当前, 心血管疾病的致死率仍然远远高于其他疾病, 且有着逐年上升的趋势[1,2]. 心脏快速磁共振成像 (Cine-MRI)是一种非侵入式医学成像技术, 被广泛用于活体心脏疾病检测[3]. 在临床诊断中, 其结果往往受心脏Cine-MRI图像分割精度的影响. 在心脏Cine-MRI图像中, 由于各部位对比度不明显, 且会受到其他组织结构和噪声的影响, 对其进行精确地分割难度较大. 目前, 心脏Cine-MRI图像分割仍依赖于专业医师的手动勾画区域, 临床效率较低.
随着计算机技术的发展, 国内外涌现出了大量的医学图像分割技术. 传统分割方法主要基于统计模型[4]和图谱法[5]针对边缘和区域进行分割, 算法效果的好坏较大程度的依赖于建模的先验和数据质量, 在一些对比度不高、边缘模糊的图像上较难得到较好的效果. 近年来, 深度学习技术快速发展, 利用深度学习方法研究医学图像分割逐渐成为主流. 2015年, Long 等人提出了全卷积神经网络分割模型(FCN)[6], 其使用了反卷积和不同层次的跳跃连接, 实现了图像像素级别的精确分割. 而U-Net[7]作者提出在不同尺度上提取更加丰富的特征, 并融合多尺度特征, 大大提高了分割性能. 以U-Net作为基础框架, U-Net++[8]以及其他改进网络[9-13]相继被提出, 并取得了较好的分割结果. DeepLab v3+[14]创新性地将深度可分离卷积应用于解码器模块, 进一步提升了语义分割的速度和准确性. 然而, 在活体心脏图像数据中, 存在大量的因心脏跳动所导致的模糊, 尤其是左心室的心内膜(LV)与心肌(MYO)的边缘, 这些边缘细节在静态图像上是存在一定程度的损失的, 直接使用现有分割网络模型对原始图像数据进行分割, 很难准确捕捉到轮廓信息. 为了解决这一问题, 本文提出了光流场与语义特征融合分割网络(OSFNet), 利用心脏运动特征增补静态图像丢失的细节信息, 同时结合语义特征实现高精度的活体心脏MRI图像分割方法.
1 模型方法本文提出的基于光流场与语义特征融合的心脏分割模型主要包括两个部分: 光流场计算心脏运动特征和深度卷积神经网络提取心脏语义特征. 下面对其原理进行详细的阐述.
1.1 光流场提取心脏运动特征光流是指图像中各像素点随时间的运动情况, 结合时间域上像素的变化和相邻帧之间的相关性确定两个连续图像的运动信息[15]. 目前, 光流已被应用于运动分割和动作识别的任务中. 在采集心脏MRI图像时, 由于心脏的舒张和运动会造成图像伪影, 利用目前的分割方法, 不能准确的计算出心脏组织轮廓边缘. 本文提出通过将光流场作为先验信息以提升模型的分割能力. 光流方法主要分为两类: 稀疏光流对图像局部像素点进行分析; 稠密光流追踪图像所有像素点的运动变化[16,17]. 要对心脏进行精准分割, 需要覆盖所有像素信息, 以保证包含所有区域运动特征. 因此, 本文采用稠密光流方法提取心脏运动特征. 稠密光流方法包括Gunnar Farneback[18]、Horn-Schunck[19]等传统算法和FlowNet[20]等深度学习算法. Horn-Schunck算法假设邻域的像素点运动速度相近, 光流场具有平滑性, 只有在图像边界才会出现光流突变, 边界敏感这一特性将有利于分割任务. 因此, 本文使用Horn-Schunck光流法提取心脏运动特征.
Horn-Schunck光流法参考光照守恒假设, 相邻时刻亮度变化表示为:
| I(x,y,t)=I(x+dx,y+dy,t+dt) | (1) |
因此, 光流约束方程可以表示为:
| ∇I⋅ω+∂tI=Ixu+Iyv+It=0 | (2) |
其中,
| minωE(u,v)=∬[(∇I⋅ω+∂tI)2+λ(‖∇u‖2+‖∇v‖2)]dxdy | (3) |
根据欧拉-拉格朗日方程(Euler-Lagrange equation)计算
| {Ix(Ixu+Iyv+It)−λΔu=0Iy(Ixu+Iyv+It)−λΔu=0Δ = ∂2∂x2+∂2∂y2 | (4) |
其中,
| {uk+1=¯uk−Ix(Ix¯uk+Iy¯vk+It)λ+I2x+I2yvk+1=¯vk−Iy(Ix¯uk+Iy¯vk+It)λ+I2x+I2y | (5) |
据此, 使用迭代式(5)可计算心脏的运动特征. 算法1具体描述了光流场的计算过程.
算法1. 光流法基本求解过程
1) 读取相邻时刻心脏图像, 初始化权重系数
2) 初始化水平和垂直光流值
3) 计算图像梯度
4) 根据光流场迭代式(5)更新
5) 返回第3)步, 直至迭代次数达到100次;
6) 输出速度场
本文提出的光流场与语义特征融合分割网络主要由编码器和解码器两部分构成. 光流场计算出的心脏运动特征与t时刻图像分别利用两个连续的卷积层提取对应特征, 融合两种特征并将其作为编码器的输入. 编码器主要用于进一步融合光流运动特征和提取的心脏图像的纹理特征. 网络模型由5个基本卷积块构成, 其中每个基本卷积块包含两层卷积操作、批标准化(batch normalization)和ReLU激活函数, 卷积核大小为3×3. 如图1所示, 每个基本卷积块后紧跟一个池化层. 其在提取高频语义特征的同时, 通过逐步缩小图像尺寸来减少网络参数数量. 值得注意的是, 池化操作无法避免特征信息的丢失, 导致数次池化操作后, 特征丢失会越来越多. 因此, 针对这个问题, 本文设计了多感受野平均池化模块. 该模块将大尺度池化操作分解为卷积与小尺度池化的组合, 主要包括3条路径: 第1条路径使用7×7大小的卷积核对图像进行下采样, 连接3×3大小的卷积和池化; 第2条路径使用3×3大小的卷积核对图像进行下采样, 再连接3×3大小的池化; 第3条路径直接使用6×6的池化层. 在实际训练中, 本文使用7×1和1×7的非对称卷积代替7×7卷积, 增加网络宽度的同时可以减少网络参数. 多感受野平均池化模块可以有效提取多尺度语义特征, 减少了特征丢失.
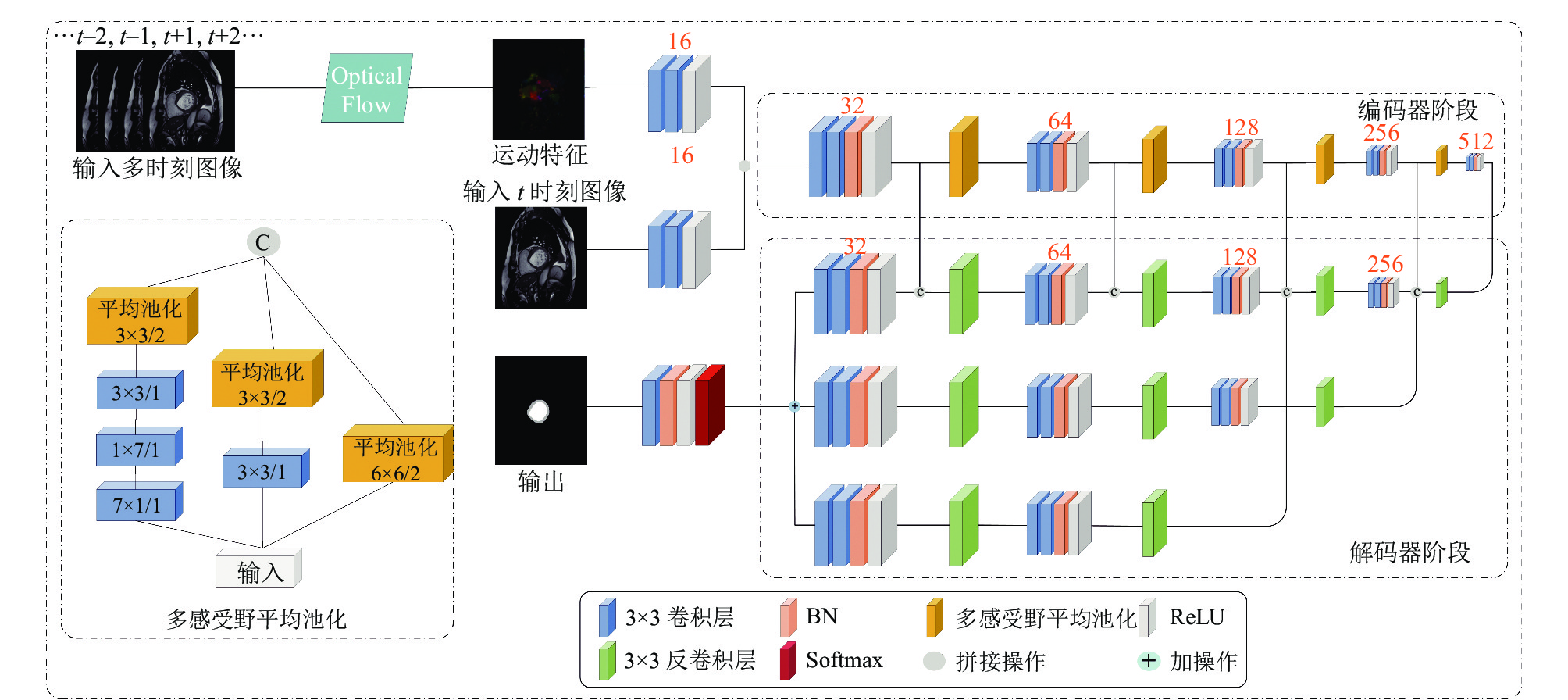
|
图 1 光流场与语义特征融合分割网络 |
在解码器阶段, 分别将编码器最后3个卷积块生成的语义特征结果进行上采样恢复, 并连接卷积块进一步提取特征, 形成了3条解码路径, 最后将恢复到原图大小的特征图进行融合, 再经Softmax层进行像素分类, 以实现分割的目的. 三路上采样操作对不同尺度的抽象特征进行恢复, 由编码器最后一个卷积块生成的最小尺度特征所构成的上采样路径中, 使用了跳跃连接的方式融合了编码器阶段所产生的相同大小的特征, 尽可能的保留了图像原始特征. 解码器阶段中所有的卷积层都使用3×3的卷积核.
2 模型的训练与评价 2.1 数据集本文所使用的数据是由法国第戎大学医院提供的ACDC (automated cardiac diagnosis challenge)公开数据集, 包含上百个心脏Cine MRI. 该数据集还包含左心室和右心室舒张末期(end diastole, ED)和收缩末期(end systole, ES)图像, 每个个体数据都有对应的由专家手动勾画的标签. 本实验首先筛选掉了所有不包括左心室的切片, 此外, 由于数据集中不同个体的图像分辨率大小存在一定差异, 为了方便网络进行训练, 对图像进行中心裁剪得到了128×128分辨率的图像并进行灰度值归一化. 数据集中符合实验要求的一共100例心脏MRI图像, 以4:1的比例将数据集划分为训练集和测试集.
2.2 实验设置本文基于TensorFlow框架对模型进行编码实现. 对于模型训练参数: batch size设置为8, 初始学习率设置为0.001, 学习率随着网络训练次数的增加逐渐减小, 实验epochs设置为400, 网络使用随机梯度下降算法(SGD)对模型进行优化. 本文使用Dice Loss作为网络的损失函数, 并使用系数为0.0001的L2正则化约束参数权重.
本文的对比实验设计为: 首先, 使用U-Net和DenseNet标准模型、加入光流场的U-Net-Flow、DenseNet-Flow、本文提出的OSFNet以及其去除光流场计算和多感受野平均池化的Basenet对左心室内膜进行分割, 以验证光流场计算方法对模型分割性能的影响. 其次, 以Basenet为基础, 分别加入多感受野平均池化模块(Basenet-m), 光流场计算模块(Basenet-Flow), 分别利用Basenet、Basenet-m和Basenet-Flow、OSFNet模型对左心室内膜与心肌进行分割, 验证本文设计的不同模块的有效性.
2.3 评价指标与定量分析本文使用Dice系数、Hausdorff距离(HD)、Jaccard相似性系数(JSC)、F1-score定量评价分割结果. Dice系数是一种集合相似度度量指标, 本文通过计算预测样本与真实样本的Dice值, 以评价分割效果, Dice系数的定义如下:
| Dice(X,Y)=2|X∩Y||X|+|Y|⇔Dice=2TPFP+2TP+FN | (6) |
其中, X表示预测结果, Y表示真实分割标签, TP表示正类样本预测为正类的部分, FP表示负类样本预测为正类的部分, FN表示正类样本预测为负类的部分. Dice描述了样本间重叠区域与非重叠区域的关系, Dice值越接近于1, 表示预测和真实之间相似程度越大, 模型分割效果越好.
F1-score是精确率(Precision)和召回率(Recall)的调和平均, 也是用来衡量分割精度的指标之一, F1-score定义为:
| F1-score=2⋅Precision⋅RecallPrecision+Recall | (7) |
| Precision=TPTP+FP | (8) |
| Recall=TPTP+FN | (9) |
召回率又称灵敏度(Sensitivity), 灵敏度越高, 模型分割正确样本的效果越好; F1-score越大, 分割结果越准确.
Hausdorff距离对分割边界敏感所以常被应用于图像分割任务中. HD是衡量两组点集之间匹配程度的一种度量, 本文使用此度量方法来评价分割轮廓的相似度, HD定义为:
| H(X,Y)=max(h(X,Y),h(Y,X)) | (10) |
| h(X,Y)=maxx∈X{miny∈Y‖x−y‖} | (11) |
| h(Y,X)=maxy∈Y{minx∈X‖y−x‖} | (12) |
其中,
JSC是两个有限样本集相似性的一种度量, 与Dice不同, 它更关注集合间共同具有的特征是否相似. JSC定义为集合交集大小与并集大小的比值:
| JSC(X,Y)=|X∩Y||X∪Y|=|X∩Y||X|+|Y|−|X∩Y| | (13) |
JSC衡量预测结果与真实标签的一致性, JSC值越大, 分割结果与真实标签越接近.
3 实验分析本文分别以左心室内膜分割和心肌分割的可视化结果与定量分析结果来阐述模型效果.
3.1 左心室内膜分割结果分析图2为多种方法分割左心室内膜轮廓可视化结果, 红色轮廓是模型预测结果, 绿色轮廓是真实标记. 可以发现, U-Net分割结果容易将心肌部分划为左心室内膜, 导致轮廓效果较其他方法差. DenseNet会将与左心室内膜灰度值相近的乳突肌分割出来, 造成异常值区域. DenseNet-Flow尽管融入了心脏的运动特征, 但对模型整体效果提升不大. Basenet相比于以上模型, 分割结果比较贴近真实标记, 而加入光流场后的OSFNet, 边缘结果更加精确.

|
图 2 左心室轮廓分割结果 |
为了更直观的体现本文方法在心脏分割任务上的性能优势, 在Dice和HD等指标上与常用模型进行对比. 表1为多个方法在测试集上对ES和ED时刻进行左心室内膜分割的定量结果. U-Net和DenseNet在Dice值上相差不大, 整体分割精度一般, ES时刻的HD标准差较大, 鲁棒性差; 在加入了光流计算方法后, 分割精度有所提高且标准差降低, 在ED时刻精度提升尤为明显, 可以看出在加入了光流场后, 加强了模型对左心室轮廓特征的学习. 本文提出的OSFNet能准确分割左心室内膜, 在多个评价指标上表现优异, 在ES和ED时刻比U-Net、DenseNet的Dice值均提高了2至3个点, 且标准差明显更低. Dice和 HD箱形图如图3所示. 在图3(a)中, U-Net-Flow比U-Net的箱长更短, 数值更稳定, 而DenseNet-Flow与DenseNet并无明显差异, 这可能是因为密集连接和光流场的效果存在叠加, Basenet-Flow的ED时刻的数据分布偏上, 平均值点较其他方法高, 整体分割效果较优. 在图3(b)中, DenseNet箱长较长, 说明整体数据分布广, 模型表现不稳定; 在加入了光流场后, 模型稳定性显著增强. 本文方法的中位线趋于下四分位, 数据分布整体靠下, 异常值较多.
| 表 1 多个方法在ES和ED时刻分割左心室内膜的定量对比 |
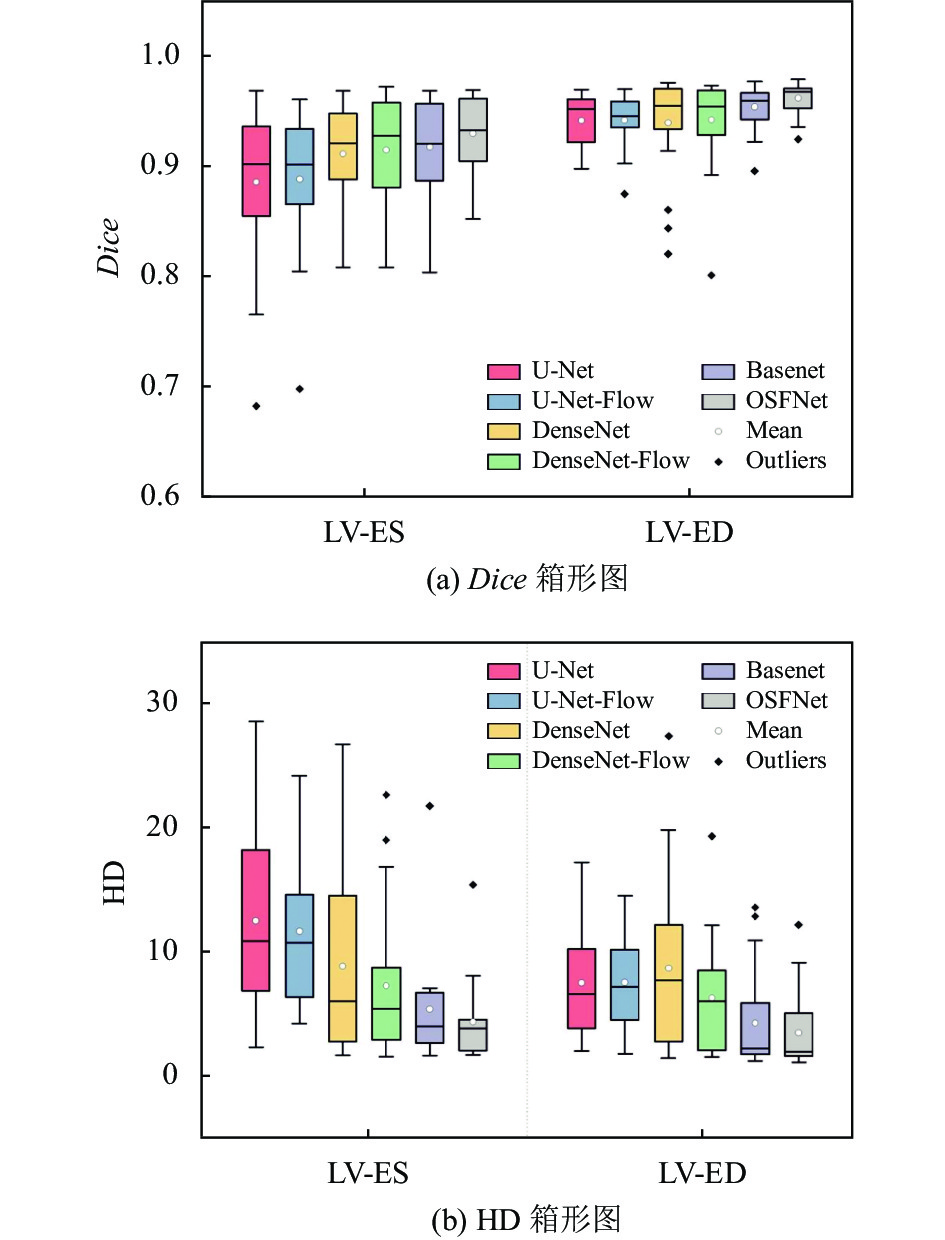
|
图 3 多个方法在ES和ED时刻分割左心室的Dice和HD箱形图 |
由于ES、ED时刻的心脏轮廓相对于运动过程中的时刻更为清晰, 为了进一步说明本文方法的效果, 表2定量分析了整个时刻不同方法的分割性能结果, DenseNet和U-Net的Dice均为0.91, 在加入光流场后, Dice、HD和JSC均有所提升, 其中HD提升显著. U-Net-Flow灵敏度最高, 这说明其前景分割准度较高. 本文方法在Dice、HD、JSC和F1-score上都表现最好, 尤其是F1-score的增幅较大, 这说明OSFNet精度较高. 图4是表2数据的箱形图, 其中DenseNet和DenseNet-Flow的箱形图相比其他方法的上四分位线和下四分位线相距较长, 在JSC指标上尤为明显, 此外, Sensitivity指标上还出现了较多离群值. U-Net-Flow在F1-score指标上四分位线与下四分位线相距较远, 且平均值最低, 说明该方法的查准率和查全率不稳定. 通过本文方法分割得到的数据分布稳定, 平均值和中位线都高于其他方法, 且离群点较少. 综上, 本文的光流场方法可以加强模型的分割效果.
| 表 2 多个方法分割左心室内膜的整个时刻定量对比 |

|
图 4 多个方法在整个时刻分割左心室的定量箱形图 |
3.2 左心室内膜和心肌的分割结果分析
图5展示了左心室内膜和心肌的分割可视化结果, 其中第一行为真实标记数据. 从图中舒张时期最后一列可以观察到, 由于左心室心腔内含有与心肌区域相近的乳突肌, 因此心室中存在一些看似黑点的组织, 导致多个方法分割结果一般, 而OSFNet模型分割结果相较于其他方法边缘更规则. 对于心脏收缩期, 左心室区域占整个图像较小, 除了Basenet分割结果有异常值出现, 其他改进方法都与真实标记轮廓相似.
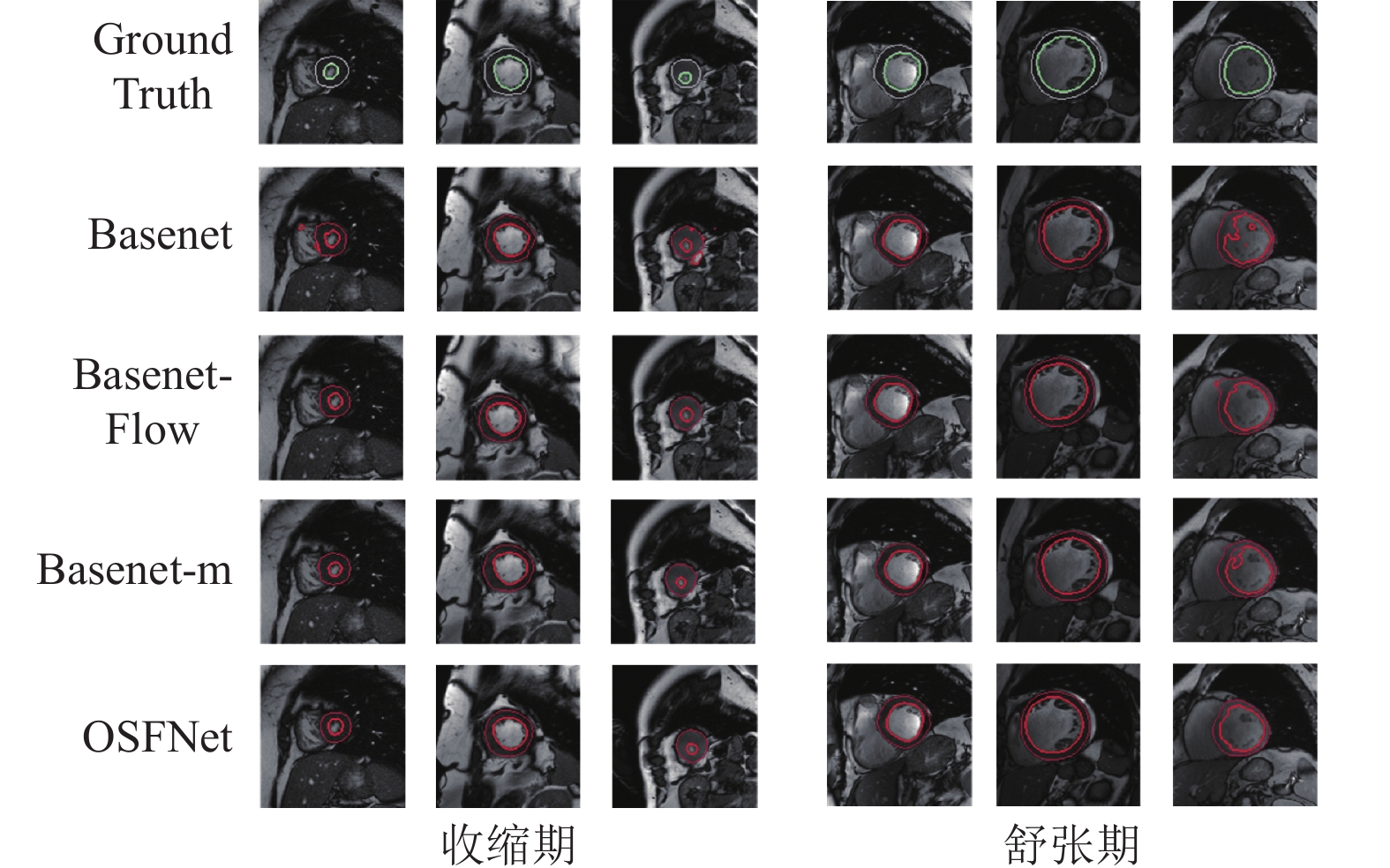
|
图 5 左心室内膜和心肌分割结果 |
本文进一步比较不同方法的分割效果, 定量结果如表3所示, 与Basenet相比, Basenet-m在心脏ES时期的分割精度提升显著, 证明加入了多感受野平均池化后获取了更多边界特征, 使得分割出的结果与实际标记数据轮廓更加接近, Basenet-Flow不仅各项指标都优于Basenet, 且Dice值高于Basenet-m. OSFNet由于加入了光流场和多感受野平均池化, 在ES时刻多个指标上都取得了最优值, 其中在HD值上体现尤为明显. 图6、图7分别是Dice值和HD值的箱形图. 在图6中, 对于ED时刻的心肌分割, 各方法中位线高度相差不大, 但在ES时刻, 其他方法的箱型图下限都比OSFNet长, 表明这几种方法对部分个体差异化较大. 并且无论对于内膜还是心肌分割, OSFNet均没有异常值. 在图7中, Basenet相比于其他方法箱型图要更长, 中位线和平均值更高, 说明加入了光流场和多感受野平均池化后, 模型对细节特征的敏感程度和模型的泛化性能得到了较好的提升.
| 表 3 在ES和ED时刻分割左心室内膜和心肌的评价指标对比 |

|
图 6 ES和ED时刻分割左心室心肌的Dice箱形图 |

|
图 7 ES和ED时刻分割左心室心肌的HD箱形图 |
同样, 为了评估模型在全时刻的分割效果, 本文在全时刻上进行了消融, 结果如表4, 相比于Basenet, OSFNet在Dice、HD和JSC上均有显著提升. 其中Basenet-Flow在多个指标上的值优于Basenet-m, 说明运动特征与纹理特征的融合更能提升模型的分割性能. 由于心肌区域边缘比内膜轮廓大, 且不规则, 占比较小, 这导致分割心肌的精度普遍没有左心室内膜高, 而由于多感受野平均池化对轮廓大的目标较为敏感, 所以Basenet-m在分割心肌上灵敏度获得了最优值. 图8是表4对应的箱形图, 从图中可观察得到, OSFNet拥有最少的离群值, 多个指标的上四分位线与下四分位线的距离比其他模型小, 说明数据波动范围小, 模型稳定性较好. 而Basenet-Flow和Basenet-m在LV的4个指标上的中位线都相近, 但在MYO上Basenet-m比较高, 这也证明了多感受野平均池化对分割的作用.
| 表 4 在整个时刻分割左心室内膜和心肌的评价指标对比 |
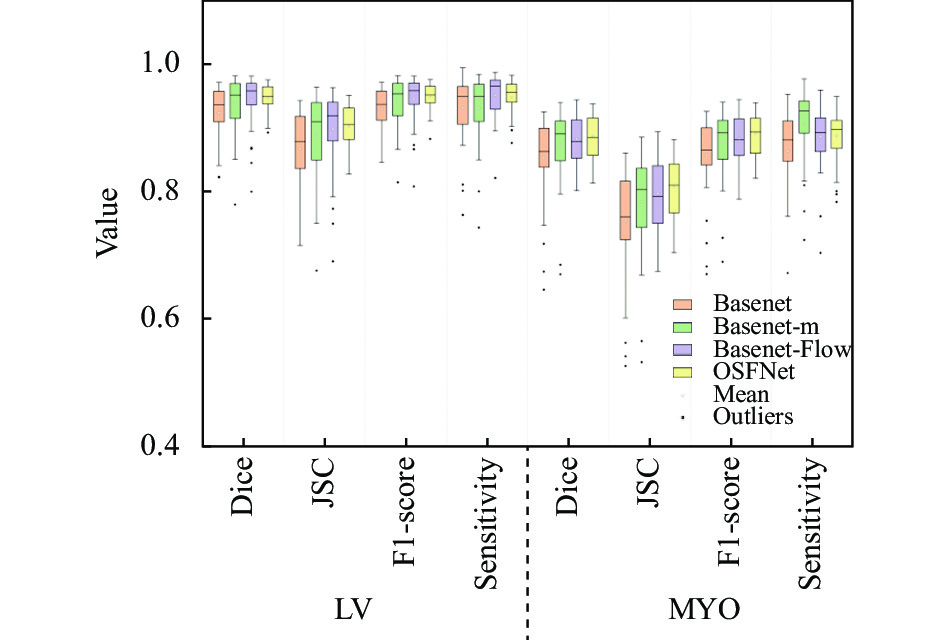
|
图 8 整个时刻分割左心室内膜和心肌的定量箱形图 |
4 结论与展望
实验结果表明, 本文提出的光流场与语义特征融合方法(OSFNet)在分割左心室内膜和心肌的任务中具有出色表现. 引入光流场后, 运动特征能够对心脏数据的纹理特征进行补充, 更有利于网络学习其分割边界. 进一步的, 由于引入了多感受野池化结构, OSFNet能够在更多尺度的特征空间搜索分割语义特征, 因此, 本文提出的多感受野平均池化融合了多尺度局部和全局特征, 可以有效减少特征丢失, 且对大轮廓心肌比较敏感, 提升了分割性能, 同时还降低了网络参数. 然而, 该方法目前还无法适用于多中心数据, 不能应用于临床, 因此扩大数据集并对模型进行调优将是未来的研究重点.
| [1] |
马文君, 马涵萍, 王运红, 等. 《2021年中国心血管病医疗质量报告》概要. 中国循环杂志, 2021, 36(11): 1041-1064. DOI:10.3969/j.issn.1000-3614.2021.11.001 |
| [2] |
《中国心血管健康与疾病报告2020》编写组. 《中国心血管健康与疾病报告2020》概述. 中国心血管病研究, 2021, 19(7): 582-590. |
| [3] |
Kalisz KR, Ansari-Gilani K. Quantification in cardiovascular MRI: A primer for radiology residents. RadioGraphics, 2020, 40(7): 1832-1833. DOI:10.1148/rg.2020200035 |
| [4] |
Okada T, Linguraru MG, Hori M, et al. Abdominal multi-organ segmentation from CT images using conditional shape-location and unsupervised intensity priors. Medical Image Analysis, 2015, 26(1): 1-18. DOI:10.1016/j.media.2015.06.009 |
| [5] |
Aljabar P, Heckemann RA, Hammers A, et al. Multi-atlas based segmentation of brain images: Atlas selection and its effect on accuracy. NeuroImage, 2009, 46(3): 726-738. DOI:10.1016/j.neuroimage.2009.02.018 |
| [6] |
Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015. 3431–3440.
|
| [7] |
Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation. Proceedings of the 18th International Conference on Medical Image Computing and Computer-assisted Intervention. Munich: Springer, 2015. 234–241.
|
| [8] |
Zhou ZW, Siddiquee MMR, Tajbakhsh N, et al. UNet++: A nested U-Net architecture for medical image segmentation. Proceedings of the 4th International Workshop Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support. Granada: Springer, 2018. 3–11.
|
| [9] |
Huang HM, Lin LF, Tong RF, et al. UNet 3+: A full-scale connected UNet for medical image segmentation. Proceedings of 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Barcelona: IEEE, 2020. 1055–1059.
|
| [10] |
Xiao X, Lian S, Luo ZM, et al. Weighted Res-UNet for high-quality retina vessel segmentation. Proceedings of the 9th International Conference on Information Technology in Medicine and Education (ITME). Hangzhou: IEEE, 2018. 327–331.
|
| [11] |
Guan S, Khan AA, Sikdar S, et al. Fully dense UNet for 2-D sparse photoacoustic tomography artifact removal. IEEE Journal of Biomedical and Health Informatics, 2020, 24(2): 568-576. DOI:10.1109/JBHI.2019.2912935 |
| [12] |
Oktay O, Schlemper J, Folgoc LL, et al. Attention U-Net: Learning where to look for the pancreas. arXiv: 1804.03999, 2018.
|
| [13] |
Wang ZY, Zou N, Shen DG, et al. Non-local U-Nets for biomedical image segmentation. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 6315-6322. DOI:10.1609/aaai.v34i04.6100 |
| [14] |
Chen LC, Zhu YK, Papandreou G, et al. Encoder-decoder with atrous separable convolution for semantic image segmentation. Proceedings of the 15th European Conference on Computer Vision (ECCV). Munich: Springer, 2018. 833–851.
|
| [15] |
Yan WJ, Wang YY, Li ZJ, et al. Left ventricle segmentation via optical-flow-net from short-axis Cine MRI: Preserving the temporal coherence of cardiac motion. Proceedings of the 21st International Conference on Medical Image Computing and Computer Assisted Intervention. Granada: Springer, 2018. 613–621.
|
| [16] |
陈震, 张道文, 张聪炫, 等. 基于深度匹配的由稀疏到稠密大位移运动光流估计. 自动化学报, 2020, 1-12. DOI:10.16383/j.aas.c190716 |
| [17] |
Brox T, Bregler C, Malik J. Large displacement optical flow. Proceedings of 2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami: IEEE, 2009. 41–48.
|
| [18] |
Farnebäck G. Two-frame motion estimation based on polynomial expansion. Proceedings of the 13th Scandinavian Conference on Image Analysis. Halmstad: Springer, 2003. 363–370.
|
| [19] |
Horn BKP, Schunck BG. Determining optical flow. Artificial Intelligence, 1981, 17(1–3): 185-203. DOI:10.1016/0004-3702(81)90024-2 |
| [20] |
Dosovitskiy A, Fischery P, Ilg E, et al. FlowNet: Learning optical flow with convolutional networks. Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015. 2758–2766.
|
 2022, Vol. 31
2022, Vol. 31



