2. 江苏省安全生产科学研究院, 南京 210016;
3. 马鞍山钢铁股份有限公司港务原料厂, 马鞍山 243021
2. Jiangsu Academy of Safety Science and Technology, Nanjing 210016, China;
3. Port Raw Material Plant of Maanshan Iron and Steel Co. Ltd., Maanshan 243021, China
多层建筑内部结构复杂, 人流密度大, 存在安全隐患, 一旦发生火灾等突发情况, 易出现拥挤、踩踏甚至伤亡等事故, 若不能高效有序地组织应急疏散, 将造成生命财产损失. 开展实战演习成本高且不易实现. 针对以上应急疏散问题, 可视化的计算机仿真提供了直观的真实环境, 且已成为主流[1-3].
目前研究应急疏散的仿真模型可分为宏观和微观两种. 宏观模型主要考虑疏散整体的影响, 在人员基数大的场景中仿真效果好, 但其缺点是不考虑疏散个体的具体行为以及它们的差异性[4]; 微观模型中, 元胞自动机[5-7]和社会力模型[8,9]是最常用的两种. Cremer等人[10]将元胞自动机模型合理应用在车辆交通流中, 实现了城市网络交通流动态过程的快速仿真. Helbing等人[11]提出的社会力模型较真实地模拟了人员疏散情况, 并将其运用在行人流的研究上. 刘景昊[12]通过微观视角研究了智能体交互问题, 采用底层分布式动态避障算法ORCA, 并引入行人瞬间能耗概念实现快速寻路, 解决了智能体与其它智能体或障碍物之间的碰撞避免问题. 周美琦等人[13]提出了一种改进元胞自动机模型的乘客疏散运动模型, 充分考虑了乘客在突发事故下疏散时的趋利避害和从众心理等. 原志路[14]在基于社会力模型的基础上, 对人员在疏散过程中的行人流变化规律进行了研究, 并对房间内部的疏散过程进行仿真实验. 蒙盾等人[15]提出一种改进A*算法的应急疏散系统, 采用邻接节点的遍历方式完成路径搜索, 并将人员密度和障碍物加入代价值的计算中, 给出了单层多出口情况下的多路径择优方案.
上述学者虽然通过不同方法对人员疏散进行了大量研究, 但均未将多智能体技术应用在机器人智能搜救室内被困人员的研究中, 鉴于此, 本文以多层建筑为背景, 采用改进的A*算法并结合多智能体技术, 对不同火灾发生点机器人如何搜救被困人员进行深入研究, 较好地模拟了不同情况下的疏散过程.
1 基本模型 1.1 火源模型火灾燃烧过程复杂, 不仅受风向、风速等影响, 而且还会产生大量有毒气体、浓烟等, 对人构成危害, 极大影响逃生效率. 为了便于研究, 本文根据张学锋等人[16]提供的模型, 将火源简化为一个圆锥模型, 并通过火源功率计算火势大小.
| D=√4Q/πqe | (1) |
| H=−1.02D+0.235Q2/5 | (2) |
其中, D为锥形底面直径; Q为火灾热释放率(kW); qe为单位面积的热释放率(kW/m2), 统一取值为500 kW/m2; H为火源高度.
现实中, 逃生人员经过火源区域会有危险状态临界值判断, 例如烟气温度超过180℃, CO浓度达到0.25%, 会因皮肤灼伤、吸入毒烟等对人构成危害. 本文统一将上述危险状态简化为生命值的衰减, 当低于某一阈值会晕倒甚至死亡.
1.2 Agent模型每个人员及机器人为一个Agent, 且都配有视觉传感器, 采用射线检测技术模拟人类视觉, 计算射线与物体的交点来确定两者距离. 根据Agent当前位置, 获取一定范围内的外界信息, 通过模拟人类视线进行环境交互, 并做出相应反应行为, 视觉模拟如图1所示. 以Agent所处位置为中心, 感知与其速度垂直方向左右90°范围内的物体.

|
图 1 视觉模拟系统 |
从Agent模型双眼视区内发射射线, 当检测到物体碰撞时, 识别它的位置和物体类型. Agent在疏散过程中, 会不时地检测是否发生碰撞, 进而实时计算Agent下一时刻的运动数据, 包括位置信息、移动速度、运动方向等, 通过从传感器接收的信息做出下一步决策. Agent模型结构如图2所示.

|
图 2 Agent模型结构 |
为了使仿真效果更加接近现实, 本文将人员Agent属性分为固有属性和动态属性, 见表1.
人员编号用于标记人员间的信息, 可通过编号搜寻到人员实时位置; 年龄影响逃生效率, 笼统划分为成年男性、成年女性、小孩、老人; 性别则为男女; 成年男性、女性耐力普遍优于小孩、老人; 位置属性为当前疏散人员所在位置; 速度属性为当前行走速度; 距离属性记录从初始位置到当前位置行走的路程; 时间属性为逃生花费的时间.
| 表 1 人员Agent属性信息 |
1.3 速度模型
本文根据各年龄段人员类型设定不同平均行走速度, 参考文献[17]的描述, 采用表2中的数据.
| 表 2 不同人员类型平均行走速度 (m/s) |
2 决策系统
机器人在智能搜救做出决策分析的过程中, 将不同年龄段人员类型分为两大类: 一类是具有完全行为能力的个体, 包括成年男性、成年女性. 另一类是具有部分行为能力的个体, 主要指小孩、老人, 逃生过程中该类个体通常需要机器人引导. 对于不同类型的人员Agent在应急疏散过程中采取的决策行为是不同的, 其决策流程如图3所示.
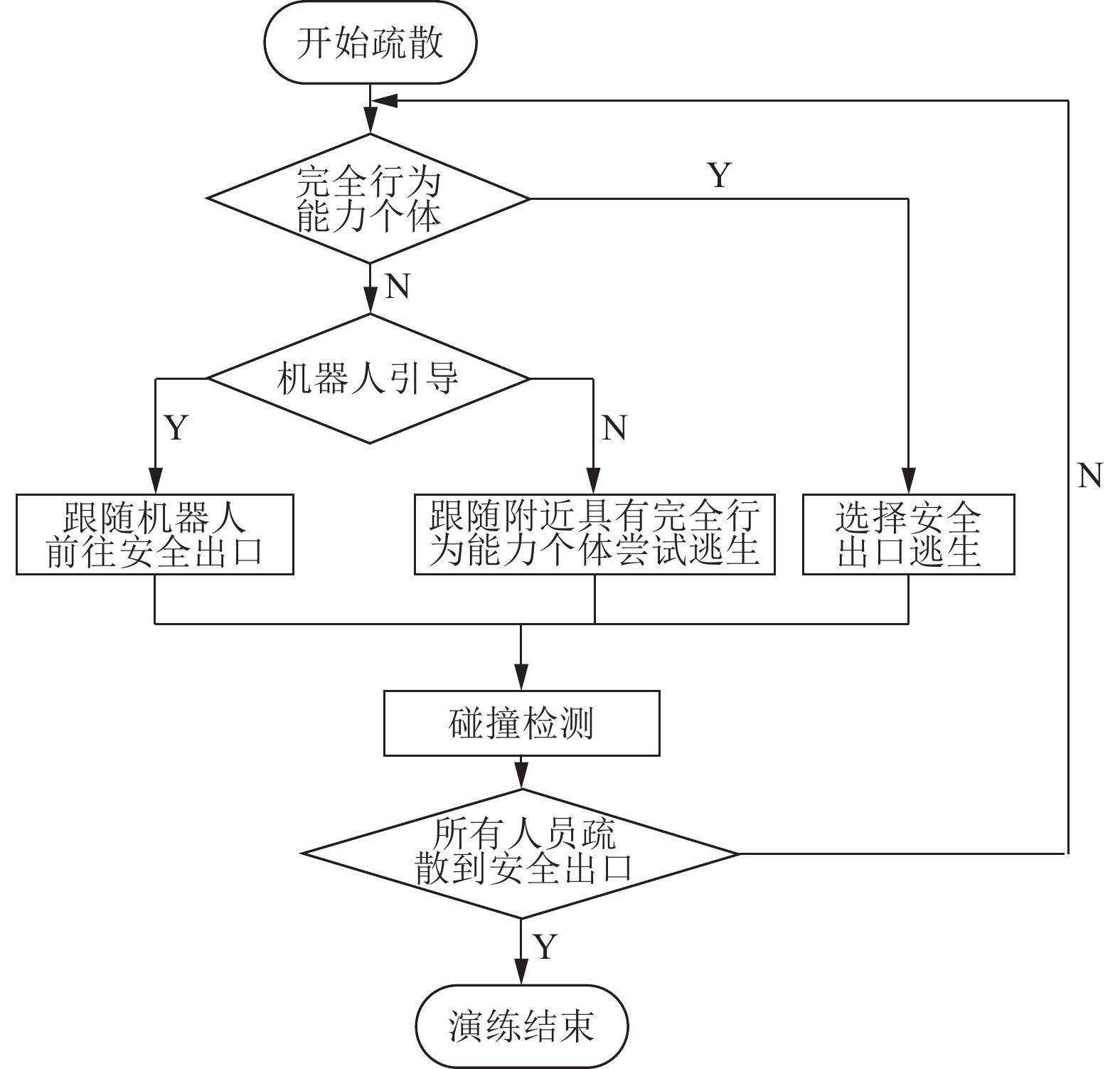
|
图 3 决策流程图 |
决策层会根据被困人员的自身状态及所处环境决定采取何种疏散行为. 若被困人员丧失行动能力或因吸入大量有毒气体导致晕厥等, 机器人发出警报, 并立即向施救人员输出该被困人员信息, 包括位置、伤亡情况、救援级别等. 若被困人员有能力逃生, 但因恐慌或浓烟迷失方向, 机器人将采取引导疏散策略, 协助被困人员到达安全出口.
3 改进A*算法 3.1 传统A*算法A*算法结合了贪心算法和Dijkstra算法, 是一种高效的启发式搜索算法[18]. 通过计算当前节点相邻的所有可达节点代价值, 选出值最小的节点作为下次搜索的父节点, 继续搜索该父节点周围可达节点, 循环往复直到搜索出目标节点, 相比于Dijkstra算法, 遍历搜索节点数更少, 运行速度更快, 提高了搜索效率. A*算法估价函数可表示为:
| f(n)=g(n)+h(n) | (3) |
其中, f(n)表示从初始点经由节点n到目标点的代价估计; g(n)表示从初始点到节点n的实际代价; h(n)是一种启发式函数, 表示从节点n到目标点的最佳路径的估计代价.
在A*算法评估函数中, g(n)为已遍历的节点, 数值固定, h(n)成为影响算法效率的关键. h(n)应满足下式:
| h(n)⩽∗h(n) | (4) |
其中, *h(n)表示节点n到目标点的真实最小代价.
通常, 启发式函数采用曼哈顿距离来计算当前节点到目标点的代价, 其公式为:
| D(i,j)=|Xi−Xj|+|Yi−Yj| | (5) |
其中, (Xi, Yi)代表节点i的坐标, (Xj, Yj)代表节点j的坐标.
A*算法搜索过程如图4所示, 其中绿色方块S代表初始点, 红色方块E代表目标点, 黑色方块代表障碍物. 首先将初始点S放入开放列表OpenList中, 所谓的OpenList基本上是一个待检查的方格列表, 目前OpenList里只有一项, 也就是S点, 后面将逐步加入更多项. 若OpenList为空, 则搜索失败. 若OpenList中存在目标点, 则搜索成功. 然后从OpenList中取f(n)值最小的节点作为当前父节点, 并将其加入到封闭列表CloseList中, CloseList中的每个方格都无需再关注. 计算与当前父节点相邻的所有可达子节点, 对每一个子节点: 若该节点在CloseList中, 则丢弃; 若该节点在OpenList中, 则检查通过当前节点计算得到的f(n)值是否更小, 如果更小则更新f(n), 并将其父节点设置为当前节点; 若该节点不在OpenList中, 则将其加入到OpenList中, 并计算f(n)值, 设置其父节点为当前节点, 如此循环. 当OpenList中出现目标点E时, 说明路径已经找到, 当OpenList中没有了数据, 则说明无合适路径.

|
图 4 A*算法搜索过程 |
传统A*算法有一定缺陷, 例如, 存在多个最小值时并不能保证搜索的路径最优; 随着地图的扩大, 其空间增长呈指数级别; 当目标点不可达时会出现大量的性能消耗; 路径平滑性较差; 若规划的路径上障碍物较多, 会紧贴障碍物, 易发生碰撞.
3.2 改进A*算法本文重点研究的是机器人对疏散效率的影响, 运用传统A*算法进行路径规划时, 通常忽略机器人体积及运动特性, 进而导致机器人途经障碍物顶点时斜穿而过, 同时规划出来的路径不平滑, 针对以上问题, 对A*算法做了如下改进:
在传统八邻域的基础上做了改进, 将当前节点周围8个相邻节点进行优先级划分, 如图5所示. 假设当前节点为O, 周围相邻节点分别为A–H.
将图5节点划分为两部分, 其中, 当前节点O周围水平竖直方向的B、D、E、G四个节点为优先遍历节点, 剩余子节点依规则遍历, 其遍历规则见表3.
针对路径不平滑问题, 引入了贝塞尔曲线对改进的A*算法规划出来的路径进行平滑处理. 根据机器人和障碍物选定一系列特征点, 通过对特征点的拟合形成初始目标路径. 机器人行走半径和横向加速度关系如下:
| ρ=1r | (6) |
| may=ν2r | (7) |
其中, ρ为对应路径曲率, r为曲率半径, m为机器人质量, 本文统一取值为5 kg, ay是机器人行走过程中的横向加速度, v为机器人步速, 取固定值1.2 m/s.
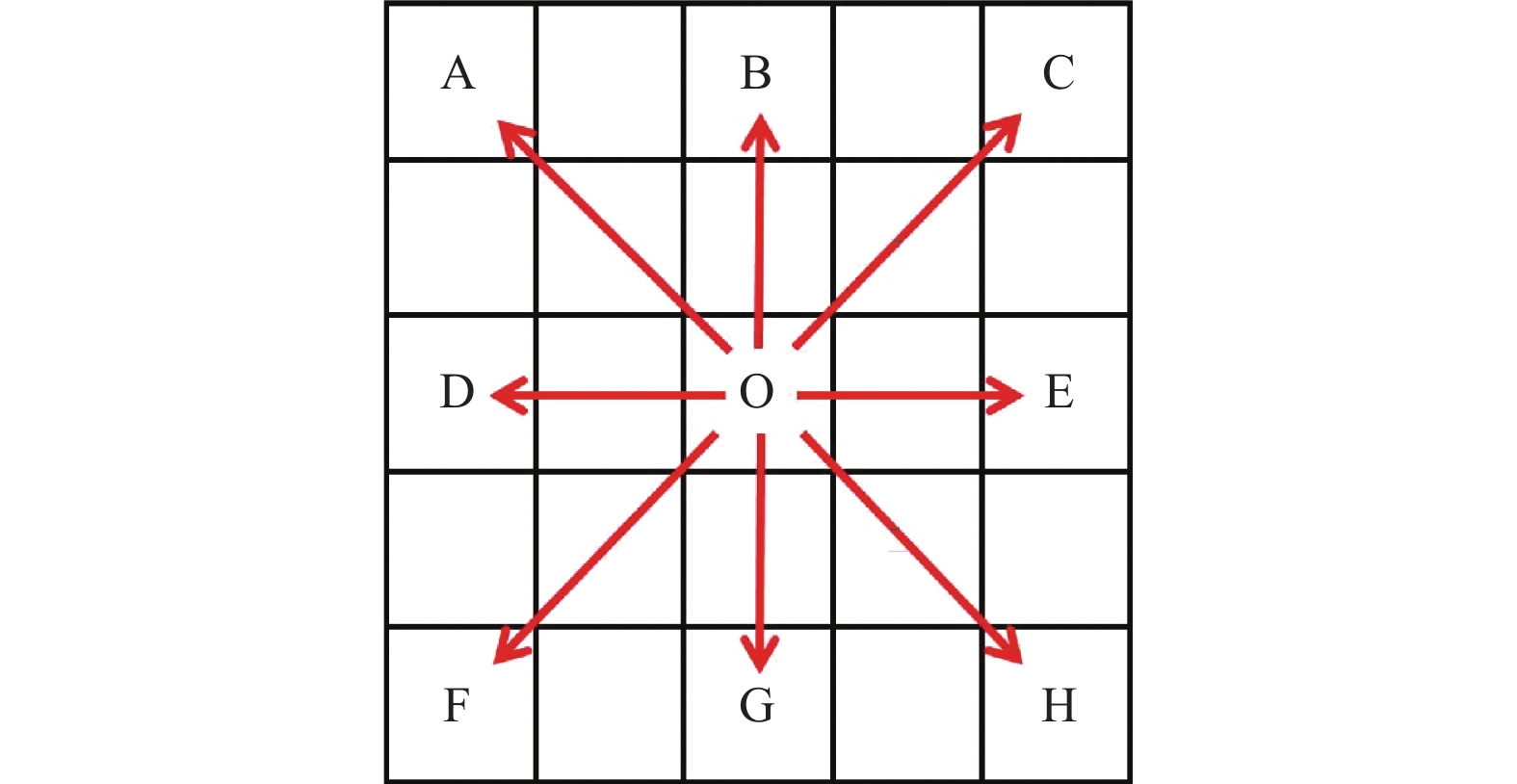
|
图 5 相邻节点优先级划分 |
| 表 3 子节点遍历规则 |
机器人的横向加速度和它的轨迹曲率呈线性关系, 在整个搜救过程中, 机器人的横向加速度连续, 则轨迹曲率也要连续, 这就要求机器人运动轨迹的拟合函数光滑可导, 因此要选择高阶贝塞尔曲线进行轨迹拟合, 其表达式为:
| B(t)=n∑i=0(ni)Pi(1−t)n−iti=(n0)P0(1−t)nt0+(n1)P1(1−t)n−1t1+⋯+(nn)Pn(1−t)0tn,t∈[0,1] | (8) |
其中, B(t)表示贝塞尔拟合曲线, t为曲线参数, Pi表示构成曲线的(i+1)个顶点坐标.
对子节点优化以及引入贝塞尔曲线, 有效避免了机器人斜穿障碍物顶点, 减少了拐角次数, 路径安全性、机器人运动效率有较大提高, 缩短了疏散中的搜救时间和路径长度. 传统A*算法和改进后的A*算法在相同条件下的仿真时间对比如图6所示.

|
图 6 仿真时间对比 |
4 仿真实例
本实例以某高校图书馆为场景, 利用三维激光点云建模, 建模主要包括数据采集、数据预处理、三维建模、纹理映射4个步骤, 具体流程如图7所示. 首先对图书馆进行扫描, 采集点云数据、纹理图片; 其次, 对采集得到的数据进行点云裁剪、降噪、精简预处理操作, 以满足3DS Max建模需求[19]; 然后, 根据点云轮廓构建图书馆主体模型; 最后, 根据三维信息提取每个面的最佳纹理信息, 并实现纹理自动映射[20].

|
图 7 3DS Max建模技术流程 |
主体框架完成后, 再对其内部结构进行细节建模, 在3DS Max建模软件中对每个独立单元重新组合, 并且将采集的纹理图片用于模型的渲染、贴图等操作中, 最终以特定的格式(.FBX)导入到Unity3D平台中, 完成与实物成比例的三维模型, 其最终三维模型如图8所示. 其中, 一楼是服务大厅, 有南北2个安全出口; 二楼是阅览室, 共有4个楼梯口, 且均连通至一楼大厅.

|
图 8 图书馆三维模型 |
首次进入仿真演练系统需要注册, 注册成功后方可登录. 注册登录界面如图9所示. 成功登录仿真演练系统后, 警报发出, 馆内人员开始疏散, 施救人员随即赶到现场指挥救援.

|
图 9 注册登录界面 |
本文对各楼层人员类型人数分布做了表4中的假设, 人员位置随机生成.
| 表 4 各楼层人员类型人数分布 |
设置机器人遍历所有楼层房间, 并开始计时. 机器人通过感知周围环境, 对室内被困人员做出决策分析. 机器人遍历完所有楼层房间以及将全部被困人员引导疏散至安全出口后, 停止计时. 疏散过程中, 可通过点击“查看实时信息”按钮, 动态查看馆内人员总数、已疏散人员数、剩余人数和演练进行时间等信息, 如图10所示.

|
图 10 仿真实时信息 |
为了更好地说明机器人个数及初始位置对疏散效率的影响, 本文较为全面地模拟了5种疏散方案, 每个机器人的种类、大小、步速等参数均是统一的, 见表5.
| 表 5 机器人搜救方案设计 |
将上述5种方案分别进行仿真实验, 实验数据曲线如图11所示.

|
图 11 不同疏散方案曲线图 |
从图11中不难看出, 疏散时间整体上会随着机器人数量的增加而呈缩减趋势, 60 s时, 馆内绝大多数人员已安全疏散; 相比于其他未着火楼层设置的机器人个数而言, 火灾发生点楼层设置的机器人个数越多, 搜救时间越短, 但当机器人数量达到一定个数后, 对搜救时间长短影响不大; 疏散前10 s没有人员抵达安全出口位置, 究其原因不难发现, 从发现火灾到疏散至安全地点期间, 有一个反应时间和逃生时间, 符合实际情况.
5 结论与展望针对多层建筑复杂的内部结构, 传统A*算法规划出的路径平滑性较差, 且通常忽略机器人体积及运动特性, 当路径上障碍物较多时, 会紧贴障碍物, 易发生碰撞等安全问题. 本文结合多智能体技术, 并提出一种子节点优先级划分的改进A*算法, 通过引入贝塞尔曲线, 有效避免了机器人斜穿障碍物顶点, 减少了拐角次数, 路径安全性、机器人运动效率有较大提高.
仿真环境中, 通过设置不同的火灾发生点, 机器人个数及初始位置, 人员速度等参数, 对影响疏散时间的相关因素进行了模拟实验, 验证了应急疏散的真实有效性. 本仿真研究利用机器人智能搜救并引导人员疏散, 在很大程度上减少了不必要的人员伤亡, 实验结果符合实际情况, 为多层建筑应急疏散预案的制定提供了参考依据.
| [1] |
郝会龙, 任鸿翔, 肖方兵. 基于A算法的虚拟船员路径规划仿真. 计算机工程与设计, 2015, 36(3): 733-737. DOI:10.16208/j.issn1000-7024.2015.03.034 |
| [2] |
阳小涛, 杨克俭, 闫春香. 虚拟人几何建模及运动控制方法的研究. 计算机与数字工程, 2008, 36(8): 132-135. |
| [3] |
王军华, 吕克志. 面向艺术与设计虚拟人技术比较研究. 计算机系统应用, 2009, 18(5): 123-127. |
| [4] |
孙迪, 周进, 高学英, 等. 地铁站内行人疏散路径选择仿真研究. 系统仿真学报, 2019, 31(9): 1819-1826. DOI:10.16182/j.issn1004731x.joss.18-0715 |
| [5] |
陈长坤, 孙华锴, 童蕴贺, 等. 基于元胞自动机的火源威胁下人员疏散模型. 中国安全生产科学技术, 2020, 16(10): 47-52. |
| [6] |
萨木哈尔·波拉提, 邹馨捷, 郝明, 等. 基于元胞自动机的人员疏散模型探讨. 安全与环境工程, 2020, 27(5): 122-127. DOI:10.13578/j.cnki.issn.1671-1556.2020.05.018 |
| [7] |
Tian HH, Wei YF, Dong LY, et al. Resolution of conflicts in cellular automaton evacuation model with the game-theory. Physica A: Statistical Mechanics and Its Applications, 2018, 503: 991-1006. DOI:10.1016/j.physa.2018.08.140 |
| [8] |
李昌华, 杨晶, 李智杰. 一种应用于人群仿真的改进社会力模型. 系统仿真学报, 2021, 33(3): 521-528. DOI:10.16182/j.issn1004731x.joss.19-0553 |
| [9] |
邓媛媛, 郑利平, 蔡瑞文. 社会行为驱动的疏散仿真方法研究. 系统仿真学报, 2020, 32(1): 130-141. DOI:10.16182/j.issn1004731x.joss.17-CACIS004 |
| [10] |
Cremer M, Ludwig J. A fast simulation model for traffic flow on the basis of Boolean operations. Mathematics and Computers in Simulation, 1986, 28(4): 297-303. DOI:10.1016/0378-4754(86)90051-0 |
| [11] |
Helbing D, Molnár P. Social force model for pedestrian dynamics. Physical Review E, 1995, 51(5): 4282-4286. DOI:10.1103/PhysRevE.51.4282 |
| [12] |
刘景昊. 基于多智能体的虚拟行人与人群仿真研究[硕士学位论文]. 合肥: 中国科学技术大学, 2019.
|
| [13] |
周美琦, 杨晓霞, 张纪会, 等. 基于改进元胞自动机模型的地铁车厢乘客疏散模拟. 复杂系统与复杂性科学, 2021, 18(3): 35-44. DOI:10.13306/j.1672-3813.2021.03.006 |
| [14] |
原志路. 基于改进社会力模型的行人流疏散仿真研究[博士学位论文]. 长春: 吉林大学, 2017.
|
| [15] |
蒙盾, 胡卓, 张华军. 基于改进A*算法的多层邮轮疏散系统仿真. 系统仿真学报, 2022, 34(6): 1375–1382.
|
| [16] |
张学锋, 白晨曦. 双层教学楼人员疏散仿真研究. 系统仿真学报, 2017, 29(5): 1070-1076. DOI:10.16182/j.issn1004731x.joss.201705019 |
| [17] |
郭海湘, 曾杨, 陈卫明. 基于社会力模型的多出口室内应急疏散仿真研究. 系统仿真学报, 2021, 33(3): 721-731. DOI:10.16182/j.issn1004731x.joss.19-0611 |
| [18] |
陶哲, 高跃飞, 郑天江, 等. 基于A*算法在蜂巢栅格地图中的路径规划研究. 中北大学学报(自然科学版), 2020, 41(4): 310-317. |
| [19] |
徐金财, 李朝奎, 陈建辉. 一种基于3ds Max与Smart 3D的三维模型构建方法. 测绘通报, 2020, 11: 61-65. DOI:10.13474/j.cnki.11-2246.2020.0355 |
| [20] |
王庆栋, 艾海滨, 张力. 利用倾斜摄影和3ds Max技术快速实现城市建模. 测绘科学, 2014, 39(6): 74-78. DOI:10.16251/j.cnki.1009-2307.2014.06.007 |
 2022, Vol. 31
2022, Vol. 31



