智能电表作为一种末端设备, 在智能电网中早已得到了广泛的应用. 智能电表记录的高分辨率数据涵盖了消费者用电行为的海量信息, 为分析用户能耗行为提供了重要参考. 同时, 电力服务部门和公司开始以用户为导向, 通过深入挖掘用电数据和客户潜在需求, 提供稳定, 安全, 便捷, 高效, 环保的个性化综合用能服务. 用户分类是智能电表数据分析的重要领域, 旨在通过智能电表数据对不同的负荷或用户进行分类. 通过对智能电表数据进行分类, 电力部门不仅可以了解区域内不同用户的特征及构成, 改善用户用电质量, 还可根据用户分布协调区域用能总量, 提高资源利用率. 因此, 用户分类在电网智能化发展和智能电表数据应用上具有重要意义, 并在能耗预测[1], 窃电检测[2]和个性化电价设计[3]等其他领域发挥着重要作用.
用户分类的方法可分为无监督分类方法和监督分类方法. 其中, 无监督分类方法以聚类[4]作为主要的分类手段, 常用的方法包括模糊C均值算法[5], 层次聚类[6]和自组织映射[7]等. 但上述方法的分类性能受算法参数, 先验知识和异常数据的影响. 因此, 无监督方法不适合大规模数据集和复杂场景下的分类任务.
监督分类方法旨在建立用能数据与用户标签之间的映射关系, 从而实现用户分类. 随着深度学习的兴起, 许多深度学习方法开始被应用于有监督的用户分类领域, 如极限学习机[8], 深度置信网络[9]和卷积神经网络[10]等. 在文献[11]中, 研究人员使用递归算法去除冗余特征, 并提出了一种基于极限学习机和支持向量机的混合网络以实现用户分类和预测. 文献[12]构建了一种基于卷积网络的分类架构, 并在该分类网络上实现了多种优化算法的性能比较. 除此之外, 文献[13]通过基于样本的过采样方法解决分类数据不平衡问题, 并在此基础上构建长短期网络提取用户特征, 输出用户类别. 该方法有效提高了在不平衡数据集上的分类精度. 但深度学习方法的提取特征多为抽象特征, 难以直观表示数据之间的相互关系. 此外, 各种分类方法在用户分类的精度仍需进一步提高.
近年来, 图神经网络[14]作为一种新兴的深度学习技术, 已成功地应用于多领域分类任务中, 如图像识别[15], 文本分类[16]和交通预测[17]等. 与现有方法相比, 图神经网络不仅可以直观地表示数据之间的关系, 而且特征学习也更加多样化. 因此, 图神经网络在用户用能分类领域提供了一条有效的思路, 但需要解决由离散数据到图数据的转化问题.
在相关工作的启发下, 本文提出了一种基于自学习边权重的图卷积网络分类方法(AEW-GCN), 实现了不同社会信息下的用户分类. 本文的主要贡献为: (1) 构建了一种自学习边权重的图卷积分类网络, 通过构建图卷积分类器, 提高了用户分类的准确率; (2) 给出了一种基于注意力机制的图转化方法, 实现了由智能电表数据到图数据的自动转换, 并自动学习图数据特征, 从而减少了对人工特征的依赖; (3) 在实际数据集中与现有分类方法进行了对比, 在不同社会信息下的分类实验验证了本文方法的有效性和优越性.
1 相关介绍 1.1 用户用能分类问题用户用能分类旨在寻找用户能耗数据与用户标签之间的最优映射函数. 用户用能分类过程如图1所示, 其主要包括用户特征的表示和用户分类两个过程. 特征表示是将实例从输入空间映射到特征空间的过程. 假设用户能耗数据为
| Cf=E(X,θe) | (1) |
其中,

|
图 1 用户用能分类过程图 |
对于已知的用户特征
| ˆY=F(Cf,θf) | (2) |
其中,
由上述特征表示和分类过程可以得出, 分类问题的实质在于寻找一组最优参数, 该组参数使得网络的分类正确率最高或误差最小.
1.2 图神经网络图是一种特殊的数据结构, 它对实例(节点)进行建模, 并表示实例之间(边)的关系. 在一个图中, 节点的数据及其邻居节点的边包含了大量的潜在信息. 图神经网络旨在从节点数据及其边中提取所需的特征, 并根据提取的特征输出相应的结果. 图神经网络的学习过程可以表示为:
| hv=fG(xv,te[v],xne[v]) | (3) |
| ov=Act(hv,xv) | (4) |
其中,
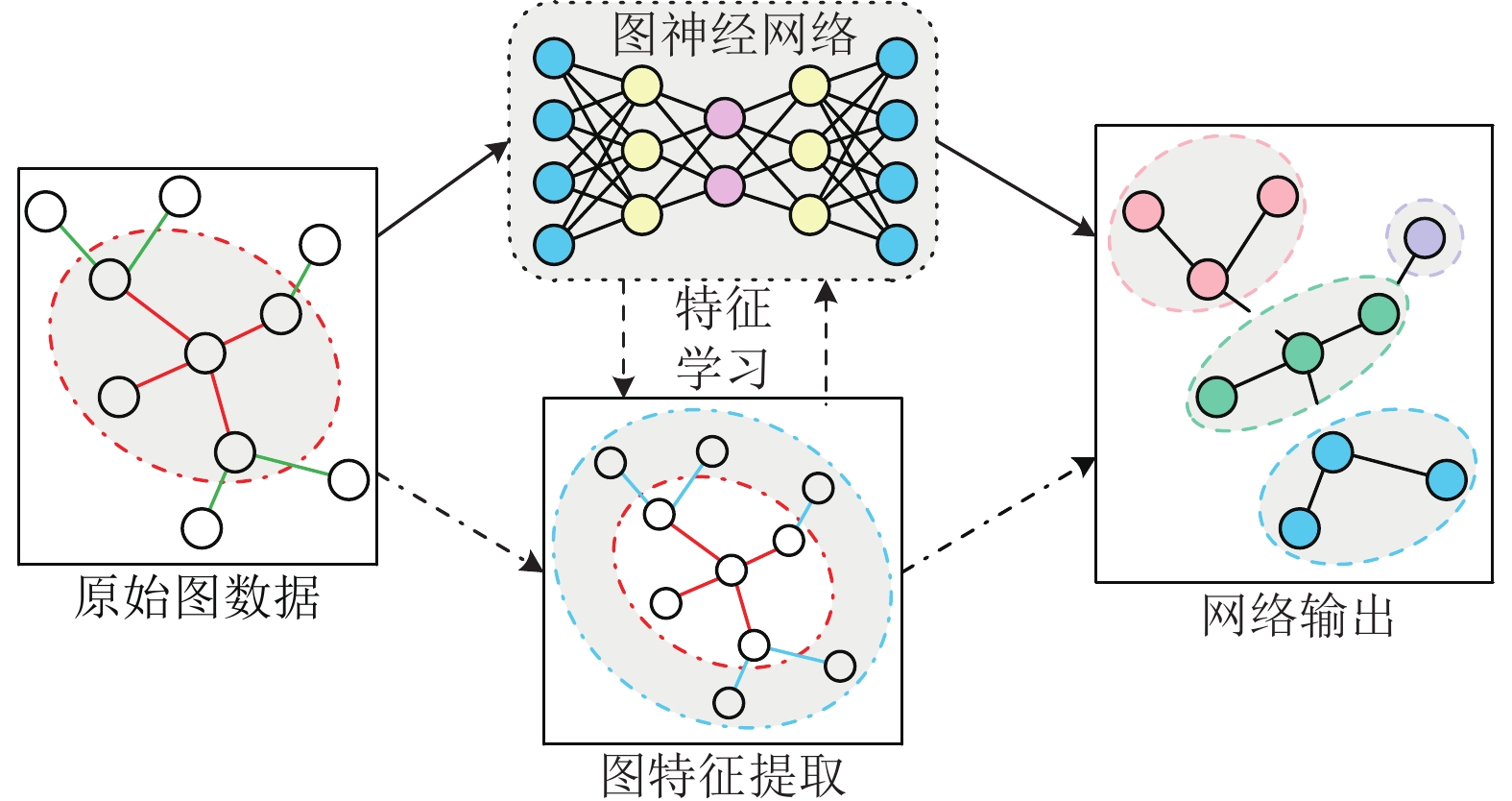
|
图 2 图神经网络学习过程 |
2 自学习边权重的图卷积分类网络
本文提出了一种自动学习边权重的图卷积分类网络(AEW-GCN), 其利用图卷积网络构建分类器, 并引入带有注意力机制图转化方法 能够有效提升用户分类的精度, 自动学习特征并减少对人工特征的依赖. 该网络由3部分组成, 分别为图初始化层、特征提取与变换层和图卷积分类层. 其中, 图初始化层完成图数据转换, 特征提取与变换层实现图上特征的提取和筛选, 图卷积分类层输出最终分类结果, 整个分类网络的架构如图3所示. 下面将对网络的每个部分展开介绍.
2.1 图初始化层由于原始用能数据不能直接被图神经网络处理, 为此, 本文建立了一个带有注意力机制的图初始化层以实现由原始数据到图数据的转化. 图初始化层主要有两个功能, 一方面, 图初始化层将原始时间序列数据转化为无向完全图; 另一方面, 注意力机制的应用使得网络能够自动学习图的边的权重参数, 并随网络更新参数. 将原始数据转化为图的过程分为以下几个步骤.
首先, 能耗数据由GRU-CNN混合层处理, 该混合层由一层GRU和CNN堆栈而成. 混合层的目的是提取原始数据的时序特征, 并输出状态参数
| R=[fgru(X)⋅d](t)=∑kfgru[x(t−k)]d(k) | (5) |
其中,

|
图 3 自学习边权重图卷积分类网络图 |
其次, 图初始化层以状态参数
| Q=R×WQ | (6) |
| K=R×WK | (7) |
| W=Softmax(QKT/√S) | (8) |
其中,
最后, 图初始化层以权重矩阵
| G=G(Xv,N,W) | (9) |
其中,
特征提取与变换层旨在提取图中的特征并输出新的特征重构图. 为了更全面地提取图数据特征, 本文引入图傅里叶变换(GFT)和离散傅里叶变换(DFT)作为特征提取方法. 其中, 图傅里叶变换可以充分考虑图结构特点, 离散傅里叶变换则提取节点数据特征. 特征提取过程可表示为:
| Gf=F(G(G)) | (10) |
其中,
特征提取完成后, 本文使用多层门控线性单元(GLU)对特征进行筛选, 为提高原始特征的利用率, 本文在特征筛选中引入跳跃连接机制, 这使得每一层GLU网络输出由当前层和它之前层的输出共同决定. 第
| hp=ReLU(fGLU(Xp)) | (11) |
| Hp=σ(∑p−1iHi+hp) | (12) |
其中,
根据筛选特征, 特征重构图可被表示为:
| Gr=G−1(F−1(Hr)) | (13) |
其中,

|
图 4 特征筛选网络架构 |
2.3 图卷积分类层
图卷积分类层实现特征重构图上的卷积运算, 并输出分类结果. 图上的卷积过程可表示为:
| (Gr⋅gc)G=Ugr((UTgr⋅gc)⊙(UTgr⋅Xgr)) | (14) |
其中,
为了减少卷积运算中的参数和计算量, 本文使用切比雪夫卷积核代替传统的图卷积核, 则图卷积过程可被重新表示为:
| yc=σ(∑θGTG(ˆΛ)) | (15) |
| ˆΛ=2λmaxΛgr−IN | (16) |
其中,
最后, 网络通过全连接层输出最后的分类结果
| ˆy=σ(Wuyc+bu) | (17) |
其中,
本文所采用的实验数据是由爱尔兰能源管制委员会(CER)[18]提供, 该委员会提供了包含了超过4300个用户530天的电力和天然气消费信息. 数据采样间隔为30 min. 为了充分证明该方法的有效性, 本文选取70%的数据进行训练, 10%的数据作为验证集, 剩余20%的数据作为测试集. 此外, CER数据集中还包含两份问卷, 问卷中包含了用户的人口统计学信息、生活方式和家庭规模等多种社会信息. 本文从问卷中选取了4种典型的社会信息, 并将每种社会信息下的不同类别作为智能电表数据的标签, 以此实现不同社会信息下智能电表数据的用户分类, 并验证所提出方法的有效性. 本文所选的4种社会信息及其类别如表1所示.
3.2 对比方法为了充分验证本文提出的方法的性能, 本文将提出的方法与3种典型的分类方法进行了比较, 下面对对比方法进行简要介绍.
(1) 支持向量机(SVM): 支持向量机是一种分类领域的典型方法, 因此, 本文将SVM方法作为对比方法之一. 在SVM方法中, 原始数据将不做任何处理直接输入至SVM网络中.
(2) 主成分分析支持向量机(PCA+SVM): PCA是一种常用的数据处理手段, 本文应用PCA方法对原始用能数据进行降维处理, 并选取一定数量的相关特征作为SVM网络的输入. 由于特征数目影响分类精度, 我们选择实验中精度最高的特征作为该方法的精度.
(3) 卷积神经网络(CNN): 与支持向量机相比, 卷积神经网络可以自动学习数据特征并输出用户类别. 本文也将其作为一种典型的分类方法进行比较.
| 表 1 智能电表数据的社会信息及分类表 |
3.3 性能指标
考虑到多个用户信息分类的不平衡性, 本文使用准确率(Acc)和F1值对模型进行用户分类性能评估. Acc代表了分类正确的样本数占样本总数的比例, 它能够客观评价模型在多类别中的分类能力. F1值是精确率(Pre)和召回率(Rec)的调和均值, 可作为模型在不平衡数据集上性能的重要参考. 在实际分类任务当中, 模型的Acc与F1越高, 表示模型的分类性能越好. 相关公式表达如下:
| Acc=∑Cc=1Dc,c∑Ca=1∑Cb=1Da,b | (18) |
| F1=2×(Pre×Rec)/(Pre+Rec) | (19) |
| Pre=TP/(TP+FP) | (20) |
| Rec=TP/(TP+FN) | (21) |
其中,
本文使用交叉熵损失函数[19]作为目标函数以评估模型的优劣, 具体表达为:
| Loss=−1JJ∑j=1M∑msgn(ˆyj=m)log(pj,m) | (22) |
其中,
在模型训练过程中, 采用Adam优化算法[20]以寻找最优参数. 与传统的梯度下降法相比, Adam优化器计算当前梯度的一阶动量和二阶动量以实现自适应参数优化, 这种优化方式使得梯度更新过程更加平滑, 具有更好的寻找最优解的能力. 决定Adam优化器的参数主要有学习率
本文方法在不同社会信息上的分类准确率和F1值如表2所示. 在4种不同社会信息中, 准确率和F1值得均值分别为74.9%和71.9%, 分类模型在#2社会信息(主要收入者是否退休)和#4社会信息(是否有孩子)的正确率均超过80%, 在#1社会信息(主要收入者年龄)的准确率超过75%, 在#3社会信息(主要收入者的社会等级)的分类准确率保持在60%左右. 其中, 在#3社会信息上的分类结果说明用户社会等级并不能显著影响用户用能行为. 从以上结果来看, 本文提出的AEW-GCN方法能够实现基于用户信息的分类任务.
| 表 2 AEW-GCN分类结果 |
表3和表4分别显示了对比方法对4种社会信息分类的准确率和F1值. 可以看出, 所有方法在4种社会信息上的分类性能分布相似, 它们均在#2社会信息和#4社会信息上表现出较好的分类性能. 这证明了这两类社会信息可以用于区分不同的用户. 在3种对比方法中, 与原始SVM方法相比, 使用主成分分析(PCA)进行特征处理的分类性能略有提高(其分类性能在Acc上提升为1.2%). 与两种SVM方法相比, CNN的分类效果得到了更好的结果, 其分类性能在两种评价指标上提高了约3.2%和3.8%. 与上述方法相比, 本文提出的方法则实现了进一步的性能提升, AEW-GCN方法的分类准确率分别提高了10.9%, 9.7%和6.5%, F1值提高了12%, 16.4%和9.2%, 这充分证明了本文所提出的方法在基于社会信息的用户分类上的有效性和优越性.
| 表 3 不同方法在4种社会信息分类的准确率 |
| 表 4 不同方法在4种社会信息分类的F1值 |
4 结语
本文提出了一种自学习边权重的图卷积网络, 实现了不同社会信息下智能电表数据的用户分类. 该方法引入注意力机制实现图的初始化, 利用包括傅里叶变换在内的多种手段进行特征提取和特征选择, 最后应用图卷积层输出分类结果. 为了证明本文方法的有效性, 我们在智能电表数据集上与其他分类方法进行了比较. 实验结果表明, 本文提出的方法取得了较好的分类性能. 在今后的工作中, 我们将进一步探讨所提方法在更多社会信息中的分类性能, 并在智能电表数据的用户分类过程中考虑环境和天气因素对用户用能行为的影响.
| [1] |
许竞文, 赵天怡, 王鹏, 等. 基于能耗监测数据的校园建筑贝叶斯能耗预测模型. 暖通空调, 2021, 51(8): 123-129. |
| [2] |
Adil M, Javaid N, Qasim U, et al. LSTM and bat-based RUSBoost approach for electricity theft detection. Applied Sciences, 2020, 10(12): 4378. DOI:10.3390/app10124378 |
| [3] |
黄海涛, 杨洋, 况夫良, 等. 基于委托-代理理论的负荷率可选择电价最优合约设计. 现代电力, 2021, 38(1): 79-86. |
| [4] |
王琳璘, 谢忠局, 陈永权, 等. 机器学习聚类组合算法及其应用. 山东农业大学学报(自然科学版), 2018, 49(3): 463-466. |
| [5] |
张丽艳, 陈映月, 韩正庆. 基于改进聚类方式的牵引负荷分类方法. 西南交通大学学报, 2020, 55(1): 27-33, 40. DOI:10.3969/j.issn.0258-2724.20180513 |
| [6] |
王保义, 胡恒, 张少敏. 差分隐私保护下面向海量用户的用电数据聚类分析. 电力系统自动化, 2018, 42(2): 121-127. DOI:10.7500/AEPS20170611006 |
| [7] |
李智勇, 吴晶莹, 吴为麟, 等. 基于自组织映射神经网络的电力用户负荷曲线聚类. 电力系统自动化, 2008, 32(15): 66-70, 78. DOI:10.3321/j.issn:1000-1026.2008.15.015 |
| [8] |
陆俊, 陈志敏, 龚钢军, 等. 基于极限学习机的居民用电行为分类分析方法. 电力系统自动化, 2019, 43(2): 97-104. DOI:10.7500/AEPS20171214003 |
| [9] |
徐春华, 陈克绪, 马建, 等. 基于深度置信网络的电力负荷识别. 电工技术学报, 2019, 34(19): 4135-4142. |
| [10] |
张玉天, 邓春宇, 刘沅昆, 等. 基于卷积神经网络的非侵入负荷辨识算法. 电网技术, 2020, 44(6): 2038-2044. |
| [11] |
Ahmad W, Ayub N, Ali T, et al. Towards short term electricity load forecasting using improved support vector machine and extreme learning machine. Energies, 2020, 13(11): 2907. DOI:10.3390/en13112907 |
| [12] |
Wang Y, Chen QX, Gan DH, et al. Deep learning-based socio-demographic information identification from smart meter data. IEEE Transactions on Smart Grid, 2019, 10(3): 2593-2602. DOI:10.1109/TSG.2018.2805723 |
| [13] |
唐子卓, 刘洋, 许立雄, 等. 基于负荷数据频域特征和LSTM网络的类别不平衡负荷典型用电模式提取方法. 电力建设, 2020, 41(8): 17-24. |
| [14] |
徐冰冰, 岑科廷, 黄俊杰, 等. 图卷积神经网络综述. 计算机学报, 2020, 43(5): 755-780. DOI:10.11897/SP.J.1016.2020.00755 |
| [15] |
Lin D, Lin JZ, Zhao L, et al. Multilabel aerial image classification with a concept attention graph neural network. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5602112. |
| [16] |
Xu SY, Xiang Y. Frog-GNN: Multi-perspective aggregation based graph neural network for few-shot text classification. Expert Systems with Applications, 2021, 176: 114795. DOI:10.1016/j.eswa.2021.114795 |
| [17] |
Bui KHN, Cho J, Yi H. Spatial-temporal graph neural network for traffic forecasting: An overview and open research issues. Applied Intelligence, 2022, 52(3): 2763-2774. DOI:10.1007/s10489-021-02587-w |
| [18] |
Irish Social Science Data Archive. Commission for energy regulation (CER) smart metering project. http://www.ucd.ie/issda/data/commissionforenergyregulationcer/.
|
| [19] |
朱峰, 徐济超, 刘玉敏, 等. 基于符号距离和交叉熵的概率犹豫模糊多属性决策方法. 控制与决策, 2020, 35(8): 1977-1986. |
| [20] |
杨观赐, 杨静, 李少波, 等. 基于Dropout与ADAM优化器的改进CNN算法. 华中科技大学学报(自然科学版), 2018, 46(7): 122-127. |
 2022, Vol. 31
2022, Vol. 31



