场景的深度信息广泛应用于SLAM^[1], 3D目标检测^[2]等算法中, 这些算法是导航任务中的关键算法, 因此深度估计任务在导航中至关重要. 本文工作聚焦于室内导航场景下的单目深度估计算法. 在室内简单场景下, 常用的深度传感器: 激光雷达、深度相机、双目相机等, 因造价昂贵应用并不广泛, 而造价低廉的单目相机和2D激光雷达成为室内导航机器人的基本配置. 但2D激光雷达提供的深度信息有限, 仅有2D平面的局部深度信息, 而导航中, 全局的稠密深度信息才更具有价值. 近期很多研究聚焦于单目深度估计, 即仅通过单目图像估计深度. 但是, 单目深度估计精度低, 对于导航场景并不适用. 因此, 本文提出一种融合2D激光雷达的单目深度估计算法, 来提高单目深度估计精度, 使其能够应用于室内导航任务中. 该算法融合2D激光雷达的尺度信息和单目图像的纹理结构信息, 使得深度估计的精度得到较高的提升.

1 概述 1.1 相关工作

近年来, 深度学习方法广泛应用于单目深度估计任务中. Eigen等人^[3] 首先将深度学习应用于深度估计任务中, 其后续的工作^[4]对上述工作进行了拓展, 在预测深度的同时完成表面法向预测和语义分割. Fu等人^[5]将连续值回归问题转化为量化的序数回归问题. Hao等人^[6]使用空洞卷积来提取多尺度信息, 并使用注意力机制来融合多尺度信息. Yin等人^[7]从重建的三维场景中随机抽取3个点, 以3个点确定的虚拟法向作为几何约束来更精确恢复三维结构. Lee等人^[8]在解码阶段使用局部平面引导层来得到原分辨率的深度图, 而不是标准的上采样层. Huynh等人^[9]将非局部共面性约束与深度注意力体(DAV)合并到网络中, 通过平面结构引导深度估计. Bhat等人^[10]提出了一种基于Transformer的结构块, 将深度范围划分为多个单元, 每个单元的中心值自适应估计每幅图像, 并将单元中心线性组合得到深度值估计. 该方法达到目前单目深度估计的最好效果.

从单幅图像估计深度缺乏绝对的尺度信息, 且精度较低, 因此, 通过稀疏的深度数据和单目图像融合来估计密集深度成为热门. Liao等人^[11]首先提出使用2D激光雷达作为额外的深度输入, 比只使用RGB图像获得更高的精度. 与文献[11]不同的是, 文献 [12–14]中使用的稀疏深度信息不具有方向性和局部性, 其使用的深度是从深度图全局随机采样的深度点或者是多线激光雷达的深度数据, 这类问题更准确地说是深度补全问题. Ma等人^[12]使用全局随机采样的深度点和RGB图像作为输入, 通过简单的编解码结构得到了更高的精度. Cheng等人^[13]提出了卷积空间传播网络, 为深度估计学习关联矩阵, 采用一个线性传播模型以循环卷积的形式传播, 并通过深度卷积神经网络学习邻近像素间的关联关系. Park等人^[14]提出了一种端到端的非局部空间传播网络, 估计每个像素的非局部邻域及其关联矩阵.

1.2 本文工作

本文主要工作如下: (1) 提出了一种融合2D激光雷达数据的单目深度估计网络; (2) 提出了一种运用通道注意力机制融合2D激光雷达特征和RGB图像特征的方法; (3) 使用跳跃连接来获得更多的细节信息; (4) 制作了带有2D激光雷达数据的深度数据集. 实验表明, 本文算法对比单目深度估计和深度补全任务均取得更好的效果.

2 基于2D激光雷达的单目深度估计网络

本文基于上述研究提出了一种端到端的融合2D激光雷达(以下简称雷达)数据的单目深度估计网络. 输入为一张RGB图像以及一张映射到二维图像的雷达数据(如图1所示). 输出为深度图(RGB图像中每个像素位置对应的深度值).

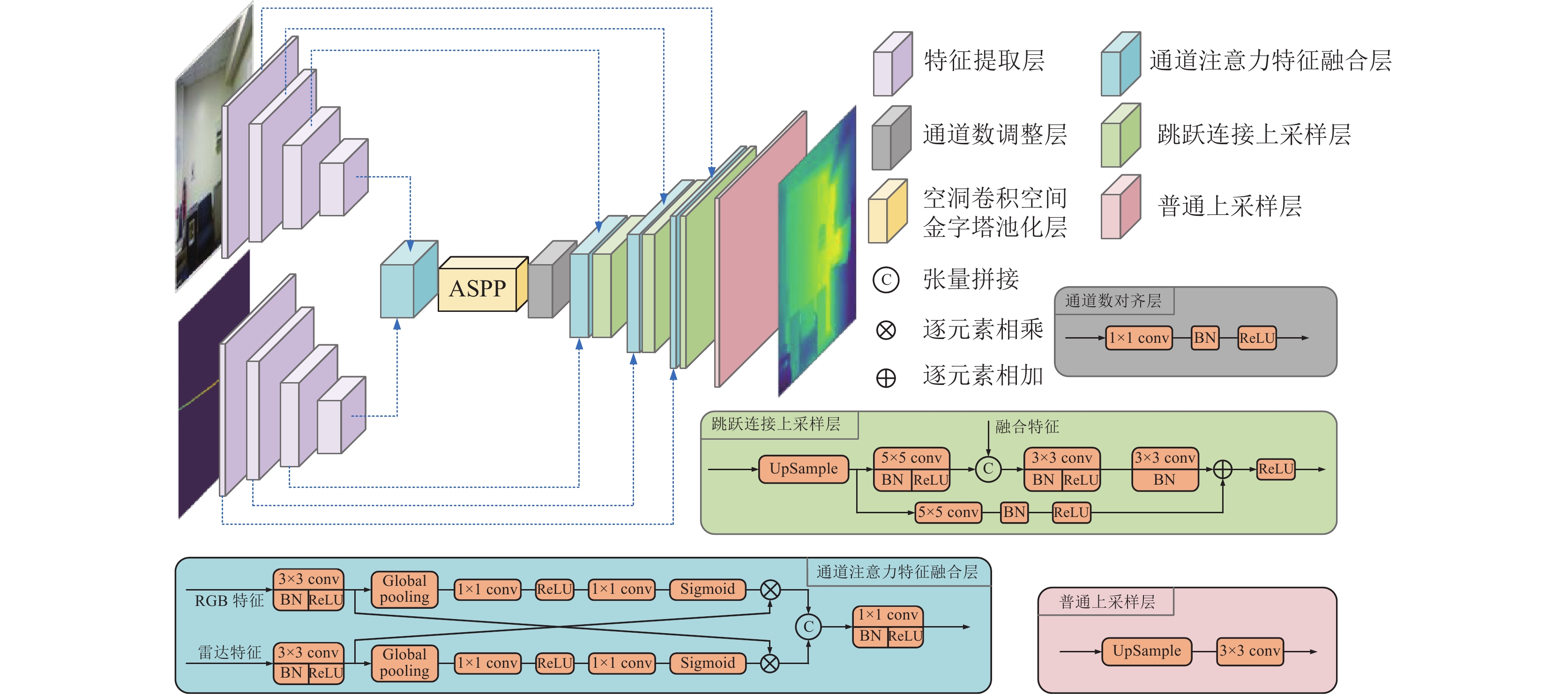
2.1 网络结构

本文的网络结构如图1所示. 首先输入的RGB图像和雷达数据分别通过特征提取网络提取出多尺度特征 $M_i^r$ , $M_i^l$ , 其中 $i = 1, 2, 3, 4$ , 分别表示4次下采样后的特征. 设输入的图像尺寸为 $W \times H$ , 则每一层特征对应的尺寸为 $[W/{2^i}, H/{2^i}]$ . 接着将特征 $M_4^r$ 和特征 $M_4^l$ 通过通道注意力特征融合模块(CAM)融合. 得到的融合特征经过ASPP^[15]增大感受野, 输出的特征通道数较大, 需要加入一层 $1 \times 1$ 卷积来改变特征通道数. 接着通过3层CAM模块以及跳跃连接上采样层将特征恢复到 $ [W/2, H/2] $ . 最后对该特征上采样, 并经过一层 $3 \times 3$ 卷积得到 $W \times H$ 的深度图.

本文为了融合RGB图像和雷达的特征, 根据文献[16]提出的通道注意力机制, 提出了一种通道注意力特征融合模块, 如图1所示. 对于提取的多尺度特征 $M_i^r$ , $M_i^l$ , 并不是每个通道都具有相同的作用, 因此, 针对特征的每个通道引入一个权重, 通过损失函数学习每个通道的权重, 使重要的特征强化, 不重要的特征减弱, 使特征指向性更强. 而RGB和雷达的特征是有关联性的, 因此, 本文将RGB与雷达的特征相互融合, 即雷达特征的权重由RGB特征产生, RGB特征的权重由雷达特征产生. 以下详细介绍该模块.

首先, 分别对RGB和雷达特征进行 $3 \times 3$ 卷积, 记得到的特征分别为 ${U^r}$ , ${U^l}$ , 尺寸分别为 ${C_r} \times W' \times H'$ , ${C_l} \times W' \times H'$ . 这里 ${C_r}$ , ${C_l}$ 为通道数, $W'$ , $H'$ 表示每个通道的长和宽. 再分别对 ${U^r}$ , ${U^l}$ 进行全局池化:

$ {\textit{z}}_c^r = {F_{sq}}(U_c^r) = \frac{1}{{W' \times H'}}\sum\limits_{i = 1}^{W'} {\sum\limits_{j = 1}^{H'} {U_c^r(i, } } j) $

(1)

$ {\textit{z}}_c^l = {F_{sq}}(U_c^l) = \frac{1}{{W' \times H'}}\sum\limits_{i = 1}^{W'} {\sum\limits_{j = 1}^{H'} {U_c^l(i, } } j) $

(2)

其中, 下标 $c$ 表示第 $c$ 个通道, ${{\textit{z}}^r}$ , ${{\textit{z}}^l}$ 为对应的输出, 尺寸分别为 ${C_r} \times 1 \times 1$ , ${C_l} \times 1 \times 1$ .

全局池化屏蔽了特征图的空间分布信息, 同时获取全局信息, 能够更加准确的计算通道的权重. 接下来通过两层全连接层, 即 $1 \times 1$ 卷积以及非线性层(Sigmoid)学习每个通道的系数:

$ {s^l} = {F_{ex}}\left( {{{\textit{z}}^r}} \right) = \sigma \left( {W_2^r\delta \left( {W_1^r{{\textit{z}}^r}} \right)} \right) $

(3)

$ {s^r} = {F_{ex}}\left( {{{\textit{z}}^l}} \right) = \sigma \left( {W_2^l\delta \left( {W_1^l{{\textit{z}}^l}} \right)} \right) $

(4)

这里 $\delta $ 为ReLU函数, $\sigma $ 为Sigmoid函数, $W_1^r$ , $W_1^l$ 分别为第1层全连接层参数, 尺寸分别为 $ \dfrac{{{C_r}}}{r} \times {C_r} $ , $ \dfrac{{{C_l}}}{r} \times {C_l} $ . $W_2^r$ , $ W_2^l $ 分别为第2层全连接层参数, 尺寸分别为 $ {C_l} \times \dfrac{{{C_r}}}{r} $ , $ {C_r} \times \dfrac{{{C_l}}}{r} $ . 这里的 $r = 16$ , 是为了减少通道个数, 计算量, ${s^r}$ , ${s^l}$ 分别对应 ${U^r}$ , ${U^l}$ 的通道权重. 得到权重后, 通过式(5)和式(6)乘上每个通道的权重:

$ \tilde U_c^r = {F_{\rm scale}}\left( {U_c^r, s_c^r} \right) = s_c^rU_c^r $

(5)

$ \tilde U_c^l = {F_{\rm scale}}\left( {U_c^l, s_c^l} \right) = s_c^lU_c^l $

(6)

这里得到的 $ {\tilde U^r} $ , ${\tilde U^l}$ 即为加权后的特征.

最后, 将得到的特征 $ {\tilde U^r} $ , ${\tilde U^l}$ 通过张量拼接操作拼接, 再经过一层 $1 \times 1$ 卷积得到最终的融合特征.

卷积神经网络中, 下采样是为了扩大感受野, 使每个卷积输出都包含较大范围的信息, 但在这个过程中图像的分辨率不断下降, 导致细节信息会逐渐丢失, 这对于要恢复和原图像相同尺寸的深度估计任务来说并无益. 因此本文引入ASPP^[15]. ASPP可以在扩大感受野的同时, 而不进行下采样, 减少下采样带来的信息丢失.

对于深度估计任务, 空间域的信息非常重要. 而网络下采样中的池化操作丢失了部分空间域信息. 因此本文借鉴文献[10,13]等的方法, 将特征提取网络提取的特征 $M_i^r$ , $M_i^l$ 通过跳跃连接的方式融入上采样过程中, 来丰富空间域的信息, 提升结果的细节信息. 如图1所示, CAM模块将 $M_i^r$ , $M_i^l$ 融合得到融合特征, 并通过图1中的跳跃连接上采样结构将融合特征通过张量拼接的方式, 融入上采样过程中.

2.2 损失函数

不同的损失函数对于最终的预测结果影响很大. 深度估计任务中常用的损失函数是计算预测深度 $\hat y$ 和真实深度 $y$ 的绝对值误差. 而单纯使用绝对值误差缺乏深度图结构信息. 因此本文为了平衡结构损失, 引入了以下损失函数:

$ L = \lambda {L_{\rm depth}} + \alpha {L_{\rm grad}} + \beta {L_{\rm normal}} + \gamma {L_{\textit{SSIM}}} $

(7)

${L_{\rm depth}}$ 为预测深度 $\hat y$ 和实际深度 $y$ 之间的L1损失:

$ {L_{\rm depth}} = \frac{1}{N}\sum\limits_i {\left| {{y_i} - {{\hat y}_i}} \right|} $

(8)

${L_{\rm grad}}$ 表示深度图梯度的L1损失:

$ {L_{\rm grad}} = \frac{1}{N}\sum\limits_i {\left| {{g_x}\left( {{y_i}, {{\hat y}_i}} \right)} \right| + \left| {{g_y}\left( {{y_i}, {{\hat y}_i}} \right)} \right|} $

(9)

其中, $ {g_x} $ 表示深度图的 $x$ 方向梯度, $ {g_y} $ 表示深度图的 $y$ 方向梯度.

${L_{\rm normal}}$ 为实际深度图的表面法向 $n$ 与预测深度图表面法向 $\hat n$ 的L1损失, 表面法向可以通过Sobel算子估计得到 $ n = ( - {\nabla _x}(y), - {\nabla _y}(y), 1) $ . 则表面法向的损失表示为:

$ {L_{\rm normal}} = \frac{1}{N}\sum\limits_i {\left| {1 - {n_i} \cdot {{\hat n}_i}} \right|} $

(10)

${L_{\textit{SSIM}}}$ 使用了结构相似性SSIM^[17], 用于衡量两幅图片的相似度指标, 因SSIM的范围是[0, 1]且为1时两幅图像一样, 所以这里损失函数定义为式(11)形式:

$ {L_{\textit{SSIM}}} = \frac{{1 - {\textit{SSIM}}(y, \hat y)}}{2} $

(11)

${\textit{SSIM}}$ 为计算两幅图像的结构相似性操作, 在计算时需将两幅图片归一化操作.

这里的系数 $\lambda , \alpha , \beta , \gamma $ 用于平衡各项损失, 本文在后续实验中取 $\lambda = 0.3$ , $\alpha = 0.4$ , $\;\beta = 1.8$ , $\gamma = 2.0$ .

3 实验分析 3.1 数据集

本文分别在公开数据集NYUDv2^[18]和自制数据集上进行了算法的验证实验.

NYUDv2数据集是使用Kinect V1深度相机采集的室内场景数据集. 数据集包含120k对RGB图和深度图样本, 654对测试样本. 原始数据的RGB图和深度图的分辨率为 $640 \times 480$ . 本文训练数据选取50k的训练样本, 使用文献[18]提供的方法填充缺失的深度值. 因本文算法需要2D激光雷达数据, 而公开数据集中没有提供, 所以本文从已有深度图中模拟雷达数据. 分为以下几个步骤: (1) 使用文献[18]提供的方法对齐深度图和RGB图并补全缺失的深度; (2) 使用文献[18]中的算法估计每张图片的重力方向; (3) 将深度图转化为3D点云图; (4) 以深度图正中心位置对应的点云为基准, 垂直重力方向作平面, 将平面截取的所有点云作为模拟的雷达数据; (5) 将模拟的雷达数据重新映射回2D图像.

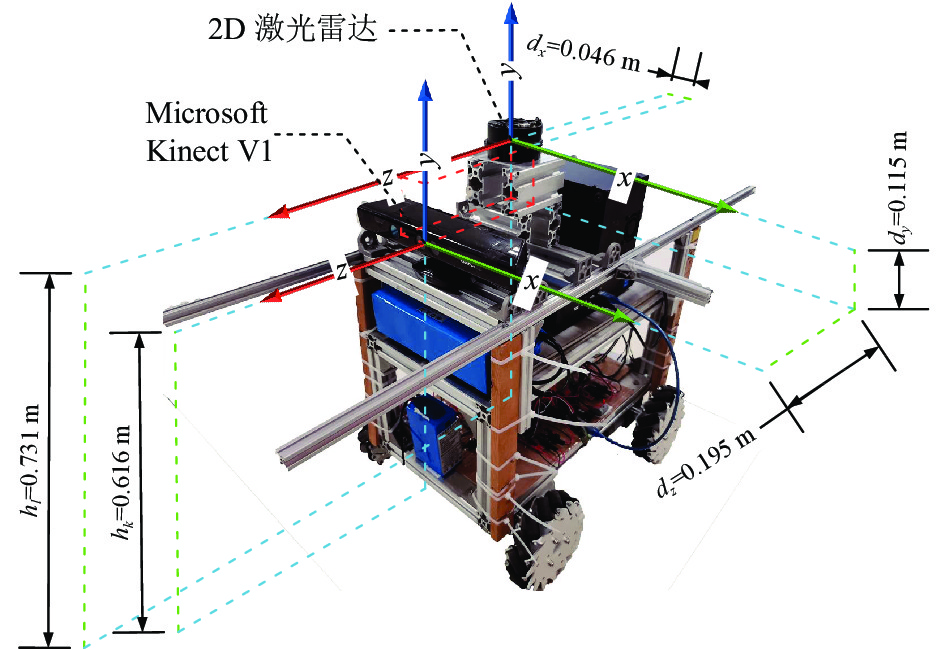
为了验证本文算法的有效性, 本文制作了带有2D激光雷达数据的数据集. 数据采集使用如图2所示的小车, 配备Kinect V1以及2D激光雷达. 采集数据前首先对深度相机进行标定, 并测量雷达和深度相机之间的相对位置. 为避免相机和雷达位姿校准, 在安装时使用水平仪进行调校, 使相机和雷达之间保持水平以及相对位姿一致.

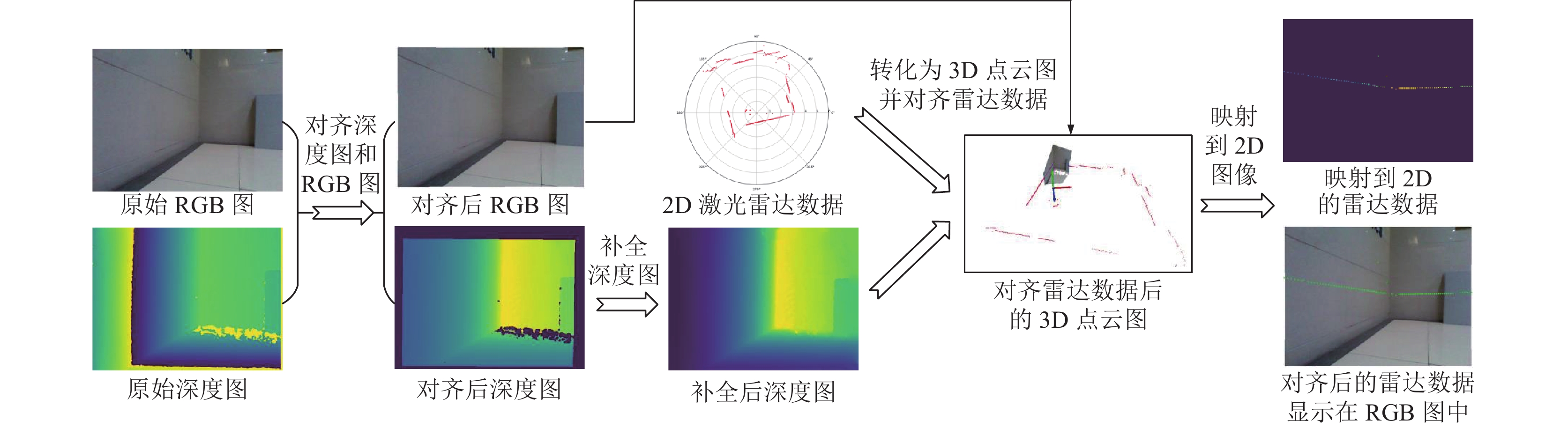
采集完数据后需对原始数据做预处理, 处理过程如图3所示. (1) 通过时间戳同步采集的原始RGB图, 深度图和雷达数据; (2) 使用文献[18]的算法对齐深度图和RGB图并补全深度图; (3) 将深度图转化为3D点云图; (4) 使用式(12)将雷达数据与深度图对齐并映射到2D图像, 映射到图像时需要去除超出图像范围的点, 以及深度值小于0的点(2D激光雷达可测量360°, 所以会出现小于0的值).

$ \left[ {\begin{array}{*{20}{c}} u \\ v \\ 1 \end{array}} \right] = \frac{1}{{r\cos \theta + {d_{\textit{z}}}}}\left[ {\begin{array}{*{20}{c}} {{f_x}}&0&{{c_x}} \\ 0&{{f_y}}&{{c_y}} \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {r\sin \theta + {d_{\textit{z}}}} \\ {{d_y}} \\ {r\cos \theta + {d_{\textit{z}}}} \end{array}} \right] $

(12)

其中, $r$ , $\theta $ 是雷达数据极坐标形式的距离和夹角. $u$ 为映射后二维图像 $x$ 轴坐标, $ u \in [0, 640), u \in N $ , $v$ 为映射后二维图像 $y$ 轴坐标, $ v \in [0, 480), v \in N $ . ${f_x}$ , ${f_y}$ , ${c_x}$ , ${c_y}$ 为相机内参. ${d_x}$ , ${d_y}$ , ${d_z}$ 为相机与雷达的相对位置, 如图2所示.

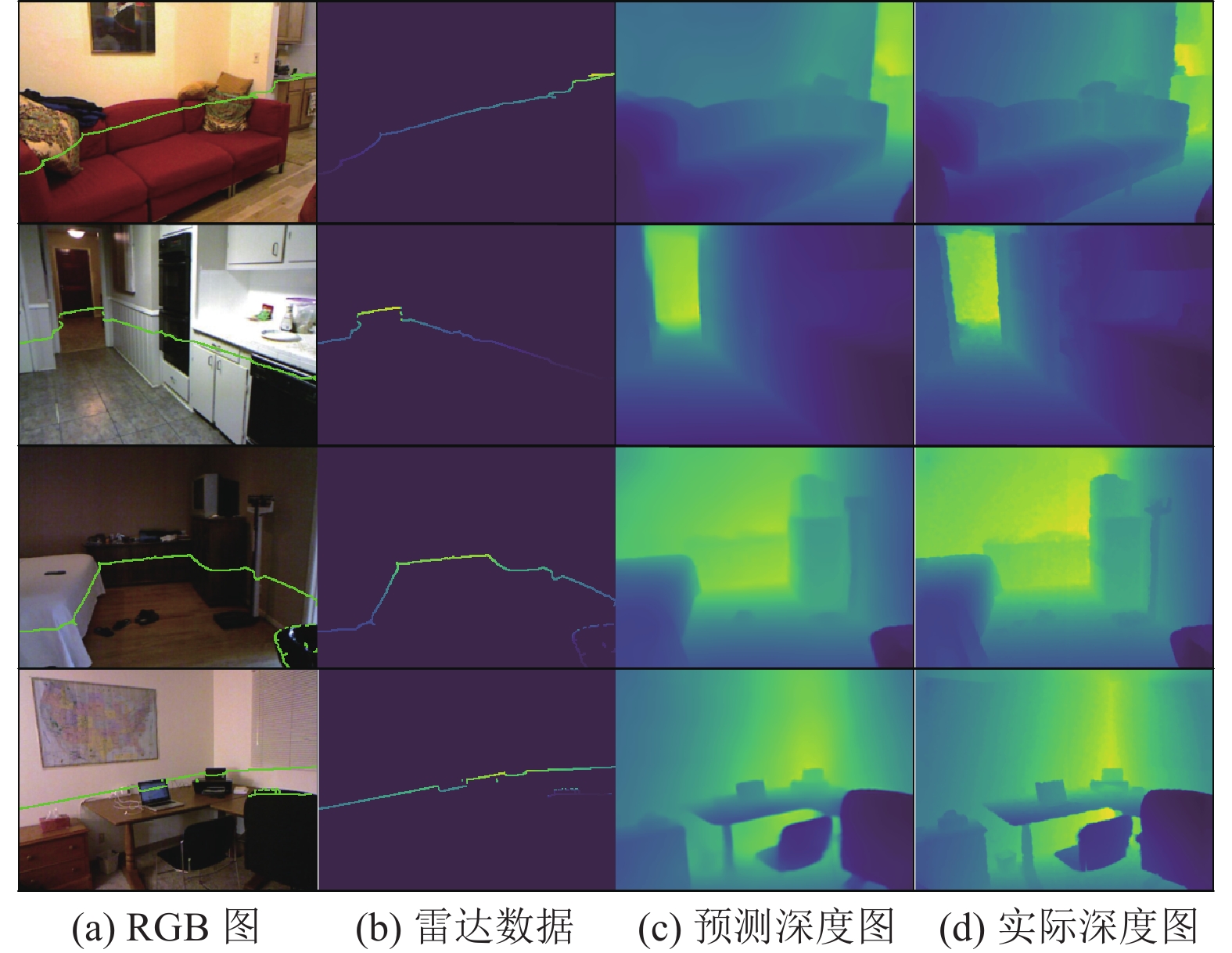
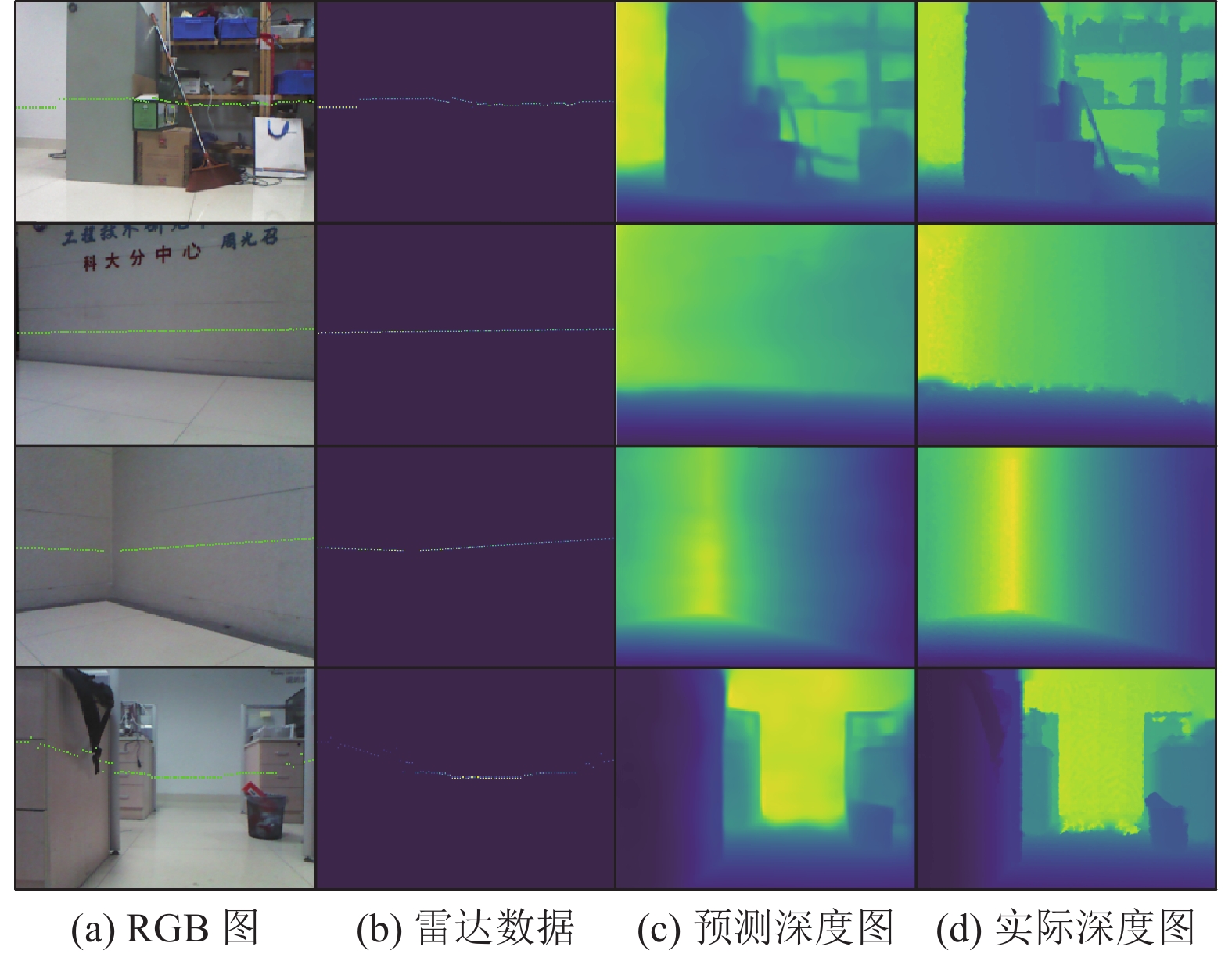
最终, 共采集24k组数据. 选取其中的16k组数据作为训练集, 800组作为测试集. 对比图4和图5中的雷达数据, 可以看出, 实际雷达数据比模拟的雷达数据更加稀疏.

3.2 与现有方法的对比实验

本文算法使用深度学习框架PyTorch 1.7实现. 训练和测试使用11 GB显存的NVIDIA GeForce GTX 1080 Ti GPU. 本文做了多组特征提取网络的对比实验, 最终, RGB图像的特征提取网络选择ResNet50^[19], 雷达数据的特征提取网络选择ResNet18达到最好的效果. 特征提取网络的参数使用ImageNet数据集上的预训练模型初始化. 采用的训练优化器是SGD, 起始的学习率设置为0.01, 并且当连续5个epoch, rel指标(见下文)没有降低, 则将学习率调整为原学习率10%. 在大约40个epoch达到稳定.

对于NYUDv2和本文自制数据集, 深度图和RGB图分辨率均为 $640 \times 480$ . 为了与文献[3]保持一致, 首先对深度图和RGB图均下采样到 $320 \times 240$ , 再以中心为基准裁剪图像, 得到 $304 \times 228$ 的输入数据. 网络输出的深度图大小也为 $304 \times 228$ .

本文采用以下几种方法对训练数据进行增强: (1) 对RGB图和深度图随机旋转, 旋转角度为 $[ - 5^\circ , 5^\circ ]$ ; (2) 对RGB图和深度图随机水平翻转, 概率为0.5; (3) 对RGB图的亮度、对比度、饱和度分别随机调整, 三者的范围均为[0.6, 1.4]; (4) 将RGB图标准化, 使用的均值为[0.485, 0.456, 0.406], 标准差为[0.229, 0.224, 0.225].

本文使用以下几个评价指标来评价深度估计算法的性能:

(1) 平均相对误差(rel): $\dfrac{1}{N}\displaystyle\sum\limits_i {\dfrac{{\left| {{y_i} - {{\hat y}_i}} \right|}}{{{y_i}}}} $

(2) 均方根误差(rms): $\dfrac{1}{N}\sqrt {\dfrac{1}{N}\displaystyle\sum\limits_i {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} } $

(3) 精确度( ${\delta ^k}$ ): $\max \left( {\dfrac{{{y_i}}}{{{{\hat y}_i}}}, \dfrac{{{{\hat y}_i}}}{{{y_i}}}} \right) < {\delta ^k},\; \delta = 1.25, \;k = 1, 2, 3$

其中, ${y_i}$ 是实际深度, ${\hat y_i}$ 是预测的深度, $N$ 是总像素个数.

为了比较已有的单目深度估计算法, 本文在公开数据集NYUDv2上测试了算法的效果. 与本文相关的深度估计算法主要有纯单目深度估计算法(仅使用RGB图像)和深度补全算法. 对于深度补全算法^[12-14], 因其原文的稀疏深度信息是全局的, 本文不与其原始效果比较. 本文将文献[12–14]的输入换成本文处理后的NYUDv2数据集训练测试. 表1为本文算法与现有算法的比较结果. 其中, *表示使用雷达数据, 其余仅使用RGB图, $ \uparrow $ 表示数值越大越好, $ \downarrow $ 表示数值越小越好从表1中可以看到, 本文提出的算法多项指标超过了目前最好的纯单目深度估计算法^[10], 并且相较于深度补全算法也有一定的提升. 相较于同样使用2D激光雷达数据的^[11], 本文在各个指标上均有较大的提升. 图4展示了部分预测结果, 从结果中看出, 本文算法能够较准确的预测图像的深度.

为了验证算法的有效性, 本文制作了带有2D激光雷达数据的深度数据集, 并对比了其他算法在本文自制数据集上的表现. 本文自制数据集主要为室内导航场景, 存在很多墙面等低纹理场景, 以及不同光照的场景, 并且雷达数据与深度数据也存在噪声误差, 所以整体难度比较大. 表2展示了不同方法在本文数据集上表现. 其中, 文献[10]不使用雷达数据. 从表中的数据可以看到, 本文的算法依旧取得了较好的效果, 并且对噪声具有鲁棒性. 图5为部分预测结果.

3.3 消融实验

为了验证雷达数据的加入带来的效果, 以及不同结构和特征提取网络带来的影响, 本文针对NYUDv2数据集做了一系列消融实验.

为了比较加入雷达数据的影响, 本文去掉了雷达特征提取部分和相关联的CAM模块, 其余保持不变, 做了对比试验, 结果如表3. 从表中可以看出, 雷达数据使rel, rms分别降低55.4%, 46.1% (越低越好), ${\delta _1}$ , ${\delta _2}$ , ${\delta _3}$ 分别提高了18.9%, 3.60%, 0.91% (越高越好).

另外, 为比较CAM模块作用, 本文将CAM模块替换为普通的张量拼接, 实验结果如表4. CAM模块使rel, rms分别降低12.7%, 7.28% (越低越好), 而 ${\delta _1}$ , ${\delta _2}$ , ${\delta _3}$ 三个指标因本来就比较高, 提升不明显.

针对不同的特征提取网络, 本文也做了几组对照实验, 如表5所示. 这里分别对比了ResNet^[19], Dense-Net^[20], MobileNetv2^[21]的影响, 其中, R表示ResNet, D表示DenseNet, M表示MobileNet, 前者表示RGB特征提取网络后者为雷达特征提取网络. 从数据中可以看到, DenseNet与ResNet结果差距不大, 且参数量较大. 而在轻量级网络MobileNetv2中, 本文的方法在大量减少参数量的同时, 精度降低较小, 且超越了已有的单目深度估计算法. 在实际运用中, 可以考虑更轻量的MobileNetv2. 后续工作将基于轻量级网络, 并结合知识蒸馏等方法压缩加速模型, 以达到导航场景的实时性要求.

4 结论与展望

本文提出了一种融合2D激光雷达的单目深度估计网络, 使用跳跃连接提高了上采样的效果, 并提出一种通过通道注意力机制融合RGB特征和雷达特征的方法. 相较于现有的单目深度估计以及深度补全方法, 均取得了更好的效果. 另外, 针对不同的结构和特征提取网络, 本文也做了一系列对照试验. 下一步研究工作将着重于将本文深度估计算法应用到SLAM以及3D目标检测中, 构建单目视觉导航系统.