单视图三维重建一直以来是计算机视觉领域里的一个热点. 随着深度学习的发展和大型3D模型数据集ShapeNet[1]的出现, 基于深度学习的三维重建成为主流. 编码器-解码器结构是目前基于深度学习三维重建的主要架构, 输入单一图片进编码器提取图像特征而后由解码器将特征向量还原成三维模型, 此结构是训练神经网络学习二维图像和三维物体之间的映射关系. 本文从MarrNet方法[2]中得到启发, 输入单一图片不直接生成特征向量而是生成2.5D中间表达(深度图、表面法向量贴图、轮廓图), 对比之下中间表达可以从图像中获得更多信息, 从而具有从复杂背景的图片中重建出三维模型的能力. 另外之前的研究都只提取了图像的全局特征, 因此重构后的三维模型精准度不高, 针对这个问题本文提出局部特征模块, 结合局部特征和全局特征生成更高质量的三维模型.
近年来, 单视图三维重建工作使用的3D表达方式主要有点云, 体素, 网格. 基于点云[3-5]的三维表达虽然易于使用CNN (convolutional neural networks)但分辨率十分受限. 基于体素[6-8]的表达因其使用太多的体素去描述物体内部看不到的部分而增加了计算量. 基于网格[9-11]的方法重构出来的三维物体较为精细, 不过这种方法受限于其固定的拓扑结构.
针对上述3种表达方式的局限性, 隐式曲面表达[12, 13]逐渐受到重视. Mescheder等人[14]则使用隐式曲面表达, 他们预测体积网格中每个单元被占用或未占用的概率, 在缓解体积网格分辨率受限的问题的同时也使最后生成的模型更平滑. Chen等人[15]同样使用SDF来完成三维重建的任务, 虽然生成了连续高质量的三维模型, 但重建细节欠佳, 不能很好的重建如三维模型孔洞处的细节. Wang等人[16]提出的DISN使用SDF作为表示, 因不仅提取了输入图片的特征更提取了局部特征使重建细节方面得到提升, 但其缺点在于只能处理纯净背景的图片, 处理复杂背景时其精度会大大降低. Thai等人[17]提出的SDFNet讨论重建精度的同时也研究了模型的泛化能力, 训练出的模型能很好的重建出训练集中未出现过的物体种类. Kleinberg等人[18]将SDF与GAN (generative adversarial networks)结合生成精度较好的三维模型.
本文提出的模型创新点有: (1)加入2.5D草图预测模块使模型可以从复杂背景图片中重建三维模型, 结合局部特征提取模块和SDF隐式表面表达可以生成更逼真的模型. (2)讨论模型的泛化能力, 研究模型是否可以重建出训练集中未出现过的物体种类, 实验结果证明加入2.5D草图预测模块有助于提升泛化能力. (3)本文采用隐式表面表达方法中最常用的SDF(signed distance function)作为三维模型的表达方式不仅估计了采样点的正负值(该点在表面外还是表面内)还估计了其到表面的距离, 可以提取任意值的等值面.
2 网络结构本文方法概况如下: 先通过采样策略为数据集ShapeNet每个三维模型采样点生成采样点点云, 之后结合图片全局特征和局部特征预测每个采样点的SDF值, 最后提取SDF值为0的面作为最终生成三维模型表面.
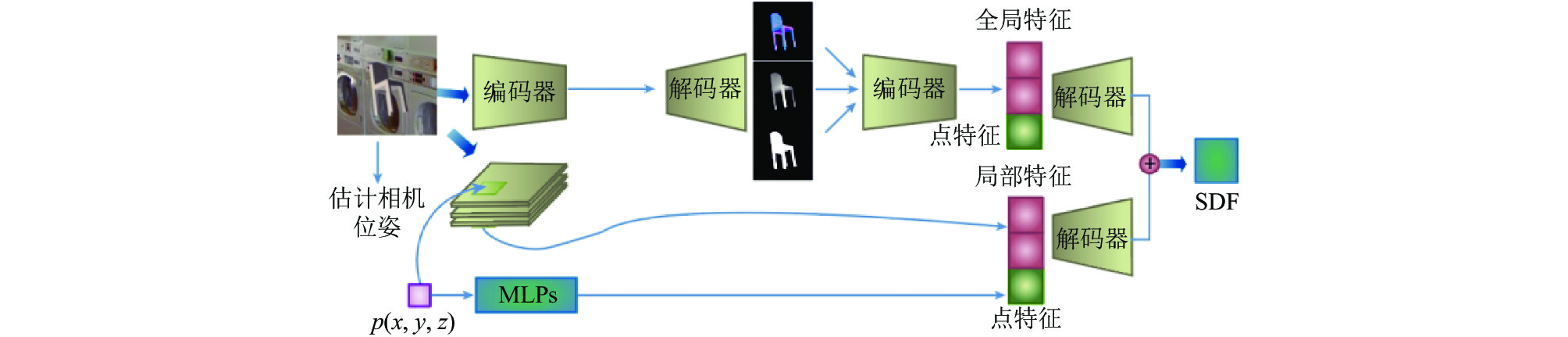
2.1 总体架构网络整体架构如图1所示, 主要包含两个模块: 相机位姿预测模块和SDF预测模块. 首先对输入的图像进行相机参数的预测. 之后将图片输入至2.5D草图模块经过编码器解码器生成2.5D草图, 再提取2.5D草图的特征作为全局特征. 接着使用之前预测到的相机参数将采样点映射到二维图像平面, 进行该采样点的局部特征提取. 最后将点特征分别与全局特征和局部特征结合, 进行降维操作后得到两路SDF值, 将这两路得出的结果连接生成最后预测的SDF值.
|
图 1 网络架构 |
2.2 相机位姿预测模块
使用ShapeNet数据集进行这个模块训练, 此模块功能为预测将默认位姿的3D模型投影至与输入图片相同位姿所需要的相机参数. 将ShapeNet数据集中各个3D模型默认位姿作为世界坐标下位姿, 并提取点云生成世界坐标下的点云. 在数据准备操作中会对ShapeNet数据集进行渲染, 会对默认位姿3D模型旋转、平移特定角度, 而后提取点云生成真实相机坐标下的点云. 相机位姿预测模块大致为输入一张图片至CNN (这里采用VGG-16)预测位姿, 将网络预测出的位姿对世界坐标下的点云进行旋转平移变换操作生成预测相机坐标下的点云, 再与真实相机坐标下的点云损失对比优化这一模块. 估计出来的相机参数用于局部特征提取. Zhou等人[19]的实验说明使用6D旋转表示法相对于四元数和欧拉角来说更容易使网络回归, 在此也采用该方法. 本文使用6D旋转表示b=(bx, by)其中bx∈R3, by∈R3 , b∈R6来表示物体位姿. 本模块预测出6D旋转表示b和位移量t, 由b通过式(1)可以计算出旋转矩阵
| Rx=N(bx),Rz=N(Rx×by),Ry=Rz×Rx | (1) |
其中, N(·)是标准化方程, ×是交叉积.
预测相机坐标下的点云和真实相机坐标下的点云之间的差距作为本模块的损失函数如式(2):
| Lcam=∑pw∈PCw‖pG−(Rpw+t)‖22∑pw∈PCw1 | (2) |
该方程本质是MSE (mean squared error), 其中PCw表示世界坐标下的点云, 而pw表示世界坐标下点云中的一个点, pG为真实相机坐标下的点, 式(2)中, pG–(Rpw+t)表示真实相机坐标下的点pG与由世界坐标系下的点pw通过旋转R和平移t变换得到的点之间的差距. 最后除总共点的个数. 相机位姿预测网络如图2.

|
图 2 相机位姿预测网络 |
2.3 SDF预测模块
SDF是一个将3D模型采样的点p=(x, y, z)映射到实数s=SDF(p)的连续函数, 其中s的正负代表在物体表面外部还是内部, s的绝对值表示这个点到物体表面距离. 再使用Marching cubes方法[20]提取0等值面作为3D物体的形状. SDF预测模块分为全局特征提取和局部特征提取两个过程.
2.3.1 全局特征提取在全局特征提取时使用了2.5D草图模块如图3所示, 以2D RGB图片作为输入预测它的2.5D草图: 表面法线、深度和轮廓, 其主要目的是从输入图像中提取出固有的物体属性, 与直接从RGB中提取特征相比, 提取出的特征更丰富, 实验表明使用这种中间表示方式可以使网络更容易处理具有复杂背景的图片, 并且因从图像中得到更丰富的信息, 网络的泛化能力也得到了提升. 在2.5D草图模块使用编码器为ResNet18 (deep residual network)将256×256 RGB图像编码成大小为8×8的512特征图, 然后通过解码器(解码器包含4组5×5全卷积层和ReLU层然后是4组1×1全卷积层和ReLU层)输出相应的深度图、表面法线、轮廓图像, 分辨率都为256×256. 将得到的2.5D草图输入到同样是ResNet18编码器中得到全局特征. 用Blender软件渲染出的2.5D草图作为地面真实计算损失函数, 训练过程中我们使用MSE损失优化2.5D表示模块.

|
图 3 2.5D草图预测模块 |
2.3.2 局部特征提取
如图4所示, 在局部特征提取模块使用编码器VGG-16 (visual geometry group). 通过相机位姿预测模块得到的相机参数将3D的点p投影到2D图像上得到点q, 在VGG-16中5个特征子图中找到q点对应的位置取下, 维度分别为64、128、256、512、512, 而后进行连接得到维度为1 472的局部特征(因为特征图尺寸不一样, 所以先采用双线性插值再取下与q点对应模块).

|
图 4 局部特征提取 |
2.3.3 预测SDF值
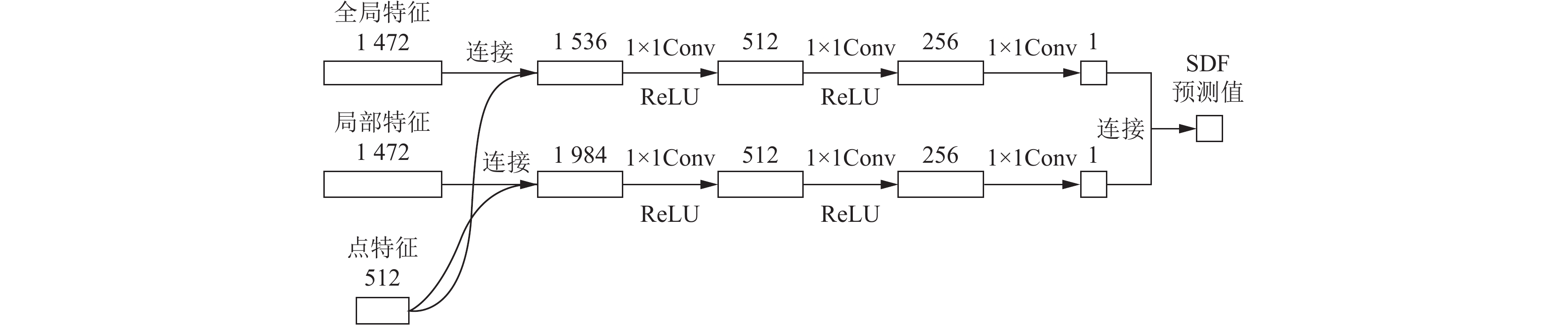
如图5所示, 当经过全局特征提取和局部特征提取之后得到全局特征维度为1 024和局部特征维度为1 472, 采样点维度初始为3经过MLP (multilayer perceptron)生成维度为512的点特征后分别与全局特征和局部特征结合. 最后通过图5中所示一系列操作分别得到两个维度为1的特征, 将得到的两个特征结合则是网络预测的SDF值.
|
图 5 通过图像特征预测SDF |
2.4 损失函数
用原始数据集ShapeNet中的三维模型先提取出点云, 而后测量出点云中各个点的SDF值作为地面真实SDF值, 而我们的网络f(·)是估计使用采样策略采样点的SDF值, 使用以下损失函数优化预测SDF值模块. SDF损失函数为式(3):
| {LSDF=∑pm|f(I,p)−SDFI(p)|m={m1,SDFI(p)<σm2,其他情况下 | (3) |
其中, f(I, p)表示以图像I和三维点p作为输入输入到本网络中, 而SDFI(p)则表示地面真实SDF值, m1和m2, 这两个值代表不同的权重,
为了生成隐式平面, 首先定义一个分辨率为256×256×256稠密3D网格将采样点点云放入其中并为网格中的每个点预测SDF值. 得到了稠密网格中每个点的SDF值之后使用Marching cubes在SDF值为0的等值面上生成对应的平面.
3 实验传统实验都是采用ShapeNet数据集中所有13种种类按照官方推荐的训练集数据集分割进行实验. 本文为了检测泛化能力, 验证网络是否可以重建出训练集中未出现的物体种类, 采用数据集中最大的3种种类(长凳、汽车、桌子)作为训练集而其余10种作为训练集. 重建结果与最先进的方法进行对比, 结果显示本文可以重构出训练集中未出现过的种类, 同时还解决了重构中细节恢复的问题.
3.1 数据集和数据准备使用ShapeNet 作为数据集, 在实验中我们使用3种种类作为训练集, 而使用另外10种种类作为测试集. 实验中地面真实深度图、法线贴图等2.5D草图我们使用Cycles光线追踪引擎在Blender中实现了自定义数据生成管道, 以2D图片为渲染对象, 生成的2.5D草图作为地面真实值与网络生成的2.5D草图计算损失. 为了生成实验中的复杂背景2D图片, 用不同的20个随机图像作背景渲染每个3D模型而后生成具有复杂背景的2D图片. 为了增加2D图像数据量, 本文通过旋转、平移特定角度生成不同角度下的3D模型再添加背景图生成2D图像. 每个三维模型旋转、平移8个特定角度, 因此每个模型生成8张具有复杂背景的2D图像. 实验中使用的点云也是由数据集ShapeNet得到的, 把数据集默认位姿提取得到的点云作为世界坐标下的点云, 而由旋转、平移不同角度后得到的三维模型中提取得到的点云作为真实相机坐标空间下的点云, 其旋转平移的相机参数则作为真实相机参数.
3.2 实现细节要生成三维模型因此更关注物体表面周边的点, 所以在训练过程中采样策略为在高斯分布N(0, 0.1)下采样2 048个点. 把采样点云装入生成的256×256×256稠密3D网格中结合图片全局特征和局部特征逐个点预测对应的SDF值, 再与真实SDF值做对比.
本文分开训练相机位姿预测网络和SDF预测网络. 相机位姿预测网络中CNN使用VGG-16, 使用式(2)作为这个模块的损失函数. 因SDF预测网络需要用到相机位姿预测网络中预测出的相机参数, 为更好训练SDF预测网络, 我们使用地面真实相机参数训练此网络. 在本模块中提取全局特征线路使用2.5D草图作为中间表达, 用Blender渲染出来的2.5D草图和网络训练得到草图对比来调优2.5D草图提取模块. 最后由局部特征、全局特征和点特征共同预测的SDF值与地面真实SDF值使用式(3)作为损失函数, 其中m1=4, m2=1,
测试阶段中, 先使用相机位姿预测模块估计相机位姿, 把预测到的位姿用于SDF预测模块预测各个点的SDF值. 所有采样点SDF已知后采用第2.5节中提及表面重建的方法生成输出模型.
3.3 评价指标对于质量评测, 使用常见的衡量指标倒角距离chamfer distance (CD)比较重建后的模型和地面真实模型. CD计算公式为式(4), 为了使用CD评判重建后模型和地面真实模型的相似度需对两个模型采样生成点云. S1和S2分别代表这两个点云, 公式中第1项代表S1点云中任意一点x到S2最小距离之和, 第2项则表示S2中任意一点y到S1最小距离之和. 所以CD值越大说明两组点云区别越大, 反之CD值越小两组点云区别越小, 重建效果越好.
| dCD(S1,S2)=∑x∈S1miny∈S2||x−y||22+∑y∈S2minx∈S1||x−y||22 | (4) |
通过渲染复杂背景图后的图片作为输入, 由2.5D草图估计网络得到对应的2.5D草图如图6. 之后再进行SDF值预测和局部特征提取等操作得到的三维模型与GenRe[21]和OccNet[12]重建出来的结果进行对比, GenRe是研究基于泛化至训练集中未出现的物体种类算法中经典的模型, 而OccNet是近期使用隐式曲面作为表达方式算法中有代表性的模型, 我们挑选出在训练集中未出现过的4种种类进行对比如图7, 对比可以很明显的看出本文的方法不仅可以恢复训练集中未见过的物体种类还可以很好的处理模型中细节的恢复, 如椅子和长椅靠背孔洞处的恢复以及飞机机翼和手枪手柄处的孔洞恢复更贴近地面真实模型. 表1则为部分未见过种类CD值对比, CD值越低表示重建效果越好, 可以看到本文方法CD值在6种种类和平均值对比中都是最低的, 表明本文重建效果优于其他两种.
4 总结与展望本文提出的网络使用SDF隐式曲面来表示三维物体, 生成后的模型相较于之前单视图三维重建方法有更为清晰的表面. 引入局部特征提取的模块使得最后生成的模型能够捕获细粒度的细节生成高质量3D模型. 我们还进行了泛化能力的实验, 通过2.5D模块和选择以视觉为中心的坐标系来测试泛化能力. 定性和定量的实验可以验证出我们的方法在重建模型的质量上和泛化能力方面都优于现有的方法.

|
图 6 输入图片和2.5D |

|
图 7 三维模型重构对比 |
| 表 1 6种训练集未出现的种类CD比较 |
| [1] |
Chang AX, Funkhouser T, Guibas L, et al. ShapeNet: An information-rich 3D model repository. arXiv: 1512.03012, 2015.
|
| [2] |
Wu JJ, Wang YF, Xue TF, et al. MarrNet: 3D shape reconstruction via 2.5D sketches. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 540–550.
|
| [3] |
Fan HQ, Su H, Guibas L. A point set generation network for 3D object reconstruction from a single image. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 2463–2471.
|
| [4] |
Mandikal P, Navaneet KL, Agarwal M, et al. 3D-LMNet: Latent embedding matching for accurate and diverse 3D point cloud reconstruction from a single image. Proceedings of British Machine Vision Conference 2018. Newcastle: BMVA Press, 2018. 1–19.
|
| [5] |
Zhang Y, Liu Z, Liu TP, et al. RealPoint3D: An efficient generation network for 3D object reconstruction from a single image. IEEE Access, 2019, 7: 57539-57549. DOI:10.1109/ACCESS.2019.2914150 |
| [6] |
Choy CB, Xu DF, Gwak J, et al. 3D-R2N2: A unified approach for single and multi-view 3D object reconstruction. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 628–644.
|
| [7] |
Girdhar R, Fouhey DF, Rodriguez M, et al. Learning a predictable and generative vector representation for objects. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 484–499.
|
| [8] |
Dai A, Qi CR, Nießner M. Shape completion using 3D-encoder-predictor CNNs and shape synthesis. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017. 6545–6554.
|
| [9] |
Pontes JK, Kong C, Sridharan S, et al. Image2Mesh: A learning framework for single image 3D reconstruction. Proceedings of 14th Asian Conference on Computer Vision. Perth: Springer, 2019. 365–381.
|
| [10] |
Groueix T, Fisher M, Kim VG, et al. A Papier-Mache approach to learning 3D surface generation. Proceedings of the IEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Salt Lake City: IEEE, 2018. 216–224.
|
| [11] |
Jack D, Pontes JK, Sridharan S, et al. Learning free-form deformations for 3D object reconstruction. Proceedings of 14th Asian Conference on Computer Vision. Perth: Springer, 2019. 317–333.
|
| [12] |
Park JJ, Florence P, Straub J, et al. DeepSDF: Learning continuous signed distance functions for shape representation. Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 165–174.
|
| [13] |
Wang JR, Fang ZY. GSIR: Generalizable 3D shape interpretation and reconstruction. Proceedings of 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 498–514.
|
| [14] |
Mescheder L, Oechsle M, Niemeyer M, et al. Occupancy networks: Learning 3D reconstruction in function space. Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2019. 4455–4465.
|
| [15] |
Chen ZQ, Zhang H. Learning implicit fields for generative shape modeling. Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 5932–5941.
|
| [16] |
Wang WY, Xu QG, Ceylan D, et al. DISN: Deep implicit surface network for high-quality single-view 3D reconstruction. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 45.
|
| [17] |
Thai A, Stojanov S, Upadhya V, et al. 3D reconstruction of novel object shapes from single image. Proceedings of 2021 International Conference on 3D Vision (3DV). London: IEEE, 2021. 85–95.
|
| [18] |
Kleineberg M, Fey M, Weichert F. Adversarial generation of continuous implicit shape representations. Proceedings of 41st Annual Conference of the European Association for Computer Graphics. Norrköping: Eurographics Association, 2020. 41–44.
|
| [19] |
Zhou Y, Barnes C, Lu JW, et al. On the continuity of rotation representations in neural networks. Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 5738–5746.
|
| [20] |
Lorensen WE, Cline HE. Marching cubes: A high resolution 3D surface construction algorithm. ACM SIGGRAPH Computer Graphics, 1987, 21(4): 163-169. DOI:10.1145/37402.37422 |
| [21] |
Zhang XM, Zhang ZT, Zhang CK, et al. Learning to reconstruct shapes from unseen classes. Proceedings of the 32nd International Conference on Neural Information Processing Systems (NeurIPS). Montréal: Curran Associates Inc., 2018. 2263–2274.
|
 2022, Vol. 31
2022, Vol. 31



