随着城市化进程的推进, 不断扩张的路网便利居民出行的同时也存在着诸多隐患, 道路的严重堵塞降低了交通系统的运转效率, 加大了交通事故发生的概率. 智慧交通系统(intelligent traffic system, ITS)[1]的出现为上述存在的问题找到了一个合理的解决方案. 精确的短时交通流预测已发展为ITS研究的重要领域之一, 高效准确的预测结果成为了助力出行者路线选择和管理者路径规划的有力保障.
短时交通流的预测模型主要可以分为4类: 基于传统统计建模的模型、机器学习模型、基于大数据驱动的深度学习模型、基于拓扑空间的图神经网络(graph neural network, GNN)模型.
基于统计方法的模型是基于数理统计的方法处理交通数据, 此类模型主要是以自回归滑动平均(autoregression moving average, ARMA)及其改进算法为代表. 杨东龙[2]利用差分自回归滑动平均(autoregression integrated moving average, ARIMA)对区间车流量进行多个时间周期的预测; 靳小飞[3]利用自回归分数整合移动平均(autogression fractionally integrated moving average, ARFIMA)分析序列的长期记忆性来预测短时交通流. 此类模型应用简单, 但适用性与实时性不强, 当实际情况与参数标定时的交通状态相差较大时, 预测误差偏高.
随着人工智能的普及, 机器学习应运而生, 此类模型可以分为基于特征的模型和状态空间模型. 前者是通过训练交通数据的回归模型进行预测分析, 张天逸等[4]利用K均值聚类(K-means clustering)来提取径向基函数(radial basis function, RBF)神经网络的中心向量, 提出了一种多维时间序列的交通流预测模型; 后者是基于系统随机性构建模型, 申启东等[5]利用马尔科夫链(Markov chain)对相关路网之间进行建模分析, 改进了权值计算公式来度量关联路段间的权值, 通过“滴滴打车”平台数据验证了模型的可靠性. 机器学习虽提高了模型的计算效率, 但关键参数的设置较为困难. 为进一步提高模型预测精度, 基于大数据驱动的深度学习模型预测交通流成为了行业新的研究热点. 克服了循环神经网络(recurrent neural network, RNN)不能保存历史状态信息问题的长短期记忆网络(long short term memory, LSTM)模型被广泛应用于时间序列预测, 产生了许多基于LSTM的短时交通流预测模型[6-9].
虽然端到端的深度学习模型可捕获交通流序列的非线性特征[10], 但却无法处理时空交通流这种具有天然图结构特性的非欧数据, 不能充分挖掘交通路网拓扑图中节点间的连接关系. 因此, 基于图卷积神经网络[11]的方法成为了挖掘交通流时空特性的有效途径. Cui等[12]提出的图卷积长短期记忆神经网络(GCN-LSTM)通过学习路网中路段之间的相互关联预测交通状态, 并将图卷积特征引入到损失函数中增强模型可解释性; Zhang等[13]提出的时空卷积图注意力网络(spatial-temporal convolutional graph attention network, ST-CGN)在路网局部空间相关性基础上考虑了全局区域间相关性, 实现了从局部到全局的全面交通流预测; Song等[14]提出一种时空同步图卷积网络模型, 该模型能有效捕捉交通状态的复杂局部时空关联和区域时空图的异质性; Zheng等[15]提出了一种结合GCN和多任务学习(multi-task learning, MTL)的异常交通数据预测混合模型, 并验证了随机缺失等异常模式下系统的鲁棒性. 虽然此类模型能挖掘路网中交通流数据的时空特征, 但单一模型的预测结果受交通流随机性扰动较大.
本文提出了基于DWT-GCN模型的短时交通流预测方法. 利用DWT算法将交通流序列分解为近似分量与细节分量, 细化交通流信息, 降低序列非平稳性; 优化路网拓扑图结构的邻接矩阵, 深度挖掘路网的时空关联; 将分解的交通流数据作为GCN的输入, 并对各组预测结果进行重构, 得到最终预测值. 利用PeMS数据库中交通流数据验证了模型预测短时交通流的有效性.
2 GCN算法图的定义为:
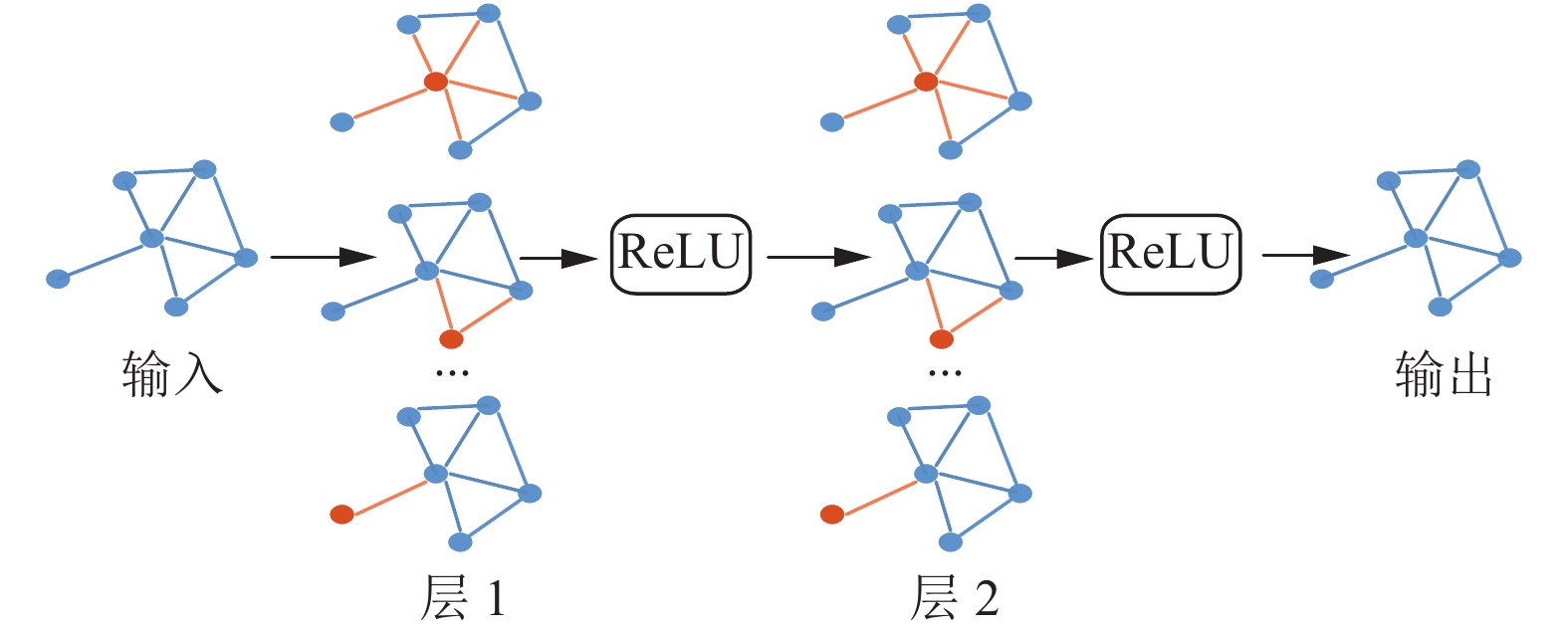
|
图 1 图卷积神经网络模型图 |
| $ {D_{ii}} = \sum\limits_j {{A_{ij}}} $ | (1) |
| $ {H^{(0)}} = X $ | (2) |
| $ {H^{(1)}} = \sigma ({D^{ - 1/2}}(A + I){D^{ - 1/2}}X{W^{(0)}}) $ | (3) |
| $ {H^{(l + 1)}} = \sigma ({D^{ - 1/2}}(A + I){D^{ - 1/2}}{H^{(l)}}{W^{(l)}}) $ | (4) |
其中,
GCN算法不仅对参数
非平稳的交通流序列在单一的预测模型下不易得到精准的预测结果, 因此结合离散小波变换降低序列随机性的特点和图神经网络挖掘非欧数据时空特征的优点, 对GCN预测模型进行优化, 基于DWT-GCN预测模型流程如图2所示.
3.1 DWT-GCN模型预测假设给定的路网有
(1)对路网输入
(2)将小波分解后的交通流量时间序列输入到GCN模型中训练, 挖掘交通流序列的时空特性. GCN模型输入
| $\begin{split} & {X_{G\_{\rm in}}} = {\left[ {\begin{array}{*{20}{c}} {{x_{1j}}{x_{2j}}{x_{3j}} \ldots {x_{Mj}}} \end{array}} \right]^{\rm T}} \\ =&{\left[ {\begin{array}{*{20}{c}} {{x_{1j}}(1)}&{{x_{1j}}(2)}& \cdots &{{x_{1j}}(t)}& \cdots &{{x_{1j}}(N)}\\ {{x_{2j}}(1)}&{{x_{2j}}(2)}& \cdots &{{x_{2j}}(t)}& \cdots &{{x_{2j}}(N)}\\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {{x_{mj}}(1)}&{{x_{mj}}(2)}& \cdots &{{x_{mj}}(t)}& \cdots &{{x_{mj}}(N)}\\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {{x_{Mj}}(1)}&{{x_{Mj}}(2)}& \cdots &{{x_{Mj}}(t)}& \cdots &{{x_{Mj}}(N)} \end{array}} \right]_{M \times N}} \end{split} $ | (5) |
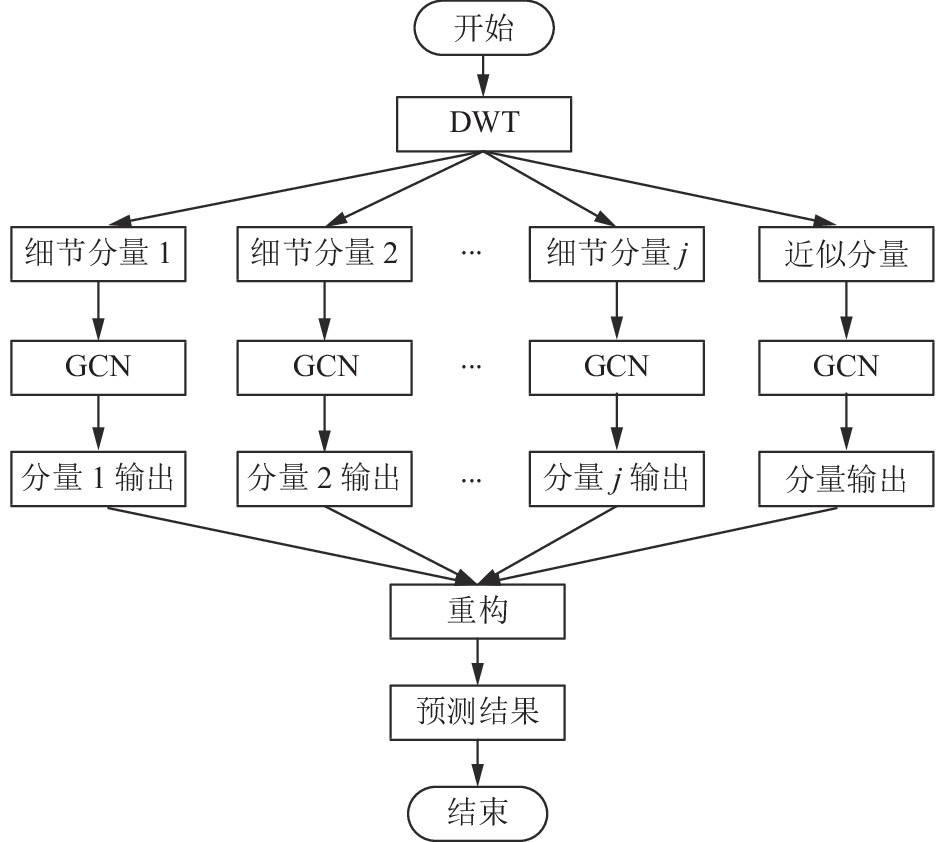
|
图 2 DWT-GCN模型流程图 |
对于路段
| $ T{R_{m\_{\rm in}}} = {\left[ {\begin{array}{*{20}{c}} {{x_{mj}}(1)}&{{x_{mj}}(2)}& \cdots &{{x_{mj}}(\tau - 1)}&{{x_{mj}}(\tau )}\\ {{x_{mj}}(2)}&{{x_{mj}}(3)}& \cdots &{{x_{mj}}(\tau )}&{{x_{mj}}(\tau + 1)}\\ \vdots & \vdots &{\ddots}& \vdots & \vdots \\ {{x_{mj}}({l_{tr}} - \tau - 1)}&{{x_{mj}}({l_{tr}} - \tau )}& \cdots &{{x_{mj}}({l_{tr}} - 3)}&{{x_{mj}}({l_{tr}} - 2)}\\ {{x_{mj}}({l_{tr}} - \tau )}&{{x_{mj}}({l_{tr}} - \tau + 1)}& \cdots &{{x_{mj}}({l_{tr}} - 2)}&{{x_{mj}}({l_{tr}} - 1)} \end{array}} \right]_{({l_{tr}} - \tau ) \times \tau }} $ | (6) |
| $ t{r_{m\_{\rm out}}} = \left[ {\begin{array}{*{20}{c}} {{x_{mj}}(\tau )}&{{x_{mj}}(\tau + 1)}& \cdots &{{x_{mj}}({l_{tr}} - 1)}&{{x_{mj}}({l_{tr}})} \end{array}} \right]_{({l_{tr}} - \tau ) \times 1}^{\rm T} $ | (7) |
| $ T{E_{m\_{\rm in}}} = {\left[ {\begin{array}{*{20}{c}} {{x_{mj}}({l_{tr}} - \tau + 1)}&{{x_{mj}}({l_{tr}} - \tau + 2)}& \cdots &{{x_{mj}}({l_{tr}} - 1)}&{{x_{mj}}({l_{tr}})} \\ {{x_{mj}}({l_{tr}} - \tau + 2)}&{{x_{mj}}({l_{tr}} - \tau + 3)}& \cdots &{{x_{mj}}({l_{tr}})}&{{x_{mj}}({l_{tr}} + 1)} \\ \vdots & \vdots &{\ddots}& \vdots & \vdots \\ {{x_{mj}}(N - \tau - 1)}&{{x_{mj}}(N - \tau )}& \cdots &{{x_{mj}}(N - 3)}&{{x_{mj}}(N - 2)} \\ {{x_{mj}}(N - \tau )}&{{x_{mj}}(N - \tau + 1)}& \cdots &{{x_{mj}}(N - 2)}&{{x_{mj}}(N - 1)} \end{array}} \right]_{({l_{te}} \times \tau )}} $ | (8) |
| $ T{R_{\rm in}} = \left[ {\begin{array}{*{20}{c}} {T{R_{1\_{\rm in}}}}\quad{T{R_{2\_{\rm in}}}}\quad \cdots \quad{T{R_{M\_{\rm in}}}} \end{array}} \right]{^{\rm {T}}} $ | (9) |
| $ T{R_{\rm out}} = \left[ {\begin{array}{*{20}{c}} {t{r_{1\_{\rm out}}}}&{t{r_{2\_{\rm out}}}}& \cdots &{t{r_{M\_{\rm out}}}} \end{array}} \right]{^{\rm T}} $ | (10) |
| $ T{E_{\rm in}} = \left[ {\begin{array}{*{20}{c}} {T{E_{1\_{\rm in}}}}&{T{E_{2\_{\rm in}}}}& \cdots &{T{E_{M\_{\rm in}}}} \end{array}} \right]{^{\rm T}} $ | (11) |
将式(9)–式(11)代入式(1)–式(4)中, 得到路网图数据的预测输出
| $ {H_j} = \left[ {\begin{array}{*{20}{c}} {{h_{1j}}}& \cdots &{{h_{mj}}}& \cdots &{{h_{Mj}}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{h_{1j}}({l_{tr}} + 1)}&{{h_{2j}}({l_{tr}} + 1)}& \cdots &{{h_{mj}}({l_{tr}} + 1)}& \cdots &{{h_{Mj}}({l_{tr}} + 1)} \\ {{h_{1j}}({l_{tr}} + 2)}&{{h_{2j}}({l_{tr}} + 2)}& \cdots &{{h_{mj}}({l_{tr}} + 2)}& \cdots &{{h_{Mj}}({l_{tr}} + 2)} \\ \vdots & \vdots &{\ddots}& \vdots &{}& \vdots \\ {{h_{1j}}(N)}&{{h_{2j}}(N)}& \cdots &{{h_{mj}}(N)}& \cdots &{{h_{Mj}}(N)} \end{array}} \right]_{{l_{te}} \times M}} $ | (12) |
(3)对各个GCN的输出结果进行重构, 得到组合模型的最终输出预测结果
| $ {H_{\rm out}} = {\left[ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{j = 1}^J {{h_{1j}}({l_{tr}} + 1)} }&{\displaystyle\sum\limits_{j = 1}^J {{h_{2j}}({l_{tr}} + 1)} }& \cdots &{\displaystyle\sum\limits_{j = 1}^J {{h_{mj}}({l_{tr}} + 1)} }& \cdots &{\displaystyle\sum\limits_{j = 1}^J {{h_{Mj}}({l_{tr}} + 1)} } \\ {\displaystyle\sum\limits_{j = 1}^J {{h_{1j}}({l_{tr}} + 2)} }&{\displaystyle\sum\limits_{j = 1}^J {{h_{2j}}({l_{tr}} + 2)} }& \cdots &{\displaystyle\sum\limits_{j = 1}^J {{h_{mj}}({l_{tr}} + 2)} }& \cdots &{\displaystyle\sum\limits_{j = 1}^J {{h_{Mj}}({l_{tr}} + 2)} } \\ \vdots & \vdots &{\ddots}& \vdots &{}& \vdots \\ {\displaystyle\sum\limits_{j = 1}^J {{h_{1j}}(N)} }&{\displaystyle\sum\limits_{j = 1}^J {{h_{2j}}(N)} }& \cdots &{\displaystyle\sum\limits_{j = 1}^J {{h_{mj}}(N)} }& \cdots &{\displaystyle\sum\limits_{j = 1}^J {{h_{Mj}}(N)} } \end{array}} \right]_{{l_{te}} \times M}} $ | (13) |
(4) GCN网络中邻接矩阵
| $ {A}{'} _{ij}=\left\{ {\begin{array}{*{20}{l}} \dfrac{1}{{d}_{ij}}+{\gamma }_{ij}, & {A}_{ij}=1且{\gamma }_{ij}\geqslant TH\\ \dfrac{1}{{d}_{ij}}, & {A}_{ij}=1且{\gamma }_{ij} < TH\\ {\gamma }_{ij}, & {A}_{ij}=0且{\gamma }_{ij}\geqslant TH\\ 0, & {A}_{ij}=0且{\gamma }_{ij} < TH\end{array}} \right. $ | (14) |
| $ {A}_{ij}=\left\{ {\begin{array}{*{20}{l}} 1, & i\in Nei(j)& 或& j\in Nei(i)\\ 0, & 其他& & \end{array}} \right. $ | (15) |
基于DWT-GCN的短时交通流预测模型一方面可以通过小波分解降低交通流序列由于外部因素导致的随机性; 另一方面, 根据改进的邻接矩阵可以有效地捕获路网拓扑图的邻近关系, 深度挖掘路网的时空特性, 更加拟合真实应用场景. 但当路网图数据过大时, 构造邻接矩阵与选择邻近路段节点的计算复杂度较大. 因此, 虽然大规模路网图数据会降低模型预测效率, 但是该模型整体能够保持较高的预测性能, 可以适用于城市公路短时交通流预测问题.
4 实验 4.1 数据来源及评价指标选用公开数据集PeMS04作为本文实验数据, 该数据集包括路网中307个节点实测交通流数据及节点之间的连接关系. 交通流数据采集时间从2018年1月1日到2018年2月28日共59天, 采样周期5分钟, 共采集16 992条交通流量. 将前49天数据为训练集, 后10天数据为验证集, 即
选择平均绝对误差(mean absolute error, MAE)和平均绝对百分比误差(mean absolute percentage error, MAPE)为模型的评价指标, 计算如式(16)–式(17)所示:
| $ MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{{\hat y}_i} - {y_i}} \right|} $ | (16) |
| $ MAPE = \frac{{100{\text{%}} }}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{{\hat y}_i} - {y_i}}}{{{y_i}}}} \right|} $ | (17) |
在PyTorch框架下搭建实验所需模型, 采用Python 3.7进行程序开发. 实验中参数设置如下: 对交通流数据进行3级小波分解得到4组分量; 训练迭代50次; 批处理为64; 预测步长
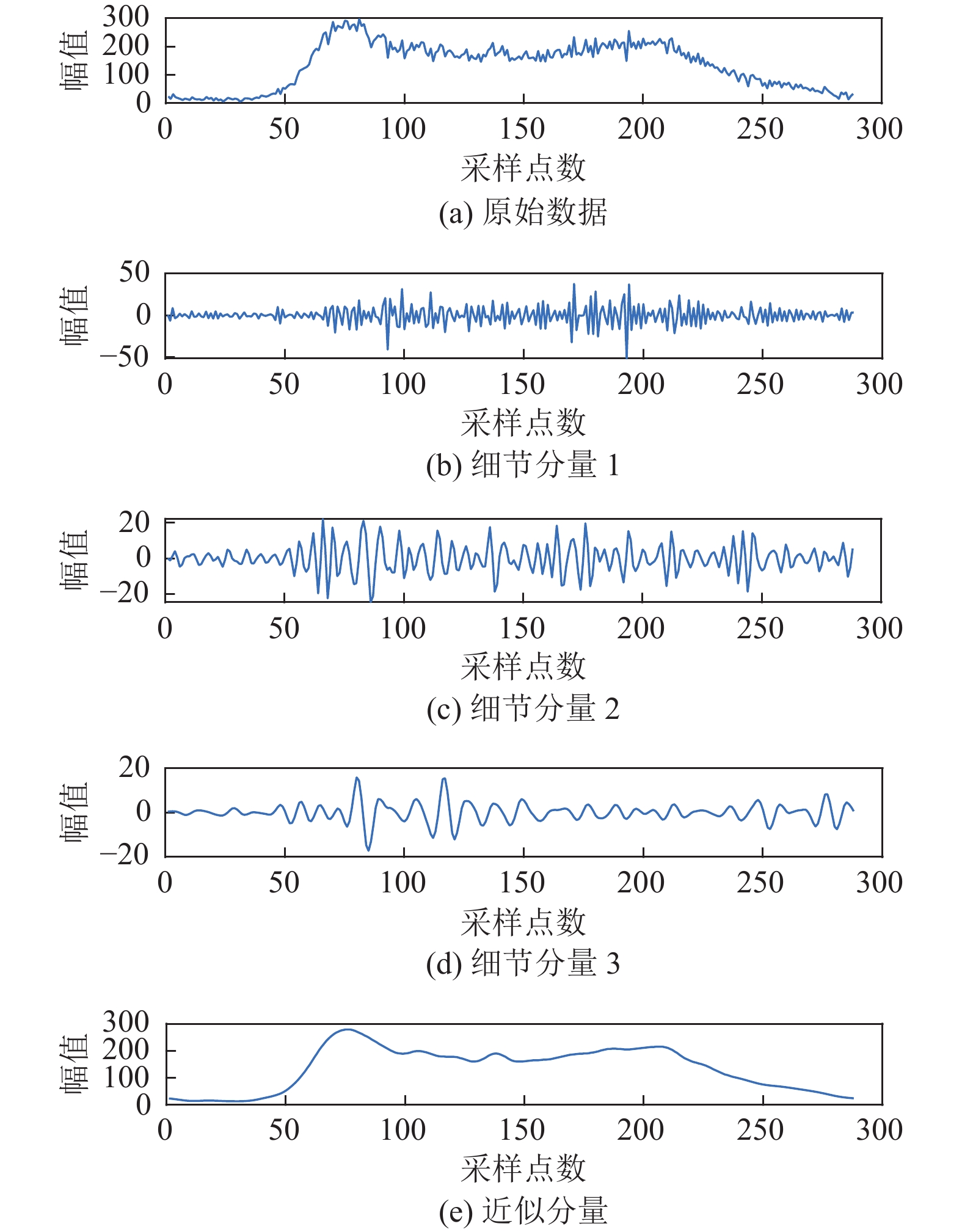
|
图 3 基于DWT分解的交通流子序列 |
4.3 模型性能分析
(1)不同模型预测结果对比
为验证模型的高效性, 选择ARIMA、小波神经网络(wavelet neural network, WNN)、GCN三种模型与本文模型进行预测结果对比分析. ARIMA模型通过前
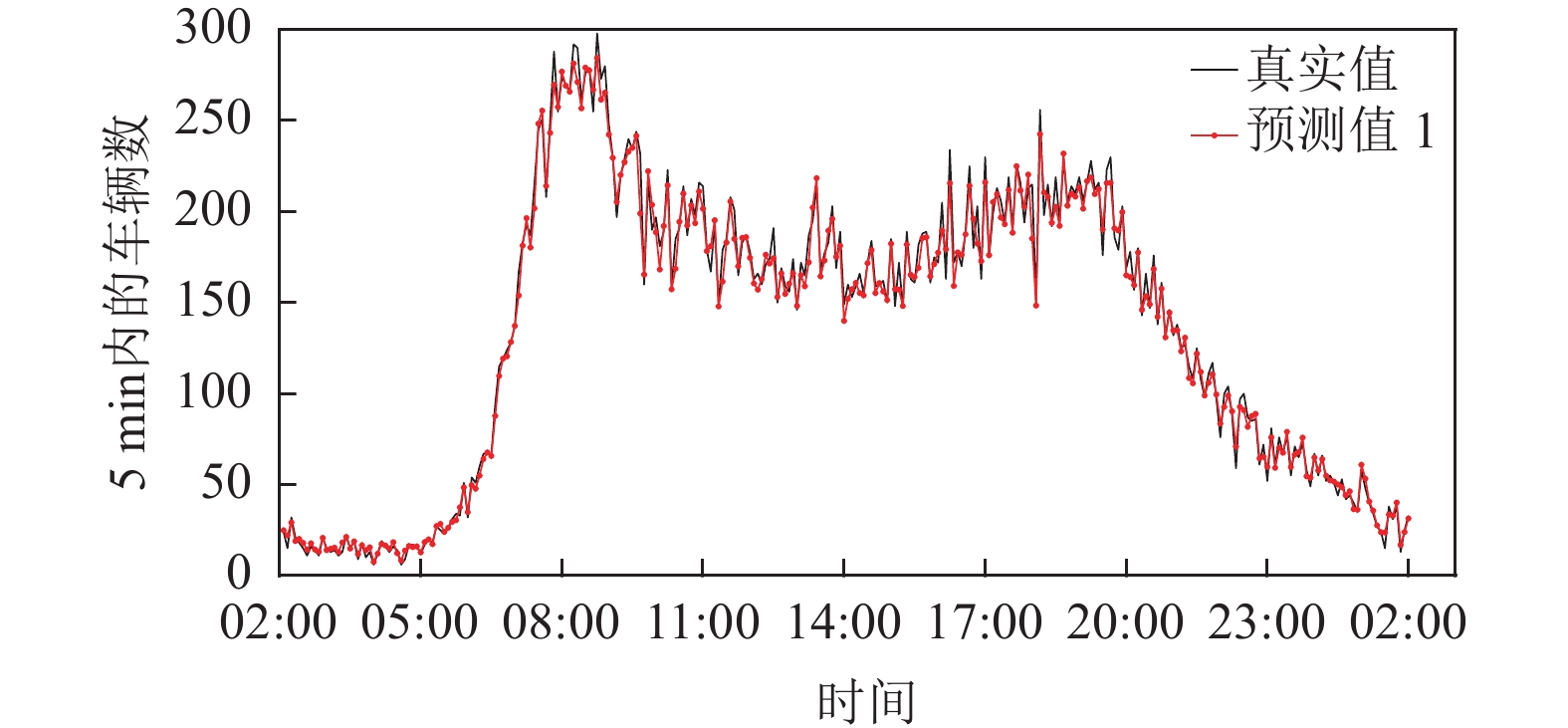
|
图 4 预测结果曲线 |
|
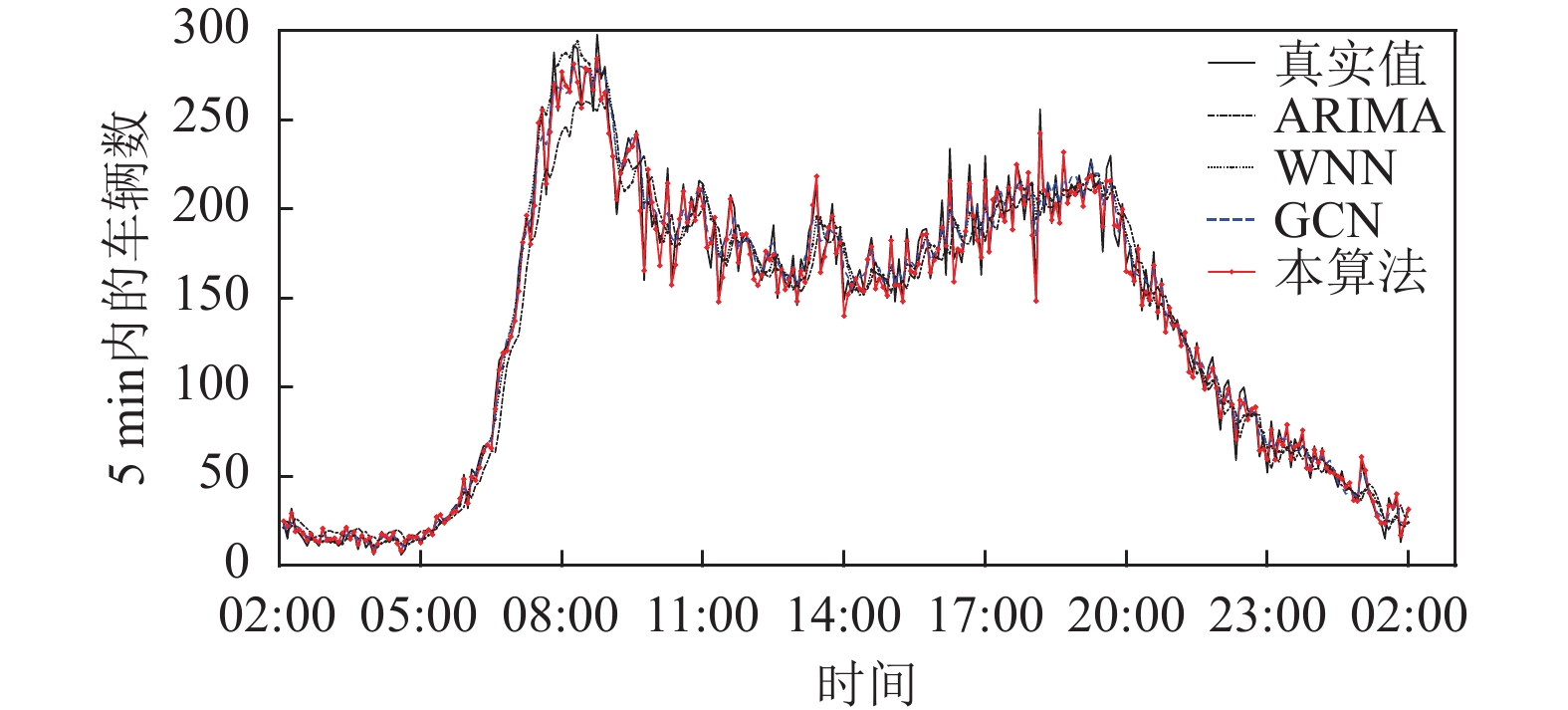
图 5 不同模型预测结果曲线对比 |
| 表 1 不同模型预测性能 |
根据图5和表1可知, ARIMA模型整体上反映了交通流数据的变化趋势, 但模型预测性能较差, 预测结果精度低; WNN模型相对于ARIMA预测精度得到了改善, 但仅考虑时间特性的模型不易挖掘交通流数据的空间特征; GCN模型利用拓扑图结构提取时空特性, 进一步强化了模型预测性能. 相比于ARIMA、WNN、GCN模型, DWT-GCN通过小波分解降低了交通流的非平稳性, 预测模型的MAE、MAPE平均降低57%和59%, 表明DWT-GCN模型预测性能好, 预测精度高, 能深度挖掘路网下交通流数据的时空特性, 反映真实的路网信息.
(2)参数分析
分析基于数据驱动的邻接矩阵
|
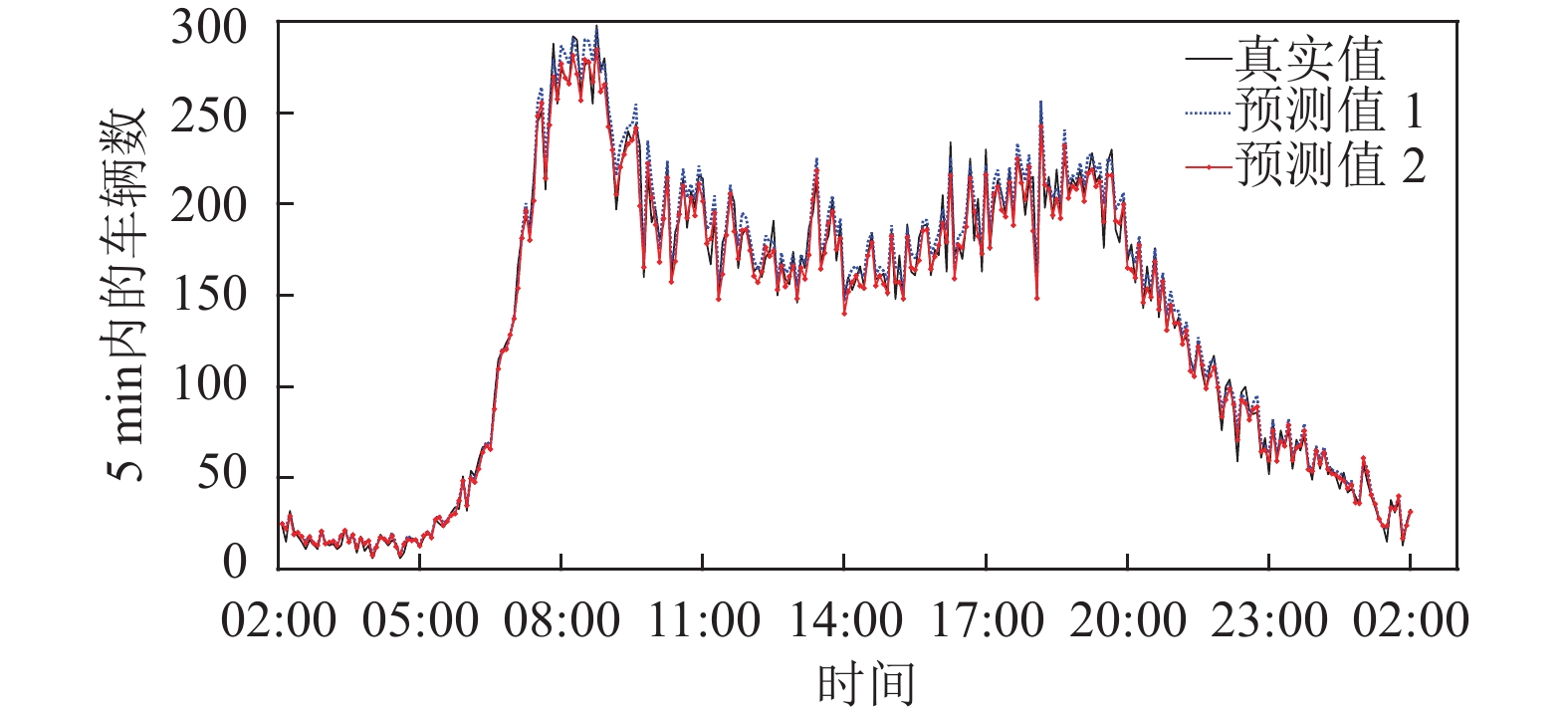
图 6 邻接矩阵修正前后预测结果曲线 |
邻接矩阵
| 表 2 不同阈值预测性能 |
在本文中, 当节点特征之间相关系数阈值取0.9时, 目标节点能够基于数据驱动选择更加邻近的路段节点, 进而聚合所选邻居节点的特征, 较大程度地提高模型的预测精度. 在PeMS数据集对应的实际路网中, 根据最佳阈值选取的邻近路段节点多数分布于目标路段节点的上下游, 根据空间距离和语义距离的分析, 相邻路段节点对具有明显邻近关系, 说明该模型预测结果符合实际路网情况, 模型能较好应用于真实场景的短时交通流预测.
5 总结本文提出了一种基于DWT-GCN的短时交通流预测模型, 该模型基于图神经网络处理非欧数据的天然优势, 通过小波分解与重构弱化交通流序列非平稳性, 并结合优化的邻接矩阵深度挖掘非欧交通流数据的时空特性, 提高了预测精度. 利用PeMS数据集的实测数据进行验证, 通过与其他基线模型预测结果对比可知, 本文提出的模型在短时交通流预测中具有较强的预测性能与可解释性. 未来可以将天气、节假日等影响交通流数据的外部因素通过注意力机制引入到模型中进一步提高模型的预测精度和泛化能力.
| [1] |
Tang SH, Kubo N, Kawanishi N, et al. Cooperative relative positioning for intelligent transportation system. International Journal of Intelligent Transportation Systems Research, 2015, 13(3): 131-142. DOI:10.1007/s13177-014-0091-2 |
| [2] |
杨东龙. 基于ARIMA模型的区间道路短时车流量预测研究. 电子设计工程, 2021, 29(13): 38-42. DOI:10.14022/j.issn1674-6236.2021.13.009 |
| [3] |
靳小飞. 基于ARFIMA混合模型的短时交通流预测研究[硕士学位论文]. 武汉: 华中科技大学, 2020.
|
| [4] |
张天逸, 孙毅然, 刘凡琪, 等. 基于K均值聚类算法与RBF神经网络的交通流预测方法. 智能计算机与应用, 2020, 10(8): 148-151. DOI:10.3969/j.issn.2095-2163.2020.08.035 |
| [5] |
申启东, 李文勇, 廉冠. 基于改进马尔可夫链的交通流预测方法. 黑龙江交通科技, 2021, 44(10): 178-181. DOI:10.16402/j.cnki.issn1008-3383.2021.10.092 |
| [6] |
罗向龙, 李丹阳, 杨彧, 等. 基于KNN-LSTM的短时交通流预测. 北京工业大学学报, 2018, 44(12): 1521-1527. |
| [7] |
李磊, 张青苗, 赵军辉, 等. 基于改进CNN-LSTM组合模型的分时段短时交通流预测. 应用科学学报, 2021, 39(2): 185-198. DOI:10.3969/j.issn.0255-8297.2021.02.001 |
| [8] |
殷礼胜, 孙双晨, 魏帅康, 等. 基于自适应VMD-Attention-BiLSTM的交通流组合预测模型. 电子测量与仪器学报, 2021, 35(7): 130-139. DOI:10.13382/j.jemi.B2003575 |
| [9] |
桂智明, 李壮壮, 郭黎敏. 基于ACGRU模型的短时交通流预测. 计算机工程与应用, 2020, 56(21): 260-265. DOI:10.3778/j.issn.1002-8331.1911-0371 |
| [10] |
王竟成, 张勇, 胡永利, 等. 基于图卷积网络的交通预测综述. 北京工业大学学报, 2021, 47(8): 954-970. DOI:10.11936/bjutxb2020120027 |
| [11] |
Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. arXiv: 1609.02907, 2016
|
| [12] |
Cui ZY, Henrickson K, Ke RM, et al. Traffic graph convolutional recurrent neural network: A deep learning framework for network-scale traffic learning and forecasting. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(11): 4883-4894. DOI:10.1109/TITS.2019.2950416 |
| [13] |
Zhang XY, Huang C, Xu Y, et al. Spatial-temporal convolutional graph attention networks for citywide traffic flow forecasting. Proceedings of the 29th ACM International Conference on Information and Knowledge Management. Online: ACM, 2020. 1853–1862.
|
| [14] |
Song C, Lin YF, Guo SN, et al. Spatial-temporal synchronous graph convolutional networks: A new framework for spatial-temporal network data forecasting. Proceedings of the 34th AAAI Conference on Artificial Intelligence. New York: AAAI, 2020. 914–921.
|
| [15] |
Zheng Q, Feng XX, Zheng HF. Robust prediction of traffic flow based on multi-task graph convolution network. 2020 IEEE 6th International Conference on Computer and Communications (ICCC). Chengdu: IEEE, 2020. 2053–2058.
|
| [16] |
Zhang N, Guan XF, Cao J, et al. Wavelet-HST: A wavelet-based higher-order spatio-temporal framework for urban traffic speed prediction. IEEE Access, 2019, 7: 118446-118458. DOI:10.1109/ACCESS.2019.2936938 |
| [17] |
倪汉杰, 蒋仲廉, 初秀民, 等. 基于DWT-LSTM的航道水位智能预测模型研究. 中国航海, 2021, 44(2): 97-102. DOI:10.3969/j.issn.1000-4653.2021.02.016 |
 2022, Vol. 31
2022, Vol. 31


