2. 中国科学院 空间应用工程与技术中心, 北京 100094;
3. 中国科学院 太空应用重点实验室, 北京 100094;
4. 中国科学院大学, 北京 100049
2. Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences, Beijing 100094, China;
3. Key Laboratory of Space Utilization, Chinese Academy of Sciences, Beijing 100094, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China
海上石油钻井是一个涉及多领域的复杂系统工程, 受地质环境等多种不可控因素的影响, 钻井过程中往往伴随着事故的发生, 如卡钻、井涌、井漏等, 严重影响了钻井作业的效率, 并且容易造成巨大的经济损失[1, 2]. 其中卡钻是在钻井过程中最常见的事故之一, 卡钻是指在钻井进程中, 由于钻柱在起下钻的过程中失去自由活动, 即钻井管柱不能上下活动也不能转动, 在井眼的某一井段遇到阻碍的钻井事故[3]. 相关钻井资料数据统计显示, 卡钻及卡钻事故的处理占整个钻井作业的40%–50%[4], 研究卡钻事故的预测方法对保障实际钻井作业的安全进行、降低施工成本具有十分重要的意义.
1 卡钻事故预测目前常用的卡钻事故预测方法大致可分为两类: (1)基于分类的方法; (2)基于时间序列信息的异常检测方法. 两类方法各有其优缺点.
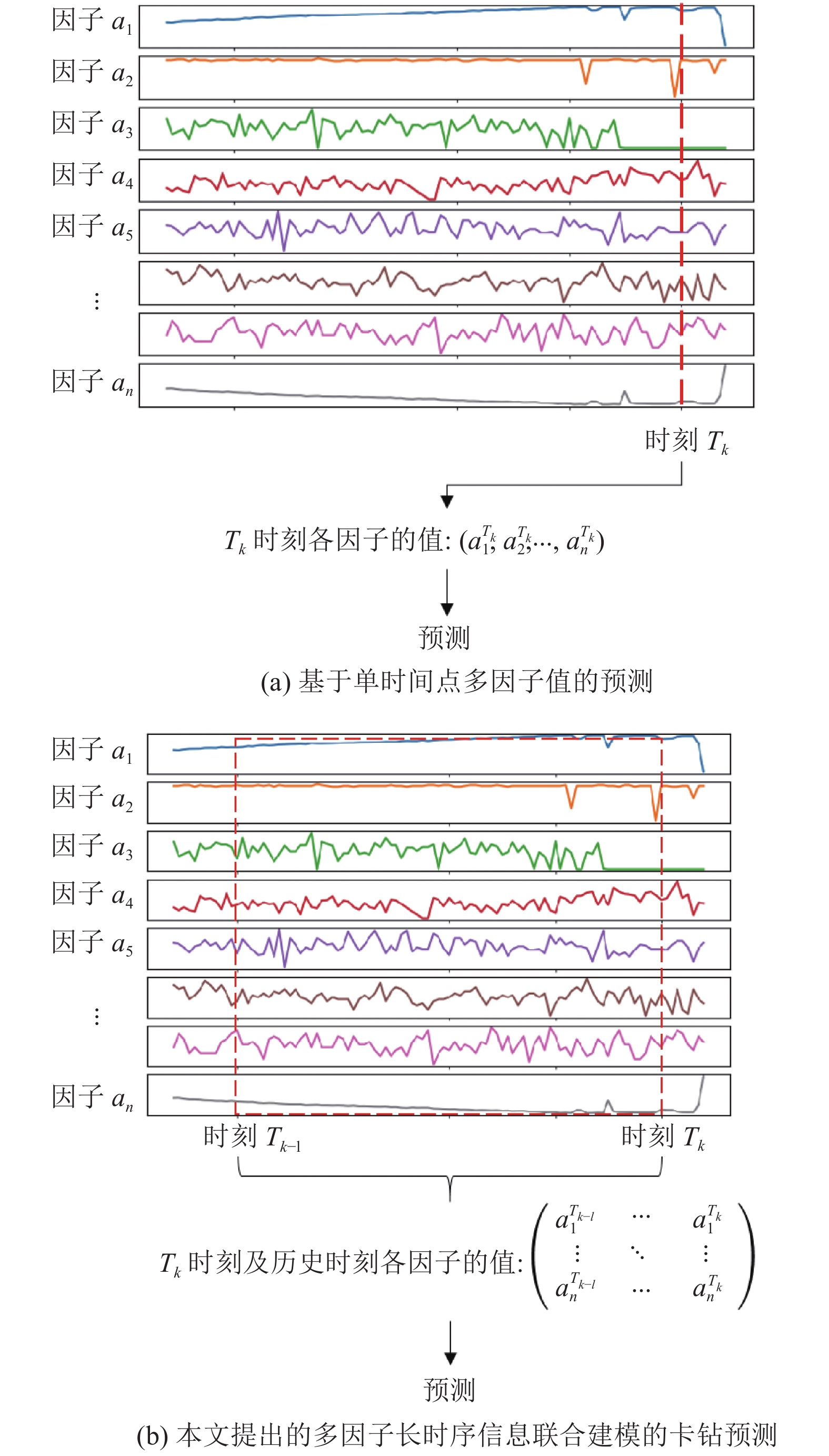
1.1 基于分类的方法基于分类的卡钻事故预测方法通过对当前单个时间点各个钻井平台监测因子的值进行正常/将发生事故的分类来预测卡钻事故, 如图1(a)所示. 刘建明等[4]通过主成分分析法(PCA)对井下测量工程参数进行降维处理, 利用随机森林(RF)模型对降维后的数据进行训练和测试, 判断是否发生卡钻事故. 苏晓眉等[5]利用PCA算法对冀东油田某井卡钻前的井下钻头实测工程参数进行降维处理, 再利用K-means聚类模型对降维后的数据进行训练测试, 该方法通过数据中心之间的距离判定卡钻事故是否发生. 刘光星等[6]分别利用单个/多个ARMA模型[7]对各个参数的监测数据进行分析, 预测卡钻事故的发生. BP神经网络[8]以及改进的BP神经网络[2]在卡钻事故预测中也被证明具有良好的效果.
1.2 基于时间序列信息的异常检测方法基于时间序列信息的异常检测方法的核心思想是对钻井平台各监测因子时序数据的异常变化进行捕捉并预警, 此类方法认为钻井事故发生前数据的异常变化可作为事故发生的征兆. Ben等[9]利用深度神经网络进行实时在线钻井状态的分类, 并使用一个离线的语义分割网络U-Net监测在线模型的表现, 当出现错分时, 对在线网络进行更新和训练, 最后使用专家经验在后处理过程对结果进行微调, 提出的方法在40口井, 3 000万条数据中, 取得了99%的分类精度. Zha等[10]仅利用井表面数据借助深度学习技术进行井下异常的判定与预测. Kaneko等[11]利用RNN构建网络用于捕捉时序上的数据关系, 在线性、非线性模拟仿真的数据中均表现较好, 其中与线性模拟数据上的测试结果相比, 非线性模拟数据上的测试结果稍差. 此外, 基于时间序列建模的异常检测方法在其他钻井事故如井喷、井漏等也有广泛的应用. Xie等[12]第一次结合大数据分析对井喷事故进行早期监测, 所研制的监测系统能够捕获和表示不同指标之间复杂的关系, 对捕捉到的异常进行预警, 现场工程师对这些消息做进一步的确认, 有效避免了事故的发生. Asarogiagbon等[13]设计了一个人工神经网络预测孔隙压力(pore pressure prediction)以提前预警钻井事故的发生.
|
图 1 基于单时间点和提出的多因子长时序信息联合建模方法的对比示意图 |
上述方法在卡钻事故预测中开展实验并取得了一定的效果, 但该类方法仍然存在两方面的局限性: (1)基于分类的方法大多数依赖于当前单个时间点钻井平台各个监测因子的值, 忽略了对监测参数长时序信息的利用, 钻井事故的发生不仅依赖于单个时间点上各监测参数的异常, 还依赖于一段时间内多个参数的变化趋势, 比如根据扭矩增加、转速降低可以有效预测卡钻事故的发生; (2)基于时间序列建模的异常检测方法将数据的异常变化视为钻井事故将要发生的征兆, 但由于地质等外在因素的不确定性, 数据的异常变化存在于整个钻井作业, 要从其中选择高置信度的异常, 需要专家人为进行筛选, 人工成本较高.
鉴于现有方法的缺点和不足, 本文拟设计一种综合考虑多因子长时序信息并且具有较高置信度预警的方法.
以卷积网络为代表的深度学习方法具有强大的空间信息建模能力, 在状态预测、故障诊断等领域中已取得了良好的效果[14-16]. 如吕召阳等[17]为克服流体力学领域中传统数学拟合方法不能很好地呈现系统非线性的问题, 基于卷积神经网络, 考虑机翼变攻角和浮沉建立了一种多变量多输出的模型, 实现了机翼气动系数的快速预测, 稳定性实验结果表明其建立的模型稳定性较好. 赵小强等[18]针对滚动轴承在强噪声环境和变工况下故障诊断效果不佳、泛化能力差的问题, 提出一种基于改进CNN的滚动轴承变工况故障诊断方法, 在凯斯西储大学轴承数据集上的变噪声实验表明其具有较好的抗噪性和更好的泛化能力. 韦延方等[19]针对直流电网故障检测正确率低、鲁棒性弱的问题, 提出了一种基于卷积神经网络(CNN)与深度卷积对抗生成网络(DCGAN)的柔性直流配电网故障检测方法, 试验结果表明其在不同工况下具有较高的监测精度.
基于上述观察与思考, 本文提出了一种多因子长时序信息联合建模的深度卷积卡钻预测方法(CNN-MFT), 本文的主要贡献如下: (1)利用卷积的平面空间信息建模能力, 同时对多个钻井监测因子及其时序信息进行联合建模; (2)为了适应性地捕捉复杂环境下不同因子对卡钻事故预测起到的关键作用, 提出的方法使用自注意力机制对长时序信息进行建模; (3)学习卡钻事故发生前的征兆信息, 能够进行高置信度的预警, 有效降低了对专家人工筛选预警点提高预警置信度后处理手段的依赖; (4)在2021年4–5月某海上钻井平台20万组实际监测数据上的测试表明了本文提出方法的有效性, 提出的方法取得了93%以上的卡钻事故预测精度.
2 CNN-MFT方法深度卷积网络具有关联多维空间数据的特性, 自注意力机制能够建模长序列的信息, 将二者结合起来应用于卡钻事故预测能够将多个钻井平台监测因子的长时序信息进行联合建模, 进行准确的卡钻事故预测.
CNN-MFT模型的整体结构如图2所示, 主要包括: (1)训练样本构建; (2)自注意力模块; (3)卷积网络构建; (4)分类器构建; (5)损失函数构造.

|
图 2 CNN-MFT网络结构示意图 |
2.1 训练样本构建
用tar(b)和tar(e)表示卡钻事故φ发生的开始时间点和结束时间点, 该区间内的数据特征为网络学习的目标特征, A={a1, a2, …, an}表示钻井平台作业中监测的n个因子, 对于当前时间点Tk, 提出的方法对多个因子的长时序信息进行联合建模, 时序长度为l的输入样本可用矩阵Hk表示:
| $ \mathop H\nolimits_k = \left( {\begin{array}{*{20}{c}} {\mathop a\nolimits_1^{\mathop T\nolimits_{k - l} } }& \cdots &{\mathop a\nolimits_1^{\mathop T\nolimits_k } } \\ \vdots & \ddots & \vdots \\ {\mathop a\nolimits_n^{\mathop T\nolimits_{k - l} } }& \cdots &{\mathop a\nolimits_n^{\mathop T\nolimits_k } } \end{array}} \right) $ | (1) |
则该样本对应标注向量为:
| $ \mathop Y\nolimits_{\mathop H\nolimits_k } = \left( {\begin{array}{*{20}{c}} {\mathop y\nolimits^{k - l} }& \cdots &{\mathop y\nolimits^k } \end{array}} \right) $ | (2) |
本文提出的CNN-MFT模型的主要目的是利用多因子的长时序历史信息提高模型对当前时刻预测的准确性, 因此在本文中:
| $ \mathop Y\nolimits_{\mathop H\nolimits_k } = \mathop y\nolimits^k $ | (3) |
即选用数据集对当前时刻Tk的标注作为训练样本Hk的标注信息.
2.2 自注意力模块自注意力机制目前在计算机视觉领域、自然语言处理领域内被广泛应用, 其最大的优点是可以对长序列信息进行建模, 并且比RNN、LSTM能记忆更长序列的信息, 且较容易训练.
CNN-MFT中使用的自注意力结构为单层的自注意力, 其主要目的是对钻井平台每个监测因子的长时序信息进行建模. 对每个训练样本Hk, 第i个因子的时序信息Xi为:
| $ \mathop X\nolimits_i = \left( {\begin{array}{*{20}{c}} {\mathop a\nolimits_i^{\mathop T\nolimits_{k - l} } }& \cdots &{\mathop a\nolimits_i^{\mathop T\nolimits_k } } \end{array}} \right) $ | (4) |
使用3个可学习的权重矩阵获取查询向量Q, 键向量K和值向量V:
| $\left\{ { \begin{gathered} Q = \mathop W\nolimits^q \cdot \left( {\begin{array}{*{20}{c}} {\mathop a\nolimits_i^{\mathop T\nolimits_{k - l} } }& \cdots &{\mathop a\nolimits_i^{\mathop T\nolimits_k } } \end{array}} \right) \\ K = \mathop W\nolimits^k \cdot \left( {\begin{array}{*{20}{c}} {\mathop a\nolimits_i^{\mathop T\nolimits_{k - l} } }& \cdots &{\mathop a\nolimits_i^{\mathop T\nolimits_k } } \end{array}} \right) \\ V = \mathop W\nolimits^v \cdot \left( {\begin{array}{*{20}{c}} {\mathop a\nolimits_i^{\mathop T\nolimits_{k - l} } }& \cdots &{\mathop a\nolimits_i^{\mathop T\nolimits_k } } \end{array}} \right) \\ \end{gathered} } \right.$ | (5) |
其中, Wq, Wk, Wv是权重矩阵, 然后利用查询向量Q和键向量K进行注意力矩阵A的计算:
| $ A = \left( {\begin{array}{*{20}{c}} {{a_{11}}}& \ldots &{{a_{1l}}} \\ \vdots & \ddots & \vdots \\ {{a_{l1}}}& \cdots &{{a_{ll}}} \end{array}} \right) = \mathop K\nolimits^{\rm T} \cdot Q $ | (6) |
其中, KT是键向量K的转置, 获得注意力矩阵之后与值向量V结合可以获得加入注意力之后的新特征.
| $ O = V \cdot A $ | (7) |
利用自注意力机制对钻井监测因子数据的时序信息建模有两个优点: 一方面其可以对长时序的信息进行建模, 同时考虑全时序的信息, 能够获得较为全局的视野; 另一方面是其在考虑时序信息的同时也能够关注每个时间点的值的信息.
2.3 卷积网络本文提出的CNN-MFT方法中, 构建卷积网络的主要目的是利用卷积可以对二维空间信息进行建模的特性对多个钻井因子的时序信息进行联合建模, 其网络结构如图2所示. 对输入的任意特征矩阵O, 网络的学习目标可以表示为:
| $ P({\textit{confidence}}, type, \mathop T\nolimits_p ) = \Psi (O) $ | (8) |
其中, Ψ为网络学习的目标函数, P为网络的预测输出, 包括预警的置信度confidence, 预警的事故类型type以及预警的时间点Tp.
网络主要由多个卷积层、池化层及激活函数ReLU组成. 卷积层的输入输出都是一个多维的矩阵, 其根据输入的多维空间的特征矩阵中局部的数据来决定输出空间中对应位置的值, 该特性赋予了卷积同时对多维空间数据进行联合建模的能力, 其可变的参数为卷积核大小、步长、是否padding等, 在此用ℓi表示第i层的卷积, 则其输入输出可表示为:
| $ \mathop O\nolimits_i = \mathop \ell \nolimits_i (\mathop O\nolimits_{i - 1} ) $ | (9) |
其中, Oi, Oi–1为该层卷积的输入和输出矩阵.
对于m层的卷积网络的输入和输出可表示为:
| $ \mathop O\nolimits_m = \mathop \ell \nolimits_1 \otimes \mathop \ell \nolimits_2 \otimes \cdots \otimes \mathop \ell \nolimits_i \otimes \cdots \otimes \mathop \ell \nolimits_m (O) $ | (10) |
其中, O为多层卷积网络的输入矩阵, 即注意力模块的输出, Om为经多层卷积提取后输出的特征矩阵, 其中包含了网络学习到的与事故强相关的异常数据的特征信息, 利用此信息可对事故是否将要发生进行有效的预测.
为了增加特征的学习速度, 保持输入输出空间数据分布的一致性, 在每层卷积之后会增加一个单独的激活函数层ReLU及batch normalization (BN)层, 此时ℓi层卷积的输入和输出可表示为:
| $ \mathop O\nolimits_i^{'} = BN\left( {{Re} {{LU}}\left( {\mathop \ell \nolimits_i \left( {\mathop O\nolimits_{i - 1} } \right)} \right)} \right) = \mathop \ell \nolimits_i^{'} (\mathop O\nolimits_{i - 1} ) $ | (11) |
对应m层卷积网络的输入输出可表示为:
| $ \mathop O\nolimits_m^{'} = \mathop \ell \nolimits_1^{'} \otimes \mathop \ell \nolimits_2^{'} \otimes \cdots \otimes \mathop \ell \nolimits_i^{'} \otimes \cdots \otimes \mathop \ell \nolimits_m^{'} (O) $ | (12) |
分类器根据卷积网络输出的特征进行分类, 它由多层的全连接层构成, 是一个神经网络分类器, 其根据卷积层网络的输出特征Om'对可能发生的钻井事故进行预测, 包括卡钻事故发生的置信度及是否会发生卡钻事故.卷积层网络输出的特征的形状为C×H×W, 其中, C为特征矩阵的通道数, H和W分别为特征矩阵的高和宽, 由于全连接层的输入是一维的向量, 在此网络中对卷积层输出的特征Om'进行如下操作:
| $ M = Ave\_Pool(\mathop O\nolimits_m{'} ) $ | (13) |
其中, Ave_Pool为平均池化, 即对特征矩阵Om'的每个通道的所有值取平均, 将特征矩阵转换为C×1的一维向量M, 输入到全连接层中进行预测:
| $ p({\textit{confidence}}, type) = f(M) $ | (14) |
转换之后的特征向量输入分类器, 输出预测结果p, 其中confidence和type表示预测的概率分布, f表示分类器学习到的拟合函数.
2.5 损失函数CNN-MFT网络的损失函数采用交叉熵函数, 其主要作用是衡量模型的预测与真实标注之间的距离或者模型预测的概率分布与真实的概率分布之间的差距, 在此采用Pi=(pi0, pi1, …, pik)表示模型对第i个样本预测的概率分布, 其中k表示预测事故类型数量, 在本文中k的值为1. Yi=(yi0, yi1, … , yik)表示第i个样本真实的概率分布, 此处的概率分布表示当前样本预测为正常、发生卡钻的概率. 则网络的损失函数可表示为:
| $ L = - \frac{1}{N}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^k {\mathop y\nolimits_i^j \log \mathop p\nolimits_i^j } } $ | (15) |
其中, N表示样本的总数量, 利用此损失函数可以衡量在每次训练过程中模型的预测与学习目标之间的差距, 根据此种差距更新网络的参数逼近学习目标, 最终获得能够有效预测钻井事故的模型.
CNN-MFT模型不同层网络的具体参数配置如表1所示.卷积层的卷积核大小为3×3, 池化层的卷积核大小为2×2, 即输入到输出降采样两倍, 两层全连接层的神经元个数分别为96和64, 正则化层的主要作用是通过在学习时以一定的概率随机丢弃神经元使得网络在学习时不依赖于某个或某几个神经元的权重信息, 从而避免过拟合, 本文中神经元的丢弃率为0.5, 在卷积层和第一层全连接层之后, 连接激活函数ReLU, 用于学习当前信息是否向下流通.
| 表 1 不同网络层具体参数配置 |
3 实验 3.1 实验数据
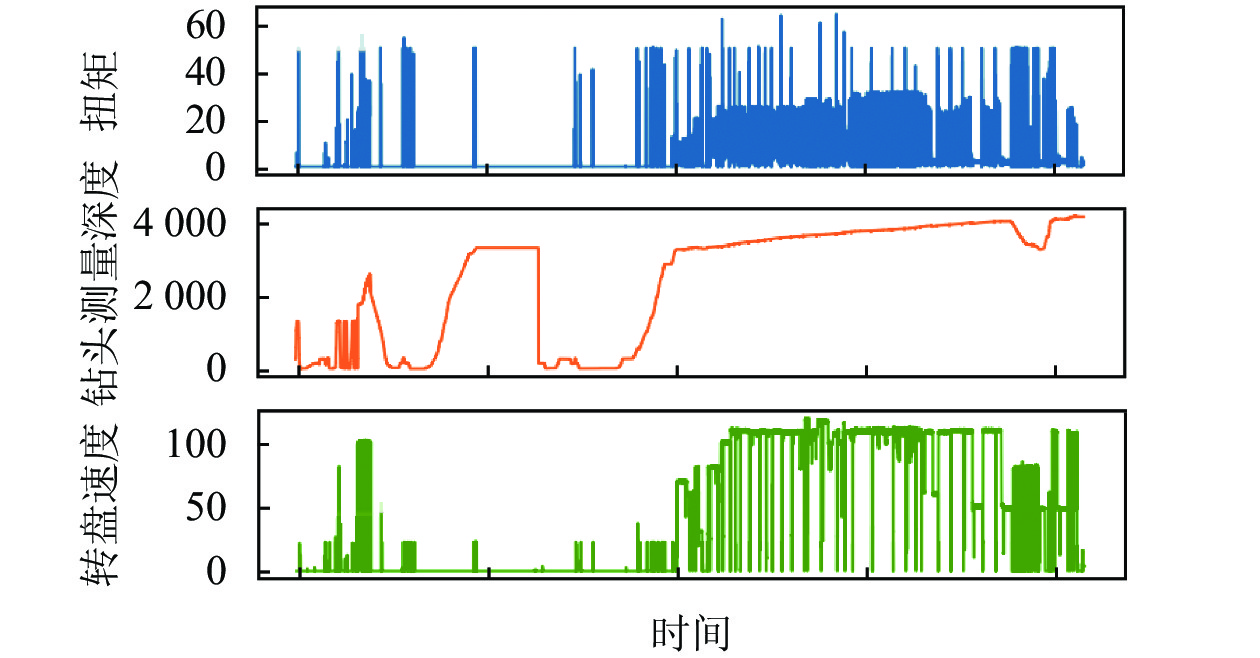
本文选用的为某海上钻井平台某区域近20天的实际监测数据, 开始时间为2021年4月18号6点47分18秒, 结束时间为2021年5月8日17点40分22秒, 包括泥浆池体积、泥浆平均流入流量、返出、泵压、大勾高度、入口泥浆平均温度、泥浆池体积变化、大勾悬重、扭矩、转盘转速、返出深度、钻头测量深度、钻压等13个监测因子, 各因子的统计信息如表2所示, 主要包括最大值、最小值、平均值和标准差. 其中值域范围最大的为泥浆平均流入流量, 最大值为5 024.07, 最小值为0; 值域范围最小的为钻压, 最大值为15.1, 最小值为0; 平均值最大的3个因子为返出深度、钻头测量深度和泥浆池体积变化, 标准差最大的3个因子为钻头测量深度、返出深度和泥浆平均流入流量, 其主要原因可能由于卡钻事故在某一段深度内频繁发生, 现场施工进行频繁起下钻, 造成该因子数据波动较大. 部分监测因子的时序变化如图3所示, 数据整体呈现出高动态、非周期性等特点.
| 表 2 钻井监测数据各因子统计信息 |
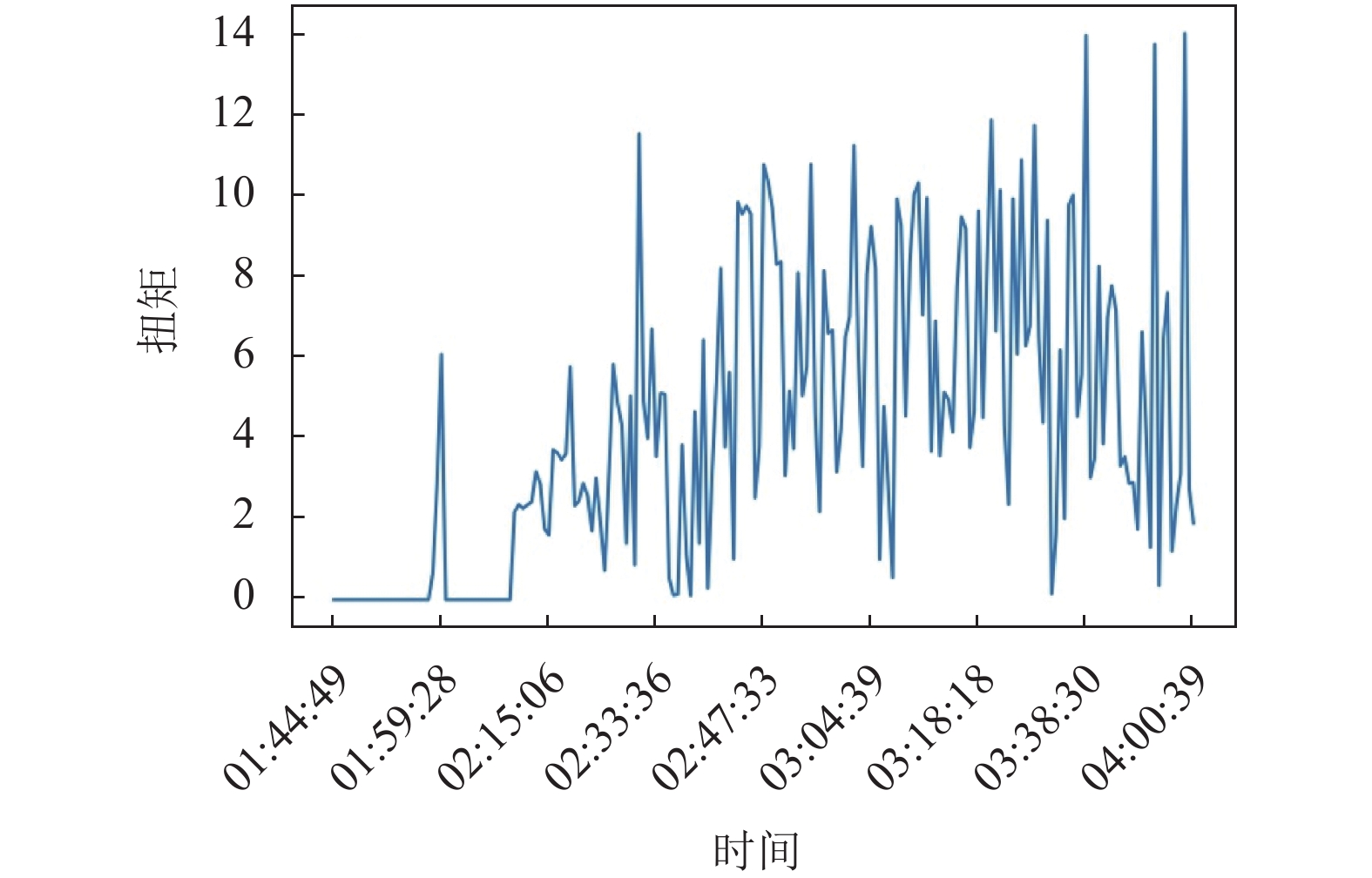
数据集任意时刻Tk对应一个标注, 其根据该钻井平台实际工作日志对卡钻事故的记录生成, 分别为正常数据(用0表示, 为负样本), 和将要发生卡钻事故的数据(用1表示, 为正样本), 其中日志记录包含每次事故发生的开始时间和结束时间, 图4、图5分别展示了日志记录的某次卡钻事故(2021年4月21日4点0分0秒)前扭矩和钻压的数据变化, 从图中可以看出, 事故发生前扭矩和钻压整体逐渐升高, 其中扭矩最高为14左右, 钻压最高为6左右.
|
图 3 数据集部分因子时序数据可视化 |
|
图 4 卡钻事故发生前扭矩数据的变化 |
数据集共包含208 504组数据, 每组数据包含13个特征, 整体正负样本分布呈不均衡状态, 其中正样本为19 300, 负样本为18 920, 在整个数据区间多数为正常数据, 少数为将要发生卡钻事故的数据.
3.2 对比方法与实验配置为充分验证本文提出算法的效果, 本节实验在相同条件下分别使用50%和70%的数据集训练不同方法, 并对比其实验结果. 本文主要选用了SVM-rbf、SVM-linear、SVM-poly、RF (随机森林)、PCA-SVM-rbf、PCA-SVM-linear、PCA-SVM-poly、PCA-RF等8种方法作为本节实验的对比方法, 它们是目前钻井事故预测中使用最多的几种方法.其中PCA为主成分分析方法, 是一种数据降维方法, 其在事故预测方法中常被用于剔除原始数据的冗余信息, 提高算法的学习效率, 在本节实验中所有使用PCA的对比方法中均取降维后的第一个主成分用于预测卡钻事故. -rbf、-linear、-poly分别代表SVM中使用的高斯核, 线性核和多项式核.

|
图 5 卡钻事故发生前钻压数据的变化 |
模型训练的初始学习率为0.000 5, 每次训练加载的样本数量为1 024, 训练的迭代次数为500, 网络的预测结果经过Softmax函数之后输出的预测向量中, 取概率最高的位置对应的类别作为预测类型(正常/卡钻). PCA、SVM-rbf、SVM-linear、SVM-poly、RF方法基于Python扩展包Sklearn实现, CNN-MFT基于PyTorch框架实现, 方法的训练和测试在1块Tesla V100上进行, 显存为32 GB, CPU的型号为Intel® Xeon® Gold 5118 CPU@2.3 GHz, 内存总量为187 GB.
3.3 评价指标本文以通用的准确率(ACC)和ROC曲线[3]作为卡钻事故预测效果的评价指标, 准确率指的是所有测试样本中被正确分类样本的比例; ROC曲线的横轴为假阳率(FPR), 含义为错误分类的正样本数量与总负样本数量的比值, 纵轴为真阳率(TPR), 含义为正确分类的正样本数量与总正样本数量的比值, ROC曲线与坐标轴围成的面积(AUC)能够反映模型在不同阈值下的卡钻事故预测性能, 此外本文还使用不同方法在训练数据集上训练一次耗费的时间来评价不同方法的时间成本.
| $ ACC=\frac{正确分类的样本数量}{测试数据样本总数量} $ | (16) |
| $ FPR=\frac{错误分类的正样本数量}{负样本总数量} $ | (17) |
| $ TPR=\frac{正确分类的正样本数量}{正样本总数量} $ | (18) |
不同方法使用50%的数据集数据训练, 在剩余50%数据上测试结果的准确率(ACC)、ROC曲线及AUC分别如表3, 图6所示.
| 表 3 50%数据训练不同方法卡钻事故预测结果对比 |

|
图 6 50%数据训练不同方法的ROC曲线 |
根据准确率评价指标, 本文提出的方法CNN-MFT取得了最高的准确率为0.934 0, 分别比SVM-rbf、SVM-linear、SVM-poly、RF、PCA-SVM-rbf、PCA-SVM-linear、PCA-SVM-poly、PCA-RF方法的准确率高出了77.72%、8.39%、19.64%、2.61%、2.50%、70.96%、20.29%、2.20%, 说明了本文提出的方法的有效性, 能够很好地预测卡钻事故的发生. 此外在SVM系列方法中采用线性核和多项式核要比采用高斯核的效果好, 这说明了在实际钻井作业中, 监测数据的分布并非是类似高斯分布等相对较均匀的分布, 也说明了钻井事故预测的复杂性. 对比不同方法使用PCA主成分分析方法降维数据前后准确率的变化可知, SVM-rbf方法在使用了PCA降维方法前后准确率变化最明显, 准确率由0.156 8增加到了0.909 0, 这说明了PCA方法对数据降维能够有效剔除数据中的冗余信息和干扰信息, 证明了PCA方法对钻井事故预测的有效性. 而SVM-linear和SVM-poly方法在使用PCA方法后, 准确率有所下降, 这主要是由于线性核和多项式核拟合的是相对较为复杂的函数, 将数据维度降为1会对此类方法的性能有所损害.
根据AUC评价指标, 在所有方法中随机森林RF方法取得了最高的AUC为0.592 0, 不同方法之间的AUC差别较小, 其中AUC指标最低的是SVM-rbf方法为0.423 2. 本文提出的CNN-MFT方法的AUC指标为0.576 8, 次于随机森林RF方法和PCA-SVM-linear方法.在使用PCA降维之后, SVM-rbf方法和SVM-linear方法的AUC指标增高, 分别由0.423 2增加至0.478 7, 由0.474 9增加至0.5919; 然后SVM-poly方法和随机森林RF方法在使用PCA降维之后, AUC指标均降低, 分别由0.538 1降低至0.449 8, 由0.592 0降低至0.5626. 此外, 由图6所示的ROC曲线可以看出, 多数方法的曲线在不同节点的波动性较大, 说明其在某些情况下效果较好, 某些数据情况下效果较差, 而本文提出的CNN-MFT方法的ROC曲线整体呈现较为稳定的趋势, 说明其在不同数据情况下算法的稳定性好.
不同方法使用50%的训练集训练一次耗费的时间如表3所示, 不同方法训练一次方法耗费的时间较短, 其中随机森林RF方法训练一次的时间最短为0.03 s, 本文提出的CNN-MFT方法在数据集上训练一次耗费的时间最长为3.8 s, 按照训练一次耗费时间长短由小到大排序为RF、PCA-RF、PCA-SVM-linear、PCA-SVM-poly、SVM-linear、PCA-SVM-rbf、SVM-poly、SVM-rbf、CNN-MFT. 本文提出的CNN-MFT方法训练时间较长的主要原因是每次预警时即要输入当前时刻数据又要输入其历史时序的数据, 输入的数据量相对其他方法要大的多. 此外使用PCA方法降维后不同方法的训练时长均减少, 主要是由于降维后整体用于训练的数据量大幅减少, 数据维度由13降为1.
3.4.2 70%数据训练实验结果分析不同方法使用70%的数据集数据训练, 在剩余30%数据上测试结果的准确率(ACC)、ROC曲线及AUC分别如表4, 图7所示.
根据ACC评价指标, 本文提出的方法CNN-MFT模型的准确率最高为0.9320, 分别比SVM-rbf、SVM-linear、SVM-poly、RF、PCA-SVM-rbf、PCA-SVM-linear、PCA-SVM-poly、PCA-RF的准确率高出了77.44%、23.08%、14.51%、2.28%、2.26%、19.3%、23.29%、2.09%, 说明了本文提出的方法的有效性, 能够很好地预测卡钻事故的发生. 对比不同方法使用PCA主成分分析方法降维数据前后准确率的变化可知, 多数方法在使用PCA降维后, 准确率提高, 其中SVM-rbf方法的准确率增加最明显, 由0.157 6增加到了0.909 4, 而SVM-poly方法的准确率在使用PCA降维之后降低, 由0.786 9降低为0.699 1.
| 表 4 70%数据训练不同方法卡钻事故预测结果对比 |
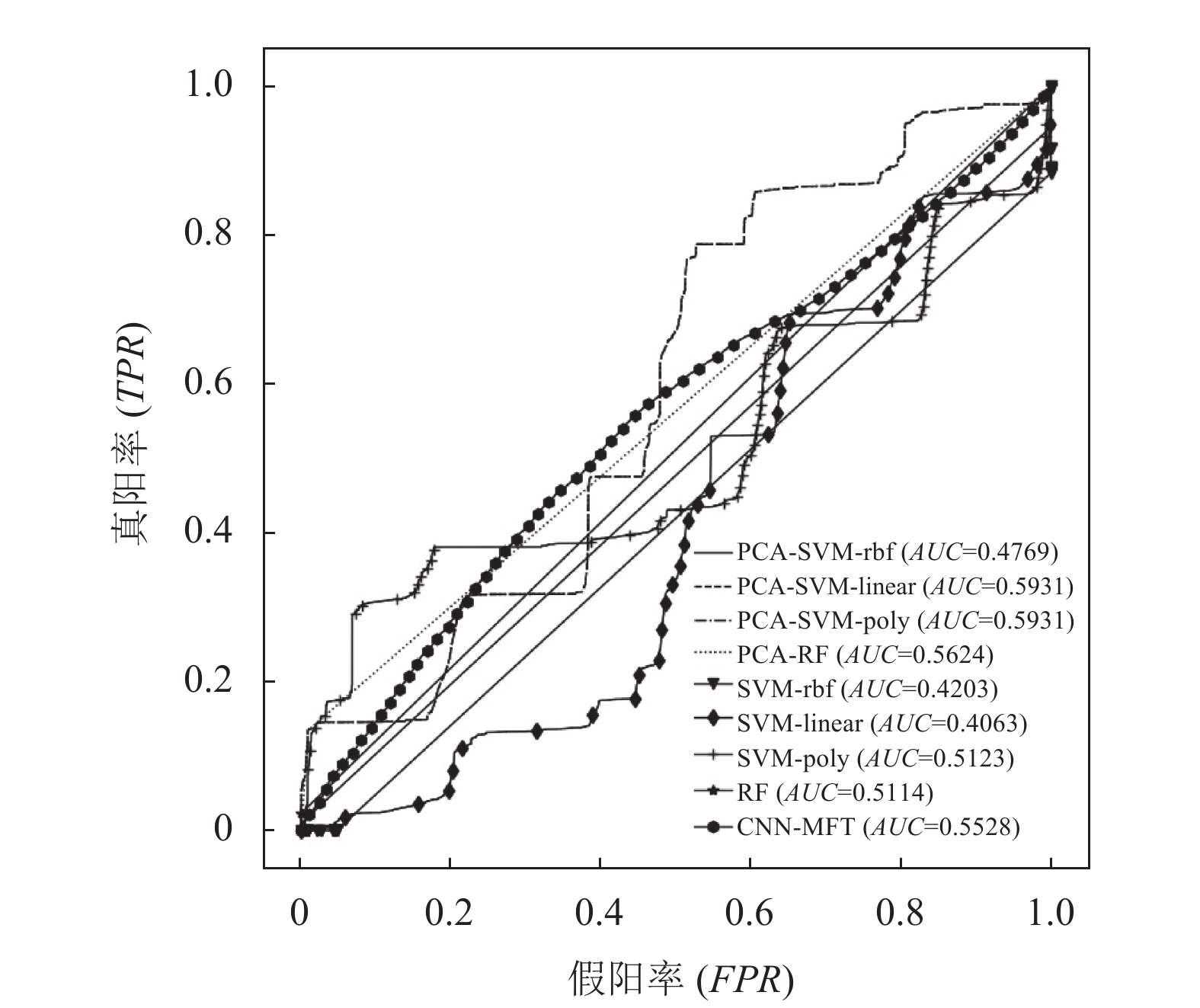
|
图 7 70%数据训练不同方法的ROC曲线 |
根据AUC评价指标, 在所有方法中PCA-SVM-linear和PCA-SVM-poly方法的该指标值最高均为0.593 1, SVM-linear最低为0.406 3, 本文提出的CNN-MFT方法的AUC指标为0.552 8, 次于PCA-SVM-linear、PCA-SVM-poly、PCA-RF. 但根据图7不同方法的ROC曲线可以看出, CNN-MFT方法的曲线整体呈较为稳定的上升趋势, 这说明在不同情况下该算法的稳定较好.
不同方法使用70%数据集数据训练一次耗费的时间如表4所示, 其中, 随机森林RF算法耗费的时间最短, 为0.044 s, CNN-MFT方法耗费的时间最长, 为5.038 s. SVM-rbf、SVM-linear、SVM-poly方法在使用PCA方法降维后, 整体训练一次耗费的时间降低, 而随机森林RF方法, 在使用PCA方法降维后时间变长, 主要是由于PCA对数据降维时耗费的时间较长.
3.4.3 50%和70%数据训练不同方法结果对比根据ACC评价指标, 对比不同方法使用50%和70%数据训练的测试结果, 多数方法卡钻事故预测的准确率下降, 包含SVM-linear、SVM-poly、PCA-SVM-poly、PCA-RF、CNN-MFT, 这说明当不改变模型的参数配置, 仅增加训练数据的规模时, 学习正常数据和卡钻事故发生前的异常数据之间边界变得困难.
根据AUC评价指标, 大部分方法的指标值降低, 包括SVM-rbf、SVM-linear、SVM-poly、RF、PCA-SVM-rb、PCA-RF、CNN-MFT, 但整体AUC指标的变化不大.
与使用50%数据集数据训练不同方法, 在使用70%数据集数据训练耗费的时间更长, 主要是由于整体训练的数据增多, 造成训练时间增长.
3.4.4 消融实验为了充分理解本文提出的方法中自注意力模块和CNN模块对卡钻事故预测的作用, 在使用50%数据训练的情况下进行了消融实验, 实验结果如表5所示.在仅使用CNN模块时, 提出的CNN-MFT网络的分类准确率为0.902 8, AUC指标为0.533 6, 结合表3结果可知, 其卡钻事故预测性能仍高于大部分对比方法, 说明了CNN模块对卡钻事故的准确预测有着重要的作用; 当自注意力模块和CNN模块同时使用时, CNN-MFT网络的分类准确率为0.934 0, AUC指标为0.576 8, 相较于仅使用CNN模块的预测结果, 分类准确率提升了0.0312, AUC指标提升了0.043 2, 分析其原因主要在于自注意力模块不可替代的长时序信息建模能力, 虽然多层的CNN也可以对长时序的信息进行建模, 但是在层与层之间存在一定的信息损失, 使用自注意力模块能更好地提升网络对于不同因子长时序信息的利用, 有效提升网络的卡钻事故预测效果.
| 表 5 使用50%数据训练消融实验结果对比 |
4 结论与展望
为了解决海上石油卡钻事故预测精度低、稳定性差、现有卡钻事故预测方法多依赖于单时间点不同监测因子的值进行预测, 未充分利用钻井监测数据长时序信息的问题, 本文提出一种多因子长时序信息联合建模的深度卷积卡钻预测方法(CNN-MFT), 通过充分利用钻井监测数据的长时序信息, 克服现有的依赖于单个时间点各因子值进行事故预测方法中事故特征缺失问题; 以多层卷积网络提取录井监测数据的多维空间信息, 结合自注意力模块进行多因子长时间序列的联合建模, 实现卡钻事故的高置信度预测, 并得出如下结论:
(1) CNN-MFT模型在使用50%和70%数据训练的情况下均取得了最高的预测准确率, 分别为0.934 0和0.932 0, 能有效地预测卡钻事故的发生;
(2) CNN-MFT方法在不使用降维方法的情况下获得了最高的准确率, 说明了其在复杂的钻井平台监测数据中具有良好的多因子长时序信息建模能力及学习能力, 证明了该方法的有效性;
(3) 综合实验结果, 本文提出的CNN-MFT方法在预测准确率上优于目前常用的SVM-rbf、SVM-linear、SVM-poly、RF、PCA-SVM-rbf、PCA-SVM-linear、PCA-SVM-poly、PCA-RF卡钻预测方法, 且方法的稳定性较强, 能够为实际钻井平台的卡钻事故预测提供技术支撑.
本文的研究尚存在一定的局限性, 虽然本文提出的方法具有较高的准确率, 但是其ROC曲线围成的面积AUC仍有一定的提升空间, 此外由于真实钻井平台卡钻事故监测数据是一个正负样本不平衡的数据, 从此角度出发研究平衡样本的算法, 进一步提升卡钻事故预测模型的性能也是一个有价值的研究方向.
| [1] |
苏兴华, 孙俊明, 高翔, 等. 基于GBDT算法的钻井机械钻速预测方法研究. 计算机应用与软件, 2019, 36(12): 87-92. DOI:10.3969/j.issn.1000-386x.2019.12.014 |
| [2] |
刘海龙, 李彤, 张奇志. 基于自适应遗传算法改进的BP神经网络卡钻事故预测. 现代电子技术, 2021, 44(15): 149-153. DOI:10.16652/j.issn.1004-373x.2021.15.030 |
| [3] |
赵志明, 邓慧静, 刘斌. 石油钻井工程事故预警研究进展. 化工设计通讯, 2021, 47(4): 180-181, 184. DOI:10.3969/j.issn.1003-6490.2021.04.089 |
| [4] |
刘建明, 李玉梅, 张涛, 等. 一种基于PCA-RF的卡钻预测方法. 北京信息科技大学学报, 2021, 36(1): 18-22. DOI:10.16508/j.cnki.11-5866/n.2021.01.004 |
| [5] |
苏晓眉, 张涛, 李玉飞, 等. 基于K-means聚类算法的沉砂卡钻预测方法研究. 钻采工艺, 2021, 44(3): 5-9. |
| [6] |
刘光星, 翟坤, 陶宇龙, 等. 单因素时间序列ARMA建模在卡钻预测中的应用研究. 重庆科技学院学报(自然科学版), 2015, 17(1): 92-96. DOI:10.19406/j.cnki.cqkjxyxbzkb.2015.01.024 |
| [7] |
刘光星, 陶宇龙, 翟坤. 时间序列在循环卡钻预测中的应用研究. 重庆科技学院学报(自然科学版), 2014, 16(5): 56-59. DOI:10.19406/j.cnki.cqkjxyxbzkb.2014.05.016 |
| [8] |
李彤, 张奇志. 基于PSO-BP的神经网络卡钻事故预测研究. 长江信息通信, 2021, 34(2): 75-77. DOI:10.3969/j.issn.1673-1131.2021.02.024 |
| [9] |
Ben YX, Han WL, James C, et al. Building a general and sustainable machine learning solution in a real-time drilling system. Proceedings of the IADC/SPE International Drilling Conference and Exhibition. Galveston: Society of Petroleum Engineers, 2020. 1–9.
|
| [10] |
Zha Y, Pham S. Monitoring downhole drilling vibrations using surface data through deep learning. Proceedings of 2018 SEG International Exposition and Annual Meeting. Anaheim: Society of Exploration Geophysicists, 2018. 2101–2105.
|
| [11] |
Kaneko T, Wada R, Ozaki M, et al. Combining physics-based and data-driven models for estimation of WOB during ultra-deep ocean drilling. Proceedings of the 37th International Conference on Ocean, Offshore and Arctic Engineering. Madrid: American Society of Mechanical Engineers, 2018. 1–10.
|
| [12] |
Xie HY, Shanmugam AK, Issa RRA. Big data analysis for monitoring of kick formation in complex underwater drilling projects. Journal of Computing in Civil Engineering, 2018, 32(5): 04018030. DOI:10.1061/(ASCE)CP.1943-5487.0000773 |
| [13] |
Osarogiagbon AU, Khan F, Venkatesan R, et al. Review and analysis of supervised machine learning algorithms for hazardous events in drilling operations. Process Safety and Environmental Protection, 2021, 147: 367-384. DOI:10.1016/j.psep.2020.09.038 |
| [14] |
万齐斌, 董方敏, 孙水发. 基于BiLSTM-Attention-CNN混合神经网络的文本分类方法. 计算机应用与软件, 2020, 37(9): 94-98, 201. DOI:10.3969/j.issn.1000-386x.2020.09.016 |
| [15] |
闫河, 董莺艳, 王鹏, 等. 基于CNN-LSTM网络的声纹识别研究. 计算机应用与软件, 2019, 36(4): 166-170. DOI:10.3969/j.issn.1000-386x.2019.04.026 |
| [16] |
朱婷, 王瑜, 肖洪兵, 等. 基于多通路CNN的多模态MRI神经胶质瘤分割. 计算机应用与软件, 2018, 35(4): 220-226. DOI:10.3969/j.issn.1000-386x.2018.04.042 |
| [17] |
吕召阳, 聂雪媛, 赵奥博. 基于CNN机翼气动系数预测. 北京航空航天大学学报. 2021: 1–10. (2021-08-16).
|
| [18] |
赵小强, 张亚洲. 利用改进卷积神经网络的滚动轴承变工况故障诊断方法. 西安交通大学学报, 2021, 55(12): 108-118. |
| [19] |
韦延方, 吴郑磊, 王鹏, 等.基于CNN与DCGAN的柔性直流配电网故障检测. 煤炭学报, 2021, 46(S2): 1201–1208.
|
 2022, Vol. 31
2022, Vol. 31


