小样本学习即从很少的例子中识别新物体类别的能力, 它展示了人类视觉智能的一个新水平. 在大量的训练数据的加持下, 视觉识别系统的准确性已经有了大幅度提高. 但是, 现实生活中有许许多多我们无法获取大量数据的情况, 当我们无法获取到大量的训练数据时, 我们应该怎么办呢. 小样本学习便在这种情况下被人们重新重视.
从很少的例子中学习新概念——是人类视觉系统的一个标志, 小样本学习便是希望学习到人类的这种能力. 例如, 给一个孩子看一张或几张袋鼠的照片, 当下次他看到袋鼠时, 他可以轻易地分辨出袋鼠. 小样本分类的目的是使利用大量可见类数据训练好的分类模型, 在面对只有少量标注数据的不可见类时依然具有较好的分类性能.
目前, 小样本学习面临着两个主要的难题, 一个是不可见类中标注数据过少的问题, 另一个是可见类和不可见类的样本类别相互独立, 将用可见类训练好的模型应用到不可见类时, 由于泛化性太差而引起的过拟合问题. 对少量的标注数据进行扩充是一种简单常用的方法, 在数据量较少的小样本学习中利用这种方法也很有效. 扩充数据的方法通常有这两种, 一种是以高斯噪声为条件[1, 2]学习数据生成器. 这种方法生成的模型问题在于对少量样本进行训练时, 往往表现欠佳. 另一种方法是利用不可见类中的无标签数据来扩充带有标签的数据. 但是这种方法扩充的标签数据准确度有时并不高, 从而影响分类效果. 我们引入了一种融合扩充标签方法, 利用同一类别中的样本数据变化规则来扩充另一类别的样本数据. 具体来说, 假如我们有两张狮子的图片, 其中一张是狮子在散步, 另一张是狮子在睡觉; 同时我们还有一张老虎在散步的照片, 我们利用狮子的姿势变换规则, 融合出一个老虎睡觉的样本, 从而达到数据扩充的目的. 这种规则不仅可以是姿势变换, 也可以是背景变换等.
面对过拟合问题, 人们利用模拟小样本训练过程的情景或元学习[3, 4]的方式来解决这一问题. 但是这些现有的方法绝大多数只关注样本整体的特征, 并没有关注样本中的局部特征. 因此Zhang等[5] 提出一种基于图像区域之间最佳匹配的小样本图像分类算法, 来关注样本的局部特征. 但是这种方法的局限性在于过分关注样本的局部特征, 反而忘记了样本的整体特征的重要性. 我们认为同时关注到样本的整体特征和局部特征, 这对于最后结果的调整是很有帮助的. 因此我们提出了一个双重特征提取方法, 该模块首先从整体出发, 关注提取样本的整体特征, 然后深入到样本的局部特征, 通过整体和局部双重特征, 关注到其中最相关的特征, 从而达到更好的分类效果.
综上所述, 我们在本文的贡献总结如下.
(1)我们引入了一种融合扩充方法, 该方法通过将同一类别样本的变换规则泛化到另一类别, 能够较好地将数据扩充至支持集, 从而实现数据扩充效果.
(2)我们提出了一个双重特征提取方法, 该方法不仅可以关注到样本的整体特征, 而且可以关注到样本的局部特征.
(3)基于(1)和(2), 我们提出了一个小样本图片分类模型: 融合扩充-双重特征提取模型. 该模型可以同时关注样本整体和局部双重特征, 找到样本中对分类最为重要的特征, 从而更好地提高小样本图片分类的准确率.
本文的其余章节组织如下: 第2节, 我们回顾了小样本学习的相关工作. 第3节正式描述我们提出的模型. 第4节, 我们进行了实验设置并对实验结果做了分析和讨论. 第5节总结了全文.
2 相关工作在描述小样本学习的文献中, 绝大多数可以分为两类: 基于度量的方法和基于优化的方法. 除此之外还有少量的其他方法.
2.1 基于度量的方法基于度量的方法首先将图像映射到一个度量空间, 然后在空间内应用某种度量方式来判别图像间的差异性. 这类方法有很多, 例如, 匹配网络[6] 基于深度特征的度量学习和外部存储器增强的神经网络启发, 通过计算支持集和查询集之间的嵌入距离生成加权最近邻分类器, 可以从小数据集中快速的学习新的概念, 同时避免微调. Snell等提出的原型网络[7]基于这样的想法: 每个类别都存在一个原型表达, 该类的原型是支持集在嵌入空间中的均值. 然后, 分类问题变成在嵌入空间中的最近邻. 关系网络[8]采用距离度量网络来学习支持和查询样本中的逐点关系. 嵌入和度量学习方法另一类少镜头学习方法旨在使用度量学习方法优化可转移嵌入. Oreshkin等[9]设计了一种TEN结构, 可以将任务相关信息引入到特征提取网站中, 同时为度量函数增加了放缩系数. Li等[10]将基础类别和少量样本的新类别一起训练, 得到每个类别的全局类别表征, 从中选择出与当前episode类别表征最相近的n个表征, 最后根据查询集样本和n个表征之间的欧氏距离进行分类. Li等受到朴素贝叶斯最近邻算法的启发, 提出了DN4网络[11], 通过比较图像与类别间的局部描述子来寻找与输入图像最相似的类别. Li等[12]提出了一种特征学习模块CTM, CTM可以提取样本特征的类内共同性和类间差异性, 从而找到与分类最为相关的特征, 提高小样本分类的准确性.
2.2 基于优化的方法基于优化的方法主要在于调整模型参数, 使其能够适应不可见类的新任务. MAML[13]是一种基于梯度优化的方法, 该算法提出的模型使用少量的梯度迭代步骤就可以学习到适用于新任务的参数, 它将元学习器设计为一个优化器, 可以学习更新模型参数, 能够匹配任何使用梯度下降法训练的模型. Antoniou等[2]对MAML进行了一定优化, 使得系统的泛化性能进一步提高, 网络的收敛速度进一步加快. LEO[14]利用编码器-解码器体系结构挖掘潜在的生成表示, 对空间中的每个点都进行分类预测, 保留训练好的参数, 使其可以在极低数据区域预测高维参数. Chen等[15]提出了一个基准模型, 用于评估小样本泛化能力, 通过实验发现若是特征提取网络能力够强, 类内差异性的作用会大大减小. Jamal等[16]提出了一种基于任务无偏思想的元学习算法, 通过基于熵减最大化的TAML和基于最小化不平等性的TAML, 提高模型的泛化能力. 在文献[17]中, Elsken等人将神经架构搜索引入到小样本学习中, 将神经架构搜索中的DARTS算法与小样本学习中的Reptile算法结合, 在训练权重参数的同时训练结构参数.
2.3 其他方法图形神经网络最初是为处理图形结构数据[6,18]上的任务而设计的. 图神经网络主要通过递归聚合和转换相邻节点来细化节点表示. 最近的方法[19-21]被提议在少镜头学习任务领域利用图神经网络. TPN[19]提出一种直推式传播网络, 将转换设置引入基于图的小样本学习. 首先将支持集和查询集输入特征网络得到特征向量, 然后将每个样本作为结点构建图模型. 利用图拉普拉斯算子处理结点间的权重, 利用图模型对查询样本进行预测. EGNN[21]提出了一种边标签图卷积神经网络, 利用样本之间的同异性来预测边缘标签特征, 以求显示类内共同性和类间差异性. DLDL[3]是在分类和回归任务中为每个实例分配离散分布而不是一个热标签的研究之一. CPNN[22]将特征和标签作为输入, 并生成框架中只有一个隐藏层的标签分布. LDLFs[23]设计了一种基于决策树算法的分布学习方法.
3 框架 3.1 问题定义小样本学习的训练集中包含了很多的类别, 每个类别都有大量样本. 训练阶段, 在训练集中随机抽取C个类别, 每个类别K个样本(总共C×K个数据), 构建一个元任务, 作为模型的支撑集; 再从这C个类中剩余的数据中抽取一批样本作为模型的查询集. 小样本学习要求模型从C×K个数据中学会如何区分这C个类别, 这样的任务被称为C-way K-shot问题.
在这里我们假设训练类为Ctrain, 测试类为Ctest. 训练类与测试类的标签是互不相交的. 我们有训练数据集Dtrain={(Ii, yi), yi ∈Ctrain}和测试数据Dtest={(Ii, yi), yi ∈Ctest}. 训练过程中, 每次都通过采样不同的元任务进行训练. 通过这种学习机制在训练数据集上学到的模型, 在对测试数据集中的查询集样本进行分类时, 也能较好地进行分类.
3.2 模型概览我们提出了一个名为融合扩充-双重特征提取的模型. 我们给出具体的模型图(图1), 以便于直观地看到模型的组成. 它由融合扩充模块、双重特征提取模块和分类模块组成.
3.2.1 融合扩充模块小样本学习需要解决的主要困难之一是支持集中数据样本过少的问题. 通过数据扩充方法, 我们可以有效地缓解这个问题. 受到文献[4]的启发, 我们引入了一种有效的数据扩充方法-融合扩充方法. 假如说有两张图片, 一张图片中的黄鹂在休息, 另一张图片中的黄鹂在飞行; 通过观察黄鹂这两种不同的状态, 我们人类在看到一只老鹰在休息时, 可以联想到老鹰飞行的画面. 这种方法就是模拟人类这种思维, 通过规则泛化来对支持集中的样本进行扩充.
融合扩充模块的具体过程如图1所示, 直观地说, 我们希望融合器通过某一类别不同样本之间的变换规则(例如不同的姿态或者背景等), 对另一种类别的样本进行扩充. 我们将融合器表示为T(I, S; WT). 其中, I表示样本示例, S表示规则向量, WT 为融合器T 的参数. 我们利用训练集中的大量样本数据来训练融合器T, 不断调整融合器的参数, 使经过融合器融合而成的样本更加有效. 对于每个类别a样本的变换规则(例如

|
图 1 融合扩充-双重特征提取模型 |
具体来说, 在元测试过程中, 我们从支持集
| Support′={(T(Ii,c1−c2;WT),yi)ni=1:(Ii,yi)∈Support′} | (1) |
| Support+=Support ∪Support′ | (2) |
我们的模型是基于度量学习的模型. 学习一个映射函数 f(·), 通过该函数将样本映射到一个嵌入空间进行分类是度量学习方法的一个最重要思想. 在嵌入空间中, 越相似的样本距离越接近, 通过Softmax分类器对嵌入点 f(I')进行分类. 该分类器通常指最后一个全连接层, 然后是Softmax层. 我们通过最小化交叉熵损失来学习此类映射和分类器权重:
| L1=−1NN∑i=1log(exp(WTyif(Ii))∑jexp(WTkf(Ii))) | (3) |
其中, Wk表示Softmax分类器的权重矩阵W的第k列.
我们通过文献[4,24]发现, 对嵌入向量和权重向量应用L2归一化, 可以让分类器具有更好的泛化性能. 因此我们首先对嵌入向量和权重向量进行L2归一化:
| ˆWk=Wk‖ | (4) |
| \hat{f}\left(I_{i}\right)=\frac{f_{\varphi}\left(I_{i}\right)}{\left\|f\left(I_{i}\right)\right\|} | (5) |
归一化后,
| {L_2} = - \frac{1}{N}\sum\limits_{i = 1}^N {\log } \left( {\frac{{\exp \left( {s \cdot \hat W_{{y_i}}^{\rm{T}} \cdot \hat f\left( {{I_i}} \right)} \right)}}{{\displaystyle\sum\limits_j {\exp } \left( {s.\hat W_k^{\rm{T}} \hat f\left( {{I_k}} \right)} \right)}}} \right) | (6) |
为了确保在特殊情况下(例如类内方差过大、类间方差太小数据分散在特征空间中), 也可以通过每个类别的一个或几个样本嵌入点构造一个稳定的决策边界, 我们在学习分类器后给出一个约束: 特征点
| L(\hat f(I),\hat W,s,Y) = - \lambda \frac{1}{N}\sum\limits_{i = 1}^N {\left\| {\hat f\left( {{I_i}} \right) - {{\hat W}_{{y_i}}}} \right\|} + {L_2} | (7) |
其中, I是训练图像, Y是标签,
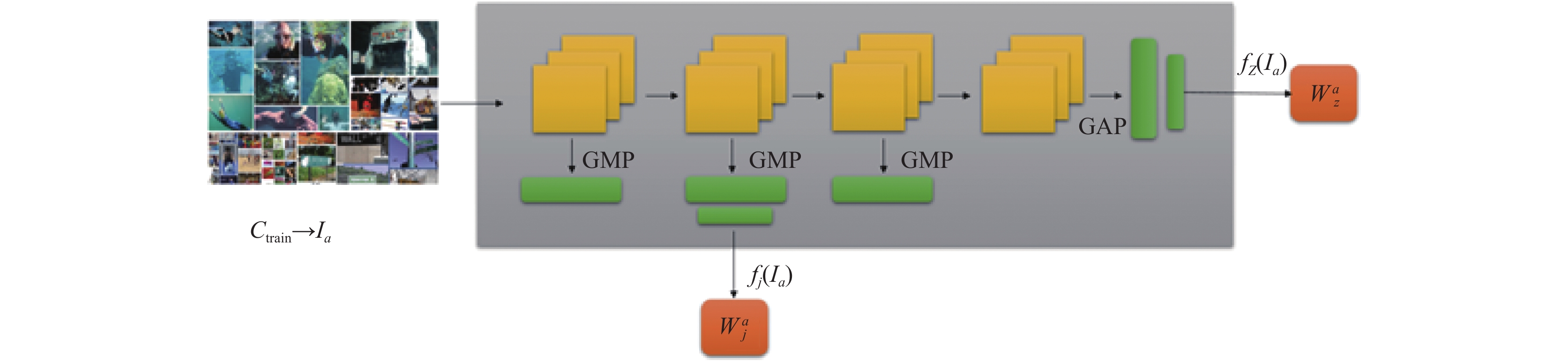
双重特征提取模块如图1所示. 从扩充后的支持集和查询集中抽取的样本, 经过双重特征提取器, 提取出整体特征和局部特征, 从而得到样本的整体权重和局部特征权重, 通过与基类权重的比较, 找到其中最为重要的分类特征, 从而实现分类. 虽然局部特征在一定程度上不如整体特征的分辨力强, 但是在可见类和不可见类之间发生转换时, 局部特征的一般性以及它的非具体性, 使得它对于描述不可见类的新概念有着非常重要的作用. 因此, 我们构建一个局部特征提取器fi(I), 用于从早期层中提取局部特征. 我们在卷积层添加了一个全局最大池层, 并连接这些层中的所有池化功能, 将它们连接到给全连接层. 我们的整体特征提取fz(I)是倒数第二层-全局池化层. 因为该层可以提供整个图像的信息.
双重特征提取器的具体过程如图2所示. 我们从经典神经网络模型的不同层构造两个特征提取器, 分别命名为局部特征提取器fi(I)和整体特征提取器fz(I), 然后通过以分类器为中心的余弦Softmax损耗, 在训练集的大量数据上联合学习这些表示. 一旦学习了表示, 我们就从新示例中提取样本的双重特征, 并将它们连接起来以构造分类器权重. 然后, 使用通过代入获得局部特征表示的损失:
| {L_j} = \left( {{{\hat f}_j}(I), {{\hat W}_j}, {s_i}, Y} \right) | (8) |
其中,
| {L_{\textit{z}}} = \left( {{{\hat f}_{\textit{z}}}(I), {{\hat W}_{\textit{z}}}, {S_{\textit{z}}}, Y} \right) | (9) |
总的来说, 可以通过最小化以下损失函数来学习多级和以分类器为中心的表示:
| {L_h} = \left( {{{\hat f}_j}(I), {{\hat W}_j}, {s_j}, Y} \right) + \left( {{{\hat f}_{\textit{z}}}(I), {{\hat W}_{\textit{z}}}, {s_{\textit{z}}}, Y} \right) | (10) |
|
图 2 局部特征提取器和整体特征提取器 |
3.2.3 分类模块
通过我们已经学习到的双重表示形式
| {f_c}(I) = \left[ {{{\hat f}_j}(I), {{\hat f}_{\textit{z}}}(I)} \right] | (11) |
基本分类器的总权重矩阵也通过相应地连接其分类器权重来获得:
| {W_b} = \left[ {{{\hat W}_j}, {{\hat W}_{\textit{z}}}} \right] | (12) |
给定一个新类别p的输入训练样本 Ip, 我们通过fc=(Ip)提取特征向量, 并直接将其用作新类别c的分类器权重
| {\hat W_p} = \frac{1}{n}\sum\limits_{i = 1}^n {{f_c}} \left( {{I_i}} \right) | (13) |
最后通过标准化得到权重向量Wp:
| {W_p} = \frac{{{{\hat W}_p}}}{{\left\| {{{\hat W}_p}} \right\|}} | (14) |
在本节中, 我们首先对实验中所用的两个数据集, 评价指标以及参数设置进行了介绍, 之后将我们提出的方法与其他基线方法进行比较. 最后我们详细分析了模型中不同模块的设置所带来的影响.
4.1 数据集我们在Mini-ImageNet和Tiered-ImageNet两个基准数据集上进行试验. 针对C-way K-shot问题, 我们在实验中设置不同的C, K值验证论文所设计模型的性能.
Mini-ImageNet数据集总共有60000张图片, 是从ImageNet数据集[25]中的大量图片提出而来, 在60000张图片共分为100个类别, 每个类别里有600张图片, 每张图片的规格为84×84. 按照传统的数据划分, 我们将64, 16和20个类别分别当作训练集, 验证集和测试集[26]. 图3为Mini-ImageNet数据集的5个类别, 每个类别5个示例.

|
图 3 Mini-ImageNet数据集示例 |
Tiered-ImageNet数据集是小样本分类的常用数据集之一. 与Mini-ImageNet一样, Tiered-ImageNet数据集也是由ImageNet数据集中的图片提取得到. 但是, Tiered-ImageNet共有608个类, 并且每个类有1281张图像. 类似于将字符分组为字母的Omniglot一样, Tiered-ImageNet将类别分为与ImageNet层次结构中较高级别的节点相对应的更广泛的类别. 根据文献[27]中使用的数据划分, 我们分别将35197和160个类别作为训练集, 验证集和测试集. 图4为Tiered-ImageNet数据集的5个示例.

|
图 4 Tiered-ImageNet数据集示例 |
4.2 实验设置
我们的代码在PyTorch深度学习平台上实现. 在5-way 1-shot和5-way 5-shot设置中实验我们的方法. 对于C-way K-shot设置, 每个epicode由C个类组成, 每个类包含K个支持样本. 为了方便比较, 我们在实验中使用ResNet-12[28]作为特征提取器. ResNet-12带有4个滤波器个数为64、128、256和512的残差块, 每个残差块由3×3个卷积层组成, 在每个残差块的末尾带有2×2最大池化层, 可以用来减小输出大小. 我们从零开始在基类上训练我们的模型90个epoch, 输入图像大小设置为84×84. 学习率从0.1开始, 每30个epoch除以10, 固定权重衰减为0.0001. 然后, 我们使用以分类器为中心的约束对模型进行进一步微调, 学习率为0.0001.
4.3 Baselines我们选取了一些经典的、具有代表性模型和目前比较先进的几个模型与我们的模型进行比较. RelationNet[8]采用距离度量网络来学习支持和查询样本中的逐点关系. 嵌入和度量学习方法另一类少镜头学习方法旨在使用度量学习方法优化可转移嵌入; CAN[29]引入了一个交叉注意网络, 该网络包含一个交叉注意模块, 可以用来突出目标区域, 从而是提取到的特征更具有代表性; DeepEMD[5]设计了一种交叉参考机制, 可以有效地减少类内背景杂波和较大外观变化的影响, 并提出学习一个结构化的全连接层, 可以对密集图像表示进行分类; CTM[12]提出了一种新的目录遍历模块, 该模块可以提取到类内相同特征和类间不同特征, 从而提高分类准确率; TapNet[30]设计了一个与任务相关的分类空间, 在该空间内进行距离度量, 而且每个类别的参考向量是通过学习更新得到的, 而不是根据训练样本的特征向量计算得到的. 除了基于度量的小样本学习方法, 我们也从基于优化和基于模型的小样本学习方法中选择几个经典模型作为参考, 包括MAML[13] 提出一个模型无关的元学习算法, 该算法适用于任何一个可使用梯度下降更新训练的模型, 并且可用于分类、回归、强化学习等场景; MTL[27]使用了一个较深的网络ResNet-12, 在预训练模型的参数固定的前提下, 对预训练模型的每层参数重新学习一个缩放和平移, 在保证预训练模型不损失特性的前提下, 重新训练了参数, 减小了模型参数; DSN[31]通过引入一个由少量样本构建的动态分类器, 为小样本学习提供了一个框架. 实验结果如表1所示.
| 表 1 FE-DF与其他方法在基准数据集上的实验结果 |
4.4 实验分类结果
从实验结果分析, 我们可以看出我们提出的融合扩充-双重特征提取模型是有效的. 与CAN相比, 我们的模型准确率有所提高, 这说明我们的双重特征提取模块和融合扩充模块是有效的. CAN中使用了一个交叉注意模块, 该模块能够突出支持集样本和查询集样本之间的主要特征, 从而提取到有效特征进行分类; 我们的双重特征提取模块目的也是突出两者直接的主要特征, 但是我们的模块通过双重特征比较, 与交叉注意模块相比更加全面、简单. ICI中提出了一种利用查询集样本扩充支持集样本的数据扩充方法, 我们的融合扩充方法与这种方法相比更加简单, 我们可以利用已有的方式对样本进行扩充, 而且我们的融合扩充方法具有一定的泛化性, 可以用在其他的小样本分类模型中.
4.5 消融实验在本节中, 我们通过一系列实验证实了融合扩充-双重特征提取模型中各个组成部分的有效性.
如表2、表3所示, 为了进一步验证融合扩充模块(FE)和双重特征提取模块(DF)的有效性, 我们将这2个模块应用于3个经典的小样本分类模型: 匹配网络[6]、原型网络[7]和关系网络[8]. 我们在Mini-ImageNet数据集上进行实验, 通过实验我们可以看到, 我们的融合扩充模块(FE)和双重特征提取模块(DF)都具有不错的泛化性, 可以提高这些原有模型的分类性能. 而且在低数据问题比较严重的1-shot中, 我们的融合扩充模块(FE)效果要比5-shot更好, 这说明数据越少, 我们的数据扩充方法效果越明显, 双重特征提取模块对于模型分类效果的提升甚至高于融合扩充模块, 这说明进行小样本分类时, 通过双重特征关注到相关性最强的特征对于分类是很重要的.
| 表 2 在不同的设置下, 融合扩充模块(FE)应用于不同网络的结果 |
| 表 3 在不同的设置下, 双重特征提取模块(DF)应用于不同网络的结果 |
如表4所示, 通过对3种不同提取特征图的方法的比较, 我们可以发现我们的双重特征提取特征图的方法总体来看是具有优势的, 同时, 通过实验比较发现, 我们的双重特征提取方法在实验中的收敛速度要更加高效.
| 表 4 5-way 5-shot下, 3种不同特征提取方法的比较 |
图5–图7显示了在5-way 5-shot设置下, 用Mini-ImageNet数据集对3个经典模型进行实验的实验结果.
通过对图5–图7的分析观察, 我们发现融合扩充模块和双重特征提取模块都能够对分类结果产生较好的提升, 这说明我们的方法是有效的, 而且我们的模块可以与任意模型搭配使用, 具有较好的泛化性. 同时, 通过图5–图7的实验结果我们可以发现, 在匹配网络、原型网络以及关系网络这3个分类模型上添加我们的模块后, 模型的收敛性能有了一定的提升, 特别是在关系网络中, 效果更为明显. 这说明我们的融合扩充模块和双重特征提取模块在一定程度上能够较好地提升模型的收敛速率.

|
图 5 在5-way 5-shot设置下, 融合扩充模块和双重特征提取模块对匹配网络的分类提升结果 |

|
图 6 在5-way 5-shot设置下, 融合扩充模块和双重特征提取模块对原型网络的分类提升结果 |

|
图 7 在5-way 5-shot设置下, 融合扩充模块和双重特征提取模块对关系网络的分类提升结果 |
5 结论
在本文中, 我们首先引入了一种融合扩充方法, 通过利用同类样本间的变化规则, 泛化到其他类别样本, 从而达到扩充数据的目的. 其次, 我们提出了一种双重特征提取方法, 通过训练不同的特征提取器, 对同一样本进行局部特征和整体特征分别进行采集, 使提取的特征更加全面有效, 从而更容易找到与分类最为相关的特征, 提高模型的分类准确度. 我们通过大量的实验证明, 与现有的基线方法相比, 我们的模型在Mini-ImageNet和Tiered-ImageNet两个基准数据集上都取得了不错的效果.
| [1] |
Mehrotra A, Dukkipati A. Generative adversarial residual pairwise networks for one shot learning. arXiv: 1703.08033, 2017.
|
| [2] |
Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks. Proceedings of the 34th International Conference on Machine Learning. Sydney: JMLR.org, 2017. 1126–1135.
|
| [3] |
Gao BB, Xing C, Xie CW, et al. Deep label distribution learning with label ambiguity. IEEE Transactions on Image Processing, 2017, 26(6): 2825-2838. DOI:10.1109/TIP.2017.2689998 |
| [4] |
Hariharan B, Girshick R. Low-shot visual recognition by shrinking and hallucinating features. Proceedings of 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 3037–3046.
|
| [5] |
Zhang C, Cai YJ, Lin GS, et al. DeepEMD: Few-shot image classification with differentiable Earth Mover’s distance and structured classifiers. Proceedings of 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 12200–12210.
|
| [6] |
Vinyals O, Blundell C, Lillicrap T, et al. Matching networks for one shot learning. Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona: Curran Associates Inc., 2016. 3637–3645.
|
| [7] |
Snell J, Swersky K, Zemel R. Prototypical networks for few-shot learning. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 4080–4090.
|
| [8] |
Ren MY, Triantafillou E, Ravi S, et al. Meta-learning for semi-supervised few-shot classification. Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach: ICLR, 2017.
|
| [9] |
Oreshkin BN, Rodriguez P, Lacoste A. TADAM: Task dependent adaptive metric for improved few-shot learning. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 719–729.
|
| [10] |
Li AX, Luo TG, Xiang T, et al. Few-shot learning with global class representations. Proceedings of 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 9714–9723.
|
| [11] |
Li WB, Wang L, Xu JL, et al. Revisiting local descriptor based image-to-class measure for few-shot learning. Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 7253–7260.
|
| [12] |
Li HY, Eigen D, Dodge S, et al. Finding task-relevant features for few-shot learning by category traversal. Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 1–10.
|
| [13] |
Antoniou A, Edwards H, Storkey AJ. How to train your MAML. Proceedings of the 7th International Conference on Learning Representations. New Orleans: OpenReview.net, 2019.
|
| [14] |
Lifchitz Y, Avrithis Y, Picard S, et al. Dense classification and implanting for few-shot learning. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2019. 9250–9259.
|
| [15] |
Chen WY, Liu YC, Kira Z, et al. A closer look at few-shot classification. Proceedings of the 7th International Conference on Learning Representations. New Orleans: OpenReview.net, 2019.
|
| [16] |
Jamal NA, Qi GJ. Task agnostic meta-learning for few-shot learning. Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 11711–11719.
|
| [17] |
Elsken T, Staffler B, Metzen JH, et al. Meta-learning of neural architectures for few-shot learning. Proceedings of 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 12362–12372.
|
| [18] |
Scarselli F, Gori M, Tsoi AC, et al. The graph neural network model. IEEE Transactions on Neural Networks, 2009, 20(1): 61-80. DOI:10.1109/TNN.2008.2005605 |
| [19] |
Liu YB, Lee J, Park M, et al. Learning to propagate labels: Transductive propagation network for few-shot learning. Proceedings of the 7th International Conference on Learning Representations. New Orleans: OpenReview.net, 2019.
|
| [20] |
Satorras VG, Estrach JB. Few-shot learning with graph neural networks. Proceedings of the 6th International Conference on Learning Representations. Vancouver: OpenReview.net, 2018.
|
| [21] |
Kim J, Kim T, Kim S, et al. Edge-labeling graph neural network for few-shot learning. Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 11–20.
|
| [22] |
Yin C, Geng X. Facial age estimation by conditional probability neural network. Proceedings of the Chinese Conference on Pattern Recognition. Beijing: Springer, 2012. 243–250.
|
| [23] |
Shen W, Zhao K, Guo YL, et al. Label distribution learning forests. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 834–843.
|
| [24] |
Qi H, Brown M, Lowe DG. Low-shot learning with imprinted weights. Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 5822–5830.
|
| [25] |
Russakovsky O, Deng J, Su H, et al. ImageNet large scale visual recognition challenge. International Journal of Computer Vision, 2015, 115(3): 211-252. DOI:10.1007/s11263-015-0816-y |
| [26] |
Ravi S, Larochelle H. Optimization as a model for few-shot learning. Proceedings of the 5th International Conference on Learning Representations. Toulon: OpenReview.net, 2017.
|
| [27] |
Sun QR, Liu YY, Chua TS, et al. Meta-transfer learning for few-shot learning. Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 403–412.
|
| [28] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [29] |
Hou RB, Chang H, Ma BP, et al. Cross attention network for few-shot classification. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Neural Information Processing Systems Foundation, 2019. 360.
|
| [30] |
Yoon SW, Seo J, Moon J. TapNet: Neural network augmented with task-adaptive projection for few-shot learning. Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 7115–7123.
|
| [31] |
Simon C, Koniusz P, Nock R, et al. Adaptive subspaces for few-shot learning. Proceedings of 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 4135–4144.
|
 2022, Vol. 31
2022, Vol. 31



