高性能计算 (high performance computing, HPC)和数据处理程序不仅在传统医药研发, 航空航天制造和气象预测中起到重要的作用, 同时与人工智能、大数据以及区块链的融合也日趋紧密. 然而, 一些高性能计算和数据处理程序, 其性能受到严重的内存延迟限制[1-3], 这是因为不规则的内存访问(内存地址不具备可识别模式)无法放入高速缓存中. 传统的解决方案是使用硬件控制的预取技术, 允许硬件检测常见的访存模式(如步长[4])将高速缓存未命中与其他处理器执行的有用工作重叠达到隐藏访存延迟的目的. 但是, 这些技术并不适用不规则的数据访存模式, 如哈希、链表等递归结构, 也不适用间接存储器访问. 在间接访存中, 其加载的地址是基于存储在数组中的索引而非归纳变量.
针对不规则的数据访问模式往往采用软件预取技术[5]. 其原理是, 使用数据结构和算法知识将指令插入程序中, 通过重叠存储器访问提前将所需数据加载至缓存中, 从而提高了程序访存性能. 过去常采取手动插入预取的方式. 然而, 这很难做到. 因为手动插入往往面临着没有严格的插入指导原则和对软件预取、硬件预取之间的相互作用关系较难理解等困难. 此外, 为了获得预取收益, 使用软件预取必须保证预取地址计算和预取数据的代价不能超过隐藏访存的延迟, 否则预取将不会带来任何好处. 因此, 为了进一步减少程序员工作, 需要设计专门的算法来自动为程序插入合适的预取.
过去针对不规则访存模式进行软件预取做了大量研究, 主要涉及预取性能研究、预取生成和预取调度3个方面.
(1) 预取性能研究. Lee等人[6]分析了软件预取和硬件预取在SPEC各个基准上的加速比以及二者之间的协同和对抗作用. 然而, 这些基准并不倾向于在其代码热点区域显示间接存储器访问, 因此无法用于间接预取性能评测. Mowry[7]使用NAS[8]并行基准测试套件的整数排序和共轭梯度基准评测间接预取性能. Ainsworth等人[9]使用HPC[10]、大数据[11]和数据库[12]也做到了. 此外, Ainsworth等人还分析了间接预取在不同体系结构和测试基准中性能差距很大的原因, 表明预取距离、内存带宽、TLB支持等因素对间接预取性能的影响. 实际上, 程序自身特点也会影响预取性能, 如程序间接预取数据规模、插入预取增加的指令开销. 本文在基于预取效益和相关程序特点的基础上, 增加了间接预取代价模型.
(2) 预取生成. Callahan等人为数据库哈希表手动插入预取[13]. 在自动预取方面, 过去针对常规步长访问模式进行预取做了很多工作[5,14], 并且已经在GCC[15]、ICC[16]等多个编译器中实现. 但是, 只有当性能超过硬件步长预取器时, 才会特别有用. Luk等人[17]实现了链表访问模式的自动预取, 但由于链表结构缺乏内存级并行性, 所以性能提升有限. Xeon Phi编译器[18] 实现了一种简单的跨步-间接存储器访问模式的算法, 但是默认情况下并未启用, 并且关于其内部工作原理的信息也很少. Mowry[7]实现了高级类C代码的间接预取, 还通过拆分循环的最后几次迭代, 消除了对循环内预取的边界检查. Ainsworth等人[9]在LLVM编译器中实现了一种可以为简单跨步-间接存储器访问模式和哈希插入预取的算法, 在错误避免和值跟踪方面做了很多工作, 但缺少预取代价分析和预取距离自动计算. 不同的是, 本文为GCC编译器设计了一个完整优化遍, 可以自动识别程序间接存储器访问模式并为之插入合适预取. 黄艳[19]提出一种面向非规则数据的线程预取与L2硬件预取优化组合策略, 减少了系统访存请求, 提高了预取准确率和相关开销. 此外, 软件预取也可以被分配到不同的线程, 以减少为预取而添加的大量额外指令的影响[20-23].
(3) 预取调度. 根据软件预取原理, 需要提前一定循环迭代次数将数据提前加载至缓存.因此进行预取调度的时机也很重要, 预取的过早或过晚都会对程序性能造成影响. Mowry等人[14]考虑内存带宽与指令数量的比率来计算预取距离, 而对于间接预取则从索引数组提前迭代次数(预取距离)隐藏访存延迟的角度研究了间接预取序列之间的调度关系[7], 但并未提出间接预取距离计算方法. 相比之下, Ainsworth等人[9]则提出了根据生成地址所需的加载次数对间接预取序列进行调度的计算方法, 但预取距离却是一个测试经验值. 不同的是, 本文提出了一种间接预取距离自动计算方法.
SW1621作为一款高性能多核处理器, 具有完全自主知识产权. 与之适配的GCC编译器针对申威CPU自主指令集进行了特定优化, 能够支持多种语言、多种编译, 同时还具有良好的可移植性, 但是在处理高延迟间接存储器访问方面还不完善. 为了进一步提高申威架构访存性能, 本文设计并实现了完整的编译器优化遍来处理中间表示的复杂性, 同时还就预取错误避免、预取代价分析和预取距离自动计算进行深入研究.
本文首先介绍了软件预取的相关背景和研究工作, 文中第1节对间接访存进行预取可行性分析以及介绍本文采用的预取调度方案; 第2节详细介绍了间接预取流程; 第3节是实验测试及分析; 最后总结全文.
1 间接预取可行性分析代码清单1展示了常见的间接存储器访问模式. 它涉及顺序移动的index_array数组, 基于index_array数组数据的函数f(x)对间接数组indir_array进行访问. 第1个数组(index_array)的索引i是标准的循环归纳变量, 以固定步长顺序移动, 可以很容易预测下一个数组地址. 但对于间接数组(indir_array)来说, 其索引是index_array[i]数据本身, 其存储器访问地址大都高度分散且不可预测.
代码清单1. 跨步间接存储器访问的一般形式
1 for ( i = 0; i < NUM_KEYS; i++) {
2 sum += indir_array[f(index_array[i])];
3 }
由于间接数组(indir_array)的地址依赖于索引数组(index_array)的数值本身, 而硬件跨步预取器无法识别这种访问模式. 但是由于常规索引数组的前向性, 在软件中可以很容易计算间接数组未来存储器访问的地址. 当f(x)是一个恒等函数时, 这表示一个简单的跨步-间接访问模式. 实际上, 在基于循环的代码中, 简单跨步-间接访问似乎是最常见的间接访存类型(也是在测试程序中观察到的唯一情况). 因此预取算法将侧重于单级间接访存模式的识别和生成预取.
选择合适的间接预取序列方案, 对提高间接预取性能至关重要. 算法将采用下述方法对简单跨步-间接访存的预取序列进行调度. 方法如代码清单所示, 直接的方式是在第2行插入针对indir_array的预取. 然而, 为了进一步优化间接预取性能, 同时在第3行以2倍预取indir_array的偏移量插入针对index_array的预取. 这保证了索引数组数据有充足时间可以加载至L1缓存, 避免了在计算间接数组预取地址时可能发生的cache miss现象, 预取偏移量(offset)的计算将在第3节说明. 此外, 由于增加对索引数组的预取干扰了硬件跨步预取器对预取距离的训练, 因此硬件预取不会对间接预取性能产生影响.
代码清单2. 间接预取序列调度
1 for ( i = 0; i < NUM_KEYS; i++) {
2 prefetch(indir_array[index_array[i+offset/2]]);
3 prefetch (index_array[i+offset]);
4 sum += indir_array[(index_array[i])];
5 }
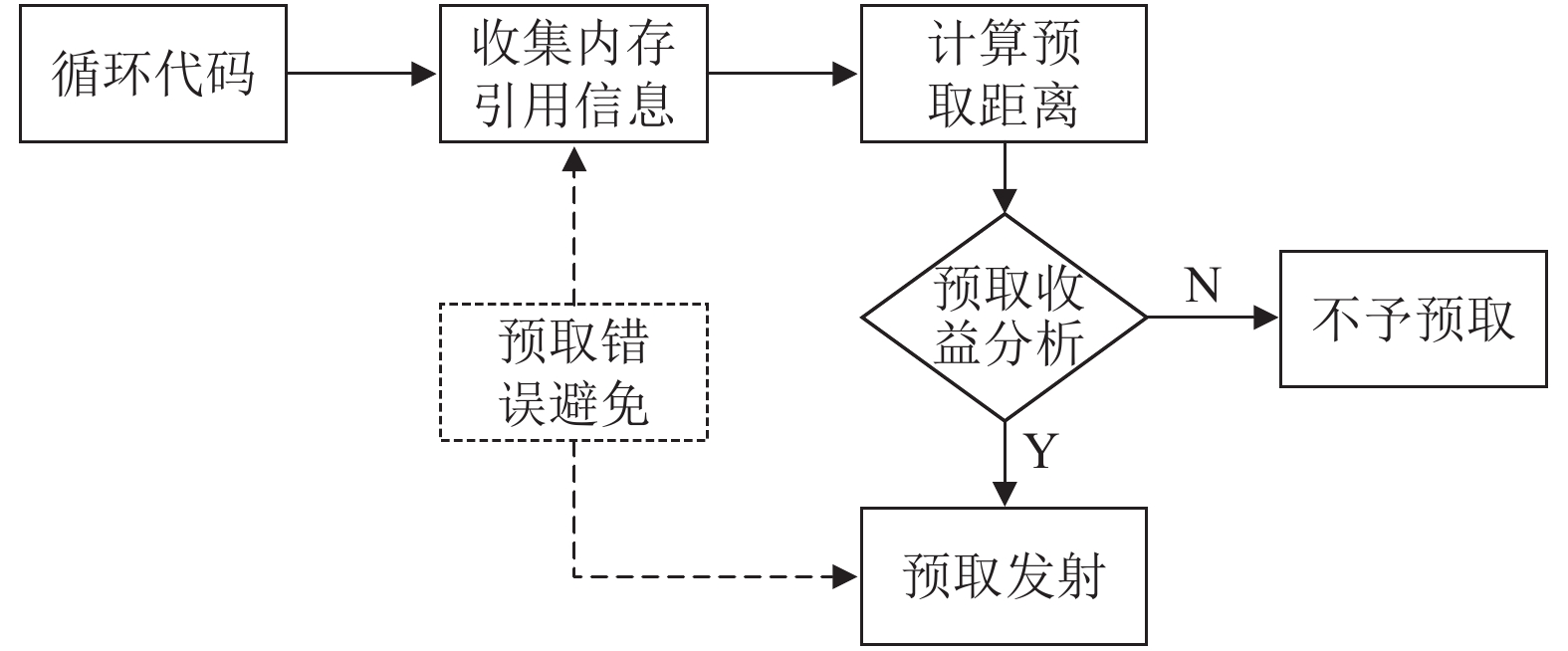
2 循环间接数组预取间接预取算法以一个完整遍集成于SWGCC编译器中, 可以基于索引数组的前向性查找间接存储器访问模式, 并为之生成软件预取. 首先描述所需的分析, 然后再插入计算预取地址的代码和发射预取. 算法主要流程如图1所示.
间接预取算法以循环作为输入, 遍历循环基本块的gimple语句序列搜集间接内存引用信息, 然后计算预取距离并进行预取收益分析, 得到合适的间接预取序列, 最后对满足收益模型的间接预取序列插入软件预取. 其中预取错误避免分为2个部分: 第1部分是在内存引用信息收集阶段排除索引数组是写数据结构的间接预取序列, 避免进行无效预取; 第2部分是在预取生成阶段, 插入限制归纳变量在有效范围的指令, 确保不出现地址越界错误.
|
图 1 间接预取算法总体框架 |
2.1 间接内存引用信息收集
间接预取算法是基于GCC编译器的tree-ssa优化框架. 在内存引用信息收集阶段, 利用gimple中间表示在静态单赋值形式(static single assignment form, SSA)形式所具有的精准的定义/使用关系, 从每一个内存引用向后深度优先搜索间接内存引用信息, 之后将其存储在由两个结构体组成的“十字链表”数据结构中. 对常规和固定布局的内存访问模式进行数据预取时, 利用数据访问的时间相关性[24]和空间相关性[25]可以有效预测未来内存访问. 但对于间接内存引用的局部性却存在两个极端: 一是所有索引值可能是相同的, 间接访存看起来似乎具有时间局部性一样. 而另一个极端中, 每个引用可能指向唯一的缓存行, 看起来又好像不具备局部性一样. 由于无法分析以上极端情况下的数据局部性, 因此决定始终预取.
算法1. 间接访存模式识别
1 foreach (bb: blocks within a loop):
2 foreach (stmt: stmts within a block):
3 if (the rhs of stmt is a memory reference)
4 prefetch = {}
//获取内存引用索引的def-stmt
5 index_stmt = get_def_stmt(rhs)
6 if ((index_ref, info, indvar)=DFS(index_stmt,loop) != null)
7 prefetch U= {indvar, index_ref, infos}
//数据结构存储内存引用信息
8 indir_refs U= prefetch
9 DFS (index_stmt, loop) {
10 candidate = {}
//间接内存引用存在常量偏移量
11 foreach (op: src_operand of index_stmt):
//获取操作数op的def-stmt
12 op_stmt = get_def_stmt(op)
//op_stmt包含内存引用
13 if (op_stmt contain a memor reference)
14 candidate U= {(index_ref, info, {infos})}
//获取索引内存引用的索引
15 index = get_index (index_ref)
//若index可以递归链表示
16 if (SCEV (loop, index))
17 candidate U={(index, {index_ref, infos}
//op_stmt不含有内存引用, 继续DFS
18 elif (op_stmt not contain memory reference)
19 if ((info, index_ref)=DFS(op_stmt, loop)!=null)
20 candidate U= {(index_ref, info, {infos})}
//选择最接近索引内存引用的归纳变量
21 indvar = closest_loop_indvar ()
//不允许非归纳变量phi节点
22 remove (candidate, contains non-induction phi)
//不允许包含函数调用
23 remove(candidate, contains function call)
//内存引用基址不可寻址
24 remove (candidate, base_addr not addressable)
25 }
分析阶段的目标是识别可以发射有效预取的间接内存引用, 并收集为其生成有效预取地址所需的所有关键信息. 算法1给出了间接访存识别的主要过程. 分析一次只考虑一个函数, 并且搜索范围限定在一个函数体, 对函数体的每一个循环嵌套结构按逆序从最内层循环开始查找有效间接内存引用. 依次遍历循环体的每一个基本块, 然后对每一个基本块的gimple语句序列依次进行迭代(算法1的1–2行). 若语句的右表达式是一个内存引用, 则根据SSA的定义/使用关系获取当前内存引用索引的唯一定义语句(算法1第5行). 使用深度优先搜索算法向后遍历定义语句的源操作数的数据依赖图(算法1第11行), 若源操作数的定义语句是一个包含内存引用的赋值语句(算法1第13行), 则利用GCC优化框架的标量演化(scalar evolution, SCEV)功能进一步判断内存引用的索引是否为一个归纳变量(算法1第16–17行). 若是一个普通赋值语句, 将继续深度递归搜索符合要求的索引内存引用(算法1第18–19行). 当没有找到一个符合要求的索引内存引用或者到达不在函数内的指令时, 将停止沿着特定路径继续搜索.
如果存在多条路径引用不同路径的归纳变量, 选择最接近索引内存引用的归纳变量(算法1第21行), 这是因为该归纳变量可能是该循环中最细粒度的内存级并行性形式, 而其他归纳变量在当前循环的每次迭代中可能仅作为一个不变量. 为了确保预取的顺利进行, 需要进一步约束间接预取序列, 使其不出现非归纳变量phi节点(算法1第22行)和函数调用(算法1第23行), 因为前者可能表示复杂的控制流, 而后者可能导致副作用. 对于一些内存引用基址是函数形参的情况也进行了预取, 前提是该形参变量具备可寻址性, 同样的内存引用的基址也必须是可寻址的(算法1第24行).
算法通过式(1)对所有内存引用地址进行解析. 具体参数含义如表1所示. 在之后的预取生成阶段, 将按照式(1)插入计算间接数组地址的相关指令.
| $ addr = base\_address + step \times indvar + delta $ | (1) |
| 表 1 内存引用地址计算公式 |
循环中所有间接内存引用信息由图2所示的两个结构体描述. 两个结构体将内存引用信息组织成“十字链表”形式, 每一个元素都是一个链表头指针, 表示一个间接访存信息group, 在同一个group的索引内存引用信息具有相同的indir_address、indir_step和indir_delta. 每一个索引内存引用存储在mem_index_ref结构体中, mem_indir_ref_group以一个refs指针指向索引内存引用, mem_index_ref以一个next指针链接属于同一group的索引内存引用.

|
图 2 描述间接内存引用的结构体 |
2.2 预取错误避免
虽然预取本身不会造成错误, 但用于间接预取地址计算的中间加载可能会导致错误. 若循环体中存在对索引数组的写数据结构, 可能会预取无效的数据. 更严重的是在对索引数组的解引用期间可能会产生非法的加载地址, 与预取操作不同, 加载指令在非法的地址上会发生内存异常, 导致程序崩溃.
为应对上述问题, 预取算法分别采取两种策略. 首先, 对循环的所有规则仿射内存引用信息进行收集和分析, 只在没有找到对索引数组的存储时, 才对该间接访存进行预取. 例如间接内存引用A[B[i]], 若循环中存在对B[i]的存储, 将舍弃对A[B[i]]的预取, 因为无法保证最终预取的数据是有效的. 其次, 在预取地址生成代码中, 将使用gimple三目运算语句检查归纳变量与前向预取距离相加之后的值是否超过其最大值.例如, 在代码清单2的第2行检查i + offset/2 < NUM_KEYS. 其中, 归纳变量的最大值作为索引数组可以被访问的最后一个元素的下标, 可以很容易在GCC的循环结构分析中获取. 此外, gimple三目运算语句在申威后端不会降级解析成跳转指令, 这减少了因指令跳转导致的额外开销.
在计算间接预取地址时, 除了可以使用普通的加载指令, 还可以使用特殊的非异常加载. 若索引内存引用类型为array_ref, 则可以将归纳变量增加一定前向预取距离的值作为内存引用新的索引, 新的内存引用将在后端生成普通加载指令, 并利用原有比较指令进行地址检查, 无需在gimple阶段进行额外的归纳变量越界检查, 既减少了指令开销, 同时也避免了代价高昂(或可能致命)的地址越界异常.
2.3 预取距离计算获得预取性能收益的关键是以一个足够大的前向预取距离对预取进行调度, 以达到隐藏访存延迟的目的. 预取距离的经典计算方法[14]在预估指令执行时间时并未考虑因插入预取带来的开销, 而在间接预取中指令开销更大. Ainsworth等人[9]认为以间接访问为特征的代码通常是受内存限制的, 其执行时间应由加载指令决定. 提出根据预取序列中加载总数和给定加载在序列中位置的计算预取序列中每个内存引用相对预取距离的比值, 但是预取距离却是一个测试值. 受经典预取距离计算方法的启发, 并进一步研究了间接内存引用数量和预取距离之间的关系, 提出根据间接预取的内存引用总数和系统内存带宽乘积与插入预取后的循环体执行时间的比率来计算预取距离, 如式(2)所示.
| $ {\text{ }}indir\_ahead{\text{ = }}\frac{{n \times L + indir\_time - 1}}{{indir\_time}} $ | (2) |
其中, n是间接预取序列中的总的内存引用数, 对应编译器常量为indir_mem_count, 若循环只有一个简单跨步-间接访存, 则n=2. L是与后端体系结构相关的访存延迟, indir_time是插入预取之后预估的循环体指令执行时间.
2.4 预取代价评估在循环数组间接预取算法中定义了两个代价模型, 用于决定是否为循环的间接访存插入预取.
代价模型1: 循环迭代次数
根据预取产生效益的原理, 若循环的迭代规模很小, 则无法隐藏访存延迟. 因此, 对于拥有高延迟的间接存储访问则需要更大的循环迭代规模才可以获得预取收益. 算法判断预估的循环的迭代次数(trip_count)和前向迭代距离(ahead distance)的比值与预设值(TRIP_COUNT_TO_INDIR_AHEAD_RATIO)的大小. 若比值小于预设值或无法预估循环迭代次数, 则不予预取. 代价模型如式(3)所示:
| $ \begin{split} &\frac{{LC}}{{indir\_ahead}} < \\ &{\textit {TRIP}}\_{\textit {COUNT}}\_{\textit {TO}}\_{\textit {INDIR}}\_{\textit {AHEAD}}\_{\textit {RATIO}} \end{split} $ | (3) |
其中, LC表示预估的循环跳脱计数, 在间接预取遍中对应变量为loop_niter; TRIP_COUNT_TO_INDIR_AHEAD_RATIO是预设的比值, 可以根据系统架构进行调整; indir_ahead为前向预取距离, 由式(2)得出.
代价模型2: CPU操作和访存操作的重叠度
基于预取效益和编译时间考虑, 若循环缺乏足够的CPU 操作与内存操作重叠, 预取不会带来显著收益. 通过将插入预取后循环预估指令数和间接预取序列内存引用总数的比值与预设值的大小比较来判断循环中内存引用数是否合理. 若比值比最小比值预设值(PREFETCH_MIN_INDIR_INSN_TO_MEM_RATIO)小则不予预取, 若出现内存引用数为零或者大于最大内存引用预设值(PREFETCH_MAX_MEM_INDIR_REFS_PER_LOOP)时, 也不予预取. 代价模型如式(4)所示:
| $ \begin{split} &\frac{{INS}}{{MEC}} <\\ &{ \textit {PREFETCH}}\_{\textit {MIN}}\_{\textit {INDIR}}\_{\textit {INSNS}}\_{\textit {TO}}\_{\textit {MEM}}\_{\textit {RATIO}} \end{split} $ | (4) |
其中, INS表示插入预取后循环预估指令数, 对应编译器变量为indir_ninsns; MEC表示循环间接预取序列的内存引用总数, 对应编译器常量为indir_mem_count; PREFETCH_MIN_INDIR_INSNS_TO_MEM_RATIO是间接预取遍预设的比值, 可根据系统架构进行设置.
2.5 预取生成在确定了生成预取的所有关键信息, 并满足了避免引入内存错误和预取收益条件后, 接下来将为间接访存插入预取. 在预取生成阶段, 将循环的gimple语句序列依次插入计算预取地址的普通语句, 并将计算获得的预取地址作为预取内建函数(_builtin_prefetch())的地址参数. 在GCC编译器后端, 将根据插入的gimple语句生成普通指令和预取指令.
首先为索引数组插入预取, 先将预取距离转换为数组前向字节数(算法2第4行). 随后插入一条加法指令, 将当前内存引用的地址与前向迭代字节数相加得到预取地址(算法2第5行), 之后将预取地址作为GCC内置预取函数(_builtin_prefetch())的地址参数用于在后端生成一个预取指令(算法2第6行).
接下来, 将为间接数组插入相关地址计算指令和发射预取. 根据前述预取调度方案, 间接数组的前向字节数为索引数组预取的前向字节数的一半, 若索引数组存在常量偏移量也必须考虑在内(算法2第7–8行). 之后插入一条将归纳变量转换为当前字节数的乘法指令(算法2第9行), 接着插入一条加法指令将其与前向字节数相加, 至此完成了归纳变量增加偏移量的计算(算法2第10行). 若索引数组内存引用是mem_ref类型, 将插入一条三目运算指令取归纳变量增加一定偏移量后的值和索引数组索引下标最大值两者之间的最小值, 使用一个加法指令将索引数组基址与上述最小值相加得到当前索引数组地址, 之后根据该地址创建一个内存引用用于加载索引值(算法2第11–13行). 若索引数组是array_ref类型, 则只需将归纳变量增加一定偏移量后的值作为索引数组新的索引即可加载当前索引值(算法2第14行). 如果间接数组存在常量偏移量, 应该使用加法指令将其与加载的索引值相加(算法2第15行). 在获得加载的索引值后, 将使用一个乘法指令转换成间接数组对应的前向字节数, 一条加法指令将间接数组基址与转换后的前向字节数相加得到间接数组预取地址(算法2第16–17行), 最后为间接数组发射一条预取指令(算法2第18行).
算法2. 预取地址计算和预取发射算法
1 foreach(group: groups within a loop):
2 foreach(indir_ref: indir_refs within a group):
3 if (could emit prefetch for index_ref)
//计算索引内存引用前向字节数
4 offt = index_step * indir_ahead
//插入计算索引预取地址指令
5 addr = insns (&index_ref + offt)
6 emit_prefetch (addr) //发射预取
//为间接内存引用发射预取
7 indir_offt = offt / 2 //间接前向字节数
//若索引内存引用有常量偏移量
8 if (index_delta!=null) indir_offt+=index_delta
//归纳变量转换前向字节数
9 indvar_step = insns (indvar*index_step)
//计算归纳变量前向偏移量
10 indvar_offt = insns (indir_step+indir_offt)
//若索引内存引用是mem_ref类型
11 min_val = insns (indvar_off <= indvar_max ? indvar_off : indvar_max)
12 index_addr =insns(index_address+min_val)
//加载索引内存引用数值
13 index_date = insns (*index_addr)
//若索引内存引用是array_ref 类型
14 index_date = insns(index_array[indvar_off])
//间接内存引用存在常量偏移量
15 if (indir_delta != null) index_date = insns (index_date + indir_delta)
//插入计算间接内存引用前向字节数指令
16 date_step = insns (index_date * indir_step)
//插入计算间接内存引用预取地址
17 indir_addr = insns (indir_address+date_step)
18 emit_prefetch (indir_addr) //发射间接预取
19 endif
3 实验测试及分析本文以SW1621处理器作为测试间接预取算法系统, 编译器为SWGCC710, 操作系统为国产深度Linux系统. 采用SPEC2006和NAS并行基准测试套件进行正确性测试, 而间接预取性能评测则采用NAS-2.3的IS和CG基准, 以及Graph500 (Seq-CSR). 对于IS和CG基准均选取CLASS = C的测试规模. 对于Graph500 (Seq-CSR)则选择在较小的图(选项-s10 -e16)和较大的图(选项-s24 -e16)上运行基准测试, 测试其在不同规模状态下的预取性能. 对于每一个基准程序重复进行5次实验.
3.1 正确性测试为了验证集成于SWGCC710编译器的间接预取算法的健壮性, 使用SPEC2006测试集的29道测试题和NAS的8个测试基准进行正确性测试. 实验结果表明, 经过间接预取优化的测试集均能通过正确性测试, 没有出现编译和执行错误.
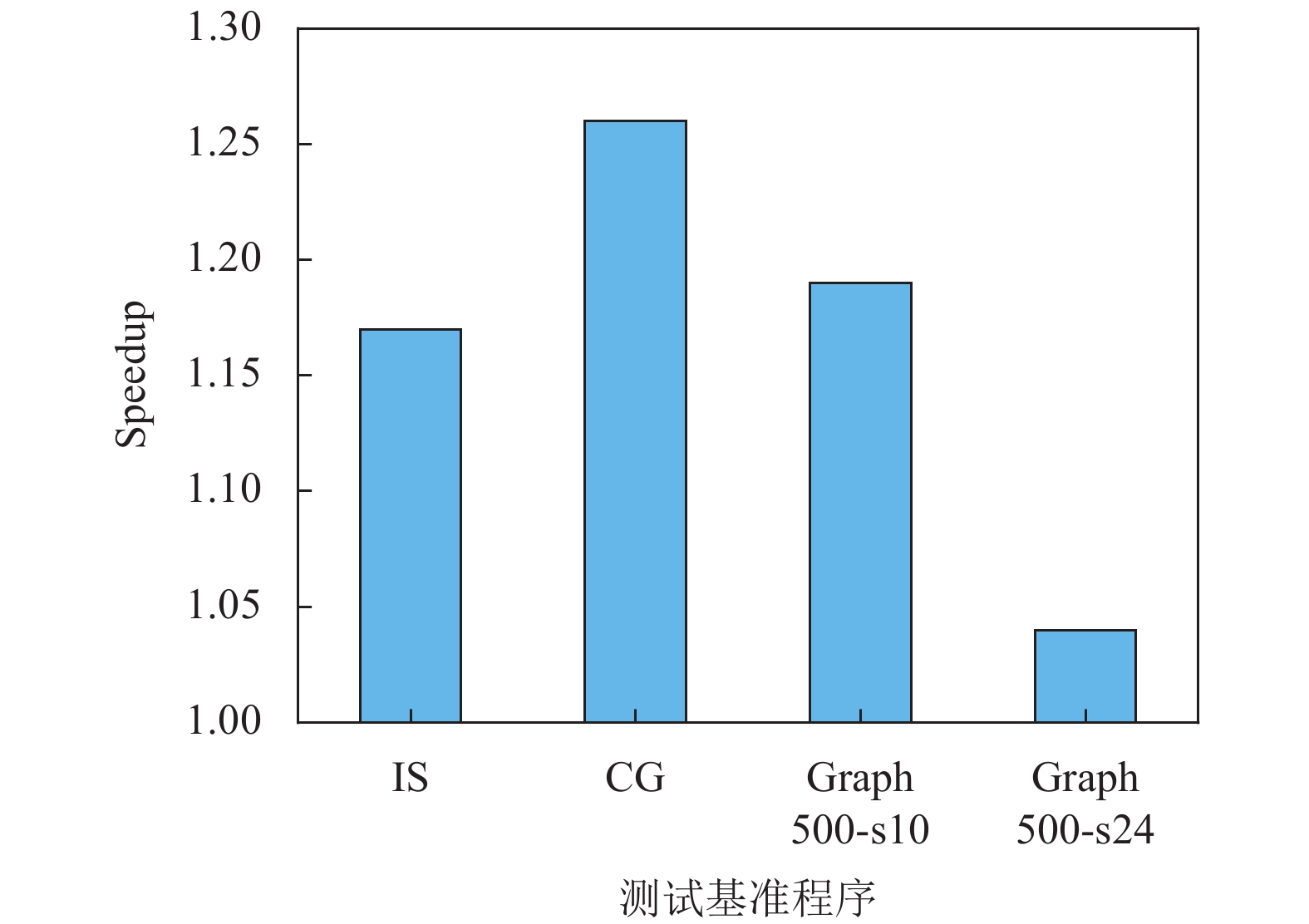
3.2 性能测试采用NAS-2.3的IS和CG基准以及Graph500(Seq-CSR)进行性能测试分析. 实验结果表明, 与编译选项为-O2 -static时的程序性能相比, 间接预取优化遍显著提高了每个应用程序的性能. 测试结果如图3所示.
|
图 3 间接预取优化遍性能加速比 |
对于拥有较为简单的跨步间接访存模式IS和CG, 分别具有17.23%和26.28%的性能提升. 而对于较为复杂的Graph500 (Seq-CSR), 在较小图中(选项为 -s16 -e)性能提升高达18.65%, 而在较大图(选项为 -s24 -e16)也有3.56%的性能提升.
在测试时发现, 当对CG基准以 CLASS=B 规模测试时, 间接预取并未产生任何加速效果, 反而降低了程序性能. 而以CLASS=C规模进行测试时, 间接预取表现出了可观的性能收益, 说明程序的间接存储器访问数据集规模对预取性能具有重要影响. 然而IS基准却表现出完全相反的结果, 当IS以CLASS=B规模进行测试具有195%的加速比, 而以CLASS=C规模测试时却仅有117%的加速比, 说明即使具有更大的数据集规模, 微体系架构的特性也会影响间接预取性能. 对于Graph500 (Seq-CSR)而言, 由于复杂的控制流分析, 自动预取遍无法对外层循环的边缘列表(最大的数据结构)进行预取, 仅可以在最内层循环中插入预取. 在-s24 -e16规下同时增加对外层循环的手工预取时, 加速比可以提高至4.27%, 因此应用程序自身特点也会影响间接预取性能.
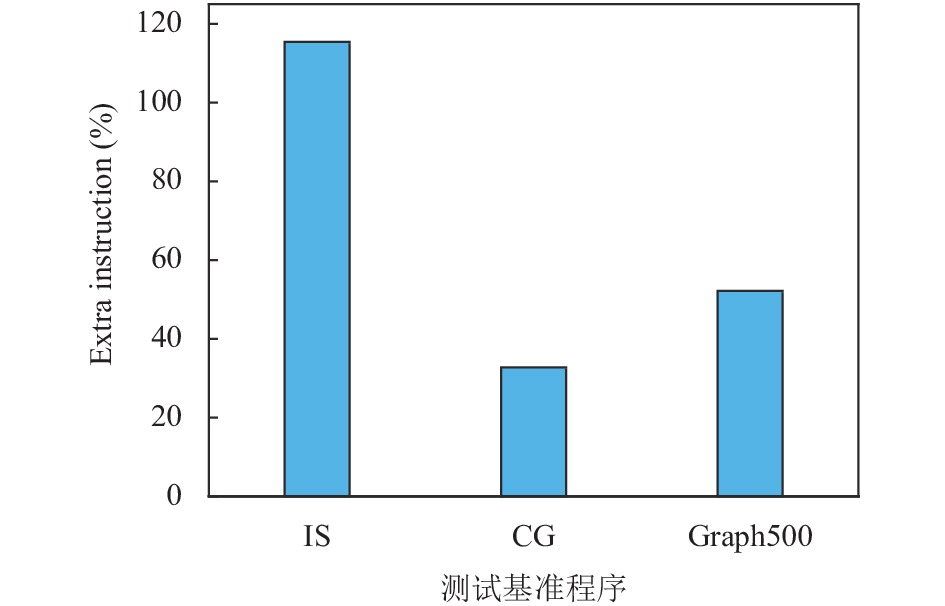
(1) 预取指令开销. 预取间接访存的另外一个比较突出的问题是指令开销. 图4显示了在SW1621上每个基准在仅隔离包含间接内存引用的循环体的动态指令计数增加情况. 通过添加软件预取, 循环体动态指令计数显著增加, 其中IS增加最多, 高达115%, 而Graph500(Seq-CSR)也增加了51%, CG增加的较少, 但也达到了32%. 通过图4可以看出, 插入预取带来的指令开销很大, 动态指令计数显著增加. 对于某些程序, 增加的指令开销将超过减少缓存未命中所带来的好处, 因此在预取距离计算和预取代价分析中均需要预估指令开销的执行时间.
|
图 4 添加软件预取后, SW1621的动态指令计数增加百分比 |
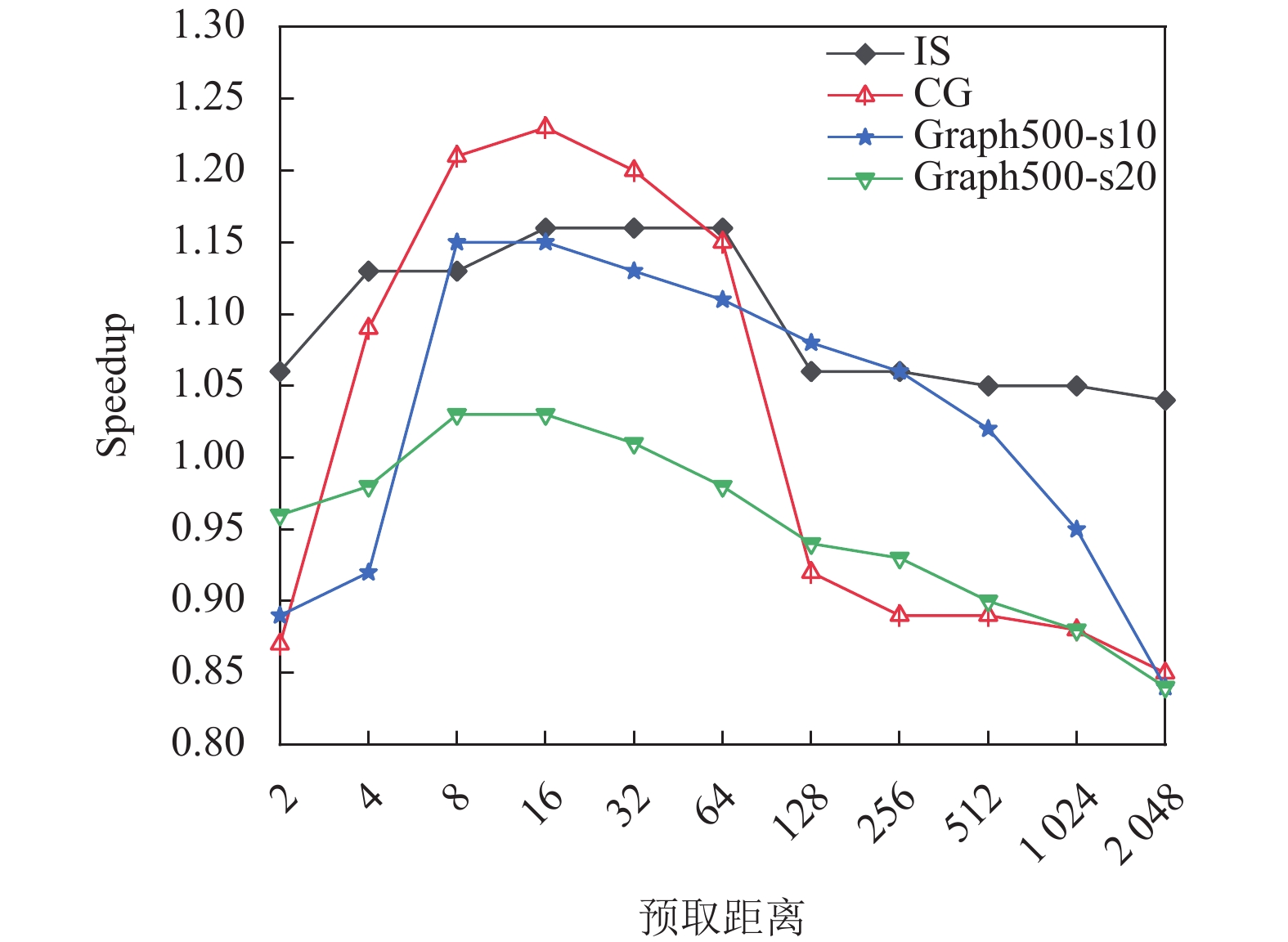
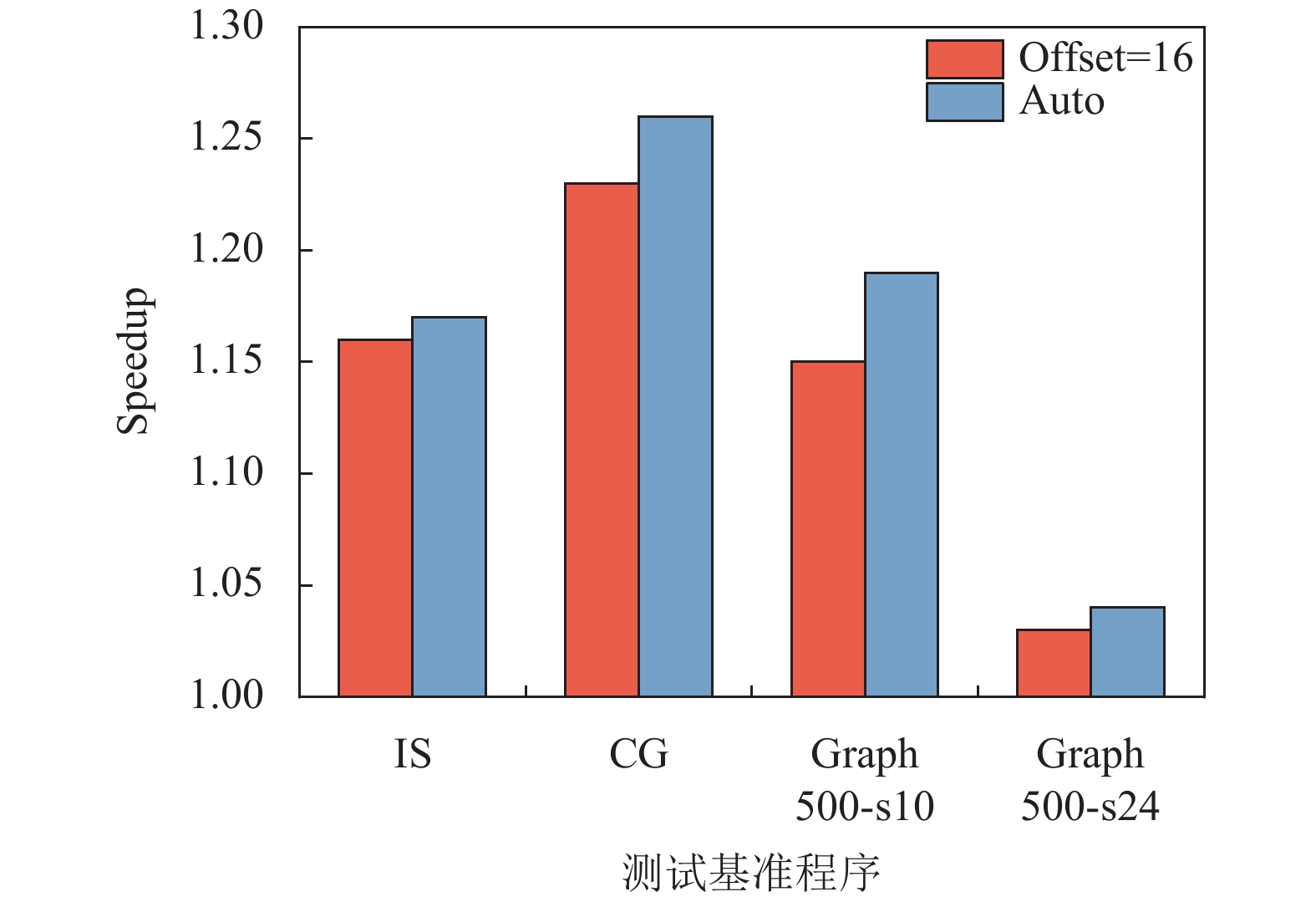
(2) 前向预取距离. 为了验证算法的预取距离计算方法的高效性, 将最好的手工设定的预取距离与自动预取计算的距离相比较. 图5给出了每个基准相对变化的前向预取距离的加速比, 表明对于每个基准前向预取距离可以是一个比较大区间中任何一个数值, 并且不同基准预取距离却具有一致性. 传统的间接预取距离设置方法就是根据不同基准测试结构设置的一个固定值, 在SW621处理器平台选取offset=16时, 每一个基准都可以获得较好的性能收益. 实际上, 通常最佳预取距离是存储器等待时间除以每次循环迭代的时间[14]. 由于每个基准程序自身特点不同, 循环指令数不同, 因插入预取增加的指令数开销也不同, 最佳预取距离并不相同, 而传统手工设定方式忽略了不同程序的特性. 算法提出的预取距离计算方法同时考虑到因预取插入带来的指令开销和程序特点, 可以计算出每个程序最接近最佳预取距离的数值. 图6给出了自动算法对每个基准的性能改进, 以及手工设定offset=16 时每个基准的预取性能. 测试结果表明, 本文提出的预取距离计算方法比手工设定可以获得更高的性能收益.
|
图 5 变化的前向预取距离加速比 |
|
图 6 自动预取和最好的手工设定offset=16 的预取性能 |
4 结束语
为了解决申威GCC编译器中缺乏间接预取自动化方法的问题, 本文设计并开发了一个完整的编译器遍来识别适合预取的间接访存模式, 并插入必要的代码计算预取地址和发射预取. 对简单跨步-间接存储器访问模式插入合适的预取, 提高了SW1621处理器对间接访问的高速缓存命中率, 显著提高了SW621访存性能.
对于一些比较复杂的循环, 其中可能包含多个简单跨步-间接访存模式, 它们具有相同的间接数组, 同时索引数组数据在同一个缓存行中(例如, B[A[i]]和B[A[i+2]]). 根据间接预取调度方案, 需要对索引数组和间接数组都进行预取, 当对其中一个索引数组(A[i])发射预取时, 也会将另外一个索引数组(A[i+2])数据加载至缓存, 如果继续对索引数组A[i+2]重复发射预取, 不仅会增加间接预取开销, 也会将其他有用数据替换出缓存, 显著降低间接预取的性能收益. 在后续工作中需要就上述问题考虑进行重用分析, 避免出现重复预取.
| [1] |
Kocberber O, Grot B, Picorel J, et al. Meet the walkers: Accelerating index traversals for in-memory databases. Proceedings of the 2013 46th Annual IEEE/ACM International Symposium on Microarchitecture. Davis: IEEE, 2013. 468–479.
|
| [2] |
Sun MM, Zhuang H, Li CL, et al. Scheduling algorithm based on prefetching in MapReduce clusters. Applied Soft Computing, 2016, 38: 1109-1118. DOI:10.1016/j.asoc.2015.04.039 |
| [3] |
Nilakant K, Dalibard V, Roy A, et al. PrefEdge: SSD prefetcher for large-scale GrapH traversal. Proceedings of International Conference on Systems and Storage. Haifa: ACM, 2014. 1–12.
|
| [4] |
Chen TF, Baer JL. Reducing memory latency via non-blocking and prefetching caches. ACM SIGPLAN Notices, 1992, 27(9): 51-61. DOI:10.1145/143371.143486 |
| [5] |
Callahan D, Kennedy K, Porterfield A. Software prefetching. ACM SIGPLAN Notices, 1991, 26(4): 40-52. DOI:10.1145/106973.106979 |
| [6] |
Lee J, Kim H, Vuduc R. When prefetching works, when it doesn't, and why. ACM Transactions on Architecture and Code Optimization, 2012, 9(1): 1-29. |
| [7] |
Mowry TC. Tolerating latency through software-controlled data prefetching[Ph.D. thesis]. Stanford: Stanford University, 1994.
|
| [8] |
Bailey DH, Barszcz E, Barton JT, et al. The NAS parallel benchmarks. The International Journal of High Performance Computing Applications, 1991, 5(3): 63-73. |
| [9] |
Ainsworth S, Jones TM. Software prefetching for indirect memory accesses. Proceedings of 2017 International Symposium on Code Generation and Optimization. Austin: ACM, 2017. 305–317.
|
| [10] |
Luszczek PR, Bailey DH, Dongarra JJ, et al. The HPC Challenge (HPCC) benchmark suite. Proceedings of 2006 ACM/IEEE Conference on Supercomputing. Tampa: ACM, 2006. 213.
|
| [11] |
Murphy RC, Wheeler KB, Barrett BW, et al. Introducing the graph 500. Cray Users Group (CUG), 2010, 19: 45-74. |
| [12] |
Balkesen C, Teubner J, Alonso G, et al. Main-memory hash joins on multi-core CPUs: Tuning to the underlying hardware. Proceedings of the 2013 IEEE 29th International Conference on Data Engineering. Brisbane: IEEE, 2013. 362–373.
|
| [13] |
Chen S, Ailamaki A, Gibbons PB, et al. Improving hash join performance through prefetching. Proceedings of the 20th International Conference on Data Engineering. Boston: IEEE, 2004. 116–127.
|
| [14] |
Mowry TC, Lam MS, Gupta A. Design and evaluation of a compiler algorithm for prefetching. ACM SIGPLAN Notices, 1992, 27(9): 62-73. DOI:10.1145/143371.143488 |
| [15] |
董钰山, 李春江, 徐颖. GCC编译器中循环数组预取优化的实现及效果. 计算机工程与应用, 2016, 52(6): 19-25. DOI:10.3778/j.issn.1002-8331.1412-0377 |
| [16] |
Krishnaiyer R. Compiler prefetching for the Intel® Xeon PhiTM coprocessor. https://www.intel.com/content/dam/develop/external/us/en/documents/5-3-prefetching-on-mic-6-326703.pdf.
|
| [17] |
Luk CK, Mowry TC. Compiler-based prefetching for recursive data structures. ACM SIGPLAN Notices, 1996, 31(9): 222-233. DOI:10.1145/248209.237190 |
| [18] |
Krishnaiyer R, Kultursay E, Chawla P, et al. Compiler-based data prefetching and streaming non-temporal store generation for the Intel® Xeon PhiTM coprocessor. Proceedings of 2013 IEEE International Symposium on Parallel & Distributed Processing, Workshops and Phd Forum. Cambridge: IEEE, 2013. 1575–1586.
|
| [19] |
黄艳, 刘海燕. 一种面向非规则数据的预取优化组合策略. 科技通报, 2016, 32(12): 163-168. |
| [20] |
张建勋, 古志民. 基于交织预取率的帮助线程预取质量调节算法. 计算机应用研究, 2019, 36(2): 430-434. |
| [21] |
Zhang JX, Gu ZM, Huang Y, et al. Helper thread prefetching control framework on chip multi-processor. International Journal of Parallel Programming, 2015, 43(2): 180-202. DOI:10.1007/s10766-013-0299-9 |
| [22] |
Selfa V, Sahuquillo J, Gómez ME, et al. Efficient selective multicore prefetching under limited memory bandwidth. Journal of Parallel and Distributed Computing, 2018, 120: 32-43. DOI:10.1016/j.jpdc.2018.05.002 |
| [23] |
Dudás Á, Juhász S, Schrádi T. Software controlled adaptive pre-execution for data prefetching. International Journal of Parallel Programming, 2012, 40(4): 381-396. DOI:10.1007/s10766-011-0190-5 |
| [24] |
Lotfi-Kamran P, Sarbazi-Azad H. Temporal prefetching. Advances in Computers, 2022, 125: 31-41. |
| [25] |
Lotfi-Kamran P, Sarbazi-Azad H. Spatial prefetching. Advances in Computers, 2022, 125: 19-29. |
 2022, Vol. 31
2022, Vol. 31



