作为一种新型的网络架构, SDN实现了集中式控制和可编程的特点, 解耦了控制层面和转发层面, 使得大型网络管理更为便捷^[1–4]. 但是, SDN的转发与控制分离的特点可能使得交换机和控制器易成为高速和低速分布式拒绝服务攻击的目标^[5].

在SDN环境中, 针对交换机和控制器的高速和低速DDoS攻击是多分类的问题. 在SDN环境下, 如何准确地识别多种不同攻击类型仍是一个较为严峻的问题. 现如今, 针对低速率和高速率DDoS攻击问题, 研究者提出了一些方法, 用于检测低速DDoS和高速DDoS攻击^[6–8]. 文献[9]提出了基于粒子群优化卷积神经的模型, 并将其用于检测高速率DDoS攻击. 文献[10]提出了一种基于信息距离度量检测低速率DDoS攻击. 信息距离度量指标可以量化网络流量在不同概率分布下的偏差, 基于SDN网络流的特性, 该文献使用广义熵的度量方法用于检测控制层的低速率DDoS攻击.

D-S证据理论是一种处理不确定信息并且实现多分类器融合的有力工具, 被广泛地用在模式识别、图像处理、风险评估、目标分类等领域^[11]. 文献[12]中, 作者结合了云模型和改进D-S证据理论, 提出了一种新的冲突参数并用于改进D-S证据理论算法, 该算法通过对探测器的证据进行修正实现多个证据最终融合. 文献[13]中, 研究者提出了一种基于不一致测量的冲突证据组合方法, 该方法引入了新的冲突系数对冲突证据进行修正, 并通过改进的组合规则获得最终的融合结果. 文献[14]中, 作者结合了希尔伯特-黄变换和传统D-S理论用于检测传统网络中DDoS攻击. 文献[15]中, 研究者使用传统的D-S证据理论算法用于检测传统网络中DDoS攻击. 文献[16]中, 研究者使用证据间距离改进D-S证据理论, 并使用SVM模型结合改进D-S证据理论算法用于检测网络中DDoS攻击.

在处理多分类器融合的过程中, 使用D-S证据理论可能会使得的融合的结果不够充分. 为了解决这一问题, 一些研究者提出修改Dempster规则方法, 主要用于解决冲突分配和管理的问题^[17-19]. 另外, 一些研究者则是通过改进基本信念分配解决上述问题, 具体改进方法是通过对不可靠的证据源进行预处理, 将经过预处理后的证据与Dempster规则进行最终的融合. 本文更倾向于第2类研究者改进D-S证据理论算法的思想. 目前, 部分研究者提出的基于D-S证据理论的DDoS攻击检测方法大多数只适用于解决传统网络下DDoS攻击安全问题. 本质上讲, 该问题属于二分类问题. 此外, 一些研究者只使用分类器的结果作为D-S基本信念分配函数(basic probability assignment, BPA), 且只使用简单的统计学方法直接对分类器结果进行权重的重新分配, 这种方式容易导致DDoS检测精度降低.

基于上述分析, 为防范SDN中高速和低速DDoS攻击, 本文提出一种SDN环境下针对控制器和交换机的多目标DDoS攻击检测方法. 首先, 为了更精确的检测SDN环境下多种不同种类的DDoS攻击, 本文使用OVO策略融合多种不同类型的二分类器构建多分类器. 其次, 为了使BPA有效的代表网络流量的初始概率分布, 代替多数研究者使用分类器的结果直接作为BPA, 本文使用OVO策略融合多个二分类器至多分类器, 结合得到二分类器的支持度与信息熵方法构建BPA. 最后, 为了更全面的衡量D-S证据间的冲突, 本文提出两种新的冲突因子包含离散因子和纯度因子用于衡量D-S证据源之间的冲突. 其中, 离散因子是通过使用OVO策略融合多个二分类器至多分类器时支持相同类别的非零概率值之间的熵值计算得到. 纯度因子是指计算使用OVO策略融合多个二分类器至多分类器后, 该多分类器内部之间支持度的Gini指数得到. 之后, 结合离散因子和纯度因子计算多个证据源的权重. 最后, 利用D-S证据理论对调整权重后的证据进行最终的融合. 综上, 本文的主要贡献如下.

(1) 为了更精确的检测SDN网络中DDoS攻击, 本文提出一种SDN环境下针对控制器和交换机的多目标DDoS攻击检测方法.

(2) 本文使用OVO策略融合多种不同类型的二分类器构建多分类器, 且二分类器的支持度与信息熵方法结合计算得到BPA.

(3) 为了更好地衡量证据内部和证据之间的冲突, 本文提出两种新的冲突因子包含离散因子和纯度因子, 用于修正D-S证据理论的证据.

本论文的结构组织如下. 第1节介绍了相关背景技术知识. 第2节介绍了本文提出的基于改进D-S理论的DDoS攻击检测方法. 第3节通过实验分析和结果证实本文提出的方法具有较好的效果. 第4节对本文提出方法进行了总结.

1 背景

本小节分为两个部分: 第1部分讲述了DDoS攻击相关背景知识, 第2部分讲述了D-S证据理论算法相关知识.

1.1 SDN环境下DDoS和LDDoS攻击

SDN实现了控制层与转发层的解耦, 具有集中式控制和可编程性等特点, 然而SDN的控制层和转发层也都面临着一些安全问题, 例如DDoS攻击等^[20].

在SDN中, 以控制器为目标的攻击者通过持续向目标主机发送新的数据包对控制器发起攻击. 攻击者发送的数据包将与交换机中的流表进行匹配, 如果数据包匹配成功, 则流表相应动作将会被执行. 否则, 交换机将向控制器发送packet_in消息. 在这种攻击方式中, 攻击者将发送大量无法与流表匹配的数据包, 使控制器处理大量packet_in消息, 导致控制器单点故障.

此外, 以交换机为目标的攻击者将向交换机发送新的数据包. 同时在idle_time时间内将持续发送与第一个数据包头部相同的数据包, 保持相关流表项一直存在交换机中. 通过持续重复这个过程, 交换机的流表项空间将被恶意无用的流表项占满, 导致正常的流表项在到达交换机时被丢弃.

以交换机和控制器为攻击目标, 其攻击发起方式主要分为两种类型, 即DDoS攻击以及LDDoS攻击. DDoS攻击是通过伪造IP地址持续不断地向攻击目标发送大量攻击流量, 而LDDoS攻击则是通过调整发送攻击的周期、攻击流量持续的时间和发送攻击流量的速率达到降低控制器和交换机服务质量的目的.

1.2 D-S证据理论

在多源数据融合中, 具有不精确推理特点的D-S证据理论是一种较有优势的技术. 目前, D-S证据理论已被广泛运用在模式识别、图像处理、多类目标分类和模式分类等领域.

D-S证据理论建立在集合框架 $\vartheta $ 基础之上, 框架 $\vartheta $ 包括了对应问题的所有结果的集合.

定义1. 假设 $\vartheta $ ={ ${A_1}, {A_2}, \cdots , {A_N}$ }是包含所有结果的集合框架, 基本信度分配函数m被定义为从集合框架 $\vartheta $ 中的幂集 ${2^\vartheta }$ 到概率区间[0, 1]的映射函数, m(A)为A的BPA, A为框架 ${2^\vartheta }$ 的任一子集, m(A)>0的集合则为焦元, 反映了在该证据下命题A的可信程度, 具体计算如式(1)所示.

$ \left\{ {\begin{array}{*{20}{l}} {m\left( \emptyset \right) = 0} \\ {\displaystyle\mathop \sum \limits_{A \in {2^\vartheta }} m\left( A \right) = 1} \end{array}} \right. $

(1)

定义2. Dempster合成法则如式(2)所示. 其中, n为证据数量, j为第j个证据, N为假设的数量, k为第k个假设, K为合成公式中[0, 1]范围内多个证据之间的冲突系数, ${m_1} \oplus {m_2} \oplus \cdots \oplus {m_n}$ 为证据之间的内积和.

$ \begin{split} & m(A)= {m}_{1}\oplus \cdots \oplus {m}_{n}\\ &\left\{ {\begin{array}{l}\dfrac{1}{1-K}{\displaystyle \sum }_{{\cap }_{k=1}^{N}{A}_{k}=A, A\subseteq {2}^{\vartheta }}{{\displaystyle \prod }}_{j=1}^{n}{m}_{j}\left({A}_{k}\right)A\ne \varnothing \\ K={\displaystyle \sum }_{{\cap }_{k=1}^{N}{A}_{k}=A, A\subseteq {2}^{\vartheta }}{{\displaystyle \prod }}_{j=1}^{n}{m}_{j}\left({A}_{k}\right)\end{array}} \right. \end{split} $

(2)

2 SDN环境下基于改进D-S理论算法检测DDoS攻击机制 2.1 设计原理

SDN网络具有转发层和控制层分离的特点使其具备传统网络不能比拟的优势, 同时也可能使得SDN中控制层和转发层遭受不同类型的DDoS攻击. 针对SDN中不同类型的DDoS攻击, 本文提出一种SDN环境下基于改进D-S理论的DDoS攻击检测方法. 该方法提出的两个因子包含离散因子和纯度因子, 用于衡量证据内部和证据之间的冲突和关联, 以此修正D-S理论算法的证据冲突. 离散因子是指在使用OVO策略进行二分类器融合成一个多分类器的过程中, 相同类别的非零支持度之间的熵值. 纯度因子指不纯度与1之间的差异绝对值. 不纯度是指每个多分类器内部不同类别的支持度之间的Gini指数. 当Gini指数越高时, 则表示多分类器内部不同类别之间的支持度分布不纯度越高, 则分类差异越为突出. 本文使用两个因子用于修正多分类器输出的结果, 使用D-S证据理论方法融合修正后的输出结果得到最终的分类结果. 检测方法整体架构图具体如图1所示.

2.2 离散因子

当OVO策略融合多个二分类器为一个多分类器过程时, 多个二分类器相同类别的非零支持度之间的离散程度影响该多分类器的分类效果. 相同类别非零支持度之间的离散因子越大, 则表示该多分类器效果越好.

本文通过M个二分类器使用OVO策略融合成一个多分类器. 此处, M=N×(N–1)/2, N指N–1种网络攻击流量和正常网络流量. 其中, 网络攻击流量包含了针对控制器和交换机的高速DDoS攻击和低速DDoS攻击. 本文通过式(3)、式(4)和式(5)计算O_i并得到BPA, 并通过式(6)和式(7)计算得到离散因子.

$ \varphi = \left( {\begin{array}{*{20}{c}} {O_{i, 1, 2}^1}& \cdots &{O_{i, 1, 2}^5} \\ \vdots & \ddots & \vdots \\ {O_{i, 4, 5}^1}& \cdots &{O_{i, 4, 5}^5} \end{array}} \right) $

(3)

$ {{\tau }}_{{i}}^j = \left( {O_{i, 1, 2}^j, O_{i, 1, 3}^j, O_{i, 1, 4}^j \cdots O_{i, 3, 4}^j, O_{i, 4, 5}^j} \right) $

(4)

$ O_i^{} = \frac{{\displaystyle\mathop \sum \nolimits_{i = 1}^{10} {{\tau }}_{{i}}^j}}{{\displaystyle\mathop \sum \nolimits_{j = 1}^5 \displaystyle\mathop \sum \nolimits_{i = 1}^{10} {{\tau }}_{{i}}^j}}=(O_i^1, O_i^2, O_i^3, O_i^4, O_i^5) $

(5)

$ H\left( {{{{\tau }}^j}} \right) = - \mathop \sum \limits_{i = 1}^{10} {{\tau }}_i^j\log {{\tau }}_i^j $

(6)

$ Dis\left( {{m_i}} \right) = \frac{{H\left( {{{{\tau }}^j}} \right)}}{{\displaystyle\mathop \sum \nolimits_{i = 1}^5 H\left( {{{{\tau }}^j}} \right)}} $

(7)

2.3 纯度因子

纯度因子通过计算多分类器内部的支持度之间的Gini指数得到. 当多分类器内部的之间支持度的纯度越低, 则多分类器的分类效果越为明显. 纯度因子的具体计算过程如式(8)和式(9)所示:

$ P\left( {O_i^{}} \right) = \sum\nolimits_{k = 1}^5 O_i^k\left( {1 - O_i^k} \right) = 1 - \mathop \sum\nolimits_{k = 1}^5 {(O_i^k)^2} $

(8)

$ Pure\left( {{m_i}} \right) = \frac{{P\left( {O_i^{}} \right)}}{{\displaystyle\mathop \sum \nolimits_{i = 1}^3 P\left( {O_i^{}} \right)}} $

(9)

2.4 D-S证据理论融合

在计算离散因子和纯度因子后, 结合两个因子将得到证据的权重. 通过式(10)和式(11)融合两个因子计算得到证据最终的权重, $\;\rho $ 的区间属于[0, 1].

$ W\left({O}_{i}\right)=\frac{\rho Dis\left({m}_{i}\right)+\left(1-\rho \right){Pure}\left({m}_{i}\right)}{ma{x}_{1\leqslant i\leqslant 5}\left\{\rho Dis\left({m}_{i}\right)+\left(1-\rho \right){Pure}\left({m}_{i}\right)\right\}}$

(10)

$ \epsilon=\left\{ {\begin{array}{l}m\left(\theta \right)=\frac{{{\displaystyle \sum }}_{\cap {\theta }_{k}=\theta }{{\displaystyle \prod }}_{i=1}^{n}{W}_{i}^{c}{m}_{i}\left({\theta }_{k}\right)}{1-{{\displaystyle \sum }}_{\cap {\theta }_{k}\ne \varnothing }{{\displaystyle \prod }}_{i=1}^{n}{W}_{i}^{c}{m}_{i}\left({\theta }_{k}\right)},\;\theta \ne \varnothing , \forall {\theta }_{k}\in \vartheta \\ m\left(\theta \right)=0,\; \theta =\varnothing \end{array} } \right.$

(11)

2.5 算法实现

SDN环境下基于改进D-S理论算法检测DDoS攻击算法具体如算法1所示.

算法1中, 首先调用RYU控制器提供的北向接口获取交换机与控制器交互的OpenFlow消息和流表项. 随后计算packert_in rate, byte_rate和paket_rate等特征. 将计算后的流表项特征记为Feature_x, 并作为二分类器的输入, 按样本类别顺序依次训练M个基分类器, 包含( ${O_{i, 1, 2}}$ , $ \text{ }{O}_{i, 1, 3} $ , $\text{ }\cdots, {O}_{i, 3, 4}$ , $ \text{ }{O}_{i, 4, 5}\text{ } $ , i=1, 2, 3). 在本文中, M=10, N=5. 训练完不同的基分类器后, 本文将10个基分类器的输出构建成一个10×5的矩阵 $\varphi $ ; 得到矩阵 $\varphi $ 后, 通过式(4), 式(5)和式(6)计算得到多分类器 $O_i^{}$ , 式(7)和式(8)计算获得第i个多分类器分类类别为j的离散因子 $Dis\left( {{m_i}} \right)$ ; 在得到多分类器 $O_i^{}$ 后, 式(9)和式(10)计算多分类器 $O_i^{}$ 内部之间的纯度因子 $Pure\left( {{m_i}} \right)$ ; 使用式(11)和式(12)结合离散因子和纯度因子得到最终调整权重后的多分类器分类结果, 获得最终的DDoS攻击检测结果.

算法1. 改进D-S证据理论检测算法

Feature_x=packert_in rate, byte_rate, paket_rate

M, N $ \leftarrow $ 5, 10

BPA, $\scriptstyle  \phi \leftarrow $ [], []

Fori in N do

　　 $\scriptstyle {O_i}$ =Binary_base(Feature_x)

　　 Forj in M do

　　　　 $\scriptstyle \varphi $ .append( $\scriptstyle {O_i}$ )

　　　　 $\scriptstyle \tau _i^j = \left( {O_{i, 1, 2}^j, O_{i, 1, 3}^j, O_{i, 1, 4}^j ,\ldots , O_{i, 3, 4}^j, O_{i, 4, 5}^j} \right)$

　　　　 $\scriptstyle Dis\left( {{m_i}} \right)$ =Dis_calculate( ${{τ }}_{{i}}^j$ )

　　 $\scriptstyle m_i^{} = O_i^{} = $ $\scriptstyle \frac{{\mathop \sum \nolimits_{i = 1}^{10} {\text{τ }}_{\text{i}}^j}}{{\mathop \sum \nolimits_{j = 1}^5 \mathop \sum \nolimits_{i = 1}^{10} {\text{τ }}_{\text{i}}^j}}$ =( $\scriptstyle O_i^1, O_i^2, O_i^3, O_i^4, O_i^5)$

　　BPA.append( $\scriptstyle m_i^{}$ )

　　 End

End

For i in BPA do

　　 Pure( $\scriptstyle {m_i}$ ) =Pure_calculate( $\scriptstyle BPA_i^{}$ )

End

R=Dempster_fusion( $\scriptstyle Dis, Pure$ )

3 实验分析

本节对提出的算法进行了实验验证及分析. 在本节中, 所提方法被命名为DFDoS-DS. 实验评估中, 通过比较精度、准确率、召回率、F-score值和混淆矩阵等指标, 本节对比了文献[13]和文献[17]的算法. 其中, 文献[13]和文献[17]的算法分别被命名为Ensemble-DS和SVM-DS.

3.1 实验设置

实验中, 本文在配置i5的CPU的计算机上运行Mininet 2.2.2软件用于生成如图2所示的网络拓扑. 此外, 本文将RYU 4.9.1作为SDN中的控制器. 本文通过设置带外模式使用Mininet软件搭建网络拓扑并连接RYU控制器. 根据相关研究工作^[21–24], 本文按如下方式生成该网络中的背景流量: 背景流量由不同协议组成, 其中TCP协议占比80%, UDP协议占比15%, ICMP协议占比5%. 同时, 背景流量中数据包的大小和速率服从泊松分布. 此外, 本文使用了两种攻击方式: (1)攻击者将通过泛洪的方式发起高速DDoS攻击, (2)攻击者通过控制(T, L, R)参数以周期性的方式发起低速LDDoS攻击, 其中, T是发起攻击周期, L是发起攻击持续脉冲长度, R是发起攻击速率^{[25, 26]}.

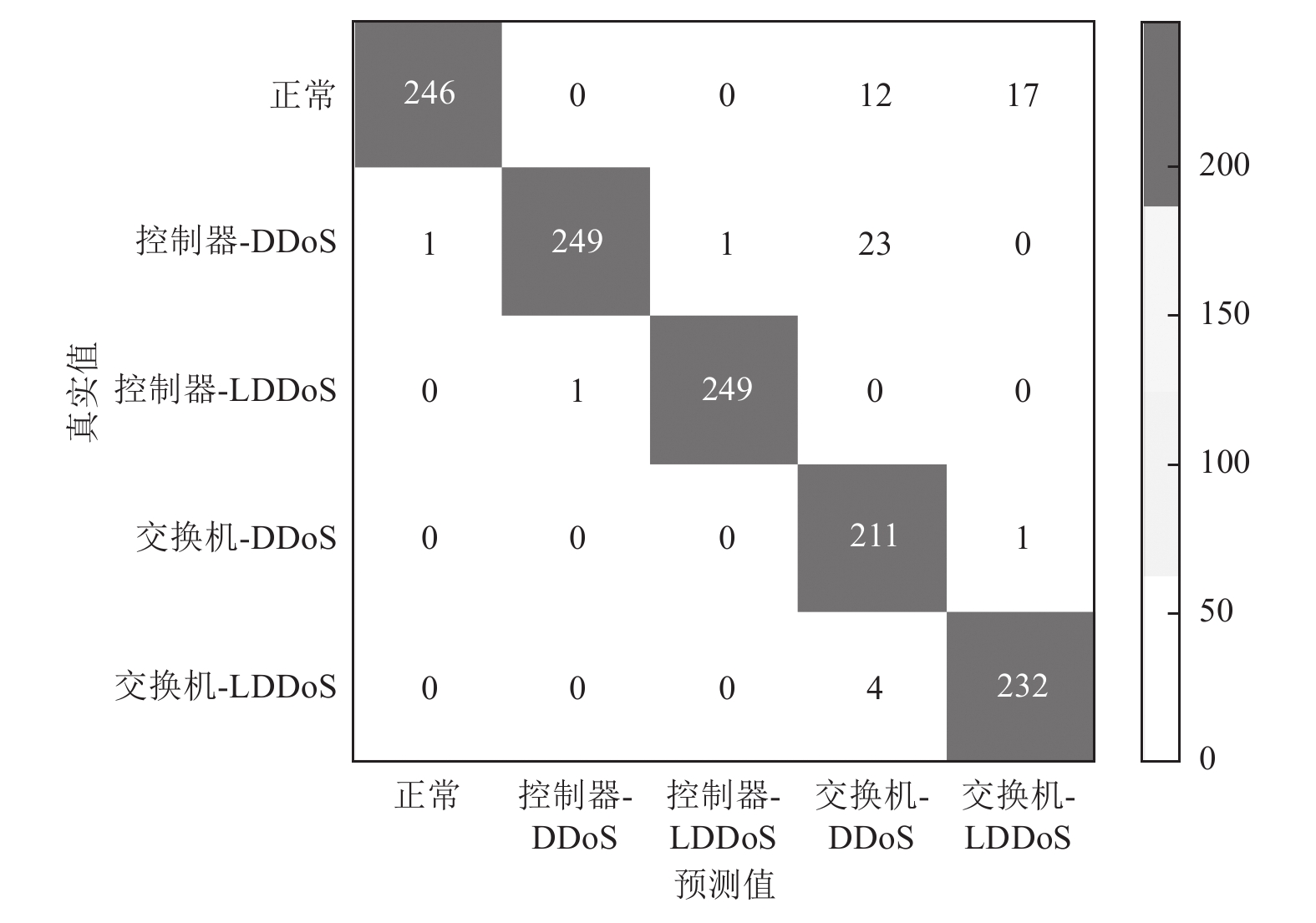
3.2 实验评估

本节对比了DFDoS-DS算法和Ensemble-DS算法以及SVM-DS算法的有效性. 在表1中, 本文通过混淆矩阵、精度、准确率、召回率以及F-score值对比DFDoS-DS算法、Ensemble-DS算法和SVM-DS算法. 图3、图4和图5是DFDoS-DS算法, Ensemble-DS算法和SVM-DS算法的混淆矩阵. 在混淆矩阵指标中, 混淆矩阵中的y轴表示样本的真实分类值,x轴则表示样本的预测分类值.

如表1所示, DFDoS-DS算法的准确率、精度召回率和F-score达到了97%、97%、98%和98%, 同时, SVM-DS的精度、准确率、召回率和F-score是62%、64%、65%和57%. 与SVM-DS比较了精度、准确率、召回率和F-score, DFDoS-DS算法增加了56%、51%、51%和72%. 同时, 相比Ensemble-DS, DFDoS-DS算法的上述指标分别增加了2%、4%、2%和3%.

4 结论

本文提出了一种SDN环境下基于改进D-S理论的DDoS攻击检测方法. 在改进D-S证据理论算法中, 本文设计了离散因子和纯度因子, 用于衡量D-S证据理论中证据源之间的冲突: 离散因子通过支持相同类别的支持度之间的熵值计算得到; 纯度因子是指多分类器内部的不同类别之间的支持度的Gini指数. 最后, 本文结合两种因子调整D-S证据源, 并通过Dempster规则融合得到最终的分类结果. 本文对别了DFDoS-DS算法和Ensemble-DS算法以及SVM-DS算法, 实验结果证明本文提出的方法取得较为优异的结果.