1 引言

随着移动互联网与大数据的发展, 数据规模也以前所未有的速度不断增长, 数据属性之间的相互关系变得复杂多样, 多维数据已是一种常见的数据发布类型^[1]. 在实际应用中, 大量的多维数据被存储在多个分布式组织中, 进行集成后, 这些多维数据将成为做出更好决策和提供高质量服务的宝贵资源.由于数据挖掘和分析技术的提升, 发布多维数据会带来很高的信息价值, 但多维数据中常包含许多隐私信息, 为了保护这些隐私信息在数据发布的过程中不被泄露, 通常会使用差分隐私保护技术. 传统的差分隐私技术将原始数据集中到一个中心服务器, 然后发布满足差分隐私的信息, 通常称其为中心化差分隐私保护(CDP). 因此中心化差分隐私技术始终基于一个可信的第三方数据收集者并保证不会窃取或泄露用户的敏感信息的前提. 然而想要找到一个真正可信的第三方数据收集者是非常困难的. 鉴此, 在缺少可信的第三方数据收集者的情况下, 本地化差分隐私(LDP)^[2-4]应运而生, 目前已在业界得到应用. 但多数的本地化差分隐私技术不适用于多维数据, 若直接将其应用于多维数据会造成通信开销较大, 可用性差等问题.

目前, 本地化差分隐私技术已经成为继中心化差分隐私技术之后一种强健的隐私保护模型. 首先, 用户对原始数据进行满足 $ \varepsilon - $ 本地化差分隐私的扰动, 然后将其传输给第三方数据收集者, 数据收集者收到扰动后的数据再进行一系列的查询和求精处理, 以得到有效的统计结果. 对本地化差分隐私的研究和应用, 主要考虑以下两个方面问题: (1) 如何设计满足 $ \varepsilon - $ 本地化差分隐私的扰动算法; (2) 数据收集者如何对收集到的数据集进行求精处理, 以提高统计结果的可用性. 本文中, 求精处理即通过基本推理和机器学习的方法来捕捉收集到数据集的联合概率分布^[5-7]的过程.

为解决数据收集阶段的隐私泄露, 本地化差分隐私保护通信开销较大以及数据收集者求精处理的问题, 本文提出了RR-LDP算法和LREMH算法, 主要工作如下:

(1) 提出了一个适用于多维数据的本地差分隐私保护算法(RR-LDP). 该算法相比直接将RAPPOR^[8]应用于多维数据上极大地降低了通信开销.

(2) 结合期望最大化(EM)算法和LASSO回归模型, 提出了一种高效的多维数据联合分布估计混合算法(LREMH). 在真实数据集上进行性能评估, 实验结果表明LREMH算法在精度和效率之间取得了平衡.

2 相关工作

Erlingsson等人^[8]提出RAPPOR应用随机响应技术和布隆过滤器来实现本地化差分隐私, 并应用在谷歌浏览器上. 苹果的差分隐私团队提出使用one-hot编码技术对敏感数据进行编码, 并部署CMS算法分析Safari中最流行的表情符号和媒体播放偏好. 文献[9]通过结合LDP与集中式数据模式, 提出具有高可用性的混合模型BLENDER. 文献[10]针对移动设备收集隐私数据问题, 构建了Harmony系统, 该系统支持满足LDP的统计分析与机器学习功能. 随机响应技术及其变体在收集分布式用户统计数据的安全性方面具有优势, 已成为LDP研究的热点. 但目前多数的LDP机制并不适用于多维且多值的数据.

Giulia等人^[11]提出基于EM的学习算法从噪声样本空间中估计联合概率分布. 然而它们的方案适用于二维数据, 当维数较高时, 数据的稀疏性会导致很大的效用损失, EM算法的复杂度也会呈指数级上升. Ren等人^[12]打破了文献[11] EM算法的局限, 将其拓展用于处理多维数据. Li等人^[13]提出使用Copula函数来模拟多维数据的联合分布, 但Copula函数不能处理小域的属性. Cormode等人^[14]将Hadamard变换应用于发布本地边缘表, 其优势是节省了通信开销, 但只适用于二进制数据. Zhang等人^[15]借鉴PriView^[16]的思想提出CLMA方法, 该方法可以在不计算满边际的情况下释放任意方向的边缘表, 并且可以处理非二进制属性. 然而, 除了隐私保护带来的噪声误差外还引入了采样误差.

3 基础知识 3.1 本地化差分隐私(LDP)

定义1. $ \varepsilon - $ 本地化差分隐私. 对于一个有 $ N $ 条记录的数据集 $ D $ , 给定随机算法 $ Q $ 满足 $ \varepsilon - $ 本地化差分隐私保护, $ R{\text{ange(}}Q{\text{)}} $ 为随机算法 $ Q $ 的取值范围, 那么算法 $ Q $ 在任意两条记录 $ {X_1} $ 和 $ {X_2} $ $ \left( {{X_1}, {X_2} \in D} \right) $ 上得到相同的输出结果 $ {X^*} $ 的概率满足:

$ P[Q({X_1}) = {X^*}] \leqslant {e^\varepsilon }P[Q({X_2}) = {X^*}] $

(1)

其中, 概率 $ P[ \cdot ] $ 表示隐私泄露风险, $ \varepsilon $ 表示隐私预算, 代表了隐私保护水平, 其值越小表示不可区分性越大, 隐私保护等级越高.

性质1. 序列组合性^[17]. 给定数据集 $ D $ 和 $ n $ 个隐私算法 $ \{ {Q_1}, \cdots, {Q_n}\} $ 且算法 ${Q_i}\;(1 \leqslant i \leqslant n)$ 满足 $ {\varepsilon _i} - $ 本地化差分隐私, 那么 $ \{ {Q_1}, \cdots, {Q_n}\} $ 在 $ D $ 上的序列组合满足 $ \varepsilon - $ 本地化差分隐私, 其中, $ \varepsilon = \displaystyle\sum\nolimits _{i = 1}^n{\varepsilon _i} $ .

3.2 随机响应技术

随机响应技术(randomized response) 是本地化差分隐私保护的主流扰动机制, 旨在调查过程中使用随机化装置, 使被调查者以一个预定的概率 $p$ 进行诚实的回答, $(1 - p )$ 的概率随意进行回答. 除被调查者以外的任何人均不知道被调查者的回答是否真实, 最后根据概率论的知识计算出敏感问题特征在人群中的真实分布情况的一种调查方法. 假设对 $ n $ 个用户的问答进行统计, 得到患病人数的统计值. 其中真实患病的比例记为 $ \pi $ , 假定回答“Yes”的人数为 $ {n_1} $ , 回答“No”的人数记为 $ {n_2} $ . 根据诚实回答的概率 $ \theta $ 可得:

$\left\{ \begin{array}{l} Pr[{x}_{i}={\text{``}}\text{Yes}\text{"}]=\pi \cdot p+(1-\pi )\cdot (1-p)\\ Pr[{x}_{i}=\text{``}\text{No}\text{"}]=(1-\pi )\cdot p+\pi \cdot (1-p) \end{array} \right.$

(2)

为了得到无偏估计, 可以采用极大似然的方法进行估计:

$ L = {[\pi \cdot p + (1 - \pi ) \cdot (1 - p)]^{{n_1}}} \cdot {[(1 - \pi ) \cdot p + \pi \cdot (1 - p)]^{n - {n_1}}} $

(3)

然后可以求得 $ \pi $ 的估计 $ \tilde \pi $ :

$ \tilde \pi = \frac{{p - 1}}{{2p - 1}} + \frac{{{n_1}}}{{\left( {2p - 1} \right)n}} $

(4)

则患病的人数 $ \tilde n $ 可估计为:

$ \tilde n = n \cdot \tilde \pi = \frac{{p - 1}}{{2p - 1}}n + \frac{{{n_1}}}{{\left( {2p - 1} \right)}} $

(5)

4 满足LDP的多维数据联合概率分布估计 4.1 设计思路

首先, 根据属性域的大小和每个取值在属性域中的位置将所有变量映射为位串, 得到的位串代表了唯一的原始记录. 然后, 通过随机响应技术进行第一次扰动, 得到的结果称作永久随机响应, 并将其保存在用户本地, 在第三方数据收集者请求数据时, 对永久随机响应的结果再做一次扰动, 得到的结果称作瞬时随机响应, 将瞬时随机响应的结果发送给第三方数据收集者. 最后, 数据收集者聚合收集到的得到随机噪声样本空间, 利用机器学习技术, 可以从中估计联合概率分布, 进行求精处理.

本文所使用的相关符号定义如表1所示.

4.2 本地差分隐私保护

在本文的本地化差分隐私保护机制设计如算法1所示, 其中包含3个关键的步骤.

算法1. RR-LDP算法

输入: 用户数据记{ $\scriptstyle {x}_{j}^{i},\;j=1, 2, \cdots, d$ }, 属性集 $\scriptstyle {A_j} $ , 随机翻转概率 $\scriptstyle f $ , 位串长度 $\scriptstyle \left| {{\Omega _j}} \right| $

输出: 随机翻转后的位串 $\scriptstyle {T^i} $

1. for $\scriptstyle 1 \leqslant j \leqslant d $

2. 根据取值将 $\scriptstyle x_j^i $ 映射为一个长为 $\scriptstyle \left| {{\Omega _j}} \right| $ 的位串 $\scriptstyle s_j^i $

3. 根据 $\scriptstyle f $ 随机翻转 $\scriptstyle s_j^i $ 中的每一位, 得到扰动后的位串 $\scriptstyle \hat s_j^i $

4. end for

5. 对 $\scriptstyle \hat s_j^i $ 进行瞬时随机扰动, 得到 $\scriptstyle T_j^i $

6. 将翻转后的每个位串连接起来得到一个 $\scriptstyle \sum\nolimits_{j = 1}^d { \left| {{\Omega _j}} \right| }$ 位的向量 $\scriptstyle {T^i} $ 并返回

(1) 假设第 $ i $ 个用户有一个包含 $ d $ 个属性的原始数据记录 $ {X^i} = \{ x_1^i, x_2^i, \cdots, x_d^i\} $ . 用属性 ${A_j}\;(1 \leqslant j \leqslant d)$ 的值域大小 $ \left| {{\Omega _j}} \right| $ 来确定预定义的位串长度, 每种属性的取值 $ {\omega _j} $ 对应位串中的一位, 进行数据转换时, 将每个属性取值所对应的那一位置1, 其余位置0, 即可该数据唯一的位串 $ s_j^i $ .

(2) 位串 $ s_j^i $ 中的每一位 $ s_j^i[b] $ 根据概率 $ f \in (0, 1) $ 按照式(6)进行随机翻转.

$ \hat s_j^i[b] = \left\{ \begin{gathered} s_j^i[b], {\text{ }}概率=1 - f \\ 0, {\text{ }} 概率=f/ 2 \\ 1, {\text{ }} 概率=f/ 2 \\ \end{gathered} \right. $

(6)

上述过程为永久随机响应. 永久随机响应可以保证用户端相互通信时的隐私安全问题, 抵御纵向攻击. 由于每条记录中所有属性的取值是独立的, 故所得到 的二进制位串可唯一代表一条记录.

(3) 初始化一个长度为 $ \left| {{\Omega _j}} \right| $ 的全0位串 $ T_j^i $ , 对 $ \hat s_j^i[b] $ 根据式(8)进行瞬时随机扰动.

$ P(T_j^i[b] = 1) = \left\{ \begin{gathered} p, {\text{ if }}\hat s_j^i[b] = 0 \\ q, {\text{ if }}\hat s_j^i[b] = 1 \\ \end{gathered} \right. $

(7)

其中, $ p \in (0, 1) $ 是当 $ \hat s_j^i[b] = 0 $ 时, $ T_j^i[b] = 1 $ 的概率, $ q \in (0, 1) $ 是当 $ \hat s_j^i[b] = 1 $ 时, $ T_j^i[b] = 1 $ 的概率.

用户 $ i $ 的每个属性的位串 $ s_j^i $ 经过永久随机响应后得到位串 $ \hat s_j^i $ , 再经过瞬时随机响应后得到 $ T_j^i $ , 将它们连接起来得到一个 $ \displaystyle\sum\nolimits_{j = 1}^d { \left| {{\Omega _j}} \right|} $ 位的向量 $ T_{}^i $ .

$ T_{}^i = \left[ {T_1^i[1], \cdots, T_1^i[\left| {{\Omega _1}} \right|]|\cdots|T_d^i[1], \cdots, T_d^i[\left| {{\Omega _d}} \right|]} \right] $

根据文献[8]的计算可以得到当 $ T_j^i[b] = 1 $ 时, $ s_j^i[b] = 1 $ 的概率为:

$ q^* = P(T_j^i[b] = 1|s_j^i[b] = 1) = 0.5f(p + q) + (1 - f)q $

(8)

当 $ T_j^i[b] = 1 $ 时, $ s_j^i[b] = 0 $ 的概率为:

$ p^* = P(T_j^i[b] = 1|s_j^i[b] = 0) = 0.5f(p + q) + (1 - f)p $

(9)

由于服务器每次请求数据时都要做一次瞬时随机响应, 所以服务此每次请求相同的数据得到的结果都是不同的, 此时就可以保证服务器不能通过多次请求数据进行推断攻击.

在本文的RR-LDP方案采用一元编码的方式进行二进制转换, 相比于RAPPOR^[8]所使用布隆过滤器进行二进制转化的方法, 本文映射后的位串长度更小且由于布隆过滤器使用哈希函数进行映射会出现哈希冲突造成映射后的位串冲突, 而RR-LDP则不会.

通信开销对比: 假设所有属性的值域都是公开的, 则RR-LDP的通信开销最小为 $ \displaystyle\sum\nolimits_{j = 1}^d { \left| {{\Omega _j}} \right|} $ , 如果直接将RAPPOR^[8]应用在多维数据上, 它会将其视为一维数据, 此时的通信开销为 $ \prod\nolimits_{j = 1}^d {\left| {{m_j}} \right|} $ .其中, $ {m_j} $ 为布隆过滤器预定义的位串长度.

4.3 隐私分析

定理1. 在用户端进行的永久随机响应过程满足 $ {\varepsilon _1} - $ 本地化差分隐私, 其隐私保护等级为:

$ {\varepsilon _1} = 2d\ln ((2 - f)/f) $

(10)

证明: 令 $ S $ 表示用户初始的位串, ${S{'}}$ 表示经过本地随机翻转的位串. $ {S_1} $ 和 $ {S_2} $ 分别代表两个不同用户的记录, 令它们的条件概率比值记作 $ RR $ , $RR = P({S{'}} = S^*|S = {S_1})/ P({S{'}} = S^*|S = {S_2})$ , 它与隐私保护等级 $ {\varepsilon _1} $ 相关. 由式(6)可以得到位串的每一位翻转的概率为 $ f/2 $ , 不翻转的概率为 $ 1 - f/2 $ , 由文献[8]可得到 $ R{R_{\max }} = {((2 - f)/f)^2} $ , 此时的隐私保护等级 $ {\varepsilon _1} = 2\ln ((2 - f)/f) $ , 其中 $ f $ 为随机翻转概率. 根据差分隐私序列组合性质^[17], $ d $ 维数据记录的本地翻转满足 $ {\varepsilon _1} - $ 本地化差分隐私, 其 $ {\varepsilon _1} = 2d\ln ((2 - f)/f) $ , 其中 $ d $ 为原始数据集 $ D $ 中属性的个数.

定理2. 在用户端进行的瞬时随机响应过程满足 $ {\varepsilon _2} - $ 本地化差分隐私, 其隐私保护等级为:

$ {\varepsilon _2} = \log \left(\frac{{q^*(1 - p^*)}}{{p^*(1 - q^*)}}\right) $

(11)

证明过程与定理1类似, 详见文献[8]. 因为相同的转换是由所有用户独立完成的, 所以上述本地化差分隐私保护适用于所有分布式用户.

4.4 基于期望最大化算法(EM)的联合分布估计算法

EM算法是在存在缺失或不完整数据的情况下获得最大似然估计的常用方法. 它特别适合于RAPPOR^[8]这种只收集它们的噪声表示且真实值未知的应用中. 文献[12]中的EM算法主要分为以下3步:

第1步: 初始化, $ P({\omega _1}{\omega _2}\cdots{\omega _k}) = 1/(\prod\nolimits_{j = 1}^k {\left| {{\Omega _d}} \right|} ) $ , 设置均匀分布分布作为初始的先验概率;

第2步: 更新, 根据式(6)得到原始位串的每一位 $ s_j^i[b] $ 翻转的概率为 $ f/2 $ , 不翻转的概率为 $ 1 - f/2 $ . 通过比较属性域与 $ \hat s_j^i $ 可得条件概率 $ P(\hat s_j^i|{\omega _j}) $ ; 由于本地化随机翻转是独立进行的, 其联合条件概率分布 $ P(\hat s_1^i\hat s_2^i\cdots\hat s_k^i| {\omega _1}{\omega _2}\cdots{\omega _k}) = \prod\nolimits_{j = 1}^k {P(\hat s_j^i|{\omega _j})} $ 可以通过组合每个属性来计算, 得到一个特定的位串组合的所有条件分布, 通过贝叶斯定理计算它们对应的后验概率 $ {P_t}({\omega _C}|\hat s_C^i) = {P_t}({\omega _C}) \cdot P(\hat s_C^i|{\omega _C})/{\Sigma _{{\omega _C}}}{P_t}({\omega _C}) \cdot P(\hat s_C^i|{\omega _C}) $ , 其中 ${P_t}({\omega _C}) = {P_t}({\omega _1}{\omega _2}\cdots{\omega _k})$ 为第t次迭代时的 $ k $ 维联合概率;

第3步: 迭代, 得到后验概率后, 通过计算后验概率的平均值来更新先验概率. 在下一次迭代中利用更新后的先验概率计算后验概率. 用上述方法进行迭代直至收敛, $max{P_t}({\omega _1}{\omega _2}\cdots{\omega _k}) - max{P_{t - 1}}({\omega _1}{\omega _2}\cdots{\omega _k}) \geqslant \delta$ .

其中 $ k $ 为指定属性, 如 $ {A_1}, {A_2}, \cdots, {A_k} $ , $ C $ 为 $ k $ 的索引集, $ C = \{ 1, 2, \cdots, k\} $ . $ {A_j} = {\omega _j} $ 或 $ {x_j} = {\omega _j} $ 都用 $ {\omega _j} $ 来表示.

EM算法具有较高的精度, 但对初始值比较敏感, 当初始值选择合适时, 上述方法能达到较好的收敛效果. 然而文献[12]将联合分布初始化为均匀分布, 显然不是最优的, 当属性个数 $ k $ 增大时, 由于 $ {\Omega _1} \times {\Omega _2} \times \cdots \times {\Omega _k} $ 中所有组合的样本空间爆发性增长, 算法的复杂度也会急剧上升, 阻碍良好的收敛. 同时多维数据呈现出的稀疏性也会带来较大的误差, 从而导致最终的估计达不到所需的效用.

4.5 基于LASSO回归的联合分布估计算法

LASSO回归最早由Tibshirani于1996年提出^[18], 文献[8]将它和最小二乘法用于收到噪声样本后的解码工作. 如第4.1节所述, 位串是原始记录的唯一代表. 随机翻转后, 本地用户会产生大量不同程度的噪声样本. 此时, 可以利用 $ \vec y = M\beta $ 来估计噪声样本空间的联合分布, 其中M是预测变量, $ \vec y $ 是响应变量, $\; \beta $ 是回归系数向量, 这里的目的是估计M上的分布, 而不是原来的域. 响应变量 $ \vec y $ 可以根据已知的随机翻转概率 $ f $ , 从位串中估计出来. 因此, 唯一的问题就是求出一个准确的回归系数 $ \;\beta $ . 基于LASSO回归的联合分布估计主要包含以下几步:

第1步: 在服务器接收到所有经过随机翻转的位串后, 对其值为1的位进行计数, 记为 $ {\hat y_i}[b] = \displaystyle\sum _{i = 1}^N\hat s_j^i[b] $ ;

第2步: 根据随机翻转概率 $ f $ , 扰动前位串中每一位为1的真实计数 $ {y_i}[b] $ 可以被估算为 $ {y_i}[b] = ({\hat y_i}[b] - fN/2)/ (1 - f) $ , 这些计数构成响应向量 $ \vec y $ , 其长度为 $\displaystyle \sum _{i = 1}^k{m_j} $ , 其中 $ {m_j} $ 为布隆过滤器预定义的位串长度;

第3步: 假设在域 $ {\Omega _j} $ 上所有的哈希函数为 $ {H_i}({\Omega _j}) = \{ {H_i}(\omega )|\forall \omega \in {\Omega _j}\} $ , 那么可以得到任意维度的候选集 $M = [{H_1}({\Omega _1}) \times {H_2}({\Omega _2}) \times \cdots\times{H_k}({\Omega _k})]$ ;

第4步: 对响应向量 $ \vec y $ 和候选矩阵M拟合一个LASSO回归模型, 然后选择非零系数作为每个候选串对应的频率. 通过将系数向量 $\; \vec \beta $ 按顺序重构为 $ k $ 维矩阵, 并除以 $ N $ , 就可以得到 $ k $ 维联合分布.

4.6 LREMH算法

基于EM的算法在样本足够的情况下, 可以表现出良好的收敛性, 但也会产生很高的复杂度. 其高复杂度是因为它迭代扫描用户的数据, 并构建一个先验分布表, 其大小为 $ N \cdot \prod {\left| {{\Omega _j}} \right|} $ . 然而, 在多维情况下, $ {\Omega _j} $ 的组合是非常稀疏的, 且有很多零项. 同时, 由于EM对初始值的选择敏感, 均匀分配的初始值会导致收敛速度较慢. 然而基于LASSO回归的联合分布估计方法可以有效地解决由于多维数据的稀疏性导致的过拟合和效率慢的问题, 但与基于EM的算法相比, 精度略有下降.

为了在精度和效率之间取得平衡, 本文提出了LREMH算法, 该算法首先用基于LASSO回归的方法估计初始值, 这样得到的初始值会比均匀分布的初始值更加精确, 同时对基于EM算法的收敛性有积极的改进作用, 然后根据LASSO回归模型计算出冗余候选项, 并消除他们, 从而提高计算效率, 最后使用EM算法进行迭代计算得到一个较为准确的估计值.

算法2. LREMH算法

输入: $\scriptstyle {A_j} $ , $\scriptstyle \left| {{\Omega _j}} \right| $ , $\scriptstyle f $ , 索引集 $\scriptstyle C $ , $\scriptstyle {T^i} $

输出: $\scriptstyle {P_0}({\omega _1}{\omega _2}\cdots{\omega _k})$

1. for each $\scriptstyle j \in C $ do

2. for each b=1, 2, $\scriptstyle \cdots$ , $\scriptstyle \left| {{\Omega _j}} \right| $ do

3. 计算 $\scriptstyle {\hat y_j}[b] = \sum _{i = 1}^NT_j^i[b] $

4. 计算 $ \scriptstyle{y_j}[b] = {{[{{\hat y}_j}[b] - N(p + 0.5fq - 0.5fp)]} \mathord{\left/ {\vphantom {{[{{\hat y}_j}[b] - N(p + 0.5fq - 0.5fp)]} {(1 - f)(q - p)}}} \right. } {(1 - f)(q - p)}} $

5. end for

6. end for

7. 令 $\scriptstyle \vec y = [{y_1}[1], \cdots, {y_1}[\left| {{\Omega _1}} \right|]|\cdots|{y_k}[1], \cdots, {y_k}[\left| {{\Omega _k}} \right|]]$

8. 令 $\scriptstyle M = [({\Omega _1}) \times ({\Omega _2}) \times \cdots({\Omega _k})]$

9. 计算 $\scriptstyle \;\vec \beta = Lasso(M, \vec y) $ /*使用回归分析计算初始值*/

10. 返回 $\scriptstyle {P_0}({\omega _1}{\omega _2}\cdots{\omega _k}) = \vec \beta /N$

11. 令 $\scriptstyle C' = \{ x|x \in C, {P_0}(x) = 0\} $

12. for each $\scriptstyle i = 1, \cdots, N$ do

13. for each $\scriptstyle j = 1, \cdots, k$ do

14.　 for each b=1, $ \scriptstyle \cdots $ , $\scriptstyle \left| {{\Omega _j}} \right| $ do

15.　　 if $\scriptstyle T_j^i[b] = 1 $

16. 　　计算 $\scriptstyle P(T_j^i|{\omega _j}) = \prod\nolimits_{b = 1}^{\left| {{\Omega _j}} \right|} {q{*^{\left| {T_j^i[b] \cdot {\text{ }}{\omega _j}[b]{\text{ }}} \right|}}} p{*^{\left| {T_j^i[b] - {\omega _j}[b]{\text{ }}} \right|}}$

17. 　　else

18. 　　计算 $\scriptstyle P(T_j^i|{\omega _j}) = \prod\nolimits_{b = 1}^{\left| {{\Omega _j}} \right|} {{{(1 - q*)}^{\left| {T_j^i[b] - {\omega _j}[b]{\text{ }}} \right|}}} {(1 - p*)^{\left| {T_j^i[b] - {\omega _j}[b]{\text{ }}} \right|}} $

19. 　　end if

20. 　end for

21. end for

22. if $\scriptstyle {\omega _1}{\omega _2}\cdots{\omega _k} \in C'$

23. 　 $\scriptstyle P(T_1^i\cdots T_k^i|{\omega _1}\cdots{\omega _k}) = 0$

24. else

25. 　　计算 $\scriptstyle P(T_1^i\cdots T_k^i|{\omega _1}\cdots{\omega _k}) = {\Pi _{j \in C}}P(T_j^i|{\omega _j})$

26. end if

27. end for

28. 初始化 t=0 /*迭代次数*/

29. repeat

30. for each $\scriptstyle i = 1, \cdots, N$ do

31.　 for each $\scriptstyle {\omega _c} \in ({\Omega _1}) \times ({\Omega _2}) \times \cdots({\Omega _k})$ do

32. 　 $\scriptstyle {P_t}({\omega _c}|T_C^i) = {P_t}({\omega _c}) \cdot P(T_C^i|{\omega _c})/{\Sigma _{{\omega _C}}}{P_t}({\omega _c}) \cdot P(T_C^i|{\omega _c}) $

33. 　end for

34. end for

35. 令 $\scriptstyle {P_{t + 1}}({\omega _c}) = \sum _{i = 1}^N{P_t}({\omega _c}|T_C^i)/N $

36. 更新t=t+1

37. 直到 $\scriptstyle max{P_t}({\omega _1}{\omega _2}\cdots{\omega _k}) - max{P_{t - 1}}({\omega _1}{\omega _2}\cdots{\omega _k}) \geqslant \delta$

38. 返回 $\scriptstyle P({A_c}) = {P_t}({\omega _c}) $

本文提出的LREMH算法主要包含以下3个步骤:

第1步: 计算初始值, 根据永久随机响应翻转概率 $f$ 和瞬时随机响应的翻转概率 $ p和q $ , 使用基于LASSO回归的联合分布方法计算初始值(第1–10行).

第2步: 消除冗余项, 利用基于LASSO回归的联合分布估计方法得到联合分布为0的属性并消除他们(第11, 22–23行).

第3步: 更新迭代, 根据永久随机响应翻转概率 $f$ 和瞬时随机响应的翻转概率 $ p和q $ , 使用基于EM的联合分布估计算法通过组合每个属性来计算得到一个特定的位串组合的所有条件分布, 通过贝叶斯定理计算它们对应的后验概率. 得到后验概率后, 通过计算后验概率的平均值来更新先验概率. 在下一次迭代中利用更新后的先验概率计算后验概率. 使用上述方法进行迭代直至收敛(第12–37行).

上述LREMH算法具有两个优势:

(1) 回归分析能够非常有效地选择稀疏的候选项. 因此, EM算法可以只计算这些稀疏候选项上的条件概率, 而不是所有候选项上的条件概率, 从而降低了时间和空间复杂度.

(2) EM算法对初值比较敏感, 尤其是在候选空间稀疏的情况下. 回归分析可以对联合分布产生较好的初始估计. 相对于均匀赋值的初值, 使用回归分析生成的初值可以进一步加快EM算法的收敛速度.

4.7 满足本地化差分隐私证明

证明. 在LREMH算法中, 所有的输入数据的都是经过RR-LDP算法处理后的数据, 且LREMH算法的整个流程中没有任何操作引入其他隐私保护和随机扰动, RR-LDP算法的永久随机响应和瞬时随机响应根据定理1和定理2证得分别满足 $ {\varepsilon _1} - $ 本地化差分隐私和 $ {\varepsilon _2} - $ 本地化差分隐私, 根据本地化差分隐私的性质1 (序列组合性)可证得, LREMH算法满足 $ \varepsilon - $ 本地化差分隐私, 其中 $ \varepsilon = {\varepsilon _1} + {\varepsilon _2} $ .

5 实验与分析 5.1 实验环境

实验中使用了两个真实数据集, NLTCS和Adult. NLTCS数据集来自美国护理调查中心, 包含21 574名残疾人不同时间段的活动. 成人数据集来自1994年美国人口普查, 包含45 222个居民的个人信息, 如性别、工资和教育水平. 在预处理中对一些连续域进行了离散化处理并删除了一些缺省值.

实验中所使用的软硬件参数如下:

(1) 操作系统: Windows 10;

(2) 硬件参数: IntelCore i5, 2.0 GHz CPU, 4 GB;

(3) 编译环境及工具: Python 2.7, PyCharm.

本文分别从数据集NLTCS和数据集Adult中采样了20%的数据和10%的数据. 算法的效率是通过计算估计时间和估计的精度来衡量的. 每组实验运行10次, 并报告平均运行时间. 为了测量精度, 本文使用了两个数据集上的平均变异距离(AVD)来量化估计的联合分布 $ P(\omega ) $ 和原始联合分布 $ Q(\omega ) $ 之间的接近程度.

$ Dis{t_{AVD}}(P, Q) = 0.5{\Sigma _{\omega \in \Omega }}|P(\omega ) - Q(\omega )| $

(12)

为了快速收敛, 将收敛间隙设置为0.001, 在瞬时响应中通常取 q=0.75, p=0.5.

5.2 安全性分析

根据第4.7节的结论, LREMH算法是满足 $ \varepsilon - $ 本地化差分隐私, 又根据本地化差分隐私的两个性质得到 $\varepsilon = {\varepsilon _1} + {\varepsilon _2} = 2d\ln ((2 - f)/f) \,+\; \log [q^*(1 - p^*)/p^*(1 - q^*)]$ , 由于本次实验的 $ p $ 和 $ q $ 是定值, 故 $ \varepsilon $ 的大小只与 $ d $ (数据记录的数量)和 $ f $ (永久随机响应的翻转概率)有关, 而两个数据集的数据记录数 $ d $ 也是确定的, 所以本次实验的安全性只与 $ f $ 相关. 从本地化差分隐私的定义可以看出 $ \varepsilon $ 越小, ${e^\varepsilon }$ 就越小, 数据记录之间的差距就越小, 就越难分辨, 安全性就越强, 反之则 $ \varepsilon $ 的值越大, 安全性就越弱, 本次实验的 $ f $ 取(0, 1), 根据式(10)可以看出随着 $ f $ 的增大 $ \varepsilon $ 的值会减小, 安全性会增强.

5.3 估计效率对比

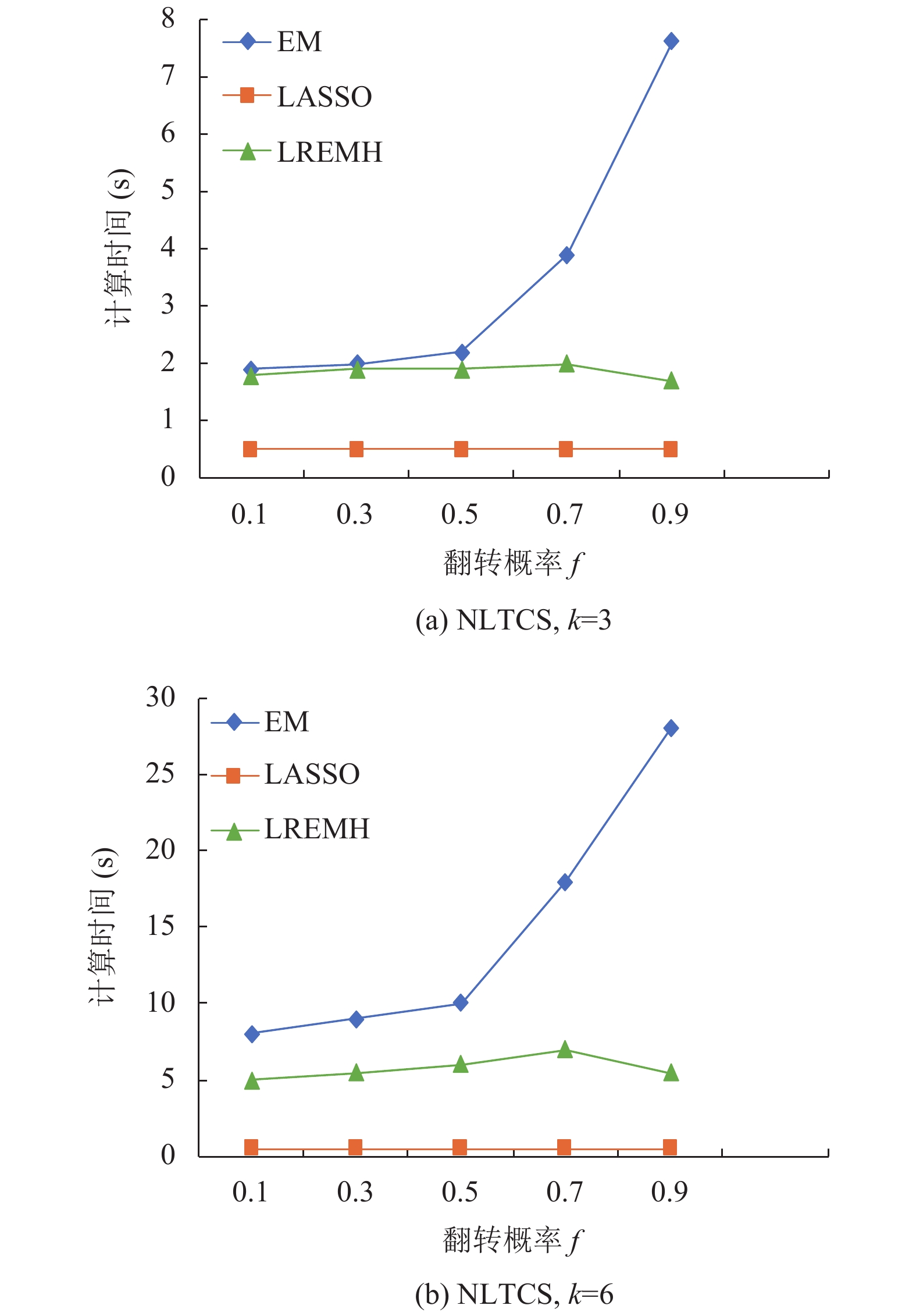
(1) NLTCS数据集: 如图1, 对于任一维度 $ k $ , LASSO回归始终比EM算法和LREMH算法快, 尤其是当 $ k $ 较大时. 由于LASSO回归的时间复杂度主要受用户数量的影响, 所以当 $ k $ 增大时, LASSO回归的计算时间增长缓慢, 而EM算法的计算时间增长较快是因为EM算法必须反复扫描每个用户的位串, 同时, 固定的收敛精度会有更多的迭代从而导致EM算法的时间消耗随着 $ f $ 的增加而增加. 相比之下, LASSO回归可以更有效地估计联合分布. 因为LASSO回归的初始估计可以大大减少候选属性空间和所需的迭代次数, 所以LREMH算法的复杂度要比EM算法小.

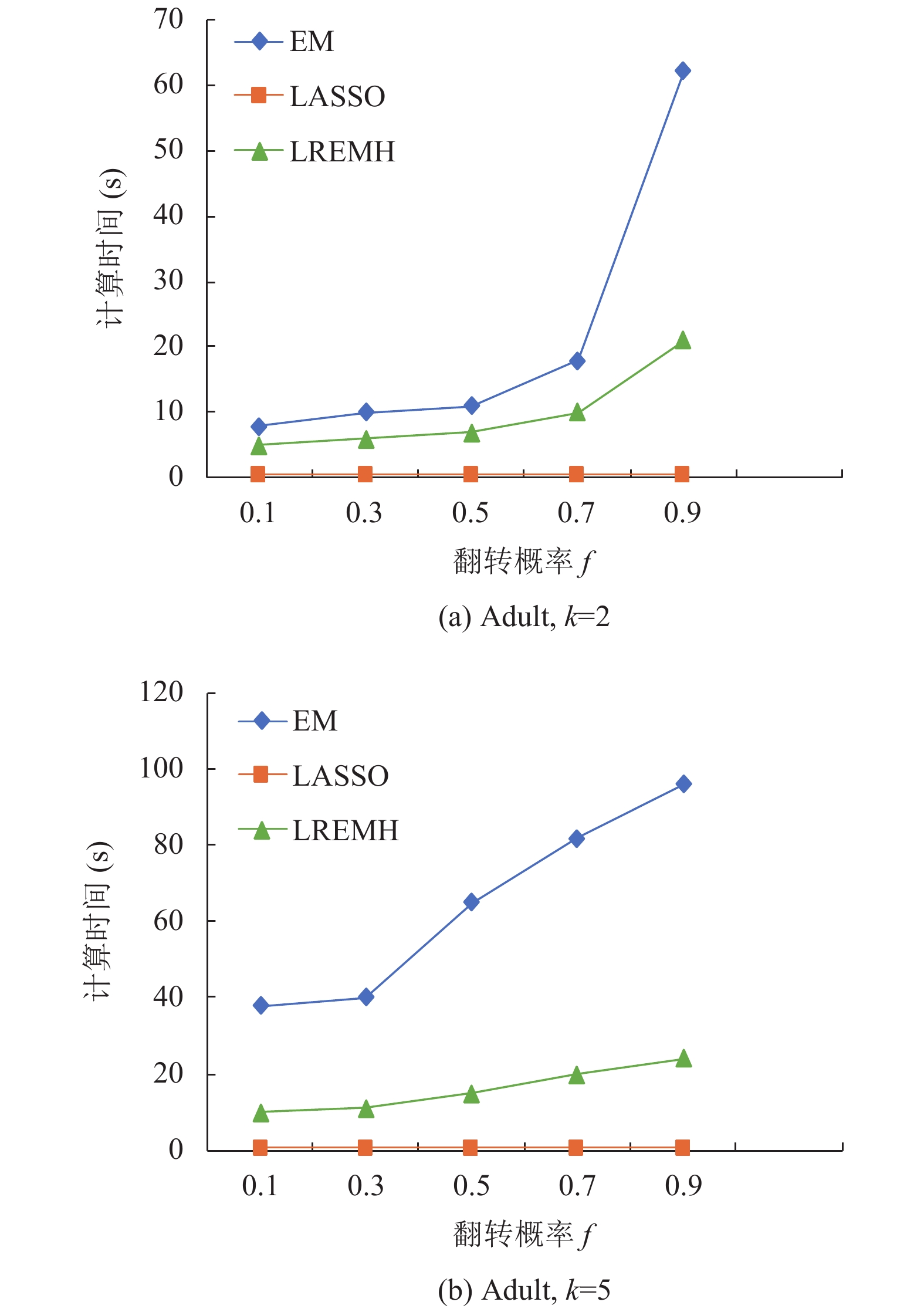
(2) Adult数据集: 如图2, EM算法在低维 $ k $ =2的情况下以可接受的复杂度运行. 当 $ k $ =5时, EM算法的时间复杂度急剧增加了几倍. 当 $ k $ 进一步增加时, 在120 s内没有返回任何结果. 然而, LASSO回归只需要几秒的时间.

5.4 估计精度对比

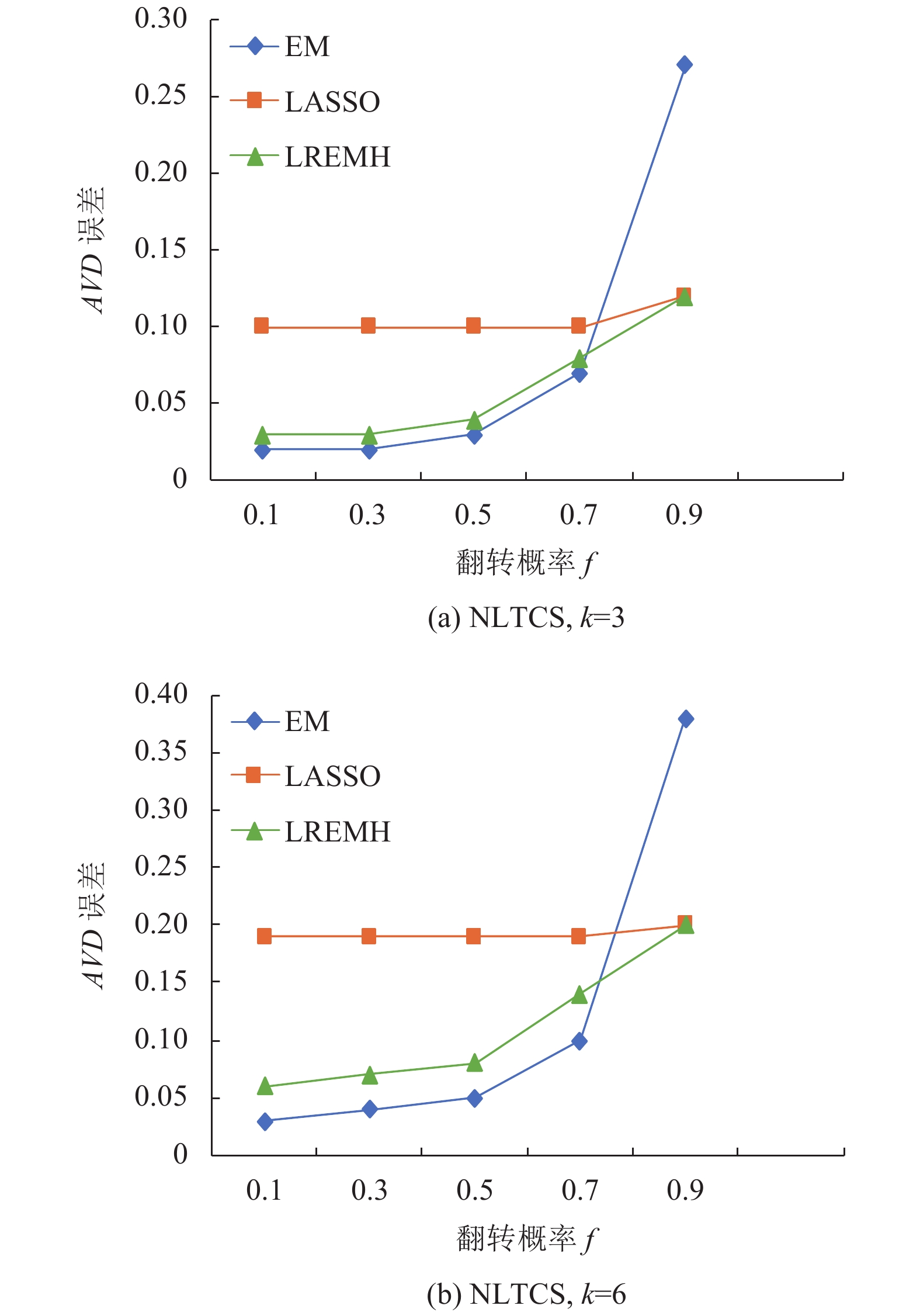
(1) NLTCS数据集: 如图3, 当 $ f $ 很小时, EM算法的AVD误差很小, 但当 $ f $ 增大时, 它会急剧增大, 高达0.28. 相比之下, 即使 $ f $ = 0.9, LASSO回归的AVD误差也保持在0.1左右. 当 $ f $ 较大时, LASSO回归的AVD误差与EM算法相当, 甚至更好. 这是因为LASSO回归在从 $ M $ 和 $ \vec y $ 估计系数时对 $ f $ 不敏感. 由于EM算法扫描每条记录的位串, 所以它对 $ f $ 很敏感, 并且容易得到某些局部最优值. 相比之下, LREMH算法在LASSO回归和EM算法之间实现了更好的权衡. 例如, 当 $ f $ 值较小时, 它的AVD误差小于LASSO回归; 当 $ f $ 值较大时, 它的AVD误差优于EM算法.

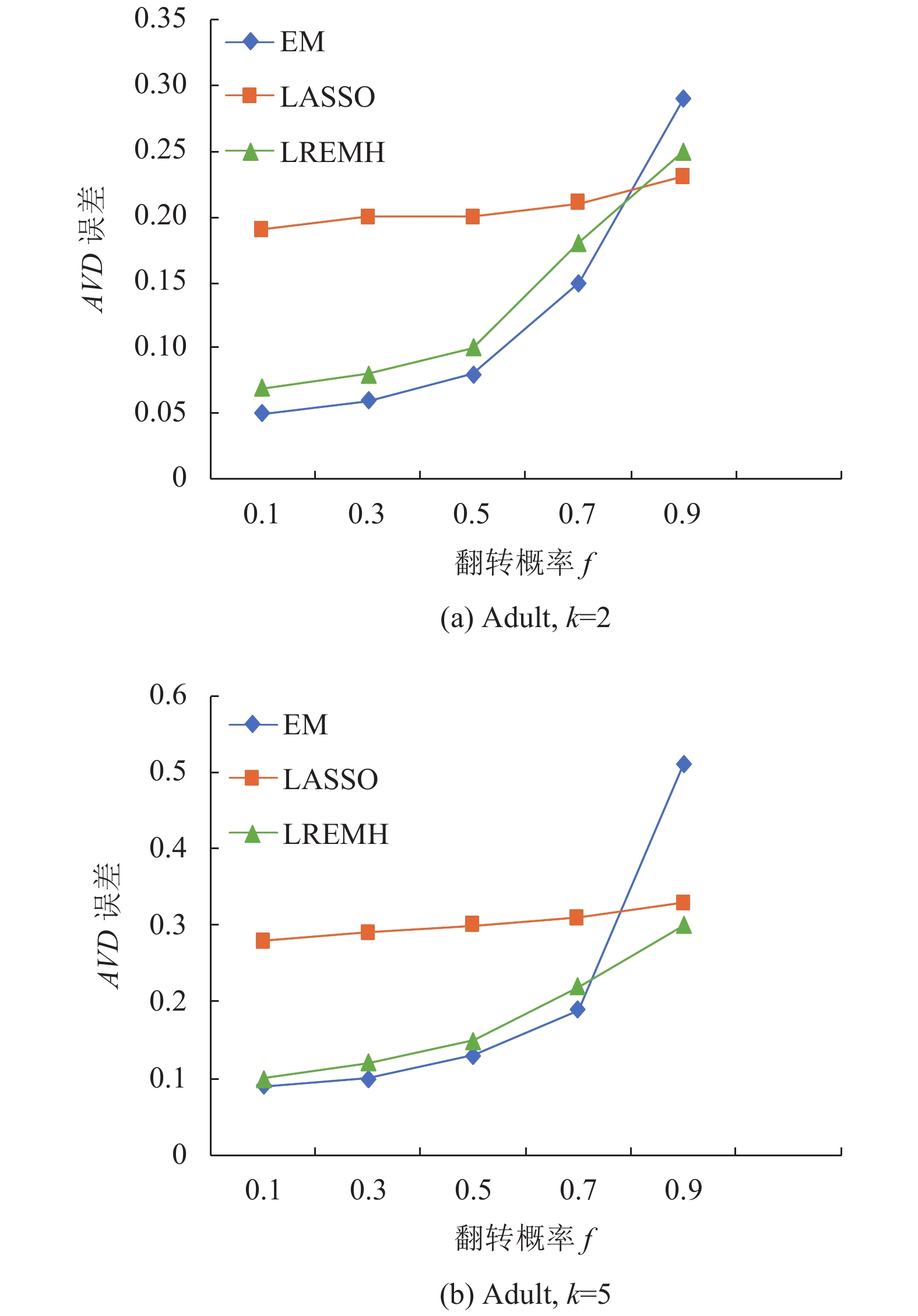
(2) Adult数据集: 如图4, 当 $ k $ = 2时, LASSO回归的AVD误差几乎不随 $ f $ 变化, 因为回归分析对 $ f $ 不敏感. 而EM算法的AVD误差而随 $ f $ 逐渐增大. 当 $ f $ 很大时, LASSO回归的趋势非常接近EM算法. 因为LREMH算法比EM算法运行的快得多且估计精度于EM算法相差不大, 所以它实现了精度和效率之间的平衡. 另外, 当 $ k $ = 5时, 估计误差也增大. 而LREMH算法可以在LASSO回归和EM算法之间进一步平衡, 因为当 $ k $ 更大时, 候选集将会更稀疏, 而LREMH算法可以有效地减少候选集的冗余和迭代次数.

根据图1, 图2可以看出LREMH算法的估计效率随着属性维度和 $ f $ 的增加而缓慢下降, 但始终处于EM算法和LASSO回归算法两者之间. 当 $ f $ >0.7时EM算法的效率急剧下降, 这是因为EM算法对 $ f $ 很敏感, 并且容易得到某些局部最优值. 由于LREMH算法使用LASSO回归快速的估计初始值, LREMH算法对 $ f $ 的敏感度要低于EM算法, 同时使用LASSO回归估计的初始值要比直接使用均匀分布的初始值更加精确, 很好的解决的EM算法对初始值敏感的问题, 而且有效地减少了迭代的次数, 这使得LREMH算法的估计效率一直比EM算法高. 根据图中可以看出, LREMH算法的估计精度随着属性维度和 $ f $ 的增加而下降, 但也在大部分情况下处于EM算法和LASSO回归算法两者之间, 当属性的维度增大时, 需要计算的候选集会变得更加稀疏, 所以EM算法的误差会随着维度和 $ f $ 的增加而增加, 由于LASSO回归只进行一次回归分析的估计, 并没有像EM算法一样进行迭代, 所以其估计的精度在大多数情况下不如EM算法, 但LREMH算法在估计初始值的同时会消除冗余候选项, 解决的初值估计问题, 减少了迭代次数, 降低了得到局部最优的概率, 所以LREMH算法在效率和精度之间取得了均衡.

并且由于 $ f $ 的值直接影响了隐私保护等级, 当 $ f $ 增加时, 隐私保护的等级就越高, 也就导致了随着 $ f $ 的增加, 3个算法估计的效率和精度都随之下降, 从图3和图4中可以直观看出当 $ f $ <0.7时, LREMH算法的估计效率和精度在LASSO回归算法和EM算法中取得了良好的均衡.

6 总结与展望

多维数据的联合概率分布估计对于数据发布具有重要作用, 本文提出的LREMH算法在满足本地化差分隐私的情况下, 结合期望最大化算法和回归分析方法消除冗余候选项, 用回归分析估计初始联合分布, 然后用期望最大化算法进行迭代计算, 直至收敛. 通过实验验证LREMH算法在精度和效率之间取得了平衡. 下一步工作将会围绕如何学习到与原始数据最为拟合的概率图模型, 如何进一步提高发布数据的可用性等方面的问题进行研究.