随着工业的发展, 空气污染已经给人民群众的生活质量和我国经济的快速发展造成了很大的影响. 对于人类的影响包括造成了一系列疾病, 甚至缩短了人类的预期寿命^{[1, 2]}. 对于城市经济发展的影响包括削弱了城市的集聚效应与规模, 减缓了城市的生产活动, 进而抑制了城市化进程^[3]. 在空气污染超标事故发生时首要解决的就是如何寻找污染源. 传统的对于空气污染源反演的方法主要是通过对企业的源排放清单进行排查. 但在源清单的获取过程中, 由于监测区域空气污染物的开放性, 使得排放清单的获取难度过大, 数据不够完全. 即便是能够获取到完备的数据, 整个污染源清单的数据量也会过于庞大, 从而导致单纯通过人力排查十分困难且低效. 为了解决源清单排查法具有的低效和盲目性的问题, 国内外学者纷纷开始寻找更优质的方法来应用到污染源的反演工作中.

根据近些年来国内外学者对于污染源反演工作的相关研究, 可以把污染源反演的方法划分为两类: 基于数理概率统计理论的反演方法和基于全局优化搜索的方法. (1)基于数理统计理论的方法是利用概率论的推理来进行污染源问题的描述, 根据推理结果的分布情况来反映污染源的概率统计^[4-6]. 郑情文^[5]利用伴随概率定位法的计算策略, 以2 km×2 km的理想开放空间为研究区域, 理想化风向和风速, 利用风洞模型实现了污染源的追踪. 这种方法对于高维问题无法快速降维导致求解时间过长. (2)基于全局优化搜索的方法是根据气体扩散的特征、气象等条件, 利用气体扩散模型, 建立目标函数, 采取启发式搜索算法对目标函数进行求解, 从而得到污染源的相关参数^[7-11]. 沈泽亚等^[7]通过对遗传算法、粒子群算法和单纯形算法的两两耦合, 分别对污染源进行了反演, 最终得到遗传算法和单纯形算法耦合时, 污染源反演的效率最高, 但准确性无法保证, 粒子群与单纯形算法耦合时, 污染源反演的准确性最高, 但效率无法保证; Thomson等^[8]采用模拟退火算法, 结合随机搜索算法对污染源进行了反演, 其反演效率较低; Ma等^[9]提出了一种将粒子群算法同吉洪诺夫规则耦合的污染源反演方法, 但是目前无法在实际中投入使用.

相比于其他群智能算法, 蚁群算法采用的是正反馈并行机制, 具有鲁棒性强, 对初值依赖性不大等优点, 在最短路径规划问题上得到了很广泛的应用. 本文创新性地将蚁群算法应用到空气污染源反演的领域中来.

虽然蚁群算法相比于其他群智能算法存在着一些优势, 但仍然存在着一些缺陷, 包括初期收敛速度较慢以及容易陷入局部最优值. 本文将针对这两个缺陷进行改进, 从而对空气污染源反演的准确性和高效性进行保证.

1 反演情景

对于污染源的参数反演需要确定污染源和监测站之间的污染物扩散关系, 这就需要一种合适的气体扩散模型来将污染物的扩散规律进行量化, 进而建立目标函数, 将空气污染源的反演问题转化为全局最优化问题.

1.1 气体扩散模型

为了和先前学者的工作保持一定的延续性, 在污染源的下风向处, 可以利用点源连续扩散的高斯烟羽模型模拟出空气在三维空间中的扩散浓度变化情况^[12]. 其表现形式如下:

$ \begin{split} C(x, y, {\textit{z}}) = & \frac{{{Q_0}}}{{2\pi u{\sigma _y}{\sigma _{\textit{z}}}}}\exp \left[ { - \frac{1}{2}{{\left( {\frac{{y - {y_0}}}{{{\sigma _y}}}} \right)}^2}} \right] \\ & \times \left\{ {{\text{exp}}\left[ { - \frac{1}{2}{{\left( {\frac{{{\textit{z}} - {H_0}}}{{{\sigma _{\textit{z}}}}}} \right)}^2}} \right] + \exp \left[ { - \frac{1}{2}{{\left( {\frac{{{\textit{z}} + {H_0}}}{{{\sigma _{\textit{z}}}}}} \right)}^2}} \right]} \right\} \\ \end{split} $

(1)

其中, $ C(x, y, {\textit{z}}) $ 表示下风向处任意一点的气体模拟浓度 ( $ \rm g/{m^3} $ ); $ {Q_0} $ 表示污染源的强度 ( $ \rm g/s $ ); $ u $ 表示平均风速 ( $ \rm m/s $ ); ${\sigma _y}$ 和 ${\sigma _{\textit{z}}}$ 分别表示平面和竖直垂直于下风向的扩散系数; $ {x_0} $ 和 $ {y_0} $ 分别表示污染源的平面坐标; $ x $ 和 $ y $ 分别表示监测站的平面坐标; ${\textit{z}}$ 表示污染源下风处任意一点的垂直坐标; $ {H_0} $ 表示污染源的高度. 在实际的空气污染监测中, 我们一般最关注的焦点是污染物在近地面的浓度分布状况, 因此本文中忽略所有的监测站的高度, 也就是令z=0, 可以得到:

$ C(x, y, 0) = \frac{{{Q_0}}}{{\pi u{\sigma _y}{\sigma _{\textit{z}}}}}\exp \left\{ { - \frac{1}{2}\left[ {{{\left( {\frac{{y - {y_0}}}{{{\sigma _y}}}} \right)}^2} + {{\left( {\frac{{{H_0}}}{{{\sigma _{\textit{z}}}}}} \right)}^2}} \right]} \right\} $

(2)

式(2)即为我们建立污染源反演模型的基础, ${\sigma _y}$ 和 ${\sigma _{\textit{z}}}$ 分别可由Pasquill-Gifford模型扩散系数方程确定. 其一般表现形式为:

$ \left\{ {\begin{split} & {\sigma _y} = {\gamma _1}x{(1 + {\lambda _1}x)^{ - 0.5}} \\ & {\sigma _{\textit{z}}} = {\gamma _2}x{(1 + {\lambda _2}x)^{ - 0.5}} \\ \end{split}} \right. $

(3)

其中, ${\gamma _1}$ , ${\lambda _1}$ , ${\gamma _2}$ , ${\lambda _2}$ 均由不同环境以及大气稳定度等级来确定^[13].

1.2 反演情景模拟

在式(2)的基础上, 假定 $ C_m^i $ 和 $C_p^i$ 分别为第个监测站的实际监测污染物浓度和通过式(2)计算模拟到的第 $i$ 个监测站所处位置的污染物浓度, 那么以此可以建立污染源参数反演的目标函数, 以平方损失函数为基础, 对每个监测站的监测浓度进行加和, 建立目标函数即反演模型^{[7, 9,10]}表现形式如下:

$ \min {L_{tar}} = \sum\limits_{i = 1}^N {{{\left( {C_m^i - C_p^i} \right)}^2}} $

(4)

根据式(4)可知, 源参数反演的问题可以转化为对目标函数 ${L_{tar}}$ 进行最优化的问题. 目标函数 ${L_{tar}}$ 越小, 表明通过反演得到的污染源的相关参数越接近真实污染源参数, 即反演结果越接近真实污染源, 反演的效果越好. 上述污染源的相关参数包括污染源的横坐标 ${x_0}$ 、纵坐标 ${y_0}$ 、源强 ${Q_0}$ 和污染源的高度 ${H_0}$ .

以沈阳市浑南区部署的若干空气质量监测站的数据为本文的数据基础. 在 $t$ 时刻, 有若干个监测站监测到某污染物浓度超标, 记录所有监测到污染物浓度超标的监测站的污染物浓度值 $C_m^i \; (i = 1, 2,\cdots, N)$ . 与此同时, 包括风速、风向等常规气象监测信息也是已知的, 从而可以确定大气稳定度等级, 然后参照文献[13]可以确定水平以及纵向的扩散系数 ${\sigma _y}$ 和 ${\sigma _{\textit{z}}}$ .

为了简化扩散模拟场景, 将整个监测的区域平面抽象成一个矩形平面, 并建立二维平面坐标系, 对每个监测站进行坐标转化, 每个监测站坐标可以以平面坐标 $\left( {{x_i}, {y_i}} \right)\left( {i = 1, 2, \cdots, N} \right)$ 来表示. 将监测到污染物浓度超标的监测站的坐标、监测的污染物浓度和当前的平均风速代入反演模型中, 即可进行污染源的反演, 最终得到污染源的4个参数结果.

2 反演模型求解

对于上述最优化问题, 本文采用改进后的ACO算法进行迭代求解, 即选取式(4)作为目标函数, 通过迭代求其最小值, 最终得到污染源的参数, 包括源强 ${Q_0}$ , 源坐标 ${x_0}$ 和 ${y_0}$ 以及源释放高度 ${H_0}$ .

2.1 传统蚁群算法

传统的ACO算法是是由意大利学者Dorigo等^[14]提出的一种人工仿生智能优化算法, 蚂蚁在觅食过程中, 会在经过的路径留下信息素, 信息素浓度高的路径会更大概率被其他蚂蚁选择, 整个种群会根据信息素的交流和传递来进行不断调整下一步的移动方向, 进而找到最佳的觅食路径.

然而传统ACO算法存在着容易陷入局部极值和收敛速度较慢的缺点. 本文设计一种机制用来对基本蚁群算法的正反馈机制进行制衡, 使其能够跳出局部极值. 同时对信息素更新机制进行调整, 使其在迭代初期能够进行更快速地收敛, 最终将其归纳为M-ACO算法.

2.2 引入选择交叉思想避免陷入局部极值

传统的蚁群算法容易陷入局部极值是因为其正反馈机制会导致如果当前解不是最优解时, 依旧会吸引其他蚂蚁更大概率选择当前解, 从而逐渐丧失了种群的多样性, 导致算法陷入局部极值. 因此, 本文类比遗传算法中的选择淘汰和交叉操作, 在每次所有蚂蚁当前这代结果求解完成后, 对整个蚁群按照目标函数值从小到大进行排序, 将值最大的1/4个体舍去, 从剩下的3/4个体中随机选择值处于中间位置的1/3个体分为两个部分, 分别从两个部分中随机选择两个个体 ${P_1}$ 和 ${P_2}$ 进行交叉操作, 参照遗传算法中的部分映射交叉形式将 ${P_1}$ 和 ${P_2}$ 的一部分进行交换, 从而形成两个新的个体, 反复操作直到新个体的数量达到原种群数量的1/4, 然后填充到之前舍去的1/4个体处, 达到维持种群多样性的目的, 具体交叉方式可如下表示:

$ \left\{ {\begin{split} & P_1^* = (A - B + 1){P_1} + (A - B){P_2} \\ & P_2^* = (A - B){P_1} + (A - B + 1){P_2} \\ \end{split}} \right. $

(5)

其中, ${P_1}$ 、 ${P_2}$ 表示所选蚂蚁个体, 包含反演源的解组成的矩阵, $P_1^*$ 、 $P_2^*$ 表示交叉后形成新的蚂蚁个体, $A$ 和 $B$ 表示交叉点, 其取值范围为(0, 1)且 $A \lt B$ .

2.3 提出奖惩因子机制加快收敛速度

传统蚁群算法中, 蚂蚁的信息素越大, 表明该蚂蚁代表的可行解越优质, 在后续的迭代过程中能够吸引劣质蚂蚁向其靠近. 在每次迭代结束后, 每只蚂蚁都会根据解的优劣程度来更新自己的信息素, 信息素更新机制可如下表示:

$ {\tau ^i}(n + 1) = (1 - \rho ){\tau ^i}(n) + \Delta {\tau ^i}(n) $

(6)

其中, $n$ 为当前迭代的次数; $\;\rho $ 表示信息素挥发因子; ${\tau ^i}(n)$ 为第 $i$ 只蚂蚁在 $n$ 次迭代开始时包含的信息素, ${\tau ^i}(n + 1)$ 为第 $i$ 只蚂蚁在 $n$ 次迭代后更新完毕的信息素, 同时也作为其在第 $n + 1$ 次迭代开始时的信息素; $\Delta {\tau ^i}\left( t \right)$ 为第 $i$ 只蚂蚁在第 $n$ 次迭代过程中获得的信息素增量, 其表现形式如下:

$ \Delta {\tau ^i}\left( n \right) = \frac{K}{{L_{tar}^i(n)}} $

(7)

其中, $K$ 为常系数, 一般取1; $L_{tar}^i(n)$ 代表第 $n$ 次迭代过程中第 $i$ 只蚂蚁求得的目标函数值.

由式(6)可知, 在传统蚁群算法中, 每只蚂蚁的信息素更新虽然会根据其解的优劣程度来区分更新, 但是在解的优劣程度相差不明显的时候, 较优解被发现的概率下降, 劣质蚂蚁无法向优质蚂蚁进行靠拢, 使得收敛速度降低. 为了加快收敛速度, 本文对信息素更新机制进行改进, 在式(7)的基础上, 提出奖惩因子机制 $m$ , 对信息素增量的计算进行修改, 可表示为:

$ \Delta {\tau ^i}\left( n \right) = m \frac{K}{{L_{tar}^i(n)}} $

(8)

$ m = \frac{{L_{tar}^i(n - 1)}}{{L_{tar}^i(n)}} $

(9)

其中, $n$ 为当前迭代的次数, $\Delta {\tau ^i}\left( t \right)$ 为第 $i$ 只蚂蚁在第 $n$ 次迭代过程中获得的信息素增量; $\;\mu $ 为奖惩系数, 其值由式(9)决定, 对于第 $i$ 只蚂蚁, 如果其 $n - 1$ 代的目标函数值 $L_{tar}^i(n - 1)$ 大于其第 $n$ 代的目标函数值 $L_{tar}^i(n)$ , 那么 $m$ 则会大于1; 反之, $m$ 则会小于1.

式(8)和式(9)共同决定了第 $i$ 只蚂蚁在第 $n$ 次迭代过程中能获得的信息素增量 $ \Delta {\tau ^i}\left( n \right) $ . 式(8)表示了目标函数值 $ L_{tar}^i(n) $ 越小的蚂蚁可以获得越多的信息素增量, 式(9)通过第 $i$ 只蚂蚁相邻两代之间的目标函数值的比值, 即奖惩系数 $\mu $ 来动态地放大或者缩小每只蚂蚁各自对应的信息素增量. 这样会使得蚂蚁在根据式(6)更新各自的信息素后, 形成两极分化的状态, 优质蚂蚁信息素更多而劣质蚂蚁信息素更少. 优质蚂蚁在后续的迭代过程中能以更大的概率被发现, 吸引劣质蚂蚁向其靠拢, 从而加快了算法的收敛速度.

2.4 M-ACO算法流程

M-ACO算法流程如图1所示, 其与传统蚁群算法流程中最大的区别在于: (1)每次迭代完毕后都需要进行选择淘汰交叉来维持种群多样性; (2)每次更新信息素时需要利用奖惩因子对每只蚂蚁的信息素增量进行放缩.整个算法过程中需要初始化的算法参数包括: 蚁群规模 $m$ , 迭代次数 $T$ , 信息素挥发因子 $\rho $ , 信息素和启发函数的重要程度因子 $\alpha $ 和 $\;\beta $ .

3 实验验证 3.1 实例背景

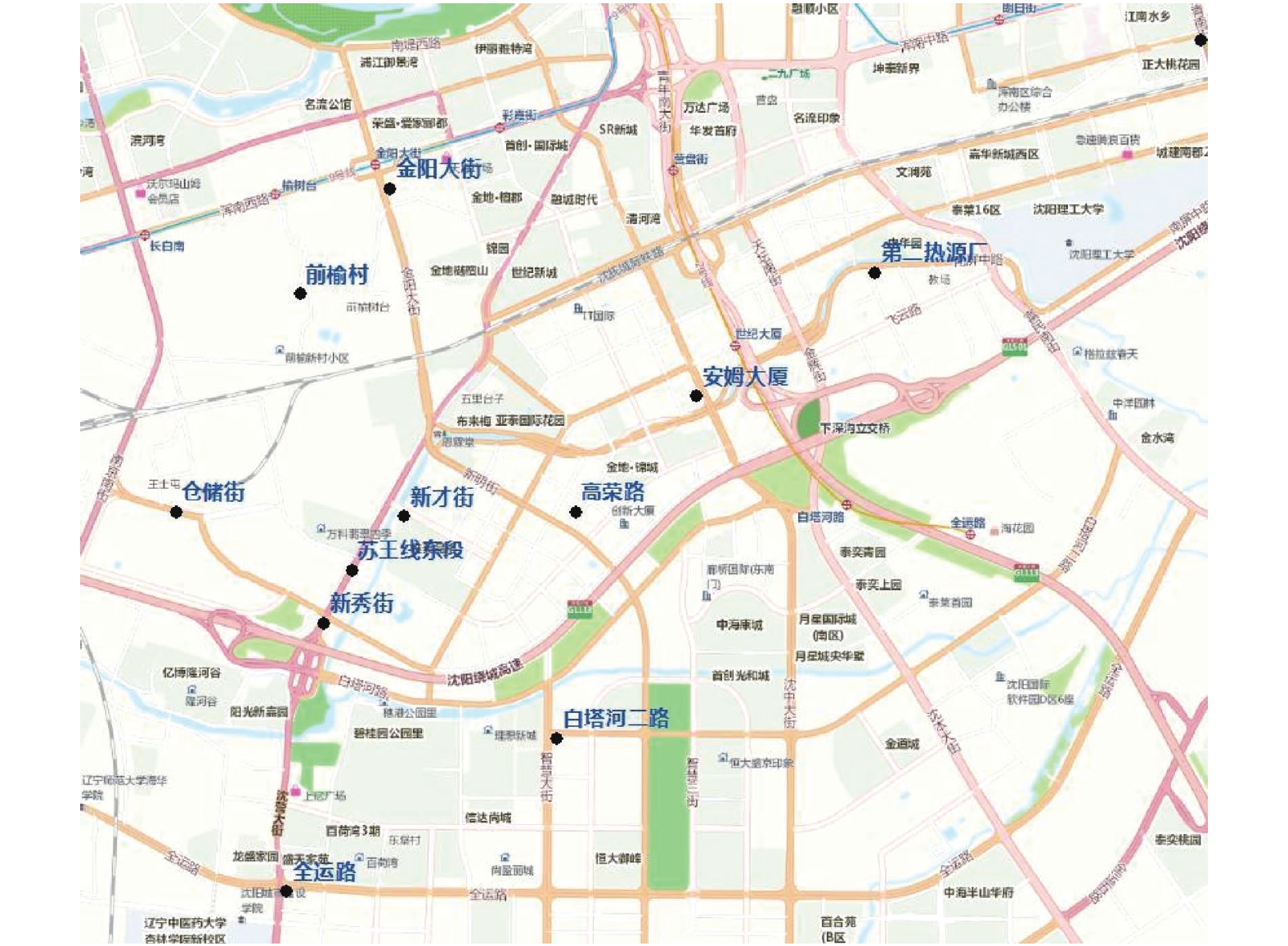
以沈阳市浑南区某区域内在2019年某日因某工厂违规排放引起的颗粒物浓度超标事件为实验实例. 该区域内存在小范围部署的11个空气监测站, 其实际部署情况如图2所示.

此次污染物浓度超标事件一共使得6个监测站监测到颗粒物浓度超标, 根据当前其他常规气象参数确定大气稳定度等级为E. 那么根据文献[13]可以得知该时刻的 ${\sigma _y}$ 和 ${\sigma _{\textit{z}}}$ 的取值如式(8)所示:

$\left\{ { \begin{split} & {\sigma _y} = 0.11x{(1 + 0.0004x)^{ - 0.5}} \\ & {\sigma _{\textit{z}}} = 0.08x{(1 + 0.0015x)^{ - 0.5}} \\ \end{split} } \right.$

(10)

已知风向为东偏北风, 为了方便确定污染源范围, 另给出上风向处一个未监测到颗粒物浓度超标的监测站作为参考监测站.

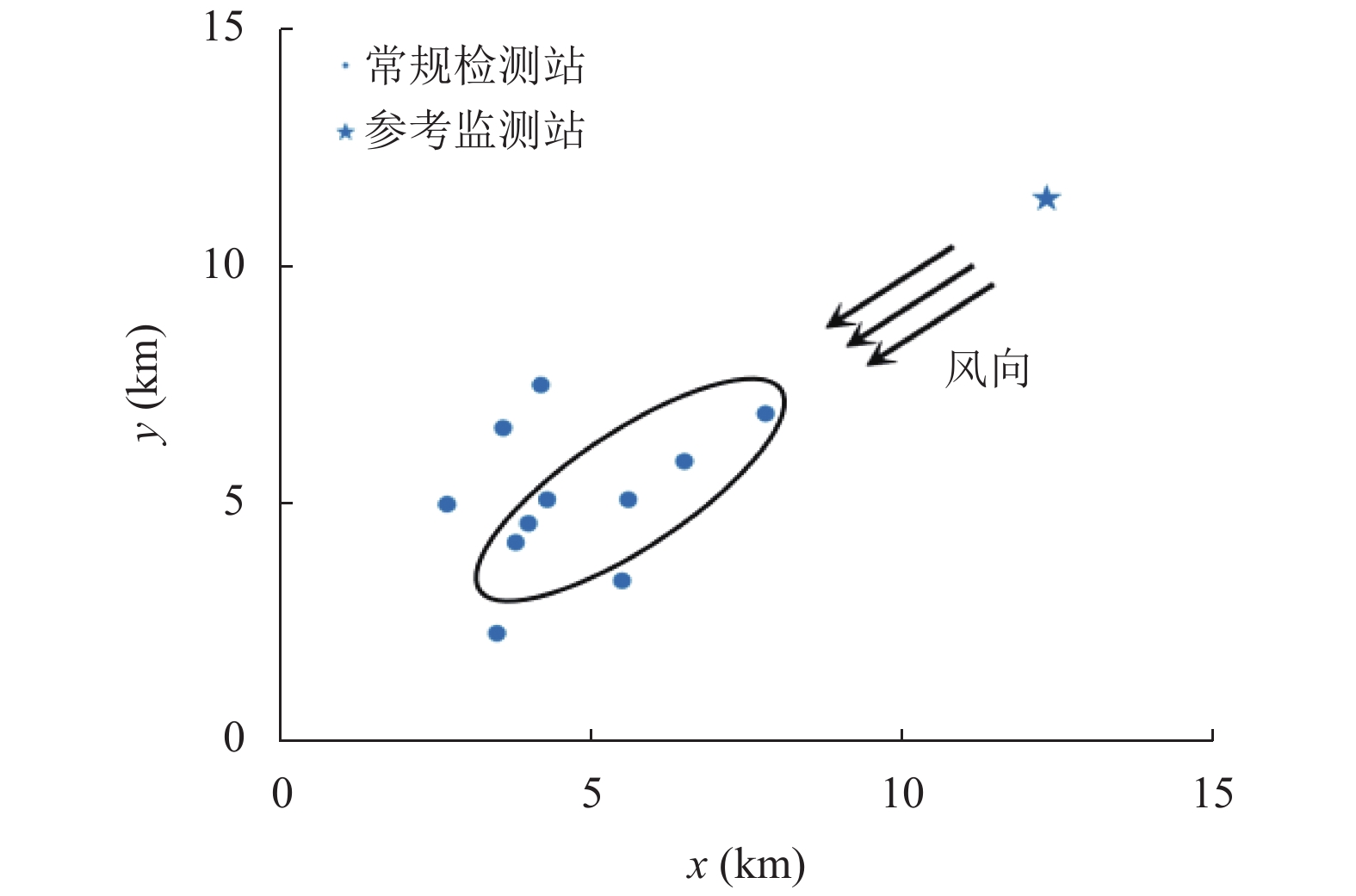
为了方便实验, 根据上述11个常规监测站以及另给出的1个参考监测站的实际部署情况, 以地图的某个点为原点, 按照监测站之间的实际距离等比例进行描点, 将其抽象成为二维平面图, 并且用圆圈框住上述监测到颗粒物浓度超标的6个监测站, 则当前整个区域内所有监测站的状态如图3所示.

将图3圆圈内的6个监测站的坐标以及此时的颗粒物监测浓度记录下来, 并将其代入式(4)中, 用来进行污染源的反演.

3.2 反演结果

通过上述实验过程, 利用Matlab软件编写ACO算法和M-ACO算法分别进行求解. 经过反复调试, 结合程序的整体运行效率和运算结果的准确性进行综合考虑, 最终决定设置迭代次数为1000, 蚁群数量为200, 信息素挥发因子为0.8, 信息素重要程度因子为1, 启发函数重要程度因子为5. 最终可以得到两种算法运算的目标函数值对比变化情况如图4所示.

由图4可以看出, 目标函数在ACO算法中在615代后达到收敛状态, 并且此收敛状态并不是全局最优状态; 而在M-ACO算法中, 142代时, 目标函数的收敛速度急剧下降, 目标函数即将陷入局部极值, 此时通过不断地交叉操作扩大搜索范围, 在243代后进一步收敛, 在336代后基本达到全局最优.

从收敛速率上来看, 目标函数在M-ACO算法的迭代过程中, 收敛效率比ACO算法要高许多, 这是由于利用奖惩因子机制更新信息素的策略, 使得优质蚂蚁个体能够积累更多的信息素, 从而放大了其被选择的概率; 而在ACO算法中, 由于各个蚂蚁之间的信息素浓度差异不够明显, 导致优质蚂蚁无法被选择到, 因此收敛速度较慢.

3.3 结果评估

通过对该次颗粒物浓度超标事件的历史记录和相关资料的进一步调查了解, 最终获得了真实污染源的4项相关参数数据, 如表1所示.

此时, 根据两种算法分别进行求解得到的反演源的4项参数值的变化情况, 同表1中真实污染源进行对比, 可以绘制出反演源中4项参数值的变化趋势, 进而直观地对比两种算法寻优结果的准确性和效率.

由图5可知, 在使用ACO算法迭代过程中, 目标函数收敛速度慢, 并且最终陷入了局部极值, 最终得到的反演源的4项参数结果与真实源4项参数结果偏差较大, 无法保证空气污染源反演的准确性和效率; 而在M-ACO算法迭代过程中, 最终得到的反演源4项参数结果更准确. 更接近真实污染源的4项参数值.

同时图5也验证了使用M-ACO算法在本次颗粒物浓度超标事件中, 可以快速准确地求出污染源的位置, 源强和排放高度等信息, 达到了空气污染源反演的目的, 证明了该算法在之后的污染源反演工作中可以进行实际应用.

由上述实验求得的每个参数的最终结果如表2所示.

根据表2中分别利用两种算法得到的反演源的4项参数值, 与真实源的4项参数值做对比, 计算出相对误差率, 如表3所示.

从表3可以看出, 使用M-ACO算法得到的反演结果的误差率明显低于使用ACO算法的误差率, 污染源反演的准确性得到了保证.

4 结论

通过上述实例, 可以发现M-ACO算法在污染源反演的准确性和效率上都比传统的ACO算法要优秀, 能够把单个空气污染源反演结果的相对误差率控制到2%以内; 同时解决了传统ACO算法因容易陷入局部极值而无法保证结果准确性的问题, 为实际的污染源定位排查工作提供有力的数据支持, 为空气污染的治理起到了关键的引导性作用, 促进了空气污染治理由凭感觉、凭经验管理转向精准化、靶向化管理, 保护了我们的空气环境.