2. 首都师范大学 信息工程学院 电子系统可靠性与数理交叉学科国家国际科技合作示范型基地, 北京 100048;
3. 首都师范大学 信息工程学院 神经计算与智能感知实验室, 北京 100048;
4. 首都师范大学 信息工程学院 北京成像理论与技术高精尖创新中心, 北京 100048;
5. 首都师范大学 心理学院, 北京 100048
2. International Science and Technology Cooperation Base of Electronic System Reliability and Mathematical Interdisciplinary, Information Engineering College, Capital Normal University, Beijing 100048, China;
3. Laboratory of Neural Computing and Intelligent Perception, Information Engineering College, Capital Normal University, Beijing 100048, China;
4. Beijing Advanced Innovation Center for Imaging Theory and Technology, Information Engineering College, Capital Normal University, Beijing 100048, China;
5. School of Psychology, Capital Normal University, Beijing 100048, China
脑电图(electroencephalogram, EEG)作为一种包含大量人体信息的多通道生理信号, 已成为脑科学研究中的重要数据[1]. 近年来, 深度学习的发展推动了计算机科学与脑科学的进一步融合, 其对EEG的特征提取方法成为EEG研究的重要手段[2-4]. 这类技术通常需要训练大量的数据来训练和优化模型, 从而构建鲁棒模型. 但是, 在EEG采集过程中, 繁琐的操作极易导致被试人员受到主观意识的影响, 从而产生眼电、心电等掩盖真实EEG的波形的噪声. 因此, 获取满足深度学习模型训练所需的数据量极其困难. 针对上述问题, 研究人员通过设计针对于EEG的生成技术, 以实现样本数量的扩充[5, 6].
目前, 样本生成模型主要包括自回归模型(auto-regressive model, AR)[6]、自动编码变分贝叶斯(variational auto-encoding Bayes, VAE)[7]、生成对抗网络(generative adversarial network, GAN)[8]以及流模型(flow-based model)[9]等. 相较而言, 前两者缺乏判别模型的指导, 因此在训练过程中极易出现生成样本单一的情况; 而流模型在训练过程中对计算资源的要求很高, 难以得到广泛应用. 综合以上分析, GAN及其相关衍生技术成为EEG生成的最佳模型. 相对而言, 传统GAN及其衍生模型的构建主要通过全连接层(fully connected layer, FC)来实现, 而FC层无法捕捉时序信号的特征和相关属性之间的复杂关联[10], 这就导致模型在处理EEG时容易丢失时间相关性信息.
为解决此问题, Abdelfattah等人[11]通过使用循环神经网络(recurrent neural network, RNN)搭建循环生成对抗网络框架(recurrent generative adversarial networks, RGAN), 从而实现多通道EEG的生成. 为验证其性能, 作者将生成EEG用于训练分类框架中并取得了较好的分类结果. 相较于其他神经网络, RNN对时序信号特性具有较强的学习能力, 能够保留时间相关信息; 但是, 由于其本身存在梯度爆炸等问题, 容易导致生成模型训练不稳定. Luo等人[12]提出conditional Wasserstein GAN (CWGAN)框架, 通过在输入生成器的随机噪声中添加辅助条件, 以用于生成EEG的微分熵(differential entropy, DE)特征, 并将其应用到情感识别任务中. 其中, 辅助条件能够加速模型的收敛速度, 从而保证模型训练的稳定性. 然而, DE只适用于情感分析任务, 具有一定的局限性. 另外, Panwar等人[13]提出class conditioned WGAN-GP (CC-WGAN-GP)模型, 并将其用于多通道EEG信号的生成. 该模型在判别器中增加了分类功能, 即在生成EEG的同时能够对其分类, 之后采用分类准确率代替损失函数来判定该模型的训练情况. 相较于已有模型, CC-WGAN-GP在模型稳定性以及样本多样性方面都有所提高, 但是, 额外的分类器增加了模型的复杂度, 从而造成模型拟合速度降低.
综上所述, 基于GAN及其衍生模型的EEG生成模型能够证明所生成样本在深度学习模型训练和优化研究中的可行性. 然而, 上述生成模型仍存在以下问题: (1)模型通常添加批标准化层(batch normalization, BN)来防止模型过拟合, 但这会导致真实样本与生成样本之间的幅值差异过大. (2)模型训练过程中易出现过拟合、模式崩溃及梯度消失等问题, 导致生成样本多样性不足; (3)模型通过增加模型复杂度来提高模型训练的稳定性, 这往往导致模型的拟合速度降低.
本文拟从以下2个方面解决上述3个问题, 具体而言: (1)在WGAN-GP网络框架下, 通过将长短期记忆网络(long short-term memory, LSTM)代替卷积神经网络(convolutional neural networks, CNN), 从而解决脑电信号生成单一的问题; 这是由于LSTM能够保留EEG信号的时间相关性特征, 从而提高生成样本中特征的多样性. 在此模型的基础上, 本文分别对网络框架的生成器和判别器的输入数据进行处理: (2)在EEG预处理阶段, 我们将标准化处理后的真实脑电信号输入至判别器, 即使其值域映射到[–1, 1] μV, 从而解决生成样本与真实样本幅值差异过大的问题. (3)考虑到EEG噪声中必然存在与真实EEG相似特征, 我们将其代替传统的高斯噪声输入至生成器, 即, 将其作为先验知识来提高生成模型的拟合速度;
为综合评估生成模型的性能, 本文采用多层次定量评估方法, 从不同角度验证其性能, 具体而言: 首先, 通过使用sliced Wasserstein distance (SWD)和mode score (MS)实现对生成模型的相似性和多样性的定量评估. 其次, 通过对比真实样本与生成样本的波形差异对其进行定性评估. 最后, 将生成样本与真实样本以不同比例混合并用于EEGNet模型的训练; 通过对分类结果的定量分析, 以验证生成模型的性能.
1 相关技术介绍为更好地阐述所提出的EEG生成方法, 本节主要阐述工作中所需的理论基础知识: 首先, 介绍WGAN以及WGAN-GP的相关知识; 其次, 介绍本文从损失函数、内部结构以及工作原理等角度对使用的网络框架—LSTM进行详细描述.
1.1 Wasserstein GANWasserstein GAN (WGAN)[14]通过将Wasserstein距离(Wasserstein distance, WD)[15]代替标准GAN中的交叉熵来作为损失函数, 以解决原始GAN中模式崩溃以及过拟合等问题.
WD又称为推土机距离(earth-mover’s distance, EMD), 定义如式(1)所示:
| $ W({P_r}, {P_g}) = \mathop {inf }\limits_{\gamma {\sim} \prod ({P_r}, {P_g})} {E_{(x, y){\sim} \gamma }}[||{x_r} - {x_g}||] $ | (1) |
其中, γ为真实样本分布Pr与生成样本分布Pg的集合, 由于该集合期望的下边界(inf)无法直接求出, 故使用Lipschitz连续代替.
定义1. Lipschitz连续: 在连续函数f(x)上额外施加一个限制, 若存在一个常数K使得定义域内的任意两个元素x1和x2都满足式(2), 则称K为f(x)的Lipschitz连续常数.
| $ |f({x_1}) - f({x_2})| \leqslant K|{x_1} - {x_2}| $ | (2) |
通过Lipschitz连续变换后, WD的定义如式(3):
| $ W({P_r}, {P_g}) = \frac{1}{K}\mathop {\sup }\limits_{||f|{|_L} \leqslant K} {E_{x {\sim} {P_r}}}[f(x)] - {E_{x {\sim} {P_g}}}[f(x)] $ | (3) |
W(Pr, Pg)即为函数f(x)的Lipschitz常数||f||L在不超过K的条件下, 对所有可能满足条件f的取到的上界x~Pr[f(x)]–Ex~Pg[f(x)]. 因此, 我们可以用一组参数来定义一系列可能的函数fω, 此时求解式(3)可以近似变成求解如下形式:
| $ K \cdot W({P_r}, {P_g}) \approx \mathop {\max }\limits_{W:||f|{|_L} \leqslant K} {E_{x {\sim} {P_r}}}[f(x)] - {E_{x {\sim} {P_g}}}[f(x)] $ | (4) |
综合以上分析, WGAN的生成器和判别器的损失函数分别如式(5)和式(6)所示:
| $ {L_G} = - {E_{x {\sim} {P_g}}}[f(x)] $ | (5) |
| $ {L_D} = {E_{x {\sim} {P_g}}}[f(x)] - {E_{x {\sim} {P_r}}}[f(x)] $ | (6) |
WGAN能够解决GAN所存在的梯度消失、生成样本单一等问题, 但Lipschitz连续的引入也带来了梯度爆炸的问题.
1.2 Wasserstein GAN-Gradient Penalty针对WGAN存在的问题, Gulrajani等人[16]在WGAN的判别器的损失函数中加入GP项, 如式(7)所示:
| $ GP = \lambda {E_{x {\sim} {{{P}}_{{{\hat x}}}}}}{[||{\nabla _x}D(x)|{|_P} - K]^2} $ | (7) |
其中, λ为超参数, 表示在真实样本xr和生成样本xg的分布连线上的随机插值取样.
因此, 其生成器的损失函数如式(8)所示:
| $L_{D}=E_{x {\sim} P_{g}}[D(x)]-E_{x {\sim} P_{r}}[D(x)]+\\ \lambda E_{x {\sim} P_{\hat{x}}}\left[\left\|\nabla_{x} D(x)\right\|_{p}-1\right]^{2}$ | (8) |
其判别器的损失函数如式(9)所示:
| $ {L_G} = - {E_{x {\sim} {P_g}}}[f(x)] $ | (9) |
总体来说, WGAN-GP (Wasserstein GAN-gradient penalty)保留了WGAN的优点, 同时, 在判别器D的损失函数上加入梯度惩罚项; 这在提升训练速度的同时, 也保证梯度更新在可控范围内, 进而降低WGAN梯度爆炸的可能性.
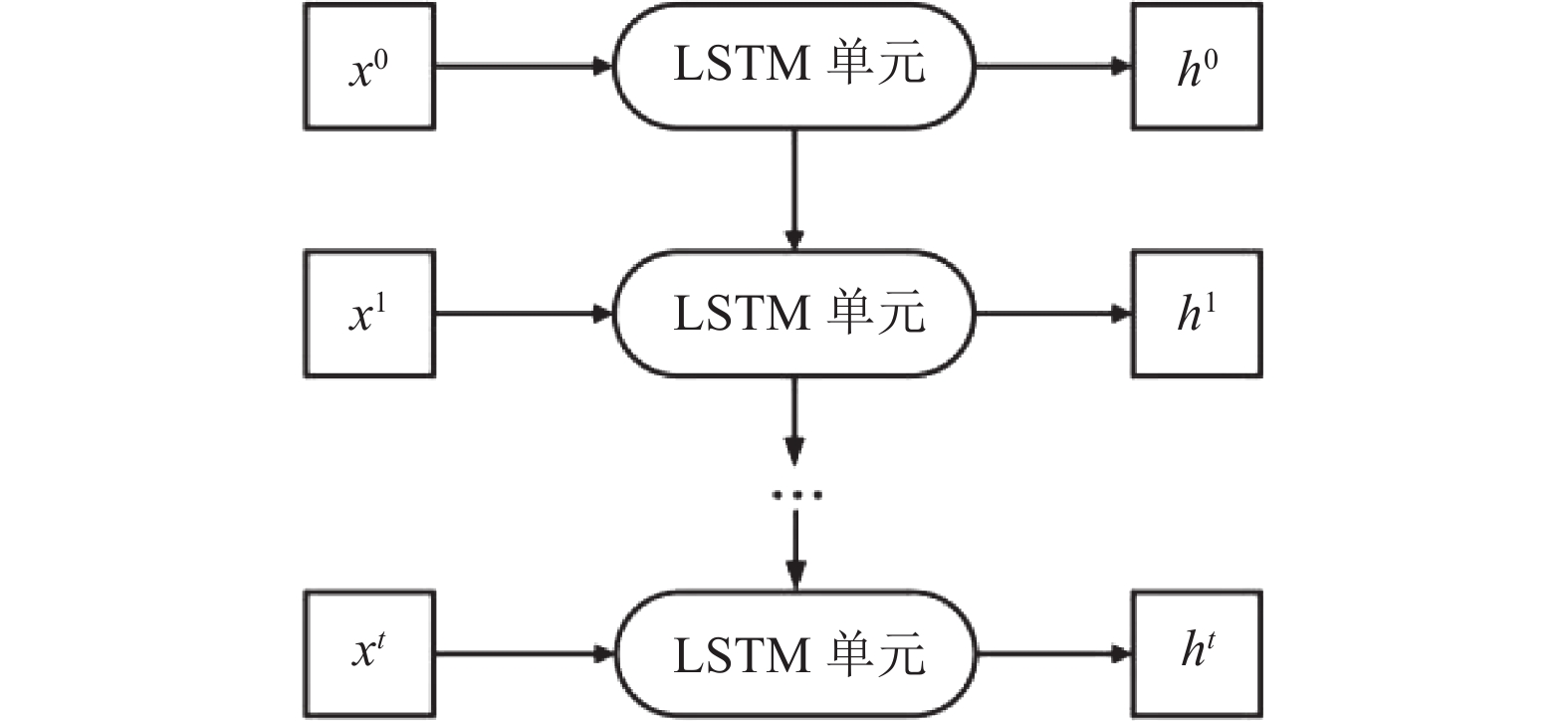
1.3 长短期记忆网络LSTM网络具有前向传播链式结构. 相较于其他处理时间序列的网络, LSTM更适用于分析长期记忆的时序信号[17, 18], 其结构如图1所示, 其中, x为输入到LSTM单元的训练数据, h为LSTM单元的输出数据.
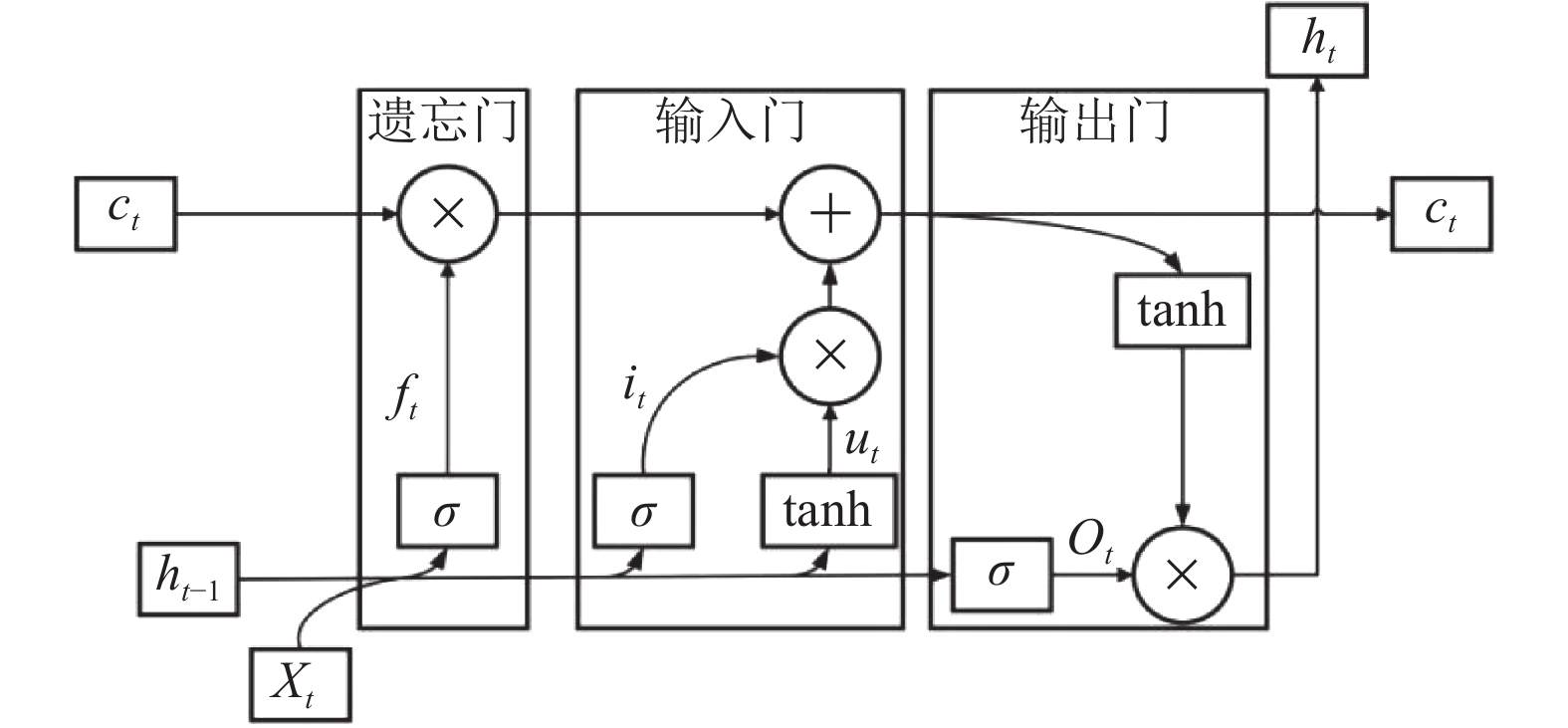
LSTM单元包含遗忘门、输入门和输出门3个部分, 其结构如图2所示, 以控制LSTM网络的记忆与遗忘[19].
|
图 1 LSTM网络结构 Fig. 1 LSTM network architecture |
|
图 2 LSTM单元结构 Fig. 2 The structure of LSTM cell |
遗忘门通过接收前一个LSTM单元的输出, 决定是否丢弃前一时刻的信息ht–1; 输入门决定当前LSTM单元需要保存的信息it, 同时生成备选更新信息ut, 将it和ut两部分相结合, 共同更新当前LSTM单元状态; 输出门决定是否输出当前LSTM单元的状态, 并获得当前LSTM的隐藏状态ht.
得益于特殊的单元结构, LSTM网络能够缓解在模型训练过程中出现的梯度爆炸和梯度消失的问题, 并且能够提取更多的时间域特征.
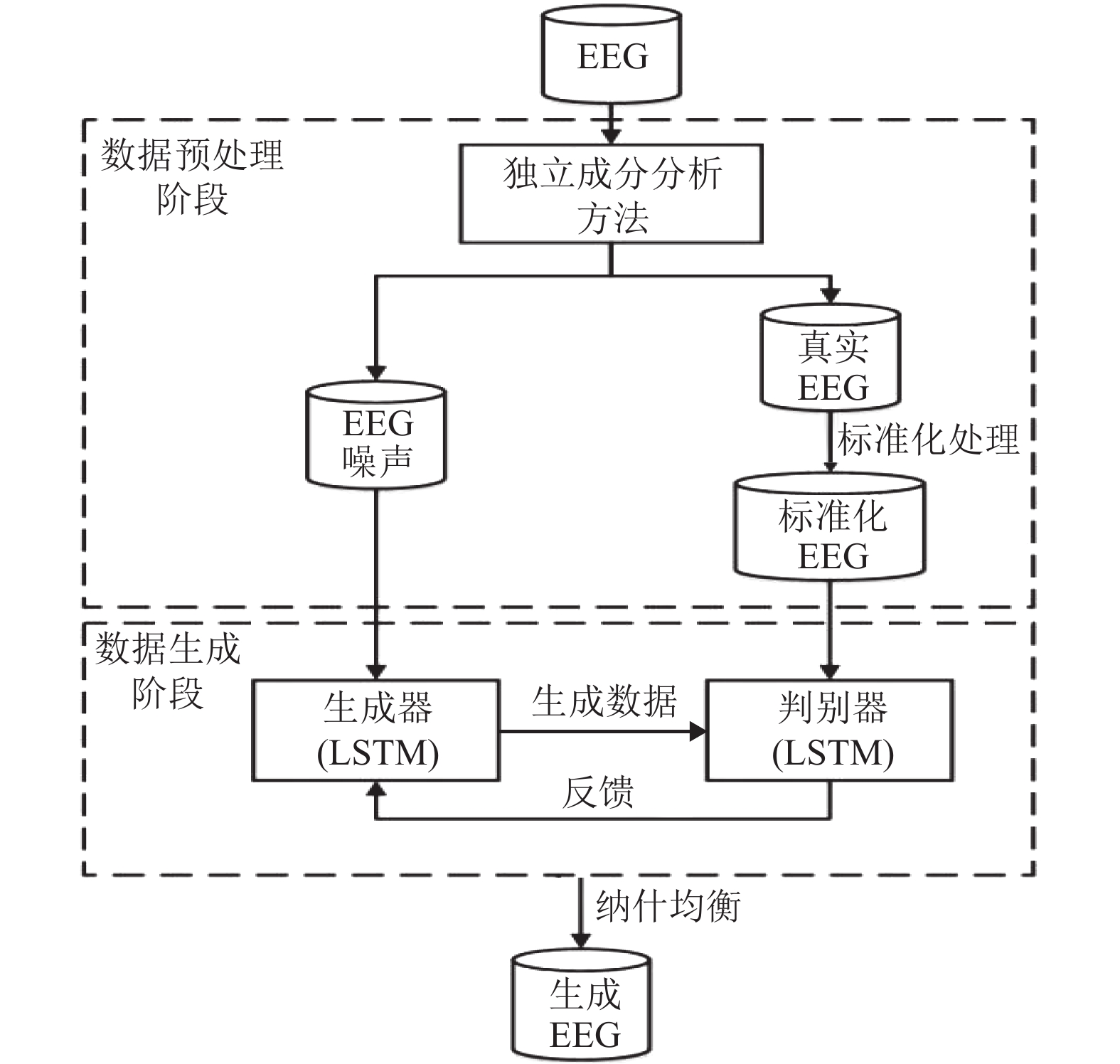
2 框架设计为解决生成EEG过程中存在的问题, 本文拟将EEG生成过程分为数据预处理阶段和数据生成两个阶段, 如图3所示. 在数据预处理阶段, 本文首先使用独立成分分析(independent component analysis, ICA)[20]对真实EEG做滤波处理, 从而将EEG数据与EEG噪声分开. 生成器采用后者作为输入数据, 这是由于后者包括被试人员的眼动、呼吸以及肌电等信号, 而这些信号中依然存在重要的特征. 因此, 我们将EEG噪声作为先验知识输入到生成器中, 从而提高模型的拟合速度; 其次, 我们对滤波后EEG信号做标准化处理, 使其值域映射到[–1, 1] μV, 从而解决生成样本与真实样本幅值差异过大的问题.
|
图 3 EEG生成流程图 Fig. 3 The flowchart of EEG generation |
在数据生成阶段, 本文通过将CNN替换成LSTM, 以构建新的生成器和判别器, 进而保证EEG中时间相关性信息的完整性, 这是由于LSTM网络具有前向传播链式结构, 包含多个LSTM单元. 相较于其他处理时间序列的网络, LSTM更适用于需要长期记忆的时序信号. 最后, 当生成器和判别器的对抗训练达到纳什均衡状态时, 生成样本的质量达到最优.
2.1 EEG噪声生成器通常将具有高斯分布的随机噪声作为输入数据, 但是由于EEG信号的特殊性, 此类噪声会导致生成模型的拟合速度降低. 本文拟将EEG噪声来代替高斯噪声作为生成器输入数据, 这是由于EEG噪声中存在与EEG信号相似的特征信息. 因此, 当其代替随机噪声, 生成器能够更高效地拟合真实样本分布.
本文采用ICA对所采集的EEG信号进行过滤, 进而分离出EEG信号和干扰噪声. ICA能够将相互独立的样本成分从混合样本中提取出来[21], 其模型一般如式(10)所示:
| $ X = A \times S $ | (10) |
其中, X是观测样本; A为系数矩阵, 包含所需分析数据的隐含特征; S代表独立源信号. 假设X服从独立性度量原则[22], 在已知A的情况下, 则有S=A−1×X=WX, 其中W=A−1一般称为分离矩阵.
2.2 EEG标准化在搭建网络框架时, 本文在生成器中嵌入BN层[23]. BN层能够将上层神经网络的输出数据分布强行转换为标准的正态分布 (mean=0, std=1), 使得输出数据分布在非线性函数较为敏感的区域, 从而避免梯度消失并且加快模型的收敛速度. 然而, BN层的转换操作能够将生成器的输出数据值域限制在 [–1, 1], 这就导致生成样本的值域远远小于真实样本的值域范围. 因此, 本文通过使用最大最小值方法将EEG信号的值域范围映射到 [–1, 1] μV, 一方面能够提高模型的收敛速度, 另一方面能够保证生成样本与真实样本的幅值在相同范围内. 最大最小值方法如式(11)所示:
| $ y = \frac{{(x - {x_{{\text{mean}}}})}}{{{x_{\max }} - {x_{\min }}}} $ | (11) |
其中, xmean为数据的均值, xmin为数据中的最小值, xmax为数据中的最大值, y为标准化后的数据.
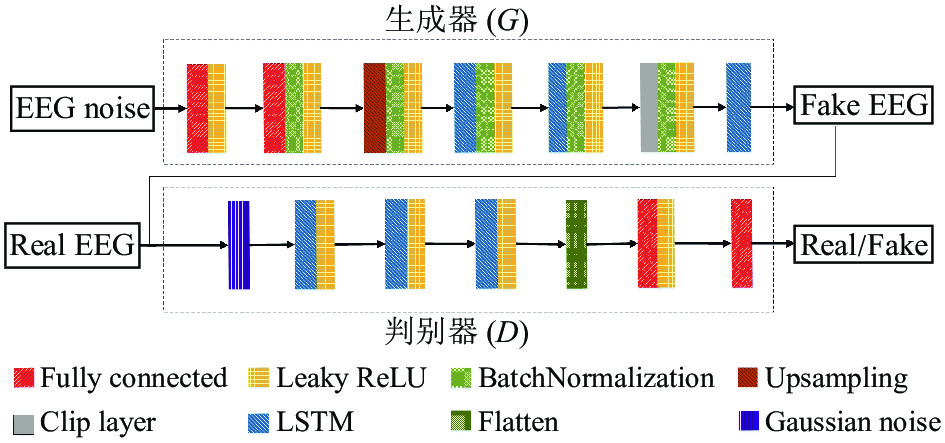
2.3 生成对抗网络设计EEG作为一种非线性、随机性强的时序信号, 其时间相关性比其他时序信号(音频、语音等)更为复杂[24, 25]. 另一方面, GAN的衍生框架大多采用FC或者CNN来提取特征[26, 27], 但二者均难以捕捉到时间序列信号的时间特征和相关属性之间的复杂关联性, 致使生成样本丢失真实样本的时间相关性信息[12], 从而导致生成样本特征单一. 本文将WGAN-GP作为基础网络框架, 使用LSTM代替CNN, 并结合第2.1节和第2.2节的创新点, 以解决目前EEG生成模型存在的问题. 改进后的网络框架如图4所示.
|
图 4 改进后的WGAN-GP网络框架 Fig. 4 The Modified WGAN-GP via LSTM and EEG Noise |
改进后的判别器体系结构如表1所示. 首先, 我们将与真实EEG维度(231×1)相同的EEG噪声信号作为生成器的输入数据, 并使用两层fully connected层将其维度逐步扩充至1×15360; 为与单元数为128的LSTM层对应, Reshape层将上层网络的输出数据转换为维度为1×120×128的三维数据; 随后, 我们采用双次插值法对三维数据进行上采样操作, 这一操作使得数据提高到1×240×128; 为满足LSTM的输入要求, Reshape层将输出维度再次转换为240×28, 然后将输出数据反馈到两层LSTM层中. 接下来, Clip层将LSTM层的输出数据整合到真实EEG的维度; 最后, 使用一层LSTM对上层输出进行整合, 使其维度满足判别器的输入维度. 此外, 本文在生成器的每一层神经网络后加入batch normalization (BN)层并使用Leaky ReLU激活函数以防止模型在训练过程中出现梯度消失等问题.
| 表 1 生成器体系结构 Table 1 The architecture of generator |
改进后的判别器体系结构如表2所示. 本文将维度为231×1真实EEG信号以及生成器的输出数据作为判别器的输入数据. 为提高判别器的稳定性, 本文通过添加高斯白噪声(mean=0, std=0.05)对输入数据进行腐蚀. Goodfellow等人[28, 29]认为, 模型不稳定的主要原因是真实样本分布和生成样本分布具有不相交的特性, 而在最优判别器的情况下, 这将导致梯度消失. 因此, 我们在判别器中加入高斯白噪声, 可以避免梯度消失, 从而提高生成模型的稳定性. 其次, 我们添加3个具有Leaky ReLU的LSTM, 以实现对EEG的时间特征提取操作; 其参数设置与生成器的LSTM层参数相对应, 从而保证判别器与生成器对数据的同步处理; 接下来, Flatten层将LSTM层的输出数据的维度降维至29568, 最后, 经过具有单神经元的Fully connected层输出判别器的鉴别结果. 本文在判别器未添加BN层, 这是由于BN层会破坏Lipschitz连续的约束范围, 导致模型出现难以收敛的现象.
| 表 2 判别器体系结构 Table 2 The architecture of discriminator |
3 实验结果分析
本文使用 Python语言和Keras (TensorFlow) 深度学习框架实现对模型的训练, 并使用Bi2015a数据集[30]作为训练数据. Bi2015a数据集包含了50名受试者在进行《大脑入侵者》游戏时的EEG记录. 该游戏在一个由36个符号(1个目标符号, 35个非目标符号)组成的网格上使用了oddball实验范例, 这些符号随机闪现以引起被试人员P300的脑电波形. 实验采用32个电极, 分别在50 ms、80 ms和110 ms三种条件下记录EEG数据. 经过初步筛选, 我们删除了15个存在损坏通道的EEG数据; 同时, 对比32个通道的P300特征, 发现C3通道的P300特征最明显. 因此, 本文使用35个被试的C3通道的数据进行实验. 在预处理阶段, 本文将未经处理的EEG信号进行降采样处理, 使其频率降至256 Hz; 同时, 为保留P300特征波形, 我们按照事件标签, 截取事件发生前100 ms至事件发生后500 ms, 共计900 ms的EEG数据, 并按照式(12)计算得到维度为231×1的训练数据.
| $ l = f \times t $ | (12) |
其中, l为分割后的数据长度, f为频率, t为时间.
本文将每一类EEG数据分割并累加, 分别得到3411、2862、2436个维度为231×1的数据. 因此, 本文使用8709个EEG样本作为训练数据.
3.1 模型评价指标 3.1.1 相似性评估方法本文采用sliced Wasserstein distance (SWD)[31]对生成样本的相似性进行评估, 如式(13)所示:
| $ {\textit{SWD}}(g, x) = \int_{{S^{d - 1}}} {WD({R_\theta }g, {R_\theta }x)} d\theta $ | (13) |
其中, S表示将样本分布映射到一维空间的空间单元, 其满足∫Sd–1dθ=1, θ表示映射角度, Rθ表示在生成样本g和真实样本x上的一维线性投影运算.
SWD通过计算两个样本分布的所有一维投影之间的WD, 来拟合样本整体的分布. SWD的值越低, 表示两种分布在外观和样本的变化上越相似.
3.1.2 多样性评估方法Mode score (MS)[32] 通过计算样本标签分布的交叉熵来评估二者之间的差异, 如式(14)所示:
| $ \begin{split} MS({P_g}) =& \exp ({E_{x\sim{P_g}}}[KL(p(y|x)||p(y)) \\ &-KL(p(y)||p(y*))]) \end{split} $ | (14) |
其中, KL表示交叉熵, x~Pg表示生成样本, p(y)表示生成样本标签y的分布, 满足p(y)=∫xp(y|x)dpg, p(y*)表示真实样本的标签分布, p(y|x)表示通过预测得到的x对标签y的分布. 若生成EEG分类特征越明显, 则p(y)的熵值越大. 因此, MS越高, 说明样本的多样性越好.
3.1.3 准确性评估方法为评估生成样本的准确性, 本文将真实EEG与生成的EEG以不同比例混合, 然后通过使用EEGNet[33]对这些数据进行分类. EEGNet将其作为激活函数以保证分类模型的稳定性[34], 如式(15)所示:
| $ f(x) = \left\{ {\begin{array}{*{20}{l}} {a({e^x} - 1)},&{{\rm{if}}(x < 0)}\\ x,&{{\rm{if}}(x \geqslant 0)} \end{array}} \right. $ | (15) |
其中, α为可调整参数, 用于控制ELU负值的饱和位置.
本文使用EEGNet对真实EEG和生成的EEG的混合数据进行分类, 从准确率、召回率、精确率等方面对生成模型进行二次定量评估.
3.2 实验结果与分析我们拟从多角度对本文所设计的生成模型进行验证, 具体包括4个实验: (1)使用叠加噪声的正弦信号模拟EEG, 验证BN层对生成样本幅值的影响; (2)使用CNN和LSTM搭建生成模型并用于生成EEG, 验证不同神经网络对生成样本多样性和相似性的影响. (3)使用EEG噪声代替高斯噪声作为生成器的输入数据, 验证EEG噪声对生成器拟合速度的影响; (4)将生成EEG与真实EEG以不同比例混合, 通过EEGNet的训练数据, 验证生成的EEG的准确性.
3.2.1 BN层对模型的影响在生成EEG时, 我们发现生成的EEG与真实EEG的值域具有明显差异. 由于其原因无法直接判定, 本文设计人工信号对生成模型进行训练, 以验证BN层对生成样本值域范围变化的影响. 我们以正弦函数(range=[−1.0, 1.0],f=(10/π) Hz)为基础函数, 并叠加一组值域为(−0.4, 0.4)的高斯白噪声(mean=0, std=1)来增加输入数据的多样性以及提升生成模型的抗干扰能力. 最后我们对信号做标准化处理, 以得到值域为[−1.0, 1.0] 的输入信号. 合成信号如图5所示.
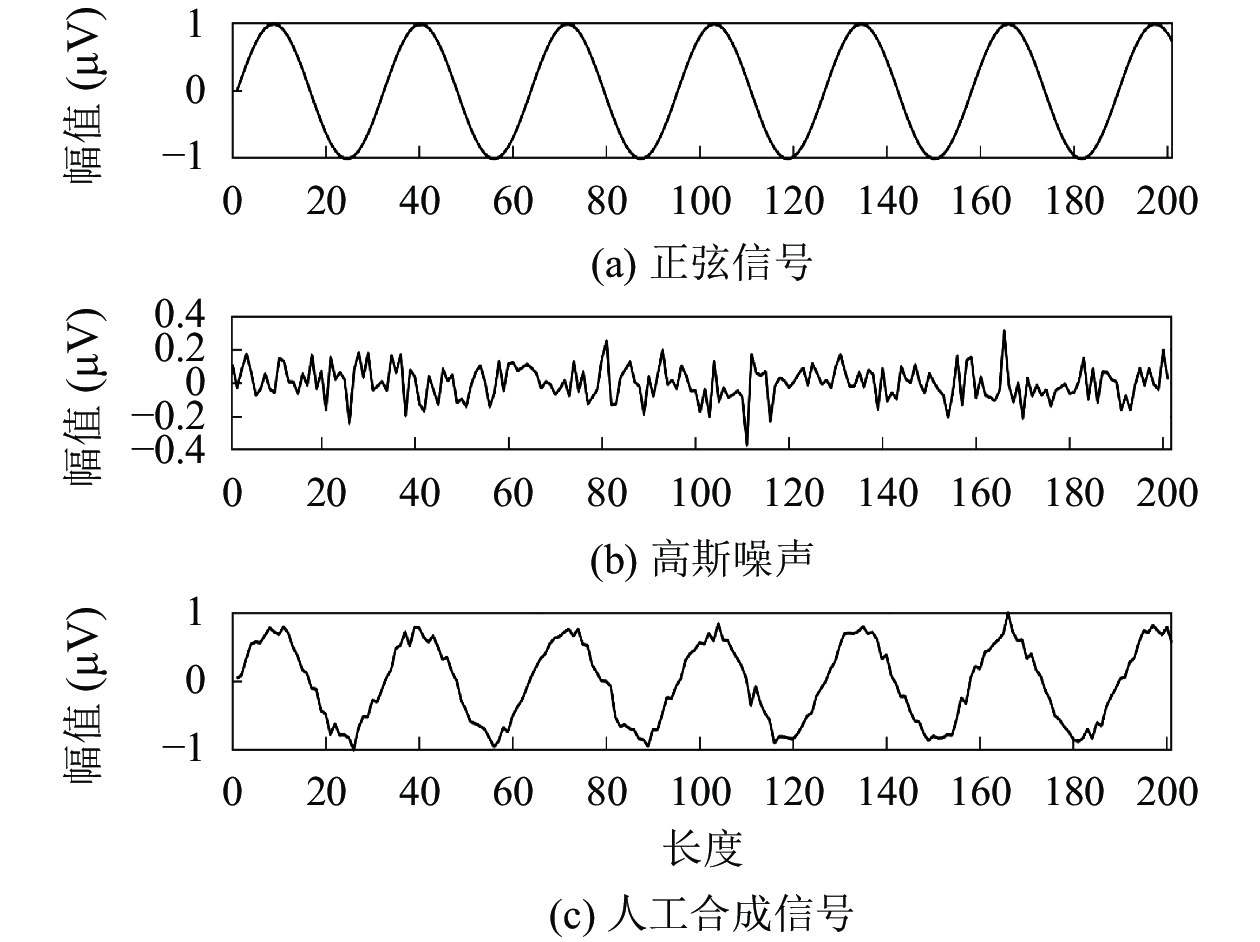
|
图 5 人工合成正弦信号 Fig. 5 Synthetic sinusoidal signal |
我们将人工信号输入到由CNN和LSTM搭建的生成框架中, 从而对比在有/无BN层情况下生成样本的值域变化, 实验结果如表3所示.
| 表 3 人工信号生成结果 Table 3 Generative results of synthetic signal |
从表3可以看出, 在加入BN层的框架中, 生成样本的幅值都比真实样本的幅值小2–50倍; 而在去掉BN层的框架中, 与真实样本的值域范围相近.
我们发现, 在保留BN层的网络框架中, 生成样本存在非周期性的随机性波形, 如图6(a)、图6(b)所示; 图6(c)、图6(d)展示了在去除BN层后所生成的波形, 可以看出, 它们具有正弦信号的形状, 但丢失了随机噪声特征, 这说明模型并未生成较为真实的信号. 实验结果表明, BN层对数据进行批标准化处理后将导致生成数据幅值变小. 但是, 在去掉BN层后, 模型出现过拟合的问题. 因此, 为解决生成样本与真实样本幅值差异的问题, 本文先对滤波后的真实EEG信号进行标准化处理, 将EEG信号的值域范围映射到 [–1, 1] μV, 再输入到判别器中.
3.2.2 不同网络框架对生成模型的影响我们通过使用CNN和LSTM搭建4种不同的生成框架WGAN-GP (GDDD、GDDL、GLDD、GLDL)以验证神经网络对生成EEG质量的影响. 其中, GD表示由CNN搭建的生成器, GL表示由LSTM搭建的生成器, DD表示由CNN搭建的判别器, DL表示由LSTM搭建的判别器; 同时, 本文通过使用SWD和MS分别对不同框架生成的EEG的相似性和多样性进行评估, 评估结果如表4所示.
由表4的客观指标可知, 对于SWD指标, 生成器或判别器任意一方使用LSTM代替2DCNN时, SWD值都有所提高, 且WGAN-GP (GDDL)比WGAN-GP (GLDD)的SWD值高0.2; GLDL的SWD值为1.9, 明显优于其他3个框架的结果, 可以证明本文算法能够生成与真实EEG更为相似的样本. 此外, 从MS值可以看出, 基于WGAN-GP (GDDL)的MS值远高于其他3个框架, 但WGAN-GP (GLDL)的值最低, 这表明相较于WGAN-GP (GLDL), WGAN-GP (GDDD)能够生成更多样化的样本. 综上所示, 定量评估结果出现了相互矛盾的问题. 经过多次实验, 我们发现生成样本的多样性和相似性结果呈负相关, 即生成样本的相似性越高, 多样性就越差.
为进一步评估生成的EEG的质量, 本文从视觉角度对基于不同框架生成的EEG波形进行分析. 从图7(a)–图7(c)可以看出, WGAN-GP (GDDD)、WGAN-GP (GDDL)以及WGAN-GP (GLDD)生成的EEG的值域范围与真实EEG的值域范围明显不符. 从图7(d)可以看出, WGAN-GP (GLDL)生成的EEG的值域范围更接近真实EEG的值域范围, 且生成EEG波形与真实EEG波形存在相似波段. 因此, 从视觉评估的角度分析, 基于WGAN-GP (GLDL)生成的EEG更接近于真实EEG.
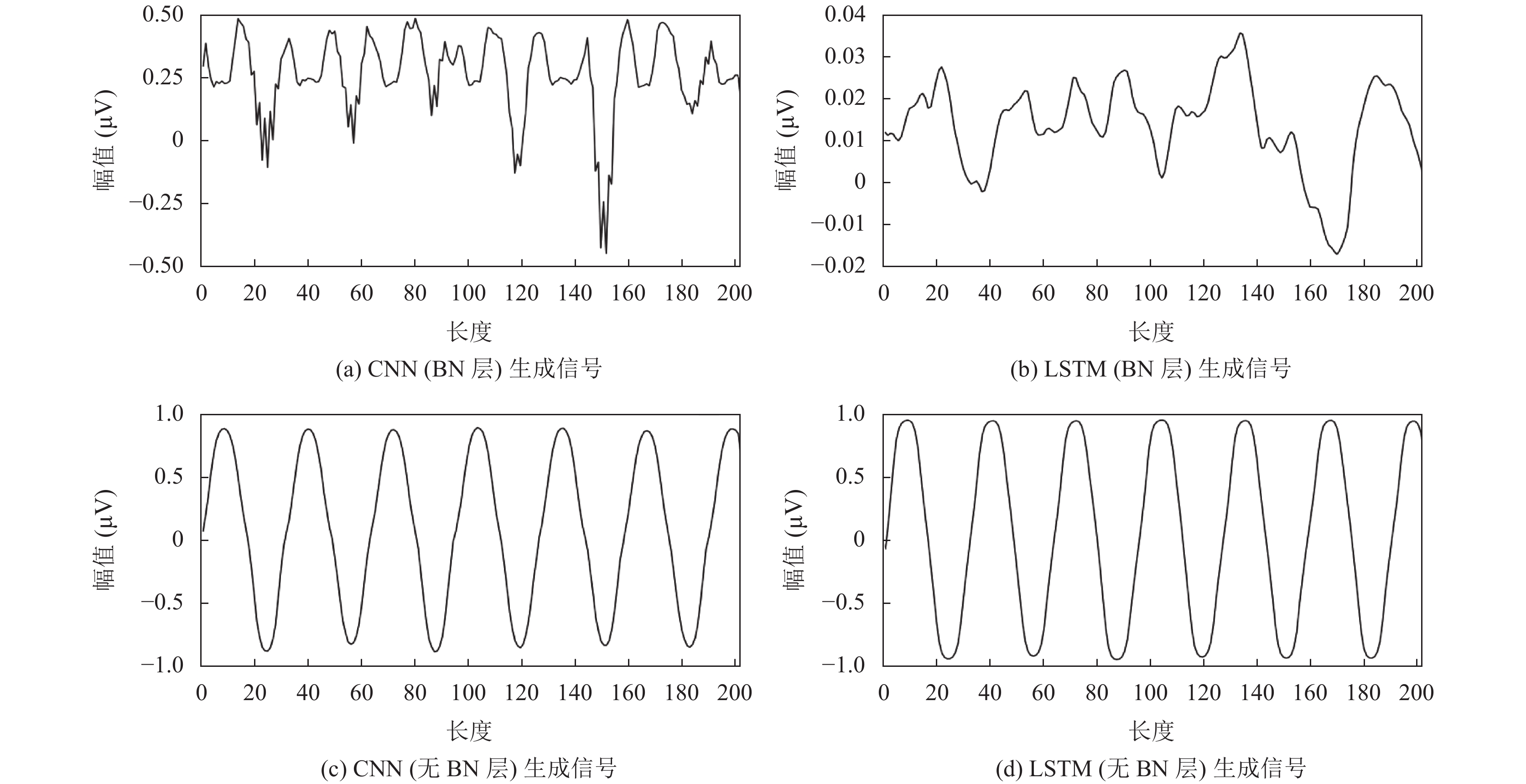
|
图 6 生成的正弦信号 Fig. 6 The generative sinusoidal signal |
| 表 4 不同网络框架生成EEG的定量评估结果 Table 4 The quantitative evaluation results of generative EEG by different network frameworks |
3.2.3 不同噪声对生成模型的影响
相较于CNN搭建的生成框架, LSTM搭建的生成框架在处理速度上更为缓慢. 为进一步提升模型的拟合速度, 本文提出WGAN-GP (GLDL+N), 即将EEG噪声输入到生成器中以用于生成EEG. 这是因为EEG噪声存在与真实EEG相似的信息, 本文将其作为先验知识来提升生成器的拟合速度. 我们记录了将不同噪声作为输入数据时, 模型的训练时间, 在结果如表5所示.
由表5可知, 相较于WGAN-GP (GLDL), WGAN-GP (GLDL+N)的训练时间缩短了1 h 42 min, 这表明EEG噪声的加入能够提高生成器的拟合速度.
为进一步评估EEG噪声对生成模型的影响, 本文使用SWD和MS对生成的样本进行定量评估, 结果如表6所示.
从表6可以看出, 相较于WGAN-GP (GLDL), WGAN-GP (GLDL+N)的MS值要高出15.56, 这证明本文的模型在应用EEG噪声训练过后可以获得多样性更好的生成样本; 但是由于生成样本的多样性和相似性结果呈负相关, 这就导致WGAN-GP (GLDL+N)的SWD值比WGAN-GP (GLDL)的SWD值高. 另一方面, 仅通过定量分析可能会存在片面性, 因此, 本文将视觉分析结果作为另一个重要指标, 其结果如图8所示. 由图可以看出, 基于WGAN-GP (GLDL+N)生成的EEG在幅度和波形上更符合真实EEG的特征.
3.2.4 EEGNet分类实验本文将CC-WGAN-GP和GLDL+N生成的EEG以不同比例与真实EEG混合对EEGNet模型进行训练, 并将分类结果与基于真实样本的分类结果相对比, 验证生成样本对分类器性能的影响. 首先, 本文使用8709个真实EEG训练EEGNet; 然后, 分别使用两个不同框架的 50%生成EEG和50%的真实EEG进行混合来训练EEGNet; 最后, 在真实EEG数据集中加入相同数量的生成样本来训练EEGNet. 实验结果如表7所示.
由表7结果分析可知, 在样本数量不变的情况下, 使用 50%的CC-WGAN-GP框架生成数据代替真实数据训练模型, 其准确率降低了10.04%, 精确率降低了3.43%, 召回率降低了9.47%, F1-score降低了10.88, AUC降低了7.86%. 实验结果表明, CC-WGAN-GP生成的样本不能够代替真实样本来训练分类模型, 反而会影响分类模型的性能. 使用50%的GLDL+N框架生成数据代替真实数据训练模型时, 其准确率、精确率、召回率相差 1%左右, F1-Score 相差 2.20%, AUC相差0.23%, 从而证明GLDL+N生成的EEG与真实 EEG相似, 能够代替真实数据作为分类器的训练数据. 此外, 将相同数量的GLDL+N框架生成的数据加入到真实数据中训练EEGNet, 准确率提高了8.5%, 精确率提高了16.5%, 召回率提高了9.25%, F1-score提高了12.73%, ROC-AUC 提高了4.37%. 由结果看出, 在增加生成数据的情况下, 模型在分类精度、稳定性以及泛化能力等方面都能够提升; 进而证明, 我们所设计的EEG生成模型能够提升分类模型的性能.

|
图 7 生成的EEG信号 Fig. 7 The generative EEG signal |
| 表 5 不同框架的训练时间对比结果 Table 5 Comparison training time of different frameworks |
| 表 6 生成样本相似性以及多样性对比结果 Table 6 Comparison of generative samples via similarity and diversity |
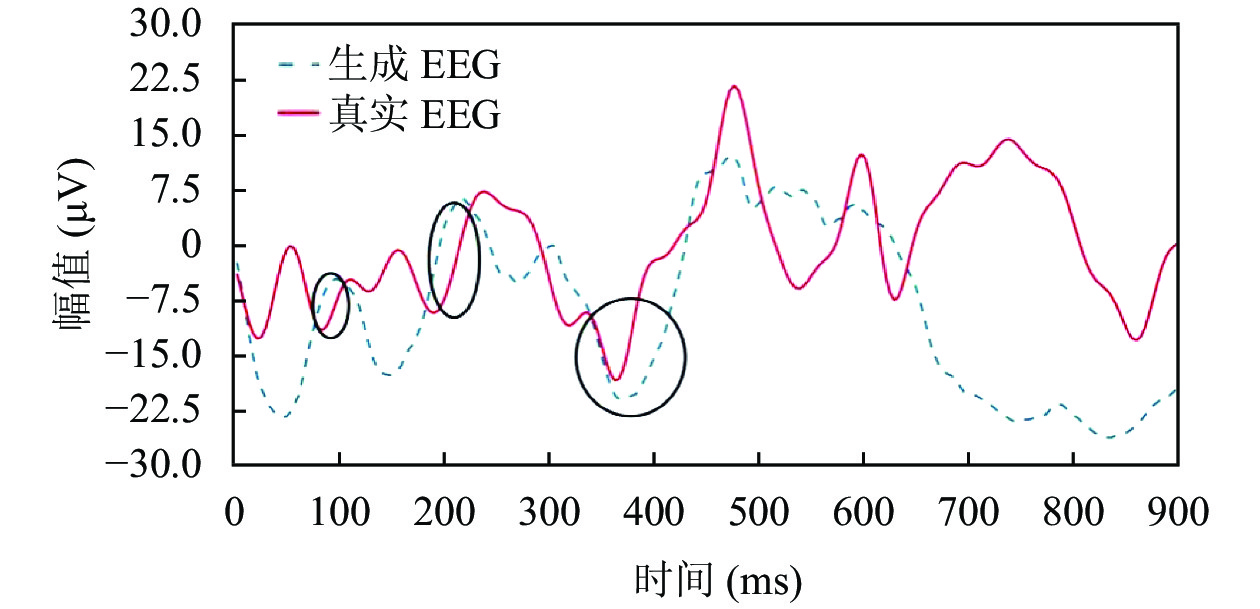
|
图 8 WGAN-GP (GLDL+N)生成的EEG波形 Fig. 8 The generative EEG of WGAN-GP(GLDL+N) |
| 表 7 基于不同混合比例的样本分类结果 (%) Table 7 The classification results using samples with different proportions |
4 结束语
本文提出一种新型EEG信号生成模型, 以解决目前存在的生成样本多样性不足、拟合速度慢以及幅值差异过大等问题. 为评估生成模型的性能, 本文从相似性、多样性、准确性以及训练时间等方面对生成模型进行评估. 与WGAN-GP相比较, 本文提出的生成模型在相似性和多样性方面的性能均有所提高. 此外, 我们使用EEGNet对模型进行二次定量评估, 分类结果表明此模型能够生成较为准确的样本, 且能够提高分类模型的性能. 本文所提出的EEG信号生成模型将为构建高性能的深度学习模型提供保证, 同时能够极大降低人力资源消耗和成本. 因此, 本研究具有十分重要的实际意义和应用价值.
目前, 本文仅完成单通道EEG生成的工作, 而在实际应用中, 基于单通道的信息可能无法满足模型泛化能力的需求. 未来, 我们将继续优化生成模型, 以用于多通道EEG信号生成, 使其能够更加有效地应用于与EEG相关的工作中, 例如, 情感识别、脑控技术等.
| [1] |
李颖洁, 李玉玲, 杨帮华. 基于脑电信号深度学习的情绪识别研究现状. 北京生物医学工程, 2020, 39(6): 634-642. DOI:10.3969/j.issn.1002-3208.2020.06.014. |
| [2] |
Bochet A, Sperdin HF, Rihs TA, et al. Early alterations of large-scale brain networks temporal dynamics in young children with autism. Communications Biology, 2021, 4(1): 968. DOI:10.1038/s42003-021-02494-3 |
| [3] |
Xu XY, Jia TY, Li Q, et al. EEG feature selection via global redundancy minimization for emotion recognition. IEEE Transactions on Affective Computing, 2021.
|
| [4] |
Song TF, Liu SY, Zheng WM, et al. Variational instance-adaptive graph for EEG emotion recognition. IEEE Transactions on Affective Computing, 2021.
|
| [5] |
Jiao YY, Deng YN, Luo Y, et al. Driver sleepiness detection from EEG and EOG signals using GAN and LSTM networks. Neurocomputing, 2020, 408: 100-111. DOI:10.1016/j.neucom.2019.05.108 |
| [6] |
Roy S, Dora S, McCreadie K A, et al. MIEEG-GAN: Generating artificial motor imagery electroencephalography signals. Proceedings of 2020 International Joint Conference on Neural Networks (IJCNN). Glasgow: IEEE, 2018. 1−8.
|
| [7] |
Kingma DP, Welling M. Auto-encoding variational Bayes. Proceedings of 2nd International Conference on Learning Representations (ICLR). Banff: ICLR, 2014. 1−14.
|
| [8] |
Goodfellow IJ, Pouget AJ, Mirza M, et al. Generative adversarial nets. Proceedings of the 27th International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2014. 2672−2680.
|
| [9] |
Kingma DP, Dhariwal P. Glow: Generative flow with invertible 1×1 convolutions. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Red Hook: MIT Press, 2018. 10236−10245.
|
| [10] |
Yu LT, Zhang WN, Wang J, et al. SeqGAN: Sequence generative adversarial nets with policy gradient. Proceedings of the 31st AAAI Conference on Artificial Intelligence. San Francisco: AAAI Press, 2017. 2852−2858.
|
| [11] |
Abdelfattah SM, Abdelrahman GM, Wang M. Augmenting the size of EEG datasets using generative adversarial networks. Proceedings of 2018 International Joint Conference on Neural Networks (IJCNN). Rio de Janeiro: IEEE, 2018. 1−6.
|
| [12] |
Luo Y, Lu BL. EEG Data augmentation for emotion recognition using a conditional wasserstein GAN. Proceedings of 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). Honolulu: IEEE, 2018. 2535−2538.
|
| [13] |
Panwar S, Rad P, Jung TP, et al. Modeling EEG data distribution with a wasserstein generative adversarial network to predict RSVP events. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2020, 28(8): 1720-1730. DOI:10.1109/TNSRE.2020.3006180 |
| [14] |
Arjovsky M, Chintala S, Bottou L. Wasserstein GAN. arXiv: 1701.07875v3, 2017.
|
| [15] |
Shi J, Zhang W, Wang YL. Shape analysis with hyperbolic wasserstein distance. Proceedings of 2016 Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas: IEEE, 2016. 5051−5061.
|
| [16] |
Gulrajani I, Ahmed F, Arjovsky M, et al. Improved training of wasserstein GANs. Proceedings of the 31st International Conference on Neural Information Processing Systems. Red Hook: MIT Press, 2017. 5767−5777.
|
| [17] |
Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166. DOI:10.1109/72.279181 |
| [18] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [19] |
Greff K, Srivastava RK, Koutník J, et al. LSTM: A search space odyssey. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(10): 2222-2232. DOI:10.1109/TNNLS.2016.2582924 |
| [20] |
Phadikar S, Sinha N, Ghosh R. Automatic EEG eye-blink artefact identification and removal technique using independent component analysis in combination with support vector machines and denoising autoencoder. IET Signal Processing, 2020, 14(6): 396-405. DOI:10.1049/iet-spr.2020.0025 |
| [21] |
高军峰, 郑崇勋, 王沛. 基于独立成分分析和流形学习的眼电伪差去除. 西安交通大学学报, 2010, 44(2): 113-118. |
| [22] |
王爽. 基于独立成分分析的碳价格分析及预测[硕士学位论文]. 西安: 陕西师范大学, 2019.
|
| [23] |
Luo P, Wang XJ, Shao WQ, et al. Towards understanding regularization in batch normalization. Proceedings of 7th International Conference on Learning Representations. New Orleans: OpenReview.net, 2019. 1−8.
|
| [24] |
Pascual S, Bonafonte A, Serr J. SEGAN: Speech enhancement generative adversarial network. Proceedings of Interspeech 2017, 18th Annual Conference of the International Speech Communication Association. Stockholm: ISCA, 2017. 3642–3646.
|
| [25] |
Donahue C, McAuley J, Puckette M. Adversarial audio synthesis. Proceedings of 7th International Conference on Learning Representations. New Orleans: OpenReview.net, 2019. 1−8.
|
| [26] |
Bousmalis K, Silberman N, Dohan D, et al. Unsupervised pixel-level domain adaptation with generative adversarial networks. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017. 95–104.
|
| [27] |
Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Proceedings of 26th Annual Conference on Neural Information Processing Systems. Lake Tahoe: MIT Press, 2012. 1097−1105.
|
| [28] |
Sutskever I, Jozefowicz R, Gregor K, et al. Towards principled unsupervised learning. arXiv: 1511.06440v1, 2015.
|
| [29] |
Salimans T, Goodfellow IJ, Zaremba W, et al. Improved techniques for training GANs. Proceedings of 30th International Conference on Neural Information Processing Systems. Red Hook: Curran Associates Inc., 2016. 2234−2242.
|
| [30] |
Korczowski L, Cederhout M, Andreev A, et al. Brain Invaders calibration-less P300-based BCI with modulation of flash duration Dataset (bi2015a). GIPSA-lab. 2019.
|
| [31] |
Lee CY, Batra T, Baig MH, et al. Sliced wasserstein discrepancy for unsupervised domain adaptation. Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2020. 10277−10287.
|
| [32] |
Shmelkov K, Schmid C, Alahari K. How good is my GAN? Proceedings of 15th European Conference on Computer Vision. Munich: Springer, 2018. 218−234.
|
| [33] |
Lawhern VJ, Solon AJ, Waytowich NR, et al. EEGNet: A compact convolutional neural network for EEG-based brain-computer interfaces. Journal of Neural Engineering, 2018, 15(5): 056013. DOI:10.1088/1741-2552/aace8c |
| [34] |
Clevert DA, Unterthiner T, Hochreiter S. Fast and accurate deep network learning by exponential linear units (ELUs). Proceedings of 4th International Conference on Learning Representations (ICLR). San Juan: ICLR, 2016. 1−8.
|
 2022, Vol. 31
2022, Vol. 31



