目前, 在工业领域中玻璃制品具有卫生、外形美观、耐高温、耐腐蚀等特点, 已在医药、卫生、化工等领域中有十分广泛的应用^[1]. 玻璃制造过程中的第一步就是将玻璃配合料熔制成均匀无气泡且符合成型要求的玻璃料滴, 玻璃料滴的质量控制直接影响产品成品率. 玻璃料滴质量的检测以往多是由人工检测, 不仅效率低还易受环境影响, 稳定性较差^[2]. 因此, 研究一种非接触式的测量方法有利于提高生产效率和产品合格率. 双目立体视觉是基于视差原理并由多幅图像获取物体三维几何信息的方法. 吴琪波^[3]通过半全局匹配算法获得图片的深度信息, 提取目标高度信息和上表面积, 得到目标物体体积. 丁嗣禹等^[4]通过插值算法填充视差图中的空洞, 用阈值分割算法提取出了堆料区域的结构信息. 梁乐^[5]通过最小切割算法提升了立体匹配算法精度, 更加完整的重建出待测物体的三维坐标信息. 料滴经过剪刀剪切后, 在下落过程中会发生空间上的偏转. 利用外截面面积和视差填充^[6]测量料滴体积及质量会产生较大误差, 三维重建方法^[7]计算较为复杂, 不能满足实时测量需求. 本文通过搭建冷态玻璃料滴测量系统, 基于双目立体视觉获得料滴的三维信息, 提出一种空间校正切片法来完成玻璃料滴的非接触式测量.

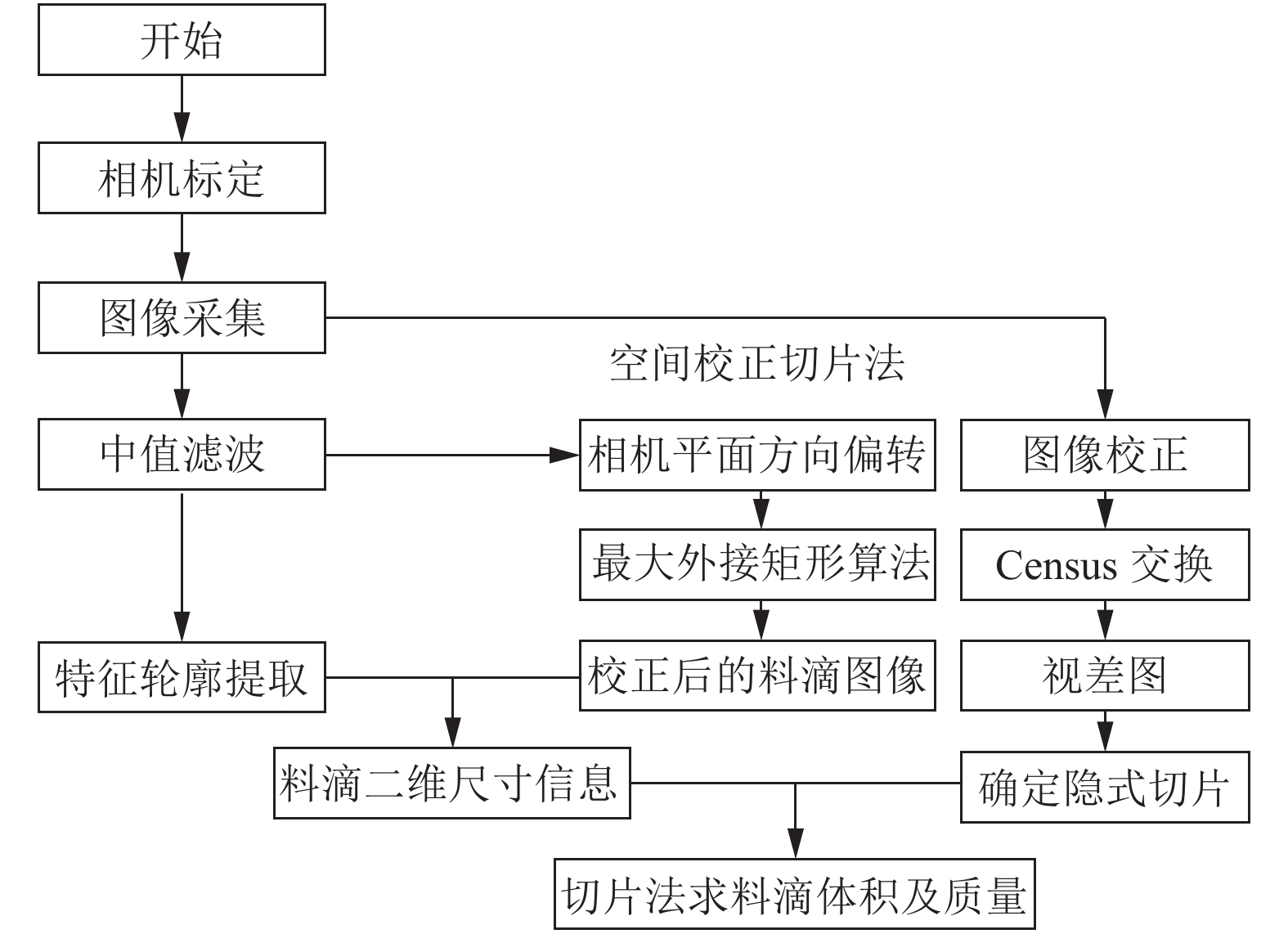
1 实验系统及双目视觉测量模型 1.1 实验系统及算法流程

实验装置如图1所示. 主要包括料滴接受装置、料滴模拟运动装置和CCD摄像头, 用密度均匀的黏土来模拟玻璃料滴, 测量采用海康威视的 2 台型号为MV-CE060-10UC摄像头进行采集, 采集下落过程中的料滴图像进行处理并获取结果.

图像处理算法主要包括5个模块: 摄像机标定、图像校正、特征轮廓提取、立体匹配和空间校正切片法求体积. 处理流程如图2所示.

1.2 双目视觉测量模型

双目立体视觉模型如图3所示. 世界坐标系中任意点 $ A(X, Y, Z) $ 在双目摄像机采集的左右图像的投影分别为 ${a_{\rm{l}}}({u_{{\rm l}}}, {v_{\rm{l}}})$ 和 ${a_{\rm{r}}}({u_{\rm{r}}}, {v_{\rm{r}}})$ . 这两个像素点坐标结合摄像机内外参数, 通过计算获得空间中待测点A的三维空间坐标.

综上所述, 整个成像系统可用式(1)表示:

$ \begin{split} &{{\textit{z}}_c}\left[ {\begin{array}{*{20}{c}} u \\ v \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{dx}}}&0&{{u_0}} \\ 0&{\dfrac{1}{{dy}}}&{{v_0}} \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} f&0&0&0 \\ 0&f&0&0 \\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} R&T \\ {{0^{\rm{T}}}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \\ 1 \end{array}} \right] = {M_2}{M_1}\left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \\ 1 \end{array}} \right] \end{split} $

(1)

2 图像处理及立体匹配 2.1 摄像机标定

首先通过张正友平面标定法^[8]得到摄像机的内外参数, 可计算求得两摄像机之间的旋转平移矩阵, 标定过程如下: 若棋盘格上有任意一点P在世界坐标系中为 $ {P_W} $ , 则点P点在左右两个摄像机坐标系中的坐标分别为:

$ \left\{ {\begin{array}{*{20}{c}} {{P_{\rm{l}}} = {P_{\rm{l}}}{P_w} + {T_{\rm{l}}}} \\ {{P_{\rm{r}}} = {P_{\rm{r}}}{P_w} + {T_{\rm{r}}}} \end{array}} \right. $

(2)

选择左摄像机坐标系为双目立体视觉系统的基准坐标系, 因此, $ {P_{\text{r}}} $ 和 ${P_{\rm{l}}}$ 应满足:

$ {P_{\rm {l}}} = {R^{\rm{T}}}({P_{\rm{r}}} - T) $

(3)

联立式(2), 式(3)可以得到左右摄像机坐标之间的变换关系:

$ \left\{ {\begin{array}{*{20}{l}} {R = {R_{\rm{r}}}R_{\rm{l}}^{ - 1}} \\ {T = {T_{\rm r}} - {R_{\rm{r}}}R_{\rm{l}}^{ - 1}{T_{\rm{l}}}} \end{array}} \right. $

(4)

其中, R和T分别为旋转矩阵和平移向量. 本次采集的标定板图像如图4所示, 拍摄多组不同位置的标定板图像, 基于Matlab中的Stereo CameraCalibration工具箱对左右相机采集到的棋盘格标定板图片完成左右相机的标定, 对多组外参数进行非线性优化, 得到立体标定最优的外参数R和T.

2.2 图像校正

由于两个相机的安装不可能完全平行, 使得左右相机获取的图片存在细微的角度偏差, 为了保证双目图像在同一平面上使左右图像对应极线平行, 以提高立体匹配速度及精度, 需要对左右相机采集到的图像进行校正. 图像的畸变使用BOUGUET校正算法对采集的图像对进行校正, 能够很好地消除相机产生的畸变和误差^[9].

2.3 特轮廓提取

中值滤波是一种空间滤波方法, 能有效抑制图像中的噪声, 料滴图像采用中值滤波能较好地保护边缘信息^[10]. 图5为料滴轮廓提取的过程, 滤波后图像如图5(b). 迭代式阈值分割是自动计算阈值, 实现简单且计算量小, 便于实时检测. 本文选择使用迭代式阈值分割算法来分割图像. 阈值分割后后图像如图5(c)所示.

2.4 融合梯度信息的Census变换立体匹配算法

Census变换的基本原理是: 在一个变换窗口内, 将窗口中每个像素的灰度值与领域像素的灰度值进行比较并映射到一个比特串. 选择一个5×5 的矩形窗口遍历整个图像, 具体定义为:

$ C{{ensu}}s(p) = { \otimes _{q \in {N_P}}}\xi (p, q) $

(5)

$ \xi (p, q)=\left\{ {\begin{array}{c}1\text{, }{I}_{{q}} \gt {I}_{P}\\ 0\text{, }{I}_{{q}}\leqslant {I}_{p}\end{array}} \right. $

(6)

用 $ \oplus $ 来表示汉明距离算子, 则基于Census变换的匹配代价计算:

$ {C_{\rm{cen}}}(p, d) = Census(p) \oplus Census(q) $

(7)

图像梯度信息包含了丰富结构信息, 能反映图像灰度变化的速度, 灰度变化较大的区域经常发生在图像的边缘位置^[11]. 在Census算法的基础上, 融入图像的梯度信息, 能够更清晰地表现图像边缘的信息, 能够增强立体匹配在边缘匹配的准确度. 融合梯度信息的Census匹配代价计算方法为:

$ {C_{\rm{grad}}}(p, d) = |{\nabla _x}{I_L}(p) - {\nabla _x}{I_R}(p, d)| + |{\nabla _y}{I_L}(p) - {\nabla _y}{I_R}(p, d)| $

(8)

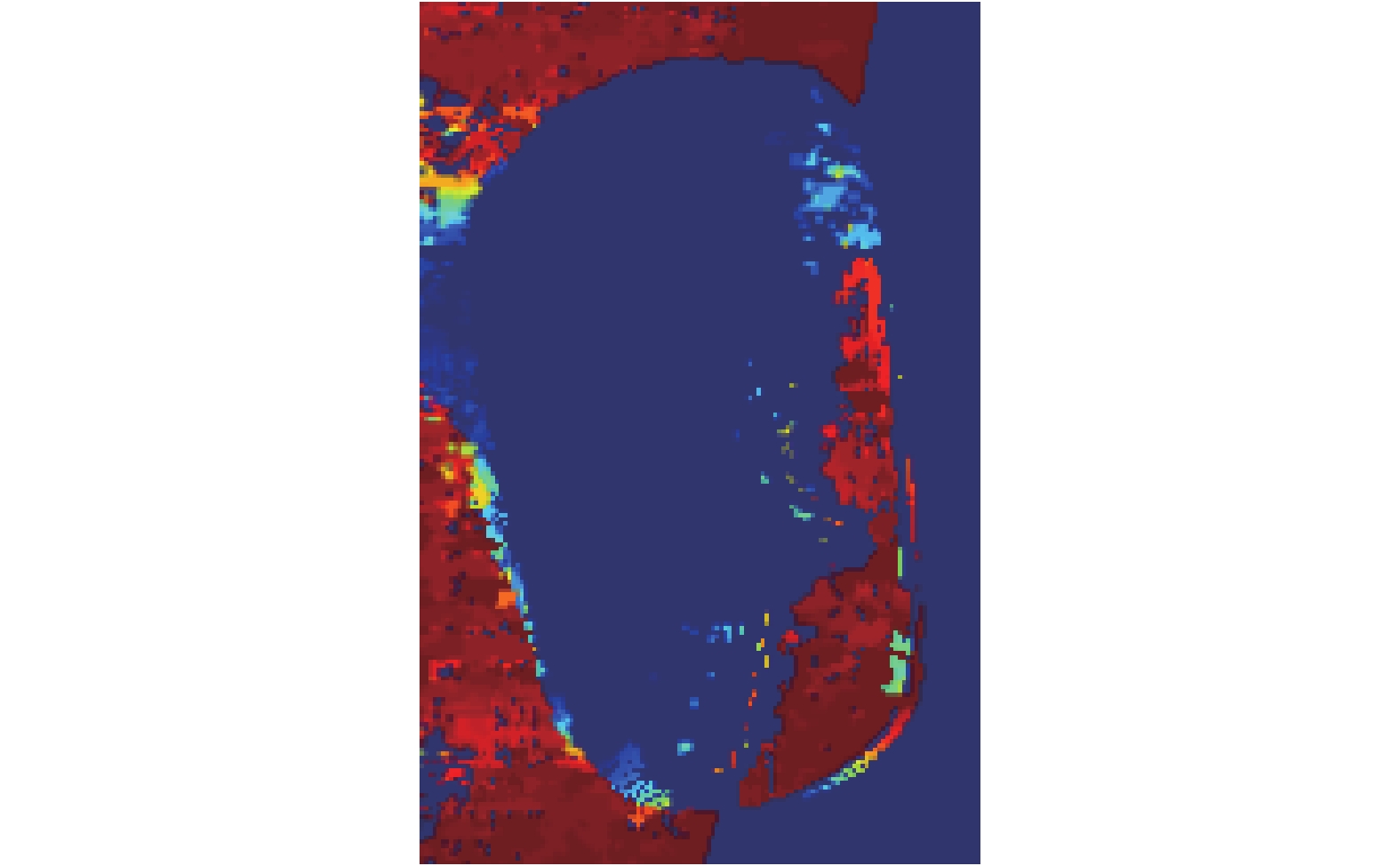
视差图如图6所示.

3 料滴体积测量方法 3.1 垂直下落状态方法分析

通过观察常见料滴形状具有回转体特征, 因此可利用其任意横截面为圆形的特征求取料滴体积并计算其质量^[12]. 如图7所示, 按水平切片法原理沿垂直方向扫描料滴图像, $ {r_e} $ 、 $ {r_s} $ 分别为料滴顶端和底端像素所在的行向量坐标, 切片厚度 $ \Delta y $ 为1 pixel; $ {d_r} $ 为切片的直径. 料滴的体积可由式(9)求得:

$ V = \sum\limits_{r = {r_s}}^{{r_e}} {\frac{{\pi d_r^2}}{4}} \Delta y $

(9)

利用 $ m = \rho v $ 计算料滴质量(g); $ \;\rho $ 为料滴的密度( $ \rm {g/c{m^3}} $ ).

3.2 空间校正切片法

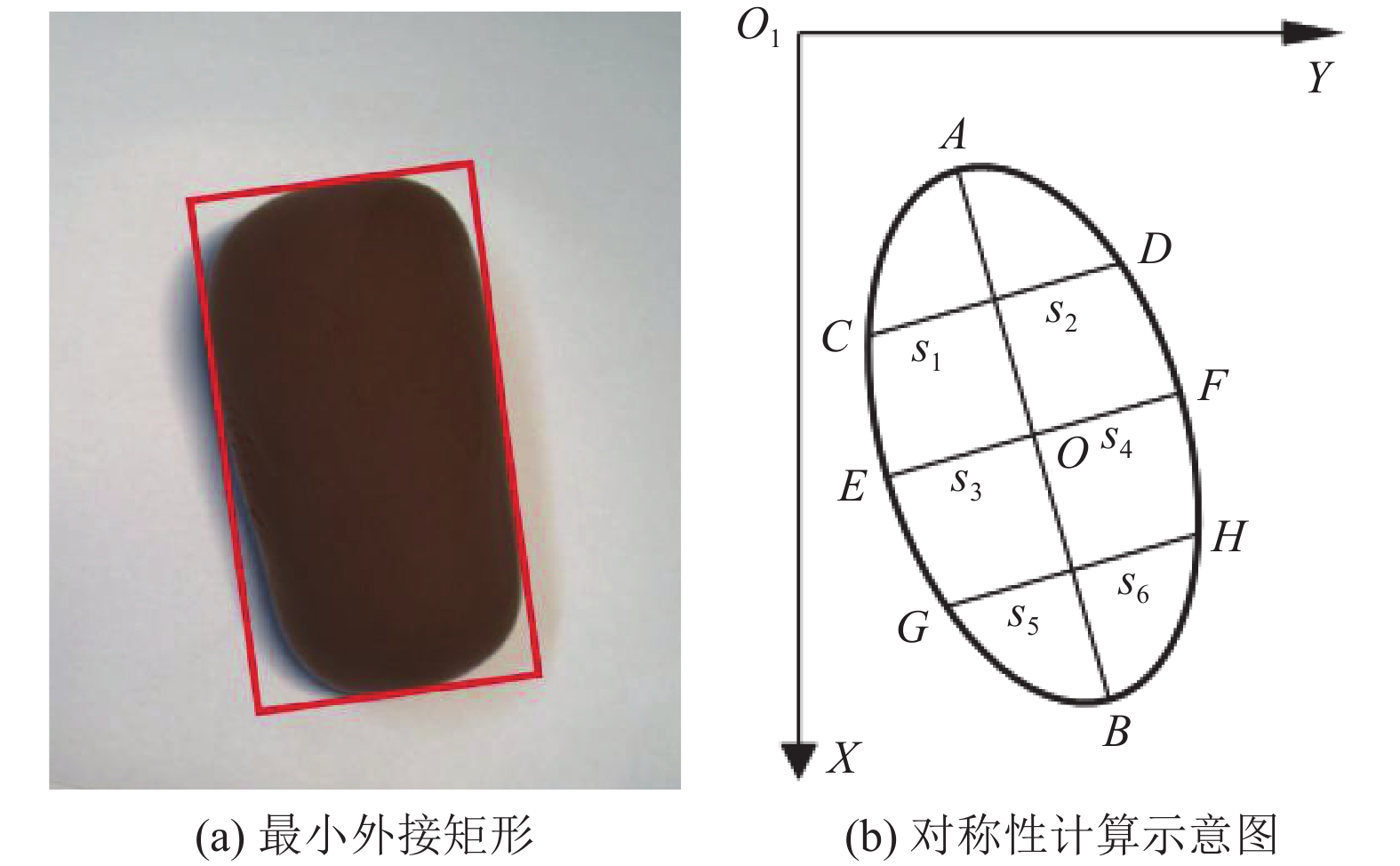
料滴经过剪刀剪切后, 在下落过程中会发生空间上的偏转, 此时将偏转方向分解为相机平面方向和相机景深方向. 当料滴对称轴发生相机平面偏转时, 料滴水平截面发生变形, 影响水平切片法计算精度. 利用最小外接矩形算法^[13]确定对称轴和偏转角度, 然后将料滴校正至水平方向. 如图8(a)所示, 图像最小外接矩形的高边角度可以反映出料滴图像的方向信息. 如图8(b)所示, 过对称轴线AB的中点O作垂线交轮廓线于E, F点, 再分别过AO, BO的中点作垂线交轮廓线于点C, D, G和H.

为了验证最小外接矩形算法选取对称轴的准确度, 引入判断料滴关于轴线是否对称的变量 $ {L_\lambda } $ :

$ {L_\lambda } = {\left( {{S_1} - {S_2}} \right)^2} + {\left( {{S_3} - {S_4}} \right)^2} + {\left( {{S_5} - {S_6}} \right)^2} $

(10)

其中, L₁, L₂, L₃, L₄, L₅和L₆, 分别为C, D, E, F, G和H到扫描直线的距离. 若 $ {L_\lambda } $ 的值越小, 则料滴关于对称轴的对称性越好. 选择合适的对称轴按切片法原理计算料滴体积.

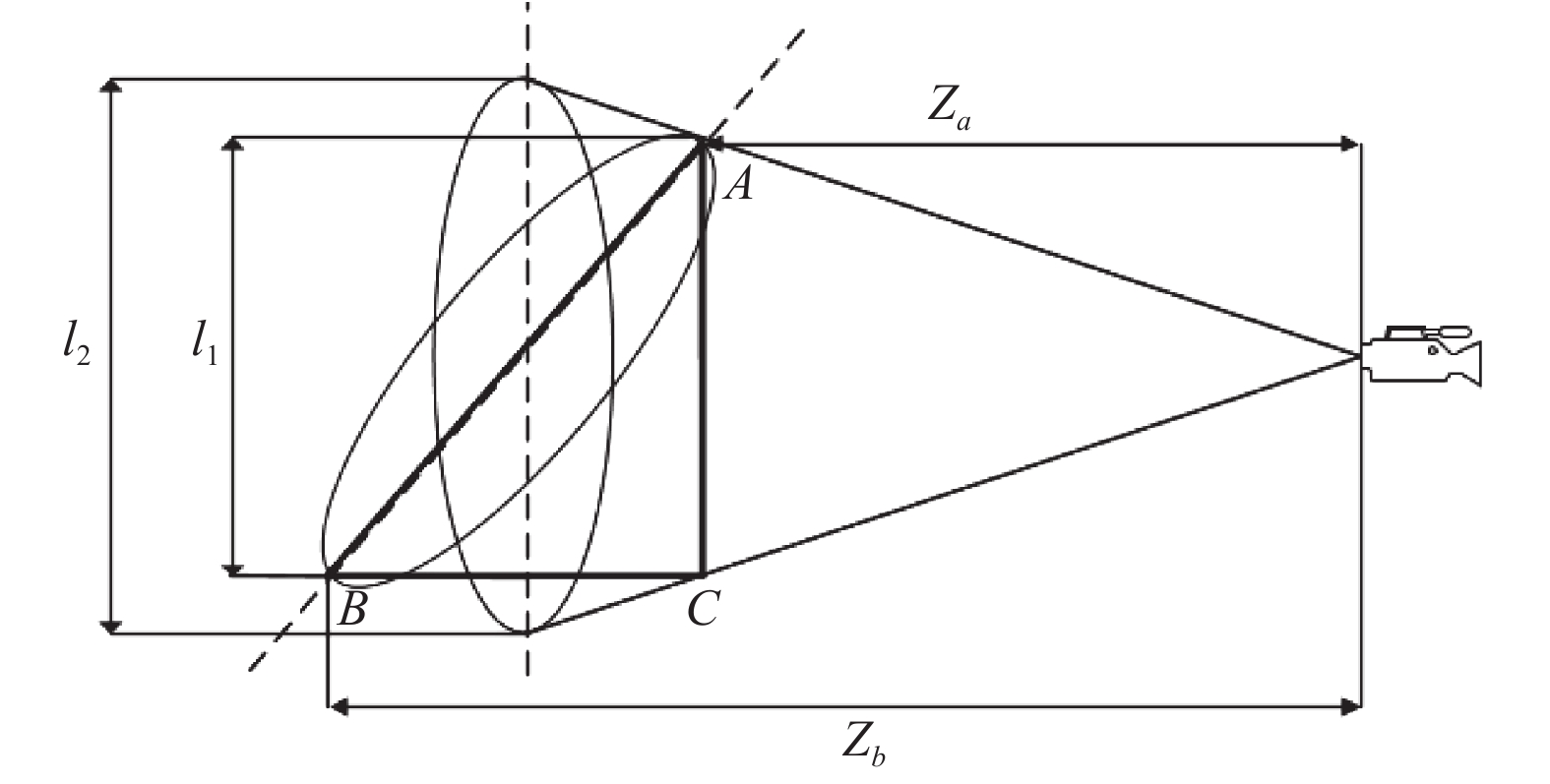
相机景深方向的偏转如图9所示, 景深方向的偏转影响了对称轴的高度, 料滴真实高度为 $ {l_2} $ , 图像上投影高度为 $ {l_1} $ , 其对称轴高度影响的是切片的数量, 影响结果的准确性. 在三角形ABC中, 利用视差变化计算出景深方向偏转的距离BC, 结合投影对称轴高度AC, 计算出料滴真实对称轴高度AB. 表达式如下:

$ {l_2} = AB = \sqrt {{{(BC)}^2} + {l_1}^2} $

(11)

$ BC = {Z_b} - {Z_a} $

(12)

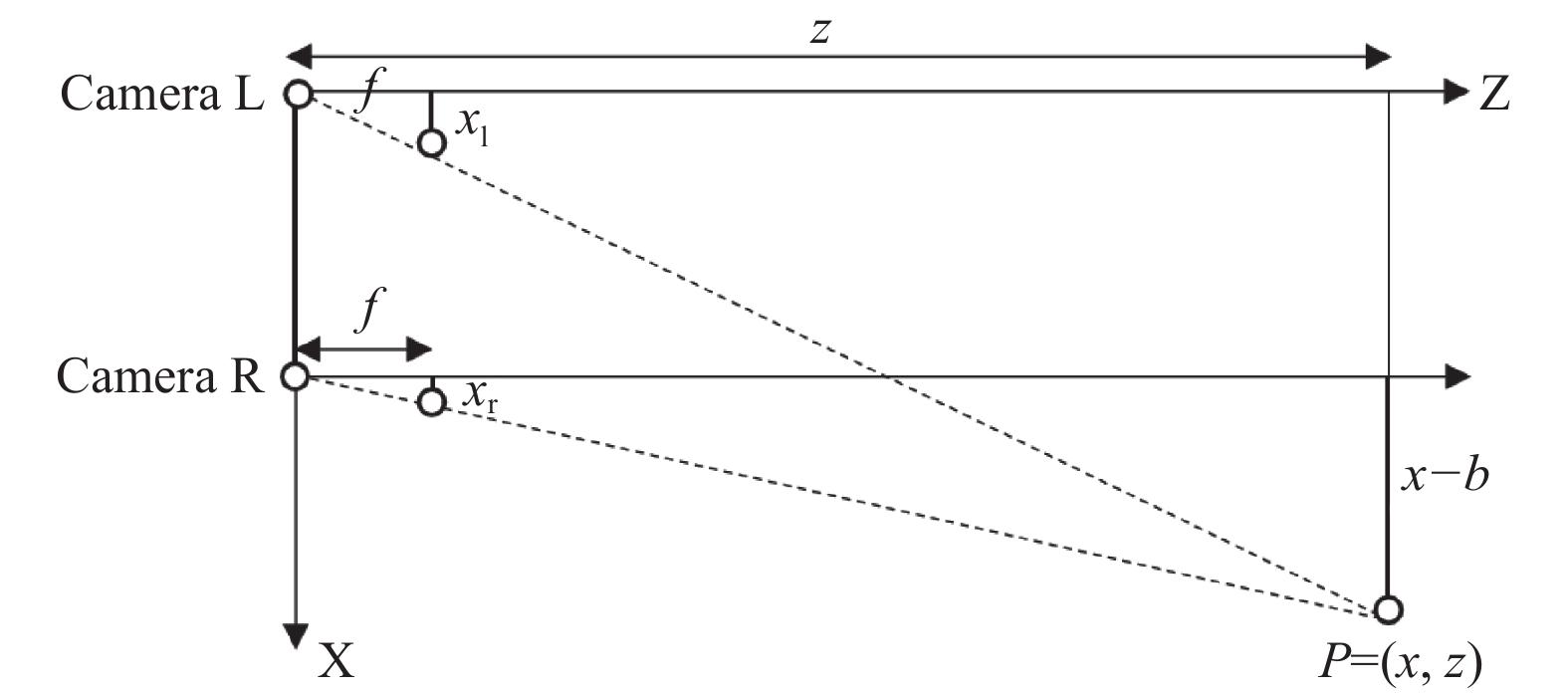
如图10双目视觉横向模式成像示意图, 景深与视差成反比, 其公式为:

$ {\textit{z}} = \frac{{f \times b}}{{({x_{\rm l}} - {x_{\rm r}})}} $

(13)

其中, $ f $ 为焦距, $ b $ 为左右摄像机之间的距离, ${x_{\rm{l}}}$ , ${x_{\rm r}}$ 分别为左右图像的像素点距离各自中心点的距离. 对于左图像的任意一个像素点 ${x_{\rm{l}}}$ , 都在右图中找到相对应的极线, 然后扫描极线找到最匹配的点 ${x_{\rm{r}}}$ , 最后计算视差, 并根据公式 ${x_{\rm{l}}} - {x_{\rm{r}}}$ 求取景深.

联立式(11), 式(12)可以得真实对称轴高度 $ {l_2} $ 表达式如下:

$ {l_2} = \sqrt {{{(Z{}_b - {Z_a})}^2} + {l_1}^2} $

(14)

其中, $ {Z_a} $ , $ {Z_b} $ 分别为料滴图像上下顶点景深.

料滴对称轴高度变化产生了如图11所示隐式切片, 隐式切片高度为 $ {l_2} - {l_1} $ , 隐式切片的直径 ${d_{\rm{r}}}$ 可计为料滴切片直径的算术平均数. 隐式切片体积V_s计算公式如下:

$ {V_s} = \frac{{\pi {{\left( {\displaystyle\sum\limits_{r = {r_s}}^{{r_e}} {{d_r}} /\left( {{r_e} - {r_s}} \right)} \right)}^2}}}{4}\Delta y\left( {{l_2} - {l_1}} \right) $

(15)

隐式切片体积可补偿在最小外接矩形切片法中因料滴发生相机景深方向偏转产生的影响.

4 实验结果与分析

为验证空间校正切片法在发生空间偏转状态下的准确性及实用性, 在实验过程中模拟3种下落状态, 分为垂直下落、发生相机平面方向偏转下落、发生空间偏转下落. 选取质量分布均匀且在常用质量区间的3个料滴分别模拟在3种状态的图像如图12所示, 其中, 编号a、d、g为垂直下落状态, 编号b、e、h为发生相机平面方向偏转下落状态, 编号c、f、i为发生空间偏转下落状态. 利用水平切片法、最小外接矩形切片法、空间校正切片法分别计算3组料滴在3种状态的测量体积, 表1所示为实验测量数据. 将由表1得到的3种方法测量体积相对误差进行比较, 结果如图13.

垂直下落的3组料滴a、d和g三种方法的相对误差均在1%以内. 对于发生相机平面方向偏转的料滴b、e和h, 水平切片法相对误差达到5%以上, 而最小外接矩形切片法相对误差降至1%–2%, 最小外接矩形切片法对发生相机平面方向偏转的料滴精确度有明显提高. 发生空间偏转的料滴c、f和i, 水平切片法误差较大, 其中料滴i相对误差达到9.25%, 最小外接矩形切片法可提高测量准确度, 其测量相对误差可降至3%左右, 而空间校正切片法可进一步测量精度, 其相对误差降至1%以内. 空间校正切片法对发生空间偏转的料滴有较为稳定的测量精度, 基本能控制在1%以内. 3种测量方法测量的平均误差与标准差如表2所示. 水平切片法测量发生偏转的料滴相对误差误差较大, 最小外接矩形切片法测量稳定性有一定提高, 空间校正切片法具有较高稳定性.

5 结论

料滴经剪刀剪切在下落过程中会发生空间偏转, 当料滴发生相机平面方向偏转后, 切片形状发生变化, 水平切片法平均误差明显上升, 最小外接矩形算法对相机平面方向偏转的料滴图像进行校正, 提高了测量精度. 当料滴发生相机景深方向偏转, 影响切片高度, 最小外接矩形切片法对有相机景深方向偏转的料滴仍具有较大误差, 空间校正切片法适用于发生空间偏转的料滴, 空间校正切片法测量的平均误差与标准差分别为0.81%和0.19. 对于发生空间偏转的料滴, 空间校正切片法具有较高的测量精度和稳定性.