扩散加权磁共振(diffusion-weighted magnetic resonance imaging, DW-MRI)是一种以非侵入性的方式, 测量活体组织内水分子扩散运动特性的成像技术. 在采集过程中, 通过改变扩散梯度强度与持续时间 (即扩散敏感因子, b值)来改变对水分子扩散运动的敏感性, 从而测定出衰减的磁共振信号. 通常利用单指数模型来衡量衰减的磁共振信号, 估计出表观扩散系数(apparent diffusion coefficient, ADC), 进而间接地反映组织细胞的微观结构^[1].

体素内不相干运动成像(intravoxel incoherent motion imaging, IVIM)是一种常用的多b值DW-MRI技术, 除了能够提供人体组织间质中水分子运动的扩散信息之外, 还能够提供源于血液微循环中的灌注信息^[2]. IVIM模型利用微循环在低b值会导致信号快速衰减这一特性, 通过建立关于b值与衰减信号的双指数模型来分离扩散和灌注运动, 估计出灌注体积分数(fraction of prefusion, f_p)、灌注或伪扩散系数(perfusion or pseudo-diffusion coefficient, D_p)和扩散系数(diffusion coefficient, D_t). 通过测定组织的扩散和灌注信息, IVIM已经在肝脏^[3]、肾脏^[4]、乳腺^[5]、心脏^[6]以及头颈部^[7]等多种灌注信息丰富的器官上用于临床研究, 在疾病早期发现及术后评价中发挥重要的作用^[8].

尽管IVIM成像技术在临床实践中取得了重大进展, 但从获得的DW信号中快速准确地估计出高质量的灌注和扩散相关参数仍然是具有挑战性的问题. 虽然在理论上更多的b值有利于提升IVIM参数估计的精度, 但是这无疑会使得图像采集时间过长, 同时过多的低b值会导致图像的信噪比(signal to noise ratio, SNR)降低. 因此解决这些缺点将有助于更加广泛地使用IVIM. Zhang等提出了一种最小化误差传播因子的优化b值采样的方法, 显著提高了通过非均匀优化采样获得的肾脏IVIM参数准确度, 降低了至少20%–30%的估计误差, 并显著提高了恶性和良性病变的区别^[9]. Huang提出了一种基于核的后滤波图像降噪方法, 与局部主成分分析法进行对比, 得到了均小于12%的偏差和变异系数的IVIM参数^[10]. Lin等利用深度图像先验的思想(deep image prior, DIP)提出了一种无监督的单图像降噪网络, 利用卷积神经网络(convolutional neural network, CNN), 将多组在b值上平均IVIM数据作为输入, 输出与原始数据b值相同数量的降噪图像, 提高了DW数据的信噪比, 得到的IVIM参数图干净平滑^[11]. Huang 等利用图像在多尺度上层内与层间的多相似性, 通过随机搜索策略将低分辨率图像映射到高分辨率图像空间中, 使得估计出的IVIM参数图像有更低的平均残差值^[12]. 上述方法中, 分别从数据优化采集策略、降低生理噪声、图像超分辨率等不同角度的数据预处理方法使IVIM参数质量得到了间接改善, 但是参数估计的准确性仍然依赖于拟合方法.

目前, IVIM最常用的拟合方法是非线性最小二乘法(nonlinear least squares method, NLLS), 即通过最小化模型的拟合信号与采集信号间的误差来优化参数, 其中最常用的是LM (Levenberg Marquardt)优化算法^[13]. 这种方法受到了来自于采集信号信噪比严重的影响. 为了提高NLLS拟合的稳定性, 一般尝试在拟合过程中根据具体估计的器官, 加入各个参数的约束项, 结果证明在参数约束范围内进行拟合, 参数的评估质量得到了提升. 但是, 不少研究表明, 利用带有约束的NLLS方法估计出来的IVIM参数常出现在约束边缘值附近, 造成了结果的偏离性. 根据组织内扩散和灌注信号衰减的特点, 通常采用分段式NLLS方法(segmented NLLS, Seg-NLLS)来提高参数估计的鲁棒性^[13-15]. Seg-NLLS首先考虑在高b值下, 组织灌注信号的贡献为0, 将双指数模型简化为单指数模型, 对扩散系数D_t进行估计. 接着利用估计好的扩散系数D_t, 推算出灌注分数f_p和灌注系数D_p. 然而NLLS方法受噪声影响严重, 特别是灌注系数D_p, 在某些局部区域, 由于噪声的影响将导致其估计结果无意义^[16-20]. Hyo在12名健康志愿者的肝脏和胰腺数据进行了可重复性测试, 实验结果表明上述基于最小二乘法得到的D_p的可重复性最差^[16]. 为了解决上述问题, 陆续有学者采用概率的思想来评估IVIM参数, 即贝叶斯概率理论(Bayesian approach, Bayes). Bayes是一种以概率先验替代最小二乘的IVIM参数求解方法, 它通过最大化给定观测信号的IVIM参数的后验概率来估计IVIM参数^[21-23]. 最近一些工作比较了各IVIM估计方法的性能, 实验结果表明Bayes方法始终优于NLLS^{[18,20,23–25]}. 然而, 虽然Bayes拥有较高的参数估计精确度, 但是该方法很容易受到组织异质性的影响, 并且估计精度强烈依赖于先验假设, 拟合时间较长. 此外, 由于以参数为优化目标, 其拟合信号与测量信号之间的误差大小难以控制^[26]. 为了解决传统IVIM参数拟合方法的缺陷, 部分学者利用人工神经网络(artificial neural network, ANN)对IVIM参数进行估计^[26-29], ANN由输出层、隐含层和输出层构成, 本质是通过高维数据的低维非线性映射, 实验结果表明ANN产生的IVIM参数图具有更好的视觉效果和较高的一致性. 然而, ANN并没有考虑到到信号之间的上下文信息, 同时ANN也容易过拟合. 针对于上述IVIM参数方法的不足, 本文提出一维动态卷积网络(DCNN), 考虑信号之间的上下文信息和b值对IVIM参数的贡献程度, 实现IVIM参数的准确估计. 仿真和真实采集两种数据集的实验表明, DCNN有更好的IVIM参数估计性能和更好的视觉质量.

1 相关技术与对比方法 1.1 体素内不相干运动模型

为了评估这些拟合方法的IVIM参数估计, 我们使用带噪声的双指数模型来测定水分子在人体大脑组织中的扩散信息和灌注信息, 该模型将DW-MRI衰减信号描述成关于b值即扩散敏感度(diffusion sensitivity, b-value)的函数. 在给定的b值下, IVIM公式如式(1):

$ S({b_n}) = S({b_0}) \cdot [{f_p}{{\rm{e}}^{ - {b_n}{D_p}}} + (1 - {f_p}){{\rm{e}}^{ - {b_n}{D_t}}}]{\text{ + }}{\varepsilon _n} $

(1)

其中, n表示b值个数, S(b_n)表示为第n个b值下的扩散加权信号, S(b₀)表示为b = 0 s/mm²时的初始信号强度. D_t为扩散系数, D_p为灌注系数, f_p为灌注体积分数, $ {\varepsilon _n} $ 表示信号含有的噪声.

1.2 非线性最小二乘法

NLLS通过最小化模型的拟合信号与采集信号间的误差平方和来优化参数, 如式(2)所示:

$ \min \sum\limits_{n = 0}^N {{{\left[ {S({b_n}) - \hat S({b_n})} \right]}^2}} $

(2)

其中, $ \hat S({b_n}) $ 表示预测的信号值. 为了提高NLLS估计的鲁棒性, 同时考虑到大脑处于一个低灌注区域组织^[28], 各IVIM参数拟合边界为: 0≤f_p≤1, 0.003≤D_p≤0.1, 0≤D_t≤0.003 mm²/s. 将IVIM模型的所有参数在一个过程中同时估计, 这种方法被称为全最小二乘法(full least squares, Full-NLLS). Seg-NLSS采用了逐步拟合的方法, 在假设高b值( $b \geqslant 200\;{\rm{s/mm^2}}$ )的情况下, D_p对信号的贡献程度很小. 在忽略D_p的情况下, 利用高b值的信号通过拟合单指数方程来确定D_t, 过程如式(3)所示:

$ S({b_n}) \approx S({b_0}) \cdot (1 - {f_p}) \cdot {{\rm{e}}^{ - {b_n}{D_t}}} = {S_{{\rm{int}}}} \cdot {{\rm{e}}^{ - {b_n}{D_t}}} $

(3)

其中, S_int代表在高b值下数据的截距. 灌注体积分数f_p再由式(4)所示计算出:

$ {f_p} = \frac{{S({b_0}) - {S_{{\rm{int}}}}}}{{S({b_0})}} $

(4)

接下来, 在得到体素点的D_t和f_p后, 再通过一次最小二乘拟合出D_p. 由于Seg-NLLS会导致偏置误差, 在本研究中将使用Full-NLLS作为基础参数拟合算法, 当体素点对应的IVIM参数超过拟合边界时, 再使用Seg-NLLS对该体素点进行估计.

1.3 贝叶斯概率法

Bayes是通过最大化IVIM参数的后验概率密度函数来估计, 并使用马尔科夫链蒙特卡罗方法(Markov chain Monte Carlo, MCMC)实现^[30]. 多参数的高斯似然函数如式(3)所示:

$ \begin{split} & p\left( {S({b_n})|{D_t},{D_p},{f_p},S({b_0}),\sigma _S^2} \right) = {\left( {2\pi \sigma _S^2} \right)^{ - N/2}} \cdot \\ & \exp \left\{ { - \frac{1}{{2\sigma _S^2}}\sum\limits_{n = 1}^N {\left[ {S({b_n}) - S({b_0})\left( {{f_p}{{\rm{e}}^{ - {b_n}{D_p}}}{\rm{ + }}\left( {1 - {f_p}} \right){{\rm{e}}^{ - {b_n}{D_t}}}} \right)} \right]} } \right\} \end{split} $

(5)

其中, D_t和D_p采用对数正态分布先验, f_p采用beta分布先验, $ \sigma _s^2 $ 代表高斯收缩的方差. 为了保证IVIM参数的一致性采用与NLLS方法一致的拟合边界. 式(5)中干扰参数S(b₀)和 $ \sigma _s^2 $ 将通过一个先验分布 $ p(S({b_0}), \sigma _s^2) $ 来消除. 先验分布如式(6)定义所示:

$ \begin{array}{*{20}{c}} {\int_0^\infty {\left( {\int_{{-}\infty }^\infty {p\left( {S({b_n}), \sigma _s^2} \right)\left. { \cdot p\left( {S({b_n})|{D_t}, {D_p}, {f_p}, S({b_0}), \sigma _s^2} \right)dS({b_0})} \right)d\sigma _s^2} } \right.} } {{{ = }}p\left( {S({b_0})|{D_t}, {D_p}, {f_p}} \right)} \end{array} $

(6)

2 材料和方法 2.1 数据集及数据处理

本文真实大脑测试临床数据集采集于哈尔滨肿瘤医院, 共计5名受试者. 所有磁共振图像均采集于飞利浦3TMRI扫描仪(Philips MR 53.0, 3.0 Tesla MRI scanner), 采集序列为平面成像自旋回波序列(EPI SE). 其采集参数如下: 分辨率(matrix size)为128×128、重复采集时间(TR)为3000 ms、回波时间(TE)为70.28 ms、切片厚度(slice thickness)为2.5 mm. 扩散敏感度b值序列为(0, 3, 5, 10, 25, 50, 75, 100, 200, 400, 600, 800 s/mm²). 本文首先利用MRIcron软件对原采集数据进行格式转换, 再使用Local PCA算法对数据切片上进行降噪. 随后使用SyN算法将各个数据配准到b₀图像上^[31], 最后为了对大脑不同感兴趣区域进行分析, 使用FSL工具对受试者大脑进行去头骨处理^[32], 再使用SPM8对灰质、白质、脑脊液进行了分割.

2.2 蒙特卡洛模拟仿真

为了训练和对比传统机器学习方法、ANN以及DCNN方法对于IVIM参数预测的性能, 我们基于蒙特卡罗模拟(Monte-Carlo simulation)方法, 分别仿真了训练模拟信号和测试仿真数据. 训练模拟信号是在真实大脑IVIM参数临床表现的限定范围里, 均匀随机选取各IVIM参数的标签 $D_t^{\rm{sim}}$ 、 $D_p^{\rm{sim}}$ 、 $f_p^{{\rm{sim}}}$ , 再利用式(1)和与真实数据集相同的扩散敏感度b值序列, 得到模拟信号数据 $x_{\rm{true}}^{\rm{sim}}$ . 其中模拟扩散参数 $D_t^{{\rm{sim}}}$ 取值范围为(0.5, 3×10⁻³ mm²/s), 模拟灌注参数 $D_p^{{\rm{sim}}}$ 取值范围为(0.003, 0.1 mm²/s), 模拟灌注体积分数 $f_p^{\rm{sim}}$ 为(0, 1). 随后, 再向每个模拟信号中加入莱斯噪声(Rician noise)模拟出与真实数据相同分布情况的训练仿真信号 $x_{\rm train}^{ \rm sim}$ , 添加噪声方法如式(7)所示:

$ x_{{\rm{train}}}^{{{\rm sim}}} = \sqrt {{{(x_{{\rm{true}}}^{{\rm{sim}}} + {G_{{N_1}}})}^2} + {G_{{N_2}}}^2} $

(7)

其中, $ {G_{{N_1}}} $ 和 $ {G_{{N_2}}} $ 满足均值为0、方差为 $ 1/SNR $ 的两不相关高斯噪声. 为了防止网络模型过拟合, 增加训练模拟信号的复杂性和多样性, SNR在(10, 120)区间随机取值.

由于IVIM数据缺乏参数的金标准, 参数估计的准确性不能直接从真实数据中确定, 但可以通过计算机模拟出测试仿真数据来评估IVIM参数估计的准确性. 为了得到真实的IVIM参数标签来评估各方法的性能, 我们将一例真实数据的大脑, 利用SPM8软件分割得到了正常人脑组织的1个灰质(gray matter, GM)、2个白质(white matter, GM)和1个脑脊液(cerebrospinal fluid, CSF)共计4个区域.

将各个区域赋予设定的真实参数, 如下所示( $D_t^{{\rm{sim}}}$ mm²/s, $D_p^{{\rm{sim}}}$ [mm²/s], $f_p^{{\rm{sim}}}$ ), 灰质(0.002, 0.07, 0.4), 白质区域1 (0.001, 0.02, 0.06), 白质区域2 (0.001, 0.03, 0.08), 脑脊液(0.002, 0.07, 0.4), 每种特定组织的参数值可以涵盖文献和研究中报道的典型值范围. 测试仿真数据的IVIM参数图分别如图1各子图所示, 同时利用式(7)向信号中添加噪声, 信噪比为(20, 30, 40, 50, 60).

2.3 网络结构

近年来, 利用人工神经网络(artificial neural network, ANN)对IVIM数据进行分析已经被报道. 然而, 这种方法并没有完全考虑IVIM参数与b值之间的关系, 也没有体素信号间上下文信息对IVIM参数的影响. 针对于此问题, 根据IVIM磁共振信号的特点, 利用动态卷积模块(dynamic convolution module, DCM)和残差网络(residual network)相结合的方式, 以提高IVIM参数的估计准确度和良好的视觉效果.

在传统的卷积中, 每个神经元的输入被描述为y=σ(ωx+b), 其中, ω代表着卷积核, σ是激活函数, b是神经元的偏置. 动态卷积核 $ \tilde \omega $ 是由一系列的并行卷积核 $ {\omega _i} $ 和相应的线性权重 $ {\eta _i} $ 聚合而成, 它能够在不增加网络深度的情况下, 通过学习于通道的线性权重 $ {\eta _i} $ , 也就是根据IVIM信号衰减特性, 自适应调整卷积核参数, 增加卷积神经网络模型的表达能力. 动态卷积核 $ \tilde \omega $ 聚合过程如式(8)所示:

$ \left\{ {\begin{array}{*{20}{l}} \tilde \omega = {\eta _1}{\omega _1} + {\eta _2}{\omega _2} + \cdot \cdot \cdot + {\eta _i}{\omega _i}{\text{ = }}\displaystyle\sum\limits_{i = 1}^N {{\eta _i}{\omega _i}}\\ {{\rm{s.t.}}}\;\;\;\;{0 \leqslant {\eta _i} \leqslant 1, }\;\;\;\;{\displaystyle\sum\limits_{i = 1}^N {{\eta _i}} {\text{ = }}1} \end{array}} \right.$

(8)

其中, N表示线性权重 $ {\eta _i} $ 和并行卷积核 $ {\omega _i} $ 的个数. 动态卷积包含权重预测模块(weight prediction module, WPM)和卷积聚合模块(convolution aggregation module, CAM). WPM系数预测模块由全局平均池化层(global average pooling, GAP)、全连接层、激活函数和Softmax组成. IVIM数据首先通过全局平均池化, 获得了由于b值导致信号衰减的整体信息, 再通过全连接层和Softmax得到线性权重 $ {\eta _i} $ . Softmax的运用能够保证线性权重 $ {\eta _i} $ 满足式(8)的条件.

此时得到的线性权重 $ {\eta _i} $ , 通过卷积聚合模块与对应的并行卷积核 $ {\omega _i} $ 进行乘积再相加来实现, 如式(8)所示聚合过程, 动态卷积流程图如图2所示.

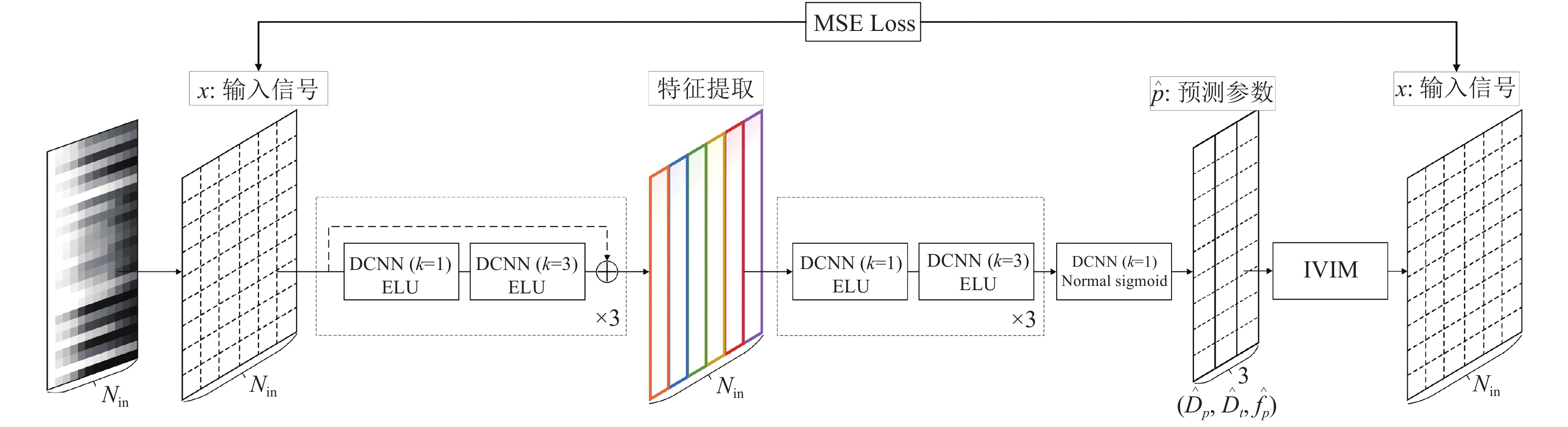
上述动态卷积的性质表明, 将原本固定且静态的卷积核替换为动态卷积核, 能够增强网络对于b值关于IVIM参数贡献程度的表达能力, 同时使用一维卷积神经网络能够学习到相邻信号中的上下文信息. 因此, 我们设计了一个基于动态卷积模块的一维卷积神经网络(dynamic convolutional neural network, DCNN)来估计IVIM参数, 详细的结构如图3所示. DCNN由6组一维动态卷积模块组成, 考虑到网络层数的加深会导致梯度消失的问题, 其中3组分别使用了残差网络. 残差网络可以将输入通道的IVIM信号衰减信息传递到输出通道, 使得残差网络中间的卷积层只需要学习残差, 避免信息遗漏.

在DCNN网络中, 利用初始信号S(b₀)对IVIM扩散加权信号S(b_n)进行归一化操作得到S(b_n)/S(b₀), 以格式为(B, N, L)的数据作为网络的输入, 其中, B是batch_size, N是b值个数, L是体素个数. 在动态卷积模块中, 网络分别采用了核大小为3的一维动态卷积和1的一维常规卷积作为IVIM参数拟合主体. 将归一化后的信号S(b_n)/S(b₀)输入到核大小为3的一维动态卷积模块中, 能够捕获相邻体素信号间上下文信息, 然后输入到核大小为1的一维常规卷积中, 以提高线性组合的拟合能力. 然后, 数据通过一个带有Sigmoid激活函数的动态卷积的网络输出层, 其卷积核为3, 输出通道数为3. 最后, 将这3个输出向量重塑为3张图像, 分别代表预测的3个IVIM参数. 另外, 输出神经元的参数用式(9)进行归一化, 以确保估计的IVIM参数在合理范围内.

$ \left\{ {\begin{array}{l} {\hat p_i} = p_i^{\rm{min}} + (p_i^{\rm{max}} - p_i^{\rm{min}}) \times {{\textit Sigmoid}}({v_i})\\ {\rm{s.t.}}\;\;\;\;{{{\hat p}_i} \in } ({\hat D_t}, {\hat D_p}, {\hat f_p}) \end{array}} \right.$

(9)

其中, $p_i^{{\rm{max}}}$ 和 $p_i^{{\rm{min}}}$ 分别代表训练仿真信号集 $x_{{\rm{train}}}^{{\rm{sim}}}$ 的各个IVIM参数的上下界, 该操作能够约束预测值的范围与假设值的范围的一致性, 并能够加快模型训练的收敛速度.

动态卷积神经网络(DCNN)将通过最小化预测信号 $ \hat x $ 和真实的归一化信号x之间的均方差来学习网络参数, 如式(10)所示:

$ {\mu ^*};{\tilde \omega ^*};{b^*} = {{\rm{argmin}}_{\mu ;\tilde \omega ;b}}\left\| {\hat x - x} \right\|_2^2 $

(10)

其中, $\; {\mu ^{\text{*}}}, {\tilde \omega ^*}, {b^*} $ 代表能使网络收敛的参数极值, $ \left\| \cdot \right\|_2^2 $ 是MSE损失函数, x是归一化后的信号值, 值大小等于S(b_n)/S(b₀), $ \hat x $ 是利用预测的IVIM参数 $ {\hat p_i} $ , 并通过式(11)得到的归一化预测信号值:

$ \hat x = {\hat f_p} \cdot {{\rm{e}}^{ - {b_n}{{\hat D}_p}}} + (1 - {\hat f_p}) \cdot {{\rm{e}}^{ - {b_n}{{\hat D}_t}}} $

(11)

3 实验设计 3.1 实验环境及训练细节

本实验采用的硬件环境, 数据预处理部分在显卡为NVIDIA-GTX 1050ti, 显存共4 GB, CPU为Intel(R) Core(TM) i7-8700, 内存共36 GB的主机上, 使用PyCharm作为本实验项目管理工具. 深度学习网络在拥有32 GB的NVIDIA Tesla V100 GPU服务器上, 使用Python 3.6语言、PyTorch 1.5工具包及Cuda 10.1驱动共同支撑的软件环境下进行加速训练. 本实验所有网络模型, 均使用学习率为1×10⁻³的Adam作为优化器, 其中batch_size为40, 共训练2000个Epoch. 为了防止过拟合, 网络训练使用了早停机制(early stopping), 当连续15个训练周期未下降则停止训练. 为了比较和量化提出方法的可重复性和稳定性, 使用相同的训练仿真数据进行了10次训练.

3.2 评价指标

为了评价不同参数估计方法对IVIM参数估计的性能, 将采用平均值(Mean)、标准差(standard deviation, Std)、相对误差(relative bias, RB)、变异系数(coefficient of variation, COV)和均方根误差(root mean square error, RMSE)作为定量标准. 其中, 由于真实图像没有绝对准确的真值标签, 我们将用平均值±标准差(Mean±Std)和COV变异系数来评定真实图像IVIM参数. 对于仿真图像而言, 我们计算出仿真图像的RB相对误差、COV变异系数和RMSE均方根误差.

以 $ {\hat P_{s, t}} $ 代表在第s个信噪比下不同参数估计方法对IVIM参数的第t个像素所对应的拟合值, 以 $P_t^{{\rm{true}}}$ 表示第t个像素所对应的真实值, 各评价指标如式(12)–式(14):

$ RB = \dfrac{1}{T}\sum\limits_{t \in L} {\dfrac{{\left[ {\dfrac{1}{S}\left( {\displaystyle\sum\nolimits_{s = 1}^S {{{\hat P}_{s, t}}} } \right) - P_t^{{\rm{true}}}} \right]}}{{P_t^{{\rm{true}}}}}} $

(12)

$ COV{\text{ = }}\frac{1}{T}\sum\limits_{t \in L} {\frac{{{\sigma _t}}}{{\dfrac{1}{S}\displaystyle\sum\nolimits_{s = 1}^S {{{\hat P}_{s, t}}} }}} $

(13)

$ {\textit{RMSE}} = \sqrt {\frac{{\displaystyle\sum\nolimits_{t \in L} {\displaystyle\sum\nolimits_{s = 1}^S {\left( {{{\hat P}_{s, t}} - P_t^{{\rm{true}}}} \right)} } }}{{S \times T}}} $

(14)

其中, $ {\sigma _t} $ 代表着不同信噪比下各参数图的方差, S是添加噪声图像的区域个数, T代表着感兴趣区域的体素点个数. 其中, COV变异系数能够反映在相同结构下的参数均匀程度, 理想的COV为0. 高COV值表示有高噪声的映射, 图像视觉质量低.

4 实验结果及分析

为了评估本文模型的有效性和稳定性, 本文与NLLS、Bayes、ANN三种不同方法对仿真测试数据集和真实的采集数据集进行了IVIM参数估计, 实验可视化和定量结果如下.

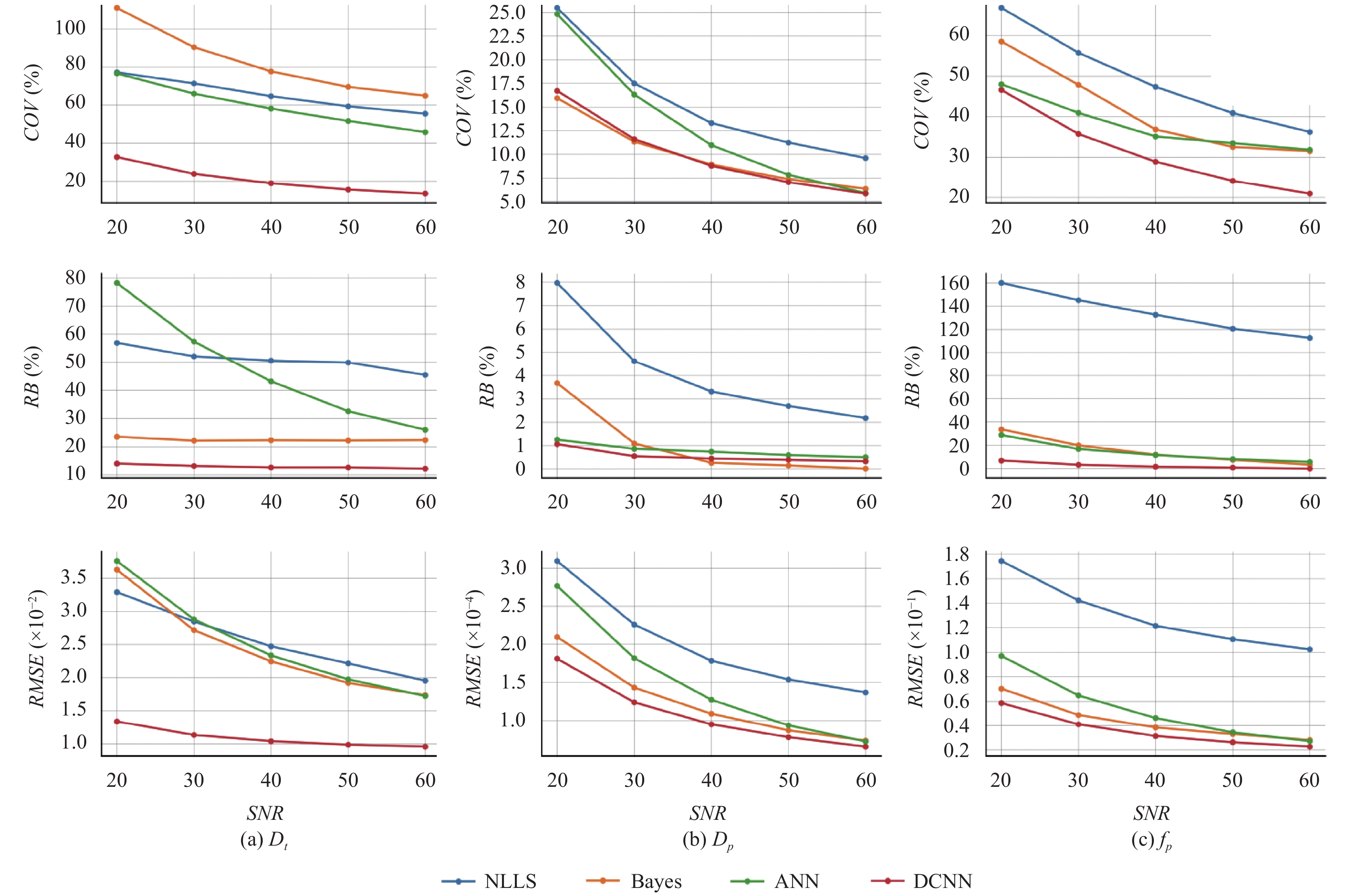
4.1 仿真测试数据

图4显示了4种IVIM估计方法对测试仿真数据在SNR为20, 30, 40, 50, 60上的参数图结果. 很明显, 基于动态卷积的方法大大提高了3个IVIM参数图的图像质量. 此外, 与传统机器学习方法(NLLS、Bayes)相比, DCNN更有效地抑制了噪声的生成, 尤其在灌注相关参数图(D_p, f_p)上, 有更清晰的纹理信息, 空间信息也损失得更少, 同时在均匀区域更加平滑. 图5是各方法对于IVIM测试仿真参数图在不同SNR下的评价指标结果图. 由图5可知, DCNN在D_p参数图的估计上全面优于NLLS、Bayes和ANN, 说明该方法在视觉质量的优越性和数值上的合理性. 对于D_p和f_p而言, RMSE和COV有大幅度的下降, 说明采用一维动态卷积神经网络在考虑上下文信息有较强的特征提取能力, 使得体素与体素点之间有更强的相关性和更强大的抗噪声能力. DCNN的RB大幅下降, 说明动态卷积模块能够学习到来自于b值的贡献权重信息, 使得不再像NLLS那样高估灌注系数数值. 除了NLLS之外, 各方法对于D_t参数图的评价指标相差不大. 但值得注意的是, 在SNR大于40的时候, Bayes的RB比DCNN小约0.25%.

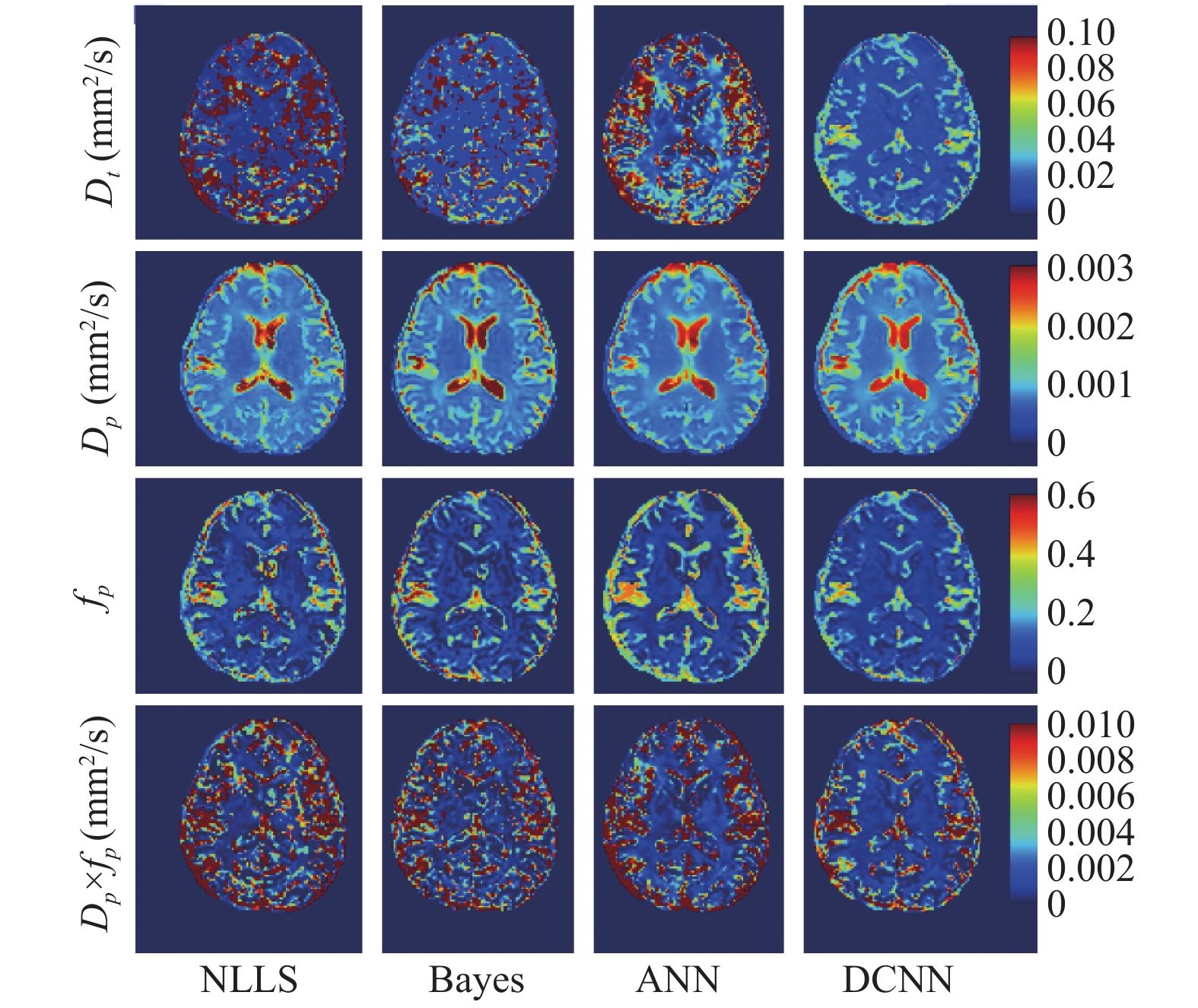
4.2 真实采集数据

图6为一健康受试者大脑的4种IVIM参数估计算法的可视化结果. 与预期的一样, 用不同方法估计的IVIM参数的变化与仿真结果一致. 整体来说, DCNN提供了最平滑、噪声最小的参数映射. 具体而言, 各种方法对于D_t的参数估计最为相似, 但是NLLS的D_t参数图显然受到了强烈的噪声影响. 两种深度学习方法(ANN, DCNN)的D_t的参数图相对于传统机器学习方法(NLLS, Bayes)相对干净、平滑, 但DCNN在灰质上的纹理结构有着更好的视觉效果. 对于灌注相关系数(D_p和f_p)而言, 不同估计方法差异较为明显. 对于D_p而言, 可以看出NLLS存在着大量的异常值. 尽管贝叶斯方法改善了D_t和f_p参数映射, 但在D_p映射中仍有许多异常值. 这是因为Bayes将NLLS估计结果作为先验, 而这种由于先验的影响导致仍然存在许多离群值是不可避免的. 对于DCNN而言, 所以生成的D_p图受异常值的影响较小, 视觉上的纹理信息丰富, 明显优于ANN神经网络. 综上所述, 我们发现DCNN可以更有效地减少异常值, 并且可以保留大部分的空间和纹理信息, 以获得最佳的视觉质量. 这验证了所提出的基于DCNN的方法可以提高IVIM参数映射的视觉质量. 除可视化结果之外, 表1总结了用不同拟合方法估计的WM和GM的IVIM参数的平均值±标准差和COV变异系数. 对于WM和GM, 不同拟合方法的参数图D_t的平均值和Std之间没有显著差异. 然而, 由所提出的动态卷积方法得到的参数映射D_p和f_p的Std和COV比其他方法要小得多, 说明该方法具有IVIM参数估计的最优稳定性.

4.3 一致性与收敛性分析

本文利用相同的训练仿真数据集, 采用随机初始化对两种深度学习方法(ANN和DCNN)独立训练了10次, 以研究不同深度学习方法性能的一致性. 图7箱型图显示了5名健康受试者在脑灰质和白质上的COV变异系数分布情况. 总的来说, DCNN和ANN的方法产生的D_t参数图有着相似的数据分布情况, 无论是在白质还是在灰质. 虽然通过DCNN模型得到的COV均值偏移量略高于ANN, 但在灰质上的四分位数范围小于ANN. 然而, 相比于ANN, DCNN得到的灌注相关参数(D_p和f_p)的COV分布有显著差异. 与仿真测试集和真实采集数据结果类似, D_p参数图在视觉上展现不同的分布. 在D_p上, ANN获得的平均COV和四分位数范围明显高于DCNN, WM和GM获得的平均COV均超过75%, 而DCNN的平均COV, GM为45.9%, WM为26.3%. 对于f_p而言, ANN获得的平均COV在GM上为88.3%, WM上为70.8%, 而DCNN在GM上为76.9%, WM上为53.1%. 实验结果表明, 基于动态卷积DCNN的方法的性能比ANN具有更好的一致性, 特别是对灌注相关参数的估计, 这表明我们提出的方法更加稳定.

图8显示了不同深度学习网络模型前500次训练损失的收敛曲线图. 由图8可知, DCNN大约在130次迭代后, 目标优化函数数值趋于稳定, 约为0.0040. 然而, ANN收敛曲线有较大幅度的振荡现象, 在300次迭代后损失函数数值约为0.0134, 说明ANN方法陷入局部解且逃逸能力不佳. 上述表明DCNN模型的收敛性和优化目标损失函数的效果要好于ANN方法.

5 结论

在本研究中, 我们提出了一个基于动态卷积的模型来提高IVIM参数估计的精度, 该模型同时考虑了不同b值的DW信号对IVIM参数估计的贡献程度以及相邻体素之间的上下文信息. 在模拟仿真和真实采集的数据集上, 实验结果表明, 相比于NLLS、Bayes和ANN方法, 本文模型估计IVIM参数的能力更佳. 该方法可以生成具有更小COV变异系数和更少离群值的IVIM参数图, 尤其是对于D_p参数图. 此外, 本文还考虑到方法的一致性, 重复实验结果表明, 本文所提出的方法比传统ANN神经网络估计结果更稳定, 满足了临床应用的实际需要. 接下来的工作中, 我们将会在更多不同疾病的受试者来验证我们的网络模型的性能评估. 同时, 我们将会考虑训练一个泛化网络, 可以接受任何器官的任何采集协议获得的DW信号, 进而实现不同采集协议下IVIM 参数的准确估计.