1 引言

由于大气的散射作用, 目标物体的反射光会受到大气中悬浮粒子、气溶胶等的吸收和散射, 并与其他方向反射的空气光混合, 最终成像设备捕获的图像会存在色彩失真、对比度降低、细节模糊等问题. 对图像进行去雾处理, 可以显著提高场景局部和全局的对比度, 纠正因空气光造成的颜色失真. 在计算机视觉、高级图像编辑、目标检测和识别等算法中, 图像去雾在一定程度上能提高算法的性能, 因此图像去雾的研究有着较高的应用价值.

图像去雾的算法主要有基于图像增强的去雾算法、基于图像复原的去雾算法和基于深度学习的去雾算法.

基于图像增强的去雾算法没有考虑到雾的浓度与场景深度成正比例的关系, 即图像雾的浓度分布是不均匀的. 因此, 增强图像对比度的去雾方法不能自适应的补偿雾图像中对比度的降低, 且容易造成部分图像信息的失真, 例如基于直方图均衡化的算法^[1]和基于Retinex的图像去雾算法^[2].

基于图像复原的图像去雾算法从雾天图像退化机制出发, 利用大气散射模型^[3], 通过求解图像降质过程的逆过程来恢复清晰图像. 尤以He等人提出的基于暗通道先验的图像去雾算法为代表, 然而该算法对于图像的天空区域和白色景物是失效的, 并且容易产生光晕效应^[4].

近年来, 深度学习的不断发展为图像处理带来了新思路, 一些基于神经网络的图像去雾算法也不断涌现. Ren等人提出了多尺度卷积神经网络的去雾方法, 通过两种尺度的网络得到更准确的介质投射率^[5]. Li等人为了避免参数因分别估计而带来误差累积的问题, 提出了多合一卷积神经网络图像去雾算法, 取得了较好的效果^[6]. 利用不同尺度的卷积核提取图像特征, 将浅层与深层的图像特征进行融合, 在一定程度上能使网络更好地学习图像的特征^[7-9].

基于深度学习的图像去雾算法利用卷积神经网络学习图像特征, 网络的深度对网络模型的性能至关重要, 层数增加, 网络可以进行更加复杂的特征学习. 但是, 在深度学习中网络层数的增加一般会导致模型过拟合、梯度消失和梯度爆炸. 残差网络的提出有效地解决了该问题, 通过短路连接(shortcut connection)机制使得网络具有学习恒等映射的能力的同时也具有学习其他映射的能力, 因此残差单元可以在输入的基础上学习到新的特征, 从而提高网络性能, 避免网络层数增加所导致的网络退化^[10]. 陈清江等人提出了一种混合残差学习与导向滤波算法在图像去雾中的应用, 但对于自然真实雾图像的去雾, 其去雾图像的视觉效果并不理想^[11]. 姜冰等人提出了适用于多场景的ResNet单幅图像去雾算法, 在GAN网络中引入残差结构用以改善网络性能^[12]. 刘仕彦等人针对去雾网络深度较深且结构复杂, 不易在嵌入式平台部署的问题, 将残差块与信息蒸馏网络(information distillation network, IDN)的信息蒸馏块作为网络的基础块, 提出了基于BP-Net网络结构的图像去雾算法^[13]. 肖进胜等人指出雾图像可以看成由清晰图像和雾层组成, 算法通过残差学习提取雾层的特征以实现图像去雾, 但网络权重参数量较大, 网络训练困难^[14].

综上所述, 针对现有去雾算法中存在的问题, 本文提出了一种改进残差神经网络的图像去雾算法, 在残差学习模块中嵌入深度可分离卷积, 有效解决网络层数增加所带来的参数量剧增和网络训练困难的问题. 算法通过所提出的网络改进模型来估计透射率, 采用四叉树分层搜索方法准确地估计大气光值. 并且利用加权引导滤波对透射率进行细化, 保留更多图像边缘信息. 实验结果表明, 本文算法能较好地实现图像去雾, 并且去雾图像边缘信息更丰富, 图像也更清晰.

2 本文去雾算法

本文去雾算法基本思路: 首先根据所提的改进网络来估计透射率, 其次利用加权引导滤波对透射率进行细化, 然后通过四叉树分层搜索方法更准确地估计大气光值, 最后根据式(1)的大气散射模型表达式来恢复出无雾清晰图像.

2.1 大气散射模型

在图像处理领域, 大气散射模型通常被用来描述雾天图像的形成. 大气散射模型可表示为:

$ {I_c}(x) = {J_c}(x)t(x) + {A_c}(1 - t(x)) $

(1)

$ t(x) = {{\rm{e}}^{ - \beta d(x)}} $

(2)

其中, $x$ 表示像素索引, ${I_c}(x)$ 为观测到的有雾图像, ${J_c}(x)$ 为去雾后的无雾场景图像. $t(x)$ 是目标对象反射光的透射率, 它由目标场景点与成像设备之间的距离确定, 光的传播距离越远, 光的散射和衰减就越大, 即 $t(x)$ 越小. 如式(2)所示 $t(x)$ 与场景深度 $d(x)$ 呈负相关, $\;\beta $ 为衰减系数. ${A_c}$ 是全局大气光, 表示大气中的环境光.

2.2 网络结构

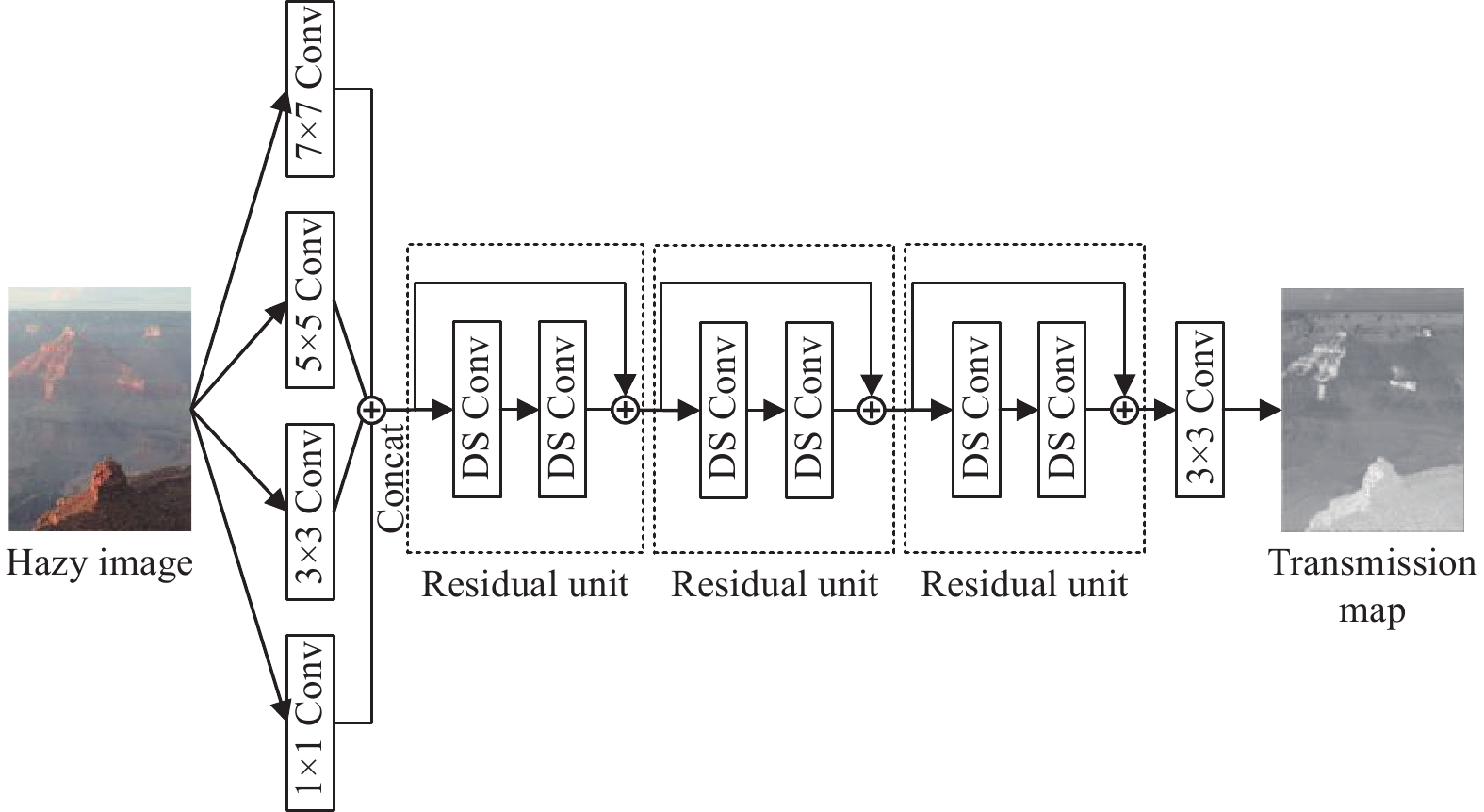
由式(1)可知, 图像去雾算法的关键在于求解介质透射率和大气光值, 然后依据散射模型进行无雾图像的恢复, 因此如何有效建立有雾图像到介质透射率的映射网络显得尤为重要. 图1所示为本文算法的网络结构图, 网络主要由多尺度特征提取模块、嵌入了深度可分离卷积的残差学习模块和输出卷积模块组成. 首先通过不同大小的并行卷积核进行有雾图像的浅层特征提取. 卷积核的尺寸设置为K×K×N, K×K为卷积核的大小, N为卷积核个数. 卷积核的大小分别为1×1、3×3、5×5和7×7, N的值为12, 步长为1, 并进行相应的填充使的输出特征图的尺寸和输入特征图的尺寸保持一致. 卷积响应公式为:

$ f_n^{l + 1} = \sigma \left( {\sum\nolimits_m {\left( {f_m^l*k_{m, n}^{l + 1}} \right) + b_n^{l + 1}} } \right) $

(3)

其中, $f_m^l$ 和 $f_n^{l{\text{ + }}1}$ 表示当前层 $l$ 和下一层 $l + 1$ 的特征映射, $k_{m, n}^{l + 1}$ 表示卷积核, 下标 $(m, n)$ 表输入特征图与输出特征图的对应关系. $b_n^{l + 1}$ 是偏置, $\sigma $ 是激活函数, 本文采用线性整流单元(rectified linear unit, ReLU)作为激活函数.

将不同尺寸卷积核提取到的特征图进行拼接, 然后送入后续的残差块. 出于网络训练参数量的考虑, 本文在残差结构中引入了深度可分离卷积(depthwise separable convolution, DS Conv), 用于替代普通的卷积. 深度可分离卷积可以做到减小参数量的同时其效果等同于普通卷积. 深度可分离卷积可以看成两部分组成: 逐通道卷积和逐点卷积, 逐通道卷积对每个输入通道应用单个滤波器, 然后使用点式卷积(简单的1×1卷积)来创建深度层的输出的线性组合^[15].

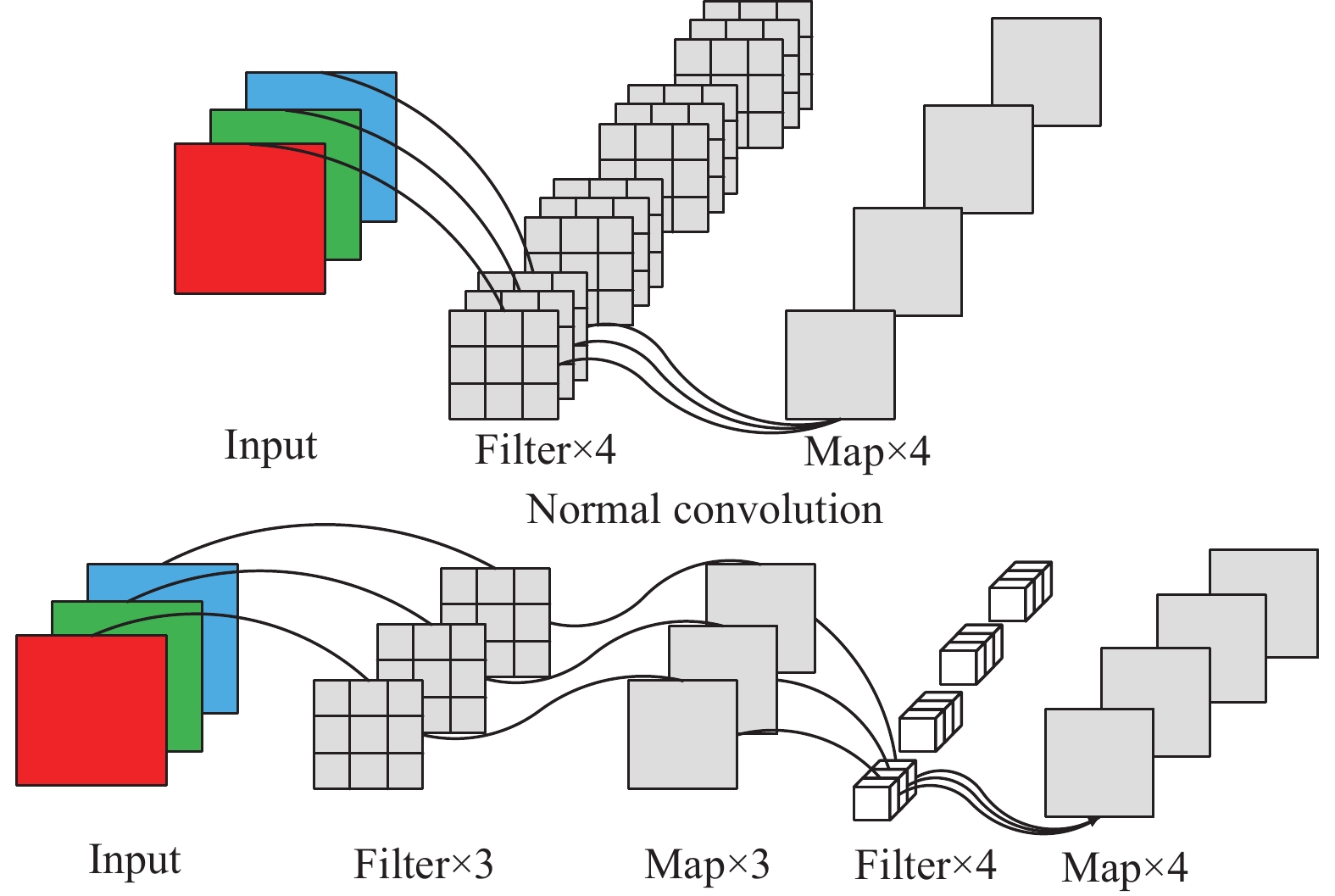
图2所示为普通卷积和深度可分离卷积的对比, 以三通道输入和3×3大小的卷积核为例, 在普通卷积中为得到4个输出特征图, 需要4个卷积核, 参数量为3×3×3×4. 而深度可分离卷积可以看成两部分, 首先3×3大小的卷积核与输入特征图进行逐通道卷积, 卷积核深度等于输入通道数; 然后将得到的特征图与1×1大小的卷积核进行逐点卷积, 卷积核个数为4, 总的参数量为3×3×3+3×1×1×4, 相比普通卷积, 深度可分离卷积可以成倍数减小参数量.

图1中的每个深度可分离卷积层中都加入了批量正则化(batch normalization, BN)和线性整流单元(ReLU). 网络模型中存在3个相同的残差单元, 每个残差单元含有两个深度可分离卷积层. 在深度可分离卷积层中, 逐通道卷积的卷积核个数为1, 大小为3×3, 逐点卷积的卷积核个数为16, 大小为1×1. 最后, 网络经过一个3×3大小的卷积核卷积输出介质投射率图.

2.3 透射率细化

为了提高去雾图像的质量, 并使恢复的无雾图像边缘得到保持, 具有更多的纹理信息, 本文对神经网络学习得到的透射率进行了细化. 与引导滤波(guided image filtering, GIF)相比, 加权引导滤波(weighted guided image filtering, WGIF)在图像边缘保持上性能更好, 且能有效减少去雾图像中的光晕伪影^[16]. WGIF在GIF的基础上引入了边缘感知权重, 边缘感知权重表达式为:

$ {\Gamma _G}(p') = \frac{1}{N}\sum\limits_{p = 1}^N {\frac{{\sigma _{G, 1}^2(p') + \varepsilon }}{{\sigma _{G, 1}^2(p) + \varepsilon }}} $

(4)

其中, G表示引导图, $\sigma _{G, 1}^2(p')$ 表示引导图G中3×3窗口区域的方差. $\varepsilon $ 是一个常量, 值为 ${(0.001 \times L)^2}$ , $L$ 为引导图像素的动态范围. 边缘感知权重 ${\Gamma _G}(p')$ 衡量像素 $p'$ 相对于整个引导图的重要性. 边缘处的像素被赋予比平坦区域像素更大的权重.

如图3所示, WGIF相较于GIF在边缘保持上性能更好, 较好地保留了图像的边缘纹理信息. 因此本文采用WGIF对神经网络特征学习得到的粗透射率图进行细化, 以此得到更精细化的透射率. 图4所示为透射率细化前后效果图及透射率用于去雾时与之对应的去雾图. 由图可知, 细化前后得到的去雾图差异较为明显, 透射率图进行细化后, 其恢复出来的无雾图像更清晰, 图中山脉轮廓也更加分明, 图像边缘得到了更好的保持. 因此, 对神经网络学习得到的透射率图进行细化是很有必要的.

2.4 大气光值估计

由于雾会造成像素强度的增加, 呈现明亮的颜色, 在式(1)中全局大气光 ${A_c}$ 通常被估计为雾图像中最亮像素的强度值. 但是这种方法在某些情况下是不恰当的, 当图像中存在比大气光更亮的对象时, 将会高估全局大气光的值.

基于图像雾区域的像素强度值较大且方差值较小这一事实, 全局大气光的估计采用基于四叉树划分的分层搜索方法. 首先, 输入的雾天图像被划分成4个矩形子区域, 分别计算每个子区域内平均像素值减去子区域内像素值的标准差, 计算的结果作为该子区域的得分. 然后选出分数最高的子区域, 并进一步将该区域划分为4个子区域. 重复上述过程, 直到区域大小小于给定的阈值(32×32). 如图5所示, 图像中红框选中的区域是利用分层搜索方法选出的最终用于计算全局大气光值的像素区域.

用于估算大气光值的区域选定后, 在该区域中计算式(5), 将使计算值最小的像素作为全局大气光的值.

$ \left\| {({I_r}(x),{I_g}(x),{I_b}(x)) - (255,255,255))} \right\| $

(5)

$ {J_c}(x) = \frac{{{I_c}(x) - {A_c}}}{{\max (t(x), 0.1)}}t(x) + {A_c} $

(6)

其中, ${I_r}(x)$ , ${I_g}(x)$ , ${I_b}(x)$ 分别对应输入有雾图像像素的3个颜色通道的像素强度值. 将估计得到的 $t(x)$ 和 $ {A_c} $ 带入式(1)得到式(6), 根据式(6)就可以计算得到无雾清晰图像.

3 实验结果与分析

算法的硬件配置和软件配置如下:

硬件配置: Intel Core i5-9400F @ 2.90 GHz CPU, Nvidia GeForce RTX 2060 GPU, 内存16 GB.

软件配置: Windows 10, TensorFlow 2.1, CUDA 10.1, Python 3.7.

3.1 数据集与网络训练

网络训练所需的数据集为NYU2 Depth Database^[17]. 根据式(1)和式(2)合成雾天图像, $A$ 的值在[0.6, 1.0]之间随机采样, $\;\beta $ 的值在[0.5, 1.5]之间随机采样. 总共合成26064张雾图像, 选取其中23231张图像用于训练, 2833张非重叠的雾图像用于测试. 图像大小为320×240. 另从互联网上收集了部分自然界真实雾天图像作为测试图像.

在训练过程中, 采用随机梯度下降法(stochastic gradient descent, SGD)和反向传播算法对网络参数优化. SGD的动量参数设置为0.9, 初始学习率设为0.001, 在迭代80个epoch后学习率设为0.0001, 损失函数为均方误差(MSE), 网络中激活函数为ReLU, 网络训练总的迭代次数为120个epoch.

3.2 不同算法的去雾对比

本节将本文算法与经典的传统图像去雾算法和深度学习去雾算法进行了对比, 图像来自RESIDE^[18]数据集和自然真实雾天图像. 对比算法涉及以下4种: DCP^[4]暗通道先验图像去雾、MSCNN^[5]多尺度神经网络图像去雾、AOD-Net^[6]多合一端到端图像去雾、Residual-GIF^[11]混合残差学习与导向滤波算法在图像去雾中的应用.

3.2.1 合成雾图像的去雾对比与分析

为了客观的评价本文算法的优劣, 本文将结构相似度(structural similarity, SSIM)和峰值信噪比(peak signal to noise ratio, PSNR)作为图像质量评价的客观指标. 结构相似度从图像亮度、对比度和结构3个方面衡量图像的相似性, SSIM值越大, 图像失真越小, 去雾性能越好. 峰值信噪比是广泛使用的图像质量客观评价指标之一, PSNR值越大, 图像受噪声影响越小, 图像质量越高.

图6为测试数据集上部分雾图像的去雾结果. DCP算法得到的去雾图像存在色彩失真, 并且在图像边缘处存在光晕效应, 造成这一现象是因为算法是基于局部透射率恒定的, 因此在图像景深发生变化时透射率的估计是不准确的, 会在物体边缘产生光晕. MSCNN算法同样也存在去雾图像颜色不真实和对比度过度增强的问题. AOD-Net算法去雾后的图像仍存在少量的雾. Residual-GIF算法和本文的算法取得了相对较好的效果, 但本文算法去雾更彻底, 并且图像的纹理信息更丰富. 为了更好地观察不同算法的去雾效果, 说明本文算法的有效性, 本文将第一幅图像的去雾图像进行了局部放大, 如图7所示. 可清晰地观察到, DCP算法和MSCNN算法去雾后的图像存在色彩失真. AOD-Net算法去雾后的图像在灯笼上仍存在少量的雾. 本文算法相对于Residual-GIF算法而言, 本文算法灯笼的边缘信息得到了更好的保持, 灯笼看上去轮廓更分明.

不同算法的PSNR和SSIM指标对比结果如表1所示. 由表可知, 相较于其他算法, 本文算法在峰值信噪比和结构相似度上均有最高的值, 这说明本文算法具有明显优势, 去雾图像受噪声干扰更小, 图像质量更好, 去雾前后的图像具有更高的相似度.

3.2.2 自然真实图像的去雾对比与分析

此部分讨论自然真实雾图像的去雾, 不同算法的自然真实雾图像去雾对比如图8所示. DCP算法在图像天空区域的去雾效果不理想, 由于DCP算法基于暗通道先验特性, 往往会高估雾的浓度, 导致在图像边缘处容易产生光晕伪影. MSCNN算法恢复的无雾图像在视觉上呈现对比度过度增强, 由第3幅图可以看出图像中树有关的边缘信息并没有得到保持, 树叶颜色偏暗, 说明MSCNN算法通过细尺度网络细化透射率的手段并不奏效. AOD-Net算法将所有中间参数都在一个统一的模型中进行估计, 一定程度上避免了参数分别估计带来误差累计的问题, 去雾图像取得了较好的效果, 但图像仍存在少量的雾. 基于残差学习的Residual-GIF算法同样也存在去雾不完全的问题. 本文算法与前几种算法相比, 去雾图像在视觉上取得了更好的效果, 不仅去雾更加彻底, 而且图像边缘保持的更好.

将图8中第2幅雾图像在不同算法下的去雾图像进行局部放大, 放大效果如图9所示. 可以清楚地看到MSCNN、AOD-Net和Residual-GIF对浓雾图像的去雾处理并不理想, 图像远景部分仍存在少量的雾. 由于图9中的图像不含天空区域, 所以DCP算法同本文算法一样都能较好地实现图像去雾. 但是, 对于含有天空区域的图像, DCP算法会存在天空区域透射率估计不准确的问题, 去雾图像存在光晕伪影, 而本文算法对于存在天空区域的图像一样能较好地实现图像去雾.

3.3 消融实验

本文分别对多尺度特征提取模块、残差模块和深度可分离卷积模块进行了消融定量分析实验, 以此验证本文网络的有效性.

为了保证消融实验中比较的公平性, 网络参数设置均保持一致. 消融实验结果如表2所示, 从结果中可以看出, 采用多尺度并行卷积模块提取图像特征并进行融合, 网络模型的性能得到了一定的提高, 同时模型中加入残差学习模块能进一步改善网络性能. 用深度可分离卷积替代普通卷积, 网络性能略微有所提高. 但是, 正如第2.2节图2所分析的那样, 深度可分离卷积相比普通卷积, 其网络模型参数量大大减小.

4 结束语

针对传统图像去雾算法中去雾不完全, 色彩失真的问题, 提出了一种改进残差神经网络的图像去雾算法. 本文新颖的在残差学习模块中嵌入深度可分离卷积, 有效避免了网络层数增加而导致模型训练困难和网络参数量剧增的问题. 本文算法还利用加权引导滤波对网络得到的透射率图进行了细化, 使得最终的去雾图像保留更多的边缘信息, 并且通过四叉树分层搜索方法准确地估计大气光值. 本文通过消融实验对比分析了网络中各个模块对整个网络的影响, 验证了所提算法的有效性和可靠性. 实验结果表明本文算法在PSNR和SSIM指标上取得了一定的提高, 并且去雾图像在主观视觉效果上也有较好的表现, 同时算法对于自然真实雾图像的去雾也能很好的适用.