工业车辆/机械的使用大幅提高了物件的装卸、堆垛、搬运效率, 然而在使用过程中也存在诸多问题. 最突出的是工业车辆/机械在作业过程中运动方向改变频繁, 回旋作动部件多, 由此给附近作业的工程人员带来较大的安全威胁; 同时此类设备往往视野盲区大, 而操作员又需同时兼顾多个操作面, 以普通叉车为例, 驾驶员有近50%的时间处于倒车状态, 很容易顾此失彼, 发生事故. 据国家质检总局和市场监管总局的统计数据显示, 2014–2018年间, 35%的事故是由于两车之间的碰撞导致, 28%的事故来自于工业车辆之间的挤压, 挤压和碰撞事故的现象相同, 最重要的原因是两者都存在视觉盲区^[1]. 工业车辆/机械引发的安全事故一旦发生, 造成人员生命财产损失, 后果影响恶劣. 如何加强工业车辆/机械的操控安全性, 避免恶性碰撞事件的发生已引发广泛关注. 全国工业车辆标准化技术委员会组织制定《GB/T 38893-2020工业车辆安全监控管理系统》已于2020年6月2日正式批准发布, 于2020年12月1日起正式实施^[2]. 本标准规定了工业车辆安全监控管理系统的构成、内容、要求、检验方法和检验项目, 对工业车辆/机械驾驶环境中的人员识别及其距离识别、减速控制等提出了要求.

随着图像采集处理设备和计算机视觉的发展, 复杂背景下人员等目标的实时监测、物体空间位置信息感知等技术变得相对成熟. 此外工业车辆在实际使用中还受到设备成本限制. 因此, 在较低的设备成本条件下, 利用机器视觉辅助工业车辆/机械实现安全预警与作业控制已成为当前需要解决的实际工程问题.

1 测距避障相关技术

工业车辆通过传感器进行车辆后方视野弱区的环境感知, 依据识别到行人、车辆等障碍物的距离及方位进行避障. 测距避障所使用的传感器不同, 其特点及适用范围也会有所区别, 按照测距避障基于传感器的不同可划分为不同技术路线, 主要包括激光雷达避障、超声波避障、红外避障和机器视觉测距避障等^[3].

1.1 激光雷达避障技术

激光雷达测距的原理是通过发射激光束, 获取被接收目标物体击中后的反射激光, 计算发射和反射的往返时间, 从而测得目标距离^[4]. 激光传感器运行性能稳定、探测距离远、测距精度高、反应速度快, 目前激光雷达测距避障技术可以达到厘米级甚至毫米级的测距精度^[5]. 康燕仁^[6]提出了一种基于雷达测距的铁路工程车防撞系统. 该系统将激光雷达、微波雷达和激光对射等周围感知信息通过ZigBee无线通信网络传给主控, 进行多信息融合与阈值比较, 最终形成报警. 然而由于激光雷达造价昂贵, 使用寿命短, 信号的处理复杂, 在遇到泥水附着在传感器的表面或较低能见度天气等特殊情况时稳定性会大大降低, 极大制约了激光雷达在工业车辆环境感知中的应用.

1.2 超声波避障技术

超声波避障是通过计算发射超声波与接受回波之间的时间差与超声波波速的乘积进行目标物距离的测量^[7]. 由于其工作原理简单、成本低, 且在一定范围内测距精度较高等优点, 超声波测距技术已经广泛应用于工业车辆避碰系统^[8]. 王琰琰等^[9]提出了STM32F407单片机的智能仓储搬运车控制系统. 提出在车身前端、左端和右端加装超声波传感器进行障碍物的检测与大小感知, 进而根据当前区域分析能否通过, 并重新规划行进路线, 实现自主避让决策. 然而超声波传感器的仅具有较短的有效探测距离, 且易受大气因素的影响, 仅适用于较近范围内的避障检测^[10].

1.3 红外避障技术

红外测距都是采用三角测距的原理. 红外发射器按照一定角度发射红外光束, 遇到物体之后, 光会反向回来, 检测到反射光之后, 通过结构上的几何三角关系, 就可以计算出物体距离^[11]. 红外传感器具有角度灵敏度高、价格便宜、结构简单且不受可见光影响等优点, 可以快速感知物体的存在^[12]. 邵小军^[13]提出了基于有源红外传感器的掘进机定位系统, 采用主动照明红外传感器结合惯性导航仪、加速度计与陀螺仪进行掘进机地下位置的精确定位和避障, 大大提高了掘进机在缺少操作者视觉控制时的定位可靠性. 然而红外传感器测距在测量物体时受环境因素影响较大, 待测物体的周围光线、方向及颜色都能导致测量误差, 影响测距精度^[14].

1.4 机器视觉测距避障技术

机器视觉测距是对视觉传感器采集到的目标物图像, 采取特定的图像处理算法对图像中的目标物信息进行分析, 进而计算得出目标物的深度距离^[15]. 本文方法属于机器视觉测距技术范畴, 相比于其他感知技术, 视觉传感器的硬件研发成熟、成本较低^[16]. 机器视觉测距技术主要在软件算法上进行研究优化, 属于被动测距, 即不需要向目标物发射信号, 不会因多车间的信号互相干扰而影响车辆的安全行驶. 另一方面, 摄像头获取的图像中信息除目标物信息外, 还包含大量附加的场景物体信息, 利用机器视觉算法识别出图像中包含的这些信息, 将会极大地提高工业车辆避碰系统的智能程度.

2 算法原理与实现

本文提出的基于双目视觉的范围内工业车辆实时避障方法主要分为以下5个步骤:

步骤1. 图像采集与矫正. 使用双目深度相机采集车辆正后方作业环境图像, 根据标定后相机的畸变系数、内参矩阵等参数对采集到的图像进行双目矫正;

步骤2. 三维立体重建. 将步骤1得到的矫正后左右视图采用SGBM算法进行立体匹配, 得到视差图, 并由匹配点的视差信息得到对应的点云图;

步骤3. 自定义有效检测范围. 对地面进行标定并拟合地面方程. 人为设定有效检测范围以及安全预警范围的长与宽, 并根据CAN通讯模块接收车辆行驶信息, 实时调整安全预警区域的大小和形状;

步骤4. 直行及转弯范围内行人距离及方位测算. 采用轻量化行人检测模型对步骤1得到的矫正后图像进行行人方位框的定位, 设计了直行及转弯测距算法对有效检测范围内的行人距离进行计算;

步骤5. 范围预警与实时规划避障. 由步骤4得到的行人距离和方位信息对比既设的安全预警范围, 判断行人所处的位置是否安全, 将比对结果通过CAN通讯模块发送至车载控制器进行车辆的自动操作, 同时将判定分析结果在车载显示器上进行实时显示.

本文提出方法的总体流程如图1所示.

2.1 图像采集与矫正

将双目深度相机固定于工业车辆正后方, 进行车辆正后方弱视野区环境图像的采集. 由双目立体视觉测距的原理可知, 要获取双目图像中目标点的距离, 就必须知道二维图像与三维空间坐标系的转换关系. 而双目深度相机标定就是通过一组图像坐标系坐标和已知其参考坐标系坐标的点建立图像坐标系中成像点与世界坐标系中目标物点的映射关系, 计算得出相机的内外参数及畸变系数, 为接下来的双目立体视觉测距提供相关未知参数解^[17].

双目相机单个摄像头的标定主要是计算出摄像头的内参矩阵M、畸变系数 ${\textit{distCoeff}}$ . 另外针对双目相机左右两个摄像头的旋转及平移位置关系, 还需要标定测量右摄像头相对于左摄像头的旋转矩阵R、平移向量T. 其中, 双目相机的畸变系数 ${\textit{distCoeff}}$ 、内参矩阵M、旋转矩阵R和平移矩阵T分别由式(1)–式(4)表示:

$ {\textit{distCoeff}} = [\begin{array}{*{20}{c}} {{k_1}}&{{k_2}}&{{p_1}}&{{p_2}}&{{k_3}} \end{array}] $

(1)

$ M{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{f_x}}&0&{{c_x}} \\ 0&{{f_y}}&{{c_y}} \\ 0&0&1 \end{array}} \right] $

(2)

$ \begin{split} R{\text{ = }}&\left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos a}&{ - \sin a} \\ 0&{\sin a}&{\cos a} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \beta }&0&{\sin \beta } \\ 0&1&0 \\ {\sin \beta }&0&{\cos \beta } \end{array}} \right]\\ &\left[ {\begin{array}{*{20}{c}} {\cos \gamma }&{ - \sin \gamma }&0 \\ {\sin \gamma }&{\cos \gamma }&0 \\ 0&0&1 \end{array}} \right] \end{split} $

(3)

$ T{\text{ = (}}{t_x}, {t_y}, {t_{\textit{z}}}{)^{\rm T}} $

(4)

其中, $ {k_1} $ 、 $ {k_2} $ 、 $ {k_3} $ 为径向畸变系数; $ {p_1} $ 、 $ {p_2} $ 为切向畸变系数; $ {c_x} $ 、 $ {c_y} $ 为主点坐标, 通常位于图像的中心附近; $ {f_x} $ 和 $ {f_y} $ 为相机在水平方向和垂直方向的焦距, 单位为像素; $ \alpha $ 、 $ \;\beta $ 、 $ \gamma $ 为右相机围绕左相机坐标系3个轴的转角; $ R $ 与 $ T $ 合并称为相机外参.

本文采用张正友标定法^[18]对双目深度相机进行标定, 得到标定后相机的最优内、外参数解. 接下来进行双目立体矫正, 首先通过单目标定得到的镜头畸变系数 ${\textit{distCoeff}}$ 分别消除左右摄像头拍摄图像的径向和切向上的镜头畸变, 然后使用Bouguet极线矫正算法^[19]对双目图像进行立体矫正(图2, 图3). 将双目标定中得到的左右摄像头的旋转矩阵R和平移向量T等数据作为Bouguet算法的输入参数, 经Bouguet算法进行双目立体矫正后, 可以得到经过重投影映射和旋转的行对准双目图像.

2.2 三维立体重建

立体匹配算法作为双目立体视觉测距算法的关键技术, 其算法效果直接影响着测距性能的好坏, 因此, 需要对采集到的双目深度相机图像采取必要的预处理措施. 对采集到的左右相机图像进行立体矫正, 得到像素行严格对准的双目图像, 这就保证了立体视觉匹配算法能够准确并快速地搜索匹配点. 此外需要对矫正后的图像进行灰度处理和滤波去噪, 以减少立体匹配算法的数据处理量. 并对双目图像边界进行延拓, 以使双目立体匹配后的视差图能够还原双目视场范围.

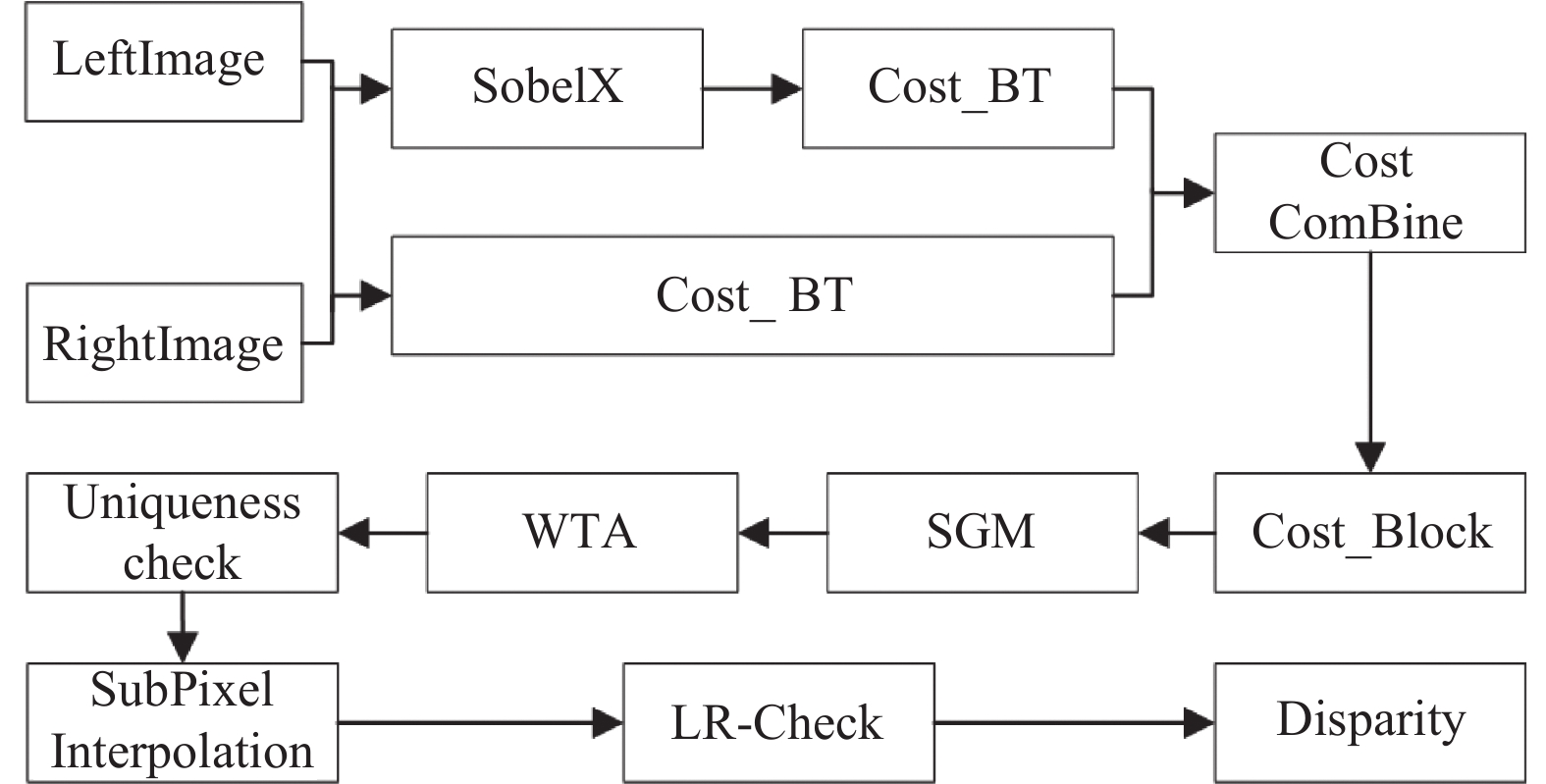
接下来, 将预处理后的双目图像输入SGBM (semi-global block matching)算法^[20]进行双目立体视觉匹配, 得到较为稠密的视差图, 具体步骤如下.

步骤1. 预处理. 使用Sobel算子对源图像进行处理, 公式为:

$ \begin{split} Sobel(x, y) =& 2[P(x + 1, y) - P(x - 1, y)] \\ & + P(x + 1, y - 1) - P(x - 1, y - 1) \\ & + P(x + 1, y + 1) - P(x - 1, y + 1) \end{split} $

(5)

其中, $ P $ 表示其原像素值, 并将经Sobel算子处理后的图像上每个原像素点 $ P $ 映射为新图像, 映射公式为:

$ \begin{split} &{P_{\rm new}} = \\ &\left\{ {\begin{array}{*{20}{l}} {0, P < - preFilterCap} \\ {P + preFilterCap, - preFilterCap \leqslant P \leqslant preFilterCap} \\ {2 \times preFilterCap, P \geqslant preFilterCap} \end{array}} \right. \end{split} $

(6)

其中, ${P_{\rm new}}$ 为新像素值, $ preFilterCap $ 为常量参数. 最终得到图像的梯度信息用于后续的代价计算.

步骤2. 代价计算. 代价计算分为两步: 一是使用采样方法对经预处理得到的图像梯度信息计算梯度代价值; 二是使用采样方法对源图像计算SAD (sum of absolute differences)代价. SAD代价计算公式如下:

$ C(x, y, d) = \sum\limits_{i = - n}^n {\sum\limits_{j = - n}^n {\left| {L(x + i, y + j) - R(x + d + i, y + j)} \right|} } $

(7)

这两个代价计算都会在选取的SAD窗口中进行计算, 窗口越大, 计算耗费的时间越多.

步骤3. 动态规划. 动态规划算法本身存在拖尾效应, 视差突变处易产生错误的匹配, 利用动态规划进行一维能量累积, 会将错误的视差信息传播给后面的路径上. 半全局算法利用多个方向上的信息, 试图消除错误信息的干扰, 能明显减弱动态规划算法产生的拖尾效应. 该算法试图通过影像上多个方向上一维路径的约束, 来建立一个全局的马尔科夫能量方程, 每个像素最终的匹配代价是所有路径信息的叠加, 每个像素的视差选择都只是简单通过WTA (winner takes all)决定的. 在每个方向上按照动态规划的思想进行能量累积, 然后将各个方向上的匹配代价相加得到总的匹配代价. 如式(8)–式(10)所示:

$ \begin{gathered} {L_{{r}}}({{p}}, d) = C({{p}}, d) + \min [{L_{{r}}}({{p - r, d), }}{L_{{r}}}({{p - r, }}d - 1) + {P_1}, \\ {L_{{r}}}(p - r, d + 1) + {P_1}, \mathop {\min }\limits_i {L_{{r}}}({{p - r}}, i) + {P_2}{{]}} - \mathop {\min }\limits_k {L_{{r}}}({{p - r}}, k) \end{gathered} $

(8)

$ {P_1}{\text{ = }}8 \times cn \times {\textit{SADWindowSize}^2} $

(9)

$ {P_2}{\text{ = 32}} \times cn \times {\textit{SADWindowSize}}^2 $

(10)

式(8)中, ${L_{{r}}}$ 为当前路径累积的代价函数; 第3项无意义, 仅是为了消除各个方向路径长度不同造成的影响; $ {P_1} $ 、 $ {P_2} $ 为像素点与相邻点视差存在较小和较大差异情况下的平滑惩罚, 且 $ {P_1} < {P_2} $ , $ {P_1} $ 、 $ {P_2} $ 分别由式(9)、式(10)表示, 其中, $ cn $ 是图像的通道数, SADWindowSize是SAD窗口大小, 数值为奇数. 将所有r方向的匹配代价相加得到总的匹配代价, 计算公式如下:

$ s(p, d) = \sum\limits_r {{L_r}(p, d)} $

(11)

步骤4. 后处理. SGBM的后处理包括置信度检测、亚像素插值、左右一致性检测. 置信度检测是利用代价立方体本身进行错误视差值的剔除, 即最佳视差值要与一定范围内的视差值在代价值上保持一定的全局最优关系, 这样可以避免算法中经常遇到的局部最优解问题. 亚像素插值的目的是让物体表面视差更加的平滑, 因为在立体匹配的时候是将双目视角所在空间粗略地分为了最大视觉差所对应的平面数, 但是真实场景却又是连续且渐变的. 左右一致性检测的目的则是为了消除左右遮挡带来的视差错误.

SGBM算法整体流程如图4所示. 图5描述了对左右视图进行双目立体匹配得到的视差图效果.

给定相机标定后的相机内参矩阵, 计算得到重投影矩阵 $ Q $ , 定义如下:

$ Q{\text{ = }}\left[ {\begin{array}{*{20}{c}} 1&0&0&{ - {c_x}} \\ 0&1&0&{ - {c_y}} \\ 0&0&0&f \\ 0&0&{ - 1/{t_x}}&{({c_x} - {{c'}_x})/{t_x}} \end{array}} \right] $

(12)

其中, 除 $ {c'_x} $ 外的所有参数都来自于左图像, $ {c'_x} $ 是左点在右图像上的 $ x $ 坐标, 当矫正正确时, 主光线在无穷远处相交, 那么 $ {c_x} = {c'_x} $ .

给定一个二维齐次点, 由SGBM算法得到的视差图中可以得到与之关联的视差 $ d $ , 通过 $ Q $ 矩阵可将该点投影至三维空间中, 公式如下:

$ Q{(x, y, d, 1)^{\rm T}} = {(X, Y, Z, W)^{\rm T}} $

(13)

在矫正正确的前提下展开式(13), 可得:

$ \left(\frac{X}{W}, \frac{Y}{W}, \frac{Z}{W}\right)= \left( - \frac{{x - {c_x}}}{d}{t_x}, -\frac{{y - {c_y}}}{d}{t_x}, -\frac{f}{d}{t_x}\right) $

(14)

该点对应的三维坐标就是 $ \left(\dfrac{X}{W}, \dfrac{Y}{W}, \dfrac{Z}{W}\right) $ , 由此完成将二维点的图像坐标到三维空间点的世界坐标的转换, 得到空间重建3D点云图.

2.3 地面标定

在图像上选取地面平面点, 在3D点云图上得到所选地面平面点所对应的空间坐标(相对左相机坐标), 设定地面参数方程如下:

$ Ax + By{\text{ + }}C = {\textit{z}} $

(15)

将多个地面平面点 $({x_1}, {y_1}, {{{{\textit{z}}}}_1}), ({x_2}, {y_2}, {{{{\textit{z}}}}_2}), \cdots, ({x_{{n}}}, {y_{{n}}}, {{{{\textit{z}}}}_{{n}}})$ 采用最小二乘法拟合出对应地面平面的参数方程^[21], 具体公式如下:

$ \left\{ {\begin{array}{*{20}{c}} {A{x_1} + B{y_1}{\text{ + }}C = {{\textit{z}}_1}} \\ {A{x_2} + B{y_2}{\text{ + }}C = {{\textit{z}}_2}} \\ {\vdots} \\ {A{x_n} + B{y_n}{\text{ + }}C = {{\textit{z}}_n}} \end{array}} \right. $

(16)

式(16)的矩阵表达方式可转换为:

$ Z{\text{ = }}X\varepsilon $

(17)

其中, $ X{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}&1 \\ {{x_2}}&{{y_2}}&1 \\ {\vdots}&{\vdots}&{\vdots} \\ {{x_n}}&{{y_n}}&1 \end{array}} \right] $ , $\varepsilon {{ = (A, B, C}}{{{)}}^{\rm T}}$ , $ Z{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{{\textit{z}}_1}} \\ {{{\textit{z}}_2}} \\ {\vdots} \\ {{{\textit{z}}_n}} \end{array}} \right] $ . 解出 $ \varepsilon $ 可得:

$ \varepsilon {\text{ = (}}{X^{\rm T}}X{)^{ - 1}}{X^{\rm T}}Z $

(18)

由此得到拟合后的地面平面参数方程.

2.4 自定义检测范围

人为设定安全预警范围, 其中包括有效检测范围的长度 $ d $ 、宽度 $ s $ 、刹车预留距离 ${l_{\rm stop}}$ 、减速预留距离 ${l_{{\text{dec}}}}$ . 而实时刹车预留距离 ${l'_{\rm stop}}$ 和实时减速预留距离 $ {l'_{{\text{dec}}}} $ 与实际车速 $ v $ 有关, 计算公式如式(19), 式(20):

$ {l'_{\rm stop}} = {l_{\rm stop}} + \frac{{v \times {t_{\rm stop}}}}{2} \times {k_{\rm stop}} $

(19)

$ {l'_{\rm dec}} = {l_{\rm dec}} + \frac{{(v + {v_{\rm stop}}) \times {t_{\rm dec}}}}{2} \times {k_{\rm dec}}\left( 当{{{l'}_{\rm dec}} > {{d}}}时,取{{d}} \right) $

(20)

其中, ${t_{\rm stop}}$ 表示刹车时间, 应和车上设置的实际参数一致; $ {t_{{\text{dec}}}} $ 表示减速时间, 应和车上设置的实际参数一致; ${v_{\rm stop}}$ 表示削减速度, 应和车上设置的实际参数一致; ${k_{\rm stop}}$ 表示刹车系数值, 需实测; $ {k_{{\text{dec}}}} $ 表示减速系数值, 需实测; 除实时车速 $ v $ 以外的其他7个参数需实际测试确定最优值.

2.5 直行及转弯范围内行人距离及方位测算

采用轻量级目标检测算法实时检测识别人等障碍物的对应位置及所属类别, 并在视频画面中框出行人位置. 根据自定义有效检测范围的长宽进行直行范围内行人方位框的投影与距离测算(第2.5.1节)和转弯范围内行人方位框的投影与距离测算(第2.5.2节).

2.5.1 直行范围内行人投影测距

工业车辆在直行倒车情况下形成矩形区域(图6), 对处于该区域范围行人方位框进行进界点计算及最佳距离测算. 主要分为以下5个步骤:

步骤1. 投影点数计算. 对人体方位框中的点按一定间隔逐像素进行遍历, 当求得像素点在左右视图中的视差大于固定阈值时, 认为该点距离较近或未能匹配成功, 需要排除; 对符合要求的点由点云图求得该点的空间位置坐标, 计算点到地面的高度, 若高度小于固定阈值, 则需排除, 由此得到行人方位框内符合投影要求的点数.

步骤2. 地面投影点坐标计算. 将步骤1中符合投影要求的点投影至地面, 由第2.3节计算得到拟合后的地面方程为 $ Ax + By + {C} = {\textit{z}} $ , 假定不在平面上的任一点的坐标为 $ P({x_i}, {y_i}, {{\textit{z}}_i}) $ , 其在平面上的投影坐标为 $P'({x_{{p}}}, {y_{{p}}}, {{{{\textit{z}}}}_{{p}}})$ . 因为投影点到当前点的向量与地面平面垂直, 根据垂直约束条件, 易知 ${y_{{p}}}, {{{{\textit{z}}}}_{{p}}}$ 满足如下条件:

$ {y_p} = \frac{B}{A}({x_p} - {x_0}) + {y_0} $

(21)

$ {{\textit{z}}_p} = - \frac{1}{A}({x_p} - {x_0}) + {{\textit{z}}_0} $

(22)

联立平面方程可以解得:

$ {x_p} = \frac{{({B^2} + 1){x_0} - A(B{y_0} - {{\textit{z}}_0} + {C})}}{{{A^2} + {B^2} + 1}} $

(23)

$ {y_p} = \frac{{({A^2} + 1){y_0} - B(A{x_0} - {{\textit{z}}_0} + D)}}{{{A^2} + {B^2} + 1}} $

(24)

$ {{\textit{z}}_p} = \frac{{({{A}^2} + {{B}^2}){{\textit{z}}_0} + ({A}{x_0} + {B}{y_0} + D)}}{{{A^2} + {B^2} + 1}} $

(25)

由此可以得到投影坐标为 $P'({x_{{p}}}, {y_{{p}}}, {{\textit{z}}_{{p}}})$ .

步骤3. 投影点距离计算. 由所求地面平面方程与相机平面的z轴分量向量相交, 易得平行于相机平面的方向向量 $x\_line({x_{x\_line}}, {y_{x\_line}}, {{\textit{z}}_{x\_line}})$ 和垂直于相机平面的方向向量 $y\_line({x_{{{y}}\_line}}, {y_{{{y}}\_line}}, {{{{\textit{z}}}}_{{{y}}\_line}})$ , 以相机投影点为基点 $({x_0}, {y_0}, {{\textit{z}}_0})$ , 将投影点与相机基点投影点在z轴方向形成的向量的长度作为该点的距离 $ {d_{P'}} $ , 即:

$ {d_{P'}} = \frac{{\left| {{{{\textit{z}}}_p} - {{{\textit{z}}}_0}} \right|}}{{{{{\textit{z}}}_{{{y}}\_line}}}} $

(26)

对行人方位框内所有符合步骤2投影要求的点的距离值进行存储, 进而得到矩阵框中符合投影要求的点的距离值列表 $ {d_{PLlist}} $ , 即:

$ {d_{PLlist}}{\text{ = }}\{ {d_{{{P'}_1}}}, {d_{{{P'}_2}}}, \cdots, {d_{{{P'}_i}}}{\text{\} }},\;1 \leqslant i \leqslant len({d_{PLlist}}) $

(27)

步骤4. 投影点进界判断. 根据步骤2所得投影点 $P'({x_{{p}}}, {y_{{p}}}, {{{{\textit{z}}}}_{{p}}})$ 的x、z方向坐标 $P''({x_{{p}}}, {{{{\textit{z}}}}_{{p}}})$ 与直行矩形区域范围内4个顶点的x、z方向坐标 ${V_{{{tl}}}}({x_{{{tl}}}}, {{{{\textit{z}}}}_{{{tl}}}})$ 、 ${V_{{{tr}}}}({x_{{{tr}}}}, {{{{\textit{z}}}}_{{{tr}}}})$ 、 ${V_{{{bl}}}}({x_{{{bl}}}}, {{{{\textit{z}}}}_{{{bl}}}})$ 、 ${V_{{{br}}}}({x_{{{br}}}}, {{{{\textit{z}}}}_{{{br}}}})$ 所呈平面向量关系, 判断是否该点是否进界, 公式如下:

$f(P'') = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} 1,(\overrightarrow {{V_{{tl}}}{V_{{tr}}}} \times \overrightarrow {{V_{{t}{{l}}}}P''} \geqslant 0,\overrightarrow { {V_{{{tr}}}}{V_{{{br}}}}} \times \overrightarrow {{V_{{tr}}}P''} \geqslant 0,\\ \overrightarrow {{V_{{{br}}}}{V_{{{bl}}}}} \times \overrightarrow {{V_{{{br}}}}P''} \geqslant 0, \overrightarrow {{V_{{{bl}}}}{V_{{{tl}}}}} \times \overrightarrow {{V_{{{bl}}}}P''} \geqslant 0) \end{array}\\ 0,\;其他 \end{array}} \right.$

(28)

若进界, 则当前进界点数加1, 并以此进行累积, 由此得到行人方位框内符合进界要求的点数.

步骤5. 范围内行人方位框的最佳距离值. 当行人方位框内同时符合投影要求与进界要求的点数高于对应的阈值时, 使用直方图距离测算方法计算该行人方位框的最佳距离. 即由符合要求的点的距离值列表计算最大和最小距离值, 除以固定直方区间宽度, 得到直方图区间个数. 将距离值列表中各点距离减去距离最小值的差, 除以区间宽度, 得到该距离所属的直方图区间号, 并且该区间内的距离数计数加1, 以此得到各区间距离数目的直方图. 以固定宽度的滑窗沿直方图由左至右以特定步长滑行, 统计每滑行一步后滑窗内的各直方图区间的距离数之和, 以及当前滑窗中心点对应的距离, 取得距离数之和最大的滑窗所对应的滑窗中心点距离作为当前行人判断框的最佳距离.

2.5.2 转弯范围内行人投影测距

工业车辆在转弯倒车情况下形成矩形区域(图7), 对处于该区域范围行人方位框进行进界点计算及最佳距离测算. 主要分为以下5个步骤.

步骤1. 确定转向中心点. 由CAN通讯模块接收车辆行驶过程中的转向角度 $ \theta $ , 再由车身长度L和圆心角 $ \theta $ 计算圆弧半径R, 即:

$ R{\text{ = }}L/\sin(\theta ) $

(29)

以相机投影点为基点 $ ({x_0}, {y_0}, {{\textit{z}}_0}) $ , 基点到圆心的距离R为直角三角形的斜边, 计算两条直角边 $ {l_1} $ (相机投影基点到车头的垂直距离)和 $ {l_2} $ (直角三角形直角顶点到圆心的水平距离), 即:

$ {l_1}{\text{ = }}R\sin(\theta ) $

(30)

$ {l_2}{\text{ = }}R{\text{cos}}(\theta ) $

(31)

将基点坐标 $ ({x_0}, {y_0}, {{\textit{z}}_0}) $ 沿 $ y\_line $ 的相反方向移动 $ {l_1} $ 个距离长度, 再沿 $ x\_line $ 方向(左转向)或 $ x\_line $ 相反方向(右转向)移动 $ {l_2} $ 个距离长度, 到转向圆心点 $ C({x'_0}, {y'_0}, {{\textit{z}}'_0}) $ .

步骤2. 投影点数计算. 同第2.5.1节步骤2.

步骤3. 投影点距离计算. 在进行转弯过程下投影点距离计算时, 由于弧形区域起始点沿线位置与相机基点沿线位置间由于转向角 $ \theta $ 的关系有一定的距离误差, 故需计算进界点的距离修正项 $ {d'_{P'}} $ , 即:

$ {d'_{P'}}{\text{ = (}}R{{ - }}R'{\text{)}} \times {\text{tan}}\theta $

(32)

进而将投影点距离相机基点沿线的弧线长度作为转弯过程下该点的距离值 $ {d_{P'}} $ , 即:

$ {d_{P'}}{\text{ = }}{\theta _{{p}}}R'{{ - }}{d'_{P'}} $

(33)

步骤4. 投影点进界判断. 由步骤2计算得到人体判定框内符合要求的点到地面的投影 $P'({x_{{p}}}, {y_{{p}}}, {{\textit{z}}_{{p}}})$ , 计算投影点到圆心的半径长度 $ R' $ , 判断该投影点是否在弧形区域宽度 $ S $ 范围内, 公式如下:

$ f(P') = \left\{ {\begin{array}{*{20}{c}} 1,\;{\left| {R' - R} \right| < \dfrac{1}{2}S} \\ 0,\;{\left| {R' - R} \right| \geqslant \dfrac{1}{2}S} \end{array}} \right. $

(34)

接下来对弧形区域宽度范围内的投影点继续判定是否该点在弧形区域长度范围内, 根据转弯区域有效作用范围的长度 $ d $ 与圆弧半径 $ R $ 的对应关系求得弧形区域长度对应的圆心角 ${\theta _{{d}}}$ , 假定相机基点 $ ({x_0}, {y_0}, {{\textit{z}}_0}) $ 与圆心 $ C({x'_0}, {y'_0}, {{\textit{z}}'_0}) $ 所成向量 $ {p_c} $ , 投影点 $P'({x_{{p}}}, {y_{{p}}}, {{\textit{z}}_{{p}}})$ 与圆心 $ C({x'_0}, {y'_0}, {{\textit{z}}'_0}) $ 的所成向量 $ {p'_c} $ , 则 $ {p_c} $ 与 $ {p'_c} $ 所成的夹角角度 $ {\theta _p} $ 计算如下:

$ {\theta _p}{\text{ = }}\arccos \left(\frac{{\left| {{p_c}} \right|\left| {{{p'}_c}} \right|}}{{{p_c}{{p'}_c}}}\right) $

(35)

判断其是否处于弧形长所在的圆心角范围内, 若 $ {\theta _p} < {\theta _d} $ , 则证明该点在弧形区域内, 进界点数计数加1, 由此得到所有的弧形区域进界点.

步骤5. 范围内行人方位框的最佳距离值. 当行人方位框内符合投影要求的点数与符合进界要求的点数均高于对应的阈值时, 通过第2.5.1节步骤5所述直方图的方法计算出最佳距离值作为转弯情况下弧形区域范围内行人方位框的最佳距离.

2.6 范围预警与实时规划避障

获取在直行(第2.5.1节)或转弯(第2.5.2节)范围内所有行人检测框的最佳距离, 将其中的最小值作为距离车尾(以相机基点为准)最近的行人距离值 ${d_{\min}}$ , 则实时刹车与减速避障规则如下:

(1)当 ${d_{\min}} > {l'_{\rm stop}}{\text{ + }}{l'_{{\text{dec}}}}$ 时, 向CAN通信设备发出安全信号;

(2)当 ${l'_{\rm stop}}{{ + }}{l'_{{\rm {dec}}}} > {d_{\min}} > {l'_{\rm stop}}$ 时, 向CAN通信设备发出减速信号;

(3)当 ${l'_{\rm stop}}{\text{ > }}{d_{\min}} > 0$ 时, 向CAN通信设备发出刹车信号.

CAN通信设备负责接收来自系统发出不同预警信号并向工业车辆控制器进行信号传递, 当行人处于刹车范围内时, 工业车辆控制器收到刹车信号使其刹车; 当行人处于制动范围内, 工业车辆控制器收到减速信号使其减速. 系统将判定分析结果结果实时在车载显示器上进行显示.

3 实验结果与分析

为了全面研究与分析基于双目定位测距的工业车辆实时避障方法的性能, 本文以普通工业叉车为例在厂区环境下开展实验, 所需硬件设备主要由车载控制器、CAN通信模块、工控机、双目深度相机、车载电源、车载显示器组成, 连接方式如图8所示.

算法模型在CPU为i5-6200U, 内存大小为4 GB的工控机上部署运行, 操作系统为Windows 10, 编程语言为C++, 编程环境为Visual Studio 2017, OpenCV版本为4.4.0, 使用OpenVINO 2021.2框架进行目标检测模型的推理加速. 此外, 双目相机经标定(第2.1节)后的结果如表1所示.

本节主要对本文提出的方法中目标检测模型性能、静态测距精度、核心检测范围进界判定、实时规划区域避障效果4个方面进行测试.

3.1 目标检测模型性能

本文采用ssd_inception^[22]作为该方法的行人检测算法模型, 并与ssd_mobilenet^[23]进行性能对比, 分别将ssd_inception与ssd_mobilenet模型进行训练、测试, 其中将3 937张行人图片和3 937张工业叉车图片划分为训练集, 将600张行人图片和600张工业叉车图片划分为测试集. 训练的批次大小为34, 周期数为25 000, 在测试集上采用平均识别精度和检测帧率作为模型检测精度和速度的验证指标. 两模型性能测试结果如表2所示.

可以看出, ssd_inception模型的模型大小和识别精度高于ssd_mobilenet模型, 检测帧率低于ssd_mobilenet模型, 因此, ssd_inception模型在推理精度上相对ssd_mobilenet模型有较大提升, 但与此同时推理速度也会相对较慢.

图9–图12展示了两种方法分别在近距离(距车尾3 m以内)、远距离(距车尾3 m之外)场景下的行人识别效果, 在近距离部分截取帧画面中, 由于距离叉车尾部较近的行人仅有部分身体出现在画面底部, 导致模型检测信息不完整, ssd_mobilenet模型对于部分行人存在漏检, 而ssd_inception模型依然可以在检测信息不完整的情况下较好地检测出出现在画面底部的行人. 在远距离部分截取帧画面中, 由于距离叉车尾部较远的行人目标较小, 对于模型检测来说像素较少, 特征不明显, 导致模型检测信息较少, ssd_mobilenet模型对于远距离下的行人依然会出现漏检情况, 而ssd_inception模可以在检测信息较少的情况下较好地检测出出现在画面中目标较小的行人.

综上所述, 在设备允许且画面无明显卡顿的情况下, 选用ssd_inception模型作为该方法的目标检测模型在近距离、远距离均能达到较好的行人检测效果.

3.2 静态测距精度

在直行倒车状况下, 标记距相机中心0.5 m、1 m、1.5 m、2 m、2.5 m、3.0 m、3.5 m、4 m、4.5 m、5 m位置, 保持叉车不动, 实验人员依次在上述位置站立, 观察记录算法计算出的距离值, 在某一位置3次测量取平均值, 计算该位置处测得的距离均值与该位置处真实距离值的平均误差, 测试结果如表3所示.

在转弯状况下, 确定叉车倒车时前轮的转弯角度为30°, 以相机中心为基本点, 以转弯角度和车头位置确定圆心, 以0.5 m为间隔, 丈量出由转弯角度所形成的2 m×5 m的弧形区域, 实验人员在该区域内匀速行走, 观测算法能否正确输出弧形范围内人员的识别和测距结果. 测试结果如表4所示.

从表3和表4可以看出, 在直行和转弯状态下, [0.5, 3.0)区间范围内, 平均测距误差在0.1 m之内, [3.0, 3.5)区间范围内, 平均测距误差在0.2 m之内. 特别地, 在转弯状态下, 算法均能识别弧形范围内人员的测距结果. 经分析可知, 测距误差与行人距离车尾的远近有关, 近距离比远距离测距误差更小, 测距较为准确, 此外远距离行人测距误差依然在可接受的误差范围之内, 证明了本文提出的测距算法的可行性.

3.3 核心检测范围进界判定

在系统界面内设置自定义核心检测范围的长度和宽度分别为5 m和2 m, 并以相机中心为基准点, 丈量出设置的自定义核心检测范围的长和宽, 实验人员在自定义核心检测区域的边界处“沾边”缓慢进入, 将人与核心检测区域按重合比例的程度划分为低度重合(身体四肢与核心区域重合)、中度重合(身体半数左右的部分与核心区域重合)、高度重合(整个身体完全与核心区域重合) 3个等级, 观察算法在不同重合比例等级下能否正常识别和定位行人. 实验结果如表5所示.

由表5可以看出, 当人与核心检测区域分别处于低度重合、中度重合及高度重合情况下, 均能识别并定位核心检测区域内的行人.

图13和图14分别表示核心检测区域长度和宽度范围内的行人进界判定效果, 可以看出, 当行人处于核心检测区域之外(进界投影点低于设定阈值)时, 不会识别并定位行人; 当行人的手部或脚部与核心检测区域稍有重合时, 会立即识别并定位到行人, 进而验证了核心检测范围进界判定算法的灵敏性和有效性.

3.4 实时规划区域避障效果

将调整好的参数值代入式(19)、式(20)中, 根据叉车倒车时的实时车速进行实时刹车距离和减速距离的计算, 并采取第2.6节中动态刹车和减速避障规则进行10 m外和10 m内的实时规划区域避障效果测试.

当人与车的距离均在10 m外时, 以不同速度倒车, 观察车遇到人后能否及时刹停, 并记录刹停后系统显示的人车距离与实际测量的人车距离. 实验结果如表6所示.

从表6可以看出, 基于测试叉车上适配好的各参数, 在10 m外以不同速度行驶时, 均能及时刹停, 且刹停时人与车尾的距离基本维持在1 m附近, 符合实时规划区域避障安全要求.

当人与车的距离均在10 m内时, 设定人与车的初始距离依次为10 m、9 m、8 m、7 m、6 m、5 m、4 m、3 m、2 m, 在不同初始距离下均以最大速度倒车, 观察车遇人能否及时刹停, 并记录刹停后系统显示的人车距离与实际测量的人车距离. 实验结果如表7所示.

从表7可以看出, 基于测试叉车上适配好的各参数, 在10 m内以最大速度行驶时, 均能及时刹停, 且刹停时人与车尾距离基本维持在0.8–1.3 m范围内, 符合实时规划避障安全要求.

此外, 在直行或转弯状态下, 当最近行人距离处于刹车、减速、安全范围内, 对应的系统界面会出现红、黄、绿3种不同颜色的边框作为实时预警提示, 并发送相应的指令信号, 通过CAN通讯模块传递至车载控制器以采取对应的措施, 实现实时避障的预警提示与制动效果.

图15和图16分别表示直行及转弯倒车情况下最近行人距离处于刹车、减速、安全范围内的预警提示效果.

4 结语

本文面对工业车辆在作业的过程中频繁出现的行人碰撞等安全问题提出了基于双目定位测距的工业车辆实时避障方法. 通过使用标定后的双目深度相机对工业车辆后方视野弱区进行实时的图像采集、Bouguet极线矫正, 进而对矫正后的图像使用SGBM算法构建视差图进行三维立体重建, 同时针对不同设备使用轻量级目标检测模型进行行人检测. 最终在人为设定的有效检测范围及安全预警范围内, 对在图像画面中的行人进行定位和测距, 并根据实时车速, 动态调整刹车、减速范围, 对处于不同安全预警范围下的行人发送不同的预警信号, 通过CAN通信设备传递至车辆控制器, 实现了工业车辆的实时规划避障. 通过4组实验测试, 结果表明, 本文提出的方法具有更精准的定位和测距性能, 能够在不同车速下对范围内的行人进行更加实时、灵敏的避障.

该方法能够为工业车辆驾驶人员提供有效、实时、智能的操作辅助. 驾驶员无需频繁回头观察, 系统即可感知后方人和物体的存在, 在显示屏实时画面的传输下, 使驾驶员轻松完成倒车操作, 大大降低人为事故发生的概率, 提升驾驶员驾驶舒适度和工作效率, 保障工业车辆作业时的安全. 未来旨在保证目标检测模型及立体匹配算法精度的前提下进一步提升其推理速度.