1 引言

医学图像配准是医学图像分析处理任务中最基本的步骤, 是指通过对一幅图像经过一系列的几何变换, 使变换后图像与参考图像处于相同的坐标空间, 以达到两幅图像中相同的组织结构在空间位置上一一对齐. 配准算法的配准精度和配准效率将直接影响后续的医疗诊断分析和研究结果. 因此, 研究快速、精准的医学图像配准算法具有重要的理论意义和临床实用价值.

传统的配准算法框架主要包含4个部分^[1]: 特征空间、搜索空间、搜索策略和相似性度量. 特征空间是指从参考图像和浮动图像中提取可用于配准的特征; 搜索空间定义了图像变换的范围和方式, 即线性变换或非线性变换; 搜索策略是指采用合适最优化算法在搜索空间中寻找最优的配准参数; 相似性度量用于评估每次变换结果的优劣, 为搜索策略的搜索方向提供依据. 在此基础上, 已有大量的配准算法被提出并被广泛用于实际临床应用, 如SyN^[2]、Demons^[3]、FSL^[4]等. 尽管这些配准算法都能取得较好的配准效果, 但是都面临着一个共同的问题: 对于每一对待配准图像对, 传统配准算法均需要从零开始迭代优化目标函数, 严重影响了配准效率^[5], 难以满足临床实时的配准需求.

近年来, 深度学习技术被广泛应用于医学图像配准. 目前, 基于深度学习的配准技术主要被分为两大类: 有监督学习配准算法和无监督学习配准算法. 有监督学习配准算法是利用已知几何变换的待配准图像对训练网络, 并通过计算网络估计的几何变换和已知几何变换的均方误差 (mean squared error, MSE) 更新网络的权重参数. 如Miao等人^[6]在ConvNet的最后一层设计一个回归器去预测二维X光和三维CT图像的刚性配准参数, 解决了现有基于灰度的二维/三维配准算法速度慢、捕获范围小等两个缺陷. 不同于回归的方法, Yang 等人^[7]采用已知几何变换的待配准图像对训练深度编解码网络, 使其能够精准预测大变形微分同胚度量映射 (large deformation diffeomorphic metric mapping, LDDMM) 配准模型^[8]中的动量, 随后通过贝叶斯概率网络求得DVF. Sokooti等人^[9]则直接使用多尺度ConvNet去估计待配准图像对的DVF, 而无需将几何变换约束至具体的配准模型. 一些作者也尝试利用ConvNet估计薄板样条模型^[10]的参数, 如Cao等人^[11]和Eppenhof等人^[12], 他们分别使用模板样条模型实现了大脑MRI图像和胸部CT图像的可变形配准. 与传统配准算法相比, 有监督学习配准算法极大地提高了配准效率, 但这类方法的配准性能十分依赖带有标签的训练数据. 然而, 获得带有标签的医学图像数据成本非常高, 并且标记信息通常利用传统配准算法获得或者人工合成, 并不精准, 因此, 限制了有监督配准算法的发展.

基于无监督学习的配准算法不需要任何标签, 其通过最小化给定的损失函数约束神经网络预测最优的DVF. Jaderberg等人^[13]提出的空域变换网络 (spatial transformer network, STN) 因其能对图像重采样并且可微而极大推动了无监督配准算法的发展. 自STN提出后, 大量无监督配准算法涌现出来. 如Balakrishnan等人^[14]提出了一个优秀的无监督配准框架VoxelMorph, 该框架使用一个类似Unet的架构估计稠密的DVF, 然后在训练过程中借助STN模块对浮动图像重采样, 并通过计算重采样后的图像和参考图像的相似性度量指导网络训练, 最终在Dice分数评价指标上取得了与SyN配准算法相当的精度. Zhao等人^[15]和Tang等人^[16]基于VoxelMorph分别设计了无监督配准框架VTN (volume tweening network) 和 ADMIR (affine and deformable medical image Registration), 他们均在可变形网络框架中新增仿射预配准模型, 使得网络能够同时执行仿射配准和可变形配准, 真正地做到端到端配准. 但是他们也存在区别, VTN框架能够级联多个可变形配准的子网络, 递进式提高配准性能. 实验结果证明了级联策略能够处理大位移形变, 提高配准的精度. 除了模型上的创新, 一些学者也致力于探索几何变换映射的微分同胚性质. 如Zhang^[17]提出使用逆一致正则化项来约束相应逆映射的差异, 并在损失函数中引入逆一致性损失和防折叠损失来保证DVF的平滑属性. Mok等人^[18]使用类似SyN算法的思想, 利用ConvNet输出一对微分同胚映射, 用于将两幅图像从两条测地线映射到两幅图像的中间地带, 实验结果表明, 该方法能够获得平滑且拓扑保持的DVF.

尽管无监督学习配准算法不需要标签数据, 并且在多个数据集上也取得了十分优秀的配准性能, 但仍存在以下问题: 1)现存的大多数无监督配准算法仅能配准单模态图像, 在多模态图像配准上, 性能低下, 且针对QSM图像和T1加权图像的配准算法仍鲜见报道. 2)现存的配准算法大多采用全局相似度量如MSE、NCC (normalized cross-correlation)、NMI (normalized mutual information)^[19] 来驱动网络学习, 但这些相似性度量并不适用于衡量QSM图像和T1加权图像的相似性, 难以驱动网络学习.

为了解决以上问题, 本文设计了RF-RegNet用于QSM图像和T1加权图像配准, 通过编码金字塔提取QSM图像和T1加权图像特征, 两个解码器分别用于估计图像对之间的局部和全局几何形变, 最后利用局部特征相似损失和DVF的正则化共同指导网络模型训练, 完成高效精确地配准.

2 RF-RegNet配准方法

分别定义F, M为在n维空间 $\Omega \subset {\mathbb{R}^n}$ 的参考图像和浮动图像, 图像配准旨在寻找到一个最优的变形场 $\hat \varphi $ 使得浮动图像与参考图像处于同一空间并且相同的组织结构在空间位置上一一对齐. 这一过程可表示为式(1):

$ \begin{split} \hat \varphi =& \arg \mathop {\min }\limits_\varphi L(F, M, \varphi ) \\ =& \arg \mathop {\min }\limits_\varphi {L_{\rm sim}}(F, M \circ \varphi ) + \lambda {L_{\rm smooth}}(\varphi ) \end{split} $

(1)

其中, $M \circ \varphi $ 代表浮动图像经过变形场 $\varphi $ 重采样后所得到的图像, ${L_{\rm sim}}( \cdot , \cdot )$ 函数用于衡量两幅图像之间的相似性, ${L_{\rm smooth}}( \cdot )$ 函数用于约束变形场平滑, $\lambda $ 为两个函数之间的平滑系数. 传统配准算法通过优化每对配准图像的目标函数寻找最优变形场, 尽管能够取得较好的配准效果, 但也极大地影响了配准效率. 本文通过深度卷积模型共享全局参数寻找最优变形场来代替特定配准对的优化过程, 这意味着只要深度卷积网络模型一旦收敛, 输入任意待配准图像对均能快速精准得到最优的变形场, 这一过程可表示为:

$ \hat \varphi = {f_\theta }(F, M) $

(2)

其中, $f$ 代表深度卷积模型学习到的映射函数, $\theta $ 为网络模型参数即卷积神经网络每层的核权重系数. 通过最小化损失函数指导网络训练, 以求得最优网络权重参数 $\hat \theta $ . 本文在U-Net网络结构的基础上, 设计了RF-RegNet实现快速精准的T1加权图像和QSM图像配准, 配准框架如图1所示. RF-RegNet的核心架构由一个编码金字塔和两个解码器构成, 编码金字塔用于提取图像的细节特征, 两个解码器分别用于估计图像对之间细小结构区域、纹理细节的局部形变和大脑整体形状、位置、大小、角度等全局形变, 通过结合局部形变和全局形变得到最优的变形场, 随后利用重采样层对浮动图像进行重采样得到配准后的图像, 并通过计算重采样后的图像和参考图像的特征相似性驱动网络学习.

2.1 编码金字塔

编码金字塔结构类似于拉普拉斯金字塔, 它是由一系列残差图像 ${L_0}, {L_1}, \cdots , {L_{n - 1}}$ 组成, 每一层图像均是高斯金字塔两个层次之间的差异, 如图2所示.

构建高斯金字塔是构建拉普拉斯金字塔的前提, 高斯金字塔是通过对原始图像逐级高斯滤波再下采样得到的, 图2中 ${G_0}$ 表示初始图像(i=0), ${G_i}$ 表示第i $(1 \leqslant i \leqslant n)$ 次高斯滤波并下采样得到的图像, 高斯金字塔的计算过程如式(3)所示:

$ {G_i} = \left\{ {\begin{array}{*{20}{c}} {D(\Phi ({G_{i - 1}})),\quad i \geqslant 1} \\ {{G_0},\quad \quad \quad \quad \;i = 0} \end{array}} \right. $

(3)

其中, $\Phi $ 表示高斯滤波算子, D表示下采样操作. 拉普拉斯金字塔每一层 ${L_i}$ 是由高斯金字塔中每一层图像 ${G_{i + 1}}$ 经过上采样、滤波之后与上一层图像 ${G_i}$ 相减得到, 这一过程被描述为:

$ {L_i} = {G_i} - U(\Phi ({G_{i + 1}})), 0 \leqslant i \leqslant n - 1 $

(4)

其中, $U$ 表示图像上采样操作. 原始图像经过下采样后压缩了图像信息, 在去除噪声的同时也保留了部分图像特征信息, 但是将图像经过上采样, 往往通过插值填补缺失的像素值, 导致难以完全恢复至原始图像. 拉普拉斯金字塔通过差值将丢失的信息记录作为图像特征, 能够捕获图像的细节和边缘特征, 因此被广泛用于图像融合、图像重建等领域.

本文使用可学习的卷积核代替编码金字塔中的高斯核, 让本文所提出的编码金字塔不仅能够捕获待配准图像对的纹理细节差异, 还能够捕获大脑微小结构的特征差异. 编码金字塔由语义编码和残差编码两部分组成, 其中, 语义编码部分将参考图像和浮动图像堆叠形成一个二通道图像作为输入, 并通过一个步长为1、4个卷积核为 $3 \times 3 \times 3$ 的卷积对其进行卷积运算, 再经过一个LeakyReLU激活函数得到初始特征图, 记为 ${S_0}$ . 随后再通过步长为2、卷积核为 $3 \times 3 \times 3$ 的步幅卷积和LeakyReLU激活函数逐级下采样, 以捕获不同特征图下的全局语义信息. 语义编码阶段共经过4次下采样, 每次下采样均使得图像尺寸减半, 图像通道数增加一倍, 将经过下采样得到的图像分别标记为 ${S_i}, i = 1, 2, 3, 4$ , 如图1编码金字塔中左半部分所示. 残差编码部分使用步长为2、卷积核为 $3 \times 3 \times 3$ 的反卷积和LeakyReLU激活函数将语义编码器所获得的特征图 ${S_i}, i = 1, 2, 3, 4$ 进行上采样得到 ${U_i}, i = 1, 2, 3, 4$ , 随后与对应的上一层特征图 ${S_i}, i = 0, 1, 2, 3$ 做差值得到差分特征图像 ${D_k}, k = 1, 2, 3, 4$ 即 ${D_k} = {S_{k{{ - }}1}} - {U_k}, k = 1, 2, 3, 4$ , 如图1编码金字塔中右半部分所示.

2.2 残差解码器和语义解码器

医学图像配准的目标旨在寻找最优的像素级几何形变参数, 需要将编码金字塔学习到的特征映射至像素空间, 因此本文使用与语义编码器和残差编码器对应的语义解码器和残差解码器去完成这一过程. 语义解码器和残差解码器均是通过步长为2、卷积核为 $3 \times 3 \times 3$ 的反卷积和LeakyReLU激活函数完成上采样操作, 但不同于语义解码器, 残差解码器利用跳跃连接层融合了残差浅层特征和残差深层特征, 加强密集预测. 在语义解码器和残差解码器的最后一层均使用一个步长为1、3个核为 $3 \times 3 \times 3$ 的卷积回归出像素级的几何形变参数, 即DVF. 最后, 将分别得到的局部DVF与全局DVF相加得到最终的DVF, 如图1解码器部分所示.

2.3 损失函数 2.3.1 上下文自相似性度量

本文使用上下文自相似性度量 (self-similarity context, SSC) 衡量重采样后的QSM图像与参考图像T1图像的相似性从而驱动卷积神经网络学习全局共享参数. 自相似性是用于描述一幅图像内的两个图像块之间的距离度量, 对于三维图像 $I$ 中任意像素点 $x, x \in I$ , 本文定义以 $x$ 为中心, 邻域半径为 $p$ 的图像块为 ${x_p}$ , 在三维方向上与图像块 ${x_p}$ 的距离为 $r$ 的图像块被定义为 $x_p^i, i = 1, 2, \cdots , 6$ , 如图3所示.

则在像素点 $x$ 的自相似性特征能够用与 ${x_p}$ 相邻且互不为对角的图像块 $x_p^i, i = 1, 2, \cdots , 6$ 两两之间的高斯核距离表示, 即:

$ {\textit{SSC}}({x_p}) = \left( \begin{gathered} {{d_{\rm gauss}}(I, x_p^1, x_p^2)} \\ {{d_{\rm gauss}}(I, x_p^1, x_p^3)} \\ {{d_{\rm gauss}}(I, x_p^1, x_p^5)} \\ {d_{\rm gauss}}(I, x_p^1, x_p^6) \\ {d_{\rm gauss}}(I, x_p^2, x_p^3) \\ {d_{\rm gauss}}(I, x_p^2, x_p^4) \\ {d_{\rm gauss}}(I, x_p^2, x_p^6) \\ {d_{\rm gauss}}(I, x_p^3, x_p^4) \\ {d_{\rm gauss}}(I, x_p^3, x_p^5) \\ {d_{\rm gauss}}(I, x_p^4, x_p^5) \\ {d_{\rm gauss}}(I, x_p^4, x_p^6) \\ {d_{\rm gauss}}(I, x_p^5, x_p^6) \\ \end{gathered} \right) $

(5)

其中, 对于以图像块 ${x_p}$ 为中心任意两个邻域图像块 ${x}_{p}^{i}, {x}_{p}^{j}, i\ne j, 且 j\ne i/2\times 2+(1-i{\text{%}}2)$ 的高斯核距离可表示为式(6):

$ {d_{\rm gauss}}(x_p^i, x_p^j) = \exp \left( { - \frac{{{D_p}(x_p^i, y_p^j)}}{{{\sigma ^2}}}} \right) $

(6)

其中, ${D}_{p}(\cdot, \cdot)$ 表示两个图像块的像素值的均方误差之和, ${\sigma ^2}$ 为所有成对图像块均方欧式距离的均值, 即:

$ {\sigma }^{2}=\frac{1}{12}{\displaystyle \sum _{j=1}^{6}{\displaystyle \sum _{i=1}^{6}{D}_{p}({x}_{i}, {x}_{j}), j\ne i, 且 j\ne i/2\times2+(1-i{\text{%}}2)}} $

(7)

提取了两幅图像的自相似特征后, 则 ${\textit{SSC}}$ 损失函数可计算为:

$ {l_{\textit{SSC}}}(F, M \circ \varphi ) = \frac{1}{N}\sum {|{\textit{SSC}}(F) - {\textit{SSC}}(M \circ \varphi )|} $

(8)

其中, $F$ 为参考图像, $M \circ \varphi $ 为浮动图像经过变形场 $\varphi $ 重采样后所得到的图像, $N$ 为图像体素总个数.

2.3.2 正则化约束

图像配准不仅要使得配准结果与参考图像尽可能相似, 同时还需要使得几何变换尽可能平滑. 不平滑的几何变换不满足微分同胚性质, 表明配准后的组织结构被破坏. 为了解决这一问题, 本文采用正则项 $R(\varphi )$ 来约束变形场平滑, 其定义如下:

$ R(\varphi ) = \sum\limits_{p \in \Omega } {||\nabla \varphi (p)|{|^2}} $

(9)

其中, $|| \cdot ||$ 为矩阵的Frobenius范数, $\nabla \varphi (p)$ 为在体素点 $p$ 处的DVF的空间梯度, 即:

$ \begin{split} \nabla \varphi (p) =& \left(\frac{{\partial \varphi (p)}}{{\partial x}}, \frac{{\partial \varphi (p)}}{{\partial y}}, \frac{{\partial \varphi (p)}}{{\partial {\textit{z}}}}\right) \\ =& \left( {\begin{array}{*{20}{c}} {\dfrac{{\partial {\varphi _x}(p)}}{{\partial x}}}&{\dfrac{{\partial {\varphi _x}(p)}}{{\partial y}}}&{\dfrac{{\partial {\varphi _x}(p)}}{{\partial {\textit{z}}}}} \\ {\dfrac{{\partial {\varphi _y}(p)}}{{\partial x}}}&{\dfrac{{\partial {\varphi _y}(p)}}{{\partial y}}}&{\dfrac{{\partial {\varphi _y}(p)}}{{\partial {\textit{z}}}}} \\ {\dfrac{{\partial {\varphi _{\textit{z}}}(p)}}{{\partial x}}}&{\dfrac{{\partial {\varphi _{\textit{z}}}(p)}}{{\partial y}}}&{\dfrac{{\partial {\varphi _{\textit{z}}}(p)}}{{\partial {\textit{z}}}}} \end{array}} \right) \end{split} $

(10)

因此, 网络模型所使用的总损失 ${l_{\rm total}}$ 如下所示:

$ {l_{\rm total}} = {l_{\textit{SSC}}}(F, M \circ \varphi ) + \lambda R(\varphi ) $

(11)

其中, $\lambda $ 为正则系数, 用于平衡相似性度量和变形场正则化.

3 实验设置及评价标准 3.1 数据描述及其预处理

本文研究所采用的模板图像为MNI152的T1加权图像, 分辨率为1 mm×1 mm×1 mm. QSM图像数据采集自贵州省人民医院, 共计104名受试者. 所有采集数据均在3T MRI (GE 750w)扫描, 使用16通道磁头线圈. 其采集参数如下: 重复采集时间/回波时间/翻转角度 $= 2.7{ \; \text{ms}}/31.7 \; {\rm ms}/1{2^ \circ }$ , 图像大小和分辨率分别为256 mm×256 mm×22 mm, 1 mm×1 mm×1 mm, 扫描时间约为3分钟. 此外, 所采集的QSM相位图还需经过相位解缠绕、背景相位去除和反演重建得到重建后的图像才能用于配准. 本文首先对相位图像进行拉普拉斯变换再进行傅里叶变换得到解缠绕相位的频域空间表示^[20], 随后利用可变卷积核半径的复杂谐波伪影去除算法进行背景相位去除^[21], 最后使用最小平方QR分解法求得磁化率^[22], 得到重建的QSM图像.

3.2 训练阶段

本文将采集自贵州省人民医院的90幅QSM图像作为训练集, 剩余的14幅QSM图像作为测试集. 训练集用于网络模型预测, 测试集用于评估模型的性能和泛化能力. 本文所提出的方法均在Keras中实现, 使用Adam优化器, 在32 GB的NVIDIA Tesla V100 GPU上进行加速训练, 共迭代5 000次, 训练约18小时左右, 初始学习率设置为0.000 1, BatchSize设置为1, 训练的总轮数Epoch设置为50, 每轮迭代次数Iteration设置为100. 训练RF-RegNet模型的步骤如算法1.

算法1. RF-RegNet网络模型训练算法

初始化:

参考图像 $\scriptstyle F$

训练数据集 $\scriptstyle S$

学习率 $\scriptstyle lr: = {10^{ - 4}}$

批次大小 $\scriptstyle Batchsize: = 1$

迭代次数 $\scriptstyle Iteration: = 100$

训练轮数 $\scriptstyle epoch: = 50$

$\scriptstyle \lambda : = 1.0$

损失函数:

$\scriptstyle {l_{\rm total}} = {l_{SSC}}(F, M \circ \varphi ) + \lambda R(\varphi )$

训练开始:

1.　 For epoch=1 to 500 do

2.　　　 随机打乱训练数据集

3.　　　 For iteration=1 to 100 do

　　　　　随机选择数据集中的一幅图像作为浮动图像M;

4. 　　　　利用网络模型预测位移矢量场DVF;

5. 　　　　依据DVF对浮动图像 $\scriptstyle M$ 进行几何变换;

6. 　　　　计算损失值并更新网络参数(每一个 $\scriptstyle {\Theta _i}$ 是配准网络模型中的可学习参数):

　　　　　　　　　　　 $\scriptstyle {\Theta _i}: = {\Theta _i} - lr\frac{{\partial loss}}{{\partial {\Theta _i}}}$

7. 　　　End for each

8. 　End for epoch

3.3 评价标准

为了有效评估QSM图像和T1加权图像配准的性能, 本文采用目标配准误差 (target registration error, TRE)^[23]、Dice分数^[24]、Hausdorff距离 (Hausdorff distance, HD) 和平均对称表面距离 (average symmetric surface distance, ASD)^[25] 来评估图像之间的表面相似性. 其中, TRE表示同一个标注点在参考图像和配准后图像的差异, 其计算方法如式 (12) 所示:

$ TRE = \sum\nolimits_{i = 1}^n {\sqrt {{{({x_i} - {x_i}')}^2} + {{({y_i} - {y_i}')}^2} + {{({{\textit{z}}_i} - {{\textit{z}}_i}')}^2}} } $

(12)

其中, $(x, y, {\textit{z}})$ 代表参考图像标记点的坐标, $(x', y', {\textit{z}}')$ 代表配准结果对应于参考图像标记点的坐标, $n$ 代表标注点的数目, 本文共标注了6个标注点.

HD用于反映两个区域的最大差异, 其定义如下:

$ HD(M_W^ * , {F^ * }) = \max \left( {\mathop {\max }\limits_{m \in M_W^ * } \mathop {\min }\limits_{f \in {F^ * }} (m - f), \mathop {\max }\limits_{f \in {F^ * }} \mathop {\min }\limits_{m \in M_W^ * } (m - f)} \right) $

(13)

其中, $M_W^{\text{*}}$ 和 ${F^{\text{*}}}$ 分别表示配准结果和参考图像中对应的解剖结构区域, HD值越低意味着两个区域越相似. 类似于HD, Dice分数用于表示两个结构区域之间的重叠程度, 其定义如下:

$ Dice = 2\frac{{|M_W^* \cap {F^ * }|}}{{|M_W^* \cup {F^*}|}} $

(14)

Dice分数的取值范围为0–1, 越高的Dice分数值意味着更好配准性能.

最后, 本文也利用ASD来评估图像之间的表面相似性, 其计算方法如式(15)所示:

$ {\textit{ASD}} = \frac{1}{{M_W^* + {F^*}}}\left( {\sum\limits_{m \in M_W^*} {d(m, {F^*})} + \sum\limits_{f \in {F^*}} {d(f, M_W^*)} } \right) $

(15)

其中, $d(x, Y)$ 为体素点 $x$ 到图像区域Y的最小欧式距离:

$ d(x, Y) = \mathop {\min }\limits_{y \in Y} x - y $

(16)

由于QSM是功能图像, 难以分割出图像局部解剖结构, 因此本文仅在全局脑部结构上进行定量评估配准的性能.

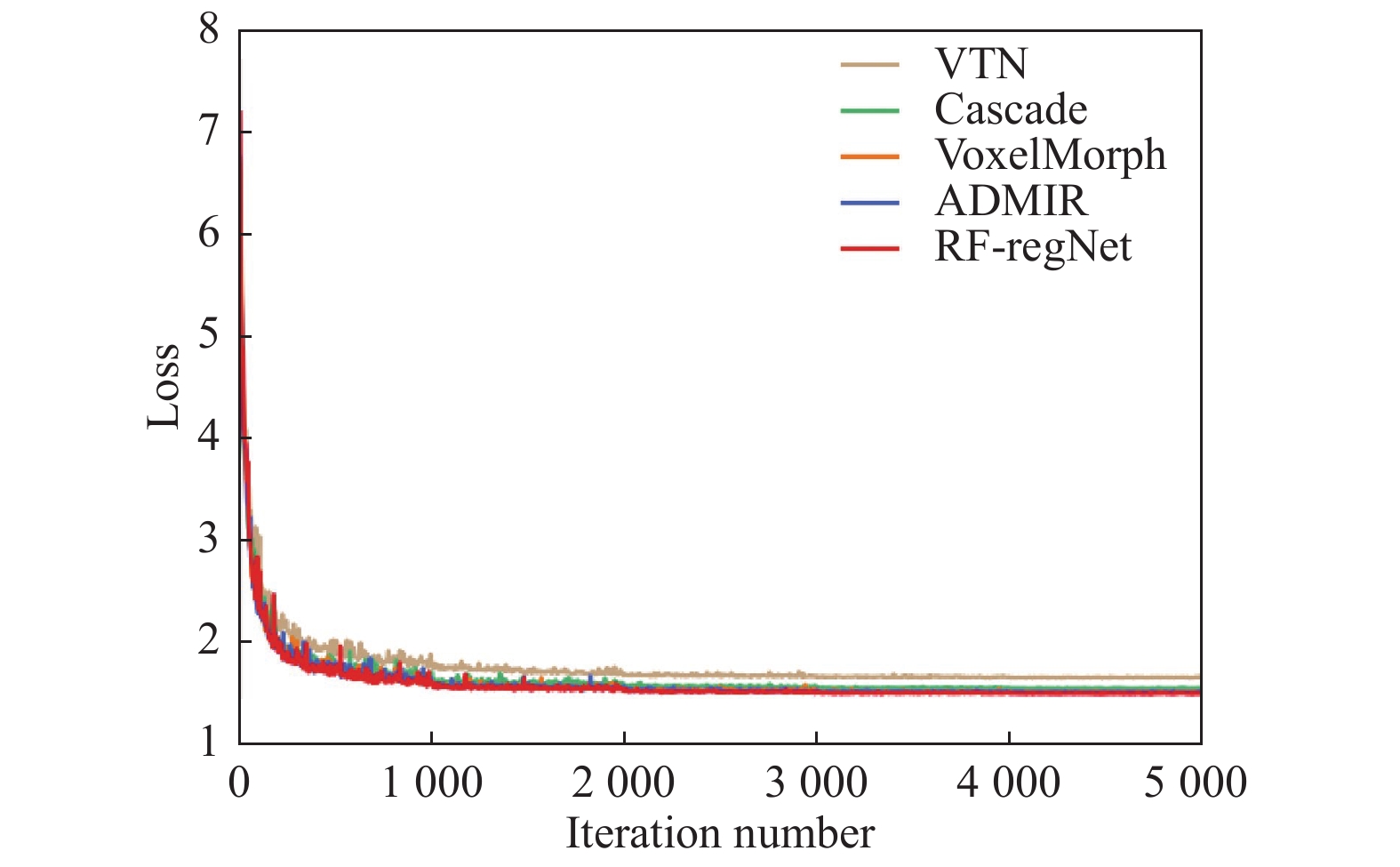
4 实验结果与定量分析

为了评估本文模型的性能, 本文与VoxelMorph、ADMIR、VTN、Cascaded^[26] 4种先进的深度学习配准算法进行了比较. 在对比实验中, 由于对比算法均是针对单模态图像配准的, 因此, 本文采用对比算法中的网络结构, 而损失函数和插值方式与本文提出的算法相同. 不同网络模型的训练过程迭代曲线如图4所示.

从图4可以看出, 相比与其他4种方法, RF-RegNet损失下降速度最快且最低. Cascade、VoxelMorph、ADMIR的损失收敛曲线有大量重叠部分, VTN的损失收敛速度最慢且难以收敛至最优值.

4.1 可视化结果

图5为5种配准算法的可视化结果, 其中第1、2列分别为参考图像和浮动图像, 后续5列分别为5种方法的配准结果并使用绿色椭圆框标记出本文方法明显改善的部分解剖区域. 从图中可以直观地看出, 5种方法在全局脑部结构上均取得了较好的配准效果, 但各个方法之间也存在明显差异. VTN、Cascaded两种方法的配准结果更为平滑, 丢失了许多的高频细节信息. VoxelMorph、ADMIR两种方法相比于VTN和Cascaded, 配准效果有一定的提升, 但依然丢失较多的细节信息. 本文所提出的方法取得了最好的视觉效果.

4.2 定量分析

为了进一步验证本文所提出的模型RF-RegNet的性能, 本文使用TRE、Dice分数、HD和ASD四种评价指标在测试集上对全局的配准结果进行了定量分析. 定量结果如表1所示.

从表1中可以直观地观察到, 本文的方法取得了最佳的平均TRE、Dice分数、HD, 其中, TRE相较于其他4种方法分别下降了35.5%、20%、5.4%、6.4%; Dice分数较其他方法分别提高了1.7%、1.1%、0.5%、0.4%; HD较其他几种方法分别降低了2.9%、3%、1.9%、1.6%; ASD较VTN、Cascaded、Voxel-Morph降低了6.2%、4.7%、1.2%, 较ADMIR方法升高了1.9%. 越高的Dice分数和越低的TRE、HD、ASD意味着更好的配准效果. 因此, 本文所提出的模型显示了最好的配准性能. 从配准所需的时间上看, VoxelMorph的网络结构最为简单, 仅包含一个编码器和一个解码器, 因此取得了最快的运行时间. VTN、ADMIR和Cascaded的设计思想均是通过堆叠多个网络模型来实现由粗到细配准, 模型参数量大, 因此需要耗费更多的时间, 本文所提出的方法所需配准时间略高于VoxelMorph, 低于其他方法, 满足临床实时的配准需求.

图6展示了5种方法分别在Dice分数、ASD、HD、TRE四个评价指标上的箱线图, 可以直观地看出, 本文提出的方法相比于其他方法的性能更为稳定, 进一步证明了RF-RegNet的优越性.

5 结论

本文针对QSM纹理结构特点, 借鉴拉普拉斯金字塔的思想, 设计了残差编码器和语义编码器, 用于提取和学习配准图像对之间的局部纹理和边缘信息的匹配变形参数. 最后, 通过重采样层重建以得到最后的配准结果. 在网络优化的过程中, 本文采用SSC的特征相似性作为损失函数驱动网络模型学习. 实验结果表明, 本文提出的方法显著提升了QSM图像和T1加权图像的配准精度. 但仍存在些许不足, 主要体现在: 在配准之前需要使用外部工具包进行预对齐, 降低了配准效率. 其次, 本文使用SSC特征相似性作为损失函数, 虽然能够较好衡量T1加权图像和QSM图像的相似性, 但是计算复杂, 致使网络训练速度缓慢.