输送线广泛应用于现代物流与生产自动化等场合. 目前, 国内输送线系统的设计开发, 仍大量采用AutoCAD等平面装配图设计、现场编程调试的基本模式, 普遍存在以下几个痛点: (1)方案设计交流缺乏有效工具, 平面装配图不直观且工作量大, 三维模型设计仿真周期长成本高; (2) PLC控制现场安装与编程调试不便; (3)大规模输送线的最优路径调度难度大、调试验证不便等.
仿真软件是解决上述问题的有效途径. 虽然国外的物流仿真软件功能十分丰富, 仿真功能强大, 但是这些软件往往价格较贵且更加注重各不同物流应用的广泛适应性, 而没有只面向输送线系统, 将布局设计、控制编程调试与仿真结合在一起的全流程仿真软件. 国内的物流设计仿真技术与国外相比还是有较大的差距, 只有一些专用设计仿真系统, 如浙江大学的张勇、范春阳等, 针对灌装输送线设计的专用系统, 提出一套快速设计方案, 完成对灌装输送机的布局设计、结构仿真与运动仿真功能, 提高灌装输送线的设计效率[1, 2]; 南京航空航天大学的薛志强、刘楠等提出一种可配置输送线系统并给出快速设计与监控方案[3, 4], 将输送线设计系统与监控系统结合在一起.
本文根据以上行业痛点, 提出一套模块化输送线设计仿真系统解决方案. 针对痛点(1)采用基于Unity3D的模块化输送线设计系统, 实现了方案设计快速沟通以及三维模型的可重用性; 针对痛点(2)采用基于模块化分布式控制器架构与软PLC技术的输送线仿真系统, 实现PLC控制编程的仿真验证, 大大提高系统的现场调试效率; 针对痛点(3)采用基于遗传算法的最优路径, 实现输送线最优路径调度与快速仿真校验.
1 设计仿真系统方案本文设计开发了模块化输送线设计仿真系统, 主要由设计模块、控制模块、调度模块与仿真模块组成. 基于Winform与Unity3D研发输送线系统设计模块, 实现输送机的模块化与输送线的设计方案的快速构建, 有效解决痛点(1); 模块化分布式控制器架构及基于Winform与软PLC技术的输送线系统研发控制模块, 可简化安装接线, 实现PLC离线编程与调试, 有效解决痛点(2); 采用基于遗传算法的输送线调度模块, 实现大规模输送线系统输送路径实时优化与调度, 有效解决痛点(3); 基于Unity3D研发输送线系统仿真模块, 以验证系统设计模块、控制模块与调度模块的可行性与有效性.
图1为输送线设计仿真系统的分层系统架构, 由系统设计管理层、仿真运行层、专用工具层与虚拟映射资源层组成, 实现对上述4大模块的层次化设计开发, 以降低系统的耦合性、提高系统的鲁棒性.

|
图 1 模块化输送线设计仿真系统分层系统架构 |
2 设计模块
建立模块化输送机及其电控装备是模块化输送线设计仿真系统的基础. 本文基于Unity3D的预制体特点, 实现了三维模型的可重用性; 基于Unity3D的三维展示, 实现了设计方案的三维可视化与有效交流.
为实现输送机模块化, 本文将输送机属性抽象为基本属性、布局属性、控制属性与仿真属性, 其中基本属性是设备的基本描述属性; 布局属性主要提供该输送机的几何与位置属性; 控制属性是面向输送机控制的传感与驱动属性; 仿真属性是面向输送线仿真的运动与状态属性. 模块化输送机属性组成如图2所示.
模块化输送机通常包括机械框架、滚筒与传感器等, 基于Unity3D的部分常见的输送机模型如表1所示.

|
图 2 输送机模块化属性组成 |
| 表 1 部分常见的输送机模型 |
系统的设计模块基于上述模块化的输送机模型, 通过Winform开发相应的人机交互, 设计人员可以快速拼装构建出客户所需的输送线系统设计方案的三维模型.
3 控制模块输送线结构模型布局构建完成后, 系统的控制采用模块化分布式架构并提供PLC编程与仿真调试等功能, 以解决PLC现场安装调试困难的痛点. 输送线系统控制模块基于软PLC技术与虚拟控制器设计开发, 由管理模块、编辑模块、编译模块与下载模块组成.
配置模块: 完成虚拟控制器输入输出接口与输送机模型的传感与控制信号的相应配置.
编辑模块: 为保证PLC程序的通用性, 系统提供了基于梯形图的PLC程序编辑方法, 界面如图3所示.

|
图 3 PLC梯形图编辑器 |
编译模块: 将梯形图通过AOV图、逻辑二叉树转成语句表[5-7], 语句表常见的操作符如表2所示.
| 表 2 语句表常见的操作符 |
下载模块: 将编译完成的PLC程序下载到对应的虚拟控制器.
4 调度模块对于规模较大的输送线系统, 物料输送路径的调度涉及最短输送路径与输送线局部阻塞时的最优路径规划, 具有实时性与动态性要求, 往往较复杂.
常见的调度算法有Dijkstra算法、Floyd算法、蚁群算法与遗传算法等[8-11], 其中Dijkstra算法的时间复杂度为O(n2), Floyd算法的时间复杂度为O(n3), 蚁群算法收敛速度相对较慢, 难以满足本系统的实时性要求. 本文采用基于优先级编码的遗传算法, 具有收敛速度快、实时性高的显著优点.
以图4所示的某输送线系统抽象的有向图为例, 讨论从入口1到出口10的最优路径规划方法, 其中圆圈代表输送机, 边代表输送机之间的连接, 边上数字代表输送机之间的当量距离.

|
图 4 某输送线系统抽象的有向图 |
4.1 基于优先级的编码与解码
编码: 以各个节点的编号

|
图 5 表示各节点优先级的染色体 |
解码: 解码过程如图6所示, 则染色体经解码的路径是
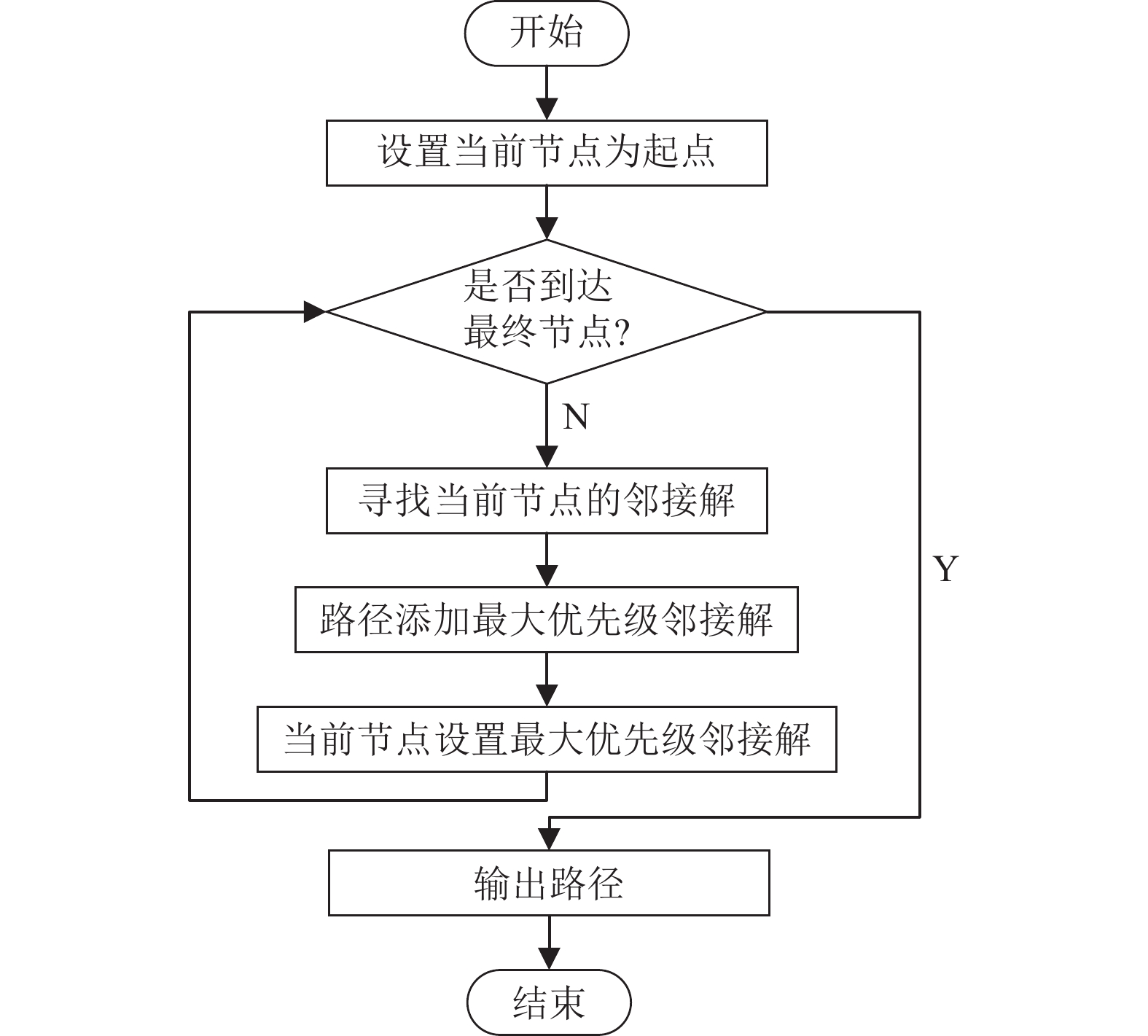
|
图 6 解码过程 |
4.2 适应度函数
该遗传算法的适应度函数如式(1)所示:
| $ eval({P_k}) = \frac{1}{{\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^m {{c_{ij}}{x_{ij}}} } }} $ | (1) |
其中,
| $ {x}_{i}{}_{j}=\left\{ {\begin{array}{l}0\text{, }节点{i}和节点{j}不直接连接\\ 1\text{, }节点i和节点j直接连接\end{array} } \right.$ | (2) |
因此图5染色体的适应度为:
| $ eval({P_k}) = \frac{1}{{\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^m {{c_{ij}}{x_{ij}}} } }}{\text{ = }}\frac{1}{{{{{c}}_{13}} + {c_{36}} + {c_{67}} + {c_{78}} + {c_{8, 10}}}} = \frac{1}{{106}} $ |
基于优先级编码的遗传算法流程如图7所示, 其中交叉操作是随机选择两个染色体, 采取部分一致交叉法; 变异操作是从父代随机选择一个染色体的, 采用两个基因位置交换的变异的方法; 选择操作采用轮盘赌选择法, 即适应度越大的染色体被选择的概率就越大.
节点1到节点10最优路径的适应度过程图如图8所示, 其中参数设置如表3所示, 最终得出的染色体如图9所示.

|
图 7 基于优先级的遗传算法处理过程 |
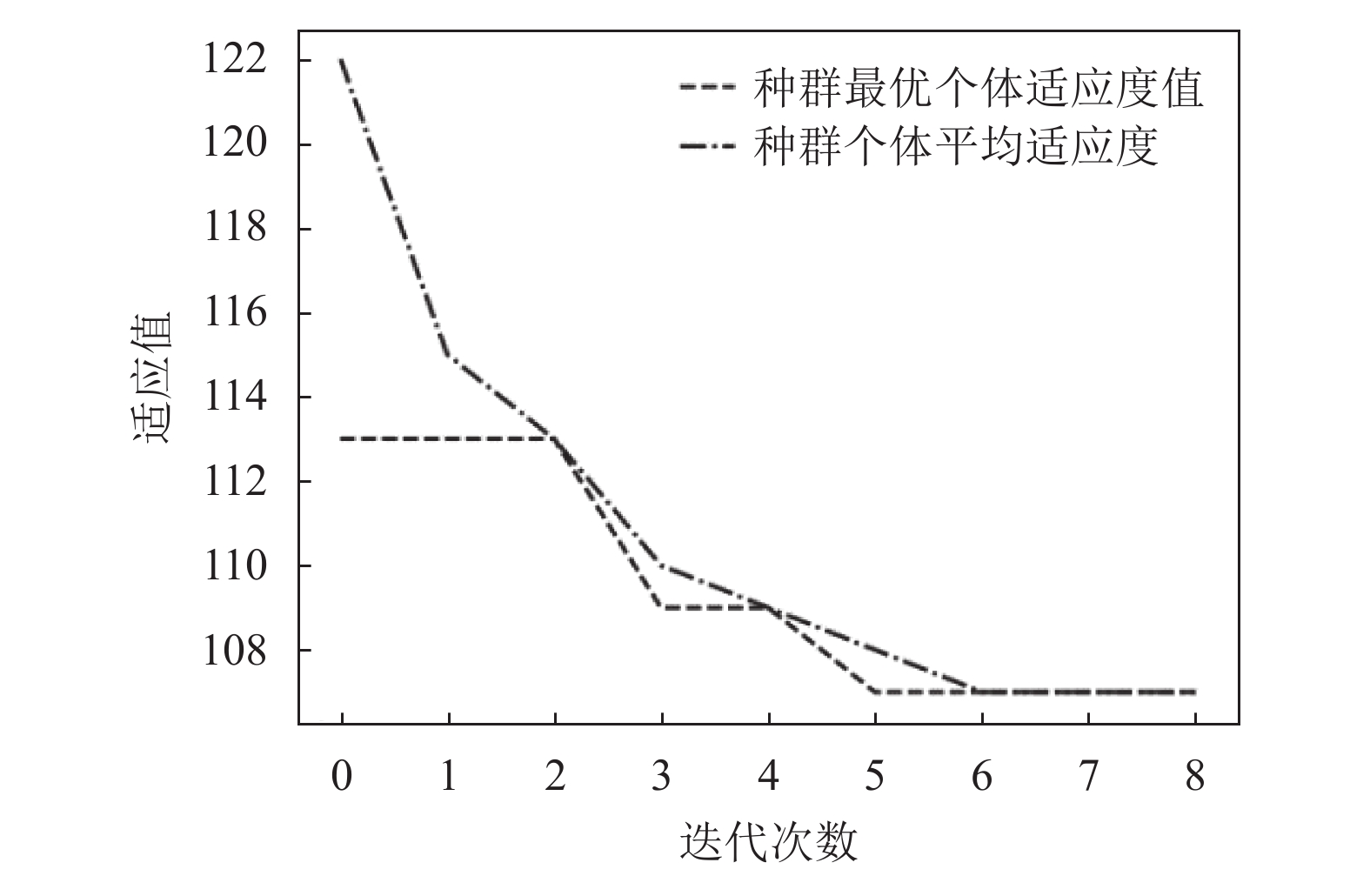
|
图 8 目标函数值(适应度) |
| 表 3 遗传算法参数设置表 |

|
图 9 最优染色体 |
最终通过解码得出节点1到节点10的最优路径为
输送线结构模型布局构建完成、控制器程序下载成功以及调度算法运算出最优路径之后, 系统的仿真模块提供了仿真验证功能, 验证输送线系统方案的可行性和PLC程序的正确性.
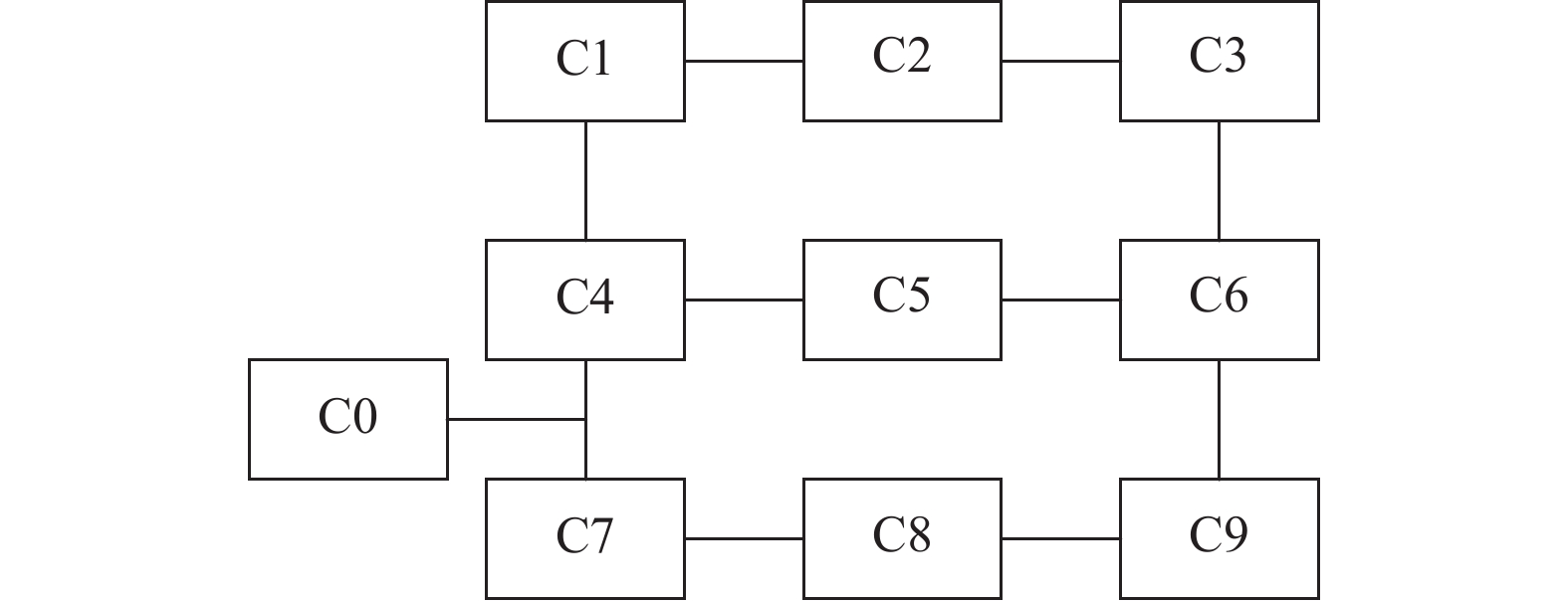
本文实验验证的输送线系统如图10所示, 由输送机、物料、控制器组成, 其中S系列为S630型号的输送机、T系列为T630型号输送机、SS系列为S1080型号输送机、C系列为控制器.

|
图 10 输送线系统平面图 |
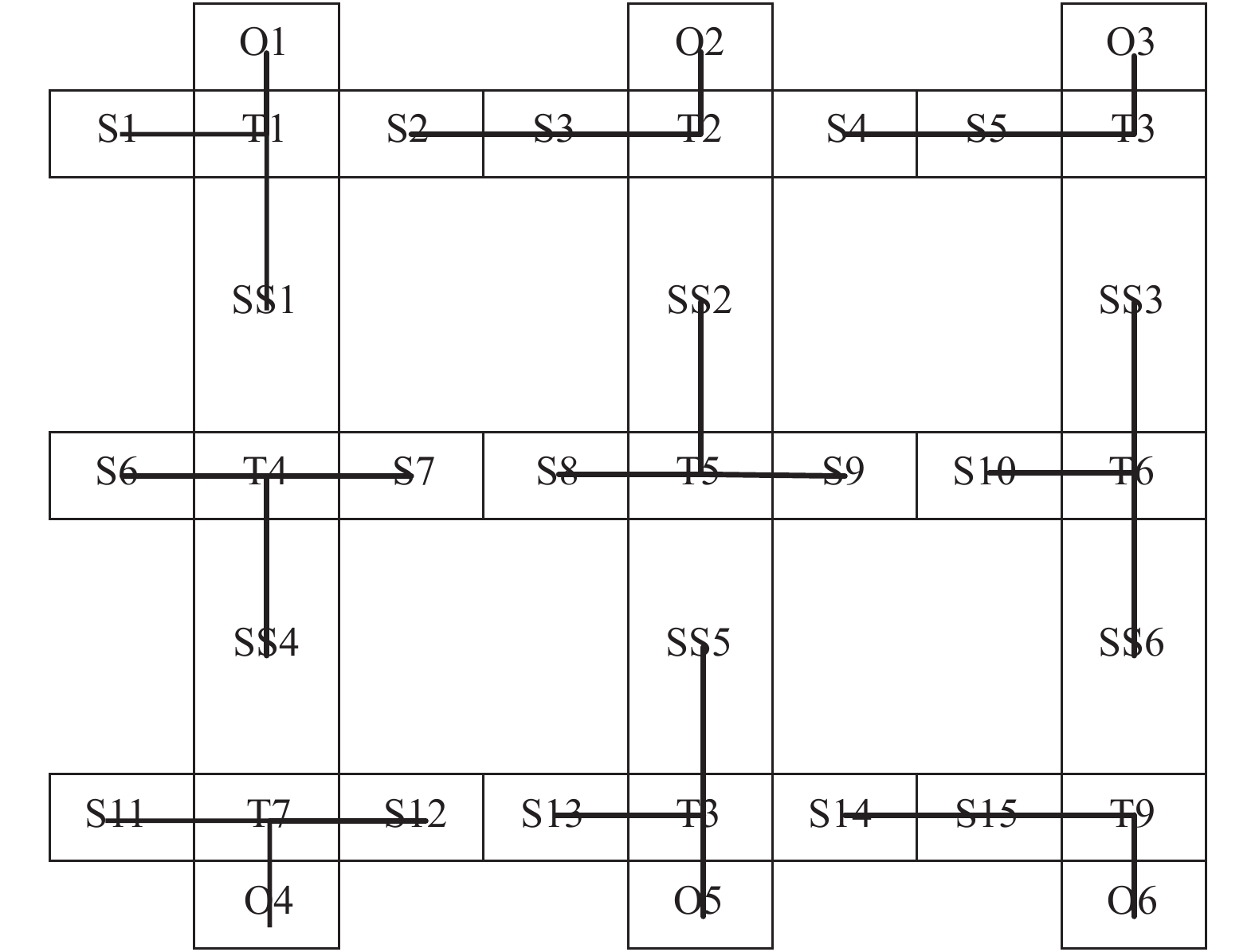
图10中, 为简化控制器之间连接, 采用了模块化分布式控制器, 各控制器及其控制的输送机连接如图11, 图12所示, 如controller1控制器控制了输送机S1、T1、SS1与O1四个输送机.
|
图 11 控制器连接图 |
根据基于优先级编码的遗传算法运算表4的任务得到的物料输送最优路径如表5所示.
基于上述最优路径, 调度计算机将路径指令发送给各对应的控制器, 最终在各PLC的控制下完成相应规划路径的输送线仿真运行过程, 如图13所示, 直观验证了系统路径规划与控制编程的正确性.
|
图 12 输送线控制器对应的输送机连接图 |
| 表 4 物料输送任务表 |
| 表 5 物料输送任务对应最优路径表 |
6 结束语
针对行业3大痛点, 本文设计研发了模块化输送线设计仿真系统, 其中研发了基于Winform与Unity3D的输送线系统设计模块, 实现输送线的三维可视化与模块化, 提高方案交流的有效性与直观性; 系统控制采用模块化分布式架构简化了现场安装接线, 通过Winform与软PLC技术, 实现了PLC控制的离线编程与调试; 基于遗传算法的输送线系统调度, 实现了较为复杂的输送路径实时优化与调度; 采用Unity3D的输送线系统仿真模块, 验证了输送线系统设计方案、控制编程与输送路径规划的可行性与正确性. 本文工作为模块化输送线系统的快速设计、离线编程、运行仿真与现场高效安装调试探索了一条有效途径.

|
图 13 输送线仿真过程 |
| [1] |
张勇. 面向灌装输送线的快速设计方法研究[博士学位论文]. 杭州: 浙江大学, 2017.
|
| [2] |
范春阳. 饮料灌装输送线专用设计系统的研究与开发[硕士学位论文]. 杭州: 浙江大学, 2011.
|
| [3] |
刘楠. 模块化可配置输送线的设计与监控系统[硕士学位论文]. 南京: 南京航空航天大学, 2019.
|
| [4] |
薛志强. 面向模块化可配置输送线的网络化控制系统仿真与设计[硕士学位论文]. 南京: 南京航空航天大学, 2018.
|
| [5] |
雷云飞, 童怀, 伍世元. 基于“逻辑二叉树”的PLC梯形图与指令表互换算法. 数字技术与应用, 2011(4): 9-10. |
| [6] |
葛芬, 吴宁. 基于AOV图及二叉树的梯形图与指令表互换算法. 南京航空航天大学学报, 2006, 38(6): 754-758. DOI:10.3969/j.issn.1005-2615.2006.06.020 |
| [7] |
谢俊达. 软PLC梯形图编程系统的研究与实现[硕士学位论文]. 湘潭: 湘潭大学, 2018.
|
| [8] |
李少波, 宋启松, 李志昂, 等. 遗传算法在机器人路径规划中的研究综述. 科学技术与工程, 2020, 20(2): 423-431. DOI:10.3969/j.issn.1671-1815.2020.02.001 |
| [9] |
吴海峰. 最短路径算法——Dijkstra及Floyd算法. 中国新通信, 2019, 21(2): 32-33. DOI:10.3969/j.issn.1673-4866.2019.02.027 |
| [10] |
徐书扬, 潘华铮, 王海江. 基于蚁群算法的旅游路线优化方案. 软件导刊, 2020, 19(9): 89-92. |
| [11] |
何国锋, 刘宇红. 改进的遗传算法在最短路径中的应用. 电脑知识与技术, 2017, 13(25): 162-164, 169. |
 2022, Vol. 31
2022, Vol. 31







