运动目标跟踪是计算机视觉中的一个重要研究领域, 旨在通过对图像中的运动目标进行检测、提取、识别等操作, 获得目标的各项运动参数并确定其位置, 从而进行下一步的分析与处理. 随着计算平台的不断升级完善以及人工智能技术的飞速发展, 行人跟踪技术在不断更新迭代的同时也变得越来越重要, 并已经广泛出现在智能视频监控、智能交通、智能人机交互、运动员比赛分析等各种场景[1, 2].
从实现方法来看, 目前主流的跟踪算法可粗略分为相关滤波类和深度学习类[3], 前者通过设计滤波模板进行预测或通过区域匹配来寻找跟踪目标的位置, 大多数情况下仅使用较为简单的手工特征. MOSSE[4]是最先出现的滤波跟踪算法, 利用目标的多个样本来进行训练, 从而得到更优秀的滤波器, 在此基础上引入核函数并不断改进优化, 又形成了CSK[5]、KCF算法[6], 在保证跟踪速度的同时, 大大提高了跟踪的准确性. 与此同时, Danelljan等人提出了C-COT算法[7], 利用神经网络提取特征, 并将学习过程推广到连续空间域, 还进一步提出改进版的ECO算法[8], 并同时更好地解决了训练过拟合的问题. 尽管相关滤波类算法在特定场景下有着优异的实时跟踪速度, 但使用的简单特征在遇到遮挡、目标形变、快速运动等复杂场景时, 易出现跟踪漂移和跟踪失败等问题.
深度学习类的算法往往更注重准确性, 多采用基于检测的跟踪(tracking-by-detection)方式. 2016年Nam等人提出的MDNet[9]利用一个轻量级的小型网络来学习跟踪目标的特征, 同时期的DeepSort[10]也是在原Sort[11]的基础上对目标提取深度特征来提高跟踪算法的准确率. Siam FC[12]则是使用了孪生网络来训练一个相似性度量函数, 以匹配候选目标作为跟踪结果. 为进一步提高Siamese类算法的跟踪速度和精度, Li等人结合RPN (region proposal network)网络提出了Siam RPN算法[13], 在跟踪阶段构造局部单目标检测任务, 并抛弃了传统的多尺度测试和在线微调. Danelljan等人提出的ATOM[14]和DiMP[15]则将目标跟踪分为目标分类和目标评价, 分别用于粗定位和精确定位, 后续又提出基于概率回归的PrDiMP[16], 根据目标状态的条件概率密度来确定目标位置, 从而进行跟踪. 这类算法在准确性上有着非常出色的表现, 但往往因为计算量过大且计算过程复杂, 在一定程度上影响了跟踪算法的速度, 导致算法不能实时运行.
针对以上问题, 本文提出一种将目标图像深浅特征融合的实时单目标行人跟踪方法. 利用目标的颜色直方图[17]来提取浅层颜色特征, 并利用YOLOv4检测模型[18]获取当前目标位置从而提取目标的深度特征, 通过计算目标的相似性和不同的距离度量对目标进行匹配更新, 并通过更新策略协调准确性与速度. 经实验验证, 本文算法可有效地在复杂场景中实现对单目标行人的长时间稳定跟踪, 同时还能达到实时跟踪的效果.
1 基于检测的跟踪算法框架 1.1 DeepSortDeepSort算法是一种采用递归卡尔曼滤波和逐帧数据关联匹配的多目标传统单一假设跟踪方法, 算法对运动目标的跟踪场景定义在一个8维状态空间
YOLO系列是实时目标检测中最具代表性的算法, 其将目标检测过程视作一个回归问题, 通过一次前向推理就可得到目标框的位置及其分类结果, 检测过程快速而高效. YOLOv4在输入端训练层面使用了Mosaic数据增强、DropBlock模块和改进后的CmBN等防止过拟合的操作, 使其能够在小目标检测和小批量数据集训练上取得更好的效果. 在YOLOv4的网络模型中, 使用CSPDarknet53作为骨干网络, 通过FPN层的上采样, 对输入检测图像的最小特征图自上而下地传递强语义特征, 同时在其后添加包含PAN结构的特征金字塔, 从最大的特征图自底向上地传递强定位特征, 从而实现对不同检测层的参数整合, 能够更好地获取目标特征并进行同时定位与分类, 提高目标检测的准确性.
本文使用YOLOv4模型作为跟踪算法的检测器, 在跟踪初始化、轨迹更新或跟踪误差较大时进行调用, 来对跟踪器进行调整与修正.

|
图 1 DeepSort基本框架 |
2 融合特征匹配与轨迹更新
目标的跟踪过程包括对跟踪目标的预测、检测、匹配以及轨迹更新, 本文将目标图像的浅层颜色特征与深度特征相融合, 共同作为预测和匹配的评价指标, 并通过提出的轨迹更新策略协调跟踪的速度与准确性.
2.1 目标预测相似性匹配跟踪目标的位置确定是跟踪过程中非常重要的一个环节, 决定了跟踪结果的准确性与可靠性. 一般情况下, 跟踪算法通过当前帧或历史帧的跟踪结果来预测或迭代搜索出下一帧的目标位置, 由于使用了先验信息来跟踪, 因此不会再进行额外的目标匹配来验证预测结果, 这在一定程度上降低了预测目标的可靠性. 而在区分出前景目标和背景之后, 目标图像所拥有的部分浅层表观特征例如颜色、形状、纹理等信息也可以是跟踪过程中重要的匹配工具, 而其中颜色特征具有比其他特征对于目标尺度、姿态的变化比较不敏感的特性. 因此将浅层颜色特征作为跟踪算法预测结果相似性匹配的一个评价指标, 并采用计算目标区域颜色直方图的方式来提取目标的颜色特征.
位置预测多采用滤波的方式, 而对于跟踪问题这样的非线性系统, 可以采用扩展卡尔曼滤波、无损卡尔曼滤波或粒子滤波, 但这三者相对来说计算量偏大, 影响实时效果. 因此本文将跟踪过程近似视为分段每两帧之间的线性过程, 并沿用DeepSort的递归卡尔曼滤波预测. 在每一帧的匹配和更新结束后, 卡尔曼滤波器首先会通过前一帧目标位置的均值与方差进行更新, 预测出当前帧目标可能会在的位置. 预测均值为DeepSort中的8维向量, 且由于卡尔曼滤波对于目标框的预测主要在于目标框运动方向和大小的变化, 而直接计算整个预测目标框区域的颜色直方图易受到相似背景的干扰而降低可靠性, 因此将目标框裁剪并缩放至50×50的大小, 再将其均分为4个部分, 分别计算目标各部分的颜色直方图Hi_pre
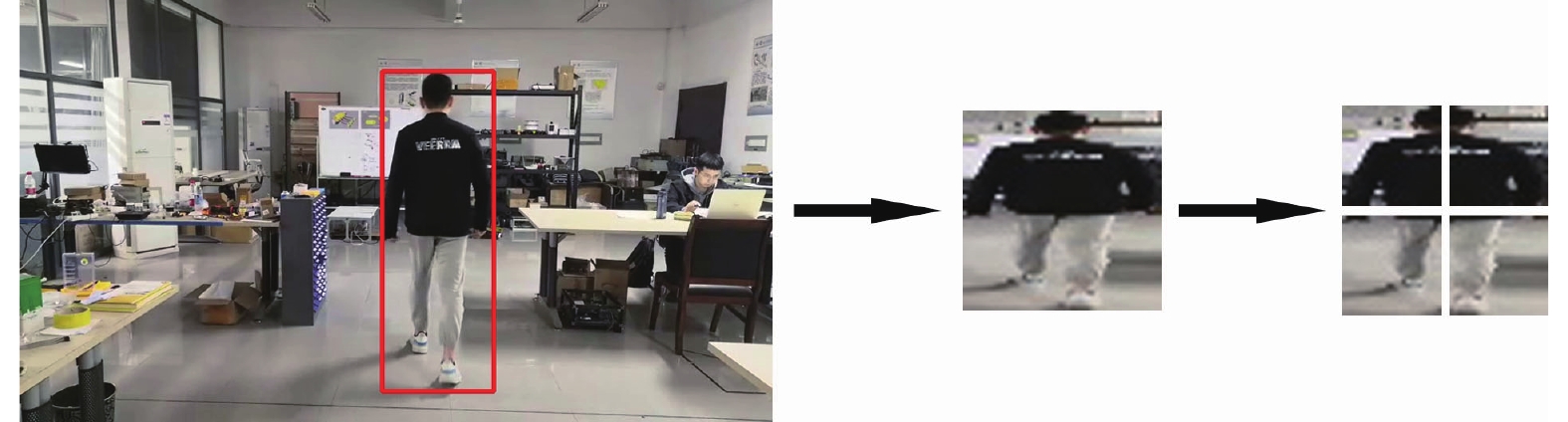
|
图 2 获取预测结果的四分颜色直方图 |
距当前帧最近的一次检测器成功调用的检测结果被储存在数组中, 此数组共储存最近5次的成功检测结果并不断更新. 与预测结果一样, 将每次的成功检测结果裁剪、缩放并分成4个部分, 分别计算相应的颜色直方图Hn_i(n=1, 2, …, 5). 把每一个预测结果的颜色直方图分别与5次检测结果的颜色直方图作对比, 由式(1)可得到预测结果的相似度Similarn, 将其中最小的相似度值作为预测结果的最终相似度, 并由此来评定当前帧跟踪目标位置预测的结果好坏.
| $ {\textit{Similar}}_n = \min \left( {\left( {\sum\limits_{j = 0}^{255} {1 - \frac{{\left| {{H_{i\_pre\_j}} - {H_{n\_i\_j}}} \right|}}{{\max ({H_{i\_pre\_j}}, {H_{n\_i\_j}})}}} } \right)/256} \right) $ | (1) |
| $ {\textit{Similar}} = \min \left( {{\textit{Similar}}_n} \right) $ | (2) |
其中, j表示像素值的大小, Hi_pre_j和Hn_i_j分别表示预测直方图和检测直方图在像素值为j时的值.
2.2 目标检测融合特征匹配如果只利用卡尔曼滤波器的预测作为跟踪结果, 则容易产生累计误差并导致跟踪失败, 因此使用YOLOv4模型作为目标检测器来提高算法的跟踪准确性. 调用检测器时, 获得当前帧的可能目标序列detection_indices, 计算检测结果的匹配代价矩阵, 该代价矩阵共由3个不同的代价部分组成, 且其中包含每一个检测结果的代价值, 并根据其中最小的代价值找出正确的跟踪目标.
第一个代价矩阵cm1首先通过式(3)计算每个检测目标与当前帧预测目标的平方马氏距离, 以获取该检测目标对于运动预测偏移位置的不确定性, 不确定性越大则说明该检测是跟踪目标的可能性越低. 再通过式(4)分别计算每个检测目标与储存的前5次成功检测的深度特征之间的最小余弦距离, 以获取目标外观特征之间的相似程度. 对两种度量分别设置距离阈值, 并利用式(5)将两种距离度量的线性加权融合作为检测目标的一个代价矩阵.
| $ maha\_{d_i} = {\left( {{d_i} - p} \right)^T}S_i^{ - 1}\left( {{d_i} - p} \right) $ | (3) |
| $ \cos \_{d_i} = \min \left\{ {1 - \frac{{{f_i} \cdot {f_{{n}}}}}{{\left\| {{f_i}} \right\|\left\| {{f_n}} \right\|}}} \right\} $ | (4) |
| $ c{m_{1\_i}} = \lambda\cdot maha\_{d_i} + \left( {1 - \lambda } \right)\cdot\cos \_{d_i} $ | (5) |
其中, di为第i个检测框位置及大小, p为目标预测位置及大小, Si为检测框与平均跟踪位置的协方差, fi为第i个检测特征向量, fn为储存的前5次成功检测的特征向量, n=1, 2, …, 5, λ为代价矩阵加权系数.
当跟踪过程某一阶段出现连续预测且预测相似性均不满足阈值时, 认为遇到目标遮挡情况, 一般情况下, 跟踪行人目标的遮挡时间大概在30–50帧左右. 由于遮挡时无法检测到目标行人而多采用预测结果直接输出, 并不对轨迹进行检测更新, 平方马氏距离则会因为协方差的累计变化而降低准确性, 容易产生误跟踪. 为解决这种情况, 再添加由当前帧和前第10次成功检测的深度特征的匹配, 由于只采用一次先验信息, 无法通过平均预测偏移来考虑检测的不确定性, 因此只计算检测结果的最小余弦距离.
| $ c{m_{2\_i}} = \min \left\{ {1 - \frac{{{f_i} \cdot {f_{10}}}}{{\left\| {{f_i}} \right\|\left\| {{f_{10}}} \right\|}}} \right\} $ | (6) |
其中, f10为前第10次成功检测的特征向量.
在跟踪算法中使用目标检测模型有助于提高算法跟踪结果的准确性, 但检测器的深度神经网络提取的抽象深度特征图无法完全准确地描述目标的特征, 且容易丢失目标的一部分浅层信息, 同时目标的空间信息也会随着网络的深度而被逐渐稀释. 为进一步提升匹配的准确性, 并充分利用目标图像的深浅信息, 同样引入颜色直方图来描述检测目标的浅层颜色特征. 计算每一个检测目标框的颜色直方图, 可以得到一个256×3的多维矩阵, 将其中每相邻两个的像素值个数取平均并赋给像素值小的像素, 从而得到128×3的多维矩阵, 以对应ReID模型对目标提取的128维深度特征. 与预测相似性一样, 计算每个检测目标与前5次成功检测的目标之间的最小相似性距离, 不同的是此处输出的是最小的不相似程度.
| $ c{m_{3\_i}} = \min \left\{ {\left( {\sum\limits_{j = 0}^{255} {\frac{{{H_{i\_j}} - {H_{n\_j}}}}{{\max \left( {{H_{i\_j}}, {H_{n\_j}}} \right)}}} } \right)/256} \right\} $ | (7) |
其中, Hi_j为第i个检测目标的第j个像素值个数, Hn_j为储存的第n个成功检测目标的第j个像素值个数.
上述距离度量分别从跟踪目标的预测偏移、深度特征、浅层特征3个方面来判断检测结果的匹配情况, 可以有效地提升匹配的准确性, 因此将三者的线性加权融合作为检测匹配的最终代价矩阵, 并通过阈值比较找出匹配的目标, 若没有代价值满足匹配阈值条件, 则说明当前帧没有与跟踪轨迹匹配的目标.
| $ {C_i} = {\omega _1} \cdot c{m_1} + {\omega _2} \cdot c{m_2} + {\omega _3} \cdot c{m_3} $ | (8) |
其中, Ci为第i个检测结果的最终代价值,
表1为分别使用不同特征进行目标匹配时, 跟踪算法在数据集上的跟踪测试精度. 在检测器识别行人目标并获取目标框后, 分别通过浅层特征、深层特征以及融合特征对跟踪目标进行匹配, 可以看出算法在使用融合特征时比单独使用深层或浅层特征具有更好的跟踪精度, 说明了融合特征能够更好地描述目标浅层颜色特征以及深层语义特征, 从而提升目标匹配和跟踪的精度.
| 表 1 不同特征匹配的跟踪精度 |
2.3 跟踪轨迹更新策略
相关滤波类的跟踪算法已经证明了它的快速性, 但误差的累计也可能造成跟踪漂移和失败, 而如果每一帧都调用检测器再进行目标匹配, 则需要极大的算法运算量, 从而无法实现对目标的实时跟踪. 为达到跟踪速度与准确性的协调统一, 本文算法首先设定在跟踪目标和轨迹初始化后, 成功检测并更新时每隔固定帧数再次调用YOLOv4检测器对跟踪轨迹进行微调, 确保跟踪的准确性. 如表2, 经过实验对比, 选择成功检测后每隔6帧再次调用检测器的方法.
| 表 2 检测器不同间隔帧数调用的跟踪结果 |
计算检测目标距离度量的代价矩阵后, 再通过级联匹配将正确的检测结果与轨迹相关联, 从而实现跟踪轨迹的更新. 每两次调用检测器之间的视频帧采用预测相似性匹配, 计算当前预测结果的相似度Similar, 并设定一个相似度阈值Simi_threshold. 若得到的相似度结果大于该阈值, 则认为当前帧的预测结果是有效的, 并将其作为当前帧的目标位置对跟踪轨迹进行更新; 若相似度小于该阈值, 则认为当前帧的预测结果不够准确, 并重新调用YOLOv4检测器, 检测并匹配当前帧的目标位置, 从而避免因预测准确性过低导致的跟踪错误.
另外, 由于跟踪目标快速运动、遮挡、背景相似等原因, 检测器在某些情况下可能出现检测不到或误检测跟踪目标的情况. 因此在调用YOLOv4检测器时会向跟踪系统反馈输入匹配的检测框个数和匹配完毕后检测框的剩余个数, 二者若相等则说明当前帧没有与跟踪轨迹相匹配的检测结果, 此时算法反馈No_Match_Detection, 并继续利用卡尔曼滤波器预测当前帧的目标位置, 且不再计算相似性匹配, 直接利用预测结果更新轨迹, 并在下一帧重新调用检测器以改善跟踪结果.
本文跟踪算法的整体框架如图3所示.
3 实验结果分析本文所进行的行人检测器网络训练以及跟踪算法验证测试均在PC主机平台上实现, 具体配置为AMD R5 3600 型号的CPU以及NVIDIA GTX 1660显卡. 测试平台为Ubuntu 16.04操作系统, 测试过程使用CUDA 10.1和OpenCV 3.4.0进行前期图像处理和结果输出.
3.1 YOLOv4行人检测器训练本文跟踪算法的目的是实现长时、实时且有效的单目标行人的运动识别与跟踪, 在检测器网络训练和跟踪算法测试过程中均只考虑对行人这个单一类别的实现效果. 因此, 本文选用PASCAL VOC 2007、2012以及INRIA DATA数据集对YOLOv4目标检测器进行训练. 3个数据集一共包含22405张图片, 其中有9 004张包含行人目标的正样本, 行人个数达到19610个, 按照8:2的比例对数据集划分训练集与测试集. 训练后的检测模型对测试集行人目标进行检测的mAP (mean average precision)为0.869, 在GPU上的检测速度可达到38 FPS, 满足算法需求.

|
图 3 本文跟踪算法的整体框架 |
3.2 跟踪算法测试数据集
由于对单目标行人进行运动跟踪需要达到一个长时且稳定的效果, 同时要体现出跟踪算法对于遮挡、目标尺度变化、目标形变、快速运动以及相似性干扰等问题的解决情况, 因此本文选择Fan等人在2019年推出的大规模单目标跟踪标准数据集LaSOT[20]中的Person类作为跟踪算法的主要测试集, 共包含20个不同场景的测试视频序列, 总时长达到35.6分钟, 每个视频序列的平均帧数为3 206帧. 同时, 为保证算法的可靠性, 以及仅对单目标行人进行跟踪的要求, 还选取了OTB100数据集[21]中33个包含行人的视频序列, 平均帧数为452帧. 两个测试数据集均具有相似目标多、目标形变明显、尺度变化和光照变化等特点.
3.3 跟踪结果分析与对比为进一步比较本文算法的单目标行人跟踪效果, 使用近年来表现出色的部分相关滤波类及深度学习类算法与本文算法来进行测试数据集的跟踪结果的对比. 跟踪测试过程中, 所有算法进行跟踪轨迹初始化的目标位置均使用数据集视频序列的第一帧真实目标位置ground truth给定. 跟踪算法获取视频序列中指定行人目标的位置以及相应的目标框, 并将后续每一帧的跟踪目标框与数据集序列的真实目标框ground truth进行比较和误差分析. 采用OPE (one pass evaluation)方法计算跟踪结果的成功率(success rate)和精度(precision)作为算法比较的主要评价指标, 并同时计算跟踪框与目标真实框的平均重叠率EAO (expected average overlap)以及跟踪速度对每种算法的跟踪效果进行评估.
不同跟踪算法在OTB100数据集和LaSOT数据集上的测试结果分别如图4和图5所示.
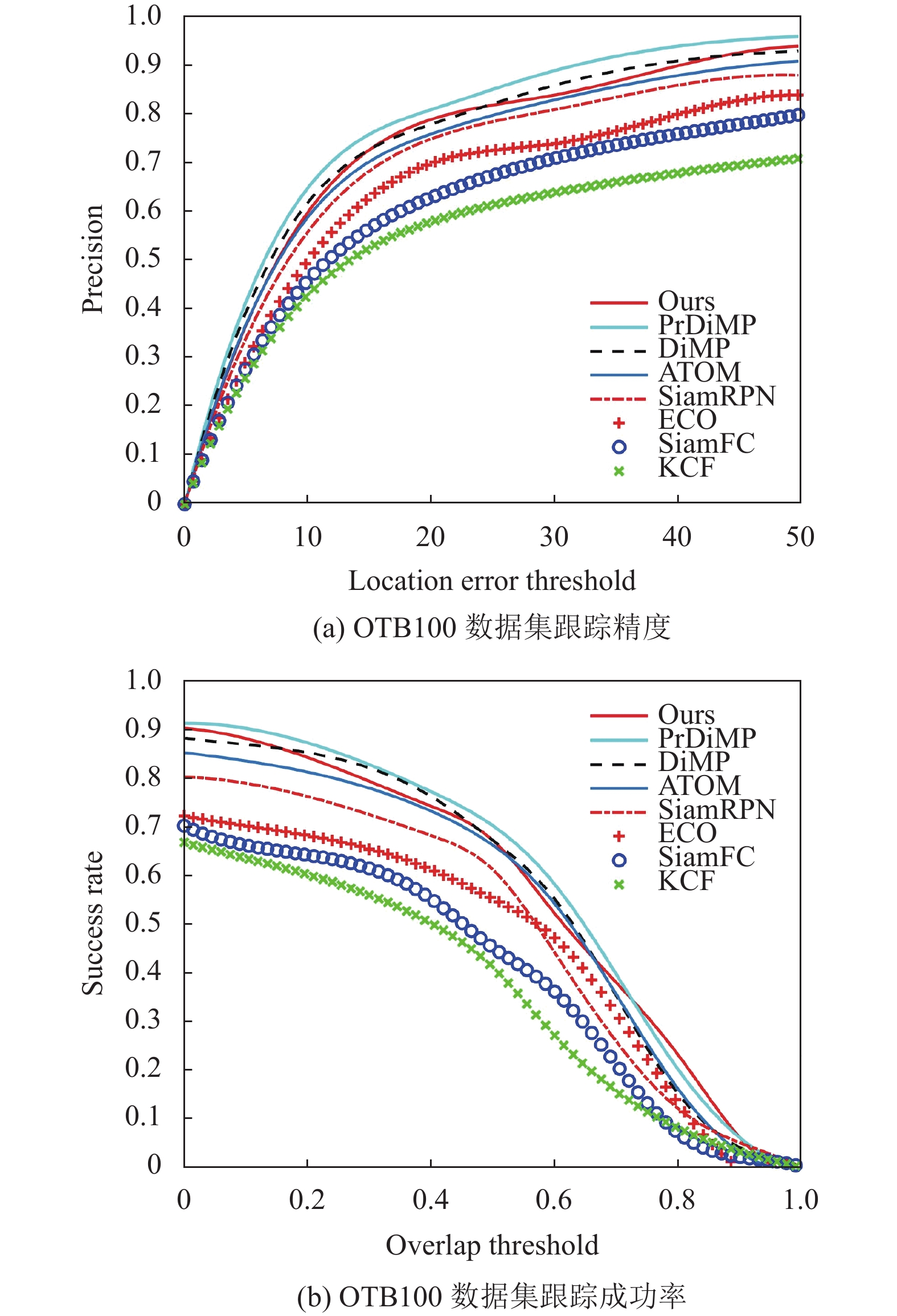
|
图 4 不同算法在OTB100数据集上测试结果 |
由于两个测试数据集的特性不同, 且OTB100数据集的视频分辨率较小, 同时真实框并不一定完全覆盖行人, 因此各类算法在测试结果上均存在一定程度的波动. 从图4和图5中可以看出, 在两个测试数据集上, 对算法分别设置不同的中心位置误差阈值和目标框重叠率阈值时, 本文算法在所有进行比较的跟踪算法中均有比较优异的表现, 在跟踪精度和成功率上远好于相关滤波类的KCF和ECO算法, 同时也要优于深度学习类的SiamFC、SiamRPN和ATOM, 与DiMP表现基本持平, 略逊于改进后的PrDiMP.
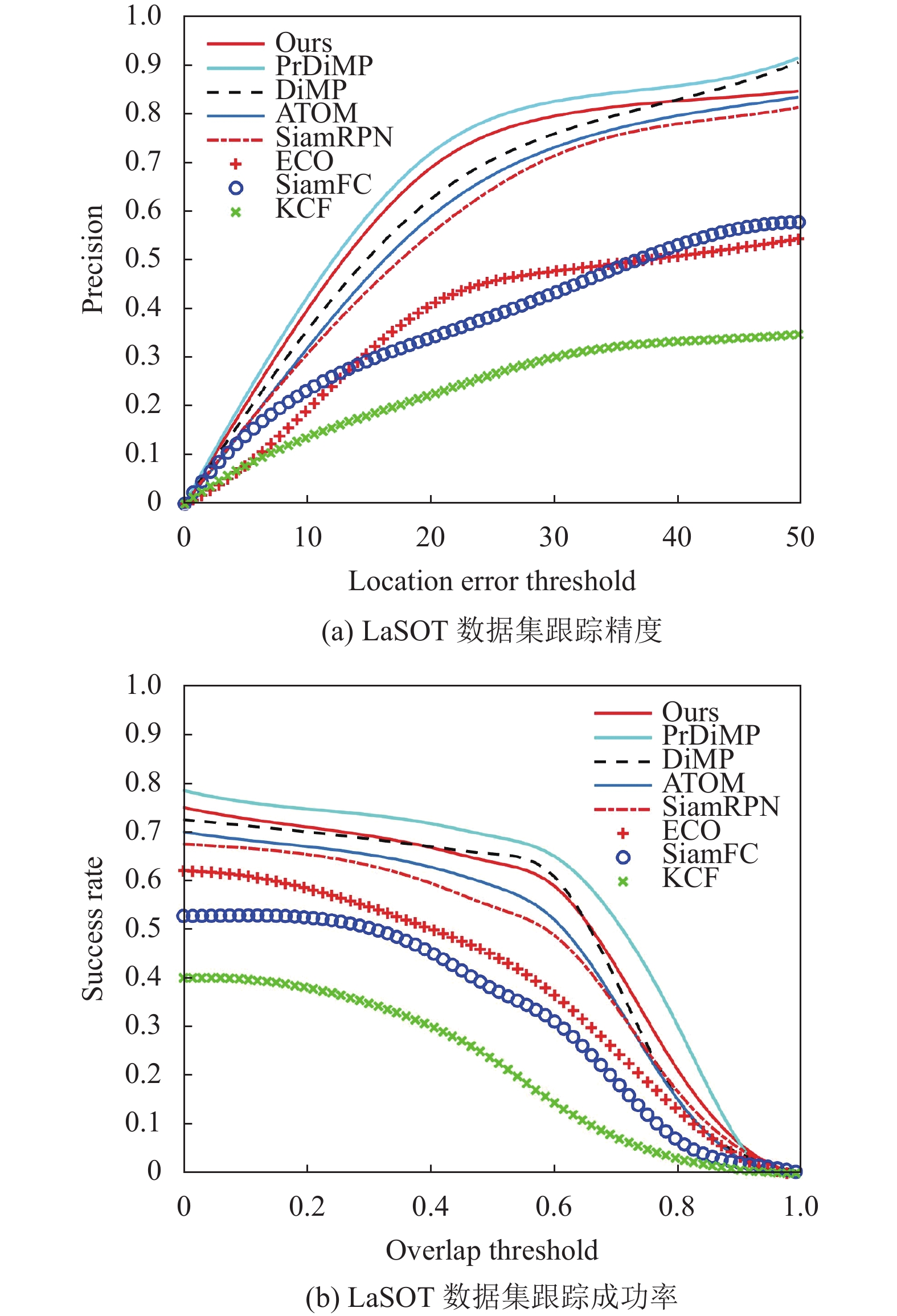
|
图 5 不同算法在LaSOT数据集上测试结果 |
表3给出了本文算法与其他比较算法在目标框中心位置误差阈值和重叠率阈值分别设置为20和0.5时的跟踪准确性和快速性的表现. 可以看出, 在两个数据集上, 本文提出的单目标跟踪算法在整体性能上均能实现比较优秀的实时跟踪效果. 融合目标图像的浅层颜色特征和深度学习特征之后, 跟踪算法的准确性相对于原DeepSort算法有了明显的提高, 在OTB100和LaSOT数据集的测试中分别提升了27.9%和21.1%. 与其他算法的对比中, PrDiMP在平均重叠率EAO上表现出色, 两个数据集测试均为最优, 但无法达到30 FPS的实时跟踪速度; KCF的跟踪速度最快, 但在准确度上却表现最差. 本文算法同时结合了准确性和快速性, 在两个数据集上的EAO分别为0.581和0.453, GPU上的测试跟踪速度分别为33.64 FPS和35.32 FPS, 能够实现实时单目标行人跟踪的效果.
图6为跟踪算法测试过程中截取的部分跟踪结果图, 左上角数字表示图片在该视频序列中的帧数, 每一帧的绿色框均为ground truth真实位置. 其中, 图6(a)和图6(b)来自LaSOT数据集, 图6(c)和图6(d)来自OTB100数据集. Person-1和David3序列的跟踪环境较为简单, 主要是目标姿态发生变化以及几帧的短时遮挡, 除了KCF和ECO会偶尔出现跟踪漂移, 以及ATOM出现误跟踪之外, 各个算法均可以比较好地定位到目标的位置. Girl2序列相对于前两个序列又增加了尺度变化和较长遮挡等属性, 可以看出ATOM在100帧时有误跟踪现象, 但随后成功进行了调整, 而ECO则在后续过程跟踪失败. Person-5是测试集中跟踪环境相对复杂的视频序列, 图像中存在多个行人对象, 同时还包括了目标快速形变、目标遮挡和相似背景干扰等跟踪过程中的难点. 这种情况下, 由于运动目标不易检测准确, 利用神经网络的深度学习类ATOM和DiMP算法以及采用了深度信息的ECO算法反而容易出现跟踪漂移或误跟踪的问题, 而本文算法则能通过位置预测和目标匹配达到比较好的跟踪效果.
| 表 3 不同算法在测试数据集上的跟踪表现 |

|
图 6 部分数据集视频序列跟踪结果 |
总体上来说, 本文算法将目标的浅层颜色特征和深度特征融合之后, 在较为复杂的场景下能够长时间稳定地对目标行人进行跟踪, 并且具有出色的跟踪准确性和实时跟踪速度, 在与目前一些主流单目标跟踪算法的比较中也表现出色, 体现出了特征融合的思想在目标跟踪领域的优势. 实验过程中, 轨迹更新策略可有效解决短时遮挡无法通过特征匹配识别目标的问题, 但在一些具有相似目标、光影变化或长时间遮挡的环境下, 偶尔会出现特征误匹配或无法匹配的情况, 此时若长时间使用预测位置进行跟踪, 则易导致跟踪漂移.
4 结论与展望通过研究相关滤波类与深度学习类跟踪算法分别在精度与速度上的不足, 为协调跟踪准确性与快速性, 同时充分利用目标图像的特征信息, 提出了一种将目标浅层颜色特征与深度特征相融合的实时单目标行人跟踪算法. 利用目标的四分颜色直方图获取浅层颜色特征, 并以此计算预测相似性进行评估, 提高预测结果的可靠性. 使用不同深浅特征计算的距离度量融合加权作为代价矩阵进行目标匹配, 同时采用新的轨迹更新策略来进行目标预测和检测, 对系统跟踪结果进行微调和修正, 从而进一步提升跟踪的准确性与实时性.
在OTB100数据集和LaSOT数据集的算法测试实验证明, 本文跟踪算法可以有效地实现对单目标行人长期且稳定的实时跟踪. 预测结果的相似性匹配和后续策略可以解决一定程度的目标遮挡问题, 进一步提高算法的鲁棒性, 但在多相似目标和长时间遮挡等情况下, 本文算法还存在一定的不足. 后续在多特征融合以及策略协同等方面还可以进一步学习与研究, 对长时间遮挡等跟踪问题实现优化.
增强出版
| [1] |
孟琭, 杨旭. 目标跟踪算法综述. 自动化学报, 2019, 45(7): 1244-1260. |
| [2] |
管皓, 薛向阳, 安志勇. 深度学习在视频目标跟踪中的应用进展与展望. 自动化学报, 2016, 42(6): 834-847. |
| [3] |
李玺, 查宇飞, 张天柱, 等. 深度学习的目标跟踪算法综述. 中国图象图形学报, 2019, 24(12): 2057-2080. DOI:10.11834/jig.190372 |
| [4] |
Bolme DS, Beveridge JR, Draper BA, et al. Visual object tracking using adaptive correlation filters. 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 2544–2550.
|
| [5] |
Henriques JF, Caseiro R, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with kernels. 12th European Conference on Computer Vision. Florence: Springer, 2012. 702–715.
|
| [6] |
Henriques JF, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 |
| [7] |
Danelljan M, Robinson A, Khan FS, et al. Beyond correlation filters: Learning continuous convolution operators for visual tracking. 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 472–488.
|
| [8] |
Danelljan M, Bhat G, Khan FS, et al. ECO: Efficient convolution operators for tracking. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017. 6931–6939.
|
| [9] |
Nam H, Han B. Learning multi-domain convolutional neural networks for visual tracking. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas: IEEE, 2016. 4293–4302.
|
| [10] |
Wojke N, Bewley A, Paulus D. Simple online and realtime tracking with a deep association metric. 2017 IEEE International Conference on Image Processing (ICIP). Beijing: IEEE, 2016. 3645–3649.
|
| [11] |
Bewley A, Ge ZY, Ott L, et al. Simple online and realtime tracking. 2016 IEEE International Conference on Image Processing (ICIP). Phoenix: IEEE, 2016. 3464–3468.
|
| [12] |
Bertinetto L, Valmadre J, Henriques JF, et al. Fully-convo-lutional siamese networks for object tracking. Computer Vision—ECCV 2016 Workshops. Amsterdam: Springer, 2016. 850−865.
|
| [13] |
Li B, Yan JJ, Wei W, et al. High performance visual tracking with siamese region proposal network. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 8971–8980.
|
| [14] |
Danelljan M, Bhat G, Khan FS, et al. ATOM: Accurate tracking by overlap maximization. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2019. 4660–4669.
|
| [15] |
Bhat G, Danelljan M, van Gool L, et al. Learning discriminative model prediction for tracking. 2019 IEEE/CVF International Conference on Computer Vision (ICCV). Seoul: IEEE, 2019. 6181–6190.
|
| [16] |
Danelljan M, van Gool L, Timofte R. Probabilistic regression for visual tracking. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle: IEEE, 2020. 7183–7192.
|
| [17] |
Zivkovic Z, Kröse B. An EM-like algorithm for color-histogram-based object tracking. Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington: IEEE Computer Society, 2004. 798–803.
|
| [18] |
Bochkovskiv A, Wang CY, Liao HYM. YOLOv4: Optimal speed and accuracy of object detection. arXiv: 2004.10934, 2020.
|
| [19] |
Ren SQ, He KM, Girshick R, et al. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137-1149. DOI:10.1109/TPAMI.2016.2577031 |
| [20] |
Fan H, Lin LT, Yang F, et al. LaSOT: A high-quality benchmark for large-scale single object tracking. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2019. 5374–5383.
|
| [21] |
Wu Y, Lim J, Yang MH. Object tracking benchmark. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848. DOI:10.1109/TPAMI.2014.2388226 |
 2022, Vol. 31
2022, Vol. 31


