2. 北京中船信息科技有限公司, 北京 100044
2. China Ship Building IT Co. Ltd., Beijing 100044, China
滚动轴承是旋转机械中易发故障的零件. 在旋转机械中由轴承损坏引起的故障约占30%. 因此, 滚动轴承故障诊断对旋转机械设备的状态监测与维护有着重要意义[1] .
传统的机器学习故障诊断方法流程包括: 数据获取, 人工设计特征, 特征提取和选择, 分类器训练. 然而, 在数据预处理阶段, 机器学习故障诊断存在一定的局限性: 为复杂操作条件下的数据人工设计特征需要耗费大量人力, 并且严重依赖领域专业知识, 难度较高. 此外, 特征挖掘和决策是分开设计的, 这种不同步的优化将消耗大量时间并限制模型的性能.
作为机器学习的一个分支, 深度学习方法旨在构建非线性转换的深度神经网络, 挖掘数据深层特征. 与传统数据驱动的机器学习方法相比, 深度学习无需大量专业知识即可自动从原始输入的简单表示中学习到隐藏的高级层次特征, 是一种端到端的模型. 基于这些优点, 深度学习在过去几年中引发了智能故障诊断的浪潮. 陈志刚等[2]提出一种改进集成深层自编码器方法, 设计了3种小波卷积自编码器对轴承振动信号进行无监督预训练和有监督微调, 最后, 为保证诊断结果的准确性和稳定性, 用加权平均法输出诊断结果. 杨平等[3]基于卷积胶囊网络, 使用带有两个卷积层的卷积网络直接对原始一维时域信号进行特征提取, 然后将其送入胶囊网络, 输出故障诊断结果. 周陈林等[4]基于提出的改进型卷积神经网络设计基本准则, 挖掘原始信号的特征, 直接用卷积神经网络在滚动轴承原始振动信号上进行“端到端”的学习训练. Ramu等[5]提出一种基于希尔伯特变换和人工神经网络的电机故障诊断方法, 首先提取信号的幅值和频率成分, 然后以最小均方误差为优化目标, 训练人工神经网络实现对故障的高精度识别. Li等[6]通过小波包变换, 将小波包系数转化为矩阵形式进而转化为像素, 形成灰度图输入到二维卷积神经网络中进行故障诊断.
在实际工业环境中, 不同的工作负载会导致同类型故障信号的内部特征分布存在巨大差异, 使得模型在某个工况下训练完成后, 在另一工况下的数据上表现不佳. 这种因数据分布不同而引起的模型性能下降现象被称为域适应问题. 深度学习要想应用到工业领域, 必须具有良好的域适应能力, 能够在变化的工况下实现高精度故障诊断. 目前, 针对深度学习故障诊断的域适应问题, 大多数研究采用迁移学习理论. Wen等[7]提出带有 51 个卷积层的 TCNN网络用于故障诊断. 该方法与迁移学习结合, 用预训练的ResNet-50 网络对原始二维振动信号进行故障诊断; 院老虎等[8]将收集到的原始振动数据转换为振动信号图作为训练样本, 用预训练的AlexNet网络进行训练和微调, 完成故障诊断任务. 陈仁祥等[9]提出一种自适应正则化迁移学习, 首先训练基分类器预测目标样本的伪标签, 然后利用联合分布对齐两域分布, 最后使用结构风险最小化框架建立的分类器完成不同工况下的故障诊断. 但是以上文献中应用的迁移学习方法仍然依赖于测试集样本的统计信息, 微调模型需要的参数量大, 且调参步骤复杂, 不具备很好的应用性. 此外, 这些研究因为重点关注模型的迁移能力而忽略了对数据特征的充分预处理过程, 没有从数据的角度挖掘出能增强网络识别能力的判别性工况特征, 缺少全面性.
因此, 针对当前研究中存在的数据预处理不充分和深度学习故障诊断方法在域适应上的局限性, 本文提出一种基于特征融合和混类增强的故障诊断方法. 贡献如下:
(1) 针对故障数据特征提取不足的问题, 提出一种特征融合方法, 在数据预处理阶段, 综合考虑原始振动信号的时频域特征、工况特征和时间差分特征, 并将这些特征与原始信号融合在一起形成新的特征向量, 增加特征多样性.
(2) 针对变工况下数据分布差异大导致模型故障识别率低的问题, 提出一种混类增强策略拓展训练数据分布, 增大训练集规模, 增加训练样本的多样性, 使模型学习到数据的本质特征, 提高模型域适应能力.
(3) 在CWRU数据集上的实验结果表明, 该方法在同工况下的预测精度高达100%, 在变工况下的平均预测精度高达93.28%, 域适应性强.
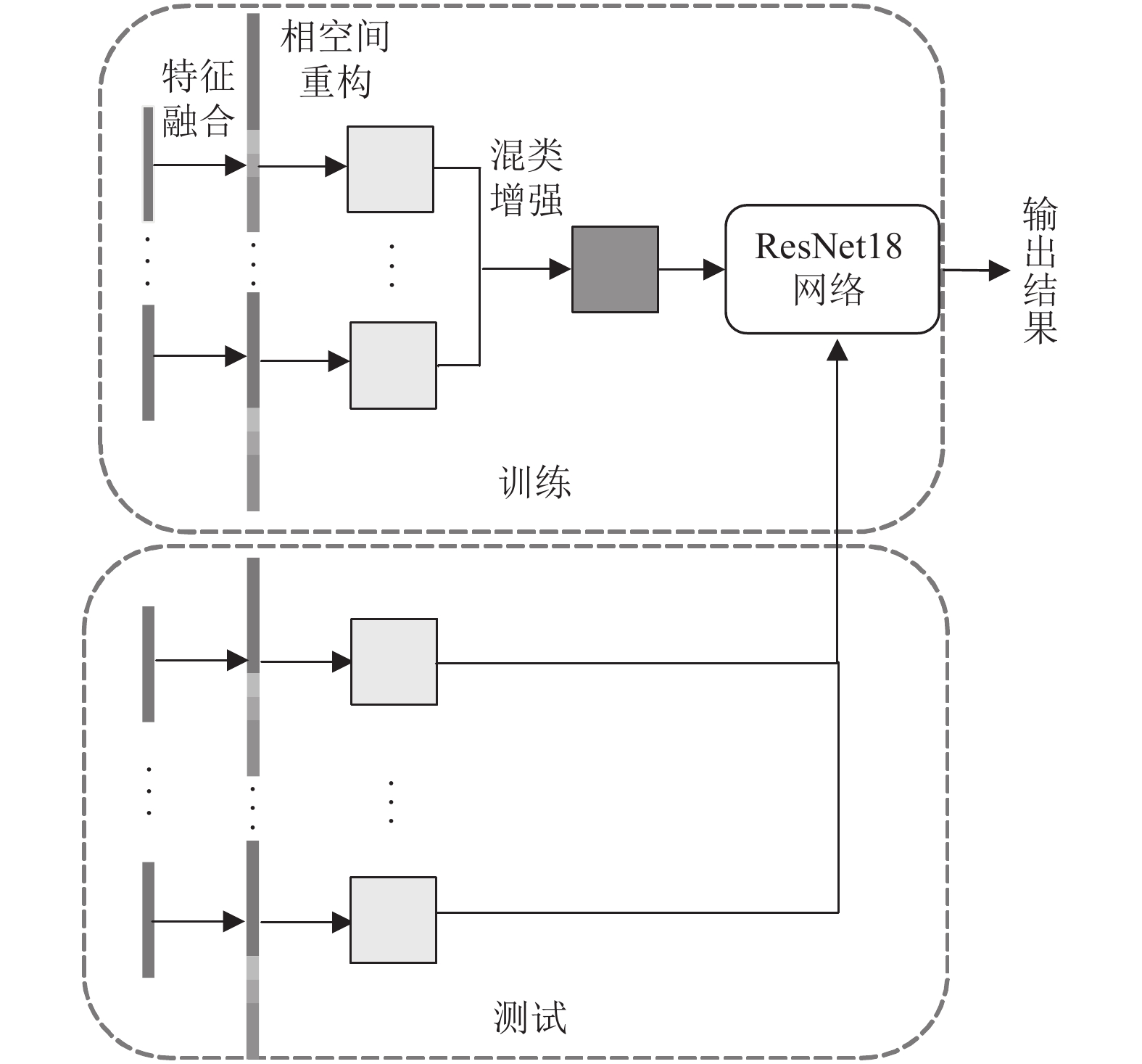
1 特征融合和混类增强模型本文提出的基于特征融合和混类增强的深度滚动轴承故障诊断方法框架如图1所示.
图1上方虚线框是训练过程, 下方虚线框是测试过程. 上方信号和下方信号来源于不同的工况, 即样本的分布不同. 在训练过程中, 原始一维振动信号经多特征融合后形成新的一维特征向量, 再经相空间重构转换成二维图像信号, 通过本文提出的混类增强策略拓展训练数据的分布, 提高模型在对抗样本上的鲁棒性. 最终, 训练好的模型可以在训练样本分布之外的测试样本上进行高精度故障诊断. 整个故障诊断流程可以概括为以下5步:
(1) 对原始信号采用时频分析方法提取时频特征, 并根据工况条件构建工况特征, 再计算时间差分特征, 然后将这3类特征与原始一维信号融合, 得到新的一维特征向量;
(2) 基于相空间重构理论, 将新的一维信号样本转换为二维图像格式, 作为神经网络的输入;
(3) 对转换后的训练样本做混类增强, 构造新的虚拟样本和虚拟标签, 扩充训练样本分布;
(4) 用混类增强后得到的样本作为训练集输入ResNet18网络中训练模型;
(5) 将训练完毕的模型在未做过混类增强的样本上测试, 获得故障诊断分类结果.
|
图 1 特征融合和混类增强故障诊断方法框架 |
1.1 特征融合方法
得益于硬件的高速发展, 现代工业设备的历史数据大多由传感器记录保存. 但是, 传感器获取的数据可能会存在异常值, 适当的故障特征提取可以减轻异常值对故障诊断的负面影响.
由于机械故障信号存在周期性脉冲, 因此提取具有信息性和判别性的时频域特征有助于提高故障数据的质量[10]. 另一方面, 故障数据的原始特征通常是固定的, 当设备在单一工况下运行时, 这些特征用于故障诊断是足够的. 当设备在变化的负载中工作时, 深度学习模型无法仅利用单工况下的固定特征掌握数据的本质信息. 由传感器在不同操作条件下观测到的帧间动态变化数据中包含大量的设备降级信息[11], 因此, 获取工况特征和时间差分特征也是有必要的.
综上所述, 本文提出一种新的特征融合方法, 在将原始信号输入模型前对数据进行预处理, 从多个角度提取多个特征, 包括时频特征、工况特征和时间差分特征, 实现多特征融合, 增加特征多样性和全面性, 为网络提供高质量的输入. 以下是对这些特征的具体描述:
(1) 原始特征: 原始一维振动信号, 由加速度计获得, 未经过任何处理, 形式为时间序列.
(2) 时频特征: 时窗信号的最大值、均值、方差、均方根值、偏度、峰度、峰值、谱偏态系数、谱峰态系数、小波系数. 对于小波系数, 本文使用db1进行8级小波包分解, 得到与故障特征频率相关的能量较高的小波系数. 每个时频特征是一个统计值, 统计出的多个时频特征可以构建形成新的一维时频特征向量. 表1给出了各个时频特征的计算公式.
| 表 1 时频特征计算公式 |
(3) 工况特征: 当前工作条件的独热(one-hot)编码. 以本文实验的4种工况为例, 独热编码对应的特征向量分别为 [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1].
(4) 时间差分特征: 由于样本是时间序列, 将每个样本看成一个时间窗, 计算该时间窗内的变化幅度特征, 构成时间差分特征向量. 具体地, 定义一个时间窗的时间序列为:
| $ X = ({x_1}, {x_2}, \cdots , {x_m}) $ |
以第一个时间点为起点, 依次从后往前求后一个时间点对应值相对于前一个时间点对应值的变化幅度, 作为新的特征, 即:
| $ a{x_i} = ({x_{i + 1}} - {x_i})/{x_i} $ | (1) |
最终得到新的时间差分特征向量为:
| $ \tilde X = (a{x_1}, a{x_2}, \cdots , a{x_{m - 1}}) $ |
为解决新的时间序列与原始时间序列的时间点错位问题(新时间序列的第i个点表示的是原始特征序列的第i+1个点相对前一时间点的变化幅度), 通过时间窗进行序列划分时, 从第2个时间窗开始, 其起始时间为上一时间窗结束时间, 这样可以保证数据变化特征的连续性.
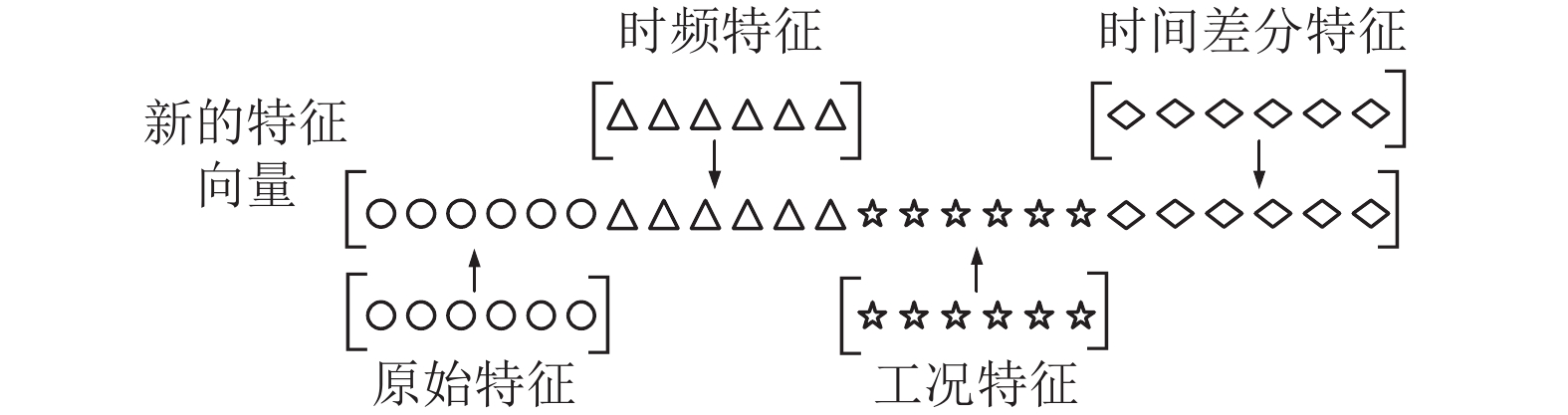
经过以上步骤后, 将提取的时频特征向量、工况特征向量和时间差分特征向量与原始一维信号拼接形成新的一维特征向量, 该向量增加了特定工况下的判别性信息, 更具全面性, 如图2所示.
|
图 2 新的特征向量 |
1.2 故障信号到图像的转换方法
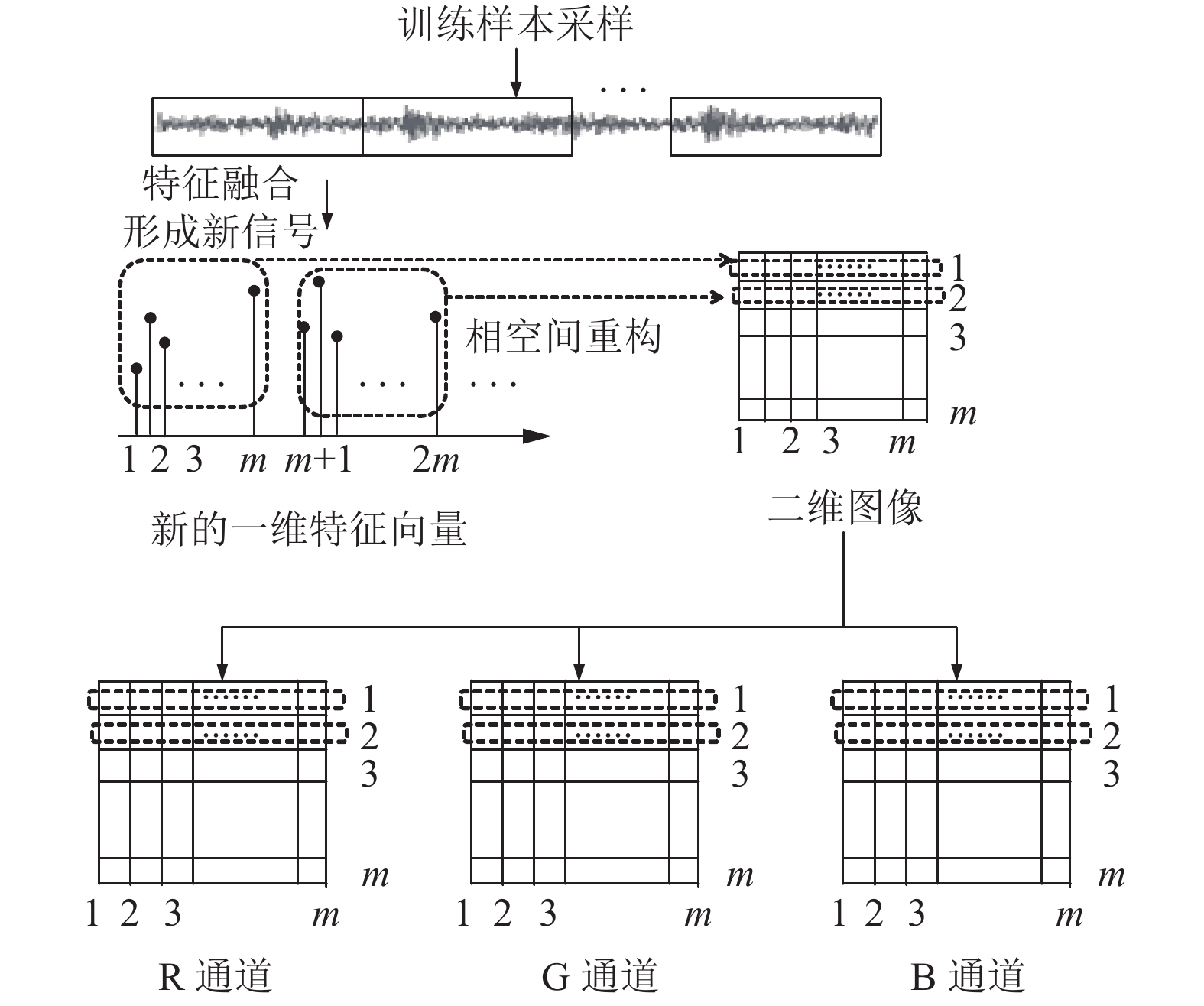
本文设计的一维振动信号到二维时频特征图像的转换过程如图3所示, 包括两个步骤:
(1) 一维振动信号采样, 经第1.1节的特征融合方法形成新的一维特征向量;
(2) 一维特征向量重构为二维图像.
以一维格式为输入数据的故障诊断方法受感受野限制, 在学习的过程中很难提取到设备故障固有模式的相关特征. 与一维信号相比, 图像是二维数据矩阵, 能够承载更强大的信息, 表示更复杂的结构分布. 为了捕获周期性信号的特征并利用深度神经网络在图像分类上的强大特征提取能力, 本文基于相空间重构理论, 将特征融合后的一维信号重构为二维图像格式作为深度神经网络的输入, 具体转换过程为:
(1) 将原始一维信号划分为n个相等的部分;
(2) 每个部分按信号图像的行顺序排列:
| $ I = \left[ {\begin{array}{*{20}{c}} {x(t)}& \cdots &{x(t + n - 1)} \\ \vdots & \ddots & \vdots \\ {x(t + (m - 1)n)}& \cdots &{x(t + mn - 1)} \end{array}} \right] $ | (2) |
其中, I表示重构后的信号图像,
| $ p_i{'} = \frac{{{p_i} - {p_{\min}}}}{{{p_{\max}} - {p_{\min}}}} \times 255 $ | (3) |
其中,
|
图 3 故障信号到图像的转换 |
1.3 深度残差网络
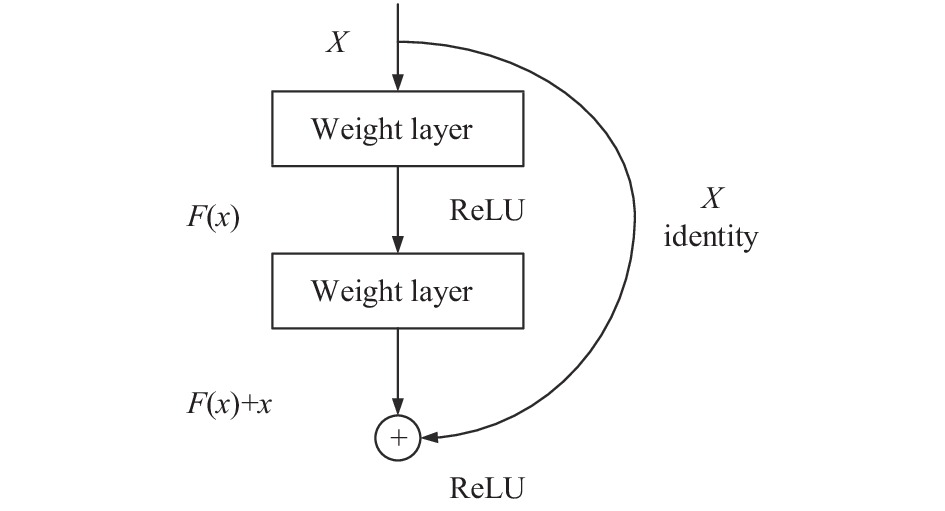
深度学习的另一个局限性在于: 网络深度的增加会带来许多优化相关问题, 如梯度爆炸、消失等. 深度残差网络(residual network, ResNet)[12]的提出有效缓解了深度神经网络模型增加层数后带来的退化问题, 从根本上杜绝了梯度消失现象, 分类和收敛性能均优于普通的深层网络结构. 因此本文采用深度残差网络作为故障诊断训练模型.深度残差网络由残差模块构建, 图4展示了残差网络块的结构.
如图4所示, 在残差块中, 输入可通过跨层的数据线路更快地向前传播, 不会给网络增加额外的参数和计算量. 残差网络通过采用这样一种跳跃连接的结构, 学习信号的差值, 在保持网络深度的同时提高了模型准确率, 并且易于优化. 由于工业落地环境要求神经网络模型有速度快、体型小的特点, ResNet18网络相较于其他ResNet50、ResNet101等网络更为轻量, 并且足够完成实验中数据场景, 因此本文选用ResNet18网络作为训练模型, 该网络有17个卷积层和1个全连接层.
|
图 4 残差网络块结构示意图 |
1.4 混类增强
深度神经网络模型训练、更新参数的依据来源于给定的训练数据, 但是在故障诊断领域, 单一工况下的训练数据只涵盖整个数据分布的一部分, 导致训练出来的网络只能在拥有类似分布的数据上表现良好, 在分布差异大的数据上表现不佳. 为了充分利用有限数据, 更好地描述数据的整个分布, 提高模型的域适应能力, 有必要进行数据增强[13]. 在计算机视觉领域, 传统的数据增强方式通过对图像进行裁剪、旋转、缩放等几何变换生成新的训练样本, 图像标签保持不变. 然而, 这样的数据增强方法存在以下局限性[14]:
(1) 生成的新样本局限于同一类别;
(2) 不同类别不同样本之间的关系没有被建模;
(3) 由于先验知识有限, 能拓展的分布也有限, 模型仍然可能会产生过拟合现象.
为解决上述问题, 本文提出一种新的混类增强方法, 改善故障诊断模型在变工况下由于数据分布不一致表现出的域适应性差的问题. 该方法是一种非常规的数据增强方式, 通过线性插值得到新的拓展数据, 即来源于训练样本邻近分布的虚拟训练样本和标签.混类增强对样本的处理过程如下:
| $ \tilde x = \lambda {x_i} + (1 - \lambda ){x_j}\; $ | (4) |
| $ \tilde y = \lambda {y_i} + (1 - \lambda ){y_j}\; $ | (5) |
其中,
混类增强具体算法如算法1.
算法1. 混类增强算法
输入: 数据集
输出: 数据集
1)
2)
3) #随机配对样本;
4)
5)
6)
为了验证本文提出方法的有效性, 在美国凯斯西储大学(CWRU)轴承实验数据上进行了测试. 关于数据集更详细的信息可在文献[15]中查看. 该数据来源于驱动端轴承, 由加速度传感器计以12 kHz的频率采集得到. 滚动轴承有4种故障类型: 内圈故障、滚动体故障、外圈故障、正常. 每种故障类型的故障直径分别为0.017 78 cm, 0.035 56 cm和0.053 34 cm, 因此, 共有10种故障标签. 表2为滚动轴承数据集的具体描述. 数据集A为在转速1 772 RPM、负载1马力下收集的振动信号, 数据集B为在转速1 750 RPM、负载2马力下收集的振动信号, 数据集C为在转速1 730 RPM、负载3马力下收集的振动信号, 数据集D为在转速1 772 RPM、1 750 RPM、1 730 RPM和负载1、2、3马力下收集的混合振动信号.
实验以1 024个采样点作为一个样本, 每种故障类型采样2 200个样本. 训练时, 长度为1 024的样本会被重塑为32×32大小的矩阵, 以二维图像格式作为ResNet18网络的输入. 训练集、验证集、测试集的划分比例为6:2:2. 模型训练的参数设置如表3所示.
| 表 2 数据集描述 |
| 表 3 参数设置 |
本文实验在Windows 10 的64位操作系统下进行, 内存为16 GB, 处理器为Intel(R) Core(TM) i7-9750H CPU. 所用深度学习框架为TensorFlow和Keras, 编程语言为Python 3.6.
2.2 单一/变工况对比分析为了验证本文所提方法的优越性, 将其与流行的WDCNN[16] 、TICNN[17]、LeNet-5网络[18]和孪生神经网络模型[19]在同一实验环境下进行单一工况、变工况对比分析. 表4给出了不同模型在单一工况下的准确率对比.
| 表 4 单一工况结果对比 (%) |
由表4可知, 在单一工况下, WDCNN、TICNN、LeNet-5和孪生神经网络模型的平均分类精度都可达到97%以上, 但是本文的混类增强模型的平均分类精度可达到100%, 优于现有的流行方法.
表5为变工况下域适应方案设置的具体描述. 其中, 源域指打上标签的训练数据, 目标域指未打标签的测试数据. 根据3种不同工况下数据集的组合, 共有6种域适应方案设置.
| 表 5 域适应方案设置 |
表6给出了变工况下各个模型在数据集A、B、C的6种域适应设置方案上对滚动轴承故障分类准确率的对比分析结果.
| 表 6 变工况结果对比 (%) |
由表6可知, WDCNN、TICNN和孪生神经网络模型在域适应方案设置中的平均精度在80%以上, LeNet-5模型的平均精度最低, 仅有66%. 受变工况操作条件影响, 这几种模型的精度与在单一工况下相比都下降了很多. 而本文方法的平均精度达到了93.28%, 比WDCNN提高了3.6%, 比One-shot提高了11.52%, 比Five-shot提高了11.43%, 比TICNN提高了8.35%, 比LeNet-5提高了27.28%, 明显改善了模型的域适应性, 提高了模型的泛化能力. 实验结表表明, 在跨域分类问题上, 基于特征融合和混类增强的深度学习滚动轴承故障诊断方法抗干扰能力强, 有效解决了故障诊断在实际工业中因跨域导致特征差异大而无法识别的问题.
2.3 消融实验分析本节设计消融实验分别探索特征融合和混类增强对故障诊断精度提升的贡献, 表7为具体对比方案. 其中, 方案1对一维信号做特征融合, 在训练模型时不加入混类增强策略; 方案2用原始一维信号重构二维图像, 不加入特征融合, 在模型训练时采用混类增强; 方案3即本文提出方法, 对一维信号做特征融合形成新的特征向量, 重构成二维图像后在训练时采用混类增强策略.
其中, 方案1对一维信号做特征融合, 在训练模型时不加入混类增强策略; 方案2用原始一维信号重构二维图像, 不加入特征融合, 在模型训练时采用混类增强; 方案3即本文提出方法, 对一维信号做特征融合形成新的特征向量, 重构成二维图像后在训练时采用混类增强策略.
| 表 7 方案对比 |
表8和表9分别展示了方案1、方案2、方案3在单一工况和变工况下的模型故障诊断分类结果.
由表8可知, 在单一工况下, 方案1和方案2都可以达到99%以上的分类精度, 但是方案3可以使模型提高到100%的分类精度, 证明了特征融合和混类增强结合的有效性, 在单工况条件下表现极佳.
| 表 8 单一工况结果对比 (%) |
| 表 9 变工况结果对比 (%) |
由表9可知, 在域适应方案设置中, 方案3的平均分类精度分别比方案1、方案2的平均分类精度高8.13%和10.8%. 在域适应设置C→A和C→B中, 方案3相较于方案1和方案2, 分类精度提升十分明显, 最大提升跨度可达28.57%.
综上, 可得出结论: 特征融合和混类增强结合的方法比仅做特征融合和仅做混类增强的方法在单一工况和变工况下具有更好的分类性能和域适应能力. 本文提出的特征融合和混类增强结合的方法对提高模型同工况下的分类精度和变工况下的域适应能力具有显著效果.
3 特征分析与可视化第2节以准确率为评价指标, 通过比较网络分类层的最终预测标签与真实标签获得模型的精度, 以此评估模型的有效性. 本节从网络的中间层出发, 用特征可视化来展示神经网络对样本特征的学习过程, 验证本文提出方法对不同故障类别的识别能力, 增加网络的可解释性.
本节采用t-SNE (t-distributed stochastic neighbor embedding)方法[20]对故障样本的分类过程进行降维和特征可视化. t-SNE方法可以将高维数据映射到适合人类直觉观察的低维空间, 是一种出色的非线性降维方法, 非常适合数据探索和可视化分析.
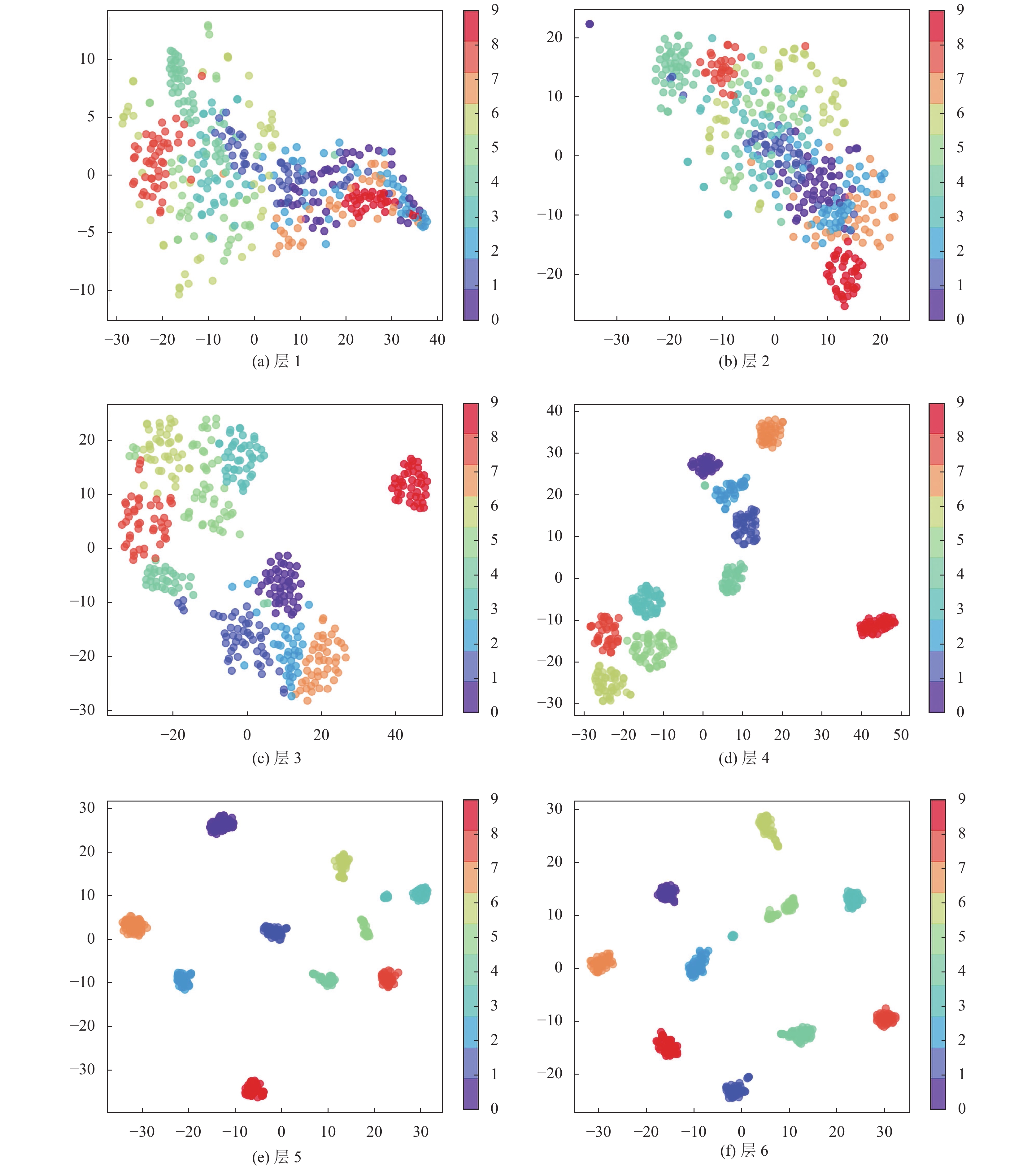
图5(a)–图5(f)以数据集D为例, 展示了测试样本在已经训练好的网络结构上从中间层到最后一个全连接层的特征分布. 图中每种颜色类别代表一类故障标签, 共有10类.
图5可以看出, 在早期的一些层中, 从图5(a)到图5(c), 特征是重叠聚合在一起的, 无法轻易区分. 从图5(d)到图5(f), 随着层数的逐渐加深, 每个类别的特征点开始聚类在一起, 10个故障的类别特征变得越来越可分割, 说明训练好的神经网络模型分类效果显著.
t-SNE可视化直观形象地展示了神经网络训练过程中层与层之间逐步提取更深层次数据内部特征的步骤, 增加了网络的可解释性, 同时验证了本文提出方法能够很好地学习到样本特征, 实现高精度的故障诊断.
4 结论与展望针对深度学习滚动轴承故障诊断模型数据预处理不充分和域适应性差的问题, 本文提出了一种基于特融合和混类增强的故障诊断方法. 该方法在深度学习的基础上加入了特征工程, 在数据预处理阶段综合考虑原始信号的时域特征、工况特征和时间差分特征, 丰富特征表示, 改善训练数据的质量. 在模型训练阶段, 提出一种混类增强策略构造虚拟样本和标签, 拓展训练数据分布, 增加训练集多样性, 并利用ResNet18强大的特征提取能力学习数据的本质特征. 实验结果表明, 该方法有效缓解了深度学习故障诊断在不同工况下故障识别率低的问题, 提高了滚动轴承故障诊断模型的域适应能力, 适合变工况下故障诊断. 在未来工作中, 将尝试优化网络结构, 进一步提高模型收敛速度.
|
图 5 特征可视化示意图 |
| [1] |
张兰芳, 张朝龙, 纪娟娟. 基于核主元分析和极端学习机的轴承故障诊断方法. 电子测量与仪器学报, 2018, 32(2): 23-29. |
| [2] |
陈志刚, 杜小磊, 王衍学, 等. 改进集成深层自编码器在轴承故障诊断中的应用. 控制与决策, 2021, 36(1): 135-142. |
| [3] |
杨平, 苏燕辰, 张振. 基于卷积胶囊网络的滚动轴承故障诊断研究. 振动与冲击, 2020, 39(4): 55-62, 68. |
| [4] |
周陈林, 董绍江, 李玲, 等. 滚动轴承多状态特征信息的改进型卷积神经网络故障诊断方法. 振动工程学报, 2020, 33(4): 854-860. |
| [5] |
Ramu SK, Irudayaraj GCR, Subramani S, et al. Broken rotor bar fault detection using Hilbert transform and neural networks applied to direct torque control of induction motor drive. IET Power Electronics, 2020, 13(15): 3328-3338. DOI:10.1049/iet-pel.2019.1543 |
| [6] |
Li GQ, Deng C, Wu J, et al. Rolling bearing fault diagnosis based on wavelet packet transform and convolutional neural network. Applied Sciences, 2020, 10(3): 770. DOI:10.3390/app10030770 |
| [7] |
Wen L, Li XY, Gao L. A transfer convolutional neural network for fault diagnosis based on ResNet-50. Neural Computing and Applications, 2020, 32(10): 6111-6124. DOI:10.1007/s00521-019-04097-w |
| [8] |
院老虎, 陈源强, 杜白雨, 等. 基于AlexNet和迁移学习的滚动轴承故障诊断研究. 机电工程, 2021, 38(8): 1016-1022. DOI:10.3969/j.issn.1001-4551.2021.08.012 |
| [9] |
陈仁祥, 朱玉清, 胡小林, 等. 自适应正则化迁移学习的不同工况下滚动轴承故障诊断. 仪器仪表学报, 2021, 42(8): 95-103. |
| [10] |
Zhao R, Yan RQ, Chen ZH, et al. Deep learning and its applications to machine health monitoring. Mechanical Systems and Signal Processing, 2019, 115: 213-237. DOI:10.1016/j.ymssp.2018.05.050 |
| [11] |
Wu YT, Yuan M, Dong SP, et al. Remaining useful life estimation of engineered systems using vanilla LSTM neural networks. Neurocomputing, 2018, 275: 167-179. DOI:10.1016/j.neucom.2017.05.063 |
| [12] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [13] |
Simard PY, LeCun YA, Denker JS, et al. Transformation invariance in pattern recognition: Tangent distance and propagation. International Journal of Imaging Systems and Technology, 2000, 11(3): 181-197. DOI:10.1002/1098-1098(2000)11:3<181::AID-IMA1003>3.0.CO;2-E |
| [14] |
Zhang HY, Cisse M, Dauphin YN, et al. Mixup: Beyond empirical risk minimization. arXiv: 1710.09412v2, 2017.
|
| [15] |
Lou XS, Loparo KA. Bearing fault diagnosis based on wavelet transform and fuzzy inference. Mechanical Systems and Signal Processing, 2004, 18(5): 1077-1095. DOI:10.1016/S0888-3270(03)00077-3 |
| [16] |
Zhang W, Peng GL, Li CH, et al. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors, 2017, 17(2): 425. DOI:10.3390/s17020425 |
| [17] |
Zhang W, Li CH, Peng GL, et al. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mechanical Systems and Signal Processing, 2018, 100: 439-453. DOI:10.1016/j.ymssp.2017.06.022 |
| [18] |
Wan LJ, Chen YW, Li HY, et al. Rolling-element bearing fault diagnosis using improved LeNet-5 network. Sensors, 2020, 20(6): 1693. DOI:10.3390/s20061693 |
| [19] |
Zhang AS, Li SB, Cui YX, et al. Limited data rolling bearing fault diagnosis with few-shot learning. IEEE Access, 2019, 7: 110895-110904. DOI:10.1109/ACCESS.2019.2934233 |
| [20] |
der Maaten LV, Hinton GE. Visualizing data using t-SNE. Journal of Machine Learning Research, 2008, 1: 1-48. |
 2022, Vol. 31
2022, Vol. 31


