计算机和网络技术的发展使得信息技术在各个行业都得到了广泛的应用, 电力系统的信息化水平在不断提高, 但同时也带来了更多的安全威胁. 据ICS-CERT报告, 近年来类似于“震网”、HaveX、BlackEngery等针对电力行业的网络安全事件在呈现稳步增长的趋势. 电力监控系统具有监控现场设备和故障处理的能力, 一旦遭受攻击, 会极大影响电力系统的正常运行. 因此保障电力监控系统的安全已经成为各级安全责任单位的重中之重. 风险评估作为检测系统安全状态的有力手段, 能够评估系统的安全风险, 利于及时制定相应的风险控制策略. 对电力监控系统进行合理的安全风险评估, 可以帮助提高电力监控系统的安全性, 有效避免灾害的发生.

从目前的研究来看, 电力系统的风险评估主要集中在对电力设备和输电网络上^[1-4], 对电力监控系统的研究较少. 梁宁波^[5]通过漏洞排查对电力监控系统进行风险管理, 但对于漏洞结果未给出明确风险评估标准; 杨鹏^[6]针对电力监控系统中的两个子系统进行安全风险分析, 但缺乏对系统整体的考虑; 梁智强等人^[7]使用AHP方法, 并结合模糊数学的原理对关键资产风险进行了评估, 但没有给出电力系统的整体风险; 曹波等人^[8]结合状态攻击图对电力监控系统的脆弱性进行评估, 但在大规模场景下攻击图易产生状态爆炸问题. 总体来看, 目前电力监控系统风险评估主要存在着系统建模不完整以及缺乏对系统整体风险的考虑的问题.

风险评估中在定性指标的评价上会表现为专家评价意见的模糊性, 影响评估结果的准确性. 因此, 云模型^[9]自提出以来, 由于其能够刻画自然语言中概念的不确定性和模糊性^[10], 已广泛应用于评估领域. 张仕斌等人^[11]引入云模型对复杂网络环境中的用户信息进行信任评估; 徐岩等人^[12]利用云模型得到定量指标对变压器各状态的隶属等级对变压器状态进行评估; 胡文平等人^[13]将正态云模型用于输变电设备故障的不确定性推理预测, 完成对电网的综合风险评估; 龙赛琴等人^[14]设计了基于云模型的多指标融合评估策略对数据中心的能效进行评估. 云模型在评估领域的应用中取得了不错的效果, 能够在一定程度上减小评价中模糊性和不确定性的影响.

云模型解决了定性指标的量化问题, 然而在综合评估时, 由于多位专家侧重点不同, 还存在着评估信息不一致的问题. 在多源信息的融合方面, 证据理论是一种有效的尝试. 证据理论能够将多源信息视为证据, 解决证据间的冲突并进行融合, 形成相对完整和一致的表达. 因而在质量评估^[15]、故障诊断^[16]、多属性决策^[17]等领域应用广泛, 能有效提高结果的准确性.

为此, 本文提出基于云模型和改进证据理论的电力监控系统综合风险评估方法. 在建立风险评估模型时充分考虑系统的特点, 使得对系统的建模更加完整; 使用云模型实现专家语言评价的有效转换, 同时使用基于冲突系数和概率距离函数的证据修正方法和基于矩阵分析的证据合成算法, 可减小证据冲突的影响和提高评估的效率.

1 构建电力监控系统风险评估模型 1.1 电力监控系统的安全性分析

典型电力监控系统的组网结构如图1所示, 3个层次的主要功能如下: 主站层能够人机交互, 可从整体上对系统的工作进行维护和管理; 网络通讯层是层次间数据交换的桥梁, 使得主站层能够快速得到现场设备层的监测信息和下发控制指令; 现场设备层主要用于监测设备的运行, 并根据上层指令对设备进行控制.

相比于传统网络系统, 电力监控系统具有节点多样性、网络异构性、应用实时性和业务连续性的特点, 因而在电力监控系统中, 可用性是其首要保障, 其次是完整性和机密性. 针对电力监控系统的特点, 本文另提出了可见性和可控性的安全属性. 可见性是指可观察过程的当前状态以便做出决策以及监视过程的当前状态并对异常事件做出警报; 可控性是防止对电力系统控制功能的影响.

威胁是系统风险产生的关键因素, 根据《工业控制网络安全风险评估规范》^[18]和电力监控系统的实际情况, 分析得到电力监控系统常见的威胁主要有非法设备的物理接入、访问权限非法获取、控制信息被篡改、未授权的网络连接、数据包重放攻击、拒绝提供服务、病毒感染、被植入木马、控制信息非法获取等^[19].

1.2 电力监控系统风险评估模型的建立

根据《信息安全风险评估规范》^[20]的定义, 信息安全风险评估是通过资产、威胁和脆弱性对信息的安全属性进行评价的过程. 本文参照该原理, 通过对系统及其安全属性进行评价以实现电力监控系统的综合风险评估. 针对电力监控系统, 将系统关键设备类比“资产”, 系统攻击方式类比于“威胁”^[21], 通过威胁对系统安全属性的影响以及系统关键设备对安全属性的依赖来对系统总体安全风险进行评估. 结合第1.1节对电力监控系统的安全性分析, 建立图2所示的电力监控系统风险评估模型.

由电力监控系统组网结构图可知, 现场设备层主要由电力一次设备组成, 对攻击者来说, 攻击成本大且收益小. 因此本文的风险评估主要针对主站层和网络通讯层, 选取的关键设备有监控终端、应用服务器、数据服务器、网络交换机、数据采集器和PLC.

各关键设备功能的不同导致与其相关的安全属性的重要程度的差异, 本文在建立关键设备层与安全属性层的联系时, 根据关键设备的功能选择其最为重要的3个安全属性建立联系, 这样既可以突出各设备的功能特性, 也便于后文各元素权重的确定.

最后根据威胁对系统的影响建立评价层与安全属性层间的联系.

1.3 电力监控系统风险评估原理

本文的电力监控系统风险评估流程如图3所示. 具体步骤如下.

(1) 收集数据: 根据建立的风险评估模型, 收集专家评价信息和系统的运行数据;

(2) 计算指标的主客观权重: 根据收集的专家意见基于FAHP方法对指标进行主观赋权, 根据系统运行数据基于修正的熵权法对指标进行客观赋权;

(3) 计算综合权重: 使用最优化模型确定主客观权重的组合系数, 对指标进行组合赋权;

(4) 综合评估: 使用云模型和改进的证据理论进行综合评估, 得到系统的风险评估结果.

2 基于组合赋权的指标权重的确定

为提高权重的准确性和评估的合理性, 以更好地反映电力监控系统的运行状态, 本文采用组合赋权的方法. 该方法能够减小专家意见的主观性影响, 又能兼顾客观数据信息, 可避免单一权重赋值方法的主导性.

2.1 基于FAHP的主观权重赋值方法

由于本文评估模型中元素多样且层次间的关联复杂, 若使用传统的AHP方法, 构造的判断矩阵维度较大, 查验矩阵一致性以及调整元素使其一致非常困难. 因此, 为避免上述问题, 本文引入了模糊AHP方法^[22]. 步骤如下.

(1) 根据表1, 专家评判构造模糊判断矩阵 $A = {({r_{ij}})_{n \times n}}$ , r_ij含义为: 对于上层某个元素, 本层与之相关的元素x_i和x_j的相对重要程度.

(2) 将矩阵 $A = {({r_{ij}})_{n \times n}}$ 按 ${f_{ij}} = \dfrac{{{r_i} - {r_j}}}{{2n}} + {\text{0}}{\text{.5}}$ 进行转换使其一致, 其中 ${r_i}$ 和 ${r_j}$ 表示对应行元素的和, 即 ${r_x} = \displaystyle\sum\limits_{k = 1}^n {{r_{xk}}}$ .

(3) 按照式(1)进行计算各要素的权重值:

$ {w_i} = \frac{1}{n} - \frac{1}{{2\alpha }} + \frac{1}{{n\alpha }}\mathop \sum \nolimits_{k = 1}^n {r_{ik}}, \; i = 1, 2, \cdots , n $

(1)

其中, ${w_i}$ 即本层第i个要素的权重值, n为总个数, ${r_{ik}}$ 模糊一致矩阵A的元素值, 参数 $\alpha$ 需满足 $\alpha \geqslant \dfrac{{n - 1}}{2}$ , $ \alpha $ 越小权重差异度越大, 本文取为 $\alpha = \dfrac{{n - 1}}{2}$ , 此时得到的各要素权重差异度最大, 即区分度最高.

2.2 基于改进熵权法的客观权重赋值方法

熵权法利用信息熵表征指标集的不确定度, 熵值大小表示各指标的变异程度. 若某个指标的信息熵越小, 表示该指标所包含的信息量越大, 则相应赋予的权重应较大. 传统的熵权法确定客观权重的步骤如下:

(1) 根据原始客观数据, 确定指标集的评价矩阵 $ R = {\left[ {{r_{ij}}} \right]_{m \times n}} $ , 其中r_ij表示第i个评估对象对第j个评价指标的评价结果.

(2) 根据式(2)对评价矩阵R进行归一化处理得到归一化后的评价矩阵 $ X = {\left[ {{x_{ij}}} \right]_{m \times n}} $ :

$ {x_{ij}} = \dfrac{{{r_{ij}}}}{{\displaystyle\sum\limits_{j = 0}^n {{r_{ij}}} }} $

(2)

(3) 根据式(3)计算得到第j个指标的熵值:

$ {e_j} = - \frac{{\text{1}}}{{Inn}}\sum\limits_{i = 1}^m {({x_{ij}}In{x_{ij}}} ), \; (j = 1, 2,\cdots, n) 　 $

(3)

(4) 由式(4)计算第j个指标的客观权重:

$ {v_j} = \dfrac{{1 - {e_j}}}{{n - \displaystyle \sum \nolimits_{j = 1}^n {e_j}}}, \; \left( {j = 1, 2, \cdots , n} \right) $

(4)

由于电力监控系统的数据不稳定, 不确定性较大, 导致指标的信息熵易接近于1. 在这种情况下, 若采用上述传统的熵权法, 结果易与现实相悖^[23]. 因此本文对该方法进行修正, 在传统计算方法中加入起修正作用的正数z, 修正的熵权法计算第j个指标的权重公式为:

$ {v_j} = \frac{{1 - {e_j} + {\textit{z}}}}{{ \displaystyle\sum \nolimits_{j = 1}^n \left( {1 - {e_j} + {\textit{z}}} \right)}}, \; \left( {j = 1, 2, \cdots , n, \; {\textit{z}} > 0} \right) $

(5)

研究表明^[23], 使用该公式进行权重计算能够成功解决传统熵权法存在的上述问题. 其中, z的值越大时修正作用越好, 本文令 ${\textit{z}}= \frac{1}{n}\displaystyle \sum \nolimits_{j = 1}^n \left( {1 - {e_j}} \right)$ .

2.3 组合权重赋值方法

组合权重赋值公式如下:

$ {\sigma _j} = \alpha {w_j} + \beta {v_j}, \; \left( {j = 1, 2, \cdots , n} \right) $

(6)

其中, w_j和v_j分别为主观权重和客观权重, $\alpha $ 和 $\;\beta $ 为权重系数, 取值范围为[0, 1], 并且 $\alpha + \beta = 1$ . 本文使用基于最小方差原理的最优化模型确定权重系数, 该模型可使主客观权重的比例达到最佳, 使得评估结果更加准确. 建立的最优化模型如下:

$ \min \mathop {B = \sum }\limits_{j = 1}^n {\left( {{\sigma _j} - {w_j}} \right)^2} + {\left( {{\sigma _j} - {v_j}} \right)^2} $

(7)

其中, B为主客观权重与组合权重的方差值, 上述模型表示求取使得式B最小的权重系数 $\alpha $ 和 $\;\beta $ . 根据微分的性质, 上式存在的唯一解, 因此根据主客观权重可唯一确定组合权重值.

3 基于云模型和证据理论的风险评估方法 3.1 证据理论 3.1.1 传统证据理论

证据理论能够有效处理问题的模糊性, 符合人类推理的决策过程, 用于风险评估可充分利用评估过程中的不确定性, 得到更为合理的评估结果, 其关键是Dempster 证据合成规则^[24]:

$ \begin{array}{l} m\left( A \right) = \\ \left\{ {\begin{array}{*{20}{l}} {0, A = \varphi } \\ \begin{array}{l} {\dfrac{{\displaystyle\sum \nolimits_{{A_i} \cap {B_j} \cap {C_k} \cdots = A} {m_1}\left( {{A_i}} \right) \cdot {m_2}\left( {{B_j}} \right) \cdot {m_3}\left( {{C_k}} \right) \cdots }}{K}, A \ne \varphi } \end{array} \end{array}} \right. \\ K = \displaystyle\mathop \sum \nolimits_{{A_i} \cap {B_j} \cap {C_k} \cdots \ne \varphi } {m_1}\left( {{A_i}} \right) \cdot {m_2}\left( {{B_j}} \right) \cdot {m_3}\left( {{C_k}} \right) \cdots \end{array} $

(8)

其中, ${m_1}, {m_2}, \cdots , {m_n}$ 表示n个独立证据, K为冲突系数, 代表证据的冲突程度.

然而, 传统证据理论在电力监控系统中应用时存在着以下问题: 由于各层元素间关系复杂, 专家评判时受主观因素的影响易出现证据冲突, 直接使用上述合成规则的计算结果可能与实际情况不符; 另外, 直接使用上述合成规则进行证据融合效率较低. 因此有必要对证据理论进行改进.

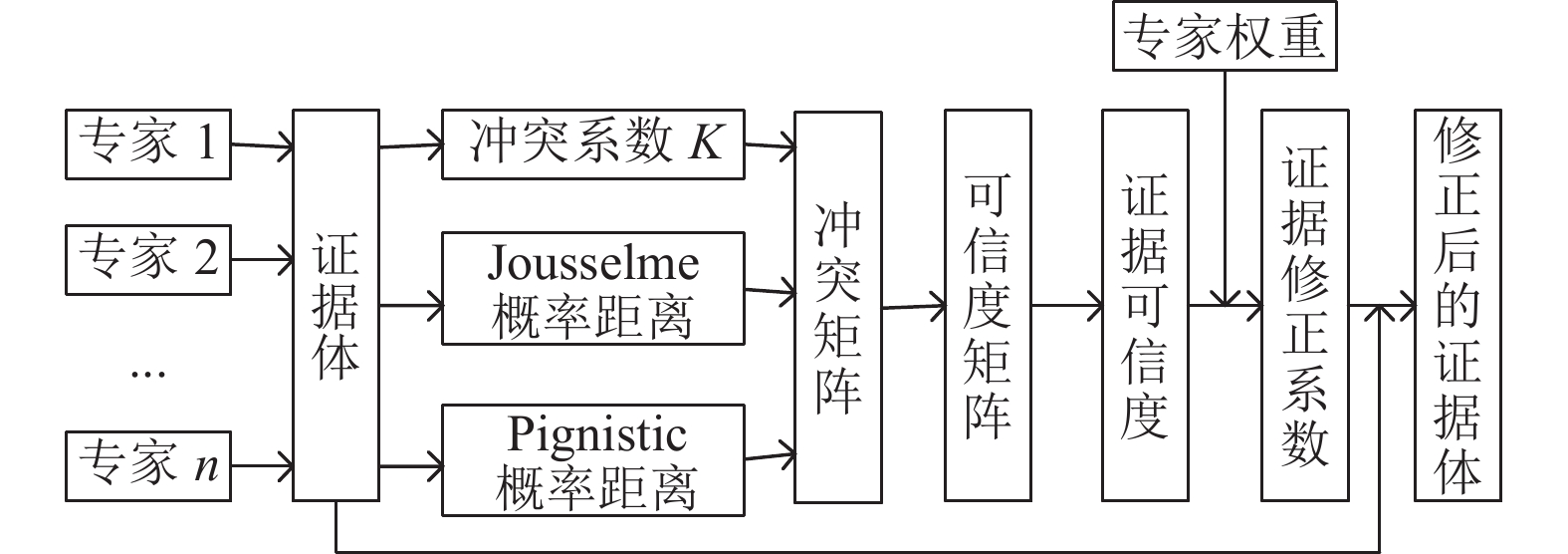
3.1.2 证据冲突修正方法

为解决证据冲突的问题, 本文引入了基于冲突系数和概率函数的证据冲突修正方法, 具体运算过程参考文献[25], 流程如图4所示.

该方法的基本原理是: 在获取原始证据体后, 根据冲突系数、Jousselme概率距离和Pignistic概率距离定义一种新的证据冲突量, 通过计算各专家的证据可信度, 结合专家权重得到各专家的证据修正系数, 对原始证据体进行修正.

3.1.3 基于矩阵分析的证据合成方法

为解决证据融合的效率问题, 本文引入了基于矩阵分析^[26]的方法, 该方法通过递推计算的方式融合专家意见, 可提高证据融合的效率.

假设有n位专家, 5个隶属等级, 根据评判得到mass矩阵为:

$ M = \left[ {\begin{array}{*{20}{c}} {{M_1}} \\ {{M_2}} \\ {\vdots} \\ {{M_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{m_{11}}}&{{m_{12}}}&{{m_{13}}}&{{m_{14}}}&{{m_{15}}} \\ {{m_{21}}}&{{m_{22}}}&{{m_{23}}}&{{m_{24}}}&{{m_{25}}} \\ {\vdots}&{\vdots}&{\vdots}&{\vdots}&{\vdots} \\ {{m_{n1}}}&{{m_{n2}}}&{{m_{n3}}}&{{m_{n4}}}&{{m_{n5}}} \end{array}} \right] $

m_ij表示第i位专家的评判中目标风险等级j的隶属度, 基于矩阵分析的证据融合流程如图5所示.

3.2 利用云模型实现mass函数的构造

在证据理论的应用中, 原始证据大都是用定性语言进行描述的, 具有较大的不确定性, 难以进行直接融合, 因此构造有效的mass函数是难点之一. 云模型刻化了定性语言值和精确数值之间随机和模糊的性质, 具有定性与定量信息转换上的优势. 因此, 本文将云模型用于构造证据理论的mass函数, 以实现专家评价从定性向定量的有效转化, 具体方法如下:

(1) 设专家的自然语言评价有r个等级, 评价值的有效论域为 $\left[ {{X_{\rm{min}}}, {X_{\rm{max}}}} \right]$ , 使用黄金分割法^[27]将评价等级转化为标准云 ${C_h}\left( {E{x_h}, E{n_h}, H{e_h}} \right)$ , 其中, h=1,…, r, 表示第n个评语等级. 再利用标准云将m位专家相对于上层元素X_i对应的第j个元素的语言评价值转化为评价云决策矩阵 ${\left[ {{C_{gij}}\left( {E{x_{gij}}, E{n_{gij}}, H{e_{gij}}} \right)} \right]_{m \times r}}$ .

(2) 结合标准云模型, 将云决策矩阵的元素转换为隶属度, 公式如下:

$ {{{\mu }}_{{g}}}{\left( {{{{x}}_{{{ij}}}}} \right)_{{h}}} = {{\rm{e}}^{ - \frac{{\left( {{{E}}{{{x}}_{{{gij}}}} - E{x_h}} \right)}}{{2{{\left( {{{E}}{{{n}}_{{h}}}} \right)}^2}}}}} $

(9)

得到的隶属度矩阵为:

$ {U_{ij}} = \left[ {\begin{array}{*{20}{c}} {{\mu _1}{{\left( {{x_{ij}}} \right)}_1}}&{{\mu _1}{{\left( {{x_{ij}}} \right)}_2}}&{\cdots}&{{\mu _1}{{\left( {{x_{ij}}} \right)}_r}} \\ {{\mu _2}{{\left( {{x_{ij}}} \right)}_1}}&{{\mu _2}{{\left( {{x_{ij}}} \right)}_2}}&{\cdots}&{{\mu _2}{{\left( {{x_{ij}}} \right)}_r}} \\ {\vdots}&{\vdots}&{\ddots}&{\vdots} \\ {{\mu _m}{{\left( {{x_{ij}}} \right)}_1}}&{{\mu _m}{{\left( {{x_{ij}}} \right)}_2}}&{\cdots}&{{\mu _m}{{\left( {{x_{ij}}} \right)}_r}} \end{array}} \right] $

(10)

然后按照式(11)进行归一化处理:

$ {m_g}{\left( {{x_{ij}}} \right)_h} = \frac{{{{{\mu }}_{{g}}}{{\left( {{{{x}}_{{{ij}}}}} \right)}_{{h}}}}}{{\displaystyle\sum \nolimits_{h = 1}^n {{{\mu }}_{{g}}}{{\left( {{{{x}}_{{{ij}}}}} \right)}_{{h}}}}} $

(11)

3.3 基于云模型-证据理论的风险评估步骤

(1) 以问卷的方式收集专家关于评价层元素对上层元素影响等级的定性评价信息.

(2) 利用第3.2节的方法将专家定性评价信息转换为隶属度矩阵也即证据理论的原始证据体.

(3) 证据冲突修正.

根据图4所示的方法计算各位专家的证据修正系数, 并对原始证据体按照式(12)进行修正:

$ {m_g}{\left( {{x_{ij}}} \right)_h}' = {\rho _g} \cdot {{{\mu }}_{{g}}}{\left( {{{{x}}_{{{ij}}}}} \right)_{{h}}} $

(12)

其中, $\;{\rho _g}$ 为第g个专家的证据修正系数.

(4) 综合评估

得到评价层元素相对于上层元素的mass矩阵后, 利用图5所示的基于矩阵分析的证据合成方法进行证据合成. 然后根据各属性的权重值 $\bar \omega = \{ {\omega _j}|j = 1, 2,\cdots, l\}$ , 得到上层第i个元素的mass函数值为:

$ m{\left( {{X_i}} \right)_h} = \mathop \sum \limits_{j = 1}^l {\omega _j} \cdot m{\left( {{x_{ij}}} \right)_h} $

(13)

根据上式自底向上进行合成, 最终得到综合风险S的mass函数值, 最大隶属等级即为系统的风险等级.

4 算例仿真 4.1 实例计算

本次仿真使用的数据来源于国网河北省电力有限公司实验网络, 该网络的拓扑图如图1所示. 该实验网络与真实网络以同样的方式运行, 将实际网络约1/20的运行流量镜像到该实验网络, 并通过人工干预的方式对其定时实施攻击.

为验证本文方法的适用性, 实验收集实验网络中监控终端、应用服务器、数据服务器、网络交换机、数据采集器和PLC的运行数据, 并邀请4位电网的工程技术人员进行专家评判, 其中, 1位正高级工程师, 2位副高级工程师, 1位中级工程师.

4.1.1 最优化组合赋权确定元素权重

计算各层元素的主客观权重并运用最优化模型进行组合, 得到各元素的权重如图6所示.

图6中, S, A1,…, A6, B1,…, B5, C1,…, C9代表图2中的各层元素.

4.1.2 专家语言评价信息转换

设专家评估有效论域为[0, 100], 分数越高表示评价指标对上层元素的影响越大, 利用黄金分割法确定的5朵标准云为: C₋₂(0, 10.31, 0.26), C₋₁(30.9, 6.37, 0.16), C₀(50, 3.93, 0.1), C₊₁(69.1, 6.37, 0.16), C₊₂(100, 10.31, 0.26).

由决策专家组成员{G1, G2, G3, G4}确定指标对上层元素的评价值, 假设隶属等级分为5级, 描述为{V_–2=很低, V_–1=低, V₀=中, V₁=高, V₂=很高}. 以可用性B1为例, 评价下层威胁对其的影响程度, 专家评价信息如表2所示.

根据标准云转化得到的云决策矩阵为:

$ V = \left[ {\begin{array}{*{20}{c}} {(50, 3.93, 0.1)}&{(100, 10.31, 0.26)}&{(69.1, 6.37, 0.16)} \\ {(50, 3.93, 0.1)}&{(69.1, 6.37, 0.16)}&{(50, 3.93, 0.1)} \\ {(50, 3.93, 0.1)}&{(50, 3.93, 0.1)}&{(50, 3.93, 0.1)} \\ {(100, 10.31, 0.26)}&{(69.1, 6.37, 0.16)}&{(30.9, 6.37, 0.16)} \end{array}} \right] $

根据式(9)–式(11), 以C1为例, 计算各等级的隶属度并归一化处理得初始mass矩阵为:

$ {M_{C1}} = \left[ {\begin{array}{*{20}{c}} {0.154}&{0.154}&{0.196}&{0.248}&{0.248} \\ {0.129}&{0.149}&{0.277}&{0.239}&{0.206} \\ {0.154}&{0.154}&{0.196}&{0.248}&{0.248} \\ {0.213}&{0.145}&{0.068}&{0.233}&{0.341} \end{array}} \right] $

4.1.3 证据冲突修正

以 $ {M_{C1}} $ 为例, 证据冲突修正步骤如下:

计算两两专家间的冲突系数K、Jousselme概率距离和Pignistic概率距离, 如表3所示.

根据表3, 利用文献[25]中的方法, 得各专家的证据可信度分别为:

Rel(G1)=1, Rel(G2)=0.9636, Rel(G3)=1, Rel(G4)=0.9395.

根据专家的经验和行业认可度确定专家权重向量 $ \lambda = \{ 0.3, 0.2, 0.4, 0.1\} $ , 则相对权重为:

$ {\lambda _{G1}} = 0.75 , {\lambda _{G2}} = 0.50 , {\lambda _{G3}} = 1 , {\lambda _{G4}} = 0.25 $

令证据可信度分配系数 $ \beta $ =0.6, 则专家G1的证据修正系数为:

$ {\rho _{G1}} = \beta \times {Re} l(G1) + (1 - \beta ) \times {\lambda _{G1}} = 0.9 $

同理得 $ \;{\rho _{G2}} = 0.78 $ , $ {\rho _{G3}} = 1 $ , $ {\rho _{G4}} = 0.66 $ .

根据式(12)得修正后的mass矩阵为:

$ {M_{C1}'} = \left[ {\begin{array}{*{20}{c}} {0.140}&{0.140}&{0.176}&{0.223}&{0.223}&{0.098} \\ {0.101}&{0.116}&{0.216}&{0.186}&{0.161}&{0.220} \\ {0.154}&{0.154}&{0.196}&{0.248}&{0.248}&0 \\ {0.141}&{0.096}&{0.045}&{0.154}&{0.225}&{0.339} \end{array}} \right] $

4.1.4 综合评估

使用图5所示方法对 ${M_{C1}'}$ 进行合成得:

mass(C1)=(0.1336, 0.1260, 0.1577, 0.2038, 0.2158, 0.1631)

同理可得mass(C2)和mass(C3). 然后结合表2的权重值, 根据式(13)求取mass(B1). 以此类推进行逐层合成, 最终得S的隶属度向量:

mass(S)=(0.0156, 0.2124, 0.3460, 0.1819, 0.2056, 0.0385)

得系统的风险等级为V₀即“中”, 该结果与系统的实际安全状态一致, 证明了所提方法的适用性.

根据各元素的mass函数值, 得各元素的风险等级评价结果如图7所示.

根据以上评价结果, 系统管理人员可明确当前系统的薄弱环节以进行针对性的防护, 防护建议如下.

(1) 系统整体的风险等级为“中”, 有提高安全性的必要, 需要对其进行安全管理. 根据系统关键设备的评估结果, 监控终端和PLC的风险评估等级为“高”, 可知系统的薄弱点集中于监控终端和PLC, 需要对两者进行针对性的管理;

(2) 对于监控终端, 评估结果表明其可见性的威胁程度较高, 且主要风险来源于拒绝服务攻击和病毒感染, 因此需要尽可能对系统加载最新的补丁, 采取有效的合规性配置, 对安全域划分的合理性进行检验, 并检查防火墙和入侵检测系统的配置安全性;

(3) 对于PLC来说, 评估结果表明其完整性的威胁程度较高, 且主要风险来源于非法设备的物理接入, 因此需加强对设备的安全边界管理和设备接入的管控措施, 同时应该严格控制机房区域的人员进出.

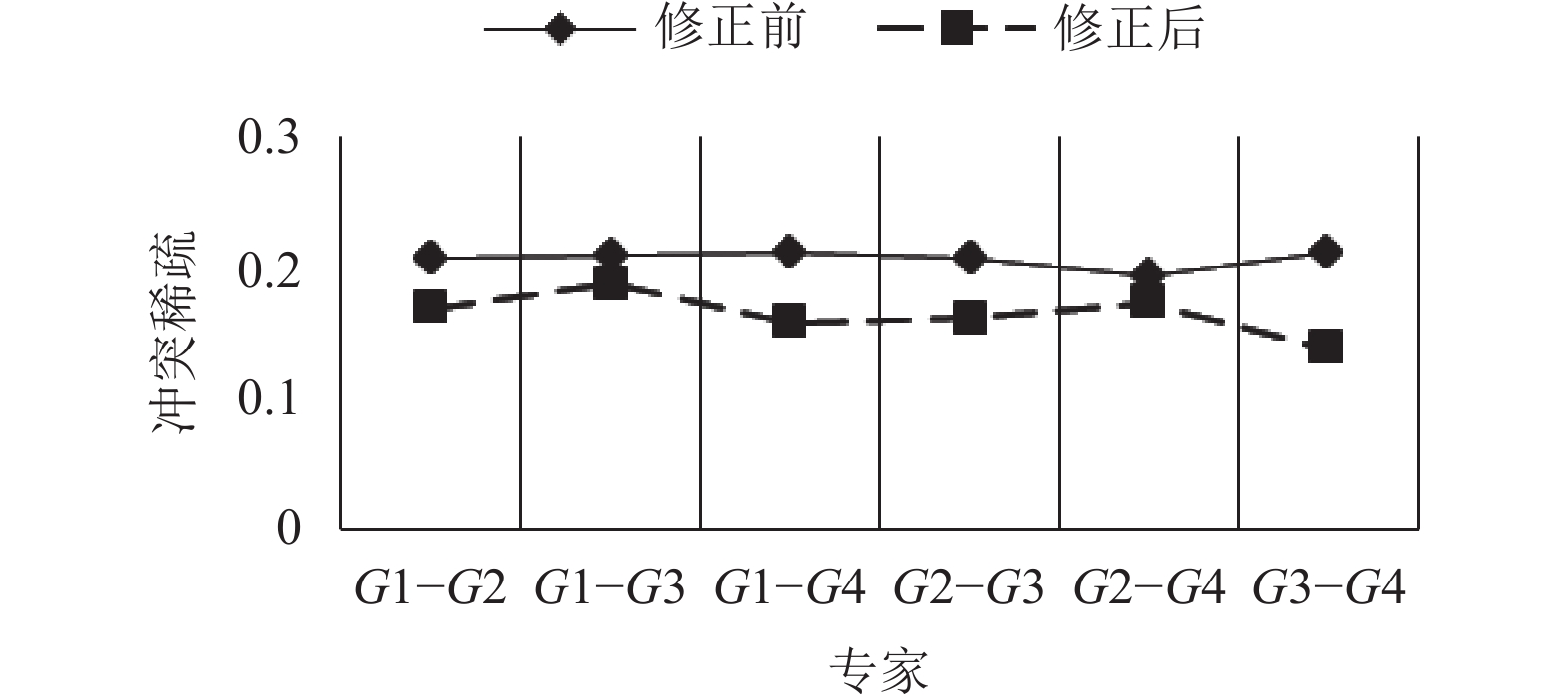
4.2 有效性分析

根据元素C1的原始mass矩阵 $ {M_{C1}} $ 和修正后的mass矩阵 ${M_{C1}'}$ , 得证据修正前后专家间的证据冲突系数如表4所示. 对比如图8所示.

由图8可知, 本文使用的证据修正方法使得专家间的证据冲突程度明显降低, 整体证据冲突系数由0.0096降低为0.0077, 证明了本文证据冲突修正方法的有效性.

同样以C1的mass矩阵 ${M_{C1}'}$ 为例, 分别使用传统方法和本文的方法进行证据合成, 得到的结果以及运行时间如表5所示.

结果表明, 传统方法和本文方法得系统可用性的风险等级结果均为“很高”, 然而对比发现, 采用本文方法的执行时间仅为传统方法的1/8, 能够大大提高数据融合的效率.

上述分析证明了本文电力监控系统风险评估方法的有效性.

5 结语

在电力监控系统的风险评估过程中, 构建评估模型时结合系统的特点进行了详细的安全性分析, 并提出了可见性和可控性的安全目标, 层次间关联和层次元素的细化使得对系统的建模更加完整; 将云模型引入证据理论, 能够充分考虑到专家评价意见的模糊性; 使用基于冲突系数和概率函数的证据冲突修正方法和矩阵分析的证据合成算法, 可在一定程度上解决证据冲突的问题和提高风险评估的效率. 本文的工作为电力监控系统的安全管理工作提供了新的思路.