1 引言

置换流水车间调度问题(permutation flow-shop scheduling problem, PFSP)是典型的生产调度问题, 当其规模大于3时已被证明是NP难问题. 群智能算法是一种新兴的元启发式计算技术, 在求解此类复杂优化问题上表现出了很大优势, 已成为越来越多研究者的关注焦点.

群智能算法从问题的很多个解开始, 不断改进直到满足终止条件为止. 由于同时从多个解出发进行寻优, 如果某个解陷入局部最优点, 其他解可能会跳出局部最优点, 因此, 该类算法在优化问题的搜索空间中具有很强的探索能力. 目前, 已有的群智能算法按照算法的基本原理大多数属于模拟群居动物行为的算法, 如粒子群算法(particle swarm optimization, PSO)^[1]、人工蜜蜂群算法(artificial bee colony, ABC) ^[2]、布谷鸟搜索算法(cuckoo search, CS)^[3]等.

PSO 算法模拟了鱼群、鸟群觅食时候有组织的群体行为. PSO算法的基本思想是在搜索空间中随机初始化一个由没有体积没有质量的粒子组成的种群, 将种群中的每个粒子视为优化问题的一个可行解, 解的好坏由适应度函数确定. 每个粒子在解空间中运动, 并由一个速度向量决定其运动的方向和位移. 算法中的每个粒子依赖本身的飞行经验并借鉴种群中其他粒子的飞行经验, 经多次迭代收敛到最优解. 在每一次迭代中, 本身的飞行经验是粒子本身迄今找到的最优解, 其他粒子的飞行经验是整个种群迄今找到的最优解. 作为一种经典的群智能算法, PSO在求解置换流水车间调度问题上得到了应用^[4-6].

人工蜂群算法是受到蜜蜂群体觅食行为的启发而提出的一种群智能算法^[2]. 在ABC中, 每个个体被分为3种类型: 雇佣蜂、跟随蜂和侦查蜂. 其中, 雇佣蜂的数量与跟随蜂的数量是一致的, 各占整个种群的一半. 每一个雇佣蜂对应某一个蜜源, 即优化问题的解, 雇佣蜂将位置信息与适应度信息分享给跟随蜂. 跟随蜂根据雇佣蜂提供的解的信息选择跟随某只蜜蜂继续挖掘高质量的解, 一般采用轮盘赌的方式选择跟随哪一只雇佣蜂. 如果某个解一直没有得到改善, 则它就变成一只侦查蜂, 在算法中用随机生成一个新解来表示一只侦查蜂. 人工蜂群算法思想简单, 参数少, 优化效果良好, 在数值优化和工程优化中得到了广泛的应用^{[7, 8]}.

CS是文献[3]中提出的一种基于布谷鸟的巢寄生性和莱维飞行机制的群智能优化算法. 在CS算法中有两种更新解的方式, 一种是布谷鸟寻找寄生巢下蛋的方式, 另一种是寄生鸟以一定的概率发现外来蛋后重新筑巢的方式. 前一种方式采用了莱维飞行的方式, 后一种方式采用随机方式或者莱维飞行的方式. 莱维飞行方式是一种长步长与短步长相结合的方式^[9]. CS也在求解置换流水车间调度问题上得到了应用^[10]. 文献[11]将CS算法与差分进化算法(differential evolution, DE)^[12]相结合, 提出了混合的CSDE算法并求解了工程优化问题.

综上, 大多数群智能算法都是受到动物行为而产生的. 近来, 一种受到群体免疫概念启发的冠状病毒群体免疫优化算法(coronavirus herd immunity optimization, CHIO)被提出来^[13]. 在自然界中, 当病毒找到宿主后, 会在人群中迅速传播和进化. 冠状病毒感染的传播速度取决于感染者如何与其他社会成员直接接触群体. 卫生部门建议用两种方法对抗病毒传播, 一种是将受感染者与他们的家人隔离, 包围社区并隔离所有他们接触的人; 另一种是利用群体免疫机制来阻止病毒传播, 即当一个群体中大部分人拥有免疫能力时, 他们对易感个体的保护行为就产生了群体免疫. 群体免疫是一种状态, 当大多数人免疫时, 人群达到这种状态, 从而防止病毒传播. CHIO 就是模拟了群体免疫策略和社会距离概念而提出的群智能算法.

本研究在原始的CHIO基础上进行了改进, 针对置换流水车间调度问题, 提出了动态改变扩展速率的策略, 提高了解的探索与开发的平衡能力. 同时, 在算法的重生阶段之后增加了基于差分进化算子的交叉阶段, 对群体进行最优解的挖掘, 提高了算法的寻优能力.

2 PFSP问题描述

PFSP的描述如下: $ n $ 个作业 $ N = \{ {J_1}, {J_2}, \cdots, {J_n}\} $ 在一系列 $ m $ 台机器 $ M = \{ {M_1}, {M_2}, \cdots, {M_m}\} $ 上依次处理. $ i $ 表示作业, $ j $ 表示机器. 每个作业由一组操作组成, 每个操作都将在特定的机器上执行, 所有作业 $ {J_i} = \{ {U_{i1}}, {U_{i2}}, \cdots, {U_{im}}\} $ 的机器加工顺序相同. 机器 $ {M_j} $ 上作业 $ {J_i} $ 的处理时间用 ${P_{ij}} \; (i = 1, 2, \cdots, n;j = 1, 2, \cdots, m)$ 表示. 每个作业只能在一台机器上处理, 每台机器一次只能处理一个作业. PFSP常见的求解目标是找到最小化最大完工时间( $ {C_{\max }} $ )的作业排列. 作业排列表示为 $ \pi = \{ {\pi _1}, {\pi _1}, \cdots, {\pi _n}\} $ . $ C({\pi _i}, m) $ 表示 $ {\pi _{\text{i}}} $ 在机器 $ m $ 上的作业完成时间.

根据以上对PFSP的描述, 给出其数学描述具体如下:

$ {{C(}}{\pi _1}{{, 1) = }}{{{P}}_{{\pi _1}, 1}} $

(1)

$ {{C(}}{\pi _i}{{, 1) = C(}}{\pi _{i - 1}}{{, 1) + }}{{{P}}_{{\pi _i}, 1}}, i = 2, \cdots, n $

(2)

$ {{C(}}{\pi _1}{{, j) = C(}}{\pi _1}{{, j - 1) + }}{{{P}}_{{\pi _1}, j}}, j = 2, \cdots, m $

(3)

$ \begin{split} {{C(}}{\pi _i}{{, j) = {\rm{max}}(C}}&({\pi _{i - 1}}{{, j), C(}}{\pi _i}{{, j - 1)) + }}{{{P}}_{{\pi _i}, j}}, \\ & i = 2, \cdots, n;j = 2, \cdots, m \end{split} $

(4)

最大化完工时间可以定义为:

$ {C_{\max }}(\pi ) = C({\pi _n}, m) $

(5)

3 混合算法设计 3.1 原始的CHIO算法

原始的CHIO算法是受到群体免疫的概念而形成的一种群智能算法^[13]. 假设优化问题搜索空间的维度是 $ D $ , 种群大小是 $ N $ . 问题的解可以用向量 $ {X^i} = (X_1^i, X_2^i, \cdots, X_D^i) $ 表示. 其中, $ i $ 是一个 $ [1, N] $ 内的随机数. 所有个体分为3种类型: 易感个体、感染个体与免疫个体.

所有个体的类型可以用向量 $ S = ({S^1}, {S^2}, \cdots, {S^N}) $ 表示. $ {S^i} = 0 $ 表示个体属于易感个体, $ {S^i} = 1 $ 表示个体属于感染个体, $ {S^i} = 2 $ 表示个体属于免疫个体. CHIO的伪代码如算法1所示. 从伪代码可以看出, CHIO算法包括3个主要阶段: 群体免疫进化阶段、群体更新阶段与重生阶段.

算法1. CHIO算法

1) 初始化种群( $ \scriptstyle X $ )、状态向量( $\scriptstyle S $ )、参数 $\scriptstyle BR $ ;

2) 　 repeat

3) 　　遍历每个个体

　　　　// 群体免疫进化阶段:

4)　　　开始遍历每个维度

5)　　　　生成随机数 $\scriptstyle r $

6)　　　　if ( $\scriptstyle r $ < ( $\scriptstyle BR/3 $ )

7)　　　　　随机选择一个感染个体

8)　　　　　根据式(6)生成新个体

9)　　　　　 $\scriptstyle isCorona(x) $ =1

10)　　　　elseif ( $\scriptstyle r $ < ( $\scriptstyle 2BR/3 $ )

11)　　　　　随机选择一个易感个体

12)　　　　　根据式(6) 生成新个体

13)　　　　else

14)　　　　　随机选择一个免疫个体

15)　　　　　根据式(6)生成新个体

16)　　　结束遍历维度

　　　　// 群体更新阶段:

17)　　　if (新个体的适应度好于原来个体的适应度)

18)　　　　对两个个体采用贪婪选择

19)　　　else

20)　　　　if (原来个体是感染的个体)

21)　　　　　记录没有改进的次数

22)　　　　endif

23)　　　if ((新个体适应度小于平均适应度) and (个体的状态等于0) 　　　　 and $\scriptstyle isCorona(x) $ )

24)　　　　将个体的状态设置为1.

25)　　　endif

26)　　　if((新个体适应度大于平均适应度) and (个体的状态等于1))

27)　　　　　将个体的状态设置为2.

28)　　　endif

　　　　// 重生阶段:

29)　　　　if (个体适应度在预定义的次数内没有得到改善)

30)　　　　　随机生成新个体替换该个体

31)　　　　endif

32)　　　　记录最佳个体

33)　　　结束遍历个体

34)　until(终止条件)

在群体免疫进化阶段, 解的每个维度依赖式(6)进行更新:

$ X_j^i(t + 1) = X_j^i(t) + \phi _j^i(X_j^i(t) - X_j^k(t)) $

(6)

其中, $ j \in (1, 2, \cdots, D) $ , $ \phi _j^i $ 是[−1, 1]区间内的一个随机数. $ k $ 是随机选择的个体, 其值是由扩展速率参数 $ BR $ 决定. 假设 $ r $ 是一个随机数, 如果 $ r \in [0, BR/3) $ , 则 $ k $ 从感染个体中随机选择; 如果 $ r \in [BR/3, 2BR/3) $ , 则 $ k $ 从易感个体中随机选择; 如果 $ r \in [2BR/3, BR) $ , 则 $ k $ 从免疫个体中随机选择.

在群体更新阶段, 每一个个体的解的适应度根据其目标函数进行计算. 所有个体的适应度可以用向量 $ F = ({F^1}, {F^2}, \cdots, {F^N}) $ 表示. 用一个向量记录感染个体的适应度没有得到改善的次数. 根据式 (7) 对状态向量进行更新:

$ {S^i} = \left\{ {\begin{array}{*{20}{l}} {1, {F^i} < {{\rm{mean}}}(F){\text{ \& }}{S^i} = 0{\text{ \& }}isCorona({X^i})} \\ {2, {F^i} \geqslant {\rm{mean}}(F){\text{ \& }}{{{S}}^i} = 1} \end{array}} \right. $

(7)

其中, $ i \in [1, N] $ , $ {\text{mean}}(F) $ 是种群的平均适应度, $ isCorona ({X^i}) $ 表示个体是否是感染者个体.

在重生阶段, 如果感染个体的适应度没有得到改善的次数到达预定义的次数, 则随机生成一个个体替换当前个体.

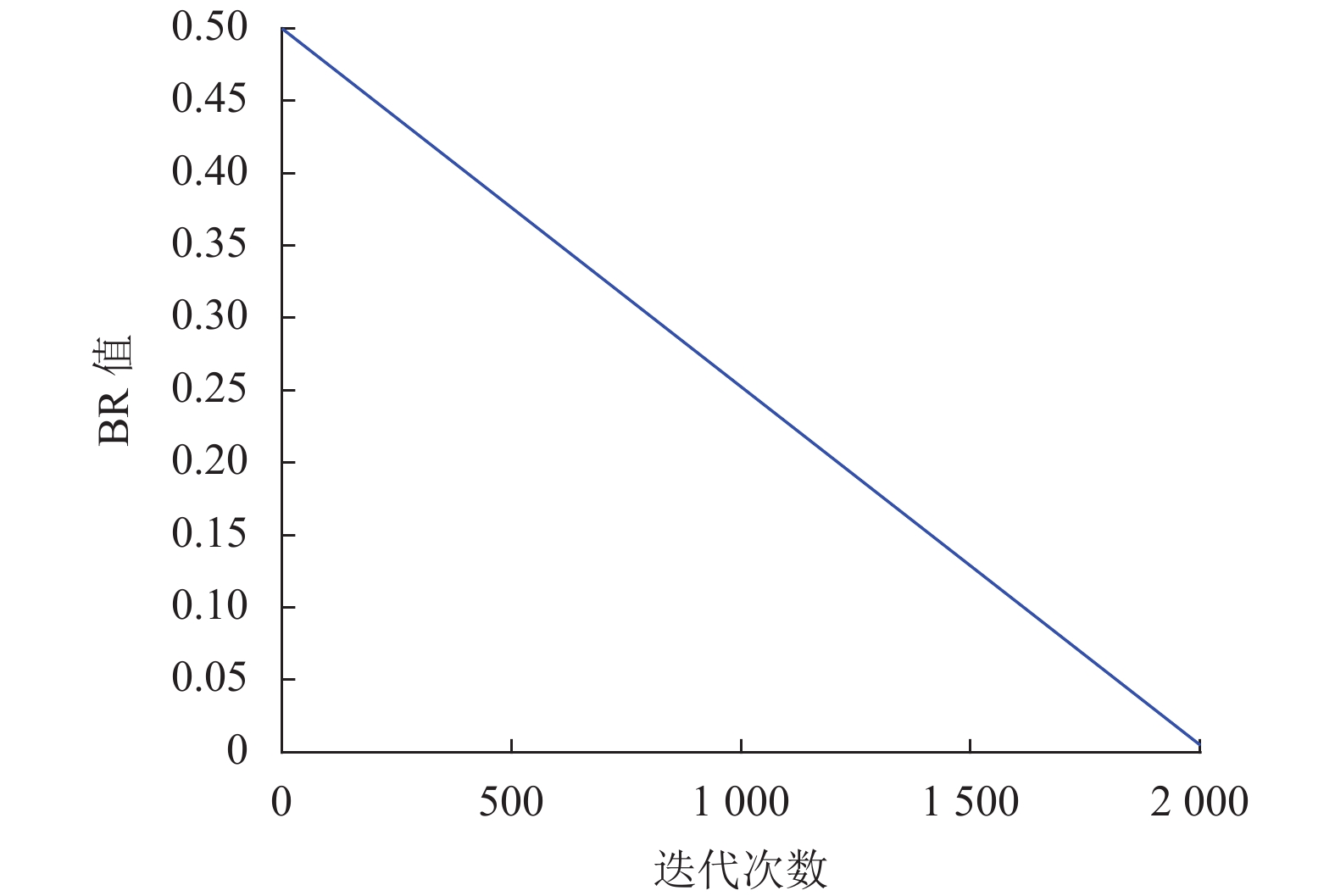
3.2 扩展速率参数设计

在原始的CHIO算法中, 扩展速率参数 $ BR $ 是一个用来决定解更新算子的重要参数, 其值越小, 算法探索能力越弱; 其值越大, 算法的探索能力越强. 在原始的CHIO算法中, $ BR $ 被设置为常数 0.01. 为了平衡算法的探索能力与开发能力, 提出一种动态调整扩展速率参数的方法, 如式(8)所示:

$ BR = B{R^{\max }} - (t/{t^{\max }}) \times (B{R^{\max }} - B{R^{\min }}) $

(8)

其中, $ B{R^{\max }} $ 是扩展速率参数的最大值, $ B{R^{\min }} $ 是扩展速率参数的最小值, $ {t^{\max }} $ 是算法的最大迭代次数, $ t $ 是算法当前的迭代次数. 图1是扩展速率参数根据式(8)从0.5动态调整到0.005的效果.

3.3 混合CHIO算法

为了增强CHIO算法的局部开发能力, 在原始算法的3个阶段后加入基于DE^[12]的解的开发阶段, 形成一种混合的CHIO算法(Hybrid CHIO, HCHIO). DE具有很强的收敛能力^[14]. 算法2给出了交叉阶段的伪代码. 图2给出了HCHIO的流程图.

算法2. 交叉算法

1) 设置参数交叉概率( $\scriptstyle CR $ )与差分权重( $\scriptstyle F $ );

2) 开始遍历个体

3)　　　开始遍历每个维度

4)　　　　　生成随机数 $\scriptstyle r $

5)　　　　　　if ( $\scriptstyle r $ < $\scriptstyle CR $ )

6)　　　　　　　根据式(9)生成新个体

7)　　　　　　endif

8)　　　结束遍历维度

9)　　　计算新个体适应度

10)　　 在新个体与原个体之间采用贪婪选择

11) 结束遍历个体

在交叉阶段, 差分变异算子是主要的操作, 该算子如式(9)所示:

$ {X_{ij}} = {X_{rj}} + F({X_{pj}} - {X_{qj}}) $

(9)

其中, $ i, {\text{ }}r, {\text{ }}p, {\text{ }}q $ 是4个区间 $ [1, N] $ 上的不同数字. $ F $ 是差分权重.

在交叉阶段, 每个个体根据交叉概率都有机会执行差分变异算子. 所以, 该阶段可以大范围挖掘最优解.

4 仿真实验 4.1 实验方案

实验采用Reeves测试集作为基准测试实例, 该测试集是一种中到大规模问题测试集^{[15, 16]}. 实验结果用每组测试集的最佳值的相对百分比偏差与平均值的相对百分比偏差表示.

每组实例上的最佳值的平均相对偏差:

$ bre = \left[ {\sum\nolimits_{i = 1}^k {(\min ({C^{\max }}) - {C^*})/{C^*}} } \right]/k $

(10)

每组实例上的平均值的平均相对偏差:

$ are = \left[ {\sum\nolimits_{i = 1}^k {({\rm{avg}}({C^{\max }}) - {C^*})/{C^*}} } \right]/k $

(11)

其中, $ {C^*} $ 是在参考文献中已知的最优结果. $ k $ 是测试集的测试实例个数.

将原始的CHIO算法^[13]、PSO算法^[1]、ABC算法^[2]、CS算法^[3]、CSDE算法^[11]以及DE算法^[12]作为对比算法. 所有算法采用最小位置值^[17]的方式实现置换流水车间调度问题解的编码与解码. 对比算法中的参数按照参考文献中进行设置. 使用适应度评估次数作为算法终止条件, 最大评估次数设置为20000. 为了得到有效的实验结果, 每种算法独立运行20次.

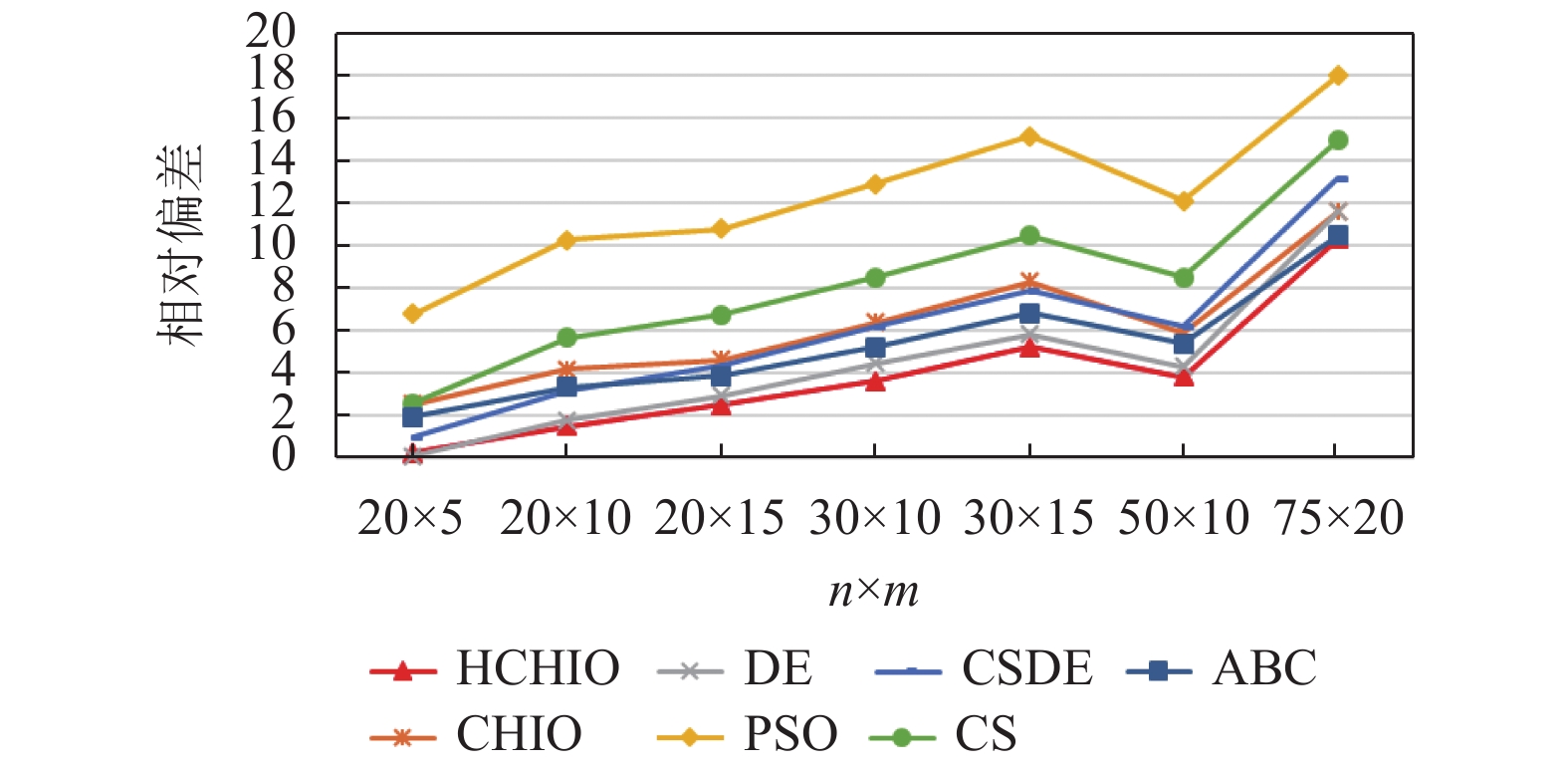
4.2 实验结果与分析

以最小化最大完工时间为优化目标在Reeves测试实例上进行实验. 表1与表2分别给出了各个算法在7组Reeves测试实例上的最佳值相对偏差与平均值相对偏差. 图3给出了不同算法在Reeves测试实例上最佳值相对偏差的折线图, 图4给出了不同算法在Reeves测试实例上平均值相对偏差的折线图.

从表1可以看出, HCHIO在7组测试集取得了最好的结果. 从表2上可以看出, HCHIO在7组测试集取得了最好的平均值. 图3与图4 以折线图的形式给出了直观的展示.

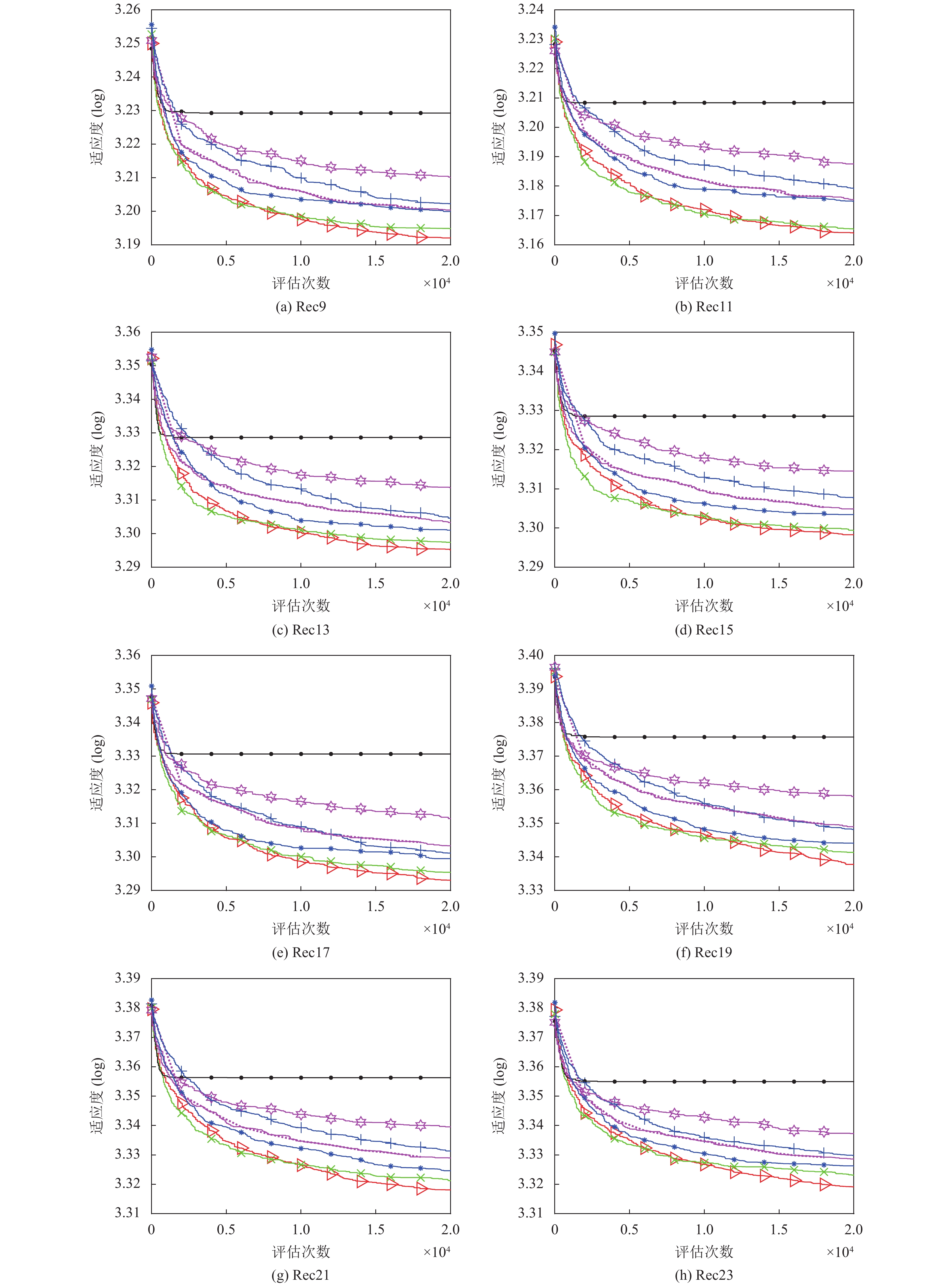
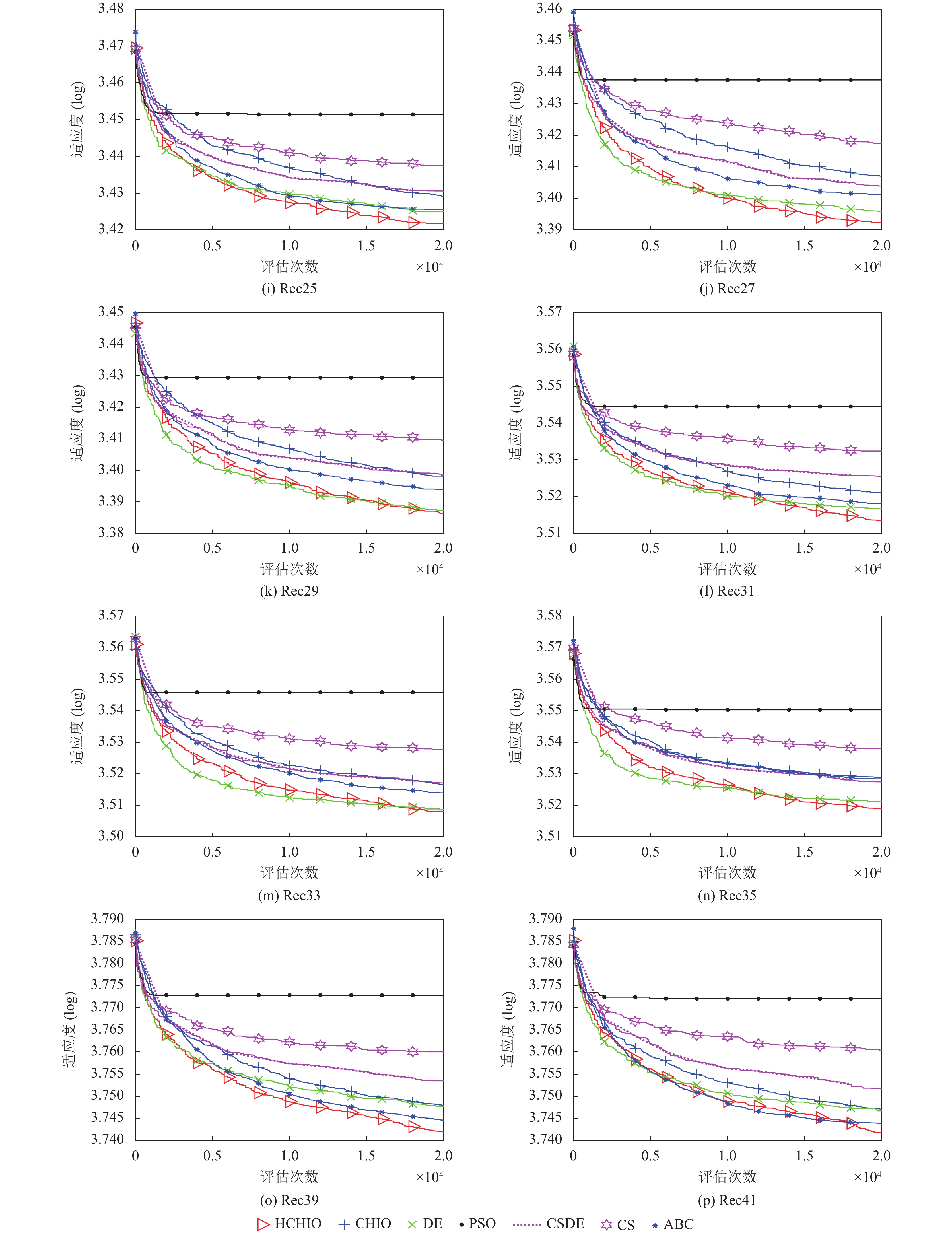
HCHIO在21个Reeves测试实例的16个单实例上取得了最好的结果, 图5给出不同算法在这16个实例上的收敛曲线. 从收敛曲线上可以清晰地看到, HCHIO 相对于其他6种比较算法具有很强的收敛性. 从收敛曲线上看出, 相对于原始的CHIO算法, 本文提出的动态改变扩展速率参数的策略与基于DE的交叉策略在寻优精度上起到了很大的改善作用.

5 结论与展望

在原始的CHIO算法的基础上采用动态改变扩展速率参数的策略以平衡解的探索能力与开发能力, 增加基于DE的交叉阶段以增强算法对最优解的开发能力, 从而形成一种混合算法. 针对PFSP问题, 以最小化最大完工时间为优化目标, 以原始CHIO算法以及其他6个智能算法作为对比算法, 在21个Reeves实例上进行了仿真实验, 实验结果表明了提出的改进策略有效提高了解的寻优能力和收敛速度.