随着物联网技术和5G技术的发展, 产生的各种新型应用, 对网络的时延和带宽提出了更高的要求. 但由于终端设备的计算和存储能力的限制, 无法处理和存储如此庞大的数据. 因此移动边缘计算[1]应运而生, MEC能有效解决时延长、能耗高和数据不安全等问题. 其中计算卸载技术[2]作为MEC的关键技术之一, 通过合理的卸载决策和资源分配策略将终端设备上运行的任务卸载到边缘服务器, 能够减少任务完成时延和设备的能耗, 提高设备性能. 而通过将D2D技术与MEC结合, 可以更进一步降低数据传输时延和能耗.
对于计算卸载技术, 目前已经出现了很多研究成果对其进行研究. 文献[3]提出了一种低复杂度的启发式算法来最小化共享频谱中的任务执行延迟. 文献[4]考虑了具有辅助节点的MEC系统, 联合优化了用户和辅助节点的计算和通信资源分配, 使总能耗降至最低. 文献[5]基于一种低复杂度的算法来降低设备能耗. 文献[6]使用线性规划的方法解决卸载决策、延迟和能耗联合优化问题. 文献[7]为了最大程度地减少任务等待时间和能耗, 提出了一种启发式算法, 该算法保证了子任务之间的依赖性并提高了任务效率. 文献[8]提出了一种基于Lyapunov优化的低复杂度的动态计算卸载在线算法, 获得了最优的卸载策略. 文献[9]考虑了包含多个忙碌智能设备和多个空闲智能设备的D2D与MEC协作系统, 基于块坐标下降法和凸优化技术的两阶段迭代算法解决卸载决策和资源分配的联合优化问题, 获得最佳卸载策略和资源分配策略, 最小化了系统的总能耗. 文献[10]建立了一个具有通信资源和计算资源约束的混合整数非线性问题, 开发了一种优化算法来解决此问题. 文献[11-13]同样考虑了在MEC环境下引入D2D技术进行协作, 来考虑任务的卸载情况 .
然而以上文献都仅考虑了单个设备上任务的卸载情况. 对于不同设备之间任务具有依赖性的研究非常少, 几乎没有. 实际上, 在不同设备上执行的任务通常也是具有相关依赖性的. 文献[14]虽然考虑了MEC系统环境下两个不同设备之间的任务相关性, 但没有考虑与D2D技术进行协作来优化系统性能. 虽然业内也在MEC环境中引入了D2D技术来优化系统性能, 但是对于MEC与D2D技术协作网络环境中不同设备任务之间任务具有相关性的研究, 就作者目前所知, 还没有相关文献对此方面进行研究. 同时, 在优化卸载决策方面文献[14]提出的算法复杂度仍然很高, 本文提出的线性搜索算法更进一步的优化了卸载决策, 并且本文将场景扩展到多设备. 因此, 本文在文献[14]的基础上进行了进一步的优化研究, 联合优化了设备任务完成时延和能耗.
本文在第1节中对系统进行了分析, 建立了通信、计算和任务依赖模型. 在第2节中运用凸优化方法得到最佳资源分配. 在第3节中提出了一种降低复杂度的线性搜索算法来优化卸载决策. 最后通过仿真实验进行性能评估.
1 系统模型 1.1 MEC与D2D协作网络系统模型本文考虑了多个设备的MEC与D2D协作网络. 如图1所示, MEC与D2D协作网络系统模型. 其中ds和d2分别表示设备S、设备2与MEC服务器之间的距离, 其中,

|
图 1 MEC与D2D协作网络系统模型 |
设备S和设备2分别具有
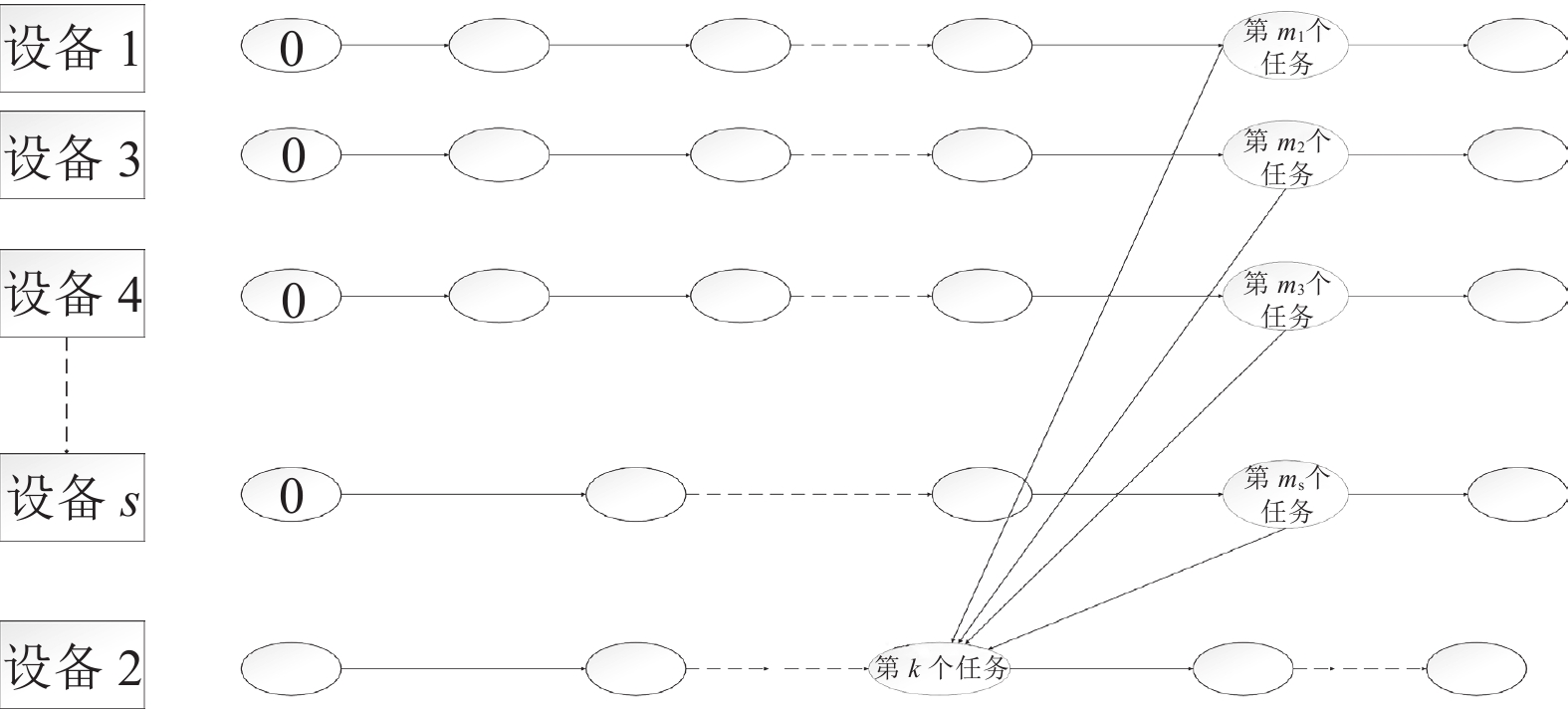
|
图 2 不同设备间调用图模型 |
采用
对于每个设备分配带宽相等的正交信道, 用
| $ \mathop R\nolimits_{i, j}^u = W\mathop {\log }\nolimits_2 \left( {1 + \frac{{\mathop p\nolimits_{i, j} \mathop h\nolimits_{i, j} }}{{\mathop \sigma \nolimits^2 }}} \right) $ | (1) |
其中,
下载速率为:
| $ \mathop R\nolimits_{i, j}^d = W\mathop {\log }\nolimits_2 \left( {1 + \frac{{\mathop p\nolimits_0 \mathop h\nolimits_{i, j} }}{{\mathop \sigma \nolimits^2 }}} \right) $ | (2) |
其中,
设备
| $ \mathop R\nolimits^{s, 2} = W\mathop {\log }\nolimits_2 \left( {1 + \frac{{\mathop p\nolimits_{\mathop m\nolimits_{{s}} + 1, s}' \mathop h\nolimits_{\mathop m\nolimits_{{s}} + 1, s}' }}{{\mathop \sigma \nolimits^2 }}} \right) $ | (3) |
其中,
信道增益为:
| $ \mathop h\nolimits_{i, j} = g\mathop {\left( {\frac{{3\times\mathop {10}\nolimits^8 }}{{4\pi \mathop F\nolimits_c \mathop d\nolimits_r }}} \right)}\nolimits^{pl} $ | (4) |
其中,
下面给出了执行和传输任务的时间和能耗.
本地执行任务
| $ \mathop t\nolimits_{i, j}^l = \frac{{\mathop L\nolimits_{i, j} }}{{\mathop f\nolimits_{i, j} }} $ | (5) |
其中,
本地完成任务
| $ \mathop e\nolimits_{i, j}^l = k\mathop L\nolimits_{i, j} \mathop {\mathop f\nolimits_{i, j} }\nolimits^2 $ | (6) |
其中,
服务器执行任务
| $ \mathop t\nolimits_{i, j}^c = \frac{{\mathop L\nolimits_{i, j} }}{{\mathop f\nolimits_0 }} $ | (7) |
其中,
将任务
| $ \mathop t\nolimits_{i, j}^u = \frac{{\mathop O\nolimits_{i - 1, j} }}{{\mathop R\nolimits_{i, j}^{{u}} }} $ | (8) |
其中,
将任务
| $ \mathop {{e}}\nolimits_{i, j}^u = \mathop p\nolimits_{i, j} \mathop t\nolimits_{i, j}^u = \frac{{\mathop \sigma \nolimits^2 \mathop t\nolimits_{i, j}^u }}{{\mathop h\nolimits_{i, j} }}\left( {\mathop 2\nolimits^{\frac{{\mathop O\nolimits_{i - 1, j} }}{{W\mathop t\nolimits_{i, j}^u }}} - 1} \right) $ | (9) |
由文献[15]可知式(9)是关于
从服务器返回到设备的下载时间:
| $ \mathop t\nolimits_{i, j}^d = \frac{{\mathop O\nolimits_{i - 1, j} }}{{\mathop R\nolimits_{i, j}^d }} $ | (10) |
将任务从设备
| $ \mathop t\nolimits_{\mathop m\nolimits_{{s}} + 1, s}^{s, 2} = \frac{{\mathop O\nolimits_{\mathop m\nolimits_{{s}} , s} }}{{\mathop R\nolimits^{s, 2} }} $ | (11) |
其中,
将任务从设备
| $ \mathop {{e}}\nolimits_{i, j}^{s, 2} = \mathop p\nolimits_{\mathop m\nolimits_{{s}} + 1, s}' \mathop t\nolimits_{\mathop m\nolimits_{{s}} + 1, s}^{s, 2} = \frac{{\mathop \sigma \nolimits^2 \mathop t\nolimits_{\mathop m\nolimits_{{s}} + 1, s}^{s, 2} }}{{\mathop h\nolimits_{\mathop m\nolimits_{{s}} + 1, s}' }}\left( {\mathop 2\nolimits^{\frac{{\mathop O\nolimits_{\mathop m\nolimits_{{s}} , s} }}{{W\mathop t\nolimits_{\mathop m\nolimits_{{s}} + 1, s}^{s, 2} }}} - 1} \right) $ | (12) |
由于设备
由以上分析可知, 设备
| $ \begin{split} \mathop T\nolimits_s =& \sum\limits_{{{i}} = 1}^{\mathop m\nolimits_{{s}} } {\left[ {\left( {1 - \mathop a\nolimits_{i, s} } \right)\mathop t\nolimits_{i, s}^l + \mathop a\nolimits_{i, s} \mathop t\nolimits_{i, s}^c } \right]} \\& +\sum\limits_{{{i}} = 1}^{\mathop m\nolimits_{{s}} {\text{ + 1}}} {\left[ {\mathop a\nolimits_{i, s} \left( {1 - \mathop a\nolimits_{i - 1, s} } \right)\mathop t\nolimits_{i, s}^u + \mathop a\nolimits_{i - 1, s} \mathop {\left( {1 - \mathop a\nolimits_{i, s} } \right)t}\nolimits_{i, s}^d } \right]} \\ \end{split} $ | (13) |
由于设备间任务的依赖关系, 在式(14)的最后一行关系式中描述了设备间任务的依赖关系. 当设备
| $ \begin{split} \mathop E\nolimits_s =& \sum\limits_{{{i}} = 1}^{\mathop m\nolimits_{{s}} } {\left[ {\left( {1 - \mathop a\nolimits_{i, s} } \right)\mathop {{e}}\nolimits_{i, s}^l + \mathop a\nolimits_{i, s} \mathop {\left( {1 - \mathop a\nolimits_{i - 1, s} } \right)e}\nolimits_{i, s}^u } \right]} \\&+ \left( {1 - \mathop a\nolimits_{\mathop m\nolimits_{{s}} , s} } \right)\left( {1 - \mathop a\nolimits_{k, 2} } \right)\mathop {{e}}\nolimits_{\mathop m\nolimits_{{s}} + 1, s}^{s, 2} + \mathop a\nolimits_{k, 2} \left( {1 - \mathop a\nolimits_{\mathop m\nolimits_{{s}} , s} } \right)\mathop {{e}}\nolimits_{\mathop m\nolimits_{{s}} + 1}^u \end{split} $ | (14) |
由于设备2的第
| $ \begin{split} \mathop T\nolimits_s^{{\text{wait}}} =& \sum\limits_{{{i}} = 1}^{\mathop m\nolimits_{{s}} } {\left[ {\left( {1 - \mathop a\nolimits_{i, s} } \right)\mathop t\nolimits_{i, s}^l + \mathop a\nolimits_{i, s} \mathop t\nolimits_{i, s}^c } \right]} \\& +\sum\limits_{{{i}} = 1}^{\mathop m\nolimits_{{s}} } {\left[ {\mathop a\nolimits_{i, s} \left( {1 - \mathop a\nolimits_{i - 1, s} } \right)\mathop t\nolimits_{i, s}^u + \mathop a\nolimits_{i - 1, s} \mathop {\left( {1 - \mathop a\nolimits_{i, s} } \right)t}\nolimits_{i, s}^d } \right]} \\& +\left( {1 - \mathop a\nolimits_{\mathop m\nolimits_{{s}} , s} } \right)\left( {1 - \mathop a\nolimits_{k, 2} } \right)\mathop t\nolimits_{\mathop m\nolimits_{{s}} + 1, s}^{s, 2} + \mathop a\nolimits_{k, 2} \left( {1 - \mathop a\nolimits_{\mathop m\nolimits_{{s}} , s} } \right)\mathop t\nolimits_{\mathop m\nolimits_{{s}} + 1, s}^u \\& +\mathop a\nolimits_{\mathop m\nolimits_{{s}} , s} \left( {1 - \mathop a\nolimits_{k, 2} } \right)\frac{{\mathop O\nolimits_{\mathop m\nolimits_{{s}} , s} }}{{\mathop R\nolimits_{k, 2}^d }} \\ \end{split} $ | (15) |
等待设备2第
| $ \begin{split} \mathop T\nolimits_2^{{\text{wait}}} =& \sum\limits_{{{i}} = 1}^{k - 1} {\left[ {\left( {1 - \mathop a\nolimits_{i, 2} } \right)\mathop t\nolimits_{i, 2}^l + \mathop a\nolimits_{i, 2} \mathop t\nolimits_{i, 2}^c } \right]} \\& +\sum\limits_{{{i}} = 1}^k {\left[ {\mathop a\nolimits_{i, 2} \left( {1 - \mathop a\nolimits_{i - 1, 2} } \right)\mathop t\nolimits_{i, 2}^u + \mathop a\nolimits_{i - 1, 2} \mathop {\left( {1 - \mathop a\nolimits_{i, 2} } \right)t}\nolimits_{i, 2}^d } \right]} \\ \end{split} $ | (16) |
令
设备2的任务完成时间为:
| $ \begin{split} \mathop T\nolimits_2 =& \max \left\{ {\mathop T\nolimits_1^{{\text{wait}}} , \mathop T\nolimits_2^{{\text{wait}}} , \cdots, \mathop T\nolimits_s^{{\text{wait}}} } \right\} \\& +\sum\limits_{{{i}} = k}^n {\left[ {\left( {1 - \mathop a\nolimits_{i, 2} } \right)\mathop t\nolimits_{i, 2}^l + \mathop a\nolimits_{i, 2} \mathop t\nolimits_{i, 2}^c } \right]} \\& +\sum\limits_{{{i}} = k + 1}^{n + 1} {\left[ {\mathop a\nolimits_{i, 2} \left( {1 - \mathop a\nolimits_{i - 1, 2} } \right)\mathop t\nolimits_{i, 2}^u + \mathop a\nolimits_{i - 1, 2} \mathop {\left( {1 - \mathop a\nolimits_{i, 2} } \right)t}\nolimits_{i, 2}^d } \right]} \\ \end{split} $ | (17) |
设备2消耗的能耗为:
| $ \mathop E\nolimits_2 = \sum\limits_{{{i}} = 1}^n {\left[ {\left( {1 - \mathop a\nolimits_{i, 2} } \right)\mathop {{e}}\nolimits_{i, 2}^l + \mathop a\nolimits_{i, 2} \mathop {\left( {1 - \mathop a\nolimits_{i - 1, 2} } \right)e}\nolimits_{i, 2}^u } \right]} $ | (18) |
设备总性能指标为:
| $ \begin{split} \eta \left( {\left\{ {\mathop a\nolimits_{i, j} } \right\}, \left\{ {\mathop p\nolimits_{i, j} } \right\}, \left\{ {\mathop f\nolimits_{i, j} } \right\}} \right) =& \mathop \eta \nolimits_1 + \mathop \eta \nolimits_2 {\rm{ + }}\cdots{\rm{ + }}\mathop \eta \nolimits_s \\ =&\mathop \beta \nolimits_1^T \mathop T\nolimits_1 + \mathop \beta \nolimits_1^E \mathop E\nolimits_1 + \mathop \beta \nolimits_2^T \mathop T\nolimits_2 \\& +\mathop \beta \nolimits_2^E \mathop T\nolimits_2 + \cdots + \mathop \beta \nolimits_s^T \mathop T\nolimits_s + \mathop \beta \nolimits_s^E \mathop E\nolimits_s \end{split} $ | (19) |
其中,
| $ \begin{split}& \mathop {0 \lt \beta }\nolimits_1^T \lt 1,\; 0 \lt \mathop \beta \nolimits_1^E \lt 1,\; \mathop {0 \lt \beta }\nolimits_2^T \lt 1,\; 0 \lt \mathop \beta \nolimits_2^E \lt 1, \cdots, \mathop {0 \lt \beta }\nolimits_s^T \lt\\& 1,\; 0 \lt \mathop \beta \nolimits_s^E \lt 1,\; \mathop \beta \nolimits_s^E = 1 - \mathop \beta \nolimits_s^T \end{split} $ |
所以问题公式化为式(20):
| $ \begin{split}& P(1)\\& \mathop {\min }\limits_{\left( {\left\{ {\mathop a\nolimits_{i, j} } \right\}, \left\{ {\mathop p\nolimits_{i, j} } \right\}, \left\{ {\mathop f\nolimits_{i, j} } \right\}} \right)} \eta \left( {\left\{ {\mathop a\nolimits_{i, j} } \right\}, \left\{ {\mathop p\nolimits_{i, j} } \right\}, \left\{ {\mathop f\nolimits_{i, j} } \right\}} \right) \end{split} $ |
| $ {\rm s.t.}\left\{ {\begin{split} & 0 \leqslant \mathop p\nolimits_{i, j} \leqslant \mathop P\nolimits_{\rm peak} , \\& 0 \leqslant \mathop p\nolimits_{\mathop m\nolimits_s + 1, s}' \leqslant \mathop P\nolimits_{\rm peak} , \\& 0 \leqslant \mathop f\nolimits_{i, j} \leqslant \mathop f\nolimits_{\rm peak} , \\& \mathop a\nolimits_{i, j} \in \left\{ {0, 1} \right\}, \forall i, j \end{split} } \right.$ | (20) |
其中, Ppeak表示设备发射功率的峰值, fpeak表示设备CPU计算能力的峰值. 由式(5), 式(8), 式(11)可知
| $ \begin{split}& P(2) \\& \mathop {\min }\limits_{\left( {\left\{ {\mathop a\nolimits_{i, j} } \right\}, \left\{ {\mathop t\nolimits_{i, j}^l } \right\}, \left\{ {\mathop t\nolimits_{i, j}^u } \right\}, \left\{ {\mathop t\nolimits_{\mathop m\nolimits_s + 1, s}^{s, 2} } \right\}, t} \right)} \eta \left( {\left\{ {\mathop a\nolimits_{i, j} } \right\}, \left\{ {\mathop t\nolimits_{i, j}^l } \right\}, \left\{ {\mathop t\nolimits_{i, j}^u } \right\}, \left\{ {\mathop t\nolimits_{\mathop m\nolimits_s + 1, s}^{s, 2} } \right\}, t} \right) \end{split} $ |
| $ {\rm s.t.}\left\{ {\begin{split} & \mathop T\nolimits_1^{{\text{wait}}} \leqslant t, \mathop T\nolimits_2^{{\text{wait}}} \leqslant t, \cdots, \mathop T\nolimits_s^{{\text{wait}}} \leqslant t \\& \frac{{\mathop L\nolimits_{i, j} }}{{\mathop f\nolimits_{\rm peak} }} \leqslant \mathop t\nolimits_{i, j}^l , \\& \dfrac{{\mathop O\nolimits_{i - 1, j} }}{{W\mathop {\log }\nolimits_2 \left( {1 + \dfrac{{\mathop p\nolimits_{\rm peak} \mathop h\nolimits_{i, j} }}{{\mathop \sigma \nolimits^2 }}} \right)}} \leqslant \mathop t\nolimits_{i, j}^u , \\& \frac{{\mathop O\nolimits_{\mathop m\nolimits_s , s} }}{{W\mathop {\log }\nolimits_2 \left( {1 + \dfrac{{\mathop p\nolimits_{\rm peak} \mathop h\nolimits_{\mathop m\nolimits_s + 1, s}' }}{{\mathop \sigma \nolimits^2 }}} \right)}} \leqslant \mathop t\nolimits_{\mathop m\nolimits_s + 1, s}^{s, 2} , \\& \mathop a\nolimits_{i, j} \in \left\{ {0, 1} \right\}, \forall i, j \\ \end{split} } \right.$ | (21) |
由于含有二进制变量
假设固定
| $ \begin{split}& P(3)\\& \mathop {\min }\limits_{\left( {\left\{ {\mathop t\nolimits_{i,j}^l } \right\},\left\{ {\mathop t\nolimits_{i,j}^u } \right\},\left\{ {\mathop t\nolimits_{\mathop m\nolimits_s + 1,s}^{s,2} } \right\},t} \right)} \eta \left( {\left\{ {\mathop t\nolimits_{i,j}^l } \right\},\left\{ {\mathop t\nolimits_{i,j}^u } \right\},\left\{ {\mathop t\nolimits_{\mathop m\nolimits_s + 1,s}^{s,2} } \right\},t} \right) \end{split} $ |
| $ {\rm s.t.}\left\{ {\begin{split} & \mathop T\nolimits_1^{{\rm{wait}}} \leqslant t,\mathop T\nolimits_2^{{\rm{wait}}} \leqslant t, \cdots ,\mathop T\nolimits_s^{{\rm{wait}}} \leqslant t\\ & \dfrac{{\mathop L\nolimits_{i,j} }}{{\mathop f\nolimits_{\rm peak} }} \leqslant \mathop t\nolimits_{i,j}^l ,\\ & \dfrac{{\mathop O\nolimits_{i - 1,j} }}{{W\mathop {\log }\nolimits_2 \left( {1 + \dfrac{{\mathop p\nolimits_{\rm peak} \mathop h\nolimits_{i,j} }}{{\mathop \sigma \nolimits^2 }}} \right)}} \leqslant \mathop t\nolimits_{i,j}^u ,\\ & \dfrac{{\mathop O\nolimits_{\mathop m\nolimits_s ,s} }}{{W\mathop {\log }\nolimits_2 \left( {1 + \dfrac{{\mathop p\nolimits_{\rm peak} \mathop h\nolimits_{\mathop m\nolimits_s + 1,s}' }}{{\mathop \sigma \nolimits^2 }}} \right)}} \leqslant \mathop t\nolimits_{\mathop m\nolimits_s + 1,s}^{s,2} , \end{split} } \right.$ | (22) |
问题
| $ \begin{split} & L\left( {\left\{ {\mathop t\nolimits_{i, j}^u } \right\}, \left\{ {\mathop t\nolimits_{i, j}^l } \right\}, \left\{ {\mathop t\nolimits_{\mathop m\nolimits_s + 1, s}^{s, 2} } \right\}, t, \mathop \lambda \nolimits_1 , \mathop \lambda \nolimits_2 , \cdots, \mathop \lambda \nolimits_s } \right)\\ & =\mathop \eta \nolimits_1 + \mathop \eta \nolimits_2 {\rm{ + }}\cdots{\rm{ + }}\mathop \eta \nolimits_s + \mathop \lambda \nolimits_1 \left( {\mathop T\nolimits_1^{{\rm{wait}}} - t} \right) \\ &\quad + \mathop \lambda \nolimits_2 \left( {\mathop T\nolimits_2^{{\rm{wait}}} - t} \right) + \cdots{\rm{ + }}\mathop \lambda \nolimits_s \left( {\mathop T\nolimits_s^{{\rm{wait}}} - t} \right) \end{split} $ | (23) |
其中,
| $ \left\{ \begin{array}{l} \mathop f\nolimits_{i,s}^* = \left\{ \begin{array}{l} \mathop f\nolimits_{\rm peak} ,\;如果\mathop \beta \nolimits_s^T + \mathop {\mathop \lambda \nolimits_s }\nolimits^* > 2k\mathop \beta \nolimits_s^E \mathop {\mathop f\nolimits_{\rm peak} }\nolimits^3 \\ \sqrt[3]{{\dfrac{{\mathop \beta \nolimits_s^T + \mathop {\mathop \lambda \nolimits_s }\nolimits^* }}{{2k\mathop \beta \nolimits_s^E }}}},\;否则 \end{array} \right.当i \in \{ 1,\cdots,\mathop m\nolimits_s \}时 \\ \mathop f\nolimits_{i,2}^* = \left\{ \begin{array}{l} \left\{ \begin{array}{l} \mathop f\nolimits_{\rm peak} ,\;如果\mathop {\mathop \lambda \nolimits_2 }\nolimits^* > 2k\mathop \beta \nolimits_2^E \mathop f\nolimits_{\rm peak} \\ \sqrt[3]{{\dfrac{{\mathop {\mathop \lambda \nolimits_2 }\nolimits^* }}{{2k\mathop \beta \nolimits_2^E }}}},\;否则 \end{array} \right.当i \in \{ 1,\cdots,k - 1\}时 \\ \left\{ \begin{array}{l} \mathop f\nolimits_{\rm peak} ,\;如果\mathop \beta \nolimits_2^T > 2k\mathop \beta \nolimits_2^E \mathop {\mathop f\nolimits_{\rm peak} }\nolimits^3 \\ \sqrt[3]{{\dfrac{{\mathop \beta \nolimits_2^T }}{{2k\mathop \beta \nolimits_2^E }}}},\;否则 \end{array} \right.当i \in \{ k,\cdots,n\}时 \end{array} \right\} \end{array} \right.{\kern 1pt} {\kern 1pt} $ | (24) |
| $ \begin{array}{l} \left\{ \begin{array}{l} \mathop p\nolimits_{i,s}^* = \left\{ \begin{array}{l} \mathop P\nolimits_{\rm peak} ,\;如果\mathop {{{h}}}\nolimits_{i,s} < \dfrac{{\mathop \sigma \nolimits^2 }}{{\mathop P\nolimits_{\rm peak} }}\left[ {\dfrac{{\mathop A\nolimits_1 }}{{ - W(\mathop { - A}\nolimits_1 \mathop e\nolimits^{ - \mathop A\nolimits_1 } )}} - 1} \right]\\ \dfrac{{\mathop \sigma \nolimits^2 }}{{\mathop h\nolimits_{i,s} }}\left[ {\dfrac{{\mathop B\nolimits_1 }}{{W(\mathop B\nolimits_1 \mathop e\nolimits^{ - 1} )}} - 1} \right],\;否则 \end{array} \right.当i \in \{ 1,\cdots,\mathop m\nolimits_s \}时 \\ \mathop p\nolimits_{i,s}^* = \left\{ \begin{array}{l} \mathop P\nolimits_{\rm peak} ,\;如果\mathop h\nolimits_{i,s} < \dfrac{{\mathop \sigma \nolimits^2 }}{{\mathop P\nolimits_{\rm peak} }}\left[ {\dfrac{{\mathop A\nolimits_2 }}{{ - W(\mathop { - A}\nolimits_2 \mathop e\nolimits^{ - \mathop A\nolimits_2 } )}} - 1} \right]\\ \dfrac{{\mathop \sigma \nolimits^2 }}{{\mathop h\nolimits_{i,s} }}\left[ {\dfrac{{\mathop B\nolimits_2 }}{{W(\mathop B\nolimits_2 \mathop e\nolimits^{ - 1} )}} - 1} \right],\;否则 \end{array} \right.\\ 或者\mathop p\nolimits_{i,s}^* = \left\{ \begin{array}{l} \mathop P\nolimits_{\rm peak} ,\;如果\mathop h\nolimits_{i,s}' < \dfrac{{\mathop \sigma \nolimits^2 }}{{\mathop P\nolimits_{\rm peak} }}\left[ {\dfrac{{\mathop A\nolimits_2 }}{{ - W(\mathop { - A}\nolimits_2 \mathop e\nolimits^{ - \mathop A\nolimits_2 } )}} - 1} \right]\\ \dfrac{{\mathop \sigma \nolimits^2 }}{{\mathop h\nolimits_{i,s}' }}\left[ {\dfrac{{\mathop B\nolimits_2' }}{{W(\mathop B\nolimits_2' \mathop e\nolimits^{ - 1} )}} - 1} \right],\;否则 \end{array} \right.当i = \mathop m\nolimits_s + 1时 \end{array} \right.\\ \left\{ \begin{array}{l} \mathop p\nolimits_{i,2}^* = \left\{ \begin{array}{l} \mathop P\nolimits_{\rm peak} ,\;如果\mathop {h}\nolimits_{i,2} < \dfrac{{\mathop \sigma \nolimits^2 }}{{\mathop P\nolimits_{\rm peak} }}\left[ {\dfrac{{\mathop A\nolimits_3 }}{{ - W(\mathop { - A}\nolimits_3 \mathop e\nolimits^{ - \mathop A\nolimits_3 } )}} - 1} \right]\\ \dfrac{{\mathop \sigma \nolimits^2 }}{{\mathop h\nolimits_{i,2} }}\left[ {\dfrac{{\mathop B\nolimits_3 }}{{W(\mathop B\nolimits_3 \mathop e\nolimits^{ - 1} )}} - 1} \right],\;否则 \end{array} \right.当i \in \{ 1,\cdots,k\}时 \\ \mathop p\nolimits_{i,2}^* = \left\{ \begin{array}{l} \mathop P\nolimits_{\rm peak} ,\;如果\mathop {h}\nolimits_{i,2} < \dfrac{{\mathop \sigma \nolimits^2 }}{{\mathop P\nolimits_{\rm peak} }}\left[ {\dfrac{{\mathop A\nolimits_4 }}{{ - W(\mathop { - A}\nolimits_4 \mathop e\nolimits^{ - \mathop A\nolimits_4 } )}} - 1} \right]\\ \dfrac{{\mathop \sigma \nolimits^2 }}{{\mathop h\nolimits_{i,2} }}\left[ {\dfrac{{\mathop B\nolimits_4 }}{{W(\mathop B\nolimits_4 \mathop e\nolimits^{ - 1} )}} - 1} \right],\;否则 \end{array} \right.当i \in \{ k + 1,\cdots,n\}时 \end{array} \right. \end{array}$ | (25) |
其中,
| $ \begin{array}{l} \mathop A\nolimits_2 = 1 + \dfrac{{\mathop {\mathop \lambda \nolimits_s }\nolimits^* }}{{\mathop \beta \nolimits_s^E \mathop P\nolimits_{{\rm{peak}}} }},\mathop B\nolimits_2 = \dfrac{{\mathop h\nolimits_{{\rm{i}},s} \mathop {\mathop \lambda \nolimits_s }\nolimits^* }}{{\mathop \beta \nolimits_s^E \mathop \sigma \nolimits^2 }} - 1,\mathop B\nolimits_2' = \dfrac{{\mathop {\rm{h}}\nolimits_{i,s}' \mathop {\mathop \lambda \nolimits_s }\nolimits^* }}{{\mathop \beta \nolimits_s^E \mathop \sigma \nolimits^2 }} - 1\\ \mathop A\nolimits_3 = 1 + \dfrac{{\mathop {\mathop \lambda \nolimits_2 }\nolimits^* }}{{\mathop \beta \nolimits_2^E \mathop P\nolimits_{{\rm{peak}}} }},\mathop B\nolimits_3 = \dfrac{{\mathop {\rm{h}}\nolimits_{i,2} \mathop {\mathop \lambda \nolimits_2 }\nolimits^* }}{{\mathop \beta \nolimits_2^E \mathop \sigma \nolimits^2 }} - 1\\ \mathop A\nolimits_4 = 1 + \dfrac{{\mathop \beta \nolimits_2^T }}{{\mathop \beta \nolimits_2^E \mathop P\nolimits_{{\rm{peak}}} }},\mathop B\nolimits_4 = \dfrac{{\mathop {\mathop {\rm{h}}\nolimits_{i,2} \beta }\nolimits_2^T }}{{\mathop \beta \nolimits_2^E \mathop \sigma \nolimits^2 }} - 1 \end{array} $ |
算法1. 固定卸载决策下求解最佳资源分配算法
1. 输入: 给定大于0的
2. 输出:
3. While True:
4. 根据最佳CPU频率的闭合表达式(24)计算
5. 根据最佳发射功率的闭合表达式(25)计算
6. 根据
7.
8. 根据梯度下降算法, 分别更新
9. 如果
10. 退出循环
11. End
3 优化卸载决策在第2节中, 给定卸载决策, 可以得出最佳资源分配, 需要搜索
定理1.
证明: 由于文章篇幅限制, 并且有许多文献都有证明了一爬策略, 这里就不再证明.
3.2 基于一爬策略的线性搜索算法在本小节中, 借鉴了文献[16]的思想, 同时基于一次爬升策略提出了一种低复杂度的线性搜索算法, 来优化卸载决策. 首先根据式(27)证明所有卸载点共享最小加权和点, 然后在找到最小加权和点的基础上寻找入口任务, 只需将两点之间的任务包括两点, 都卸载到服务器, 如图3所示.

|
图 3 一次爬升策略 |
公式如下, 设备有m个任务:
| $ \begin{split} \eta \left( {i, {{o}}} \right) =& \mathop \beta \nolimits^E \left[ {\sum\limits_{h = 1}^{i - 1} {\mathop e\nolimits_h^l } + \mathop e\nolimits_{i - 1, i}^u + \sum\limits_{k = o{\text{ + }}1}^m {\mathop e\nolimits_k^l } } \right] \\&+ \mathop \beta \nolimits^T \left[ {\sum\limits_{h = 1}^{i - 1} {\mathop t\nolimits_h^l } + \mathop t\nolimits_{i - 1, i}^u + \sum\limits_{k = i}^o {\mathop t\nolimits_k^c } + \mathop t\nolimits_{o, o + 1}^d + \sum\limits_{k = o + 1}^m {\mathop t\nolimits_{{k}}^l } } \right] \end{split} $ | (26) |
| $ \mathop \eta \nolimits_i = \left\{ \begin{array}{l} \mathop {\min }\limits_{1 \leqslant {{o}} \leqslant m} \left\{ {\eta \left( {i,{{o}}} \right)} \right\},如果\;\;\;i = 1\\ \mathop \eta \nolimits_i - \mathop \beta \nolimits^E \mathop e\nolimits_{i - 2,i - 1}^u + \mathop \beta \nolimits^E \left( {\mathop e\nolimits_{i - 1}^l + \mathop e\nolimits_{i - 1,i}^u } \right) {\kern 1pt} \\ -\mathop \beta \nolimits^T \left( {\mathop {{t}}\nolimits_{i - 2,i - 1}^u + \mathop t\nolimits_{i - 1}^c } \right) + \mathop \beta \nolimits^T \left( {\mathop {{t}}\nolimits_{i - 1,i}^u + \mathop t\nolimits_{i - 1}^l } \right),\;否则 \end{array} \right. $ | (27) |
其中,
定理2. 所有卸载点共享最小加权和点
证明: 假设当任务
当
| $ \begin{split} \eta (j,j) =& \mathop \beta \nolimits^E \left[\sum\limits_{{{h}} = 1}^{j - 1} {\mathop e\nolimits_h^l } + \mathop e\nolimits_{j - 1,j}^u + \sum\limits_{k = j + 1}^m {\mathop e\nolimits_k^l } \right] \\&+ \mathop \beta \nolimits^T \left[\sum\limits_{h = 1}^{j - 1} {\mathop {{t}}\nolimits_h^l } + \mathop t\nolimits_{j - 1,j}^u + \mathop {{t}}\nolimits_j^c + \mathop t\nolimits_{j,j + 1}^d + \sum\limits_{k = j + 1}^m {\mathop {{t}}\nolimits_k^l } \right] \end{split} $ | (28) |
卸载任务
| $ \begin{split} \eta (j,j + 1) =& \mathop \beta \nolimits^E \left[\sum\limits_{{{h}} = 1}^{j - 1} {\mathop e\nolimits_{{h}}^l } + \mathop e\nolimits_{j - 1,j}^u + \sum\limits_{k = j + 2}^{{m}} {\mathop e\nolimits_k^l } \right] \\&+ \mathop \beta \nolimits^T \left[\sum\limits_{h = 1}^{j - 1} {\mathop {{t}}\nolimits_h^l } + \mathop t\nolimits_{j - 1,j}^u + \mathop {{t}}\nolimits_j^c + \mathop {{t}}\nolimits_{j + 1}^c + \mathop t\nolimits_{j + 1,j + 2}^d + \sum\limits_{k = j + 2}^M {\mathop {{t}}\nolimits_k^l } \right] \end{split} $ | (29) |
卸载任务
| $ \begin{split} \eta (j,o) =& \mathop \beta \nolimits^E \left[\sum\limits_{{{h}} = 1}^{j - 1} {\mathop e\nolimits_h^l } + \mathop e\nolimits_{j - 1,j}^u + \sum\limits_{k = o + 1}^{{m}} {\mathop e\nolimits_k^l } \right] \\& +\mathop \beta \nolimits^T \left[\sum\limits_{h = 1}^{j - 1} {\mathop {{t}}\nolimits_h^l } + \mathop t\nolimits_{j - 1,j}^u + \mathop {{t}}\nolimits_j^c + \cdots + \mathop {{t}}\nolimits_o^c + \mathop t\nolimits_{o,o + 1}^d + \sum\limits_{k = o + 1}^M {\mathop {{t}}\nolimits_k^l } \right] \end{split} $ | (30) |
卸载任务
| $ \begin{split} \eta (j,{{m}}) =& \mathop \beta \nolimits^E \left[\sum\limits_{{{h}} = 1}^{j - 1} {\mathop e\nolimits_h^l } + \mathop e\nolimits_{j - 1,j}^u \right] \\& +\mathop \beta \nolimits^T \left[\sum\limits_{h = 1}^{j - 1} {\mathop {{t}}\nolimits_i^l } + \mathop t\nolimits_{j - 1,j}^u + \mathop {{t}}\nolimits_j^c + \cdots + \mathop {{t}}\nolimits_m^c + \mathop t\nolimits_{m,m + 1}^d \right] \end{split} $ | (31) |
因为当
| $ \begin{split}& \eta (j,{{o}}) \leqslant \eta (j,j) \Rightarrow \\& \mathop \beta \nolimits^T [\mathop {{t}}\nolimits_{j + 1}^c + \cdots + \mathop {{t}}\nolimits_o^c + \mathop t\nolimits_{o,o + 1}^d ] \leqslant \mathop \beta \nolimits^E [\mathop e\nolimits_{j + 1}^l + \cdots + \mathop e\nolimits_o^l ] \\& +\mathop \beta \nolimits^T [\mathop t\nolimits_{j,j + 1}^d + \mathop {{t}}\nolimits_{j + 1}^l + \cdots + \mathop {{t}}\nolimits_o^l ]\\& \eta (j,o) \leqslant \eta (j,j{{ + }}1) \Rightarrow \\& \mathop \beta \nolimits^T [\mathop {{t}}\nolimits_{j + 2}^c + \cdots + \mathop {{t}}\nolimits_o^c + \mathop t\nolimits_{o,o + 1}^d ] \leqslant \mathop \beta \nolimits^E [\mathop e\nolimits_{j + 2}^l + \cdots + \mathop e\nolimits_o^l ] \\& +\mathop \beta \nolimits^T [\mathop t\nolimits_{j + 1,j + 2}^d + \mathop {{t}}\nolimits_{j + 2}^l + \cdots + \mathop {{t}}\nolimits_o^l ]\\& \eta (j,o) \leqslant \eta (j,j{{ + }}2) \Rightarrow \\& \mathop \beta \nolimits^T [\mathop {{t}}\nolimits_{j + 3}^c + \cdots + \mathop {{t}}\nolimits_o^c + \mathop t\nolimits_{o,o + 1}^d ] \leqslant \mathop \beta \nolimits^E [\mathop e\nolimits_{j + 3}^l + \cdots + \mathop e\nolimits_o^l ] \\&+ \mathop \beta \nolimits^T [\mathop t\nolimits_{j + 2,j + 3}^d + \mathop {{t}}\nolimits_{j + 3}^l + \cdots + \mathop {{t}}\nolimits_o^l ]\\& \cdots \\& \eta (j,o) \leqslant \eta (j,o{{ + }}1) \Rightarrow \\& \mathop \beta \nolimits^E [\mathop e\nolimits_{o + 1}^l ] + \mathop \beta \nolimits^T [\mathop t\nolimits_{o,o + 1}^d + \mathop {{t}}\nolimits_{o + 1}^l ] \leqslant \mathop \beta \nolimits^T [\mathop {{t}}\nolimits_{o + 1}^c + \mathop {{t}}\nolimits_{o + 1,o + 2}^d ]\\& \eta (j,o) \leqslant \eta (j,o{{ + 2}}) \Rightarrow \\& \mathop \beta \nolimits^E [\mathop e\nolimits_{o + 1}^l + \mathop e\nolimits_{o + 2}^l ] + \mathop \beta \nolimits^T [\mathop t\nolimits_{o,o + 1}^d + \mathop {{t}}\nolimits_{o + 1}^l + \mathop {{t}}\nolimits_{o + 2}^l ] \leqslant \\& \mathop \beta \nolimits^T [\mathop {{t}}\nolimits_{o + 1}^c + \mathop {{t}}\nolimits_{o + 2}^c + \mathop {{t}}\nolimits_{o + 2,o + 3}^d ]\\& \cdots \\& \eta (j,o) \leqslant \eta (j,m) \Rightarrow \\& \mathop \beta \nolimits^E [\mathop e\nolimits_{o + 1}^l + \cdots + \mathop e\nolimits_{{m}}^l ] + \mathop \beta \nolimits^T [\mathop t\nolimits_{o,o + 1}^d + \mathop {{t}}\nolimits_{o + 1}^l + \cdots + \mathop {{t}}\nolimits_m^l ] \leqslant \\& \mathop \beta \nolimits^T [\mathop {{t}}\nolimits_{o + 1}^c + \cdots + \mathop {{t}}\nolimits_{{m}}^c + \mathop {{t}}\nolimits_{m,m + 1}^d ] \end{split} $ | (32) |
当
| $ \begin{split}& \mathop {\eta (j{{ + }}1, j + 1) = \beta }\nolimits^E \left[\sum\limits_{{{h}} = 1}^j {\mathop e\nolimits_h^l } + \mathop e\nolimits_{j, j{{ + }}1}^u + \sum\limits_{k = j + 2}^m {\mathop e\nolimits_k^l } \right] \\& +\mathop \beta \nolimits^T \left[\sum\limits_{h = 1}^j {\mathop {{t}}\nolimits_h^l } + \mathop t\nolimits_{j, j{{ + }}1}^u + \mathop {{t}}\nolimits_{j{{ + }}1}^c + \mathop t\nolimits_{j + 1, j + 2}^d + \sum\limits_{{{k}} = j + 2}^m {\mathop {{t}}\nolimits_k^l } \right] \\ \end{split} $ | (33) |
卸载任务
| $ \begin{split}& \mathop {\eta (j + 1, {{o}}) = \beta }\nolimits^E \left[\sum\limits_{h = 1}^j {\mathop e\nolimits_h^l } + \mathop e\nolimits_{j, j + 1}^u + \sum\limits_{k = o + 1}^m {\mathop e\nolimits_k^l } \right] \\& +\mathop \beta \nolimits^T \left[\sum\limits_{h = 1}^j {\mathop {{t}}\nolimits_h^l } + \mathop t\nolimits_{j, j + 1}^u + \mathop {{t}}\nolimits_{j + 1}^c + \cdots + \mathop {{t}}\nolimits_o^c + \mathop t\nolimits_{o, o + 1}^d + \sum\limits_{k = o + 1}^m {\mathop {{t}}\nolimits_k^l } \right] \\ \end{split} $ | (34) |
卸载任务
| $ \begin{split}& \mathop {\eta (j + 1, {{m}}) = \beta }\nolimits^E \left[\sum\limits_{h = 1}^j {\mathop e\nolimits_h^l } + \mathop e\nolimits_{j, j + 1}^u \right] \\& +\mathop \beta \nolimits^T \left[\sum\limits_{h = 1}^j {\mathop {{t}}\nolimits_h^l } + \mathop t\nolimits_{j, j + 1}^u + \mathop {{t}}\nolimits_{j + 1}^c + \cdots + \mathop {{t}}\nolimits_m^c + \mathop t\nolimits_{m, m + 1}^d \right] \\ \end{split} $ | (35) |
当
| $ \begin{split}& \eta (j + 1,{{o}}) \leqslant \eta (j + 1,j{{ + }}1) \Rightarrow \\& \mathop \beta \nolimits^T [\mathop {{t}}\nolimits_{j + 2}^c + \cdots + \mathop {{t}}\nolimits_o^c + \mathop t\nolimits_{o,o + 1}^d ] \leqslant \mathop \beta \nolimits^E [\mathop e\nolimits_{j + 2}^l + \cdots + \mathop e\nolimits_o^l ] \\& +\mathop \beta \nolimits^T [\mathop t\nolimits_{j + 1,j + 2}^d + \mathop {{t}}\nolimits_{j + 2}^l + \cdots + \mathop {{t}}\nolimits_o^l ]\\& \eta (j + 1,o) \leqslant \eta (j + 1,j{{ + }}2) \Rightarrow \\& \mathop \beta \nolimits^T [\mathop {{t}}\nolimits_{j + 3}^c + \cdots + \mathop {{t}}\nolimits_o^c + \mathop t\nolimits_{o,o + 1}^d ] \leqslant \mathop \beta \nolimits^E [\mathop e\nolimits_{j + 3}^l + \cdots + \mathop e\nolimits_o^l ] \\& +\mathop \beta \nolimits^T [\mathop t\nolimits_{j + 2,j + 3}^d + \mathop {{t}}\nolimits_{j + 3}^l + \cdots + \mathop {{t}}\nolimits_o^l ]\\& \cdots \\& \eta (j + 1,o) \leqslant \eta (j + 1,o{{ + }}1) \Rightarrow \\& \mathop \beta \nolimits^E [\mathop e\nolimits_{o + 1}^l ] + \mathop \beta \nolimits^T [\mathop t\nolimits_{o,o + 1}^d + \mathop {{t}}\nolimits_{o + 1}^l ] \le \mathop \beta \nolimits^T [\mathop {{t}}\nolimits_{o + 1}^c + \mathop {{t}}\nolimits_{o + 1,o + 2}^d ]\\& \cdots \\& \eta (j + 1,o) \leqslant \eta (j + 1,M) \Rightarrow \\& \mathop \beta \nolimits^E [\mathop e\nolimits_{o + 1}^l + \cdots + \mathop e\nolimits_m^l ] + \mathop \beta \nolimits^T [\mathop t\nolimits_{o,o + 1}^d + \mathop {{t}}\nolimits_{o + 1}^l + \cdots + \mathop {{t}}\nolimits_m^l ] \leqslant \\& \mathop \beta \nolimits^T [\mathop {{t}}\nolimits_{o + 1}^c + \cdots + \mathop {{t}}\nolimits_m^c + \mathop {{t}}\nolimits_{m,m + 1}^d ] \end{split} $ | (36) |
从而得出所有卸载点共享最小加权和点
从定理2可知, 只需遍历
| $ \begin{gathered} \mathop {\mathop \eta \nolimits_h = \max \{ \eta }\nolimits_1 , \cdots, \mathop \eta \nolimits_o \} \end{gathered} $ | (37) |
基于定理1和定理2, 可以通过提出的线性搜索算法快速地找到最小加权和点
算法2. 低复杂度线性搜索算法
1. 输入: 根据式(33)计算
2. 输出:
3. For
4. 根据算法1计算出最优
5. 然后分别计算设备能耗和时间
6. 根据能耗、时间和式(26)计算
7. If
8.
9. End
10. 找到
11.
12. For
13. 根据
14. End
15. 根据公式
在这一节, 将进行数值模拟来评估所提的卸载算法, 关注的性能指标是两设备的总性能(时延和能耗的加权和最小), 用ETC表示, 其中每个设备的性能用设备完成任务所消耗的能耗和时间的加权和表示, 实验数据值的大小参考了文献[14]进行了设置.
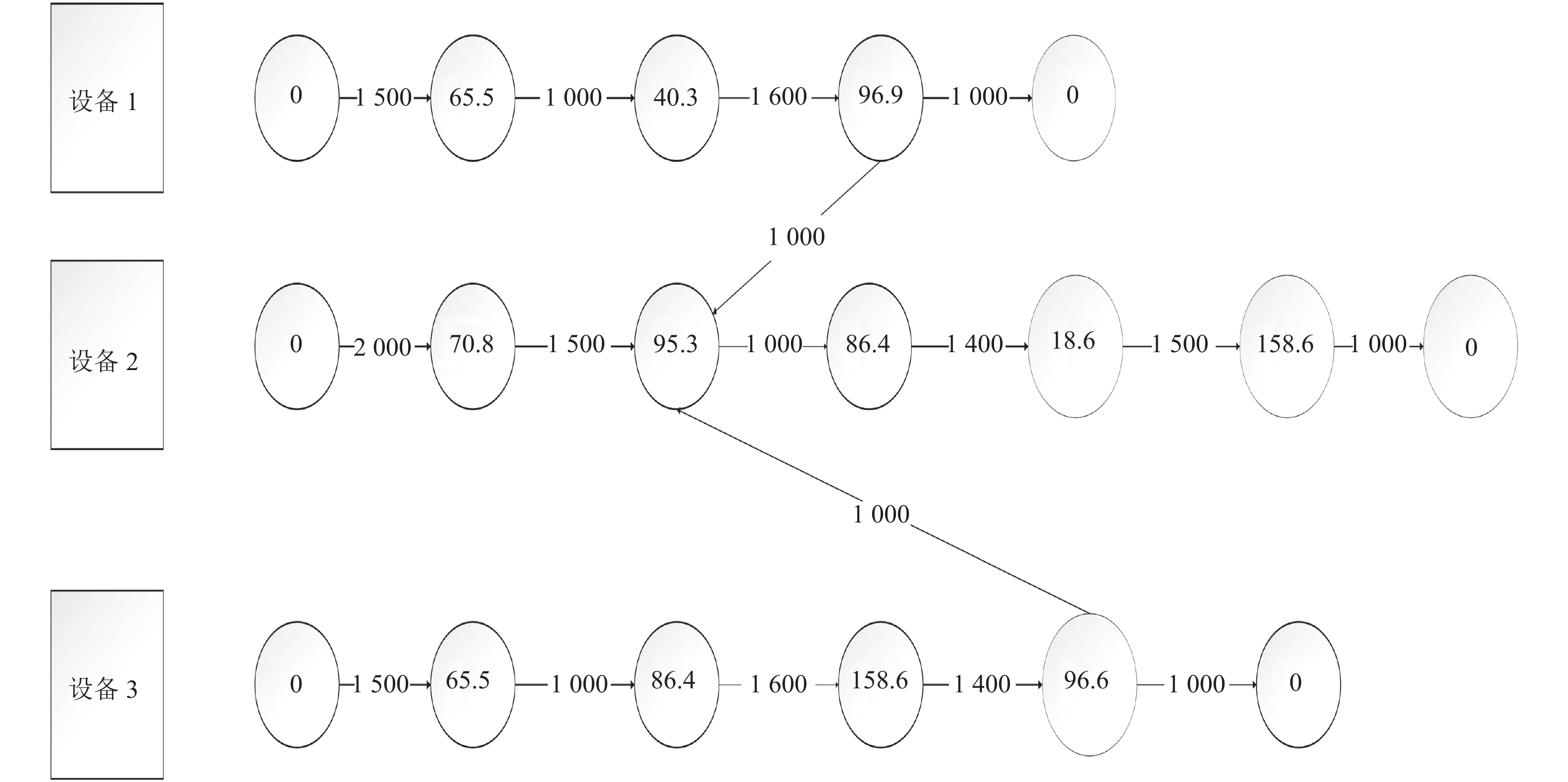
图4为每个设备的任务调用图, 每个节点代表一个任务, 节点权值为完成此任务的计算量, 边权值表示输入和输出数据的大小. 这里将设备1、设备2和设备3的实际任务数量分别设置为3、4和5, 每个设备引入了两个虚拟任务. 服务器的发射功率
根据第3节列出的信道增益公式, 公式中的一些参数设置为:
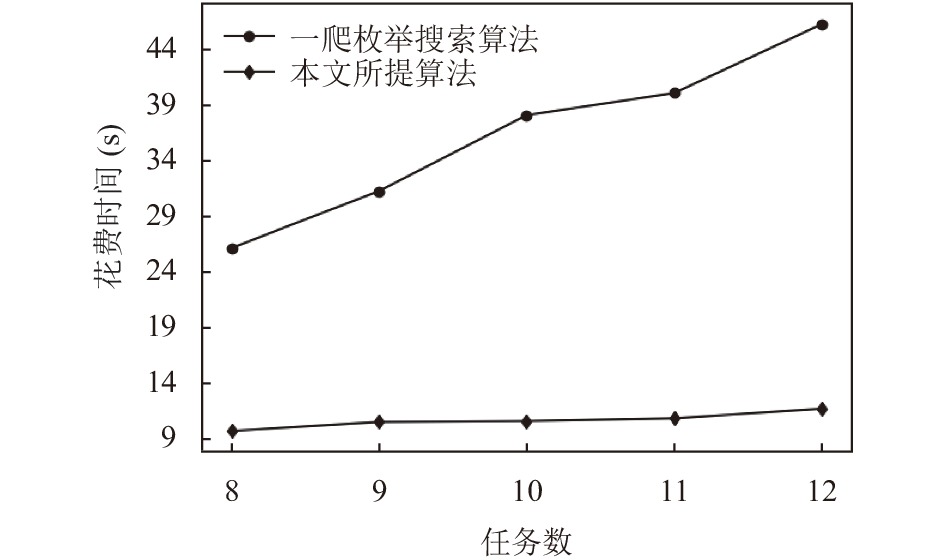
在图5中, 首先进行了本文所提的算法和一爬策略枚举搜索算法的比较. 通过图5可以观察到, 随着任务数的增多获得最佳卸载策略所花费的时间, 本文所提算法的性能要优于一爬枚举搜索算法. 在相同的任务数下, 本文所提的算法获得最优卸载策略的时间明显小于一爬策略枚举搜索算法明.
|
图 4 实验模型和参数 |
|
图 5 两种算法对比曲线图 |
接下来, 本文给出了当
从图6(a)可以观察到, 当固定其他距离时, 随着距离
图6(b)显示了距离

|
图 6 与其他算法的对比 |
图6(c)显示了距离
通过以上对比分析, 本文所提的算法明显优于其他基准算法, 同时与D2D技术协作可以显着提高系统的性能.
5 结论与展望本文研究了MEC与D2D技术协作系统环境下不同设备之间具有任务依赖性的最优的资源分配和优化任务卸载决策问题, 来最小化设备的能耗和任务完成时间的加权和, 为了解决该问题, 提出了一种低复杂度的在线任务卸载算法, 获得了最优计算卸载策略. 最后通过数值实验表明, 本文所提的算法明显优于其他基准算法. 下一步将对多设备多服务器场景进行研究.
| [1] |
Abbas N, Zhang Y, Taherkordi A, et al. Mobile edge computing: A survey. IEEE Internet of Things Journal, 2018, 5(1): 450-465. DOI:10.1109/JIOT.2017.2750180 |
| [2] |
Flores H, Hui P, Tarkoma S, et al. Mobile code offloading: From concept to practice and beyond. IEEE Communications Magazine, 2015, 53(3): 80-88. DOI:10.1109/MCOM.2015.7060486 |
| [3] |
Saleem U, Liu Y, Jangsher S, et al. Latency minimization for D2D-enabled partial computation offloading in mobile edge computing. IEEE Transactions on Vehicular Technology, 2020, 69(4): 4472-4486. DOI:10.1109/TVT.2020.2978027 |
| [4] |
Cao XW, Wang F, Xu J, et al. Joint computation and communication cooperation for energy-efficient mobile edge computing. IEEE Internet of Things Journal, 2019, 6(3): 4188-4200. DOI:10.1109/JIOT.2018.2875246 |
| [5] |
Zhou JZ, Zhang X, Wang WB, et al. Energy-efficient collaborative task offloading in D2D-assisted mobile edge computing networks. Proceedings of 2019 IEEE Wireless Communications and Networking Conference. Marrakesh, Morocco: IEEE, 2019. 1–6.
|
| [6] |
Mahmoodi SE, Uma RN, Subbalakshmi KP. Optimal joint scheduling and cloud offloading for mobile applications. IEEE Transactions on Cloud Computing, 2019, 7(2): 301-313. DOI:10.1109/TCC.2016.2560808 |
| [7] |
Han YP, Zhao ZW, Mo JW, et al. Efficient task offloading with dependency guarantees in ultra-dense edge networks. Proceedings of 2019 IEEE Global Communications Conference. Waikoloa: IEEE, 2019. 1–6.
|
| [8] |
Li ML, Chen T, Zeng JX, et al. D2D-assisted computation offloading for mobile edge computing systems with energy harvesting. Proceedings of the 20th International Conference on Parallel and Distributed Computing, Applications and Technologies, Gold Coast: IEEE, 2019. 90–95.
|
| [9] |
Li Y, Xu GC, Ge JQ, et al. Jointly optimizing helpers selection and resource allocation in D2D mobile edge computing. Proceedings of 2020 IEEE Wireless Communications and Networking Conference. Seoul: IEEE, 2020. 1–6.
|
| [10] |
He YH, Ren JK, Yu GD, et al. Joint computation offloading and resource allocation in D2D enabled MEC networks. Proceedings of 2019 IEEE international Conference on Communications. Shanghai: IEEE, 2019. 1–6.
|
| [11] |
Xing H, Liu L, Xu J, et al. Joint task assignment and resource allocation for D2D-enabled mobile-edge computing. IEEE Transactions on Communications, 2019, 67(6): 4193-4207. DOI:10.1109/TCOMM.2019.2903088 |
| [12] |
He YH, Ren JK, Yu GD, et al. D2D communications meet mobile edge computing for enhanced computation capacity in cellular networks. IEEE Transactions on Wireless Communications, 2019, 18(3): 1750-1763. DOI:10.1109/TWC.2019.2896999 |
| [13] |
Saleem U, Liu Y, Jangsher S, et al. Mobility-aware joint task scheduling and resource allocation for cooperative mobile edge computing. IEEE Transactions on Wireless Communications, 2021, 20(1): 360-374. DOI:10.1109/TWC.2020.3024538 |
| [14] |
Yan J, Bi SZ, Zhang YJA. Optimal offloading and resource allocation in mobile-edge computing with inter-user task dependency. Proceedings of 2018 IEEE Global Communications Conference. Abu Dhabi: IEEE, 2018. 1–8.
|
| [15] |
Boyd S, Vandenberghe L. Convex Optimization. Cambridge: Cambridge University Press, 2004.
|
| [16] |
Zhang Y, Liu H, Jiao L, et al. To offload or not to offload: An efficient code partition algorithm for mobile cloud computing. Proceedings of the 2012 IEEE 1st International Conference on Cloud Networking. Paris: IEEE, 2012. 80–86.
|
 2022, Vol. 31
2022, Vol. 31


