计算机系统应用  2022, Vol. 31 Issue (8): 292-297   PDF    
引用本文
刘诗仪, 刘改, 吴峰. 基于深度神经网络的字典学习. 计算机系统应用, 2022, 31(8): 292-297.http://www.c-s-a.org.cn/1003-3254/8619.html   
Liu SY, Liu G, Wu F. Deep Neural Network-based Dictionary Learning. Computer Systems and Applications, 2022, 31(8): 292-297(in Chinese).http://www.c-s-a.org.cn/1003-3254/8619.html   
基于深度神经网络的字典学习
刘诗仪, 刘改, 吴峰     
西安工程大学 计算机科学学院, 西安 710699
收稿日期：2021-11-07; 修改日期：2021-12-02; 采用时间：2021-12-14; csa 在线出版时间：2022-05-31
基金项目：西安市科技计划(2020KJRC0027); 国家环境保护近岸海域生态环境重点实验室开放研究课题(202110)
通讯作者：刘诗仪, E-mail: 190721051@stu.xpu.edu.cn.
摘要：字典学习通常采用线性函数捕获数据潜在特征, 该方式无法充分提取数据的内在特征结构, 近年来深度学习方法因其强大的特征表示能力而备受关注, 由此本文提出一种结合深度学习与字典学习的非线性特征表示策略, 基于深度神经网络的字典学习(deep neural network-based dictionary learning, DNNDL). DNNDL将字典学习模块融入传统深度学习网络结构中, 在通过自编码器进行映射获取的低维嵌入空间中同时学习数据字典及在其上的稀疏表示系数, 从而实现端到端方式的数据潜在特征提取. DNNDL可为已有数据以及样本外点数据生成紧凑且具判别性的表示. DNNDL不仅是一种新的深度学习网络结构, 并且可将其看作为字典学习和深度学习相结合的统一框架. 通过在4个真实数据集上进行的大量实验, 验证表明所提方法较常用方法具有更好数据表示能力.
关键词: 字典学习    深度学习    稀疏表示    特征提取    
Deep Neural Network-based Dictionary Learning
LIU Shi-Yi, LIU Gai, WU Feng     
School of Computer Science , Xi’an Polytechnic University, Xi’an 710699, China
Abstract: Although dictionary learning mostly uses linear functions to capture potential features of data, this method cannot fully extract the inherent feature structure of data. Deep learning has received widespread attention in recent years due to its outstanding feature representation ability. Therefore, this study proposes a nonlinear feature representation strategy combining deep learning with dictionary learning, i.e., deep neural network-based dictionary learning (DNNDL). DNNDL integrates the dictionary learning module into the traditional deep learning network structure and simultaneously learns the data dictionary and the sparse representation coefficients on it in the low-dimensional embedded space mapped by the autoencoder, thereby achieving end-to-end potential data feature extraction. It can generate compact and discriminant representations of existing data as well as out-of-sample point data. DNNDL not only is a new deep learning network structure but also can be regarded as a unified framework of dictionary learning and deep learning. A large number of experiments on four real data sets show that the proposed method has a better data representation capability than those of conventional methods.
Key words: dictionary learning     deep learning     sparse representation     feature extraction    

机器学习任务如分类、聚类等的性能很大程度上依赖于数据表示的结果, 表示学习将原始数据自动转换为能被计算机处理与运算的特征表示, 现已成功应用于语音识别[1-3]、目标识别[4, 5]和自然语言处理[6, 7]等任务. 字典学习作为表示学习的重要组成部分, 其主要通过为样本数据找到合适的数据字典并将原始数据转化为稀疏表示形式. 合适的数据字典可有效降低数据表示的冗余度并提升数据的判别性. 稀疏表示中只有少量的元素为非零值, 因此字典学习以全新的思想对高维数据进行压缩. 字典学习因其优秀的数据特征表示能力和对数据内在特征的自动提取, 在图像处理、信号还原、模式聚类和模式识别等领域彰显出卓越的应用效果和价值. 字典学习在数据特征提取的应用上备受关注, 但由于传统字典学习基于矩阵优化而开展, 因此学习效果受到线性模型形式的限制, 在面对复杂数据时, 无法有效提取出其中的非线性特征.

近些年, 有关深度学习的研究[8-10]表明, 深度学习网络可以很好地生成非线性数据特征表示, 这正是现阶段字典学习所欠缺的特性. 基于深度神经网络的算法[9]利用5层的BP神经网络对图像进行特征提取, 图像的一个像素对应一个神经元, 一张图像由无数个神经元铺满, 通过对图像的逐层卷积计算得到其复杂的非线性特征. 因此, 研究者集中于字典学习与深度神经网络相结合的方向.

Yu等[11]提出一种基于扩展稀疏模型的图像识别框架, 卷积神经网络在样本数据上进行的预训练, 作为特征提取方法与字典学习相结合, 该方法使字典学习过多地依赖于卷积网络的初始化, 并且采用交替迭代的优化方法, 未能形成一个统一的网络进行训练, 因此所获得的特征不稳定且耗时较长. Lu等[12]提出一种基于图像集的特征和字典学习方法, 从原始人脸图像集中学习判别特征和字典, 从而联合利用判别信息进行人脸识别, 将全连接层网络与字典学习算法结合. 但实验中所使用的深度卷积网络是预先训练的, 未参与到字典学习的训练中, 深度学习网络仅被用作特征提取的手段, 没有将其端到端的良好特性应用到, 字典学习和深度学习之间的关系仍然是独立的, 没有表现出两者之间的内在联系. 虽然这些方法都考虑到与深度学习相结合, 但它们并未构建一个统一的网络框架与联合的优化目标, 并且忽视深度学习非线性映射的重要性, 因此没有充分利用深度学习在特征提取方面的优势.

为解决上述问题, 本文提出DNNDL网络模型, 该模型主要解决字典学习中非线性特征的提取问题. DNNDL采用端到端的方式联合优化稀疏表示系数矩阵与神经网络参数, 首先将原始数据输入至深度学习网络获得数据非线性表示, 深度学习网络的映射作为字典学习的输入通过稀疏约束获得原始数据的近似表示, 稀疏系数即为数据的潜在特征.

1 相关工作

本文所提算法涉及字典学习和深度学习, 本节中分别对其进行简要介绍.

1.1 字典学习

数据字典是根据样本数据的结构学习获得的特征向量矩阵, 该矩阵的列向量为字典的基. 在满足一定重构误差的条件下, 利用最少的基对数据进行近似表示, 如式(1)所示. 因此要求基应具有较强的泛化表示能力, 减少数据冗余的同时提升表示质量. 在字典学习中, 基的数量通常远远大于待表示数据的数量. 在表示数据过程中使用的基越少, 则说明字典可以更稀疏地表示数据. 因此, 稀疏表示的效果与字典的选择密切相关.

$ X = D\Lambda $ (1)

其中, $ X \in {\mathbb{R}^{d \times n}} $ 是原始数据. D是待学习的字典, $ D \in {\mathbb{R}^{d \times k}} $ , 其中, k是字典基的数量. Λ是稀疏系数矩阵, $ \Lambda \in {\mathbb{R}^{k \times n}} $ . 字典学习的目的是寻找基的最优集合并以尽可能稀疏的方式表示原始数据, 形式化表示为:

$ \mathop {\min }\limits_{D, \Lambda } \left\| {X - D\Lambda } \right\|_F^2 \;\; {\rm{s.t.}} \; {\left\| \Lambda \right\|_0} \leqslant \varepsilon $ (2)

目前存在两种主流的字典构建策略: 分析字典法[13-16]和学习字典法[17]. 分析字典法是一种预先确定的字典方法, 包括超完全离散余弦变换字典[14]和傅立叶字典[15]等. 这些方法易于实现, 但数据的表示形式简单且无法实现自适应, 导致分析字典无法被广泛用于不同类型与来源的数据. 通过机器学习策略从给定的数据中获得特定字典的学习字典法具有较强的自适应能力, 即使面对不同的数据集也能学习获得性能优秀的字典, 如最优方向法[18]、广义主成分分析算法[19]和K奇异值分解算法(K-singular value decomposition, K-SVD)[20]等. 其中K-SVD算法在字典选择中采用正交匹配追踪方法, 并在此基础上获得稀疏表示Λ. 因其字典更新的独特性, 该算法有效地提高了从样本数据中学习特征表示的能力, 但K-SVD算法侧重于学习字典的表示能力而忽略字典的判别能力. Pham等[21]提出半监督字典学习算法, 通过将类别信息融入优化目标更好得到样本数据的特性. Yang等[22]提出一种结构字典学习算法, 将费舍尔判别法作为稀疏表示约束引入字典学习, 从而提高图像识别能力.

随着深度神经网络在图像识别领域的成功应用, 一些研究人员观察到深度神经网络结构所代表的特征更加抽象和紧凑. Singhal等[23]利用深度置信网络实现深度学习与字典学习的结合. 深度字典学习[24]专注于将深度学习和字典学习范式相结合, 通过构建更深层次的字典学习架构进行数据特征提取. 深度字典学习通过将单层字典学习问题贪婪化转换解决多层字典的学习, 即使用前一层的表示作为下一层学习的输入虽然将深度学习的概念融入到字典学习中以提高其性能, 但该方法并未重视深度神经网络中的非线性映射, 多层字典学习依旧以线性规划为基础.

1.2 深度学习

在深度神经网络的模型训练过程中, 网络参数根据优化目标采用梯度下降算法进行自适应更新. 非线性响应函数的使用可实现数据中的内在特征表示, 并逐步将初始的低级特征表示转化为高级特征表示. 从而获得更加抽象和具判别性的特征, 最终建立层次化的特征表达体系.

由于监督学习需要大量标记数据, 因此很难应用于大规模数据中. 无监督学习可有效解决该问题, 如自编码器(autoencoder, AE)[25]. AE通过编码层高效地计算数据特征, 并通过相应的解码层对数据进行重构, 在重构的过程中就能提取数据的内在特征. AE在特征学习中无需使用任何标签信息, 因此具有更广泛的应用. AE通过对样本数据的非线性映射可以提取出数据中最具代表性的特征, 而字典学习将大量的冗余特征去除, 只保留与样本数据最相关的解释特征, 简化模型的同时, 保留样本数据中最重要的信息. 因此通过DNNDL网络表示的特征可以揭示数据中的内蕴几何关系, 以将每个映射的样本表示为其他样本的组合, 降低模型复杂度.

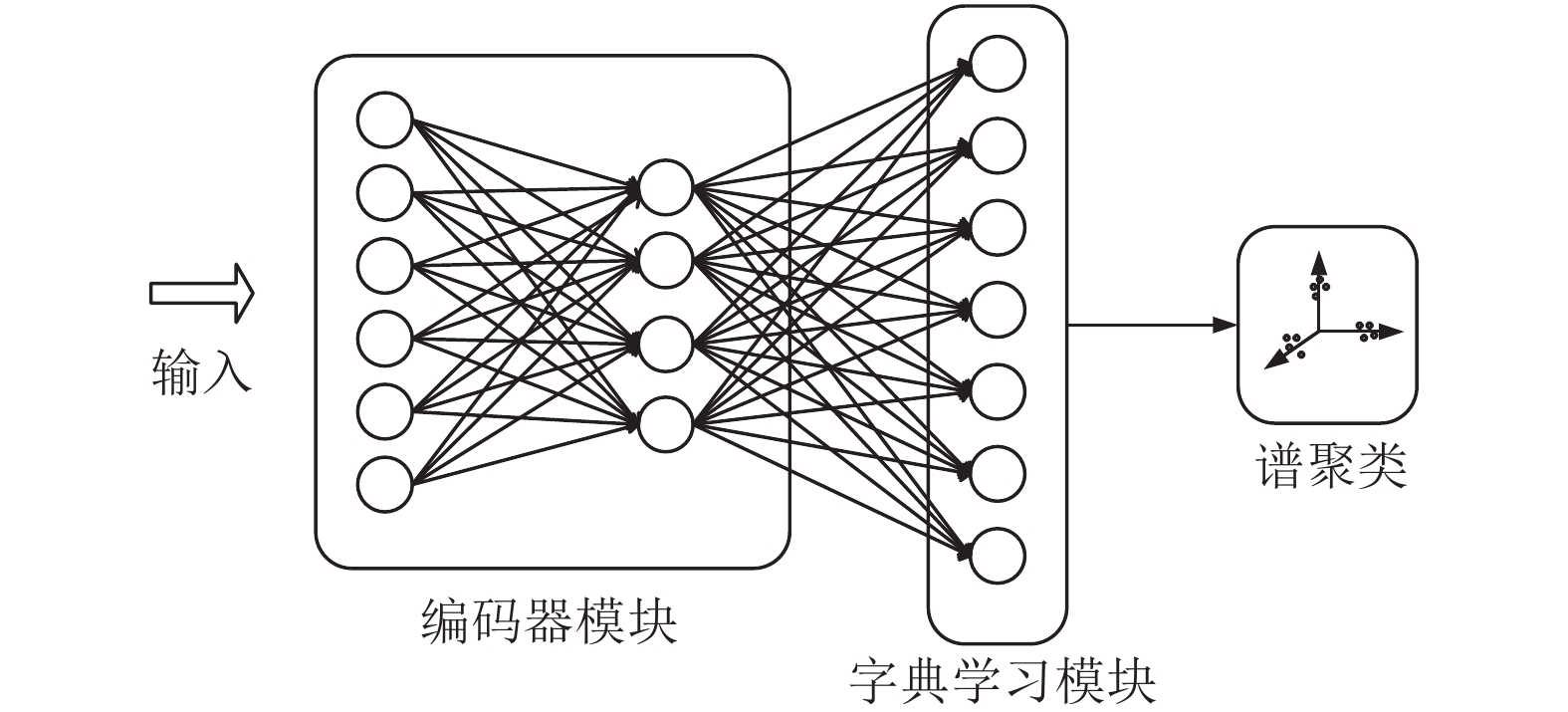
2 模型与算法

在本节将介绍提出的DNNDL方法, 其结构如图1所示, DNNDL主要由3个部分组成, 编码器模块、字典学习模块和谱聚类模块. 编码器模块采用自编码器中的编码器部分, 利用编码器模块实现从样本数据到低维空间表示的非线性映射. 字典学习模块将编码器模块的输出作为输入进行字典和稀疏表示的学习, 发现样本数据隐含的特定结构并提取特征, 最终输出稀疏系数矩阵. 谱聚类是通过对样本数据的相似度矩阵[26]的特征向量进行聚类, 从而达到聚类目的. 谱聚类模块采用谱聚类算法将稀疏系数矩阵作为数据的相似度矩阵进行聚类, 得到聚类结果. DNNDL的优化问题包含如下两个部分.

图 1 DNNDL框架图

第1部分L1的设计是为最小化字典和稀疏系数矩阵重建的表示与原始数据之间的重构误差, 从而尽可能地保留原始数据的内在信息. 同时对稀疏表示矩阵Λ进行约束, 使其具有稀疏性. 定义DNNDL的字典损失L1为:

$ {{L} _1} = \frac{1}{{2N}}\left\| {X - D\Lambda } \right\|_F^2 + \frac{1}{N}{\left\| \Lambda \right\|_p} $ (3)

其中, N为输入数据的样本个数, $ {\Vert \cdot\Vert }_{p} $ 表示 $ {l_p} $ 范数, 在机器学习中常采用 $ {l_1} $ 范数和 $ {l_2} $ 范数[27], 本文选用 $ {l_1} $ 范数, 有两个原因. 一方面, $ {l_1} $ 范数表示向量中各个元素绝对值之和, 主要用于产生稀疏权值矩阵, 符合本文算法对保持Λ稀疏性的要求, 也就是需要Λ中有更少的非零项; 另一方面, 在研究 $ {l_2} $ 范数的评价中, 实验表明, 它在DNNDL网络中的聚类效果相对低于 $ {l_1} $ 范数.

第2部分L2的设计是为了避免在迭代过程中模型收敛到平凡解, 去除深度神经网络潜在空间中的任意比例因子, 因此通过增加适当的约束项, 来约束解的范围.

$ {L_2} = \frac{1}{4}\left\| {{X^{\rm{T}}}X - 1} \right\|_2^2 $ (4)

因此, DNNDL网络中的损失函数形式如下:

$ L = {{L} _1} + \lambda {{L} _2} $ (5)

其中, $ \lambda $ 是一个为正的权衡参数. 在DNNDL中, 公式中X经过编码器部分获得. 假设编码器部分有M+1层, 则有M个非线性变换. 定义网络的输入为 $ {h^{(0)}} \in {\mathbb{R}^d} $ , 第m层的输出如下:

$ {h^{(m)}} = g({W^{(m)}}{h^{(m - 1)}} + {b^{(m)}}) $ (6)

其中, m=1, 2, …, M, $ {h^{(m)}} \in {\mathbb{R}^{{d^{(m)}}}} $ , 其中 $ {d^{(m)}} $ 为 $ {h^{(m)}} $ 的维数. $ g(\cdot) $ 是一个非线性激活函数. $ {W^{(m)}} \in {\mathbb{R}^{{d^{(m)}} \times {d^{(m - 1)}}}} $ 和 ${b^{(m)}} \in {\mathbb{R}^{{d^{(m)}}}}$ 表示深度神经网络中第m层的权重和相关偏差. 编码器部分的输出就表示为 $ {h^{(M)}} $ . 具体来说, 本文算法的优化问题可以转化为式(7):

$ \frac{1}{{2N}}\left\| {X - D\Lambda } \right\|_F^2 + \frac{1}{N}{\left\| \Lambda \right\|_1} + \frac{\lambda }{4}\left\| {({h^{{{(M)}^{\rm{T}}}}}{h^{(M)}} - 1} \right\|_2^2 $ (7)

上述损失函数在保证DNNDL表示稀疏性的同时还可以优化网络对原始数据的重构, 并且解决网络中由于平凡解导致网络崩溃的问题, 如 $ {h^{(M)}} = 0 $ . 字典学习在深度神经网络的潜在表示空间中进行稀疏表示, 而不是在原始数据中. 通过在潜在空间进行非线性变换, 数据变得更有利于稀疏重构. 此外, DNNDL通过反向传播上述损失函数, 不断学习和优化网络中的参数. 显然, 字典学习是深度学习的补充, 可以在谱聚类中表现出更好的性能.

3 实验分析

本文在不同的图像数据集上对所提出的DNNDL算法进行实验, 并从4个聚类性能指标方面与6种常用的稀疏表示方法进行比较, 验证本文所提方法的有效性.

3.1 数据集

The extended Yale B (EYaleB)[28]面部数据集由38名被测者在64种不同光照条件下采集的正面面孔图像组成, 共2432张图像, 图像大小为48×32.

ORL人脸数据集[28]包含40名被测者的不同面部表情和不同光照条件下的10张图像, 每张图像的像素大小为32×32.

COIL-20物品数据库[29]包含20个不同物品和每个物品的72张不同图像, 每张图像的大小为32×32.

COIL-100数据集[29]由100个不同物品的图像组成, 每个物品有72张不同图像. 图像的像素大小为32×32.

3.2 参数及指标

算法运行环境: PyCharm2020; 加速环境: cuda_10.2.89_441.22; 操作系统: Windows 10; 深度学习框架: TensorFlow 1.15.0; 语言环境: Python 3.7.

实验参数: 本文实验采用Adam优化算法. DNNDL网络由两层以修正线性单元[30]为激活函数的编码器和字典学习网络组成. 在编码器部分, 第1层和第2层节点数分别设为10和20. 第1层的内核大小设置为5×5, 第2层的内核大小为3×3. 步长固定为2. 选择用于字典学习的原子数是50个. 损耗函数L1中的 $ {\lambda _1} $ 设为0.5, 损耗函数L2中的 $ {\lambda _2} $ 设为0.25. 学习率设置为 $ 1.0 \times {10^{ - 4}} $ , 模型的训练迭代次数为700.

评价指标: 本文采用4种广泛应用于聚类算法的评价指标[31]来进行对比实验, 即准确度(ACC)、归一化互信息(NMI)、调整兰德系数(ARI)和F值(F-score). 这4种指标的值越高, 表明实验性能越好.

3.3 对比试验

为了验证本文算法的性能和有效性, 对比当前主流稀疏表示的聚类算法, 来对提出算法性能进行验证. 低秩表示(low rank representation, LRR)[32]、低秩子空间聚类(low rank subspace clustering, LRSC)[33]、稀疏子空间聚类(sparse subspace clustering, SSC)[34]、核稀疏子空间聚类(kernel sparse subspace clustering, KSSC)[35]、SSC采用正交匹配追踪(SSC-OMP)[36]和深度字典学习(DDL)[24]方法进行对比实验.

3.4 实验结果

DNNDL在4个数据集与其他6种算法的实验结果列于表1, 其中以粗体显示最佳效果. 实验分析如下.

表 1 不同数据集上不同算法的聚类结果对比 (%)

SSC主要思想是假设高维空间中的数据属于低维子空间, 能够在低维子空间中对数据进行线性表示, 从而揭示数据所在的本质子空间. 然而它却忽略数据的非线性特征, 因此本文提出的融合非线性特征的DNNDL算法可以更好地获取数据复杂的内在特征, 较于SSC性能更好.

DDL专注于将深度学习的网络结构应用于字典学习中, 通过构建更深层次的字典学习网络架构进行数据特征提取. 尽管该方法融入深度学习的多层思想, 但并未重视深度神经网络中的非线性映射, 多层字典学习依旧以线性规划为基础. 本文方法将深度学习和字典学习相融合, 可以得到更好的特征提取效果. 通过对比, 可以看出本文提出的模型在ACC、NMI、ARI和F值评价指标上有一定的提升, 验证了DNNDL的有效性. 从表1中可以看出, DNNDL是提取数据内在特征的更强大的方法, 该方法在聚类应用中取得满意的效果, 深度学习和字典学习相结合的策略可以有效地提取数据的判别特征.

4 结论与展望

本文提出一个可训练的端到端的特征学习框架DNNDL, 其将AE和字典学习进行有机结合学习数据的稀疏表示, 并利用谱聚类的结果验证数据特征学习的效果. 本文在4个图像数据集上进行了实验, 以全面评估算法性能. 实验结果表明, DNNDL在4组数据集上均有较好的聚类性能, 说明该方法能够有效地提取数据的判别性特征. 在未来, 我们将致力于设计更好的训练策略, 进一步提升特征学习的效率.

参考文献
[1]
朱学超,张飞,高鹭,等. 基于残差网络和门控卷积网络的语音识别研究. 计算机工程与应用, 2022, 58(7): 185-191.
[2]
胡文轩, 王秋林, 李松, 等. 基于端到端的多语种语音识别研究. 信号处理, 2021, 37(10): 1816-1824.
[3]
赵刚, 朱文娟, 胡碧灵, 等. 多维度特征融合的教学行为智能分析模式构建. 电化教育研究, 2020, 41(10): 36-44.
[4]
耿艺宁, 刘帅师, 刘泰廷, 等. 基于计算机视觉的行人检测技术综述. 计算机应用, 2021, 41(S1): 43-50.
[5]
谢晓方, 刘厚君, 张龙杰, 等. 融合轻量级YOLOv4与KCF算法的红外舰船目标识别. 兵器装备工程学报, 2021, 42(6): 175-182. DOI:10.11809/bqzbgcxb2021.06.031
[6]
李舟军, 范宇, 吴贤杰. 面向自然语言处理的预训练技术研究综述. 计算机科学, 2020, 47(3): 162-173. DOI:10.11896/jsjkx.191000167
[7]
Zhou M, Duan N, Liu SJ, et al. Progress in Neural NLP: Modeling, Learning, and Reasoning. Engineering, 2020, 6(3): 275–290.
[8]
Deng C, Yang E, Liu T, et al. Unsupervised semantic-preserving adversarial hashing for image search. IEEE Transactions on Image Processing, 2019, 28(8): 4032-4044. DOI:10.1109/TIP.2019.2903661
[9]
宋晓茹, 吴雪, 高嵩, 等. 基于深度神经网络的手写数字识别模拟研究. 科学技术与工程, 2019, 19(5): 193-196. DOI:10.3969/j.issn.1671-1815.2019.05.029
[10]
Ji P, Zhang T, Li HD, et al. Deep subspace clustering networks. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: ACM, 2017. 23–32
[11]
Yu S, Zhang T, Ma C, et al. Learning a discriminative dictionary with CNN for image classification. Proceedings of the 23rd International Conference on Neural Information Processing. Springer International Publishing. Kyoto: Springer, 2016. 185–194.
[12]
Lu JW, Wang G, Zhou J. Simultaneous feature and dictionary learning for image set based face recognition. IEEE Transactions on Image Processing, 2017, 26(8): 4042-4054. DOI:10.1109/TIP.2017.2713940
[13]
王军浩, 闫德勤, 刘德山, 等. 融合极端学习机的判别性分析字典学习算法. 计算机科学, 2020, 47(5): 137-143. DOI:10.11896/jsjkx.190600090
[14]
Yang J, Xie QL. Image denoising method based on DCT over-complete dictionary and the MOD algorithm. Computer and Digital Engineering, 2012, 40(5): 100-103.
[15]
Cheung SC, Shin JY, Lau Y, et al. Dictionary learning in Fourier-transform scanning tunneling spectroscopy. Nature Communications, 2020, 11(1): 1081. DOI:10.1038/s41467-020-14633-1
[16]
Tang W, Panahi A, Krim H, et al. Analysis dictionary learning based classification: Structure for robustness. IEEE Transactions on Image Processing, 2019, 28(12): 6035-6046. DOI:10.1109/TIP.2019.2919409
[17]
Mairal J, Bach F, Ponce J, et al. Non-local sparse models for image restoration. 2009 IEEE 12th International Conference on Computer Vision. Kyoto: IEEE, 2009. 2272–2279.
[18]
Cai ST, Weng SJ, Luo BL, et al. A dictionary-learning algorithm based on method of optimal directions and approximate K-SVD. 2016 35th Chinese Control Conference. Chengdu: IEEE, 2016. 6957–6961.
[19]
Liu Q, Zhang CM, Guo Q, et al. Adaptive sparse coding on PCA dictionary for image denoising. The Visual Computer, 2016, 32(4): 535-549. DOI:10.1007/s00371-015-1087-x
[20]
Zhang Q, Li BX. Discriminative K-SVD for dictionary learning in face recognition. 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 2691–2698.
[21]
Pham DS, Venkatesh S. Joint learning and dictionary construction for pattern recognition. IEEE Conference on Computer Vision and Pattern Recognition. Anchorage: IEEE, 2008. 1–8.
[22]
Yang M, Zhang L, Feng XC, et al. Fisher discrimination dictionary learning for sparse representation. IEEE International Conference on Computer Vision. Barcelona: IEEE, 2011. 543–550.
[23]
Singhal V, Gogna A, Majumdar A. Deep dictionary learning vs deep belief network vs stacked autoencoder: An empirical analysis. 23rd International Conference on Neural Information Processing. Kyoto: Springer, 2016. 337–344.
[24]
Singhal V, Aggarwal HK, Tariyal S, et al. Discriminative robust deep dictionary learning for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(9): 5274-5283. DOI:10.1109/TGRS.2017.2704590
[25]
Hinton GE, Salakhutdinov RR. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647
[26]
白璐, 赵鑫, 孔钰婷, 等. 谱聚类算法研究综述. 计算机工程与应用, 2021, 57(14): 15-26. DOI:10.3778/j.issn.1002-8331.2103-0547
[27]
Deng C, Xue YM, Liu XL, et al. Active transfer learning network: A unified deep joint spectral-spatial feature learning model for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(3): 1741-1754. DOI:10.1109/TGRS.2018.2868851
[28]
Zhang JJ, Li CG, You C, et al. Self-supervised convolutional subspace clustering network. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2019. 5468–5477.
[29]
Yang JW, Parikh D, Batra D. Joint unsupervised learning of deep representations and image clusters. IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 5147–5156.
[30]
Dahl GE, Sainath TN, Hinton GE. Improving deep neural networks for LVCSR using rectified linear units and dropout. IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver: IEEE, 2013. 8609–8613.
[31]
Niu C, Zhang J, Wang G, et al. GATCluster: Self-supervised Gaussian-attention network for image clustering. 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 735–751.
[32]
Liu GC, Lin ZC, Yu Y. Robust subspace segmentation by low-rank representation. Proceedings of the 26th International Conference on Machine Learning. Haifa: ICML, 2010. 663–670.
[33]
Vidal R, Favaro P. Low rank subspace clustering (LRSC). Pattern Recognition Letters, 2014, 43: 47-61. DOI:10.1016/j.patrec.2013.08.006
[34]
Xie GS, Zhang XY, Yan SC, et al. SDE: A novel selective, discriminative and equalizing feature representation for visual recognition. International Journal of Computer Vision, 2017, 124(2): 145-168. DOI:10.1007/s11263-017-1007-9
[35]
Patel VM, Vidal R. Kernel sparse subspace clustering. Proceedings of IEEE International Conference on Image Processing. Paris: IEEE, 2014. 2849–2853.
[36]
You C, Robinson DP, Vidal R. Scalable sparse subspace clustering by orthogonal matching pursuit. Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 3918–3927.