2. 巴州翱翔无人飞行器科技有限公司, 库尔勒 841000
2. Bazhou AoXiang Pilot Technology Co. Ltd., Korla 841000, China
空间目标观测是目标编目、碎片碰撞预警和轨道预报方面的主要手段[1-3]. 一些免费的轨道目标观测与分析软件在三维可视化和任务适用性方面存在差距, 大型软件如STK (satellite tool kit)虽然可用于二次开发, 但这种方式不仅需要支付组件购置费, 要求研究者具备一定的专业知识以及多种计算机语言编程能力, 而且操作较为繁琐, 熟练使用需要一定的学习周期, 开发的成品以需要下载安装的软件为主[4]. Cesium作为一款性能良好、基于WebGL技术的跨平台三维开发框架, 能够在三维虚拟地球场景中叠加丰富的矢量和模型信息, 实现空间数据分析和三维可视化场景的创建, 同时还支持在浏览器端的无插件浏览交互[5]. 本软件基于Cesium开源库设计, 搭建了高分辨瓦片地图服务器, 使用浏览器/服务器(B/S)架构及WebGL技术实现了目标预报观测三维可视化平台, 使用户在任意联网终端都能通过浏览器对空间目标进行观测计算和场景展示[6, 7].
1 平台实现架构Cesium是一个完全开源的基于WebGL的JavaScript框架, 它能够基于多种浏览器进行网页端的2维、2.5维和3维可视化展示, 支持调用地理信息联盟指定的空间数据规范下的WMS、WMTS、ArcGIS等多种地图服务层[8]. 本软件设计基于B/S方式, 在前端进行3维数据可视化展示, 后端实现文件共享和必要的计算功能. 根据各个层次实现的功能的不同, 文献[5]把系统整体分为客户层、服务层以及数据存储层3个层次. 本平台系统整体架构实现如图1所示.

|
图 1 软件平台实现框架 |
客户层中的表现层通过网页形式对系统整体实现在各种主流浏览器端展示, 同时通过 HTML5 和 CSS文件实现网页内容和网页样式的调整与设计, 因此, 客户层的模块整体可分为3个方面: 一是三维场景的显示, 主要体现在三维数字地球、卫星航迹、卫星实时位置动态可视化效果的呈现, 同时包括对地球本身的鼠标动作响应等基本操作; 二是用户对图层工具的操作界面, 包括功能菜单、对话框的设置和曲线图的展示; 三是程序层中使用 JavaScript 语言提供的各个JS功能文件及模块接口, 例如 Cesium 框架提供的三维可视化场景接口以及编程实现的JS功能函数等. 本设计的服务层实现了基于JQuery-Ajax对JSON数据文件的交互功能和基于地图服务对地图文件的访问接口. 数据存储层主要负责对客户端需要查找的数据进行存储, 本设计采用 GeoJSON数据格式将站址信息、图标与模型信息、航迹数据等信息存储在服务器中的静态文件夹中[9]; 采用高分辨卫星地图瓦片数据对数字地球进行显示. Cesium的地图接口需要一个已发布的服务器访问地址, 它链接到地图瓦片文件[10]. 瓦片地图是一种用瓦片金字塔结构来组织数据的地图服务方式, 它将地图切割成许多较小的瓦片块, 并根据目前的视角范围提供快速的显示效果, 从而大大提高地图在浏览器端的加载速度[11, 12].
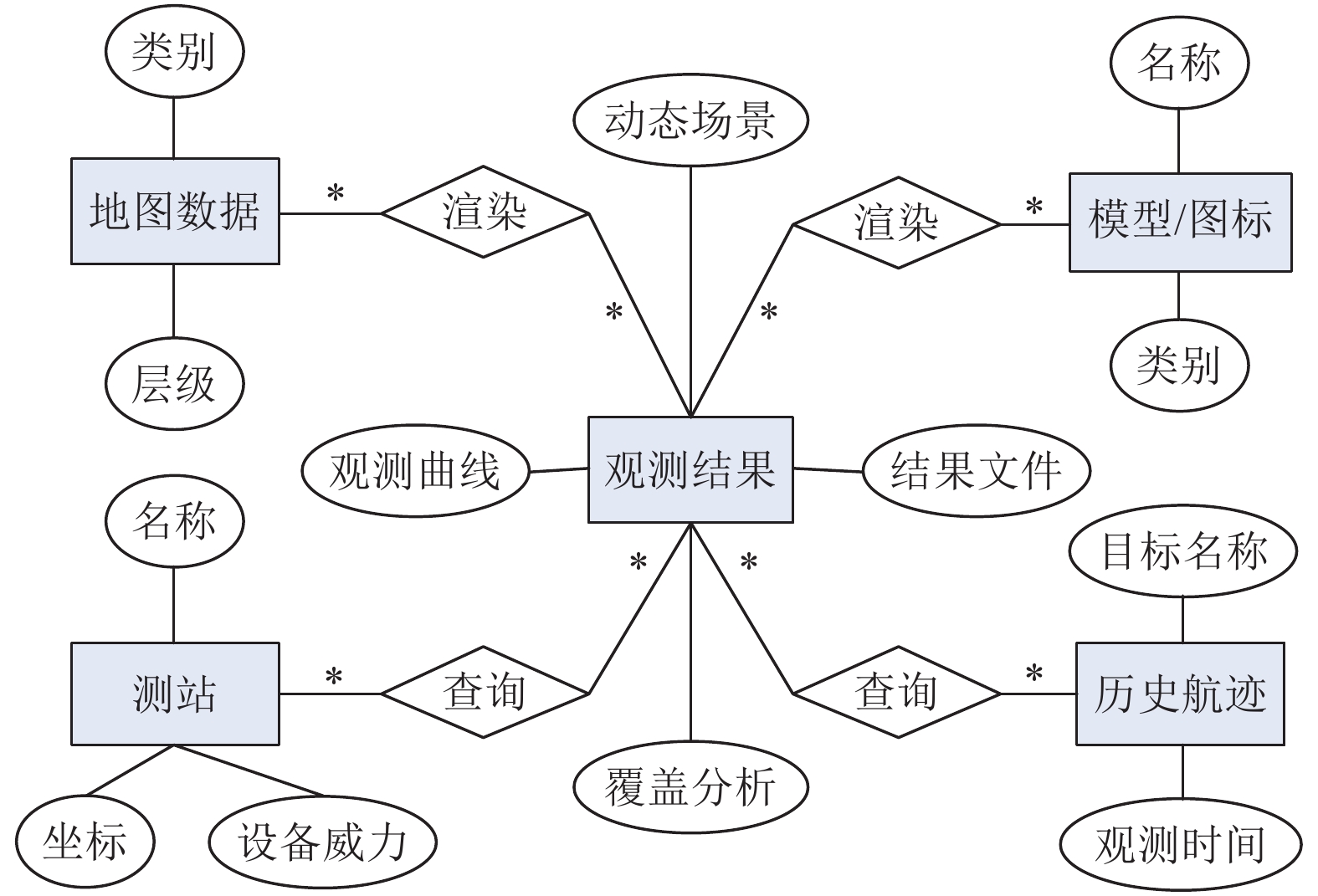
本平台观测结果的生成与展示基于数据库模型实现. 实体对象包括观测结果、地图数据、测站、模型/图标和历史航迹. 其中高分辨瓦片地图数据和目标三维模型用于二维和三维动态场景渲染; 测站信息包含测站名称、站址坐标和观测设备威力指标等属性, 用于目标观测时对设备可见性和覆盖情况进行分析; 历史航迹则提供了数据查询功能. 基于数据库设计的E-R流图如图2所示.
|
图 2 软件平台数据库E-R流图 |
2 轨道计算与观测分析
对空间目标的观测需要获取卫星的入站和出站时间, 掌握目标的观测角和距离信息; 在计算得到目标的空间坐标后, 还需要转换成测站极坐标系, 以此作为观测天线的引导数据文件. 以下介绍TLE两行根数格式、SGP4轨道计算模型和站心系坐标转换.
2.1 TLE与SGP4模型TLE两行根数格式由北美航天国防司令部(North American aerospace defence command, NORAD)公布, 对应瞬时轨道坐标系, 其相应的轨道预报算法由一般摄动法(即解析法)简化得到. 将TLE数据应用于SGP4模型, 可成功预报轨道周期小于225 min的空间目标, 解算出目标在任意时刻的空间位置和速度[13].
卫星星历的结构为3行, 首行数据为卫星名称; 后面两行则存储了卫星相关数据, 每行69个字符, 包括0–9、A–Z (大写)、空格、点和正负号. 第2、3行的格式说明如表1和表2所示.
| 表 1 第2行格式描述 |
| 表 2 第3行格式描述 |
SGP4/SDP4是由NORAD开发的一种轨道预报模型, 代码公布以来, 经过了多次修正, 2006年Vallado, David等人对所有版本进行了总结, 提供了与美国国防部完全兼容的程序代码[14]. 除了地球中心引力, 在轨卫星还受到各种摄动力的影响, 主要包括: (1)大气阻力摄动的影响. 大气阻力摄动是非引力摄动之一, 人造卫星特别是近地轨道卫星, 在地球附加的空间飞行受到大气阻力产生的摄动, 使卫星轨道的大小和形状不断变化. (2)地球非球形引力的影响. 在二体问题中, 只需考虑地球对卫星的中心引力; 实际上, 由于地球质量分布不均匀, 对卫星还产生扁率摄动、形变摄动等影响. (3)太阳、月球及其他行星引力的影响. 在SGP4模型中, 这些摄动力均有对应算法进行修正, 考虑了地球扁率, 日月引力的长期和周期摄动, 以及大气阻力引起的轨道衰退, 以保证预测轨道的精度[15].
2.2 球心直角坐标到站心极坐标的转换经过轨道计算得到的空间目标位置是不同时间点的球心直角坐标, 如果用于测站对空间在轨目标的观测, 需要转换成站心极坐标. 转换包含两个步骤, 一是球心直角坐标到站心地平直角坐标的转换, 二是站心地平直角坐标到站心极坐标的转换[16].
设测站的大地坐标经纬度为(
| $ \begin{split} \left( {\begin{array}{*{20}{c}} x \\ y \\ {\textit{z}} \end{array}} \right) =& \left( {\begin{array}{*{20}{c}} { - \sin {B_0} \cos {L_0}}&{ - \sin {B_0} \sin {L_0}}&{\cos{B_0}} \\ { - \sin{L_0}}&{\cos{L_0}}&{\text{0}} \\ {\cos{B_0}\cos{L_0}}&{\cos{B_0}\sin{L_0}}&{\sin{B_0}} \end{array}} \right) \\ & \cdot \left( {\begin{array}{*{20}{c}} {X - {X_0}} \\ {Y - {Y_0}} \\ {Z - {Z_0}} \end{array}} \right) \end{split} $ | (1) |
将球心直角坐标(
| $ \left( {\begin{array}{*{20}{c}} x \\ y \\ {\textit{z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {R\sin E\cos A} \\ {R\sin E\sin A} \\ {R\cos E} \end{array}} \right) $ | (2) |
解得:
| $ \left( {\begin{array}{*{20}{c}} R \\ A \\ E \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\sqrt {{x^2} + {y^2} + {{\textit{z}}^2}} } \\ {{\tan^{ - 1}}{y \mathord{\left/ {\vphantom {y x}} \right. } x}} \\ {{\tan^{ - 1}}{{\sqrt {{x^2} + {y^2}} } \mathord{\left/ {\vphantom {{\sqrt {{x^2} + {y^2}} } {\textit{z}}}} \right. } {\textit{z}}}} \end{array}} \right) $ | (3) |
得到站心极坐标后, 结合目标入站时间, 可引导观测设备的天线指向, 实现空间在轨目标的跟踪测量.
3 可视化实现 3.1 目标场景动态显示三维场景的创建主要由创建容器、加载三维控件、添加地图地形服务、加载三维模型或在线数据图层服务 4 个部分组成, 在页面容器创建之后, 通过调用 Cesium 的 Viewer函数初始化三维场景控件[17]. Viewer函数中有多达几十个参数设置项, 这些参数决定了场景部件的显示方式, 其中最主要的参数是通过设置imageryProvider参数访问我们提供的地图数据. Cesium支持多种服务来源的高精度影像(地图)数据的加载和渲染[18]. 在本设计中, 搭建了高分辨的离线地图服务器, 通过Cesium的TMS (瓦片地图服务) 接口访问地图服务的URL, 然后在Viewer函数中为imageryProvider参数指定这一图层服务. 经过以上设置. 就可以在浏览器窗口显示一个完整的三维数字地球了.
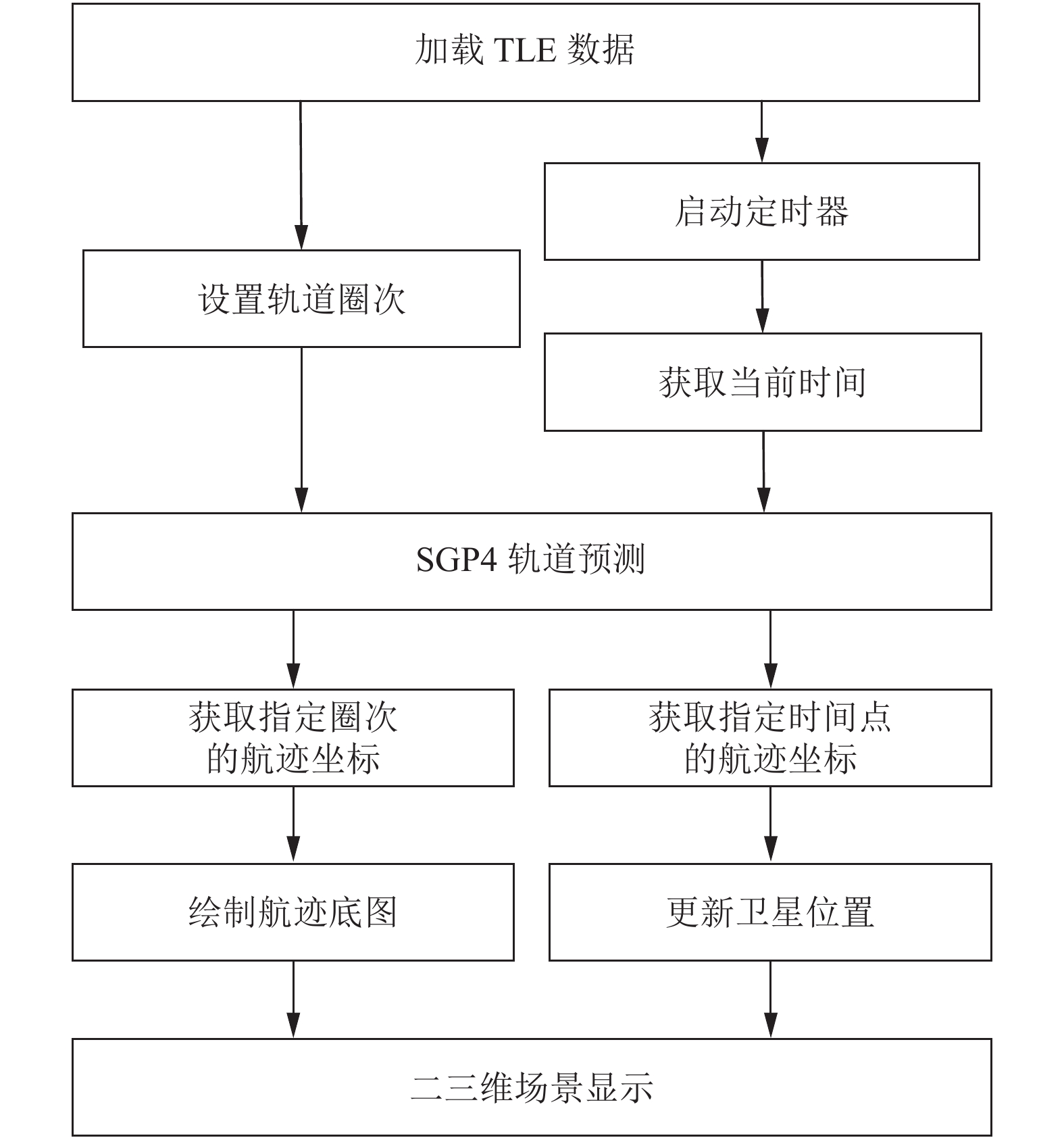
软件中通过功能函数showSatPos(tle)实现目标的动态场景显示. 首先从轨道根数tle中提取卫星周期, 根据设置的圈次数, 得到卫星从当前时刻到结束时刻的显示时间长度, 然后调用函数getSatelliteInfo()返回该时间长度内指定时间间隔的观测信息.函数getSatelliteInfo()接收的参数包括tle根数、时间戳和测站坐标信息, 利用SGP4模型计算后返回结果对象, 对象中包含了目标的空间坐标和测站观测的极坐标. 场景中显示的目标三维航迹和模型数据通过Cesium提供的Entity对象的add()方法实现; 根据绘制需要, 可指定该方法的绘制参数, 包括点(point)、线(polyline)、图片(image)、模型(model)、标签(lable)以及它们的空间坐标(position)等. 本设计中使用线实体(polyline)绘制目标航迹, 通过加载卫星模型实时更新目标位置. Cesium中目前支持gltf和bgltf两种格式的模型数据, 可以借助3ds Max软件从其他格式的模型文件转换得到[19, 20]. 为了显示卫星的移动效果, 使用定时器更新卫星的位置[21]. 在本软件中, 利用JavaScript提供的setInterval()函数, 通过设置回调函数和时间间隔, 实现了指定的目标位置更新效果.场景动态显示的流程如图3所示.
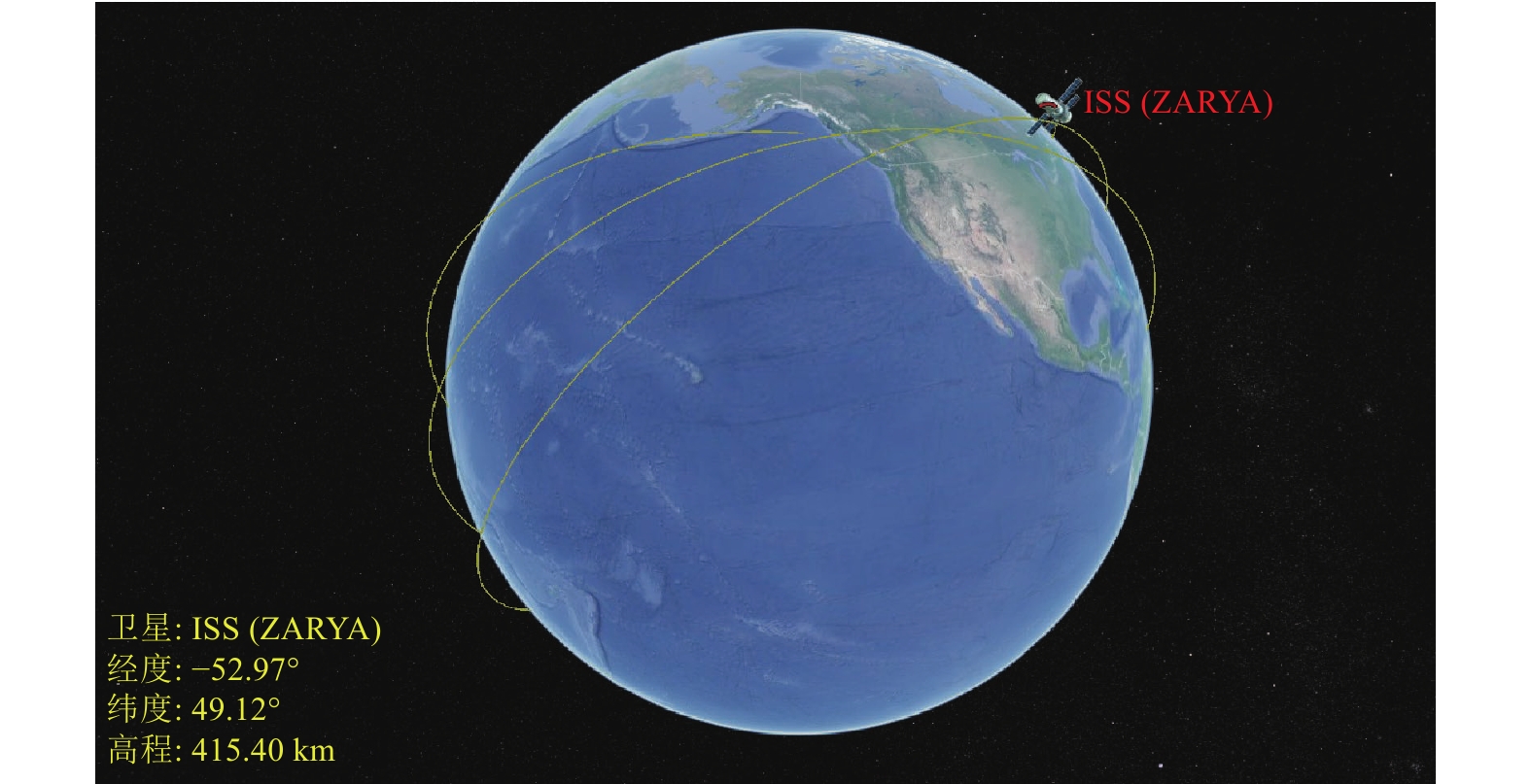
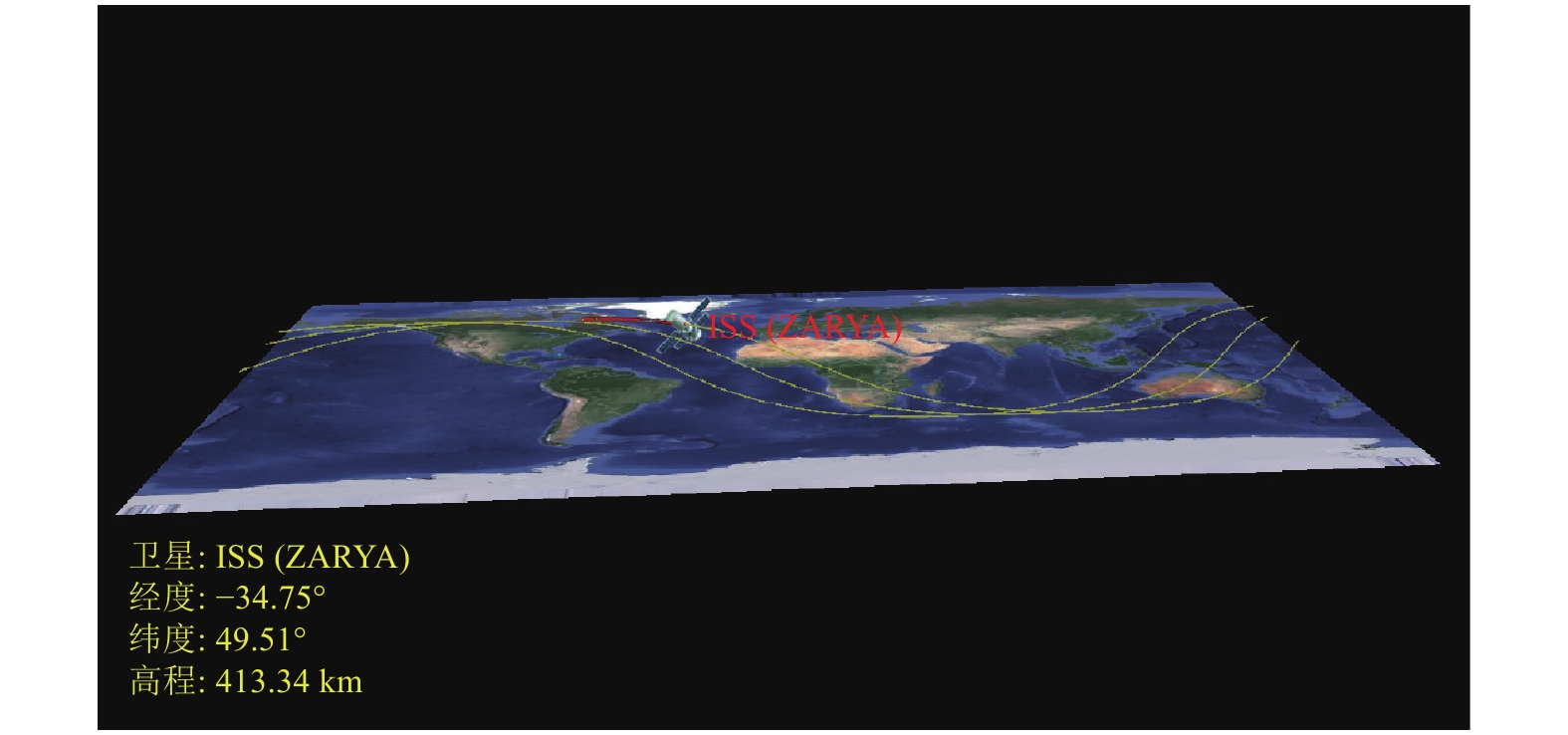
为了获取不同视图的显示效果, 场景中利用小窗增加了二维全景地图的显示, 显示的航迹地图和目标位置与三维场景保持同步. 二维显示窗口可拖放至屏幕任意位置, 同时支持地图缩放功能. 图4和图5分别为场景3D和2.5D显示效果.
3.2 目标观测可视化目标的可见性是指目标进入测站的观测视角范围内. 通常要求目标的观测仰角大于0°, 观测距离则由观测设备的探测威力决定. 目标可见性计算时, 从参数设置对话框输入观测约束条件. 软件实现的流程如图6所示.
|
图 3 场景动态显示流程 |
|
图 4 场景动态显示效果(3D) |
|
图 5 场景动态显示效果(2.5D) |
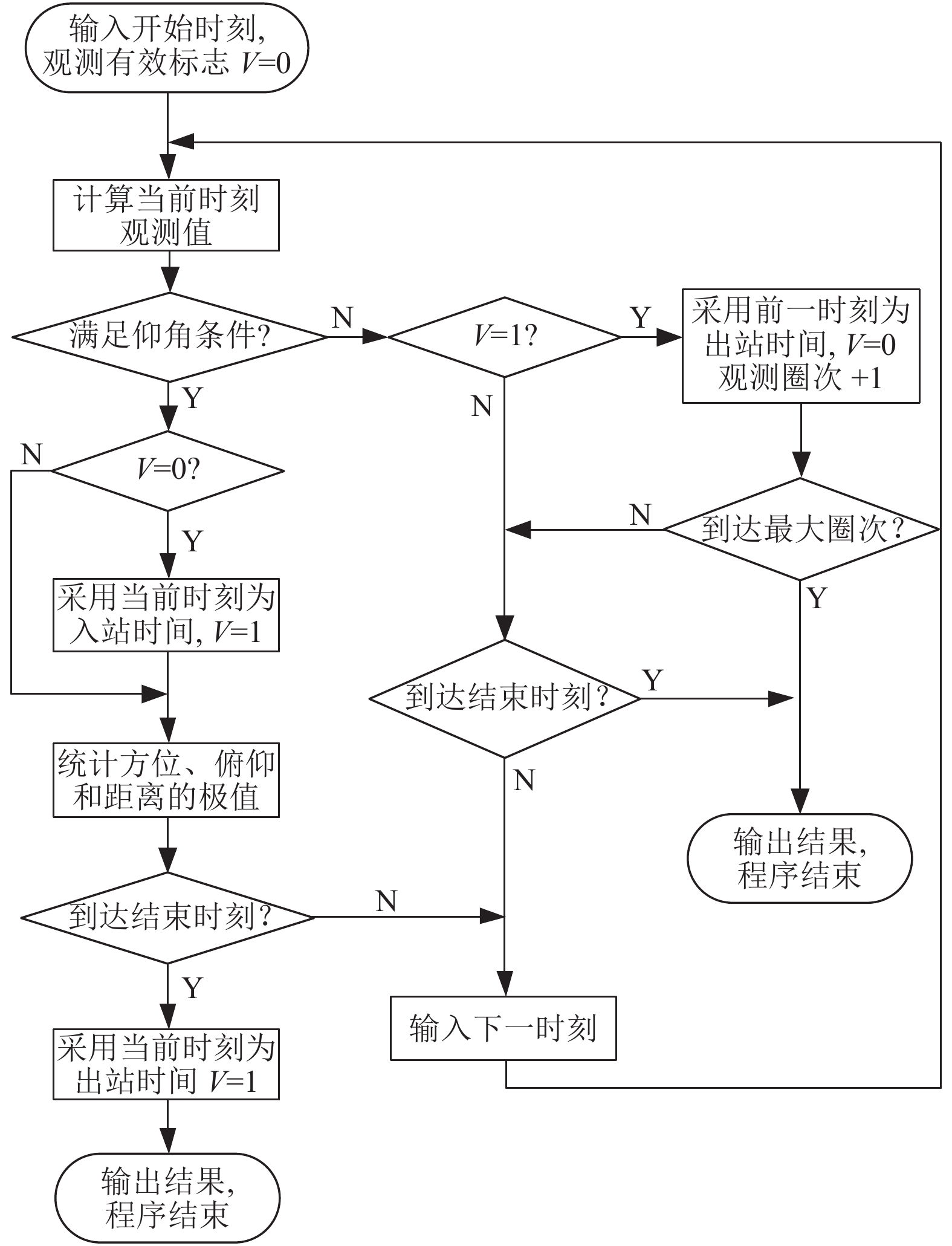
观测约束条件包括测站坐标、起止时间、最低仰角和最大圈数等信息. 计算过程使用了getSatelliteInfo()函数功能, 输出观测结果时, 对数据进行了统计和筛选, 以获取每个观测圈次的入站和出站时间、观测方位角范围、最高仰角、最远距离和持续时间等信息. 用程序实现的统计和筛选流程如图7所示. 程序中设置了观测有效标志变量V, 初始化为0, 如果当前时刻计算的结果符合测站的仰角观测条件则置V=1. 通过该标志变量的变化, 可以统计和记录观测时段的起止时刻. 另外, 程序中还通过初始设置极大极小值的方法, 实现了边计算边统计观测结果中方位、俯仰和距离的极值, 避免了二次遍历数据, 提升了计算效率. 在统计结果中, 选中指定的一行观测数据, 可以对结果进行三维可视化、测站覆盖分析或曲线图显示, 也可以保存为本地数据文件. 在三维可视化显示时, 通过第3.1节中描述的Cesium的线实体实现了测站的可见航迹绘制; 在查询和计算当前测站相对于空间目标的观测距离后, 作为半径参数, 通过绘制Cesium的ellipsoid实体实现了测站的覆盖分析效果. 参数设置与统计结果通过图8的对话框实现.

|
图 6 目标可见性显示流程 |
从CelesTrak网站下载Landsat9卫星TLE轨道根数进行计算, 图8中的数据表格内容为该卫星从2021年11月4日到5日的可见圈次计算结果.表格中每一行给出了符合条件的起止时间、最高仰角、最远距离、方位角变化范围和持续时间. 选择某个圈次后, 可以输出文本格式的轨道数据文件, 文件记录了目标在每个时间点的空间位置、速度、大地坐标、站心系极坐标等内容.
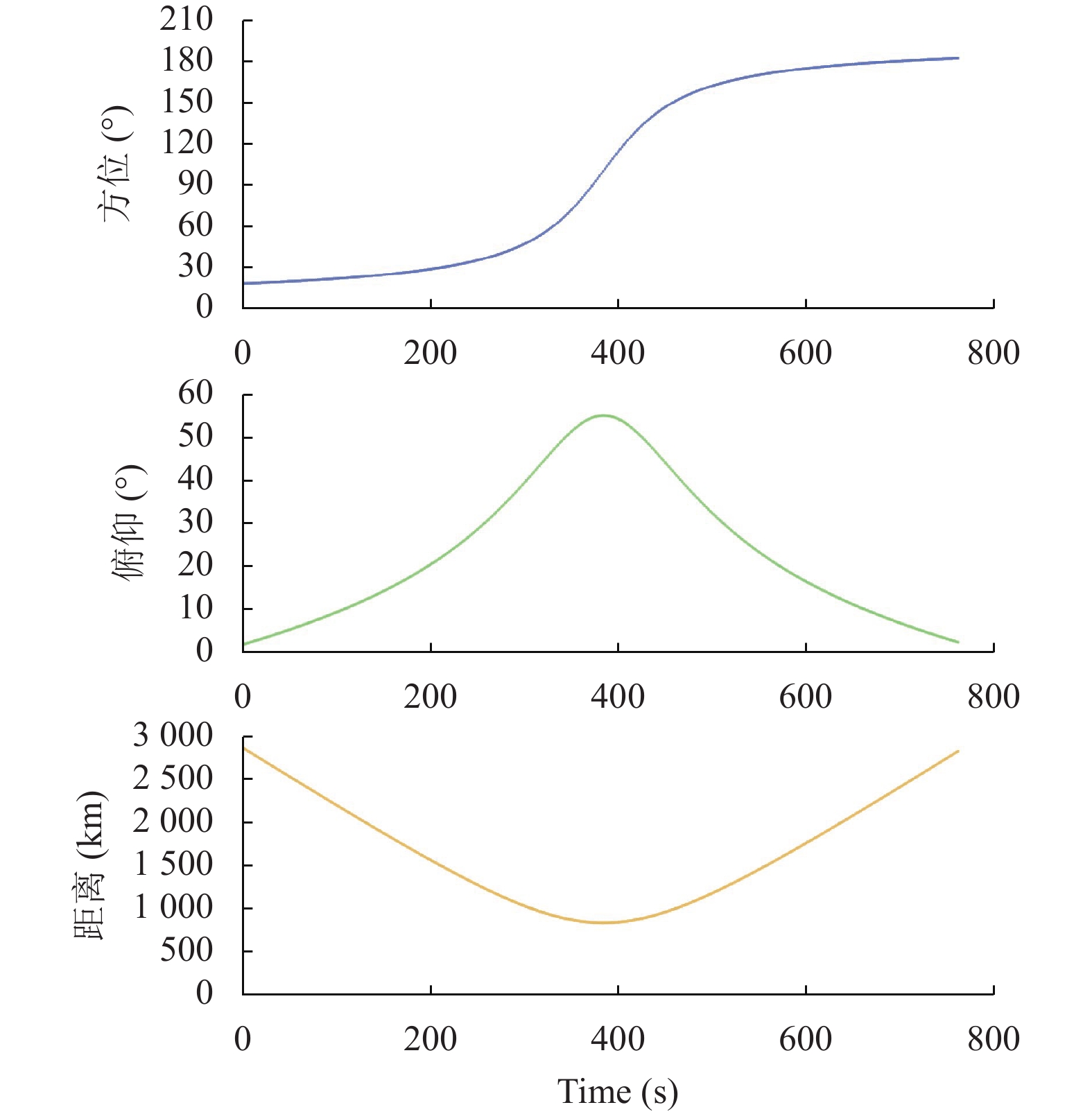
观测结果曲线如图9所示. 图中横轴为时间, 纵轴为方位、俯仰和距离, 曲线图支持缩放功能, 可保存为本地图片文件; 图中的数据还可以导出为Excel表格文件, 方便用户使用.
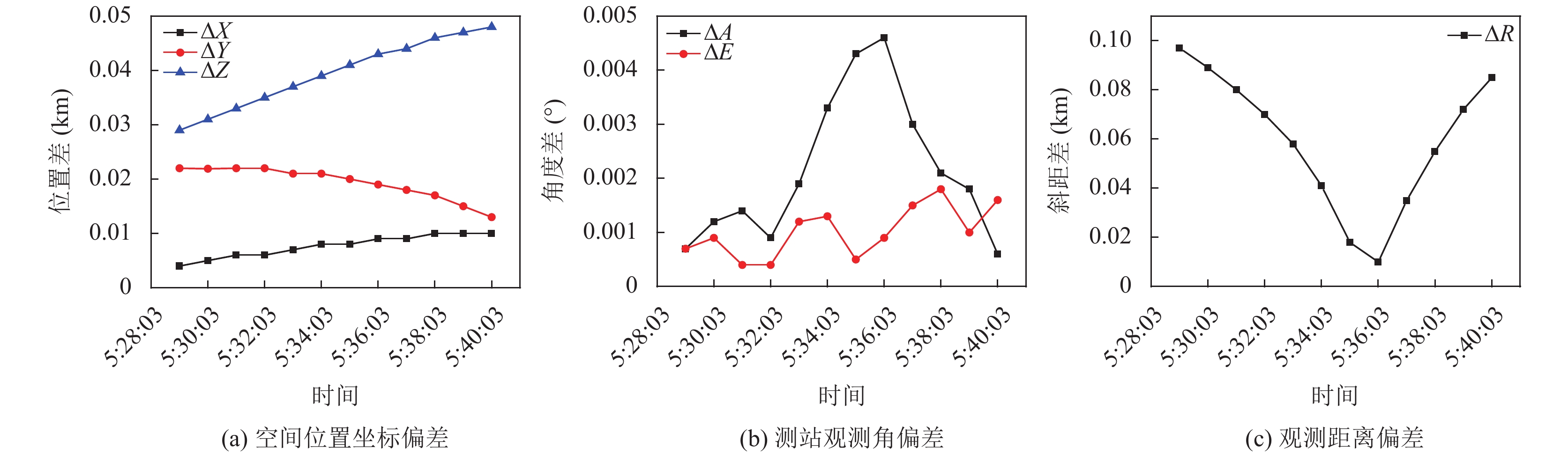
4 观测数据精度验证为了验证平台软件得到的观测数据的可信度, 利用TLE轨道根数和SGP4模型, 分别以STK仿真工具和平台软件计算OCEANSAT-2卫星(轨道高度约730 km)的预报和观测数据. 卫星对测站12可见的时间为UTC时间2021年11月4日05时29分03秒至05时40分03秒, 设置计算步长为60 s, 假设测站12的大地坐标为经度92.7501°, 纬度37.030°, 高程1397.59 m. 得到观测目标的球心坐标和转换后的站心极坐标后, 以STK软件的计算结果为基准, 验证平台软件计算结果的精度[22]. 表3为球心坐标的计算结果, 表4为站心极坐标的计算结果; 图10为STK与可视化平台计算结果比对后的偏差曲线.
|
图 7 观测统计与筛选流程图 |

|
图 8 参数设置与统计结果对话框 |
|
图 9 测站12的观测曲线 |
从图10的偏差曲线可以得出, 平台软件与STK分别计算的卫星球心坐标位置差小于50 m; 站心极坐标的方位差小于0.005°, 俯仰差小于0.002°, 星站距离差小于100 m, 表明平台软件的计算结果与STK相吻合, 可以满足使用要求.
为了比较观测软件与STK在三维动态显示时的系统资源使用情况, 使用Windows任务管理器对两个软件在自动运行时进行监测. 测试的电脑CPU为Intel core i7 8550u@1.8GHz, 内存16 GB, Intel UHD620集成显卡. 经过一段时间后运行流畅, 可观察得到两个软件对CPU、内存和GPU的近似占用率. 图11为运行时的资源占用情况截图. 表5对两个软件的基本性能做了对比.
从测试情况看, 两个软件对CPU的占用率基本相同, 保持在10%以内; 在内存和GPU的使用方面, 观测软件相比STK偏高, 其原因是观测平台软件使用了高分辨率的地图和场景数据, 渲染时占用了较多的内存和GPU资源. 在多用户支持方面, 观测平台不受限制, 而STK只能通过二次开发接口提供有限支持.
|
图 10 可视化平台与STK计算结果偏差 |
| 表 3 OCEANSAT-2卫星的预报结果(球心坐标)(km) |
| 表 4 OCEANSAT-2卫星的预报结果(站心极坐标) |
| 表 5 可视化平台与STK基本性能对比 |

|
图 11 资源使用情况截图 |
5 结束语
随着我国航天事业的快速发展, 对空间目标的观测需求逐步增多, 为满足各测量站对空间目标的常规和应急观测任务, 设计开发了基于Web访问技术、具有三维可视化功能的轨道目标观测平台. 本软件基于Cesium开发库进行设计, 采用浏览器/服务器架构, 搭建了高分辨离线瓦片地图服务器, 增强了三维场景配置的灵活性, 同时使数据共享更加方便. 该软件已多次应用于实际观测任务, 结果表明, 软件的跨平台特性使其能够适用于国产化软件环境, 计算精度满足使用要求.
| [1] |
夏胜夫, 陈俊宇, 雷祥旭, 等. 空间碎片天基监测图像仿真研究. 空间科学学报, 2020, 40(6): 1084-1090. DOI:10.11728/cjss2020.06.1084 |
| [2] |
杜建丽. 面向空间碎片编目的天基监测系统研究[博士学位论文]. 武汉: 武汉大学, 2018.
|
| [3] |
张海峰, 龙明亮, 邓华荣, 等. 地基空间碎片激光测距技术发展与应用(特邀). 光子学报, 2020, 49(11): 1149004. DOI:10.3788/gzxb20204911.1149004 |
| [4] |
张彧. 基于Cesium平台的导航卫星轨道模拟与可视化[硕士学位论文]. 上海: 华东师范大学, 2017.
|
| [5] |
赵慧峰. 基于Cesium的三维展示与查询平台开发[硕士学位论文]. 徐州: 中国矿业大学, 2019.
|
| [6] |
高云成. 基于Cesium的WebGIS三维客户端实现技术研究[硕士学位论文]. 西安: 西安电子科技大学, 2014.
|
| [7] |
杨菁, 陈冰凌, 王文鹏, 等. 基于Cesium的三维可视化场景建设及发布技术的研究. 测绘通报, 2021(S1): 50-53. |
| [8] |
韩昕熠. 基于Cesium的多维动态可视化技术研究[硕士学位论文]. 西安: 西安科技大学, 2019.
|
| [9] |
王东兴, 朱翊. GeoJSON在异构地理信息数据集成中的应用. 测绘与空间地理信息, 2018, 41(6): 138-140, 146. DOI:10.3969/j.issn.1672-5867.2018.06.041 |
| [10] |
袁凌, 刘建成, 潘磊, 等. 基于Cesium和谷歌影像的风电场地形三维可视化. 地理空间信息, 2020, 18(12): 1-4. DOI:10.3969/j.issn.1672-4623.2020.12.001 |
| [11] |
王尊. 地理信息应急服务中矢量瓦片技术研究与实现[硕士学位论文]. 天津: 天津师范大学, 2020.
|
| [12] |
毕硕本, 陈烨洲, 贡毓成, 等. 基于cesium的热带气旋灾害信息可视化研究. 系统仿真学报, 2021, 33(2): 472-483. DOI:10.16182/j.issn1004731x.joss.19-0547 |
| [13] |
赵广宇, 桑吉章, 陈俊宇, 等. 利用稀疏角度数据改进空间目标TLE轨道预报精度. 测绘地理信息, 2021, 46(S1): 301-304. DOI:10.14188/j.2095-6045.2019214 |
| [14] |
韦栋, 赵长印. SGP4/SDP4模型精度分析. 天文学报, 2009, 50(3): 332-339. DOI:10.3321/j.issn:0001-5245.2009.03.010 |
| [15] |
Vallado DA, Crawford P, Hujsak R, et al. Revisiting spacetrack report #3. AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Keystone: AIAA, 2006.
|
| [16] |
孙宏, 刘欣. 基于GPS定位的飞机航迹矢量算法. 科技和产业, 2021, 21(8): 235-237. DOI:10.3969/j.issn.1671-1807.2021.08.040 |
| [17] |
杨明奇, 周程, 付立军, 等. 融合Cesium和Geoserver的地质数据形变监测可视化方法. 计算机系统应用, 2021, 30(11): 179-187. DOI:10.15888/j.cnki.csa.008179 |
| [18] |
魏世轩. 基于Cesium的空间数据展示与查询关键技术研究. 城市勘测, 2021(3): 5-8. DOI:10.3969/j.issn.1672-8262.2021.03.001 |
| [19] |
王金娜, 焦学军, 宋会传, 等. 基于CESIUM的露天矿山实景三维智能监管技术研究. 地理空间信息, 2021, 19(8): 93-96. DOI:10.3969/j.issn.1672-4623.2021.08.025 |
| [20] |
熊英, 高月明. 面向Web应用的三维模型格式转换技术研究. 城市勘测, 2020(6): 59-63. DOI:10.3969/j.issn.1672-8262.2020.06.013 |
| [21] |
曹衍龙, 汪杰. HTML5/CSS3/JavaScript技术大全. 北京: 人民邮电出版社, 2018.
|
| [22] |
刁宁辉, 刘建强, 孙从容, 等. 基于SGP4模型的卫星轨道计算. 遥感信息, 2012, 27(4): 64-70. DOI:10.3969/j.issn.1000-3177.2012.04.011 |
 2022, Vol. 31
2022, Vol. 31



