2. 四川大学华西医院 超声医学科, 成都 610041
2. Department of Ultrasound Medicine, West China Hospital of Sichuan University, Chengdu 610041, China
颈部淋巴结会受甲状腺病变细胞转移的影响而发生病变. 发生肿瘤转移的淋巴结, 肿瘤细胞会通过淋巴管首先聚集于边缘窦, 继而逐渐侵入淋巴结实质; 其可破坏淋巴结正常的动静脉结构, 诱导新生血管的形成. 肿瘤细胞的转移会影响颈部淋巴结的血流情况. 基于超声造影(contrast-enhanced ultrasound, CEUS)可以通过造影剂判断血流灌注的信息, 辅助医生进行病情诊断[1].
传统的灌注曲线(时间强度曲线, TIC)是基于病灶区域每帧取强度值的平均值而沿时间轴成时间序列而得. 然而, 由于感兴趣区域(region of interest, ROI)的灌注强度可能并不均匀, 这样将使提取的特征不准确[2]. 因此, 本文对感兴趣区域进行像素级分析, 即视频的一个坐标将沿时间轴拟合一条时间强度曲线. 所有感兴趣区域内的曲线对一个灌注特征(达峰时间、峰值等)进行提取可以形成一个二维矩阵. 二维矩阵可以进行编码显示成图, 也可以进一步提取更深层次的信息来进行可视化.
本文主要的创新实验是, 基于达峰时间(time to peak, TTP)二维矩阵进行研究, 猜测感兴趣区域中相距不远的达峰时间接近的两坐标可能存在流向先后的关联性并因此寻找血流流向的信息, 来进行灌注流向的成像可视化.
1 相关技术与研究现状 1.1 研究现状探头固定时, 颈部淋巴结采集的造影视频, 目标跟踪过程是不考虑尺度变化的. 比如, Zhang等人在2011年认为颈部淋巴结在探头不动的情况主要会受呼吸作用影响而做类似周期性的运动, 而直接利用基于块匹配的方法来进行目标跟踪[3]. 其利用了最小化绝对差和(sum of absolute difference, SAD). 基于光流法也能进行目标跟踪, 但是对光照要求太过严格[4]. Ta等人在2012年利用了基于互信息的方法来进行目标跟踪[5]. 然而互信息始终计算量太大, 并且也不能很好地处理异常帧. 而后, 林细林等人2018年利用了感知压缩跟踪[6], 该方法通过改进可以处理异常帧的情况[7], 但压缩感知跟踪的跟踪结果位置不够精确, 甚至位置还会跑得很远[8]. 由此本文实验了KCF (核相关滤波)算法来进行目标跟踪, 其利用了相关滤波理论与核函数技术, 使得目标跟踪很鲁邦而且计算量不会很大[9].
时间强度曲线可以反映血液中的造影剂浓度变化. Zhang等人早期就对感兴趣区域提取亮度灰度值的平均值, 随帧数生成时间强度曲线(time intensity curves, TIC), 提取出达峰时间、峰值(peak value, PI)等灌注参数来分析视频[3]. Gaia分析类风湿性关节炎时, 指出可以利用像素级的时间强度曲线, 即每个坐标点拟合一条曲线. 然后对每一个灌注参数可以生成一个二维矩阵, 可以编码成像来帮助医生诊断病情. 其拟合曲线时利用的是Gamma公式[10]. 王本刚等人分析肝脏病例也进行了基于像素的时间强度曲线分析, 不过只是利用了savgol滤波器进行曲线拟合[2]. 这些文献没有研究怎么样将没有很好灌注趋势的曲线筛除, 本文将对此进行研究.
针对灌注流向问题, 本文尝试利用流线与向量场来进行实验. 自Brian 等提出线积分卷积 (line integral convolution, LIC)的方法后, 对向量场进行可视化大部分是利用了LIC方法及其变体[11]. 虽然Wegenkittl 等人提出 Oriented LIC 方法来使结果纹理含有方向指向信息[12]. 但本文病例感兴趣区域太小, 因此不能用该方法表示方向. 本文使用了Brain提出的基本的LIC方法, 同时利用颜色编码来表示坐标的先后关系.
1.2 相关技术第1步. 对淋巴结进行目标跟踪.
实验中所采集的超声造影视频都为双模式并排显示, 如图1所示, 左为超声灰阶B模式, 右为超声造影模式. 目标跟踪在灰阶B模式上面进行, 然后再将位置信息应用到彩色造影模式中以分析灌注情况.

|
图 1 双模式视频帧 |
由于淋巴结主要是因为呼吸会产生运动, 但没有明显尺度变化. 所以可以由医生进行感兴趣区域的标记, 然后提取出掩膜mask以便在视频中进行目标跟踪, 如图2所示.
这里手工标定的帧由医生选取, 被用来做目标跟踪的起始帧, 被称为“参考帧”. 参考帧不一定是原视频的第1帧.
本文选择核相关滤波(kernelized correlation filters, KCF)[9]和Kalman滤波结合的方式进行目标跟踪[13].
第2步. 进行像素级的时间强度曲线拟合.
基本思路是: 在B模式对淋巴结进行目标跟踪后, 将位置信息用到造影模式. 造影模式ROI每一个坐标沿着时间轴都能拟合一条时间强度曲线. 本文利用Gamma公式模型, 同时也研究怎么筛选符合灌注特征的曲线.
第3步. 提取灌注特征参数. 因为是基于像素的分析, 所以对符合标准的曲线提取灌注参数(达峰时间、峰值等), 形成二维矩阵. 对二维矩阵可以编码成像显示, 辅助医生诊断病情.
第4步. 利用TTP参数二维矩阵可视化灌注流向情况. 设种子点为TTP值低于设定阈值的坐标点. 先找种子坐标点, 每个种子点会找一条流线, 这些流线可以进行可视化. 实验也尝试了利用流线信息生成向量场, 并利用线积分卷积的方式可视化.

|
图 2 提取mask掩膜示意图 |
2 病灶跟踪 2.1 淋巴结关于目标跟踪方面的特点
探头固定的情况下, 视频灰阶B模式相邻两帧之间的运动变化很小可以忽略, 整体运动以呼吸运动的影响为主, 而呼吸运动可以看成周期运动[3]. 在视频中淋巴结很少发生巨大的尺度变化(即缩放变化), 也不会有大的形变(指形状改变成另外的样子).
灰阶B模式采用的是基波, 造影模式采用的是谐波. 造影剂的浓度变化会使彩色造影部分的亮度跟着改变. 这也会对灰阶B模式产生影响, 但亮度不会发生很大变化.
视频中会出现短暂的异常帧, 持续时间很短, 并且之后目标形态会恢复正常. 异常帧常是由于信号噪声、病人的较强的呼吸引来的其他平面信息等因素而导致的, 主要表现是目标细节暂时丢失.
总结下来, 没有异常帧时可以利用简单目标跟踪方法(如基于灰度的模板匹配)来处理. 有异常帧时就要考虑如何检测与处理异常帧.
2.2 目标跟踪模型传统的基于灰度的模板匹配(如最小化绝对差和SAD、最小化平均绝对差MAD、最大化归一化互相关NCC等)进行目标跟踪, 一帧一帧更换参考模板的可以渐变地跟踪目标. 但是, 其并没有提出好的检测异常帧的方法.
基于要处理异常帧的思路, 本文选择了相关滤波的方法进行目标跟踪.
相关滤波的思想是利用信号的相关性, 设计一个滤波模板, 利用模板与目标候选区做相关运算生成响应图, 响应图上值越大的位置越可能是待搜索帧的目标位置. 相关滤波跟踪的优点是可以利用卷积计算在傅里叶域的性质减少计算量.
用KCF (核相关滤波)进行目标跟踪, 利用HOG特征会对光照变化有鲁邦性, 异常帧检测可以利用响应图的峰值旁瓣比(peak to sidelobe ratio, PSR)[9].
峰值旁瓣比公式为[14]:
| $ {\textit{PSR}} = \frac{{{g_{\max }} - {\mu _s}}}{{{\delta _s}}} $ | (1) |
其中,
卡尔曼滤波器是一种高效的递归滤波器, 能够从一系列不完全包含噪声的测量中, 估计出动态系统的状态[13]. 其常用在轨迹预测与目标定位中. 对于一般的线性随机系统, 可表示为:
| $ {x_k} = {F_{k - 1}}{x_{k - 1}} + {G_{k - 1}}{w_{k - 1}} $ | (2) |
| $ {{\textit{z}}_k} = {H_k}{x_k} + {v_k} $ | (3) |
其中,
上述模型是线性的Kalman滤波模型, 常有5个基本公式. 用Kalman滤波进行数据的滤波, 可以从后验结果得到最终的数据滤波结果, 比如滤波后的曲线数据; 用Kalman滤波进行预测, 可以从先验结果里得到预测结果, 比如预测的位置信息.
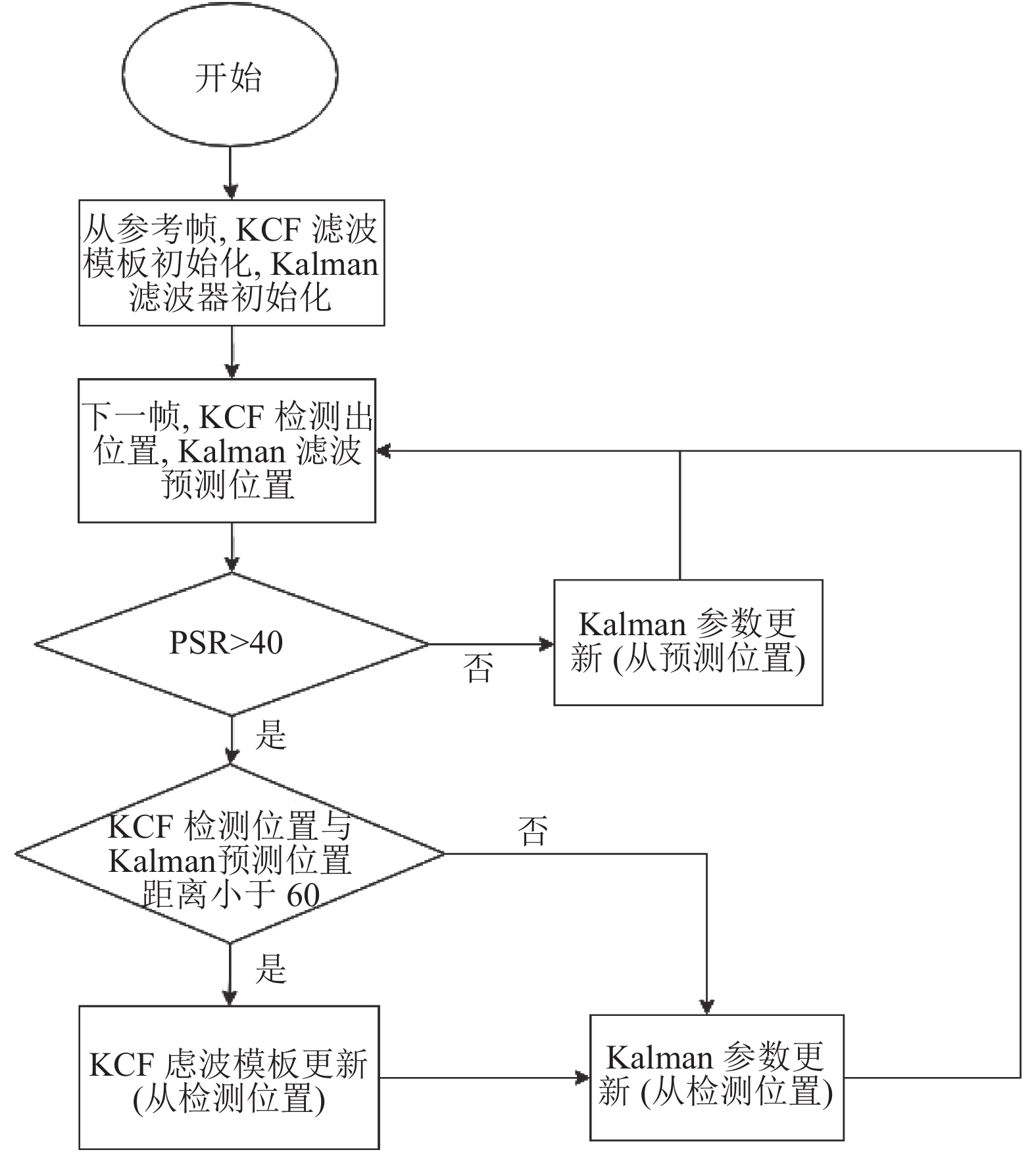
2.4 总的目标跟踪思路视频中大部分时间淋巴结的运动速度都是较慢的, 但突发情况时会发生较快的运动. 较快的运动就会有一些帧中目标变得模糊, 或产生伪影. 因此建立线性的卡尔曼模型来检测目标是否运动过快, 一旦速度超过阈值, 就不对KCF滤波模板进行更新[7].
最终, KCF的模板大小为长宽96 像素. 如果图像太小, 模板边长要适当变小. PSR的最小阈值为40, Kalman预测位置与相关滤波检测位置的欧式距离最大阈值为60 像素.
如果上述两阈值条件都满足, 才更新KCF的滤波模板. 对于Kalman模型的参数更新, 如果某帧不满足PSR最小阈值就用Kalman预测位置更新; 如果满足PSR最小阈值, 就用KCF检测位置更新. 目标跟踪中的更新操作流程如图3所示.
|
图 3 目标跟踪中的更新操作流程 |
3 进行像素级的时间强度曲线拟合 3.1 二维平滑窗口的选择
时间强度曲线是每个坐标都沿时间轴提取一条曲线. 但是会出现大量坐标的数据不能曲线拟合成功.
针对该问题, 猜测淋巴结内部各结构会随着呼吸相对于淋巴结整体发生很细微的运动. 考虑利用一个二维平滑窗口, 将呼吸引起的细微运动的轨迹笼罩住, 窗口内提取平均值. 平均值的变化就能符合灌注趋势了. 这里平滑窗口高宽是“29×29”.
3.2 TIC曲线数据的提取TIC (time-intensity curve)曲线即时间强度曲线. 将造影图片从RGB颜色空间转换为“HSV”颜色空间[15]. 生成H分量的直方图之后发现数据分布集中在很窄的一段, 如图4, 即造影部分色调都比较接近. 因此, 图像的色调不存在太多信息, 饱和度又不能说明亮度变化. 最终选择了“HSV”的“V”分量(缩放到[0, 255])来表示“强度”.
每一坐标点可以沿时间轴得到一条TIC曲线的原始数据. 当TIC的原始数据得到之后, 会首先采用S-G平滑滤波(Savitsky-Golay滤波器)[2], 多项式阶数是2, 窗口大小是81 (原视频帧率是10 fps, 所以这里代表8.1 s). 滤波目的是减弱噪声.

|
图 4 一帧造影与其HSV空间的H分量的直方图 |
3.3 基于Gamma公式的曲线拟合
Gamma模型公式[10]为:
| $ {{Y}}(t) = \left\{ {\begin{array}{*{20}{l}} B,&{t < AT} \\ {A{{(t - AT)}^C}{{\rm{e}}^{ - k(t - AT)}} + B},&{t \geqslant AT} \end{array}} \right. $ | (4) |
其中,
利用Gamma公式进行曲线拟合, 可以描述造影剂在血管中的洗入(wash-in, 表现为曲线上升)与洗出(wash-out, 表现为曲线下降)的时间段情况, 便于提取相关的灌注特征参数, 如图5所示.

|
图 5 原数据和Gamma拟合图 |
3.4 曲线数据的筛选之粗筛选与细筛选
并非ROI内所有的点都能很好地拟合曲线, 考虑原因是并非所有区域都是液态的有血流经过的区域. 因此, 需要将不符合的曲线数据筛除.
这里考虑用“粗筛选-细筛选”的方式, 只有两种筛选都通过的曲线才能用于以后的实验.
第1步, 粗筛选.
粗筛选大致分两个思路, 两个子筛选条件都满足了才算通过粗筛选. 一个是真实值的判断, 一个是缩放值的判断.
(1)真实值判断, 就是对曲线原数据的峰值、起始值判断大小.
比如在实验中, 峰值不能小于30, 曲线起始值不大于100. 这里注意由于利用HSV的方法, 所有曲线中强度值范围可统一为[0, 255], 如图6所示.

|
图 6 真实值判断示意图 |
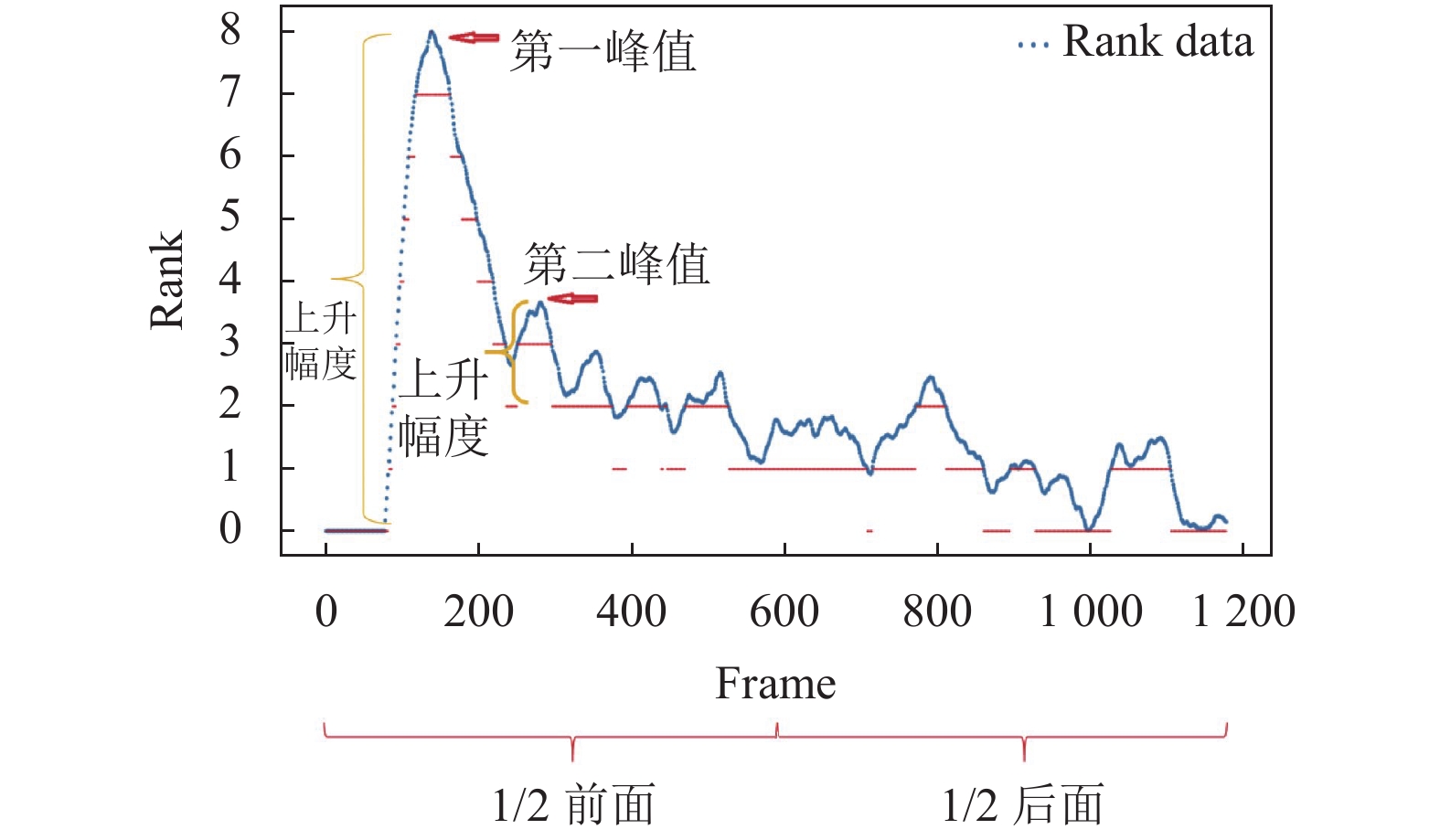
(2)缩放值判断, 将曲线原数据值缩放到[0, n], n为正整数, 这里为8. 对数据中的第2峰值、后面(1/2时间之后)最大值、起伏过程中的上升幅度、起伏过程中的异常上升总次数等进行判断.
比如实验中, 第2峰值在数据后面不能大于5, 在前面不能相比之前的波谷上升超过3. 后端1/5时间段最大值不能是6. 上升幅度大于3为异常上升, 异常上升次数不能多于3个, 如图7所示.
|
图 7 缩放值判断示意图 |
第2步, 细筛选.
满足粗筛选的曲线再次用细筛选进行处理. 细筛选是利用Gamma公式去拟合数据, 根据拟合情况对数据进行最后筛选.
因为“R-squared”一般应用于线性拟合中的拟合度评价准则, 所以没有使用在这里[16]. 本文的拟合度的评价准则如下:
(1) NRMSE, 即归一化的RMSE (均方根误差).
这里RMSE公式为:
| $ {\textit{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({r_i} - {f_i})}^2}} } $ | (5) |
其中,
而NRMSE的公式为:
| $ {\textit{NRMSE}} = \frac{\textit{RMSE}}{{\max ({f_i})}} $ | (6) |
(2) Adjusted Cosine即修正的余弦相似性[17]. 公式为:
| $ {{adcosine = }}\frac{{\displaystyle\sum {\left( {{r_i} - u} \right)\left( {{f_i} - u} \right)} }}{{\sqrt {\displaystyle\sum {{{\left( {{r_i} - u} \right)}^2}} } \sqrt {\displaystyle\sum {{{\left( {{f_i} - u} \right)}^2}} } }} $ | (7) |
其中,
考虑到拟合的曲线可能会直接平滑掉起伏频率高的数据段, 可能出现NRMSE小但是跟原数据根本就不像的情况. 因此, 利用余弦相似度进行衡量, 这里设置的最小阈值为0.75.
4 提取灌注特征参数 4.1 提取2-D灌注参数特征对于一条TIC曲线可以提取灌注参数, 而参数大致分两类[5]: (1)基于时间的, 如TTP (达峰时间)、MTT(平均渡越时间); (2)基于数值的, 如AUC (曲线下面积)、PI (峰值).
在视频中, 像素级提取时间强度曲线, 则对于一个灌注特征参数可得到一个二维矩阵, 可称为“灌注参数二维矩阵”.
另外, 曲线拟合成功与失败的坐标需要记录下来, 下文需要使用.
4.2 灌注参数二维矩阵的可视化曲线拟合成功的点才能进行正常的颜色编码来可视化, 失败的坐标点将会设置为黑色.
首先会将参数二维矩阵中成功的坐标的值统一缩放到[0, 240]之间. 因为在HSV颜色空间中, 色调分量H从“0到240”会对应“红到蓝”. 将S和V统一设置为1 (或满值), 不同坐标点只需设置各自的H分量, 便可得到一张彩色图.
然后, 对缩放后的二维矩阵进行编码可显示成图片. 不过, 颜色编码方式需结合实际情况指定.
比如, 对于TTP (达峰时间)来说, 达峰时间越小就说明达峰时间早, 越早越是医生感兴趣的越偏向暖色(红色). 此这一类数据采取“蓝到红, 大到小”的编码方法, 如图8.

|
图 8 TTP二维矩阵成像图 |
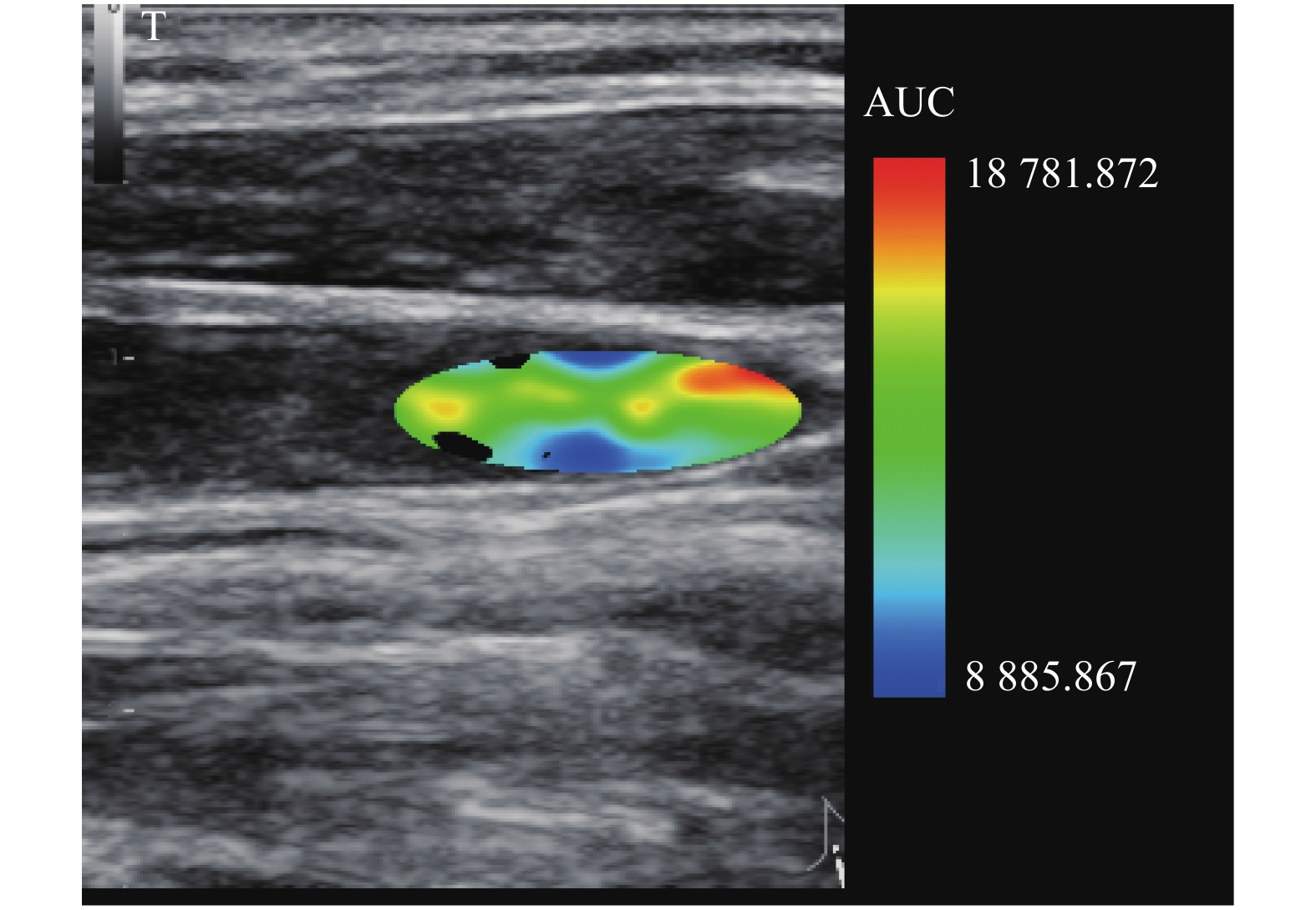
而对于AUC (曲线下面积), 值越大说明灌注总量越大, 越表示医生感兴趣的而偏暖色(红色). 因此这一类数据采取“蓝到红, 小到大”的编码方法, 如图9.
|
图 9 AUC二维矩阵成像图 |
5 基于达峰时间的灌注流向估计与可视化 5.1 灌注方向的求法
灌注大致方向对于病情的判断是有帮助的. 所以, 为了可视化灌注方向, 本课题利用了达峰时间二维矩阵进行估计. 总体思路是, 造影会从TTP小的地方流向TTP大一点的地方.
5.2 流线种子点的选取针对达峰时间二维矩阵, 设置一个TTP最大阈值, 将低于最大阈值的区域提取出来作为种子点.
对于TTP二维矩阵查找最大值maxValue和最小值minValue, 然后阈值Th为:
| $ Th = minValue + \left( {maxValue - minValue} \right) \times frac $ | (8) |
其中, frac为“0”到“1”之间的小数, 这里frac设置为0.3.
5.3 每条流线的生成流线是一条其上任意一点的矢量方向都与流线相切的曲线. 流线方程定义如下[18]:
| $ \frac{{d\mu \left( \tau \right)}}{{d\tau }} = v\left( {\mu \left( \tau \right)} \right) $ | (9) |
其中,
本文一条流线可以利用一组具有先后顺序的采样点来确定. 这里利用链表的形式给出, 为了理解, 这里借用C++的容器表示.
class Point{
int x;
int y;
};
std::vector<Point> streamlineList; //即一条流线的点组成的list.
而这里寻找流线的思想: 每个点以自己为起点找下一个符合的点, 并以找到的点为起点再找下一个点. 如图10(a), 一条流线的例子, 从A点开始, 直到F点结束就形成了一条流线的采样点.

|
图 10 寻找流线示意图 |
每次一个点为起点寻找下一个点时, 找大于该点且时间差为“0.2”或“0.3”秒的最小值(两个点不能同时发生, 所以时间差要有最小阈值), 搜索范围并不是采用固定的8邻域, 而是以当前点为中心, 一层一层(1、2到3的顺序)地搜寻外围的邻域点, 直到找到一个TTP大于该点且超过一定数值的最小值.
如图10(b), 以当前点P搜索下一个候选点的过程如下:
(1)设当前参考点为P, 并设置预定标准为下一点是该点值是比当前参考点大0.2的点的最小值.
(2)搜索P点的8邻域点, 如图中标记为“1”的那些点. 如果找到预定标准的候选点就结束; 否则将当前点和其8邻域点加入一个点群pointGroup, 然后进行第(3)步;
(3)继续搜索pointGroup点群的4邻域点(比如上次搜索标记为“1”, 这次搜索标记为“2”的那些点). 当前参考点依旧为中心点P (即第(1)步的点). 如果找到预定标准的点就结束; 否则就将其周围点加入pointGroup点群, 重复本步骤. 另外, 此步骤中pointGroup点群的长度大于限制值或ROI内所有点都已经遍历也会终止.
5.4 流线显示找到每条流线采样点中, 一条流线上每相邻的两个点可能在图上空间不相邻, 可以利用Bresenham直线算法用一条近似直线的像素点连接两点[19].
可问题是, 方向怎么表示. 图像小, 不考虑用箭头表示流向, 而利用TTP参数成像图里的颜色(色调)不同进行标记.
另外, 对区域中每一个坐标点统计有多少条流线经过(遍历所有曲线得出), 可以生成一个流线计数二维矩阵, 流线经过比较多的区域有很大可能是有血管的区域. 由于流线计数图亮度低的区域的细节看不清. 可以利用log增强技术来提高低灰度区域的对比度.
流线图、流线计数图以及流线计数图log增强图都显示在图11中.

|
图 11 流线结果显示 |
6 生成向量场并可视化 6.1 生成向量场
不同的种子点会有不同的流线, 可生成大小与原参数成像图相同的向量场, 每个坐标点有一个向量, 为了表示每一个坐标点的造影剂在下一时刻的可能去向[18].
一条流线可以利用Bresenham直线算法填充空隙, 然后从前到后依次指向, 每个非终止点可以指向流线上下一点而成向量. 而每一条流线的终点会设置成零向量.
可以用一张mask来表明某坐标是否已经因为一条流线经过而被赋值过. 遍历每一条流线, 然后在向量场相应位置修改向量值. 只有流线经过的点有非零的向量, 其他点向量都为零向量. 当出现某个点有多条流线经过的时候, 选取流线计数大的下一个点来作为下一个最优指向.
6.2 线积分卷积LIC技术根据向量场, 用一维滤波器沿流线卷积白噪声图像, 合成纹理. 该纹理与向量场的向量方向高度相关.
其生成过程需要输入向量场和一张噪声图(通常是白噪声)[11], 如图12所示.
其基本思想是, LIC会选择噪声图像作为输入背景纹理, 然后对每一个坐标点正反向去各追踪一条流线, 流线上的每一个像素点根据卷积核算出的权重来进行卷积计算, 得出纹理值. 而采用不同的核函数, 加之不同的背景噪声, 最终得到的效果也不一样[20], 本实验选择的是盒型核与白噪声.

|
图 12 LIC图生成示意图 |
6.3 灌注流向的向量场成像
生成LIC图时要对零向量区域进行一步抑制, 缩小其亮度范围, 利用了TTP成像图的颜色来着色表示坐标点的先后关系(越接近暖色即红色, 则达峰时间越小).
如图13, 是对上面流线图的例子进行计算的结果. 其纹理显示了向量场的大致状态.

|
图 13 LIC结果图 |
7 实验结果分析 7.1 数据
本课题所选择的病例视频由四川成都华西医院提供, 造影剂采用意大利博莱科公司生产的第二代造影剂声诺维. 所有病例来自于同一个迈瑞的机器. 采集期间, 探头固定, 嘱患者固定体位, 平稳呼吸, 勿做吞咽动作. 目前实验数据共18例病例, 12例良、6例恶.
7.2 曲线拟合筛选后的有效点面积占比如表1所示, 18例视频都进行了实验. 有效坐标点是上文曲线拟合成功坐标点. 有效坐标点占比是有效坐标点数占ROI内总点数的比重.
| 表 1 有效坐标点占比结果 |
对于造影视频, 符合灌注趋势的坐标应是有血流经过的坐标. 有效坐标点占比太小则合格血管的覆盖面积太少.
因为本文的重点是探寻灌注流向信息可视方法, 所以实验的数据不是很多. 但在已有的数据中, 大部分良性视频的有效成功点数占比为“50%–100%”, 而有一半的恶性视频的有效成功点数占比为“0–50%”. 如果发生了有效成功点占比低于50%的事情, 样本极有可能是恶性的, 也可能是采集异常, 可标记为“可疑的”.
7.3 4种不同面积占比的视频的灌注可视化结果如图14, 观察不同的拟合成功点占比下灌注情况可视化结果. 其中, 每一行图片为一个视频的结果, 从上而下有效坐标占比依次为“0–20%”“20%–50%”“50%–80%”“80%–100%”. 每一行从左到右分别为TTP成像图、流线图、流线技术图(log增强)、LIC结果图.
当有效坐标点占比过于小时(低于50%时), 有关灌注情况的效果会很差. 因此, 建议观察流向信息时, 有效坐标占比要超过50%.
7.4 总的结果分析当确定ROI内基本是血管时, 可以将有效坐标点占比小(比如低于50%)的视频标记为“可疑”视频供医生分析. 有效坐标点(拟合曲线成功的坐标)占比太小, 不建议进行灌注可视化. 利用上述方法寻找到的流线, 流线图与流线计数图非常类似于血管的分布, 应具有一定的研究价值.

|
图 14 4种不同有效点面积占比的结果 |
8 结论与展望
本文研究了对造影视频的灌注特征的提取与可视化. 提取灌注参数(达峰时间、峰值等)来编码成像可以协助医生分析病情, 使用流线等方法可视化造影剂在ROI内的流向信息. 结果中流线图与流线计数图中的线条类似血管, 应具有一定的研究意义.
经历了目标跟踪、时间强度曲线拟合、灌注参数提取、根据达峰时间二维矩阵进行灌注情况可视化共4个步骤. 目标跟踪根据视频的特点而选择了KCF与Kalman滤波结合的方式. 时间强度曲线拟合是像素级的, 经历了粗细筛选的方式, 将符合灌注特征的曲线留下来. 灌注参数提取主要是提取达峰时间、峰值等. 像素级的曲线拟合与提取参数可以形成一个二维矩阵, 可颜色编码成像显示, 也可做一些处理提取特征. 根据达峰时间二维矩阵, 做了流向情况可视化, 最后可得到流向可视化.
做流向情况可视化时, 有效坐标占比要大于50%才能有较好的可视化效果.
未来更进一步的实验将是: 更好的曲线拟合公式与筛选方式, 因为目前Gamma公式可能并非对灌注情况描述最佳的公式, 虽然达峰时间误差小但峰值处并不能很好地贴合原数据; 根据参数二维矩阵更好的寻找流线的方式, 目前寻找流线的方式还需要进行更进一步的标准; 使用更多的数据, 只有数据量足够才能找到更精确的标准.
| [1] |
杨琛, 彭婵娟. 超声造影定量评价体系及其影响因素分析. 中国肿瘤, 2016, 25(3): 212-218. DOI:10.11735/j.issn.1004-0242.2016.03.A012 |
| [2] |
王本刚, 丁红, 彭诗云, 等. 基于S-G滤波的超声造影分析参数灌注成像. 中国生物医学工程学报, 2018, 37(4): 429-434. DOI:10.3969/j.issn.0258-8021.2018.04.006 |
| [3] |
Zhang J, Ding MY, Meng F, et al. Respiratory motion correction in free-breathing ultrasound image sequence for quantification of hepatic perfusion. Medical Physics, 2011, 38(8): 4737-4748. DOI:10.1118/1.3606456 |
| [4] |
Horn BKP, Schunck BG. Determining optical flow. Artificial Intelligence, 1981, 17(1–3): 185-203. DOI:10.1016/0004-3702(81)90024-2 |
| [5] |
Ta CN, Kono Y, Barback CV, et al. Automating tumor classification with pixel-by-pixel contrast-enhanced ultrasound perfusion kinetics. Journal of Vacuum Science & Technology. B, Nanotechnology & Microelectronics: Materials, Processing, Measurement, & Phenomena: JVST B, 2012, 30(2): 2C103. |
| [6] |
林细林, 张麒, 韩红. 运用超声造影特征选择的淋巴结良恶性鉴别. 自动化仪表, 2018, 39(6): 58-61. |
| [7] |
金晓康. 复杂场景下鲁棒的单目标跟踪算法研究[硕士学位论文]. 长沙: 长沙理工大学, 2019.
|
| [8] |
Zhang KH, Zhang L, Yang MH. Real-time compressive tracking. Berlin Heidelberg: Springer, 2012.
|
| [9] |
Henriques JF, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 |
| [10] |
Rizzo G, Raffeiner B, Coran A, et al. Pixel-based approach to assess contrast-enhanced ultrasound kinetics parameters for differential diagnosis of rheumatoid arthritis. Journal of Medical Imaging, 2015, 2(3): 034503. DOI:10.1117/1.JMI.2.3.034503 |
| [11] |
刘振东, 刘海行, 苏天赟, 等. 基于LIC的海流动态模拟与可视化. 海洋通报, 2019, 38(2): 179-185. DOI:10.11840/j.issn.1001-6392.2019.02.008 |
| [12] |
Wegenkittl R, Groller E, Purgathofer W. Animating flow fields: Rendering of oriented line integral convolution.Computer Animation. Los Alamitos: IEEE, 1997.
|
| [13] |
戴文丰. 基于卡尔曼滤波算法的声源目标跟踪研究[硕士学位论文]. 广州: 华南理工大学, 2020.
|
| [14] |
Bolme DS, Beveridge JR, Draper BA, et al. Visual object tracking using adaptive correlation filters. 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 2544–2550.
|
| [15] |
刘轲. 基于局部特征匹配的颜色传递方法研究[硕士学位论文]. 赣州: 江西理工大学, 2021.
|
| [16] |
徐秦, 薛茜, 徐睿. 浅论曲线拟合中的相关指数R2. 中国卫生统计, 1992(6): 44-45. |
| [17] |
嵇晓声, 刘宴兵, 罗来明. 协同过滤中基于用户兴趣度的相似性度量方法. 计算机应用, 2010, 30(10): 2618-2620. |
| [18] |
左少华. 海洋流场数据的可视化技术研究[硕士学位论文]. 杭州: 浙江工业大学, 2020.
|
| [19] |
王宝仁, 李金松, 吕国娜, 等. 基于Bresenham算法的快速直线脉冲增量插补算法. 机床与液压, 2018, 46(20): 155-158. DOI:10.3969/j.issn.1001-3881.2018.20.036 |
| [20] |
Cabral B, Leedom LC. Imaging vector fields using line integral convolution. Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques. Anaheim: ACM, 1993. 263–270.
|
 2022, Vol. 31
2022, Vol. 31


