交通安全问题长期是交通领域的难题, 根据世界卫生组织的数据, 全球每年因道路交通事故造成的死亡人数约为140万, 90%的交通事故是人为失误造成的[1, 2]. 利用自动驾驶技术辅助人工驾驶, 将是解决交通安全问题的有效手段.
根据当前智能化车辆在行业内的发展趋势, 可以预见未来一段时间的智能车辆还是以L2–L3等级的辅助驾驶为主, 开发合适的驾驶辅助系统将是这一阶段的主要目标. 据不完全统计, 换道导致的事故占到了总事故数的27%[3], 引发换道交通事故的主要原因是前车的不规范行车(例如未按照要求开启转向灯)以及后车驾驶员的注意力分散导致未能及时察觉前车意图. 因此, 实时识别周围车辆换道行为并为驾驶员提供预警将有效提升道路交通安全水平, 识别结果还可进一步用于智能路径规划等方面.
车辆换道行为分为强制换道和自由换道. 当驾驶员必须改变车道以完成预定路线时, 强制换道发生. 自由换道通常由于驾驶员以低于期望的速度跟随另一辆车辆, 试图通过换道来寻求更佳的驾驶感受. 强制换道是与驾驶环境密切相关, 通常可以通过环境感知来获取变道意向, 而自由换道行为识别则更具挑战性, 也是本文所研究的问题.
随着机器学习算法的兴起, 车辆自由换道行为识别已经成为近年来研究的热点. 早在2010年Schubert等人使用非连续卡尔曼滤波与基于贝叶斯网络决策方法通过车载传感器收集的数据实现了车辆环境感知, 实时评估交通状况, 为驾驶员提供换道建议[4]. 由于车辆的连续行为与语音识别过程的相似性, Li等人在语音识别模型的基础上改进了隐马尔科夫模型(hidden Markov model, HMM), 结合贝叶斯滤波(Bayesian filtering, BF)来输出识别结果, 提出的HMM-BF框架较原始HMM对于左右换道具有更高的识别精度[5]. Xia等人提出了一种用于自动驾驶的仿人变道意图理解模型, 通过模拟人类视觉系统的选择性注意机制, 模拟驾驶员对周围车辆的注意力集中方式, 从而识别驾驶员的变道意图[6]. Husen等人建议使用基于语言学的句法识别方法, 利用上下文无关文法来识别驾驶员意图, 以提高驾驶员和乘客的安全[7]. 为解决识别率低、实时性差等问题, Yu等人提出了一种基于深度学习的5G智能交通系统中自动车辆和手动车辆混合使用的交通安全解决方案, 改善了混合交通环境下的车道变更问题[8]. Lee等人提出使用卷积神经网络来对车道换道意图进行推理和预测, 它的输入是来自雷达和摄像头的图像[9]. Li等人设计了一个多模态分层逆强化学习框架, 从真实世界的交互式驾驶轨迹数据中学习联合驾驶模式-意图运动模型, 仿真结果表明该方法对涉及交互行为的驾驶行为识别预测具有较高的精度[10].
车辆换道行为识别对实时性与准确性要求较高, 而隐马尔科夫模型得益于其计算简单、精度高、训练量较少等特点, 在车辆换道识别领域具有广阔的应用前景. 本文研究的要点在于结合车辆自由换道行为的特点对隐马尔科夫模型进行改进, 提高识别精度的同时兼顾计算量以满足实时性要求.
1 基于HMM的车辆行为识别方法隐马尔科夫模型是一种基于贝叶斯理论, 通过外部可观测数据描述含有隐含状态的马尔科夫过程的统计模型[11]. 隐马尔科夫模型作为经典的时间序列模型被广泛应用在自然语言处理领域. 由于车辆行为也是随时间变化, 符合时序模型的特点, 伴随无人驾驶技术的兴起, 近年来HMM也被应用于车辆行为识别领域.
1.1 隐马尔科夫模型概述如图1所示, HMM每个时间步都一一对应着两组变量, 其中上方的变量为隐状态, qt表示系统在t时刻的状态. 在车辆行为识别领域, 这些状态包括换道、超车等, 这些状态对于传感器是不可直接观测的, 所以该状态被称为隐状态, 其取值集合记为Q, 隐状态会随时间按一定概率变化. 下方的变量为观测状态, ot表示系统在t时刻的观测, 在车辆行为识别领域为传感器可以直接获取的车辆数据, 包括速度、加速度等. 观测变量可以是离散的, 也可以是连续的, 对于离散的观测变量, 取值集合记为O, 同一时刻的观测变量按一定概率关联于隐状态变量. 一个完整的车辆行为对应一段连续的驾驶状态, 图1中T为完整序列的时间步长.

|
图 1 HMM结构示意图 |
HMM参数可以由λ描述, λ={A,B,π,M,N}, M代表观测状态数, N代表隐状态数, 其他参数含义见表1, 参数解释如图2所示.
| 表 1 HMM参数 |
1.2 HMM解决车辆换道行为识别问题
HMM主要包含3大问题, 分别为隐状态概率计算、隐状态过程求解和参数学习问题. 在车辆换道行为识别中, 通常采用Baum-Welch算法进行参数学习, 利用收集的车辆观测数据进行隐状态概率求解, 通常采用Forward-backward算法来实现[11]. 在本文中换道行为被分为3类, 即左换道、右换道与车道保持.

|
图 2 HMM概率转换模型 |
模型参数
| $ P(O|\lambda ) = \sum\limits_{i = 1}^N {{\alpha _t}(i){\beta _t}(i)} $ | (1) |
其中,
| $ {\alpha _{{t}}}(i) = P({o_1}, {o_2}, {o_3},\cdots,{o_t}, {i_t} = {q_i}|\lambda ) $ | (2) |
| $ {\beta _{{t}}}(i) = P({o_{{{t + }}1}}, {o_{t + 2}}, {o_{t + 3}},\cdots,{o_T}|{i_t} = {q_i}, \lambda ) $ | (3) |
上述提到需要计算当前状态分属3类行为的概率, 意味着我们需要3组不同的HMM参数, 左换道λ1、车道保持λ2以及右换道λ3. 参数学习问题在换道行为识别中表现为在给定3类模型参数初值后通过对应行为数据训练集对每组参数迭代更新, 即每组确定一个描述已知观测序列的最优参数组合使得训练数据在该模型下输出的概率值最大. 我们定义两个重要参数
| $ {\gamma _{{t}}}{{(i) = P(}}{i_t}{\text{ = }}{q_i}{\text{|}}{ O}, \lambda {\text{) = }}\frac{{{\alpha _t}(i){\beta _t}(i)}}{{\displaystyle\mathop \sum\limits _{j = 1}^N {\alpha _t}(j){\beta _t}(j)}} $ | (4) |
| $ \begin{split} {\xi _t}(i, j) =& {{P(}}{i_t}{\text{ = }}{q_i}{\text{, }}{i_{t + 1}}{\text{ = }}{q_j}{\text{|}}{ O}, \lambda {\text{)}} \\ =&\frac{{{\alpha _t}(i){a _{ij}}{b_j}({o_{t + 1}}){\beta _{t + 1}}(j)}}{{\displaystyle\mathop \sum\limits_{i = 1}^N \displaystyle\mathop \sum\limits_{j = 1}^N {\alpha _t}(i){a _{ij}}{b_j}({o_{t + 1}}){\beta _{t + 1}}(j)}} \end{split} $ | (5) |
各参数迭代更新公式为:
| $ {\pi _{{i}}} = \frac{{{{P(}}{ O}, {i_1}{\text{ = }}{q_i}{\text{|}}\hat \lambda {\text{)}}}}{{{{P(}}{ O}|\hat \lambda {\text{)}}}} = {\gamma _1}({{i}}) $ | (6) |
| $ {a_{ij}}{\text{ = }}\frac{{\displaystyle\mathop \sum\limits_{t = 1}^{T - 1} P(O, {i_t}{\text{ = }}{q_i}, {i_{t + 1}}{\text{ = }}{q_j}|\hat \lambda )}}{{\displaystyle\mathop \sum\limits_{t = 1}^{T - 1} P(O, {i_t}{\text{ = }}{q_i}|\hat \lambda )}} = \frac{{\displaystyle\mathop \sum\limits_{t = 1}^{T - 1} {\xi _t}(i, j)}}{{\displaystyle\mathop \sum\limits_{t = 1}^{T - 1} {\gamma _{{t}}}({{i}})}} $ | (7) |
| $ {b_j}{{(k) = }}\frac{{\displaystyle\mathop \sum\limits_{t = 1}^T P(O, {i_t}{\text{ = }}{q_j}|\hat \lambda ){ I}({o_t}{\text{ = }}{v_k})}}{{\displaystyle\mathop \sum\limits_{t = 1}^T P(O, {i_t}{\text{ = }}{q_j}|\hat \lambda )}} = \frac{{\displaystyle\mathop \sum\limits_{{t = 1},\;{o_t}{\text{ = }}{v_k}}^{T} {\gamma _{{t}}}({{j}})}}{{\displaystyle\mathop \sum\limits_{t = 1}^{T} {\gamma _{{t}}}({{j}})}} $ | (8) |
利用HMM进行换道识别通常需要用K-means聚类算法对原始数据进行预分类, 确定有限个观测行为类别后再进行隐状态划分. 但由于车辆运动是一个时间连续行为, 其运动观测状态不是简单地有限划分, 若采用离散化的表征方式将大大减少原始数据的特性, 降低最终精度. 因此我们需要一个新的连续化表征方法来最大化保留原始数据特征, 提高模型识别精度.
1.3 基于高斯混合隐马尔科夫模型的车辆换道行为识别高斯混合模型(Gaussian mixture model, GMM)是指利用多个单高斯模型进行线性叠加形成的分布模型, 通过调整单高斯模型参数以及加权系数可以近似表达任意连续的分布特征. 通常一个混合模型可以使用任意概率分布, 选用高斯混合模型是因为高斯分布具备良好的数学性质以及计算性能. 结合车辆运动的数据多维、连续的特点, 高斯混合模型可以最大化契合该特点, 与HMM相结合形成高斯混合隐马尔科夫模型(Gaussian mixture hidden Markov model, GM-HMM).
该模型参数仍可记为
| $ {b_j}{{(o) = }}\sum\limits_{m = 1}^M {{c_{jm}}N(o|{\mu _{jm}}, {U_{jm}})} $ | (9) |
其中, o为观测量, M为隐状j包含的混合高斯元个数,
| $ N(o|{\mu _{jm}}, {U_{jm}}) = \frac{1}{{\sqrt {{{(2\pi )}^G}|{U_{jm}}|} }}\exp \left[ - \frac{{(o - {\mu _{jm}}){{(o - {\mu _{jm}})}^T}}}{{2{U_{jm}}}}\right] $ | (10) |
其中, G为观测变量维数, 初始概率分布π和状态转移概率矩阵A与离散隐马尔科夫模型的训练公式相同. 其它高斯混合隐马尔科夫模型参数的重估公式为:
| $ {\hat c_{jm}} = \frac{{\displaystyle\sum\limits_{t = 1}^T {{\gamma _t}(j, m)} }}{{\displaystyle\sum\limits_{t = 1}^T {\displaystyle\sum\limits_{m = 1}^M {{\gamma _t}(j, m)} } }} $ | (11) |
| $ {\hat \mu _{jm}} = \frac{{\displaystyle\sum\limits_{t = 1}^T {{\gamma _t}(j, m)} \times {o_t}}}{{\displaystyle\sum\limits_{t = 1}^T {{\gamma _t}(j, m)} }} $ | (12) |
| $ {\hat U_{jm}} = \frac{{\displaystyle\sum\limits_{t = 1}^T {{\gamma _t}(j, m)({o_t} - {\mu _{jm}})} {{({o_t} - {\mu _{jm}})}^T}}}{{\displaystyle\sum\limits_{t = 1}^T {{\gamma _t}(j, m)} }} $ | (13) |
其中,
| $ {\gamma _t}(j, m) = \frac{{{\alpha _t}(j){\beta _t}(j)}}{{\displaystyle\sum\limits_{j = 1}^N {{\alpha _t}(j){\beta _t}(j)} }} \times \frac{{{c_{jm}}N({\text{o}}|{\mu _{jm}}, {U_{jm}})}}{{\displaystyle\sum\limits_{m = 1}^M {{c_{jm}}N({\text{o}}|{\mu _{jm}}, {U_{jm}})} }} $ | (14) |
虽然现有计算机性能相较以往得到了极大提升, 但由于行为识别的时效性要求较高, 因此在考虑精度的同时也要兼顾计算量. 从GM-HMM的模型构成及参数计算方法可以发现, 模型的计算量主要与隐状态数量、观测数据维数、观测数据时间序列长度和高斯混合数相关. 这些参数越小则计算量越小, 但是考虑到模型的识别效果, 这些参数并不是越小越好.
2 实验数据集NGSIM数据集是美国联邦公路管理局收集的道路行车数据, 包含高速公路US-101, I-80, 城市道路Lankershim Boulevard 和 Peachtree Street行车数据, 数据集共记录了11850526车辆帧数据, 每秒记录10帧数据[12]. 我们选取了高速公路I-80的3个时段, 每个时段15分钟, 共计45分钟5316辆车数据进行实验, 如图3所示.
I-80数据收集于加利福尼亚州旧金山湾区, 研究区域长约500 m (1640英尺), 由6条高速公路车道以及进出口闸道组成, 其中包括一条高载客率车辆车道(HOV), 除进口闸道存在斜坡弯道, 其余道路皆为平直道路, 适合进行车辆行为分析.

|
图 3 I-80道路示意图 |
2.1 数据平滑处理
NGSIM数据集是通过安装在道路两侧高处摄像头记录视频数据, 利用视频图像处理的方法得出具体车辆的信息, 包括车辆位置、速度、加速度、车长以及车宽等数据. 由于视频处理算法的局限性, 所获取的数据存在一定的噪声干扰, 我们需要采用数据处理方法来尽量得到真实的数据值.
常用的数据平滑方法有移动平均法、加权移动平均法、指数移动平均法、SG滤波(Savitzky Golay filter)等, 根据Thiemann等人的研究[13], 对称指数移动平均法(symmetric exponential moving average, SEMA)对于处理该数据集的效果比较显著, 因此这里我们采用该方法对车辆的轨迹数据进行平滑处理.
| $ {X_i} = \frac{{\displaystyle\sum\limits_{k = i - D}^{i + D} {{X_k}\exp ( - |i - k|/\Delta )} }}{{\displaystyle\sum\limits_{k = i - D}^{i + D} {\exp ( - |i - k|/\Delta )} }} $ | (15) |
| $ \Delta {\text{ = }}\frac{T}{{{d}}} $ | (16) |
| $ D = \min \{ 3\Delta , i - 1, l - i\} $ | (17) |
其中, T是移动平均幅度, 我们一般选取0.5 s, D为平滑窗口宽度, d为数据时间间隔0.1 s, l是车辆轨迹时刻总数,

|
图 4 横向位置平滑处理 |
2.2 数据筛选
原有完整数据集包含了所有车辆类型在所有车道的完整轨迹, 但是实验需要的是普通车辆的自由换道行为数据, 因此我们有必要对数据进行筛选, 我们按照以下5点对数据进行了处理.
(1)实验数据集包含进出口闸道以及辅助车道的信息, 涉及强制换道, 我们剔除车道编号为6, 7, 8的车辆数据.
(2)原始数据集包含大型车辆, 普通小汽车以及摩托车数据, 我们剔除车辆类别为1的摩托车数据.
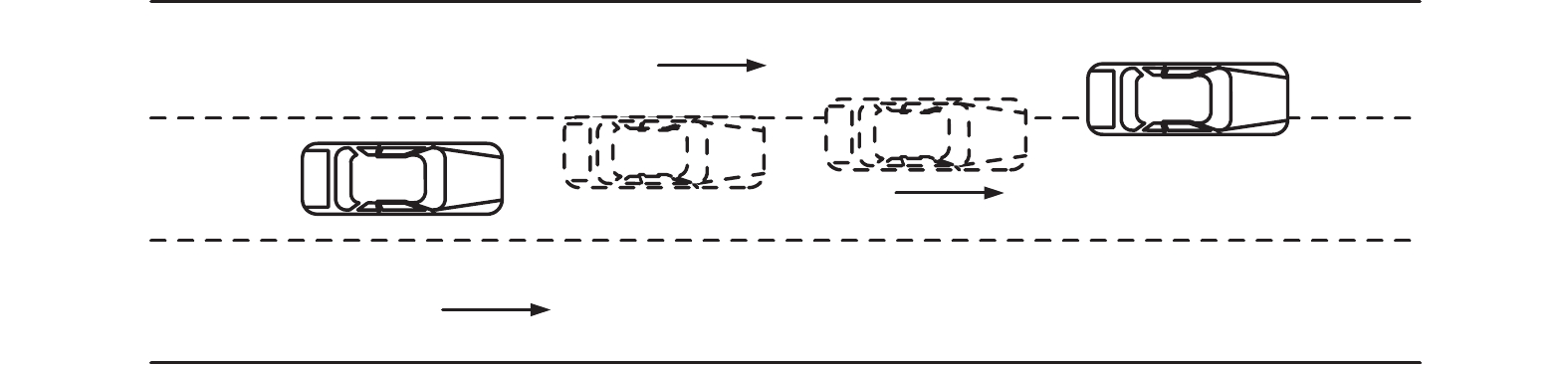
(3)换道行为通常在5 s内完成[14], 我们选取车辆中心越过车道边线的时刻作为换道行为结束的标志(参考图5), 提取往前5 s的轨迹作为我们实验数据, 由于考虑到信息冗余, 我们将10 Hz的采样率降为2 Hz, 即时间间隔为0.5 s, 观测序列长度T=10.
|
图 5 换道示意图 |
(4)通过车道编号的变化区分左右换道与非换道数据, 分别保存.
(5)按照7:3的训练数据与测试数据比例随机抽取车辆数据作为训练集与测试集.
最终通过以上处理得到左换道训练数据384组, 左换道测试数据164组, 右换道训练数据67组, 右换道测试数据29组, 非换道训练数据1 500组, 非换道测试数据642组. 这里右换道数据较少的原因是最右侧为进出口闸道以及辅助车道, 涉及的强制换道较多, 在数据筛选过程中被清除.
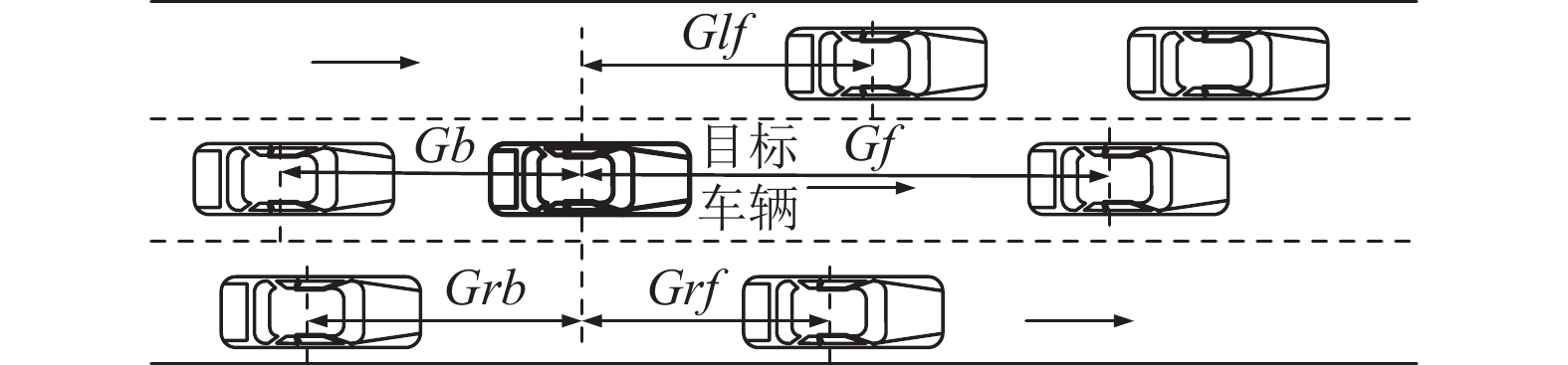
3 实验分析 3.1 模型观测变量选择根据现有文献表明[15, 16], 影响车辆换道的主要因素有目标车辆车速、前车车速、左右车道上最近前后车辆与本车纵向位置差(图6中Glf, Grf, Grb, Gf, Gb)以及速度差. Liu等人还利用了车辆与道路中心线的偏转角, 车辆与车道两侧边线距离等变量作为了观测变量[17]. 本实验将对相关变量进行控制变量法试验, 最终选定最优的观测变量.
|
图 6 观测变量示意图 |
3.2 模型参数制定
(1)模型数与隐藏状态数N
在HMM中, 隐藏状态数一般根据经验指定. 在本文中根据换道行为数确定, 即隐藏状态数 N=3.
(2)高斯混合数M
GM-HMM中的高斯混合模型是指用多层高斯分布的概率密度函数拟合车辆行为, 不同高斯混合数会对模型计算量以及识别精度产生影响, 因此我们选取了M=1, 3, 5, 7作为实验选项, 隐藏状态的高斯分布权重系数C根据M的值等值设定.
(3)初始状态概率π和状态转移概率A
通常情况下π和A的初始值可以任意设置, 对最终结果影响不大, 在本文中设定初始值为π=(1, 0, 0), A={0.33, 0.33, 0.34; 0.33, 0.33, 0.34; 0.33, 0.33, 0.34}.
3.3 实验结果分析在特征参数控制变量法寻优过程中, 我们选择高斯混合数M=1, 高斯权重C=1, 即单高斯模型作为评判观测变量的基础参数(单高斯模型具有比较好的数据拟合能力, 能描绘大部分场景), 将观测变量作为因变量, 识别准确度与训练迭代次数作为评判指标(计算复杂度主要集中在训练阶段), 目的是寻找最优的特征变量. 最终选定目标车辆与两侧车道前车的速度差, 与当前车道以及两侧车道后车的位置差(两侧车道中一侧不存在时其参数数值使用较小数代替, 若车道存在对应车辆不存在时, 其参数数值使用较大数代替), 目标车辆偏转角, 当前车道与前车车头时距共7维数据作为观测变量.
进行HMM换道识别实验时选取K-means算法对车辆观测状态进行离散化, 离散点数K对识别结果有较大影响, 因此我们设定K=10, 20, 30进行多次实验, 以验证高斯混合隐马尔科夫模型的性能提升. 图7展示了不同K值下的HMM预测精度与不同M值下的GM-HMM预测精度, 结果展示了对于车辆换道问题, GM-HMM相比传统HMM具有更高的识别精度.

|
图 7 HMM与GM-HMM识别精度对比 |
在确定改进后的识别模型精度上有提升后, 我们通过改变高斯混合数M来分析不同的高斯混合数对识别精度以及训练迭代次数的影响, 以研究该识别算法的实际应用前景. 图8展示了训练过程中参数收敛情况, 图9展示了不同M下的实验结果, 我们可以看出当M=1或者M=7 (即高斯混合数等于数据维数)时的准确度较高, 且M=7时的准确度会略高于M=1时, 但M=7时的迭代次数明显高于M=1
表2中的数据为对应的3个换道模型计算单个样本概率取对数的结果, 按照取条件概率最大的类作为换道行为的识别结果, 我们选取每行数值最大的作为识别结果, 加粗表示. 通过测试集数据验证, M=1下的平均识别精度为90.6%, M=7下的平均识别精度为91.8%, 整体达到了较高的精度, 未来如果加入与驾驶员相关的观测变量将有望达到更高的识别精度.

|
图 8 左换道训练过程 |

|
图 9 不同高斯混合数实验结果 |
| 表 2 单个测试样本计算结果 |
4 结论与展望
本文通过NGSIM数据集对隐马尔科夫模型与高斯混合模型的结合产物高斯混合隐马尔科夫模型在自由换道行为识别上的应用做了研究. 通过控制变量法确定了以目标车辆与两侧车道前车的速度差, 与当前车道以及两侧车道后车的位置差, 与当前车道前车车头时距以及目标车辆偏转角共7维数据作为观测变量. 与HMM识别模型的对照实验体现了GM-HMM识别模型精度上的提升, 同时还对不同高斯混合数下的精度与计算量进行了评估, 结果表明单高斯模型下的综合性能是最好的, 而当高斯混合数等于观测数据维数时精度从单高斯的90.6%提升到了91.8%, 但对应的平均训练迭代次数也由6次提升到了24次. 在今后实际应用中, 高斯混合数的选择应结合车载计算器性能来平衡精度与计算量. 最后本文仅研究了高速道路下的自由换道识别, 未来将考虑城市道路下的自由换道识别, 将此方法应用于更广的领域.
| [1] |
Yang ZK, Zhang WP, Feng J. Predicting multiple types of traffic accident severity with explanations: A multi-task deep learning framework. Safety Science, 2022, 146: 105522. DOI:10.1016/j.ssci.2021.105522 |
| [2] |
World Health Organization. Global status report on road safety 2018: Summary. WHO/NMH/NVI/18.20, Geneva: World Health Organization, 2018.
|
| [3] |
国家统计局. 中国统计年鉴 2020. 北京: 中国统计出版社, 2020.
|
| [4] |
Schubert R, Schulze K, Wanielik G. Situation assessment for automatic lane-change maneuvers. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(3): 607-616. DOI:10.1109/TITS.2010.2049353 |
| [5] |
Li KQ, Wang X, Xu YC, et al. Lane changing intention recognition based on speech recognition models. Transportation Research Part C: Emerging Technologies, 2016, 69: 497-514. DOI:10.1016/j.trc.2015.11.007 |
| [6] |
Xia YJ, Qu ZW, Sun Z, et al. A human-like model to understand surrounding vehicles’ lane changing intentions for autonomous driving. IEEE Transactions on Vehicular Technology, 2021, 70(5): 4178-4189. DOI:10.1109/TVT.2021.3073407 |
| [7] |
Husen MN, Lee S. Continuous car driving intention recognition with syntactic pattern approach. Proceedings of 2016 International Conference on Information and Communication Technology. Kuala Lumpur: IEEE, 2016. 71–76.
|
| [8] |
Yu KP, Lin L, Alazab M, et al. Deep learning-based traffic safety solution for a mixture of autonomous and manual vehicles in a 5G-enabled intelligent transportation system. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(7): 4337-4347. DOI:10.1109/TITS.2020.3042504 |
| [9] |
Lee D, Kwon YP, McMains S, et al. Convolution neural network-based lane change intention prediction of surrounding vehicles for ACC. Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems. Yokohama: IEEE, 2017. 1–6.
|
| [10] |
Li DC, Wu YJ, Bai B, et al. Behavior and interaction-aware motion planning for autonomous driving vehicles based on hierarchical intention and motion prediction. Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems. Rhodes: IEEE, 2020. 1–8.
|
| [11] |
李航. 统计学习方法. 北京: 清华大学出版社, 2012.
|
| [12] |
Colyar J, Halkias J. US highway 80 dataset. Technical Report, Washington: Federal Highway Administration, 2007.
|
| [13] |
Thiemann C, Treiber M, Kesting A. Estimating acceleration and lane-changing dynamics from next generation simulation trajectory data. Transportation Research Record: Journal of the Transportation Research Board, 2008, 2088(1): 90-101. DOI:10.3141/2088-10 |
| [14] |
张良, 陈诗慧, 张伟. 驾驶员换道执行持续时间研究. 工业工程与管理, 2014, 19(4): 109-114. DOI:10.3969/j.issn.1007-5429.2014.04.016 |
| [15] |
Jin H, Duan CG, Liu Y, et al. Gauss mixture hidden Markov model to characterise and model discretionary lane-change behaviours for autonomous vehicles. IET Intelligent Transport Systems, 2020, 14(5): 401-411. DOI:10.1049/iet-its.2019.0446 |
| [16] |
Deng Q, Wang J, Hillebrand K, et al. Prediction performance of lane changing behaviors: A study of combining environmental and eye-tracking data in a driving simulator. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(8): 3561-3570. DOI:10.1109/TITS.2019.2937287 |
| [17] |
Liu SW, Zheng K, Zhao L, et al. A driving intention prediction method based on hidden Markov model for autonomous driving. Computer Communications, 2020, 157: 143-149. DOI:10.1016/j.comcom.2020.04.021 |
 2022, Vol. 31
2022, Vol. 31



