计算机系统应用  2022, Vol. 31 Issue (8): 319-326   PDF    
引用本文
何灿, 袁国武, 吴昊. 基于自注意力孪生网络的野生蛇细粒度分类. 计算机系统应用, 2022, 31(8): 319-326.http://www.c-s-a.org.cn/1003-3254/8609.html   
He C, Yuan GW, Wu H. Fine-grained Classification of Wild Snakes Based on Self-attention Siamese Network. Computer Systems and Applications, 2022, 31(8): 319-326(in Chinese).http://www.c-s-a.org.cn/1003-3254/8609.html   
基于自注意力孪生网络的野生蛇细粒度分类
何灿, 袁国武, 吴昊     
云南大学 信息学院, 昆明 650500
收稿日期：2021-10-28; 修改日期：2021-11-29; 采用时间：2021-12-13; csa 在线出版时间：2022-04-18
基金项目：国家自然科学基金地区项目(62061049); 云南省应用基础研究计划重点项目(202001BB050032); 云南省应用基础研究计划面上项目(2018FB100)
通讯作者：吴昊, E-mail: wuhao19820311@163.com.
摘要：野生蛇的分类相较于其他细粒度图像分类更加困难和复杂, 这是因为蛇姿势各异、变化急促、常处于运动或盘曲状态, 很难根据蛇的局部特征去判断并分类. 为了解决这个问题, 本文将自注意力机制应用野生蛇细粒度图像分类, 从而解决卷积神经网络因层数加深造成的过于专注局部而忽略全局信息问题. 通过Swin Transformer (Swin-T)进行迁移学习获得细粒度特征提取模型. 为了进一步研究自注意力机制在元学习领域的性能, 本文改进特征提取模型搭建孪生网络并构造元学习器对少量样本进行学习和分类. 相较于其他方法, 本方法减少了元学习在特征提取时所造成的时间和空间开销, 提高了元学习分类的准确率和效率并增加了元学习的自主学习性.
关键词: 自注意力机制    孪生网络    元学习    细粒度分类    野生蛇分类    图像分类    注意力机制    
Fine-grained Classification of Wild Snakes Based on Self-attention Siamese Network
HE Can, YUAN Guo-Wu, WU Hao     
School of Information Science and Engineering, Yunnan University, Kunming 650500, China
Foundation item: National Natural Science Foundation of China(No.62061049); General Project of Yunnan Applied Basic Research Program(No. 2018FB100 ); Key Projects of the Applied Basic Research Program of Yunnan Province(No.202001BB050032)
Abstract: Compared with other fine-grained image classifications, that of wild snakes is more difficult and complicated, as it is difficult to judge and classify snakes by their local characteristics due to their different postures, rapid posture changes, and usual status of motion or coiling. In response, this study applies the self-attention mechanism to fine-grained wild snake image classification to solve the problem that the convolutional neural network focuses too much on the local parts to ignore the global information due to the increasing number of layers. Transfer learning is implemented through Swin Transformer (Swin-T) to obtain a fine-grained feature extraction model. To further study the performance of the self-attention mechanism in meta-learning, this study improves the feature extraction model, builds a Siamese network, and construct a meta-learner to learn and classify a small number of samples. Compared with other methods, the proposed method reduces the time and space consumption caused by feature extraction, improves the accuracy and efficiency of meta-learning classification, and increases the learning autonomy of meta-learning.
Key words: self-attention mechanism     Siamese network     meta-learning     fine-grained classification     wild snake classification     image classification     attentional mechanism    

1 前言

野生蛇分类属于细粒度图像分类的范畴, 蛇体态多变、形状不一、纹理丰富、外观相似, 相较于粗粒度分类任务, 蛇分类具有类间差异小、类内差异大的特点. 野生蛇的原始图片因光线、遮挡、背景混乱、拍摄角度等不确定因素也会加大细粒度分类的难度. 野生蛇分布在海拔高、地形复杂的茂密丛林中, 具有极强的毒性, 因此对野生蛇的数据采集充满难度和危险. 传统的细粒度分类, 通常需要借助大量的人工标注信息, 然而对于海量图片处理时则难以处理. 细粒度图像存在许多肉眼难以获取的局部特征, 但这些局部特征却存在一定的关联, 如何有效地提取这些差异特征之间的关联是本文研究的重点. 细粒度图像分类是计算机视觉中的一个基本的视觉识别分类问题, 在过去的几年里得到了广泛的研究[1, 2]. 通过神经网络对蛇进行分类不仅可以提取肉眼难以发现的细微特征还能够快速、高效处理细粒度分类样本. 卷积神经网络考虑的区域过于局部, 从而忽略了局部区域之间的相互关联性. 例如, 利用卷积神经网络网络单独对蛇的头部、身体、尾部都很难确定蛇的类别, 只有从蛇的全身来看才能得以区分. 卷积神经网络不能很好处理局部和整体之间的关系, 并且随着网络层数的增加所获取的空间信息会进一步损失[3, 4]. 本文将自注意力机制应用到细粒度图像分类, 优化卷积神经网络忽略全局信息的问题[5].

对于人类而言认识新事物仅仅需要一到两个图片或者概念, 然而对于最好的深度神经网络其数据集也是成千上万张[6]. 不仅需要对数据图像进行标签化还需浪费大量的时间来训练模型. 小样本学习是元学习的一个重要分支, 是指给定一个少样本图像分类任务T, 在该任务中包括数据集D={Dtrain, Dtest}. 把Dtrain称之为少量样本学习的支持集, 也称为训练集其一般由一到数十张图片组成; 把 Dtest称为测试集, 也称为查询集. 一般来说, 少量样本学习考虑的是一个N-way K-shot的分类问题. 其中, N表示Dtrain中类别的个数, K表示每个类别有K个样本, 支持集Dtrain的样本数为Dtrain = NK. 如何在半监督或无监督的条件下解决小样本学习细粒度分类的问题, 是本文研究的另一重点[1,7, 8]. 小样本学习利用极少的数据对网络进行训练并且在能够保证准确率的情况下尽可能地减少训练的数据量[3], 在很多网络中通常只用一张图片作为训练的数据集, 最后对比提取的特征向量, 进而判断测试集图像的类别. 对比以往的小样本学习方法, 本文提出在细粒度分类方向做小样本学习研究. 细粒度图像的差异大多体现在局部细微之处, 难点主要在于两个方面: 一个是准确定位图像中具有辨别性的关键区域, 二是从检测到的关键区域中提取有效特征[6]. 如何有效地检测图像中的前景图像, 从中挖掘局部细节并在这些区域上提取关键的特征信息, 是细粒度图像分类的难点[9]. 基于卷积神经网络的模型在细粒度分类方面有很大的局限性[10], 本文使用了基于自注意力机制的Swin Transformer (Swin-T). Swin-T是Transformer在图像领域的又一出色的网络, 其通过层级化的设计和翻转窗口有效地弥补卷积神经网络过于专注局部的弊端, 并且在分类、分割等领域都优于大部分的卷积神经网络模型[11]. 此外, Swin-T对Vision Transformer做进一步提升, 主要改善了Vision Transformer的token数目固定且单一的缺点、增加了窗口之间的信息交互. 通过实验结果对比, 获得了优于卷积神经网络的Transformer特征提取网络模型[4,12, 13], 最终本文选择了Swin-T作为孪生网络的主干网并改进Swin-T在孪生网络方面的不足从而与孪生网络进行适配. 因此, 本文提出了利用自注意力机制对蛇的细微差别进行检测[7,14], 通过迁移学习对比不同网络获得最佳特征提取网络模型并作为搭建孪生网络的主干网, 将孪生网络提取出的特征向量送入本文构造的元学习器中, 元学习器对这两组特征向量做对比和分类[15].

2 相关工作 2.1 细粒度分类

神经网络在细粒度分类方向取得了长足的进步[16], 近年的研究大多是弱监督分类, 其难点在于分离背景干扰因素并提取局部特征. 早期的工作主要依赖先验信息如局部标注、边界框等人工注释. 另一部分工作则仅通过图像级别的注释来定位有区别的部位. Jaderberg等人[11]提出了空间变换网络来进行仿射变换从而对全局特征应用特征池化方法得到进一步改进. 但是, 仿射变换只能执行旋转、剪切、缩放和翻译[17]. 当支持集和测试集的图片差异较大时, 即便二者是来自同一类的图片, 也很难有效区分图片的差异. 在本文中, 通过迁移学习获得自注意力特征提取主干网, 通过多头自注意力机制来获取局部特征以及这些局部特征之间的关联[18, 19]来改进空间变换网络的缺陷.

2.2 元学习

在近几年, 元学习领域取得了极大的进步. Vinyals等人[7]提出了匹配网络方法, 该方法通过在标记的支持集添加嵌入函数来预测未标记的查询集. 通过计算支持集和查询集上特征的余弦距离得出查询集上和支持集最接近的那一类, 从而完成少量样本学习. Ravi等人[20]则在匹配网络上进一步改进, 提出了元学习的方法. 该方法通过long short term memory训练支持集更新分类器, 然后在每一次迭代上训练自定义模型[14]. 孪生网络由Koch等人[1]提出, 其包含两个权重完全相同的网络, 首先通过图像验证任务训练网络学习样本的判别特征, 然后对于新任务的样本直接使用训练好的模型提取特征向量进行比较, 搭建简单且在很多场景任务中达到了不错的效果. Vinyals等人[7]提出的matching networks在孪生网络基础上引入了加权机制, 即对每两个样本通过欧式距离计算相似性, 并对这些相似性分数通过Softmax函数进行归一化操作. Antouniou等人[21]提出使用改进GAN网络, 先训练模型来评估数据的概率分布, 然后随机采样直接无监督生成数据, 来弥补数据不足的缺点. Liu等人[22]提出可以简单地旋转一个类中的所有图像, 来将这个旋转后的类的图像与父类区分开来从而作为一个新类, 同时也高效地增加了训练过程中可以采样的样本数量. Chen等人[23]突出针对一次学习问题, 提出了Self-Jig算法, 这是一个两阶段方法, 首先在训练集中利用带变迁的源域图片采用网格划分的方式将图片划分成多个区块, 然后随机替换掉部分区块实现数据增强, 并以此训练一个基准网络. 在目标域以同样的方式将有标签支持集和无标签查询集合成为新的图片, 并赋予新图片支持集的标签再训练网络模型. Hariharan等人[8]提出一种表征学习和数据增强方法, 通过构造三元组并利用生成对抗网络产生的新数据添加正则化项来严格限制编码器学习的有效信息. 原型网络[14]是将输入图像映射到一个潜在空间, 其中一个类别的原型是对支持集中所有相同类别图像的向量化样例数据取均值得到的, 然后再通过计算查询集图像的向量化值与类别原型之间的欧式距离从而预测查询集合的类别. 换句话说, 原型网络认为在映射后空间中距离越近的样例属于同一类别的可能性越大, 反之, 则认为不属于同一类别. 关系网络[24]是通过一个神经网络来计算不同样例之间的距离.

2.3 元学习细粒度分类

Transformer首次提出是应用到机器翻译[25]领域中, 在当前的研究工作中Transformer成为自然语言处理领域的基础架构[26], 并取得了不错的结果. 基于此, 很多工作尝试将Transformers引入计算机视觉处理领域. Vision Transformer首次提出了视觉变换架构, 将图像分割成固定数量的块, 在每个块内做注意力运算并取得了优于卷积神经网络的结果[7]. Data-efficient Image Transformers通过数据增强和强分类, 通过对比结果减少了训练所花费的时间提高了分类的效率. Liu等人[4]提出Swin-T, 该方法是在Vision Transformer的基础上加入了多模态融合并结合卷积神经网络层次化设计的思想. 通过翻转窗口达到不同窗口之间的信息交互, 为了减少Transformer结构的复杂度又设计了在每个切片内做自注意力计算, 并使每个切片与周围切片进行信息交互和融合, 这也使其复杂度相较于此前Transformer网络减少到了线性复杂度的级别. 此外, 相较于Vision Transformer, Swin-T能够处理高分辨率图片[4], 取得了更好的效果. 在本文中, 构造细粒度数据集并命名Snake set (S-set), 通过改进Swin-T模型在S-set数据集上进行迁移学习获得特征提取网络进而作为搭建孪生网络的主干网.

3 方法 3.1 构建孪生网络

以注意力机制为基础的Transformer模型被越来越多地应用到图像领域, 且比以卷积神经网络为基础的网络模型效果要更好. 这主要是因为卷积神经网络网络随着层数的加深特征会逐渐丢失. 尽管近年又提出了残差网结构但是对于深层网络仍然容易产生过拟合[6,27]. 在Transformer中, 图片被分为各个不同的切片在每个切片内应用自注意力机制不仅实现了每次输入数据的可控性也解决了图片相对于文本数据维度过多的问题. 在计算自注意力时通过加入相对位置偏置B来计算每一个头的相关性:

$ Attention(Q, K, V) = {\textit{Softmax}}(Q{K^{\rm{T}}}/\sqrt d + B)V $ (1)

其中, $ Q, K, V $ 是query, key, value矩阵; d是query/key的维度. 通过在本实验细粒度数据集上对比不同模型的效果, 最终选择改进Swin-T作为孪生网络的主干网, 孪生网络通过构建两组权重、参数相同的孪生模型. 一组为支持集的特征提取网络[4,7], 另一组作为提取测试集图像的特征提取网络.

为了使Swin-T契合到本文搭建的孪生网络中, 本文改写并定义了Swin-T的损失函数部分. Swin-T作为特征提取网络, 共有4个模块, 前2个模块提取低维特征, 其权重占比较小; 后2个模块提取高维特征, 其中第3个模块权重占比最大. 这是因为对于低维特征而言, 其维度小、包含的高维信息过少, 对于高维特征而言, 其维度高、已丢失了大部分低维信息. 通过对第3个模块的权重设置, 同时兼顾高维和低维特征. 本文改写了4个提取特征模块后的损失部分, 去掉平均池化层和全连接层, 新增标准化层对特征进行归一化从而将Swin-T与孪生网络进行适配. 将改进过的Swin-T作为孪生网络特征提取网络模型, 并设置两组孪生网络特征提取网络权重相同、参数一致.

3.2 特征向量相似度

孪生特征提取网络提取到相应数据集的特征后, 为了进一步确定两个输入孪生网络的图片是否属于同一类, 本文使用了余弦距离和欧式距离.

$ Loss(\theta )=\frac{a\cdot b}{\parallel a\parallel \cdot\parallel b\parallel } $ (2)

其中, a和b分别代表两组孪生网络提取出来的特征向量, Loss( $ \theta $ )表示两组向量的余弦距离. 余弦距离也称为余弦相似度, 通过计算两个向量之间的夹角值得到余弦相似度, 再用一减去余弦相似度从而得到余弦距离[28]. 如果两个特征向量的余弦相似度值为零或负数, 则余弦距离为大于一的值, 说明提取这两个特征向量的图像不属于同一类. 如果两个特征向量的余弦相似度为一, 则余弦距离为零, 说明提取这两个特征向量的图像为同一类. 通过这样设置, 使余弦距离为非负值, 其值在[0, 2]的区间上, 从而在数值上符合认知逻辑, 也进一步优化了整个计算的过程. 当两个特征向量越相似, 余弦相似度越高, 余弦距离越大; 当两个特征向量差异越大, 余弦相似度越低, 余弦距离越小. 再通过设置合适的阈值对余弦距离进行判断, 大于这个阈值的则认为这两个特征向量对应的图像属于同一类, 反之, 则属于不同类.

$ Loss(X, Y) = \sqrt {\sum\limits_1^n {({x_i} - {y_i})} } $ (3)

其中, X, Y分别代表两组孪生网络提取出的特征向量, n表示特征向量的长度, i表示两组特征向量对应的数值, 范围从1到n. 欧式距离的一种定义方式是通过计算两个向量对应各项的差的平方之和后开方所得的值; 还有一种方式是通过计算两个向量对应各项差的平方和. 根据其定义当孪生网络提取的两个特征向量越接近时, 欧式距离的值越小; 反之, 欧式距离则越大. 总体来说, 余弦距离体现的是两个特征向量的方向差异, 而欧式距离体现的是两个特征向量数值上的绝对差异. 通过余弦距离和欧式距离的综合考量, 优化孪生网络提取的两个特征向量的比较方法.

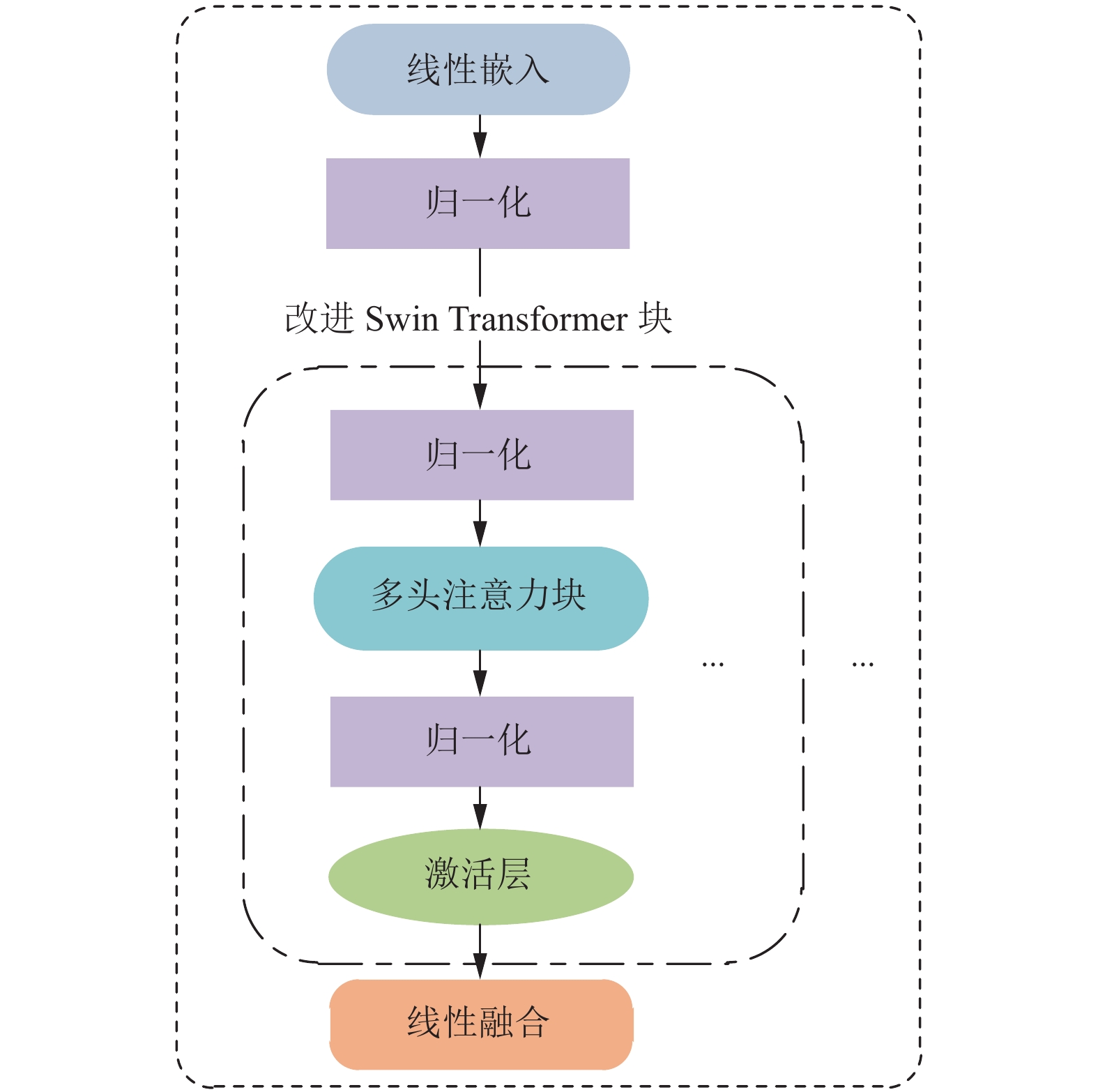
3.3 改进Swin Transformer

Swin Transformer (Swin-T)选择ImageNet数据集上进行训练和测试. 在图1中, 通过改进Swin-T与孪生网络进行适配, 并进一步提升特征提取的效率. 首先通过迁移学习对本文使用的数据集Snake set进行训练, 得到提取本实验细粒度数据集的能力. 在迁移学习得到特征提取网络模型后, 为了使迁移学习的模型能够与孪生网络进行匹配, 只需要迁移后的模型具备特征提取能力, 因此, 舍弃了模型中损失计算部分和分类部分, 之后送到元学习器中进行特征对比.

图 1 改进Swin Transformer模型

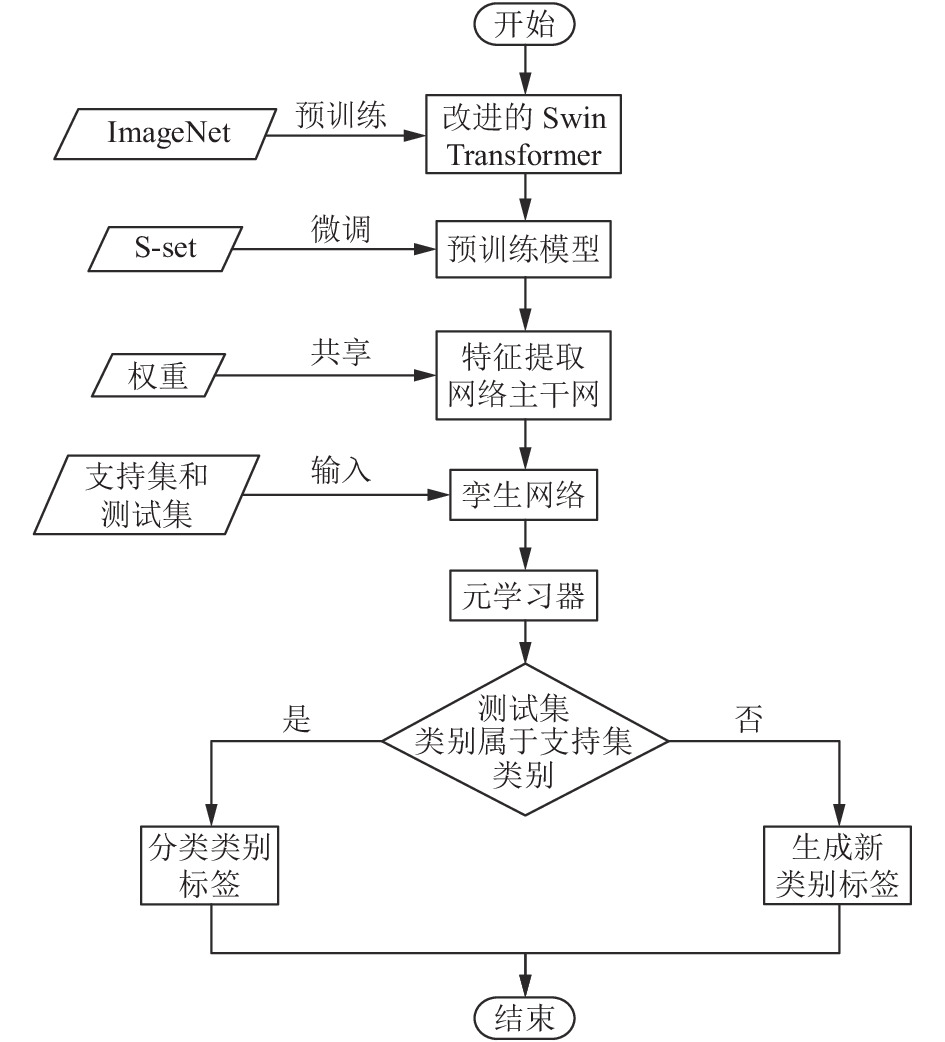
图 2 模型流程图

Swin-T提出的翻转窗口注意力方法相较于之前的Transformer网络将复杂度缩小到了线性级别. 在本文中通过应用翻转窗口极大地减少了特征提取的时间.

$ \Omega (MSA) = 4hw{C^2} + 2{(hw)^2}C $ (4)
$ \Omega (W - MSA) = 4hw{C^2} + 2{M^2}hwC $ (5)

式(5)是对式(4)即Swin-T之前的注意力计算复杂度的改进, 计算量级从二次方减少到一次方; h、w分别表示整幅图片切片的行数和列数, hw表示切片数; M表示窗口分割的切片数; C表示特征的通道数.MSA表示多头注意力; W–MSA表示翻转多头注意力.

3.4 元学习器

元学习器对来自孪生网络的特征向量做对比分类. 通过余弦距离和欧式距离综合应用对支持集和测试集的特征向量做对比, 并设置合适的阈值, 对大于阈值的两个向量, 则认为属于同一类, 反之, 则属于不同类. 此外, 对于不同类的测试集图片为其赋予新的标签, 单独列为一个新的类别, 从而增强元学习的自主学习性.

$ Loss(c) = Loss(\theta ) \wedge Loss(X, Y) $ (6)

由式(2)和式(3)求得的两个结果做逻辑与运算, 得到两组特征向量的对比结果 $ Loss(c) $ , c为类别信息. 只有在余弦距离和欧式距离的结果都为正的情况下, 元学习器才认为这两组特征向量属于同一类.

3.5 实验模型

在图2所示的模型流程图中, 首先模型通过在ImageNet上预训练得到改进的Swin-T. 为了使改进的Swin-T更好地获取野生蛇的特征, 通过在Snake set上微调模型的权重参数, 从而得特征提取模型. 然后将两组特征提取模型共享权重作为孪生网络的主干网来搭建孪生网络. 之后输入支持集和测试集到孪生网络提取特征向量, 并将孪生网络提取出来的两组特征向量送入元学习器进行对比和分类. 如果测试集类别与支持集类别相同, 则输出分类类别标签, 否则生成新类别标签. 在图3的模型中, 左侧数据集包含支持集和测试集, 支持集共有5种野生蛇类别, 每个类别包含5张图片; 测试集只有一个类别, 每个类别包含一张图片. 改进的Swin-T包含两个完全相同的特征提取网络, 这两个特征提取网络权重、参数一样. 将孪生网络提取的特征向量送入元学习器, 元学习器由预测部分和类别生成部分构成. 预测部分完成对测试集特征的对比和预测, 这里对比方法使用了余弦距离和欧式距离, 如果与支持集中所有类别对比后超过阈值则认为是同一类. 如果与支持集中的所有类别对比后的值小于阈值则认为属于不同类别, 并生成新的标签, 从而形成一个新类.

图 3 实验模型

4 实验 4.1 数据集

在微软亚洲研究院提出的Swin-T中, 使用ImageNet作为数据集. 在本实验中, 制作了如图4的野生蛇数据集, 共17389张图片, 其中训练集与测试集按照9:1的比例进行划分, 将其命名为Snake set. 划分后的训练集含有15650张图片, 测试集含1739张图片. 将数据集初始化为384×384大小的尺寸, 在训练模型时通过旋转、裁剪、插值对图像进一步增强[29]. 在Snake set数据集上对比了当前在细粒度分类方面效果较好的主干网, 包括Res-Net、DenseNet、EfficientNet和Swin-T等, 在未经微调的前提下, 对比不同主干网在Snake set数据集上的分类准确率, 包含15650张训练集图片以及1739张测试集图片. 结果证明使用注意力共17389张图片, 其中训练集图片为15650张、测试集1739张机制的Swin-T效果要明显好于其他卷积神经网络模型, 因此本文选择Swin-T作为搭建孪生网络的主干网, 并对Swin-T网络作进一步改进.

图 4 S-set数据集示例图

4.2 主干网络对比

如表1所示, 根据实验结果对比, 本文选择基于Transformer结构的Swin-T作为孪生网络的主干网. 近年来注意力机制在自然语言领域取得了巨大的进步, 同时应用到计算机视觉和图像处理领域一样取得了不错的成果. 弥补了以往基于卷积神经网络结构的缺陷, Swin-T将图片作为一个切片输入, 增强局部信息交互, 在切片内做注意力运算, 这样的Transformer网络结构对于大多图像领域的研究都具有很好的应用前景.

表 1 主干网实验结果

为了使Swin-T具备更好的效果, 本文探索了不同Swin-T模块对实验结果的影响, 第3个Swin-T模块能够有效提取特征同时减少时间消耗, 因此将第3个Swin-T块的权重设置最高. 在模型提取信息后, 使用一个规范层使其值归一化, 经过上述操作得到一个一维的、长为221184的特征向量. 此外, 为了进一步确定特征向量的长度对元学习器分类的影响, 又在规范层后加一个平均池化层, 得到一维的、长为1024的特征向量. 实验结果证明, 特征向量长度越长越有利于元学习器的对比分类[4,12,30].

4.3 模型改进

根据前面介绍的方法中, 本文从多方面改进了Swin Transformer, 保留了模型在分类前的全部网络结构, 并重新写了分类部分和损失部分的函数. 整个模型由3部分组成, 首先特征提取模块将原始图像映射到特征空间. 把特征空间输入元学习器并对查询集中的图像进行预测. 特征提取层使用Swin-T模型, 该模型分为4个模块每个模块又对应不同数目的注意力层. 其4个模块分别对应2层、2层、18层、2层; 并且每个模块分别对应的多头注意力数目为6、12、24、48. 模型的输入图片尺寸为384×384像素. 通过特征提取层最终得到一维的、长为221181的特征向量, 在每一层提取特征后使用一个mlp层, mlp层最重要的作用就是控制输出的维度数使其保持一个较慢的速度增加. 每个mlp层由全连接层、GELU激活层、drop层组成.

特征提取得到特征空间后再通过构建元学习器对特征进行预测和分类. 首先通过特征提取模型搭建孪生网络提取支持集和测试集的图像特征向量, 将提取到的特征向量送入元学习器, 对测试集样本做类别预测. 元学习器对两组特征向量计算余弦距离和欧式距离, 余弦距离从两组特征向量的角度方面进行对比; 欧式距离从距离方面对两组特征向量进行对比. 在计算余弦距离和欧式距离时设置合适的阈值, 从而大于这个阈值的两个特征向量则认为是来自于同一类的图片; 而小于这个阈值的两个特征向量则认为来自不同类的图片. 若确定某个特征向量是来自于不同类的图片, 则为其添加新标签, 从而丰富元学习的可扩展性和自主学习性, 使其更加符合元学习的特点[31].

4.4 实验结果

为了评估模型的准确率, 本实验构造单图片测试集. 单图片测试集即在测试集中包含一张测试的图片, 当测试集图片类别不属于支持集中的任一类别时, 其分类结果为新类别. 最后, 通过统计测试集中的分类结果作为评价模型的指标.

如表2所示, 在单图片实验中, 本文设置了7组实验数据, 每一组支持集中包含5个类别, 每个类别有5张图片. 每一组测试集中有一个类别, 包含一张图片. 在第1组实验中, 测试集的蛇类别与支持集中第1类蛇的类别相同, 分类结果为第1类. 在第2组实验中, 测试集的蛇类别与支持集中第2类蛇的类别相同, 分类结果为第2类. 在第3组、第4组、第5组实验中, 测试集的蛇类别分别与支持集中第3类、第4类、第5类蛇的类别相同, 分类结果为第3类、第4类、第5类. 为了更好验证基于自注意力机制的孪生网络模型在细粒度分类中的效果, 在第6组和第7组实验中, 设置测试集蛇类别与支持集5种蛇类别均不相同, 实验结果经元学习器生成了新的类别标签, 即新类1和新类2.

表 2 单图片实验结果

为了进一步与其他细粒度分类模型的对比, 本实验设置多图片测试集. 多图片测试集中包含1000张图片, 将分类准确率作为模型的评价指标.

表 3 多图片实验结果

如表3所示, 在第1组到第5组对比实验中, 分别对比了bilinear convolutional neural networks (B-CNN)、discriminative filter bank within a CNN (DFL–CNN)、weakly supervised data augmentation network (WS-DAN)、progressive multi-granularity (PMG)共4种细粒度分类网络在野生蛇图片上的分类效果. 通过单图片和多图片测试验证了基于自注意力机制的孪生网络在小样本学习和细粒度分类方向的优势.

4.5 模型环境

本实验使用的设备参数如下: 操作系统为Ubuntu18.04环境, 深度学习环境和框架为Cuda 10.1、Cudnn 7、PyTorch 1.7.1、Torchvision 0.8.2、Cudatoolkit 10.1; 显卡2080ti、32 GB内存

4.6 模型参数

在进行迁移学习训练模型时, 训练参数设置为300轮, 每轮输入4张图片; 每20轮进行一次预热学习, 预热学习率为5E–7; 权重衰减率为0.05; 基础学习率为5E–3, 最小学习率为5E–6.

模型参数设置如下, 通道数为4, 嵌入通道数为96, 模型四个模块的深度分别为2, 2, 18, 2, 4个块的自注意力头数分别为6, 12, 24, 48; 窗口大小为7×7个切片, 自注意力机制的偏置设为true.

5 总结

本文主要研究基于自注意力机制的孪生网络模型在细粒度分类的小样本学习方法. 首先通过迁移学习得到提取本实验细粒度数据集的网络模型权重. 将迁移学习后的网络模型作为孪生网络的主干网, 通过构建元学习器对孪生网络提取的两组特征向量做对比和分类. 本实验探索了基于自注意力机制的网络模型在细粒度图像的分类效果, 相较于卷积神经网络模型, 本文获得了更高的准确率和效率.

参考文献
[1]
Koch G, Zemel R, Salakhutdinov R. Siamese neural networks for one-shot image recognition. Proceedings of the 32nd International Conference on Machine Learning. Lille, 2015. 1–27.
[2]
Li D, Hu J, Wang CH, et al. Involution: Inverting the inherence of convolution for visual recognition. Proceedings of 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 12316–12325.
[3]
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Proceedings of the 26th Annual Conference on Neural Information Processing Systems 2012. Lake Tahoe: NIPS, 2012. 1106–1114.
[4]
Liu Z, Lin YT, Cao Y, et al. Swin transformer: Hierarchical vision transformer using shifted windows. arXiv: 2103.14030, 2021.
[5]
Itti L, Koch C, Niebur E. A model of saliency-based visual attention for rapid scene analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(11): 1254-1259. DOI:10.1109/34.730558
[6]
Ankile LL, Heggland MF, Krange K. Deep convolutional neural networks: A survey of the foundations, selected improvements, and some current applications. arXiv: 2011.12960, 2020.
[7]
Vinyals O, Blundell C, Lillicrap T, et al. Matching networks for one shot learning. Proceedings of the Annual Conference on Neural Information Processing Systems 2016. Barcelona: NIPS, 2016. 3630–3638.
[8]
Hariharan B, Girshick R. Low-shot visual recognition by shrinking and hallucinating features. Proceedings of 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 3037–3046.
[9]
Howard AG, Zhu ML, Chen B, et al. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv: 1704.04861, 2017.
[10]
Singh B, Li HD, Sharma A, et al. R-FCN-3000 at 30fps: Decoupling detection and classification. Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 1081–1090.
[11]
Jaderberg M, Simonyan K, Zisserman A. Spatial transformer networks. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2015. 2017–2025.
[12]
Dosovitskiy A, Beyer L, Kolesnikov A, et al. An image is worth 16×16 words: Transformers for image recognition at scale. arXiv: 2010.11929, 2020.
[13]
Rensink RA. The dynamic representation of scenes. Visual Cognition, 2000, 7(1–3): 17-42. DOI:10.1080/135062800394667
[14]
Snell J, Swersky K, Zemel R. Prototypical networks for few-shot learning. Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach: NIPS, 2017. 4077–4087.
[15]
Hu J, Shen L, Sun G. Squeeze-and-excitation networks. Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 7132–7141.
[16]
Wei XS, Wu JX, Cui Q. Deep learning for fine-grained image analysis: A survey. arXiv: 1907.03069, 2019.
[17]
Lin TY, RoyChowdhury A, Maji S. Bilinear CNN models for fine-grained visual recognition. Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015. 1449–1457.
[18]
Han D, Kim J, Kim J. Deep pyramidal residual networks. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 6307–6315.
[19]
Wu YK, Zhang B, Yu G, et al. Object-aware long-short-range spatial alignment for few-shot fine-grained image classification. arXiv: 2108.13098, 2021.
[20]
Ravi S, Larochelle H. Optimization as a model for few-shot learning. Proceedings of the ICLR 2017. Toulon: ICLR, 2017.
[21]
Antoniou A, Storkey A, Edwards H. Data augmentation generative adversarial networks. arXiv: 1711.04340, 2018.
[22]
Liu JL, Chao F, Lin CM. Task augmentation by rotating for meta-learning. arXiv: 2003.00804, 2020.
[23]
Chen ZT, Fu YW, Chen KY, et al. Image block augmentation for one-shot learning. Proceedings of the AAAI Conference on Artificial Intelligence. Honolulu: AAAI, 2019. 3379–3386.
[24]
Sung F, Yang YX, Zhang L, et al. Learning to compare: Relation network for few-shot learning. Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 1199–1208.
[25]
Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate. arXiv: 1409.0473, 2016.
[26]
LeCun Y, Boser B, Denker JS, et al. Backpropagation applied to handwritten zip code recognition. Neural Computation, 1989, 1(4): 541-551. DOI:10.1162/neco.1989.1.4.541
[27]
He KM, Zhang XY, Ren SQ, et al. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1904-1916. DOI:10.1109/TPAMI.2015.2389824
[28]
Chen D, Miao DQ. Control distance IoU and control distance IoU loss function for better bounding box regression. arXiv: 2103.11696, 2021.
[29]
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. Proceedings of the 3rd International Conference on Learning Representations. San Diego: ICLR, 2015.
[30]
Xu K, Ba JL, Kiros R, et al. Show, attend and tell: Neural image caption generation with visual attention. Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lille: PMLR, 2015. 2048–2057.
[31]
Kullback-leibler divergence explained. https://www.Countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained. (2017-05-10).