2. 江汉大学 人工智能研究院, 武汉 430056
2. Artificial Intelligence Institute, Jianghan University, Wuhan 430056, China
随着大数据时代的到来, 移动互联网已融入到人们日常生活的各方面之中[1]. 截至2020年12月, 我国网民规模为9.89亿, 互联网普及率高达70.4%, 较2020年3月提升5.9个百分点, 其中农村网民规模为3.09亿, 较2020年3月增长5 471万; 农村地区互联网普及率为55.9%, 较2020年3月提升9.7个百分点[2]. 新浪微博(以下简称“微博”)作为一个流量较大的网络社交平台, 具有传播速度快, 范围广, 监管不严等特征, 使微博称为各类谣言的温床. 《2021年2月微博辟谣月度工作报告》统计微博辟谣数据显示, 2021年2月, 微博站方共有效处理不实信息5 331条, 当月发布微博辟谣信息51条. 微博辟谣及话题阅读于2月1日至2月28日, 话题阅读量增长0.6亿, 总阅读数93.9亿[3]. 高便利性及样本数量大导致舆情传播的预防难度很大. 此类信息造成了严重的社会负面影响, 带来了极大的社会危害. 因此, 微博信息的分类及不良信息的快速定位和处理是社会关注的焦点问题之一.
1 相关工作当前针对微博信息分类及不良信息的快速定位和处理问题, 存在一系列文献分析算法来处理高维微博信息数据[4-6], 如支持向量机(support vector machine, SVM)[7], 朴素贝叶斯(naive Bayesian)[8]. 其中, SVM作为一种高效的二分类模型, 由于其具有较好地解决少量样本的精准分类问题, 被广泛应用于处理各种分类问题. 蔡坤烨等[9]建立了基于 SVM 的多参数预测模型, 验证了该模型的有效性. Zhu等[10]提出了利用 SVM预测模型进行在线诊断, 并验证了该方法的有效性.
而SVM的性能受其关键参数的影响较大, 需进行参数寻优. Jiao等[11]提出利用改进的狼群算法优化SVM预测模型参数. 黄斌[12]将改进后的GM(1, 1)和 SVM 进行最优化权重组合, 通过案例验证了该模型的有效性. Yang 等[13]提出了一种利用蚁群算法(ant colony optimization, ACO)来优化 SVM 分类模型, 验证了该模型的有效性. 然而, 这些寻优算法在处理高维微博信息数据仍存在一定的局限性, 如: GWO全局开发能力弱, 探索空间易重复, 浪费计算资源; ACO收敛速度慢, 易陷入局部最优. 且上述基于SVM的分类方法均建立在完善的网络数据条件下, 而真实的网络数据爬取当中, 可能存在样本数量不平均的现象, 会导致SVM出现较大的分类误差问题. 因此, 本文提出非线性多分类均衡支持向量机 (balanced SVM, BSVM) 以减小样本量不平衡引起的误差, 再采用遗传-改进粒子群优化算法(genetic algorithm-improved particle swarm optimization, GA-IPSO) 优化 BSVM 的参数, 对微博评论数据进行分类, 以获得更好的分类效果.
2 问题描述由于现实网络中评论信息对时效性要求较高, 则快速准确的分类算法对于微博舆情的控制具有重要意义. 此类算法可考虑两方面内容:
(1) 小样本及时处理;
(2) 分类算法快速收敛.
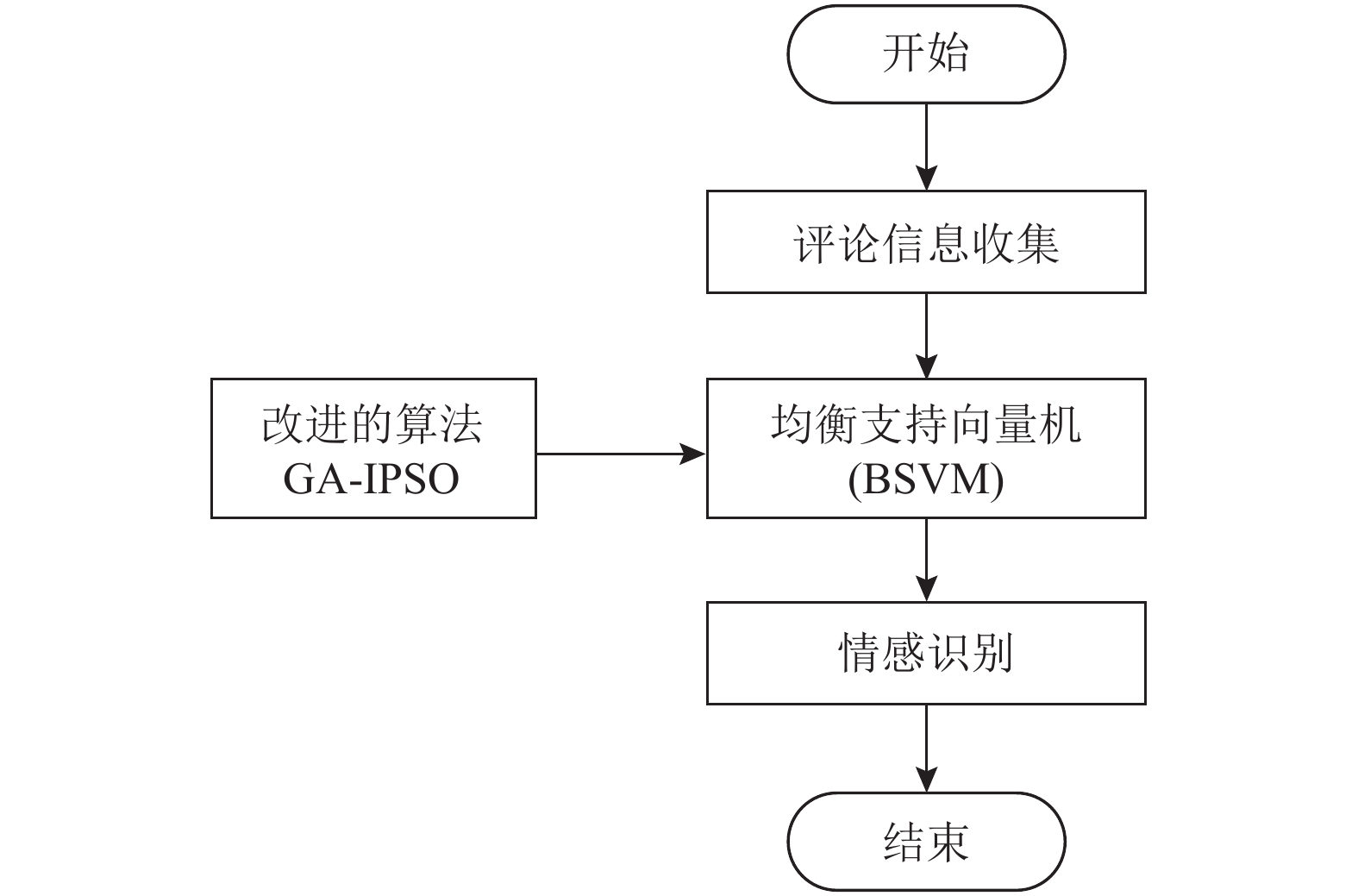
在舆情传播的前期收集样本数据时, 由于评论信息相对较少, 可能出现样本类数量相对不足且不均衡的情况. 针对该种情况下微博评论信息的及时分类问题, 本文提出BSVM以尽可能降低由于样本量不均衡而引起的误差, 从而提升分类准确率. 此外, SVM的分类效果受其参数的影响较大, 本文通过GA-IPSO算法来优化BSVM的关键参数, 提出GA-IPSO-BSVM的微博评论分类模型, 其具体流程如图1所示.
3 改进粒子群优化算法(GA-IPSO)粒子群算法(particle swarm optimization, PSO)由Kennedy和Eberhar于1995年提出, 是一种基于群体智能进化优化算法[14]. 该算法通过分析模拟鸟群, 昆虫, 鱼群等动物种群的觅食习惯, 考虑将每个动物个体看成所求寻优问题的一个解(即: 相当于问题中的粒子), 每个粒子具有速度和位置两个属性值, 通过种群个体间的合作, 种群之间的信息共享来寻找所求问题的最优解, 用于求解优化问题. 其表达式为式(1)和式(2):
| $ {V^{k + 1}} = \omega V_{id}^k + {c_1}{r_1}^k(Pbest_{id}^k - X_{id}^k) + {c_2}{r_2}^k(Gbest_{id}^k - X_{id}^k) $ | (1) |
| $ X_{id}^{k + 1} = X_{id}^k + V_{id}^{k + 1} $ | (2) |
其中, 粒子位置信息为
|
图 1 GA-IPSO-BSVM的微博评论分类模型 |
由于PSO算法在收敛过程中存在大量聚集的低速粒子, 这些粒子既不加速算法的收敛也无法探索新区域, 导致粒子陷入局部最优的概率较高, 且在迭代过程中仍消耗了大量资源, 降低了算法的收敛速度. 此外, PSO是一种易陷入局部最优的算法模型, 导致算法无法实现全局最优.
基于上述两个问题为克服微博评论信息快速分类, 本文提出了两种改进方法:
1) 引入粒子淘汰机制. 在训练的迭代初期, 出现收敛趋势时, 存在大量的低速且远离最优解的粒子, 而这些粒子的探索范围常远离最优解范围, 迭代其所需大量的计算量且收益率低, 于是在迭代前期采用GA算法, 通过粒子淘汰机制, 在迭代前期定期将适应度最差且速度最慢的粒子淘汰删除, 节约系统资源并极大加速收敛速度.
2) 改变粒子的拓扑结构. 当GA迭代次数D为:
| $ D = {T_{\max }}\left\lceil {\frac{1}{{1 + {{\rm{e}}^{ - n}}}} - 0.4} \right\rceil $ | (3) |
其中,
当粒子完成聚类后按照聚类结果进行PSO算法, 每个粒子在当前社区进行寻优, 最终各区域最优粒子组成为优秀群体的初始粒子种群开始PSO算法, 该算法的优势为: 即使存在社区的粒子陷入局部最优, 其他社区的粒子仍然能够在解空间内继续寻找最优解, 较好地保证了解的全局最优性.
在引入上述两种改进机制后, 本文提出粒子群算法的改进GA-IPSO算法. 首先该算法在粒子迭代的迭代前期使用GA算法, 在粒子迭代过程中删除掉适应度相对较差或边缘的惰性粒子, 其次在迭代中期进行K均值聚类算法对于剩余粒子进行粒子分区, 在每个社区中进行粒子群算法直到粒子收敛. 最后在迭代后期将所有社区中最优粒子组合成一个新的优秀粒子群体进行最终迭代, 获取最优解.
GA-IPSO算法步骤可以描述为:
(1) 初始化解空间中所有的初始粒子种群.
(2) 将粒子种群进行GA算法进化, 在该进化过程中, 分别记录不同迭代次数下不同粒子不同位置的适应度, 并将适应度进行排序.
(3) 按照粒子淘汰机制所设定的淘汰比例将适应度最低的批次粒子定义为惰性粒子.
(4) 删除惰性粒子, 并将剩下粒子种群定义为活跃粒子种群.
(5) 将活跃粒子种群进行K-均值聚类, 种群依照聚类结果进行社区划分, 定义为: 活跃A社区, 活跃B社区, …, 活跃N社区.
(6) 每个粒子在其所在社区中进行PSO算法的迭代, 直到算法收敛或达到最大迭代次数, 再定义各自社区中所有粒子位置中适应度最高的位置为优秀粒子, 并记录为: A社区优秀粒子, B社区优秀粒子, C社区优秀粒子, …, N社区优秀粒子.
(7) 将所有的优秀粒子组成为粒子群体, 定义为优秀群体, 优秀群体进行PSO算法迭代, 直至算法收敛或达到最大迭代次数, 从而得到最优解.
4 非线性多分类均衡支持向量机(BSVM)的建立 4.1 SVM简介SVM算法是Vapnik于1995年提出的一种基于统计学习理论的机器学习方法[15]. 其结构简单, 训练时间少, 具有良好的泛化能力, 所需的训练样本少, 精度也较高, SVM分类的基本思想可表述为: 给定两类样本点, 寻找最优线性超平面使两类样本点分离, 且最大化超平面和距离分类平面最近的样本点之间的距离.
在线性可分条件下, SVM可表述为:
对于给定数据集:
| $ \{ {x_i}, {y_i}\} \text{, } i = 1, 2, \cdots, N, {y_i} \in \{ - 1, 1\} , {x_i} \in {{\rm{R}}^n} $ | (4) |
分类超平面的函数为:
| $ w \times x + b = 0 $ | (5) |
归一化处理之后, 满足:
| $ {\xi _i} \gt 0, \; i = 1, 2, 3, \cdots, N $ | (6) |
其中, x是输入向量; w是权重向量; b是分类阈值. 整理后可将求取该超平面的问题转化为求解问题:
| $ {y_i}(w \times {x_i} + b = 0) = 1 \text{, } i = 1, 2, 3, \cdots , N $ | (7) |
| $ L = \min \frac{1}{2}|w{|^2} $ | (8) |
对于线性不可分条件下, 引入惩罚因子C和松弛变量
| $ {f}{(x)}={sgn}\left({\displaystyle \sum _{i=1}^{N}{\alpha }_{i}^{*}}{y}_{i}(\varphi ({x}_{i})\cdot \phi (x)+{b}^{\text{*}}\right) $ | (9) |
将高维空间中的点积运算替换成核函数:
| $ K({x_i} \cdot x) = \phi ({x_i}) \cdot \phi (x) $ | (10) |
则最优分类函数可表示为:
| $ {f{(x)}} = {{sgn}} \left(\sum\limits_{i = 1}^N {\alpha _i^*} {y_i}K({x_i} \cdot x) + {b^{\text{*}}}\right) $ | (11) |
在SVM中, 核函数的引入解决了因数据维度过高且线性不可分导致计算能力不足的缺陷. 一般核函数的选择对于问题的求解极为重要, 常见的核函数有线性核(linear), 多项式核(poly), 双曲正切核(Sigmoid), 高斯径向基核(rbf)等.
线性核函数和多项式核函数在非线性数据上的性能不稳定: 若数据相对线性可分, 则性能效果较好; 若如环状非线性数据一样完全不可分, 则性能效果较差. 在线性数据集上, 即使存在有扰动项干扰, 线性核函数和多项式核函数的分类效果仍较好, 可知多项式核函数在线性数据集上功能更强. 双曲正切核在非线性数据上强于两个线性核函数, 但效果不如高斯径向基核函数, 在线性核函数上表现较差, 对扰动项的抵抗较弱[16], 高斯径向基核函数在全部数据集上的表现都较优, 对扰动项的抵抗力也较强[17]. 综上分析, 本文对于位置分布未知的数据分类任务, 选择高斯径向基核函数作为SVM模型中的核函数.
SVM多分类方法主要包括2种: 一种是直接求解法, 但该方法的时间复杂度高, 实现起来较为困难, 且存在大量数据待处理的情况下计算性能不足的问题; 另一种是将多分类问题转化成多个二分类问题. 本文选择第2种方法, 常见的转化方式有一对一OAO (one against one)[18], 多对多, 有向环形图和二叉树等方法. 在上述二分转化方法中, 由于所需构造的二叉树数量不同, 二叉树结构的多分类方法训练的二分类器的数量也不尽相同, 本文采用偏二叉树的结构实现多层分类, 先将所有样本分为第一类和其他类, 再在剩下类别中重复此操作直到所有类别都单独分为一个叶子节点, 最终完成多层分类.
4.2 建立非线性多分类均衡支持向量机(BSVM)SVM作为一种常用的变形预测模型[19], 在处理高维数据, 非线性问题上具有良好的鲁棒性和泛化能力. 由于微博数据存在获取容易和样本数量不均衡的特性, 本文提出非线性多分类均衡支持向量机BSVM以降低微博样本量不平衡引起的误差问题.
| $ \left\{ {\begin{split} &\min \left(\frac{1}{2}||\omega |{|^2} + C\sum\limits_{i = 1}^N {{\theta _{{y_i}}}{\xi _i}} \right)\\ & {\rm{s.t.}}\left\{ {\begin{array}{*{20}{l}} {{y_i}(\omega \cdot \phi ({x_i}) + b) \geqslant 1 - {\xi _i}} \\ {{\xi _i} \geqslant 0} \end{array}} \right. \end{split}} \right.$ | (12) |
其中,
为克服SVM算法超参数选择速度慢, 易陷入局部最优问题, 本文结合PSO的快速收敛性和SVM多维出来高可靠性的特点, 提出改进的GA-IPSO算法对BSVM模型进行超参数寻优, 以实现微博信息的快速准确分类.
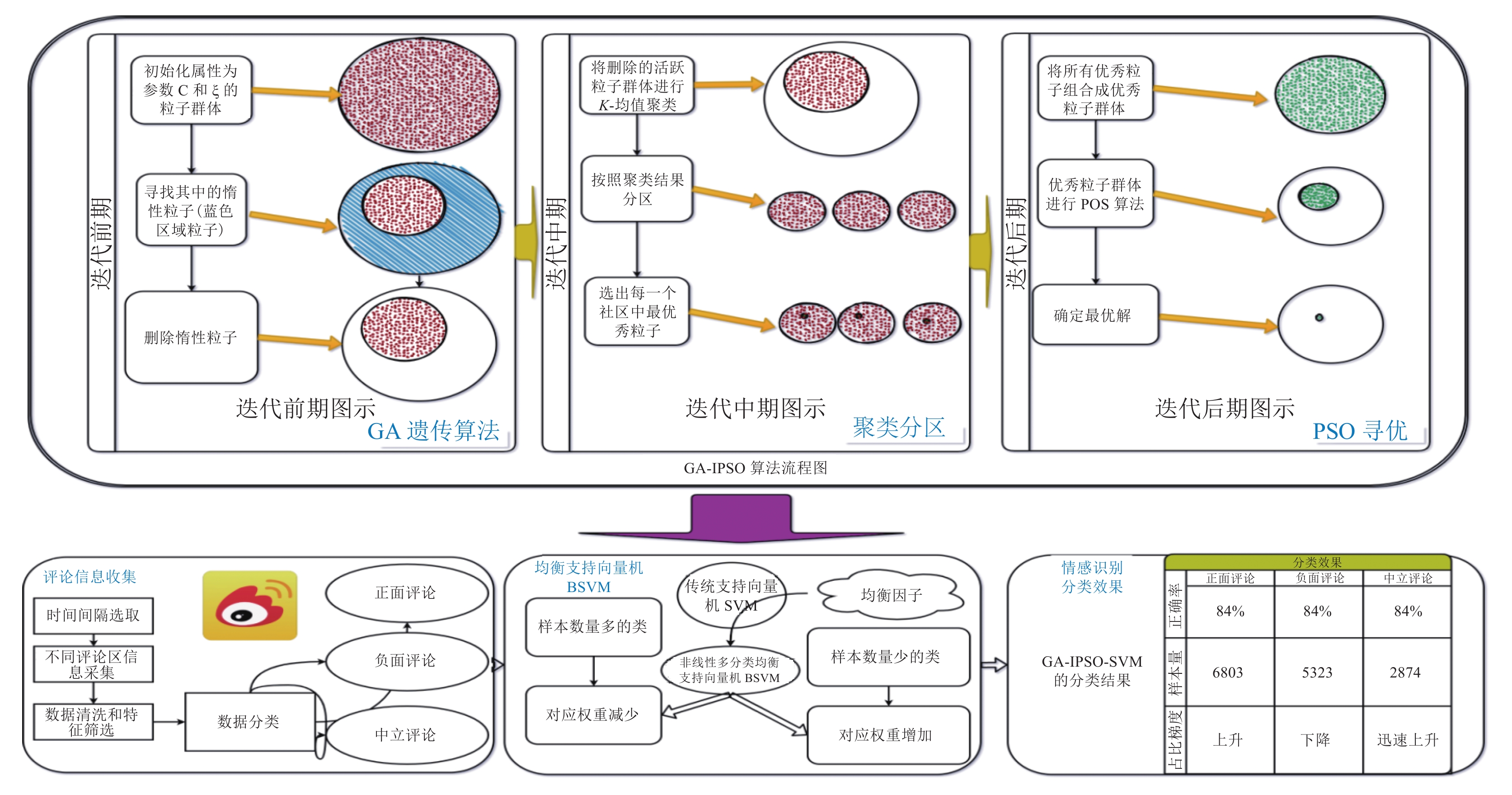
当前研究多集中于针对PSO算法中惯性权重的动态改变[20], 但每一次惯性权重的计算需都花费一定的系统资源. 因此, 本文提出基于引入GA和新拓扑结构的PSO以获得更好的参数寻优效果, 又提出非线性多分类均衡支持向量机BSVM以减少样本量不平衡引起的误差. 具体实施流程如图2所示.
|
图 2 GA-IPSO-BSVM具体实施流程图 |
6 GA-IPSO-BSVM算法对比验证
设置解决n维问题时在迭代次数D时聚类, K-均值聚类类别数量为Z=4. 将GA-IPSO-BSVM算法与传统PSO算法进行对比, 验证粒子淘汰机制和聚类分区机制引入的有效性, 使用函数为Shaffer函数的
| $ \left\{ {\begin{split} &{f_6}({x_1}, {x_2}) = 0.5 + \frac{{{{\sin }^2}\sqrt {x_1^2 + x_2^2 - 0.5} }}{{{{\left[1.0 + 0.01(x_1^2 + x_2^2)\right]}^2}}}\\ & x_1 \gt - 100, x_2 \lt 100 \end{split}} \right. $ | (13) |
| $\left\{ {\begin{split} &{f_7} = {\left(x_1^2 + x_2^2\right)^{0.25}}\left[{\sin ^2}\left(50{\left(x_1^2 + x_2^2\right)^{0.1}}\right) + 1.0\right]\\ & x_1 \gt - 100, x_2 \lt 100 \end{split} } \right.$ | (14) |
其中, 函数只有唯一极值点
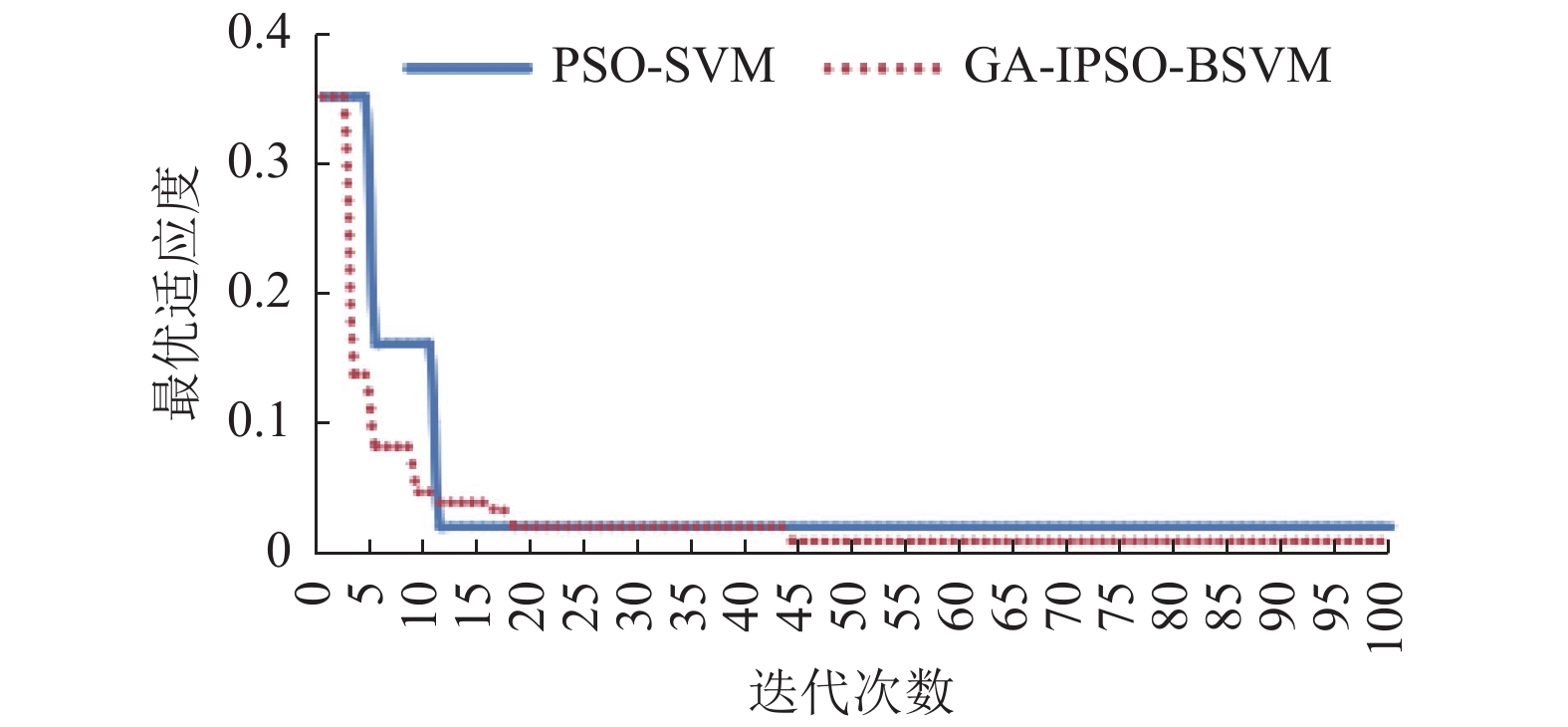
从图3可看出, 两种算法在第20次迭代时均找到了同一适应度的位置, 适应度为0.018, 然而GA-IPSO-BSVM算法在第45次粒子收敛时不再陷入局部最优, 找到了适应度更好的位置, 适应度为0.007, 而未改进的PSO算法直到达到最大迭代次数仍陷入局部最优.
|
图 3 f6函数寻优效果对比 |
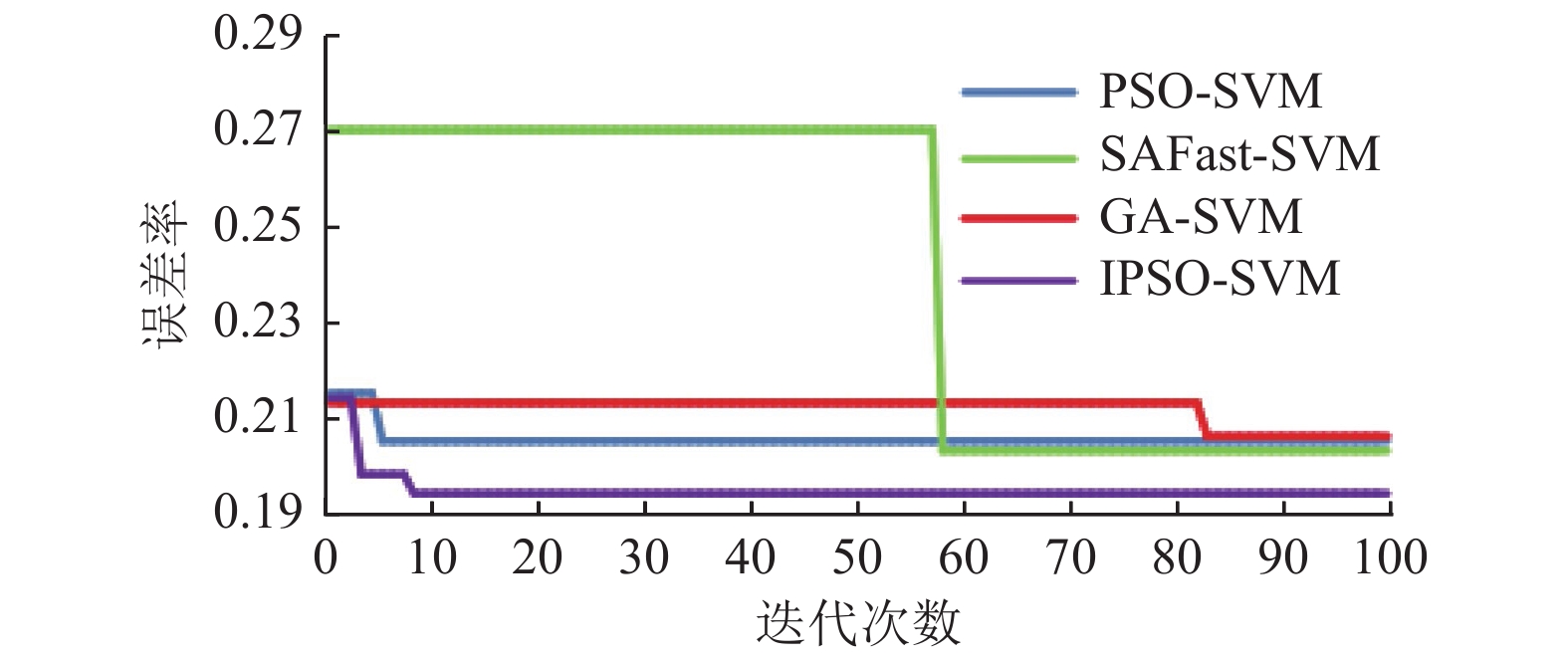
从图4可看出, 两种算法在第83次迭代时都找到了同一适应度的位置, 适应度为0.01. 然而GA-IPSO-BSVM算法在第15次迭代之后, 在任何一个相同的迭代次数下都能找到比原算法适应度更高的位置, 说明GA-IPSO-BSVM算法收敛速度更快.
综合上述结果看出, GA-IPSO-BSVM算法能够有效地加快粒子收敛速度, 且避免陷入局部最优, 更易找到全局最优点.

|
图 4 f7函数寻优效果对比 |
7 微博评论信息分类的实验设计和结果分析 7.1 数据来源
由于微博评论信息具有复杂性, 用户的年纪跨度和信息渠道的不同, 用户发博的随机性, 单用户多次发表评论的不确定性等多个特征, 导致数据可能产生噪声干扰, 本文每隔一小时对于10个不同的评论区间进行信息采集, 再经过数据清洗和特征筛选后得到离散型7维数据和3个二值数据. 其中, 离散型7维数据能够较为完整地反映出当前微博评论信息的相关信息, 其包括: 评论时间, 昨天发博数, 阅读数, 阅读人数, 互动数, 关注数, 粉丝数; 二值数据记录用户类别, 主要包括用户性别, 用户是否加V, 用户是否认证. 再通过所提出的GA-IPSO-SVM算法可预测一个3种分类的输出结果, 包括: “正面结果”“负面结果”“中立结果”. 最后, 本文基于这3种分类输出结果得到分类准确率.
7.2 分类效果本文将16 000条数据按照4:1的比例分为训练集和测试集, 检验模型识别的准确率. 表1列出不同评论的分类正确率, 样本数量.
SVM的核函数采用RBF核函数. IPSO优化参数均设置为: 粒子初始种群数量100, 最大迭代次数1 000, 惯性因子w设置为0.8, 学习因子c1, c2分别设置为0.5和0.7. GA优化参数设置为交叉概率为0.9, 变异概率为1E–7.
| 表 1 不同评论样本数据及其分类正确率 |
7.3 多种算法效果对比
用GA-IPSO-SVM算法与BPNN算法[21], CNN算法[22], SAFsat-LSSVM算法[23]对相同微博评论信息进行实验对比, 如图5所示.
|
图 5 多种算法对于微博评论信息分类的效果对比 |
由图5结果可看出, 在分类准确率方面, 本文使用的GA-IPSO-SVM更高; 在收敛速度方面GA-IPSO-SVM迭代次数上更少, 所使用的的模型能找出全局最优的SVM超参数, 较好地克服了PSO易陷入局部最优解的缺陷, 在微博评论信息的分类任务上可以进行快速有效的处理.
并进行不同模型在不同时间段的造成误差的均方根误差(root mean squared error, RMSE)和平均绝对相对误差(mean absolute percentage error, MAPE)进行比较, RMSE和MAPE计算公式分别为:
| $ {\textit{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} } $ | (15) |
| $ {\textit{MAPE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left|\frac{{{{\hat y}_i} - {y_i}}}{{{y_i}}}\right|} \times 100{\text{%}} $ | (16) |
其中,
表2为基于BPNN, CNN, SAFast-SVM和GA-IPSO-BSVM对于微博评论数据分类的效果对比, 从中可以看出在RMSE误差衡量标准当中, GA-IPSO-SVM的误差显著低于BPNN的18.63和CNN的15.769, 略低于SAFast-LSSVM的8.674, 是RMSE标准下精度最高的算法. 且在MAPE误差衡量标准中, GA-IPSO-SVM的误差显著低于BPNN的0.385和CNN的0.294, 低于SAFast-LSSVM的0.187, 是MAPE标准下精度最高的算法. 实验证明相对于传统算法, GA-IPSO-SVM在寻优精度上有更好的表现.
8 结束语针对微博评论信息的分类任务, 利用相关数据, 本文提出了采用多分类偏二叉树结构的GA-IPSO-SVM对信息进行分类的方法, 模型通过粒子淘汰机制的引入节约了迭代大量无用粒子的时间, 使粒子的收敛速度更快, 能在一定程度上完成快速寻优, 基于聚类算法的粒子分区机制引入使粒子不再局部最优的能力更强. 最终在多个公开数据集及微博信息分类上进行相较传统算法的对比验证, 本文提出的算法具有更高的分类精度和有效性.
| 表 2 各种分类算法的误差值 |
| [1] |
黄炎宁. 数字媒体与新闻“信息娱乐化”: 以中国三份报纸官方微博的内容分析为例. 新闻大学, 2013(5): 54-64. |
| [2] |
CNNIC. CNNIC发布第47次《中国互联网络发展状况统计报告》. http://cnnic.cn/gywm/xwzx/rdxw/20172017_7084/202102/t20210203_71364.htm. (2021-02-03).
|
| [3] |
微博. 微博辟谣月度工作报告(2021年2月). https://weibo.com/ttarticle/p/show?id=2309404616101991678467. (2021-03-18).
|
| [4] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [5] |
Kim Y. Convolutional neural networks for sentence classification. Proceedings of 2014 Conference on Empirical Methods in Natural Language Processing. Doha, Qatar: Association for Computational Linguistics, 2014. 1746–1751.
|
| [6] |
王文凯, 王黎明, 柴玉梅. 基于卷积神经网络和Tree-LSTM的微博情感分析. 计算机应用研究, 2019, 36(5): 1371-1375. |
| [7] |
Keerthi SS, Shevade SK, Bhattacharyya C, et al. Improvements to Platt’s SMO algorithm for SVM classifier design. Neural Computation, 2001, 13(3): 637-649. DOI:10.1162/089976601300014493 |
| [8] |
林江豪, 阳爱民, 周咏梅, 等. 一种基于朴素贝叶斯的微博情感分类. 计算机工程与科学, 2012, 34(9): 160-165. |
| [9] |
蔡坤烨, 蔡景, 周迪, 等. 基于SVM方法的APU故障预测方法. 南京航空航天大学学报, 2019, 51(4): 466-473. |
| [10] |
Zhu YJ, Yu XM, Yang BH. The research on sensor fault diagnosis based on the SVM prediction model. Applied Mechanics and Materials, 2014, 596: 528-531. DOI:10.4028/www.scientific.net/AMM.596.528 |
| [11] |
Jiao XX, Jing B, Li J, et al. Research on remaining useful life prediction of fuel pump based on adaptive differential evaluation grey wolf optimizer-support vector machine. Chinese Journal of Scientific Instrument, 2018, 39(8): 43-52. |
| [12] |
黄斌. 基于改进GM(1, 1)和SVM的轨道电路故障最优组合预测模型研究. 铁道科学与工程学报, 2019, 16(11): 2852-2858. |
| [13] |
Yang DL, Liu YL, Li SB, et al. Gear fault diagnosis based on support vector machine optimized by artificial bee colony algorithm. Mechanism and Machine Theory, 2015, 90: 219-229. DOI:10.1016/j.mechmachtheory.2015.03.013 |
| [14] |
Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of IEEE International Conference on Networks. Piscataway: IEEE, 1995. 1942–1948.
|
| [15] |
Cortes C, Vapnik V. Support-vector networks. Machine Learning, 1995, 20(3): 273–297.
|
| [16] |
朱树先, 张仁杰. 支持向量机核函数选择的研究. 科学技术与工程, 2008, 8(16): 4513-4517. DOI:10.3969/j.issn.1671-1815.2008.16.021 |
| [17] |
汪廷华, 陈峻婷. 核函数的选择研究综述. 计算机工程与设计, 2012, 33(3): 1181-1186. DOI:10.3969/j.issn.1000-7024.2012.03.068 |
| [18] |
Ranaee V, Ebrahimzadeh A, Ghaderi R. Application of the PSO–SVM model for recognition of control chart patterns. ISA Transactions, 2010, 49(4): 577–586.
|
| [19] |
American College of Cardiology Foundation, American Heart Association Task Force on Practice Guidelines, American Association for Thoracic Surgery, et al. 2010 ACCF/AHA/AATS/ACR/ASA/SCA/SCAI/SIR/STS/SVM guidelines for the diagnosis and management of patients with thoracic aortic disease: Executive summary. Journal of the American College of Cardiology, 2010, 55(14): 1509-1544. DOI:10.1016/j.jacc.2010.02.010 |
| [20] |
雷秀娟, 史忠科, 周亦鹏. PSO优化算法演变及其融合策略. 计算机工程与应用, 2007, 43(7): 90-92. DOI:10.3321/j.issn:1002-8331.2007.07.028 |
| [21] |
Ghose DK, Panda SS, Swain PC. Prediction of water table depth in western region, Orissa using BPNN and RBFN neural networks. Journal of Hydrology, 2010, 394(3–4): 296-304. DOI:10.1016/j.jhydrol.2010.09.003 |
| [22] |
Shin HC, Roth HR, Gao MC, et al. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Transactions on Medical Imaging, 2016, 35(5): 1285-1298. DOI:10.1109/TMI.2016.2528162 |
| [23] |
刘静. 基于AFSA-LSSVM的短时交通流量预测. 计算机工程与应用, 2013(17): 226-229. DOI:10.3778/j.issn.1002-8331.1211-0182 |
 2022, Vol. 31
2022, Vol. 31



