随着人机交互技术的发展, 用户界面的呈现方式越来越多样化, 如何为用户打造高效、满意的用户界面是界面设计的热点. 界面质量是界面设计有效性和用户满意度的关键因素, 布局方式更是界面质量的重要组成部分. 影响布局方式的主要因素是界面元素本身所要表达信息量的大小、用户的生理行为及心理认知等人因特性因素, 界面设计不仅需要满足用户生理特性的基本需求, 更是需要满足心理特性的认知层, 进而发展到人机系统设计中偏重用户体验的感性层[1]. 目前基于管理平台界面设计中以用户体验为导向的设计差距还较大, 因此优化用户界面设计对于提升平台系统可用性及满意度具有重要意义.
1 相关工作界面中布局方式所构成信息理解的难易程度决定了用户对于界面布局认知的准确性和高效性[2], 良好的布局方式有助于提升用户的认知效率. 目前针对界面布局优化的方向主要有两种: 一种是通过主观测量数据优化界面, 另一种则是利用算法等技术手段进行界面布局设计. 前者, 许永生等人[3]通过模拟实验测量驾驶员的注意力分配情况, 通过主观量表工作负荷以及访谈对高铁操纵台布局进行优化; 后者, Wu等人[4]建立误差因子-视觉感知-界面布局的关联模型并利用遗传算法寻求最优解进行界面优化; 康慧[5]基于工效学及美度评价原则建立布局准则, 并运用遗传算法对产品界面布局进行优化; 刘昕等人[6]引用改进粒子群算法提出了我国飞行员人机布局优化新方法; 国外, Diego-Mas等人[7]使用眼动跟踪、鼠标移动和切片树的遗传算法对界面进行布局优化; Oulasvirta等人[8]对用户界面设计中元素组合优化的方法进行阐述. 近年来在用户认知过程中有关认知负荷的研究越来越受到学者重视, 袁义凡[9]归纳了近10年认知负荷在界面设计中应用研究的热点领域、重点、研究趋势等, 表明负荷大小是影响界面可用性设计和提升用户体验的重要因素之一. 然而, 目前将认知负荷引入界面布局优化的研究并不多.
界面布局优化本身属于多目标优化问题, 遗传算法、粒子群算法、蚁群算法等启发式算法已在许多布局优化问题研究中得到了应用. 赵子健等人[10]运用蚁群算法对操纵器布局进行优化排列, 叶坤武等人[11]引入带有惯性权重的粒子群算法对飞机驾驶舱界面布局进行优化. 但算法之间各有优劣, 遗传算法可以求全局最优解, 但收敛速度较慢, 局部搜索能力较差、控制变量较多; 群智能优化算法因易操作、鲁棒性强等优点被广泛应用, 典型的群智能优化算法有粒子群算法、蚁群算法, 但是粒子群对于参数的设置依赖性较强, 易陷入局部最优解中; 蚁群算法计算量较大, 收敛速度较慢且容易局部最优; Xue等人[12]受麻雀觅食和反捕食行为的启发提出了麻雀搜索算法(sparrow search algorithm, SSA), 该算法结构简单且控制参数较少, 收敛速度快、稳定性好、全局搜索能力强, 可以满足全局的搜索能力和局部探索能力, 在进行优化问题时具有良好的性能, 一定程度上提升了优化搜索空间的探索利用能力. 李雅丽等人[13]使用标准基准测试函数对2010年以来新提出的6种典型群智能优化算法进行分析, 结果表明SSA各方面性能优于其他算法. 因此本文运用SSA对所建立的优化目标函数进行求解.
界面布局优化问题受到很多学者的研究, 并出现许多相关的应用案例, 但针对客观的工效学布局原则与用户心理认知规律相结合进行研究的较少. 针对用户界面布局优化问题, 本文建立了融合认知负荷以及界面美度计算为设计原则的多目标优化模型, 利用SSA模拟种群的捕食和反捕食过程, 生成界面优化布局解集. 以某铁路建造智能化协同管理平台首页为例, 展开优化方案的生成, 并通过生理测量数据建立布局与认知负荷之间的评价目标函数, 最后选取20名用户对初始方案及优化方案进行评价验证, 本文流程如图1所示.
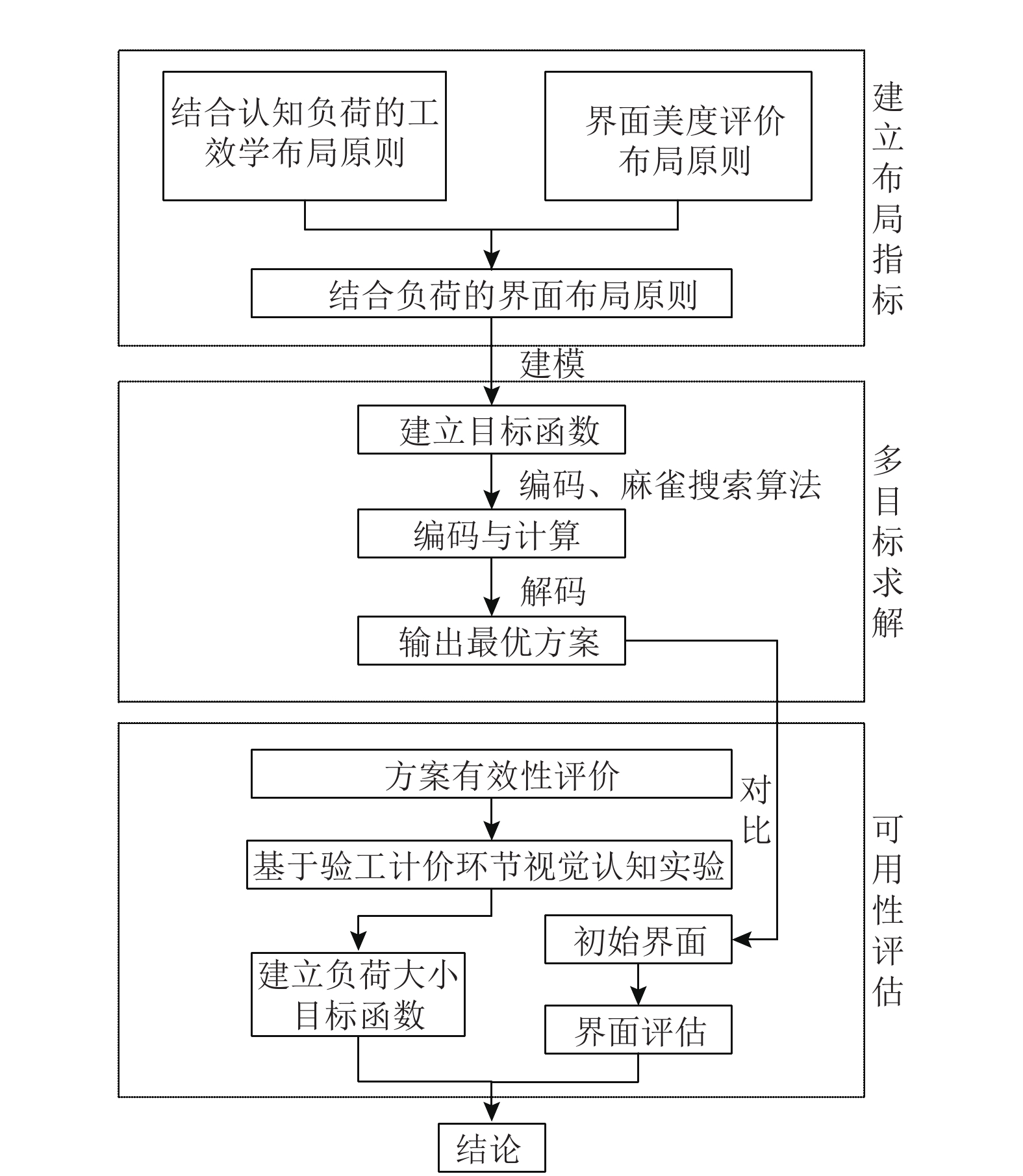
|
图 1 结合负荷的界面布局优化流程图 |
2 建立界面布局设计原则
人机界面交互过程中, 用户作为界面信息的接收者和使用者, 始终是人机交互中的核心要素. 界面布局是将元素按可行性约束放置于界面中, 影响其设计的因素众多, 需要综合考虑人机关系、人的认知模式、系统功能、界面设计美学、计算机技术、信息识别和获取等多方面的因素[14]. 在用户认知模型支持下, 需要同时满足用户心理及生理的前提下并综合考虑用户认知过程中会受到的影响因素[15]. 界面设计在不断发展过程中, 形成了许多通用的界面布局设计原则: Sanders等人[16]建立了界面信息元素排列的基本设计原则; Wickens等人[17]提出了邻近相容原则, 要求相关元素应紧密的呈现在一起, 此外还需考虑到各元素的使用频率.
2.1 结合认知负荷的工效学布局原则人机界面中的负荷主要存在于用户认知过程中, 随着界面信息数量的增多或信息难度的上升, 会加大用户在认知过程中的负荷量, 容易造成误操作等失误情形. 认知负荷理论划分了外在认知负荷、内在认知负荷和相关认知负荷3种类型的认知负荷. 李晶等人[18]在均衡认知负荷中提出要减少外在认知负荷, 保持内在认知负荷, 增加相关认知负荷. 本文首先归纳了调节界面中外在认知负荷的策略, 与工效学原则进行结合并形成界面工效学基本布局原则.
外在认知负荷主要受信息元素的布局呈现方式影响, 因此界面布局设计中应着重关注如何降低外在认知负荷的策略. 界面设计中形成认知负荷的原因有: 信息量超过工作记忆; 信息难度超过认知加工水平; 注意力资源分配不均等. 因此界面设计中需要根据元素的重要程度来进行排列, 把重要元素放置在最佳视觉区域; 人的工作记忆有限, 因此需要减少无关信息干扰, 界面中可以利用邻近减负原则来减少不必要的设计. 调节外在认知负荷策略布局设计原则如表1所示.
界面布局优化最理想的结果是将每一个信息元素放置在最优位置, 充分发挥人机效率, 但布局原则之间会存在相互重叠, 为避免这种情况, 需要添加系数进行调控, 从而对设计原则进行优先排序. 布局优化要求优化方案整体评价最高, 布局原则约束下需要使目标函数得到最大值. 在优化模型中可以得出重要度越高、使用越频繁则需要靠近视觉最佳布置点, 加权值也就越大. 本文通过调节认知负荷策略原则, 确定界面元素操作顺序、重要程度、使用频率以及元素间相关性的设计原则, 由此建立目标函数如式(1)所示:
| $\left\{ { \begin{split} & H{(i)}_{\rm best}=\max\left[{\displaystyle \sum _{i=1}^{n}({\omega }_{1i}{S}_{i}+{\omega }_{2i}\cdot{P}_{i}+{O}_{i})}\right]\\ &{\omega _{1i}} = 1 - 1/n\\ &{\omega _{2i}} = 1 - {d_{ia}}/{d_{a\max}} \end{split} } \right. $ | (1) |
其中,
| 表 1 调节外在认知负荷策略及布局设计原则 |
① 将界面元素按照一定的操作顺序放置, 有助于提升用户认知效率. 根据视觉认知规律, 元素应当按照从左到右或从上到下进行排列. 操作顺序矩阵
| $ C = {C_{ij}} = \left[ {\begin{array}{*{20}{c}} {{C_{11}}}&{{C_{12}}}& \cdots &{{C_{1d}}} \\ {{C_{21}}}&{{C_{22}}}& \cdots &{{C_{2d}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{C_{n1}}}&{{C_{n2}}}& \cdots &{{C_{nd}}} \end{array}} \right] $ | (2) |
矩阵中,
| $ {S}_{i}={\displaystyle \sum _{j=1}^{d}\left[{C}_{ij}\Bigg/{\displaystyle \sum _{i=1}^{n}{C}_{ij}\cdot{\omega }_{1i}}\right]} $ | (3) |
其中,
② 重要度由专家进行评价, 重要度矩阵可以表示为:
| $ I = {I_{ij}} = \left[ {\begin{array}{*{20}{c}} {{I_{11}}}&{{I_{12}}}& \cdots &{{I_{1h}}} \\ {{I_{21}}}&{{I_{22}}}& \cdots &{{I_{2h}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{I_{n1}}}&{{I_{n2}}}& \cdots &{{I_{nh}}} \end{array}} \right] $ | (4) |
矩阵中,
信息元素的操作频率矩阵
| $ F = {f_{ij}} = \left[ {\begin{array}{*{20}{c}} {{f_{11}}}&{{f_{12}}}& \cdots &{{f_{1r}}} \\ {{f_{21}}}&{{f_{22}}}& \cdots &{{f_{2r}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{f_{n1}}}&{{f_{n2}}}& \cdots &{{f_{nr}}} \end{array}} \right] $ | (5) |
矩阵中,
| $ {\omega _{\textit{z}}} = {\left[ {\begin{array}{*{20}{c}} {{\omega _{{\textit{z}}1}}}&{{\omega _{{\textit{z}}2}}}& \cdots &{{\omega _{{\textit{z}}r}}} \end{array}} \right]^{\rm T}} $ |
元素
| $ {P_i} = {I_i} + {Z_i} $ | (6) |
③ 相关性是反映信息元素之间关系的密切程度, 关系紧密的应靠近布置, 因此相关度矩阵可以表示为:
| $ O = {O_{ij}} = \left[ {\begin{array}{*{20}{c}} {{O_{11}}}&{{O_{12}}}& \cdots &{{O_{1n}}} \\ {{O_{21}}}&{{O_{22}}}& \cdots &{{O_{2n}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{O_{n1}}}&{{O_{n2}}}& \cdots &{{O_{nn}}} \end{array}} \right] $ | (7) |
矩阵中,
| $ {O_i} = \sum\limits_{j = i + 1}^n {({O_{ij}}/{d_{ij}})} $ | (8) |
Ngo等人[19]在图形显示上制定了14种审美指标: 平衡、均衡、对称、顺序、凝聚力、统一性、比例、简单性、密度、规律性、经济性、均匀性、节奏性、顺序性和复杂性. 周蕾等人[20]从界面的感性意象出发对美度计算进行定量分析, 建立界面美度的感性意象结构, 根据界面的平衡度、比例美度、简洁美和呼应美度4个方面进行12个美度指标的建立, 进一步完善了美度评价指标. 根据已有研究中的美度指标, 并针对于项目管理平台凝聚成12个美度感性词汇, 并邀请专家进行项目建设管理平台界面美度的语义进行评价, 根据最后的评价结果, 选取了简洁、统一、协调、舒适4个美度指标如表2, 以此构建界面美度评价目标函数:
| $ \begin{split} {F_{\max}} =& {\varepsilon _1}{\theta _1}\left( {1 - \left( {\left| {\frac{{{w_L} - {w_R}}}{{\max\left( {|{w_L} - {w_R}|} \right)}}} \right| + \left| {\frac{{{w_T} - {w_B}}}{{\max(\left| {{w_T} - {w_B}} \right|)}}} \right|} \right)/2} \right) +{\varepsilon _2}{\theta _2}\left( {1 - ({n_{\rm vertical}} + {n_{\rm hon{{z}}ontal}})/4n} \right) \hfill \\ &+ {\varepsilon _3}{\theta _3}\left( {1 - 2\left| {0.5 - \frac{{\displaystyle\sum\limits_i^n {{a_i}} }}{{{a_{\rm lrame}}}}} \right|} \right) + {\varepsilon _4}{\theta _4}\left( {1 - \left( {\frac{{{P_L} - {P_R}}}{{\max\left( {\left| {{P_L}} \right|, \left| {{P_R}} \right|} \right)}} + \frac{{{P_U} - {P_D}}}{{\max\left( {\left| {{P_U}} \right|, \left| {{P_D}} \right|} \right)}}} \right)/2} \right) \end{split} $ | (9) |
其中,
首先建立界面元素布局坐标系, 通过简化处理降低目标函数求解的难度, 将信息元素转化为矩阵形状, 在二维坐标上进行设计布局. 将界面大小设为1920 px×1080 px (px代表像素)的矩形, 将需要放置的信息元素抽象为矩阵, 长和宽已知, 各信息元素在界面中和坐标轴平行.
针对布局优化问题, 上述建立了结合认知负荷的工效学以及美度计算的界面布局设计原则, 并将布局原则量化转为可进行计算的数学建模指标进行编码, 建立如下的优化目标函数:
| $ H{(i)}_{\rm best}=\max\left[{\displaystyle \sum _{i=1}^{n}({\omega }_{1i}{S}_{i}+{\omega }_{2i}\cdot{P}_{i}+{O}_{i})\cdot \mu +\nu \cdot {F}_{\max}}\right] $ | (10) |
设界面中有
| $ {d_{ij}} = \sqrt {\mathop {\left( {{x_i} - {x_j}} \right)}\nolimits^2 + \mathop {\left( {{y_i} - {y_j}} \right)}\nolimits^2 } $ | (11) |
最后求解得到满足设计原则的设计变量, 即信息元素坐标系集
| 表 2 界面布局美度评价度量指标[20] |

|
图 2 界面布局示意图 |
(1)间距约束: 信息元素应该保持一定的距离, 即要满足公式:
| $ \left\{ {\begin{array}{*{20}{c}} {\left| {{A_x} - {B_x}} \right| - \dfrac{{{A_i}}}{2} - \dfrac{{{A_j}}}{2} - {d_{x\min}} \geqslant 0} \\ {\left| {{A_y} - {B_y}} \right| - \dfrac{{{B_i}}}{2} - \dfrac{{{B_j}}}{2} - {d_{y\min}} \geqslant 0} \end{array}} \right. $ | (12) |
(2)边界约束: 保证信息元素与界面边界保持一定的距离, 即要满足公式:
| $ \left\{ {\begin{array}{*{20}{c}} {{d_{a\min}} + \dfrac{{{A_i}}}{2} \leqslant {x_A} \leqslant L - \dfrac{{{A_i}}}{2} - {d_{a\min}}} \\ {{d_{b\min}} + \dfrac{{{B_i}}}{2} \leqslant {y_A} \leqslant W - \dfrac{{{B_i}}}{2} - {d_{b\min}}} \end{array}} \right. $ | (13) |
其中,
本文运用SSA对目标函数全局寻找最优解, 适应度函数值最大时得到最优参数, 算法流程具体如图3所示.

|
图 3 麻雀搜索算法流程图 |
Step 1. 初始化变量和麻雀搜索算法各参数, 设置种群规模以及迭代次数.
Step 2. 计算初始适应度值, 得出初始适应度的极值及位置并且进行标记.
Step 3. 计算预警值. 在算法中, 发现者为整个麻雀种群寻找食物并对所有追随者提供捕食方向, 因此具有较好适应度值的发现者会优先获取食物, 而且发现者可以获取更大的觅食搜索范围.
以预警值大小更新发现者的位置, 在每次迭代中, 发现者的位置更新如下:
| $ X_{i, j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {X_{i, j}^t \cdot \exp\left(\dfrac{{ - i}}{{\alpha \cdot ite{r_{\max}}}}\right)}, \quad{\rm if} \;{{R_2} < ST}\\ {X_{i, j}^t + Q \cdot L}, \qquad\qquad\quad\; {\rm if}\; {{R_2} \geqslant ST} \end{array}} \right. $ | (14) |
其中,
追随者是适应度比较差的个体, 它们监视发现者寻找食物, 为竞争食物会改变当前的位置. 更新追随者的位置, 根据式(15)更新追随者的位置.
| $ X_{i, j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {Q \cdot \exp\left(\dfrac{{X_{\rm worst}^t - X_{i, j}^t}}{{{i^2}}}\right)},\;\;\quad\quad {\rm if}\; {i > n/2} \\ {X_p^{t + 1} + \left| {X_{ij}^t - X_P^{t + 1}} \right| \cdot {A^ + } \cdot L},\quad {\rm otherwise} \end{array}} \right.$ | (15) |
其中,
在模拟实验中, 我们假设意识到危险的麻雀占总数的10%–20%. 这些麻雀最初的位置是在种群中随机产生的. 根据式(16)更新位置, 数学模型可以表示为:
| $ X_{ij}^{t + 1} = \left\{ {\begin{array}{*{20}{c}} {X_{\rm best}^t + \beta \cdot \left| {X_{ij}^t - X_{\rm best}^t} \right|}, \\ {X_{ij}^t + K \cdot \left(\dfrac{{\left| {X_{ij}^t - X_{\rm worst}^t} \right|}}{{({f_i} - {f_w}) + \varepsilon }}\right)}, \end{array}} \right. \begin{array}{*{20}{c}} {\rm if} \\ {\rm if} \end{array} \begin{array}{*{20}{c}} {{f_i} > {f_g}} \\ {{f_i} = {f_g}} \end{array} $ | (16) |
为简单起见, 当
本文以某铁路项目管理平台首页为研究对象, 对所提方法进行验证. 首先以平台界面首页为目标任务构建任务模型, 通过专家对信息元素的评价获取该目标任务所需要的任务信息元素以及之间关系. 首先对该平台首页所包含的决策信息元素: 系统名称、数字工厂、验工计价、物资管理、进度报表、合同管理、变更设计、质量工程、竣工资料、用户管理、系统设置以及平台菜单进行编码, 根据各个信息元素类型不同, 将每个类型以及同类元素进行标准化设定, 如表3所示.
| 表 3 12个待布局元素的编码以及重要度、使用频率 |
邀请平台专家针对各决策元素进行打分以此确定布局元素之间的重要度、使用频率以及元素之间的相关性, 布局与本身之间的相关性为1, 所有确定的评分数据都确定在[0, 1]之间, 待布局元素之间的影响因素越大则数值越大. 将评价结果进行综合计算, 重要度、使用频率见表3, 待布局元素间的相关性见表4.
通过上述步骤完成对布局元素的编码、界面以及待布局元素尺寸的定义以及相关数据的计算, 再设定SSA控制参数: 迭代的最大次数为3 000, 种群大小设置为300 (n=300), 发现者数量和SD分别占20%和10%, ST=0.8, 通过问卷调研以及专家打分确定加权系数, 将数据输入SSA中, 运用Matlab R2019b进行辅助优化计算求解, 根据初始信息和约束条件, 得到适应度随迭代次数的变化曲线如图4所示.
从图4中可得, 在迭代至20次左右时获得最优解, 此时12个待布局元素在界面中的位置见表5.
| 表 4 12个待布局元素间的相关性 |
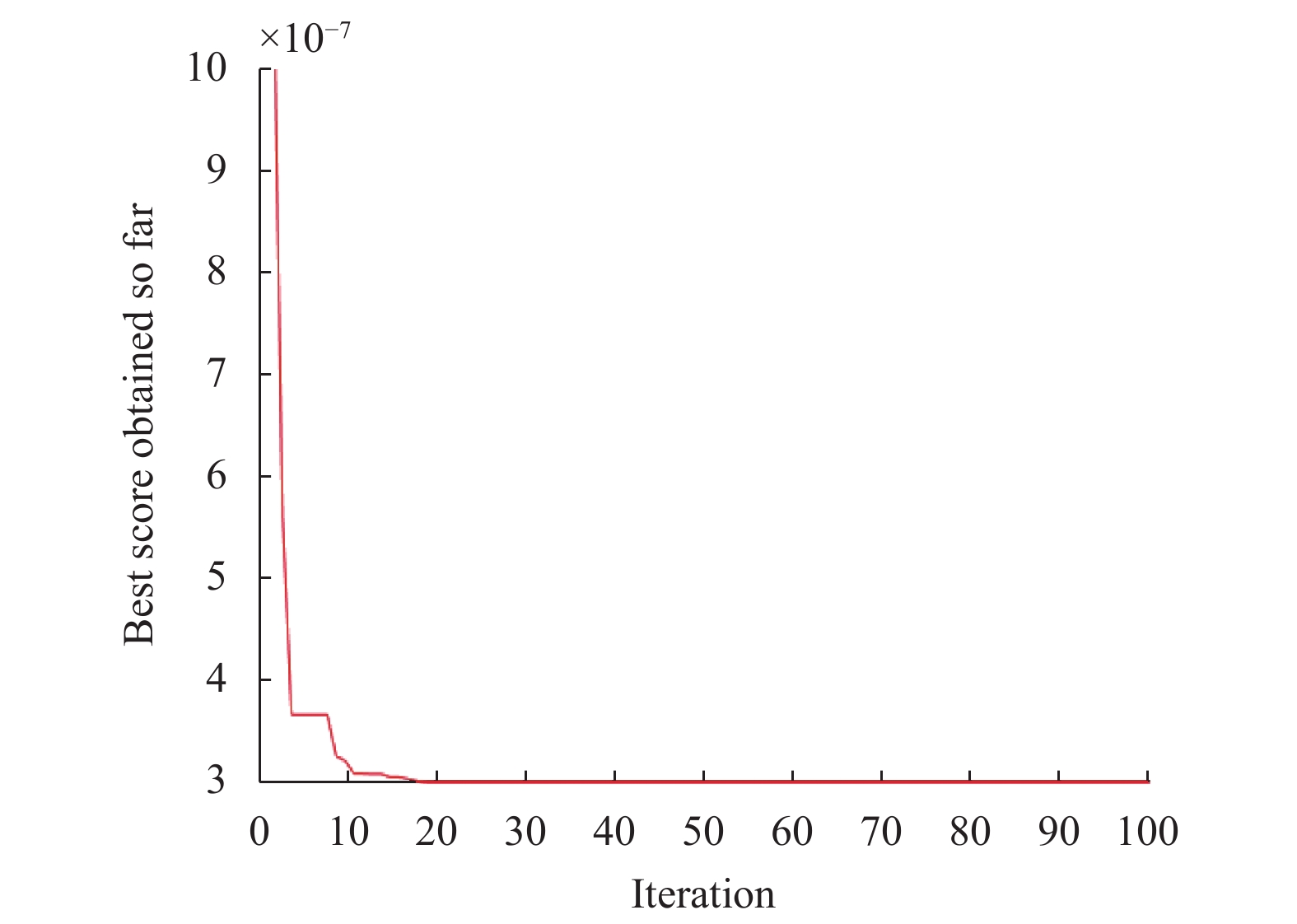
|
图 4 适应度随迭代次数的变化曲线 |
| 表 5 计算结果布局 |
结合表5的数据, 将重要度及使用频率高的放置在视觉认知的最佳位置, 按相关性与操作顺序确定了布局元素之间的位置和距离关系, 从上到下进行纵向排列得到优化后的布局方案如图5所示.
4.2 方案有效性评价为验证本文方法的有效性, 运用眼动生理测量实验进行分析验证. Holsanova等人[21]指出不同布局对于眼睛运动行为有显著影响, 且已有眼动指标被证实与认知负荷具有显著相关性. 本文首先归纳出5种常用布局方式以及6种眼动指标, 运用方差分析计算F比求证不同布局与所选眼动指标之间是否具有相关性, 并以眼动数据构建计算负荷量大小的评价函数, 用以计算不同布局间负荷量的大小.

|
图 5 两种界面布局方案 |
从现有项目管理平台界面中归纳出5种常用的界面布局方式: 上下型、左右型、厂字型、口字型、T字型, 以验工计价界面为例形成实验样本, 如图6所示. 选取6种眼动指标: 注视点数目、每秒注视点数量、平均注视持续时间、平均扫视长度、平均扫视速度以及扫视总长度. 由易到难设计5种实验任务: 流程审批、清单内计价、量差计价、变更设计、价差计价, 测量用户在界面认知过程中眼睛运动行为数据.

|
图 6 布局结构示意图 |
为避免被试者因界面有序浏览顺序而影响实验结果, 本文采用拉丁方设计实验. 选取20名来自工业设计专业的硕士研究生, 年龄(25±3.5)岁, 视力正常或矫正视力正常. 实验首先确定自变量是不同布局设计, 因变量是眼动数据, 根据拉丁方设计, 随机将行与列调换形成拉丁方表格, 如图7所示.

|
图 7 实验处理顺序的分配方案 |
通过5种布局方式6种眼动指标进行双因素无交互作用方差分析计算F比, 有关布局方式与眼动指标的F比值为:
| $ \left\{ {\begin{gathered} {F_1}{\text{ = }}\frac{{M{S_A}}}{{M{S_E}}} = {S_A} \cdot {S_E} \cdot (a - 1)(b - 1) \hfill \\ {F_2}{\text{ = }}\frac{{M{S_B}}}{{M{S_E}}} = {S_B} \cdot {S_E} \cdot (a - 1)(b - 1) \hfill \\ \end{gathered}} \right. $ |
| 表 6 双因素方差显著性计算分析 |
实验获取到20名被试人员的眼动指标数据, 由此建立测量眼动负荷的目标函数:
| $ f(x) = a \cdot {L_{dn}} $ | (17) |
| $ {L_{dn}} = \left[ {\begin{array}{*{20}{c}} {{L_{11}}}&{{L_{12}}}& \cdots &{{L_{1n}}} \\ {{L_{21}}}&{{L_{22}}}& \cdots &{{L_{2n}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{L_{d1}}}&{{L_{d2}}}& \cdots &{{L_{dn}}} \end{array}} \right] $ | (18) |
| $ a = \left[ {\begin{array}{*{20}{c}} {{{\bar L}_{11}}}&{{{\bar L}_{11}}}& \cdots &{{{\bar L}_{11}}} \\ {{{\bar L}_{11}}}&{{{\bar L}_{11}}}& \cdots &{{{\bar L}_{11}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{{\bar L}_{11}}}&{{{\bar L}_{11}}}& \cdots &{{{\bar L}_{11}}} \end{array}} \right] $ | (19) |
根据数据结果求得
计算结果显示优化后的布局数值低于初始布局数值, 表明本文基于SSA的界面布局优化模型后的界面相对于初始界面, 降低用户认知负荷量, 提升用户认知效率, 增强了界面的可用性.
| 表 7 测量负荷大小结果 |
5 结语
本文以降低用户认知过程中的负荷大小及减少界面设计的主观性为目标, 建立融合眼动负荷的界面布局设计原则并运用SSA进行优化设计. 该方法综合考虑到界面对用户影响因素, 从客观的界面布局基本原则及用户主观认知出发, 建立结合认知负荷的工效学和美度计算的目标优化函数, 通过对信息元素的合理布局, 提升用户的认知效率, 降低用户认知过程中负荷大小, 增加用户对界面的满意度, 提升了系统平台的可用性. 此次研究还未考虑到布局元素的颜色、动效等视觉因素对用户认知过程负荷大小的影响, 后续的研究中会进一步探索并完善该研究.
| [1] |
邓丽, 王国华, 余隋怀. 遗传-蚁群算法求解司钻控制室操纵器布局优化. 工程设计学报, 2016, 23(2): 143-151. DOI:10.3785/j.issn.1006-754X.2016.02.007 |
| [2] |
李晶, 郁舒兰, 刘玮. 基于眼动追踪的数控界面布局认知特性评价. 计算机辅助设计与图形学学报, 2017, 29(7): 1334-1342. DOI:10.3969/j.issn.1003-9775.2017.07.020 |
| [3] |
许永生, 李丽丽, 吴尤荻, 等. 基于注意力分配的高铁操纵台界面布局优化设计. 西南交通大学学报, 2022, 57(2): 401–409.
|
| [4] |
Wu XL, Chen Y. Correlation between error factors, visual perception, and interface layout—Taking digital instrument control equipment of nuclear power safety injection system as an optimization example. International Journal of Pattern Recognition and Artificial Intelligence, 2020, 34(5): 2055012. DOI:10.1142/S0218001420550125 |
| [5] |
康慧, 杨随先, 邓淑文, 等. 产品操作界面元素布局多目标优化设计. 包装工程, 2020, 41(8): 149-153, 172. |
| [6] |
刘昕, 余隋怀, 初建杰, 等. 改进PSO的飞机驾驶舱组合排序人机布局优化. 计算机工程与应用, 2015, 51(7): 1-6. DOI:10.3778/j.issn.1002-8331.1409-0243 |
| [7] |
Diego-Mas JA, Garzon-Leal D, Poveda-Bautista R, et al. User-interfaces layout optimization using eye-tracking, mouse movements and genetic algorithms. Applied Ergonomics, 2019, 78: 197-209. DOI:10.1016/j.apergo.2019.03.004 |
| [8] |
Oulasvirta A, Dayama NR, Shiripour M, et al. Combinatorial optimization of graphical user interface designs. Proceedings of the IEEE, 2020, 108(3): 434-464. DOI:10.1109/JPROC.2020.2969687 |
| [9] |
袁义凡. 近十年认知负荷在界面设计中的应用研究综述. 设计, 2020, 33(17): 116-118. DOI:10.3969/j.issn.1003-0069.2020.17.036 |
| [10] |
赵子健, 吕健, 金昱潼, 等. 人因特性驱动蚁群算法的操作界面布局优化. 组合机床与自动化加工技术, 2020(5): 124-127, 131. |
| [11] |
叶坤武, 包涵, 魏思东. 基于视觉注意力分配的飞机驾驶舱人机界面布局优化. 南京航空航天大学学报, 2018, 50(3): 416-421. |
| [12] |
Xue JK, Shen B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Systems Science & Control Engineering, 2020, 8(1): 22-34. |
| [13] |
李雅丽, 王淑琴, 陈倩茹, 等. 若干新型群智能优化算法的对比研究. 计算机工程与应用, 2020, 56(22): 1-12. DOI:10.3778/j.issn.1002-8331.2006-0291 |
| [14] |
沈擎阳, 薛澄岐, 牛亚峰. 基于ERP的人机交互界面设计方法研究. 设计, 2018(6): 134-135. DOI:10.3969/j.issn.1003-0069.2018.06.045 |
| [15] |
李雪楠, 赵江洪, 赵丹华. 基于用户认知偏好的3D打印软件界面交互设计. 机械设计, 2018, 35(7): 124-128. |
| [16] |
Sanders MS, McCormick EJ. 工程和设计中的人因学, 第7版. 清华大学出版社, 2009.
|
| [17] |
Wickens CD, Carswell CM. The proximity compatibility principle: Its psychological foundation and relevance to display design. Human Factors: The Journal of the Human Factors and Ergonomics Society, 1995, 37(3): 473–494.
|
| [18] |
李晶, 薛澄岐, 王海燕, 等. 均衡时间压力的人机界面信息编码. 计算机辅助设计与图形学学报, 2013, 25(7): 1022-1028. DOI:10.3969/j.issn.1003-9775.2013.07.012 |
| [19] |
Ngo DCL, Teo LS, Byrne JG. Modelling interface aesthetics. Information Sciences, 2003, 152: 25-46. DOI:10.1016/S0020-0255(02)00404-8 |
| [20] |
周蕾, 薛澄岐, 汤文成, 等. 界面元素布局设计的美度评价方法. 计算机辅助设计与图形学学报, 2013, 25(5): 758-766. DOI:10.3969/j.issn.1003-9775.2013.05.022 |
| [21] |
Holsanova J, Holmberg N, Holmqvist K. Reading information graphics: The role of spatial contiguity and dual attentional guidance. Applied Cognitive Psychology, 2009, 23(9): 1215-1226. DOI:10.1002/acp.1525 |
 2022, Vol. 31
2022, Vol. 31



