细心观察会发现身边的事物都存在着微小的变化, 这其中蕴含着事物本身重要的信息, 准确捕捉这些变化有助于把握事物的本质^{[1, 2]}. 视频放大技术借助复可控金字塔对帧图像进行运动分析, 给予了人们掌握目标变化情况的机会, 利用相机记录下微小运动, 再对视频信号进行处理, 可以放大振动的幅度, 观察边缘的形变情况, 这对于医学及工程等领域有重大意义. 例如, 从脉搏的微弱跳动情况中检测心率^[3], 从大楼墙体的振动中可监测建筑健康情况^[4], 分析桥梁的振动情况可避免事故的发生^[5]等.

但视频的放大倍数是有限的, 并且随着放大倍数的增加, 放大视频的画面质量会进一步降低. 这是由于复可控金字塔每一尺度的相移极限不同, 对于一部分尺度, 放大后的相移信号会超出该尺度的相移上限, 导致伪影及模糊^[6]. 目前最先进的改进算法^[6]通过改变部分尺度的放大因子, 在一定程度上提升了画面质量, 但也存在着参数依赖人工设定的问题. 本文提出了一种基于多尺度滤波的视频放大算法, 针对目标存在大小运动混叠的情况, 首先利用加速度滤波^[7]去除大运动干扰, 通过建立视频帧图像空间波长与振动位移间的联系, 无须人工设定参数, 自适应调整金字塔各尺度的放大因子, 从而减轻放大视频画面中的伪影及模糊, 提升画面质量.

1 视频运动放大

按照视角不同, 视频运动放大技术可总结为3类: 拉格朗日法、欧拉法以及欧拉拉格朗日混合法. 目前的视频运动放大方法大都基于欧拉视角. 拉格朗日法依赖于流体动力学, 通过感兴趣粒子的运动轨迹来研究相关的物理特性. Liu等人^[8]提出了第一个基于拉格朗日视角的视频放大方法. 通过匹配帧间特征点及基于光流的运动估计方法, 来区分背景运动和感兴趣的目标运动, 并对目标运动进行放大. 然而该方法中使用的光流估计的计算量过大.

欧拉方法不采用目标追踪, 而是分析图像中固定像素的位置随时间的变化. 欧拉线性视频放大方法^[1]利用拉普拉斯金字塔实现视频帧序列的空间分解, 并对空间频带进行时域滤波, 提取目标频率的微小振动信号. 但该方法会放大视频噪声, 并且对于运动放大来说, 只支持较小的放大因子. 因此Wadhwa等人^[9]提出了基于相位的视频放大算法, 通过复可控金字塔得到各尺度各方向的相位变化, 从而解决了噪声问题, 并通过扩展复可控金字塔提升了放大因子的上限, 但也增加了计算成本和时间. 对此, Wadhwa等人^[10] 又提出了Risez金字塔方法加快运行速度. 由于无法区分微小变化信号和大运动信号, 上述视频放大方法只适用于目标和相机之间相对稳定的情况, 即视频画面中只存在目标自身的微小运动.

然而目标包含大运动的情景也是需要研究的, 如人在跑步时的心率情况. 如何去除大运动对微小变化的干扰成为了关键问题. Bai等人^[11]通过用户指定大运动所在范围, 采用追踪和图形切割的方式去除大运动. 采用欧拉拉格朗日混合法的DVMAG^[12]通过拉格朗日方法追踪感兴趣区域来去除大运动, 并通过欧拉方法对感兴趣区域的振动进行提取和放大. 缺点在于需要人工圈定感兴趣区域, 而且其中的拉格朗日方法需要巨大的计算量. Kooij等人^[13]引入了深度信息, 通过检测相同深度层的像素变化来确定要放大的区域. 该方法在目标的深度不连续或目标不平稳时将难以实现.

Zhang等人^[7]提出了一个假设, 即大运动在小变化的时间尺度上是线性的, 实现了放大慢速大运动上的微小加速度变化. 该方法通过复可控金字塔提取局部相位信息, 各尺度的放大因子都是相同的, 但复可控金字塔中各尺度的空间支持是不同的, 由于视频放大倍数的上限是根据最大尺度决定的, 对于部分尺度, 其相位信号乘以放大因子后可能会超出其空间支持, 导致输出视频的伪影及模糊, 这意味着部分尺度的放大因子应该进行相应的调整. Xue等人^[6]针对该问题对加速度放大算法^[7]进行了改进, 通过人工设定截止波长将复可控金字塔的尺度分成两组, 缩小一组的放大因子, 而另一组的放大因子保持不变, 以尽可能满足所有尺度的限制条件. 该方法的不足之处在于其截止波长依赖人工设定, 无法准确反映各尺度的放大上限, 不能在放大效果满足需求的前提下达到较好的画面质量.

2 基于多尺度滤波的视频放大算法

本文针对大小运动混叠的场景, 提出了一种基于多尺度滤波的视频放大算法, 算法流程图如图1所示, 首先利用复可控金字塔对视频帧序列进行空间分解, 得到不同尺度不同方向的子带信号, 通过加速度滤波^[7]去除大运动干扰, 得到目标频率的微小振动信号. 然后设计一个多尺度滤波器, 通过建立各尺度空间波长 $ {\lambda _n} $ 和运动位移 $ \delta (t) $ 的联系, 自适应调整各尺度的放大因子 $ {\alpha _n} $ . 再利用相位展开技术对每层的相位差信号进行相位校正, 避免卷积过程中的伪影. 最后将输出信号与对应尺度的 $ {\alpha _n} $ 相乘, 重建复可控金字塔, 并输出放大视频.

2.1 空间分解

复可控金字塔是一种能将图像分解成一系列在位置、空间尺度以及方向上同时定位的基函数表示^[14], 得到图像的局部幅度谱与局部相位谱, 其中包括高通残差、低通残差及不同尺度 $ n $ 、不同方向 $ \theta $ , 如式(1).

$ I(x, y) \otimes {\psi _{n, \theta }} = {A_{n, \theta }}(x, y){{\rm{e}}^{i{\phi _{n, \theta }}(x, y)}} $

(1)

其中, $ I(x, y) $ 为图像原始信号, $ {\psi _{n, \theta }} $ 为金字塔滤波器, $ {A_{n, \theta }}(x, y) $ 为幅度信息, $ {\phi _{n, \theta }}(x, y) $ 为相位信息. 视频放大算法主要处理中间不同尺度不同方向的相位, 保证局部的微小相位处理等效于局部的运动处理. 而高通残差与低通残差在最终金字塔重建视频合成输出时被利用. 运动信息包含在相位中, 因此, 通过处理局部相位差信号就可以实现对视频局部运动的处理.

2.2 加速度滤波

在本文所研究问题中, 由于目标存在大小运动混叠的情况, 提取出目标频率对应的相位信号 $ {\phi _\omega }(x, y) $ 后, 其中包含大运动和微小运动, 利用加速度滤波^[9]去除其中的大运动干扰:

$ \frac{{{\partial ^2}I(x, y, t)}}{{\partial {t^2}}} \otimes G(x, y, t) = I(x, y, t) \otimes \frac{{{\partial ^2}G(x, y, t)}}{{\partial {t^2}}} $

(2)

$ {\phi _\omega }'(x, y, t) = {\phi _\omega }(x, y, t) \otimes \frac{{{\partial ^2}G(x, y, t)}}{{\partial {t^2}}} $

(3)

其中, $ G(x, y, t) $ 是高斯滤波器, $ \dfrac{{{\partial ^2}G(x, y, t)}}{{\partial {t^2}}} $ 为拉普拉斯滤波器, 即加速度滤波器, $ {\phi _\omega }'(x, y) $ 为加速度滤波后得到的微小运动的相位信号.

2.3 多尺度滤波

在视频放大算法中, 最终得到放大后的信号为:

$ {\hat \phi _\omega }(x, y, t) = {\phi _\omega }(x, y, t) + \alpha {\phi _\omega }'(x, y, t) $

(4)

其中, $ \alpha $ 为放大因子.

然而放大因子 $ \alpha $ 不能无限大, Wadhwa等人^[9]用高斯窗的标准差 $ \sigma $ 作为边界, 其边界条件为:

$ \alpha \delta (t) < \sigma $

(5)

由于高斯窗标准差 $ \sigma $ 与空间频率 $ {\omega _n} $ 存在关系 $ 4\sigma \approx \dfrac{{{n_p}}}{{{\omega _n}}} $ , 且波长 $ {\lambda _n} = \dfrac{1}{{{\omega _n}}} $ , 式(5)可转变为:

$ {\alpha _n}\delta (t) < \frac{{{n_p}{\lambda _n}}}{4} $

(6)

其中, $ \delta (t) $ 为振动位移, ${\lambda _n}$ 是尺度 $ n $ 的空间波长, 在1/4倍频程复可控金字塔中, $ {n_p} \approx 3 $ , 因此尺度 $ n $ 的放大因子 $ {\alpha _n} $ 边界为:

$ {\alpha _n} < \frac{{3{\lambda _n}}}{{4\delta (t)}} $

(7)

从式(7)可知, 对一特定视频, $ \delta (t) $ 为定值, 当前尺度的放大因子的上限与空间波长 ${\lambda _n}$ 有关, ${\lambda _n}$ 由式(8)可得:

$ {\lambda _n} = \frac{{{\lambda _N}}}{{{s^{N - n}}}} $

(8)

其中, ${\lambda _N}$ 为金字塔最大尺度的空间波长, $ s $ 是金字塔的尺度因子.

由此可知初始设定的放大因子不一定适用于所有尺度, 当较小空间波长的子带使用相同的放大因子放大时, 可能会超过其空间支持, 从而导致输出视频产生伪影及模糊. 因此需要调整较小空间波长的放大因子.

针对这一点, Xue等人^[6]通过人工设定截止波长 ${\lambda _c}$ , 将金字塔的尺度分为两组, 较大空间波长的放大因子不变, 而较小空间波长的放大因子按照式(9)的方式进行相应缩小.

$ {\alpha _n} = \left\{ {\begin{array}{*{20}{l}} {\alpha, \; {\lambda _n} \geqslant {\lambda _c}} \\ {\alpha \cdot \dfrac{{{\lambda _n}}}{{{\lambda _c}}}{\text{ }}, \;{\lambda _n} < {\lambda _c}} \end{array}} \right. $

(9)

人工设定 ${\lambda _c}$ 所产生的分组是固定的, 不同的初始放大因子, 可能会导致某些尺度无谓的缩小或者某些尺度本该缩小的放大因子却没有缩小, 以致最终放大视频的总体放大倍数不能满足需求或画面质量没有得到较好的提升.

Xue等人^[6]只考虑到了视频的空间特性, 而视频放大针对的是视频中目标的微小运动, 在多尺度滤波时应当考虑到目标的运动特性. 本文算法提出了一种新的多尺度滤波方法, 结合视频的空间特性和目标的小运动位移实现对各尺度放大因子的自适应调整. 由式(7)可得, 各尺度的放大因子 $ {\alpha _n} $ 的最大值为 $ {\alpha _n}_{\max } = \dfrac{{3{\lambda _n}}}{{4\delta (t)}} $ , 可建立起放大因子与视频的空间波长 ${\lambda _n}$ 和目标的微小位移 $ \delta (t) $ 之间的联系, 通过 ${\lambda _n}$ 和 $ \delta (t) $ 计算出 $ {\alpha _{n\max }} $ , 结合初始放大因子 $ \alpha $ , 能够更为合适地调整 $ {\alpha _n} $ , 可避免Xue等人^[6]人工设定 ${\lambda _c}$ 所产生的问题. 当 $ \alpha $ 小于当前尺度的上限 $ {\alpha _{n\max }} $ 时无须调整, 当 $ \alpha $ 大于 $ {\alpha _{n\max }} $ 时则缩小为 $ {\alpha _{n\max }} $ , 如式(10).

$ {\alpha _n} = {\alpha ^{u({\alpha _{n\max }} - \alpha )}}{\alpha _{n\max }}^{u(\alpha - {\alpha _{n\max }})} $

(10)

其中, $ {\alpha _n}_{\max } = \dfrac{{3{\lambda _n}}}{{4\delta (t)}} $ , $ u( \cdot ) $ 为阶跃函数.

关于小运动位移 $ \delta (t) $ , Peng等人^[15]通过推导图像强度 $ I(x, y, t) $ 转换为频域信号 $ F(x, y, t) $ 的过程, 得到运动位移 $ \delta (t) $ 与相位差 $\Delta \phi$ 的关系, 无须计算相位梯度而直接将相位变化转化为位移.

$ F(x, y, t) = I(x, y, t) \otimes g(x, y;\lambda , \psi , \sigma , \gamma ) $

(11)

其中, $ g(x, y;\lambda , \psi , \sigma , \gamma ) $ 为Gabor函数, 是一个高斯包络的正弦窗函数, 正弦函数是调谐函数, 高斯包络函数是窗函数, $ \lambda $ 为正弦的波长, $ \psi $ 是调谐函数的相位偏移量, $ \gamma $ 是空间长宽比, $ \sigma $ 表示高斯函数的标准差.

以水平方向的位移为例, 式(11)可以通过积分计算, 得到:

$ \phi (F(x, y, {t_0})) = - 2\pi \frac{x}{\lambda } + \phi ' $

(12)

$ \phi (F(x, y, {t_0} + \Delta t)) = - 2\pi \frac{{x + \Delta x}}{\lambda } + \phi ' $

(13)

由上述两公式可得相位差 $ \Delta \phi $ :

$ \Delta \phi = \frac{{2\pi \Delta x}}{\lambda } $

(14)

因此小运动位移 $ \delta (t) $ 可由式(15)获得:

$ \Delta \phi = \frac{{2\pi \delta (t)}}{\lambda } $

(15)

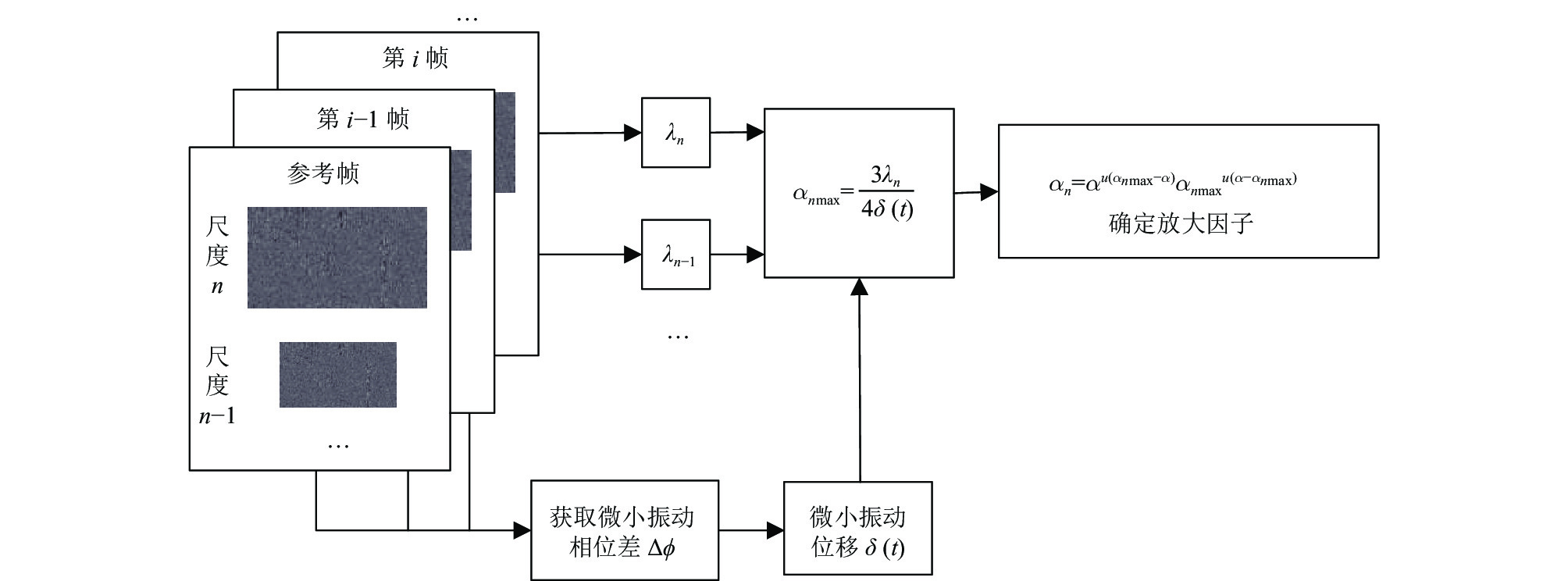
如图2所示, 各尺度的放大因子便可确定.

2.4 视频放大

利用相位展开技术对各尺度的振动信号进行相位校正后得到信号 $ {\phi _n}'(x, y, t) $ , 分别乘以自适应调整后的放大因子 $ {\alpha _n} $ , 得到放大后的相位信号 $ {\phi _{mag}}_n $ , 如式(16).

$ {\phi _{mag}}_n(x, y, t) = {\phi _n}(x, y, t) + {\alpha _n}{\phi _n}'(x, y, t) $

(16)

结合输入视频的高通残差与低通残差, 进行金字塔重构, 并输出放大视频.

3 实验结果及分析

对于大小运动混叠的场景, 分别采用模拟小球视频和真实目标视频进行实验来验证本算法的性能. 实验计算机为i7-6700处理器, 12 GB内存, 在Matlab 2019a开发实现, 真实目标视频均来自加速度放大算法^[7]中的公开数据. 采用八方向的1/4倍频程带宽复可控金字塔, 与文献[7]的加速度放大算法(EVAM)、文献[6]提出的多尺度自适应算法的原始代码输出的结果进行对比.

与文献[6]的做法保持一致, 由于需要缩小金字塔部分尺度的放大因子以适应其相移极限, 导致整体放大效果随之减小, 因此, 实验将适当提高预设放大倍数以达到相近的放大效果. 实验参数如表1所示.

3.1 实验结果

(1)模拟小球视频

本文模拟了一个包含大运动的合成小球视频. 小球从画面左侧向右以1像素每帧的速度进行水平方向的大运动, 同时在其竖直方向有一定频率的微小振动, 速度满足 $ {v_i} = A\sin \left( {2\pi i\dfrac{f}{{{f_r}}}} \right) $ , 其中 $ A = 1 $ 像素, $ f = 4 $ 周期/帧, $ {f_r} = 30 $ 帧/秒. 视频长度共200帧. 并令 $ A = 4 $ 像素模拟其真实放大视频GroundTruth.

如图3所示, 相比文献[6]的算法, 本文算法的放大结果更接近GroundTruth.

(2)真实目标视频

本节实验所用的4个视频均来自加速度放大^[7], 拍摄的相机处于稳定状态, 视频中的目标存在振动的同时还存在大运动, 均在图中黄线位置取时空切片图. 视频1如图4所示, 该视频中有一个玩具在向前行进, 同时存在竖直方向的振动. 图5是一个飞行状态的无人机, 水平行进的同时存在竖直方向的振动. 图6所显示的是人走近相机的同时手部在微微震颤的场景. 图7则是人转身时的手部震颤场景.

实验放大结果图表明, 3种算法都能够对目标的微小运动而非大运动进行放大. 图中红色方框部分能够看出, 文献[7]的算法所生成的放大视频的画面最为模糊, 目标的轮廓不甚清晰, 文献[6]提出的算法与本文算法所生成的放大视频的画面则更为清晰, 证明本文算法达到了提升放大视频画面质量的效果.

3.2 图像质量评价

本文选择5种通用的图像质量评价标准^[16]对视频放大结果进行比较, 包括SpEED^[17], SSIM^[18], VIF^[19], IFC^[20]以及PSNR^[21]. 对各放大视频的所有帧求上述5种评价指标的平均值, 其中SpEED的值越小表示图像质量越高, 其余指标则是值越大表示图像质量越高.

表2记录了对各真实目标视频放大结果的评价, 本文算法的结果均优于文献[7], 其中仅无人机视频的实验结果不及文献[6], 原因在第3.3节进行了说明. 其余视频的画面质量均优于文献[6], 从式(9)中可知, 文献[6]以当前尺度的空间波长与截止波长的比值作为缩小的比例调整放大因子, 因此 $ {\lambda _c} $ 的取值会影响 $ {\alpha _n} $ 的大小, 由于人工设定 $ {\lambda _c} $ 不能达到足够的精确度, 缩小后的结果不一定能够满足相移极限的要求, 也就不能较好地提升画面质量.

3.3 各尺度放大因子对比

以视频2为例, 金字塔共21层, 比较文献[6]与本文实验结果的第11到17层的放大因子. 如表3所示, 在初始放大因子 $ \alpha $ 不同时, 本文算法能够根据 $ \alpha $ 更加合理地自适应调整各尺度的放大因子, 而文献[6]的算法则是通过人工设定截止波长, 将金字塔的尺度划分为两组, 15层及以下的放大因子被缩小, 16层及以上的放大因子保持为 $ \alpha $ .

对放大视频进行图像质量评价, 结果如表4所示, 当 $ \alpha {\text{ = 8}} $ 时, 本文的画面质量虽不及文献[6], 但文献[6]将原本无须缩小的放大因子缩小, 大大降低了总体的放大效果, 无法满足观测要求, 便需要提高初始放大因子. 而当 $ \alpha $ 提升到16时, 本文算法的总体放大倍数与文献[6]很相近, 保证了各尺度的放大因子不超过其上限, 因此画面质量优于文献[6]. 由此可知, 文献[6]的算法并不能做到合理的调整 $ {\alpha _n} $ , 显然, 本文算法更具有优势.

4 结论

本文提出了一个基于多尺度滤波的视频放大算法, 通过建立图像空间波长与视频微小运动位移间的关系, 对复可控金字塔各尺度的放大因子实现完全自适应调整, 以保证各尺度的放大信号都保持在相移极限内, 以减轻放大视频的伪影及模糊. 经实验验证, 本文算法与对比算法相比, 无须人工设定参数, 并能够有效提高放大视频的画面质量, 在总体放大效果和画面质量的平衡上有明显的优势.