1 引言

超分辨率重建(super-resolution, SR)技术旨在通过特定的约束函数把低分辨率图像重建为高分辨率图像. 由于图像生成容易受到设备, 天气, 光照和环境等因素的干扰只能获得低分辨率图像, 然而高分辨率图像往往含有更丰富的信息, 具有极大价值. 提高图像分辨率的最直接手段就是改善成像设备, 但是这种方式会加重个人和中小企业的成本负担. 而图像超分辨率重建技术是通过编程算法对低分辨率图像进行处理得到高分辨率图像, 这种方法成本极低, 因此图像超分辨率技术被广泛应用于智能监控、国防军事、医学图像和遥感卫星等领域中.

图像超分辨率重建技术方法大致可以分为3类: 基于插值^[1], 基于重建^[2]和基于学习^[3]. 基于插值的方法通过子像素和周围像素的空间位置关系利用数学公式推导插入新像素点, 基于插值的方法有最近邻插值, 双线性插值和双三次插值(bicubic), 这种插值方法实现简单快捷. 基于重建的方法是对图像的整体信息通过数学方式进行结合然后重建出高分辨率图像, 常用的方法有迭代反投影法(IBP)^[4], 凸集投影法(POCS)^[5]和最大后验概率估计法(MAP)^[6]. 基于学习^[7-9]的图像超分辨率重建方法通过学习低分辨率图像和高分辨率图像之间的映射关系, 得到大量先验知识来指导图像重建. 上述都属于基于传统方法, 算法简单, 处理速度快, 但是存在着边缘纹理模糊, 图像效果不好的问题.

近年来, 通过结合卷积神经网络, 学习低分辨率图像和高分辨率图像之间的复杂关系, 达到了更好的重建效果. Dong等人^[10]提出了深度卷积网络的图像超分辨率(super-resolution convolutional neural network, SRCNN)重建模型, 结合卷积神经网络通过端到端的训练方式, 大大提高了重建图像质量, 但是由于SRCNN在网络模型中使用双三次插值的方法实现对图像的放大操作, 会破坏图像原有的细节信息, 导致重建效果还不够理想. 因此在SRCNN的基础上, Dong等人^[11]提出了加速图像超分辨率重建的卷积神经网络(fast super-resolution convolutional neural networks, FSRCNN)模型, 在网络层最后引入反卷积层代替双三次插值对输入图像进行尺寸放大, 并且使用更小的卷积核和更多的卷积层达到加快模型速度的目的. Shi等人^[12]提出了一种基于亚像素卷积网络的ESPCN, 将亚像素卷积引入到图像上采样工作中, 提高了图像重建效果.

本文针对FSRCNN模型中存在的图像特征信息提取不充分和反卷积上采样带来的人工冗余信息问题, 提出了一种多尺度融合卷积神经网络, 首先在浅层特征提取阶段设计了一种多尺度融合通道, 增强对图像中的高频有用信息特征的提取能力; 其次在图像重建部分使用亚像素卷积代替反卷积层进行上采样, 避免反卷积层的人工冗余信息引入. 实验结果表明, 与FSR-CNN模型相比, 在Set5和Set14数据集中, 2倍放大因子下的PSNR值和SSIM值平均提高了0.14 dB、0.001 0, 在3倍放大因子下平均提高0.48 dB、0.009 1.

2 相关工作 2.1 FSRCNN模型

图1为FSRCNN的网络结构, 其中, ${\rm Conv} \left(x, y, {\textit{z}}\right)$ 中, x代表卷积核大小, y代表卷积层输出通道, z代表卷积层输入通道. 分为5层: 第1层对低分辨率图像进行特征提取, 卷积核大小是5, 输入通道为1, 输出通道是56. 第2层是缩减层, 减少模型的参数量, 提高算法速度. 第3层是学习映射层, 对图像信息进行非线性学习. 第4层是扩大层, 增加图像特征图数量. 第5层是反卷积层, 对图像上采样得到重建图像.

2.2 子像素卷积

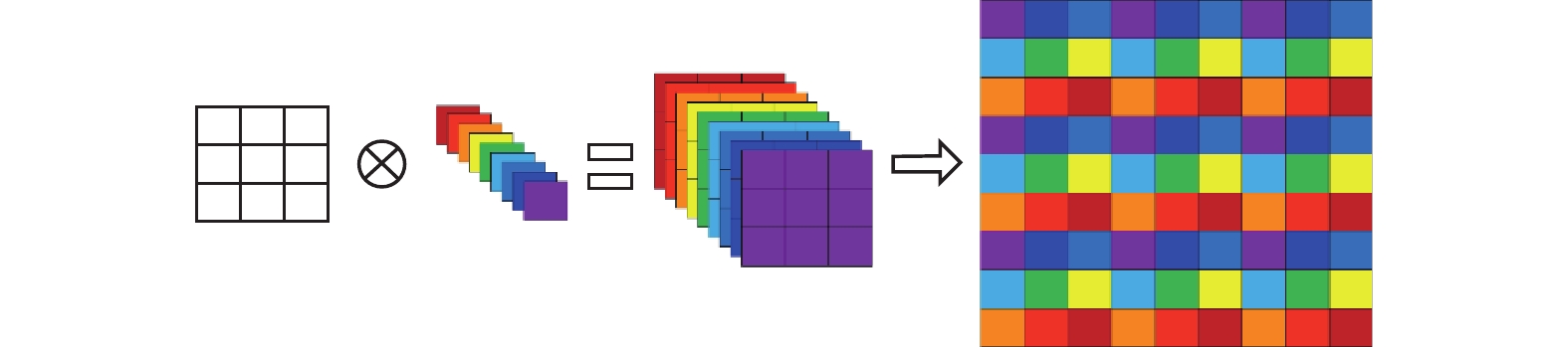
子像素卷积又称像素重排序(pixel shuffle), 像素重排是将不同通道的特征图排序到同一个通道上, 以此达到对图像的像素增多的目的. 如图2为子像素卷积对图像重建过程, 假设低分辨率图像大小为3×3大小, 若想得到一个9×9大小的图像, 即需要对原本的图像放大3倍, 首先使用1×1大小的卷积核对原低分辨率图像进行卷积操作, 生成 $ {3}^{2} $ =9个3×3大小的特征图, 然后将这9个相同尺寸特征图进行像素的重新排列, 拼成一个放大3倍的高分辨率图像.

3 基于多尺度融合卷积神经网络的图像超分辨率重建算法 3.1 网络结构

如图3所示为本文网络结构, 分为5层: 第1层为本文算法设计的一种多尺度特征融合提取通道, 引用不同大小尺寸的卷积核对低像素图像进行特征提取, 提高对图像中不同尺度的高频有用信息的提取能力. 第5层为子像素卷积重建层, 引入了子像素卷积的方法对图像进行重建, 抑制反卷积层带来的人工信息冗余问题, 提高图像的重建质量.

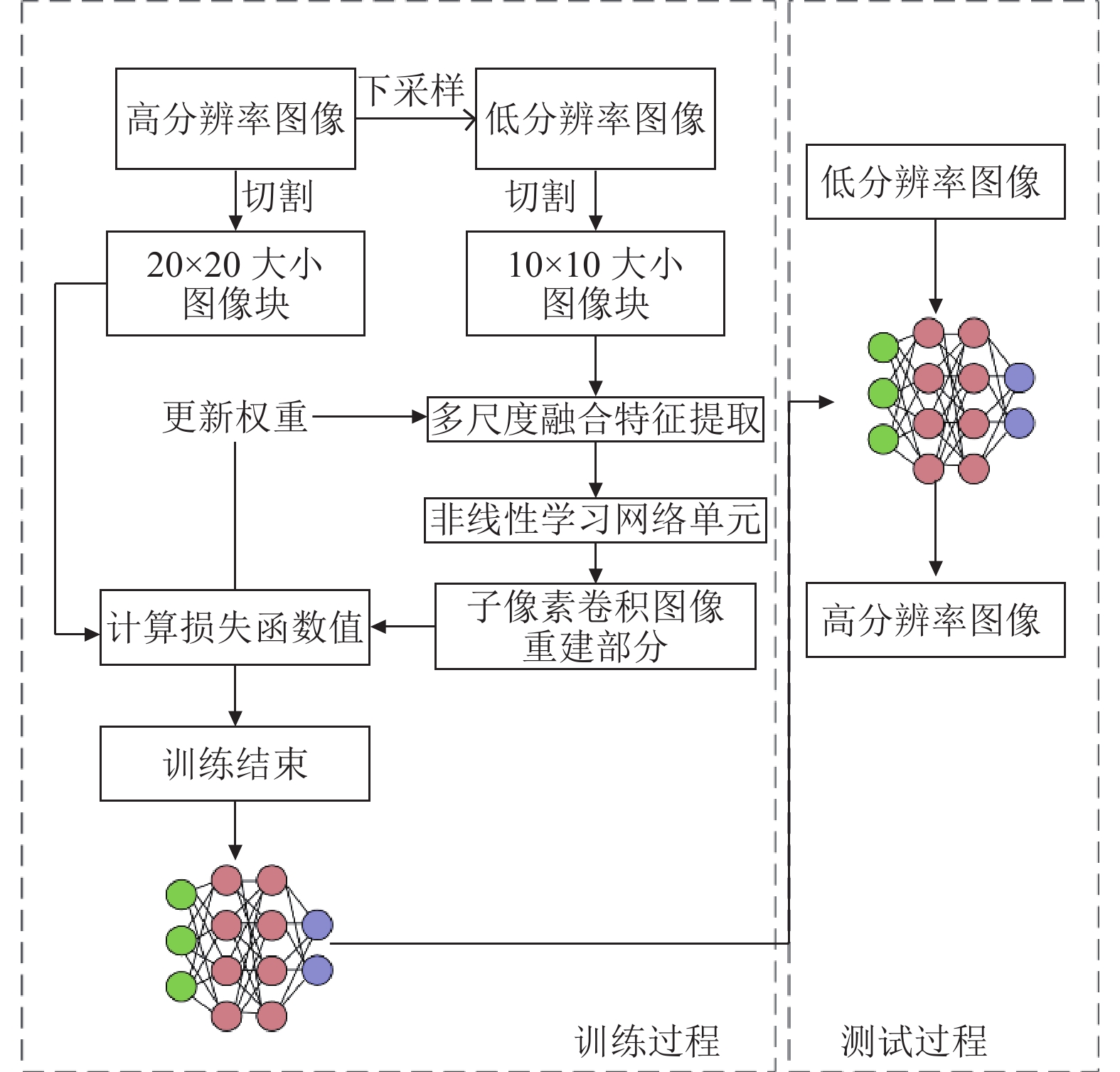
为实现图像超分辨率重建, 需要对算法卷积神经网络模型进行训练. 如图4所示, 训练过程首先将高分辨率图像下采样得到低分辨率图像, 将高分辨率图像和低分辨率图像分别切割, 获得若干成对对应训练样本, 将高分辨率图像和低分辨率图像成对输入卷积神经网络中进行训练, 通过损失函数指导卷积神经网络更新权重, 经过多轮迭代, 最终得到图像超分辨率重建模型. 在测试阶段, 将低分辨率图像送入训练完成的模型, 即可重建出高分辨率图像.

综上, 本文在FSRCNN模型的基础上设计了一种了多分支融合特征提取通道, 提高算法对图像有用信息的提取能力; 在图像重建部分, 使用子像素卷积代替反卷积, 实现对图像的重建, 抑制人工冗余信息的引入.

3.2 多尺度特征融合提取通道

在FSRCNN模型使用了一层56个5×5大小卷积核的卷积层进行特征提取工作, 本文设计了一种多尺度融合特征提取通道, 结合跳跃连接和特征融合操作, 使用3个不同大小的卷积核分别对输入图像进行特征提取. 针对图像的易模糊边缘轮廓和细节特征的提取难度问题, 如图5所示为多尺度特征提取通道的结构图. 第一个通道为56个1×1大小的卷积核, 获得图像的细节特征, 具体实现公式为:

$ \begin{array}{c}{F}_{11}\left(Y\right)={W}_{11}\times{I}_{LR}+{B}_{11} \end{array} $

(1)

其中, $ {F}_{11}\left(Y\right) $ 表示第一通道卷积层输出的特征图, $ {W}_{11} $ 表示第一通道卷积层的权重, $ {B}_{11} $ 表示偏置项.

第2通道和第3通道分别为28个3×3和5×5大小卷积核进行特征提取并拼接到一起, 第2通道的具体实现公式为:

$ \begin{array}{c}{F}_{12}\left(Y\right)={W}_{12}\times{I}_{LR}+{B}_{12}\end{array} $

(2)

其中, $ {F}_{12}\left(Y\right) $ 表示第2通道卷积层输出的特征图, $ {W}_{12} $ 表示第2通道卷积层的权重, $ {B}_{12} $ 表示偏置项. 第3通道的具体实现公式为:

$ \begin{array}{c}{F}_{13}\left(Y\right)={W}_{13}\times{I}_{LR}+{B}_{13}\end{array} $

(3)

其中, $ {F}_{13}\left(Y\right) $ 表示第3通道卷积层输出的特征图, $ {W}_{13} $ 表示第3通道卷积层的权重, $ {B}_{13} $ 表示偏置项.

由于第2通道和第3通道分别采用了3×3和5×5的卷积核进行特征提取, 不同尺寸的卷积核可以获得不同尺度的特征信息, 通过Contact操作将不同的特征信息进行拼接, 具体实现公式为:

$ \begin{array}{c}{F}_{23}\left(Y\right)={F}_{12}\left(Y\right)+{F}_{13}\left(Y\right)\end{array} $

(4)

之后将不同尺度的特征信息通过长跳跃连接(LSC)操作进行特征融合从而保证图像信息的流通性和完整性. 具体实现公式为:

$ \begin{array}{c}{{F}_{1}\left(Y\right)=W}_{14}\left({F}_{12}\left(Y\right)+{F}_{13}\left(Y\right)\right)+{B}_{1}\end{array} $

(5)

其中, $ {F}_{1}\left(Y\right) $ 表示特征融合后得到的特征图, $ {W}_{14} $ 表示特征融合层的权重, $ {B}_{1} $ 表示该层的偏置项. 相比FSR-CNN模型^[11]仅有一个5×5大小的卷积核作为特征提取通道, 多尺度特征融合特征提取通道对图像的不同尺度的信息提取更充分, 加强了算法网络模型的特征提取能力.

3.3 子像素卷积上采样

在算法的图像重建部分, 反卷积操作实现了对图像的放大, 在重建过程中使用反卷积填充图像内容, 使得图像内容变得丰富, 然而反卷积存在过多人工冗余信息引入的问题, 为了解决这个问题, 我们在图像重建部分引用子像素卷积替代反卷积实现对图像的上采样过程.

如图6所示, 首先使用1×1的卷积对扩大图像输入通道, 然后通过像素重排扩大图像的分辨率. 若子像素卷积重建之前有 $ r\times r $ 个通道特征图, 则通过使用子像素卷积重建会将 $ r\times r $ 个特征图通过特定的排序规则重新生成一副 $ w\times r $ , $ h\times r $ 的图像.

3.4 损失函数和激活函数

本文算法采用MSE损失函数, 即均方损失函数. 经过超分辨率重建神经网络重建得到的图像 $ f\left({x}_{i}\right) $ 和真值图像 $ {y}_{i} $ , 通过对网络模型进行训练使损失函数的值减小从而指导低像素图像重建出更好效果的高分辨率图像. MSE损失函数如式(6)所示:

$ \begin{array}{c}{\textit{MSE}}=\frac{1}{m}\displaystyle\sum _{i=1}^{m}{\left({y}_{i}-f\left({x}_{i}\right)\right)}^{2}\end{array} $

(6)

使用的激活函数为PReLU^[13], 即带参数的ReLU函数, 避免ReLU函数中零梯度坏死特性, 并且还可以实现更高的准确率, PReLU激活函数表达式如式(7):

$ \begin{array}{c}\rho \left({Y}_{i}\right)=\left\{\begin{array}{l}{Y}_{i},\;  x > 0\\ {\lambda Y}_{i},\;  x\leqslant 0,\lambda \in \left[\mathrm{0, 1}\right]\end{array}\right.\end{array} $

(7)

其中, Y_i是第i通道的输出, λ为PReLU的参数, 且会随着训练次数的增加而不断更新.

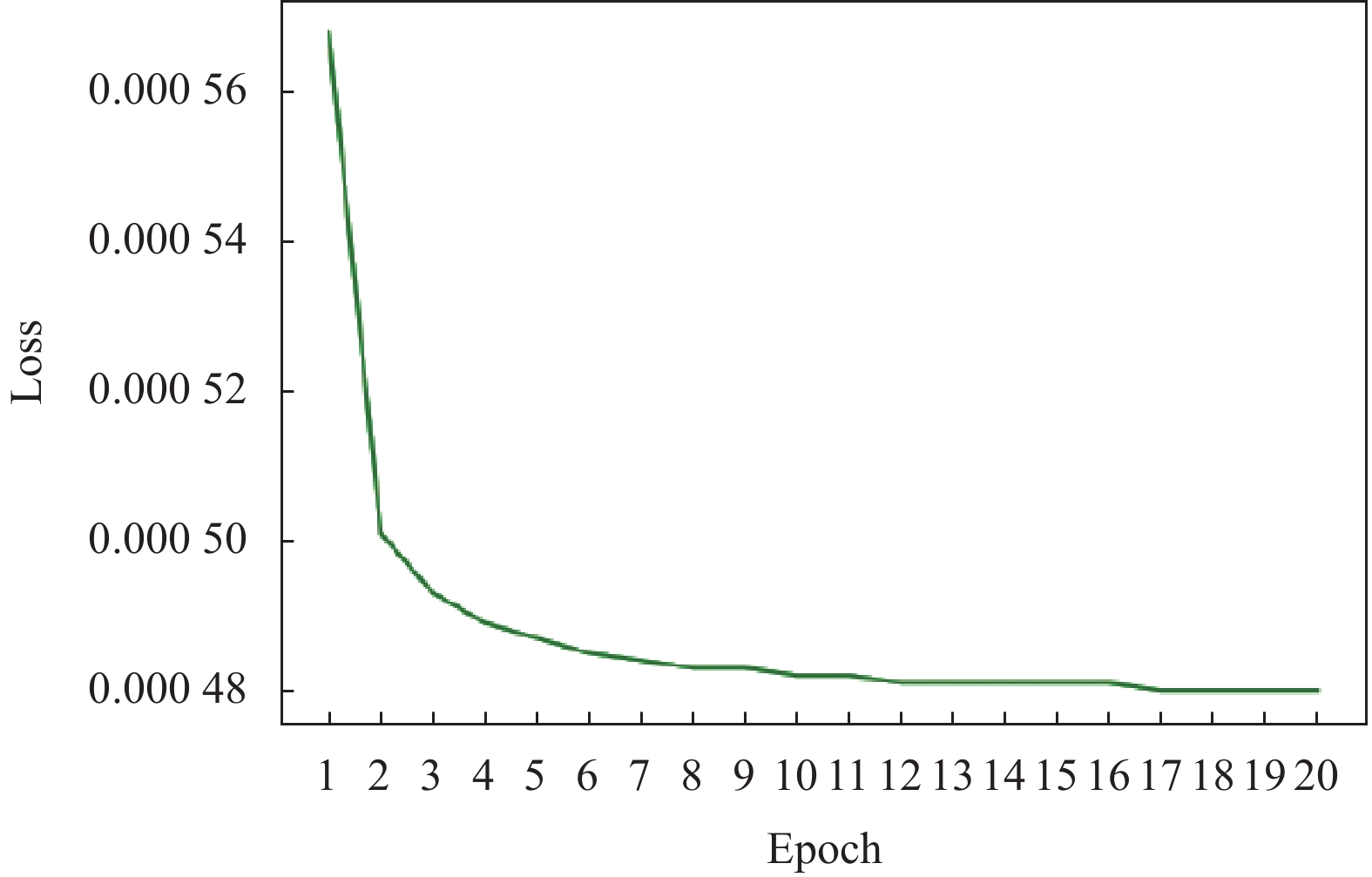
如图7, 图8所示为本文算法训练阶段的损失函数收敛曲线图. 放大因子为×2时, 在迭代到17时, 损失函数收敛. 当放大因子为×3时, 训练迭代到18代时, 损失函数收敛.

4 实验 4.1 实验数据以及设置

实验用91-image数据集对模型进行训练, 首先对输入的图片进行数据增强, 将图像旋转90°、180°、270°, 并缩小0.9、0.8、0.7、0.6倍, 实现对数据集扩充的目的.

测试集: 选用Set5^[14]和Set14^[15]公开数据集作为测试集进行效果度量.

本文算法采用Adam (Adam optimization algorithm)来优化损失函数, 学习率设置为0.000 1, 训练的批处理大小为16, 训练迭代次数设置为20次. 深度学习框架为PyTorch 1.2, 实验的操作系统是Ubuntu 16.04, 服务器是内存8 GB的Tesla P4.

4.2 评价指标

本文采用峰值信噪比(PSNR)^[16]和结构相似度(SSIM)^[17]作为重建效果的评价指标, PSNR值越大证明重建图像比真值图像失真越少. PSNR的公式如式(9):

$ \begin{array}{c}{\textit{MSE}}=\dfrac{1}{{H}{W}}\displaystyle\sum _{{i}=1}^{{H}}\displaystyle\sum _{{j}=1}^{{W}}{\left[{X}\left({i}, {j}\right)-{Y}\left({i}, {j}\right)\right]}^{2}\end{array} $

(8)

$ \begin{array}{c}{\textit{PSNR}}=10{\log}_{10}\left(\dfrac{{\left({2}^{n}-1\right)}^{2}}{\textit{MSE}}\right)\end{array} $

(9)

其中, MSE表示均方误差, $ H $ 和 $ W $ 分别表示图像的长度和宽度, $ X\left(i, j\right) $ 表示真值图像, $ Y(i, j) $ 表示重建后的图像. 峰值信噪比的单位为dB, 值越大表示重建效果越好.

SSIM也常用来评价图像重建效果, SSIM用来评价重建图像与真值图像的结构相似性, 值越大代表相似性越高, 重建效果越好. SSIM的计算公式为:

$ \begin{array}{c}{\textit{SSIM}}\left(H, L\right)=\dfrac{\left(2{\mu }_{H}{\mu }_{L}+{c}_{1}\right)\left(2{\sigma }_{HL}+{c}_{2}\right)}{\left({\mu }_{H}^{2}+{\mu }_{L}^{2}+{c}_{1}\right)\left({\sigma }_{H}^{2}+{\sigma }_{L}^{2}+{c}_{2}\right)}\end{array} $

(10)

其中, $ \;{\mu }_{H} $ 、 $ {\mu }_{L} $ 分别表示图像 $ H $ 和 $ L $ 的均值, $ {\sigma }_{H} $ 、 $ {\sigma }_{L} $ 分别表示图像 $ H $ 和 $ L $ 的标准差, $ {\sigma }_{H}^{2} $ 、 $ {\sigma }_{L}^{2} $ 分别表示图像 $ H $ 和 $ L $ 的方差, $ {\sigma }_{HL} $ 表示图像 $ H $ 和 $ L $ 协方差. $ {c}_{1} $ , $ {c}_{2} $ 和 $ {c}_{3} $ 为常数.

4.3 与其它方法比较

本文在Set5和Set14数据集上, 对比了Bicubic、SRCNN^[10]、FSRCNN^[11]. 由表1和表2可以看出, 从客观评价标准出发, 对比不同算法, 本文算法的重建质量优于其他几种算法. 相较于FSRCNN算法, 在Set5测试集上, 当放大因子为×2和×3时, PSNR值分别提高了0.15 dB和0.57 dB. 在Set14测试集上分别提高了0.13 dB、0.39 dB. 在Set5测试集上, 当放大因子为×2和×3时, SSIM值分别提高了0.001 9和0.010 8. 在Set14测试集上,SSIM值分别提高了0.000 2和0.007 5.

如图9和图10所示, 图像通过不同的超分辨率重建算法获得了不同的效果图, 可以看到, 相较于传统的Bicubic算法, SRCNN对图像重建质量提升了很多, FSRCNN改善了图像的纹理细节并且避免了噪声对图像细节的影响, 而本文所提出的算法较之原来的方法保留更多的图像细节特征, 这主要是得益于多尺度特征融合通道对特征提取能力的提高和子像素卷积对人工冗余信息的抑制作用.

5 结语

本文提出了一种基于多尺度卷积神经网络的图像超分辨率重建算法, 在算法的特征提取阶段, 设计了多通道多尺度特征提取方法, 分别使用1×1、3×3和5×5大小的卷积核, 对图像的不同特征运用不同尺寸的卷积操作, 并结合跳跃链接和特征融合操作, 提高对图像特征信息的感知能力. 在图像重建阶段, 使用子像素卷积避免反卷积层引用过多的人工冗余信息, 提高重建图像的质量. 下一步将研究在网络结构中结合图像的全局信息和局部信息, 在训练阶段充分利用高分辨率图像中的高频有用信息指导图像重建过程, 从而提高重建图像的质量.