受各种记录设备所固有的物理限制, 大多数真实世界中获取到的图像都包含了一定程度的噪声和失真[1], 下面的模型可以描述期望图像退化至观测图像的过程:
| $ y = A{\textit{z}} + e $ | (1) |
其中,
一类常见的去噪算法基于某些特定变换域, 例如傅里叶变换、快速傅里叶变换、离散余弦变换、小波变换, 这类算法主要利用稀疏性, 使用较少的非零系数来表示信号. 确定变换域后还需要确定阈值, 阈值函数一般有硬阈值和软阈值两种选择[2]. 硬阈值方法将小波系数全部切除, 其余的全部保留, 软阈值方法为了避免频域中的阶跃, 将保留的系数都减去了阈值.
另一类方法基于空域, 直接在原图像上进行处理, 这类方法还可分为局部和非局部两种. 常见的局部方法包括高斯滤波器、最小均方滤波器、双边滤波器、维纳滤波器, 局部算法的基本思想是利用像素之间的相关性, 而像素的相关性会由于噪声水平变高而严重受损, 因此局部方法在高噪声条件下表现不佳. 非局部方法中最常用的是非局部均值滤波(NLM), 它利用了图像的非局部相似性, 是一种典型的逐点去噪算法[3].
图信号处理的方法为图像去噪提供了一种新思路. 非局部图变换算法通过图信号处理在图像块中构造出数据自适应的变换域用于去噪, 并在深度图像去噪问题中表现优秀[4]. Meyer等人利用图拉普拉斯矩阵的低维特征向量进行去噪[5]. Yan等人提出了GNNLG, 在非局部方法的基础上, 结合图拉普拉斯先验项进行去噪[6].
目前基于图信号的去噪的研究中, 主要方法都是通过图像块匹配后, 使用图信号的方法对每一个图像块分别进行去噪, 关于图像块的去噪比较类似于传统方法中基于变换域的方法, 本质上是利用图傅里叶变换得到一个新的变换域. 而本文所提出的算法虽然同样基于图信号处理, 但更类似于基于空域方法, 直接针对图像本身设计滤波器得到去噪图像.
在本文的方法中, 首先选择适当的相似性度量, 计算出图像对应的权重矩阵以及拉普拉斯矩阵, 根据所得矩阵的滤波效果, 提出了一个基于图信号的目标函数, 这个目标函数使用权重矩阵来拟合数据保真度项, 并同时加入拉普拉斯先验项以确保恢复信号的平滑性. 我们随后说明了所提出的目标函数的合理性, 并最终使用迭代的方式对优化问题进行快速求解.
本文的其余安排如下: 首先在第2节中介绍准备工作, 然后在第3节中提出并详细描述了我们的算法, 并分别在第4节和第5节中介绍实验和结论.
2 准备工作 2.1 图信号处理的相关概念根据图信号处理的相关理论, 可以将图像建模为无向加权图
| $ {r_i} = \left[ {{x_{i, 1}}, {x_{i, 2}}, {y_i}} \right] $ | (2) |
其中,
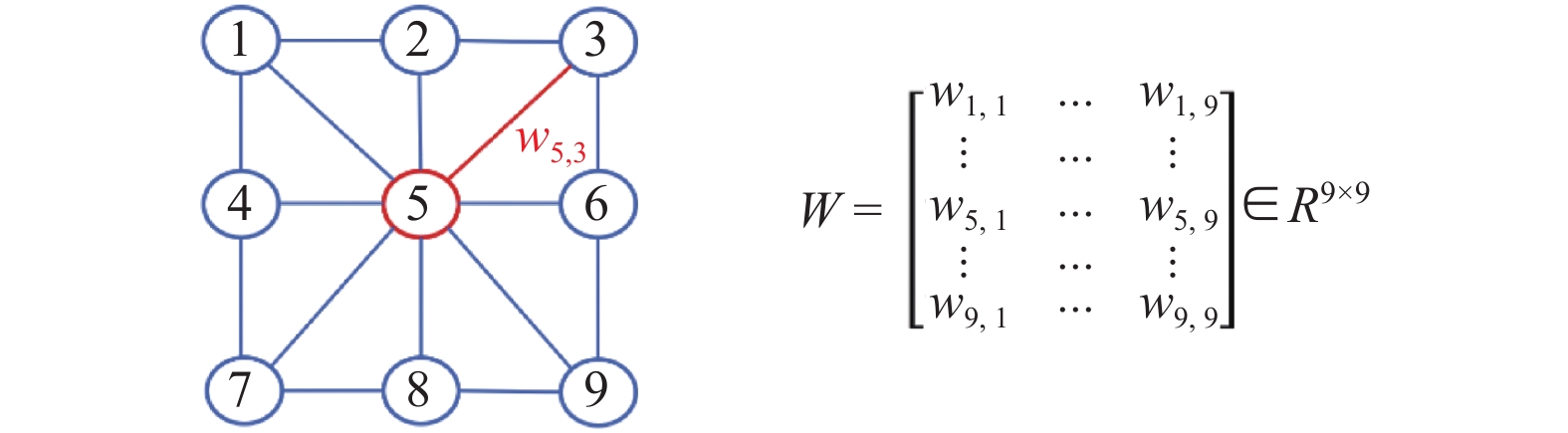
|
图 1 图像的图结构与其对应的权重矩阵 |
确定图权重的一种常用方法是使用距离的指数衰减函数, 即:
| $ {w_{i, j}} = \exp \left( { - dist\left( {{r_i}, {r_j}} \right)/{h^2}} \right) $ | (3) |
其中,
关于常用的距离度量在表1中给出, 所列举距离度量的直观图形解释如图2所示. 由于经典回归滤波器对感兴趣信号的底层结构缺乏更强的适应性, 双边滤波器在低信噪比情况下无法提供有效性能, 因此在后文中均选择非局部均值滤波器作为权重矩阵中的距离度量
| 表 1 常用的距离度量 |
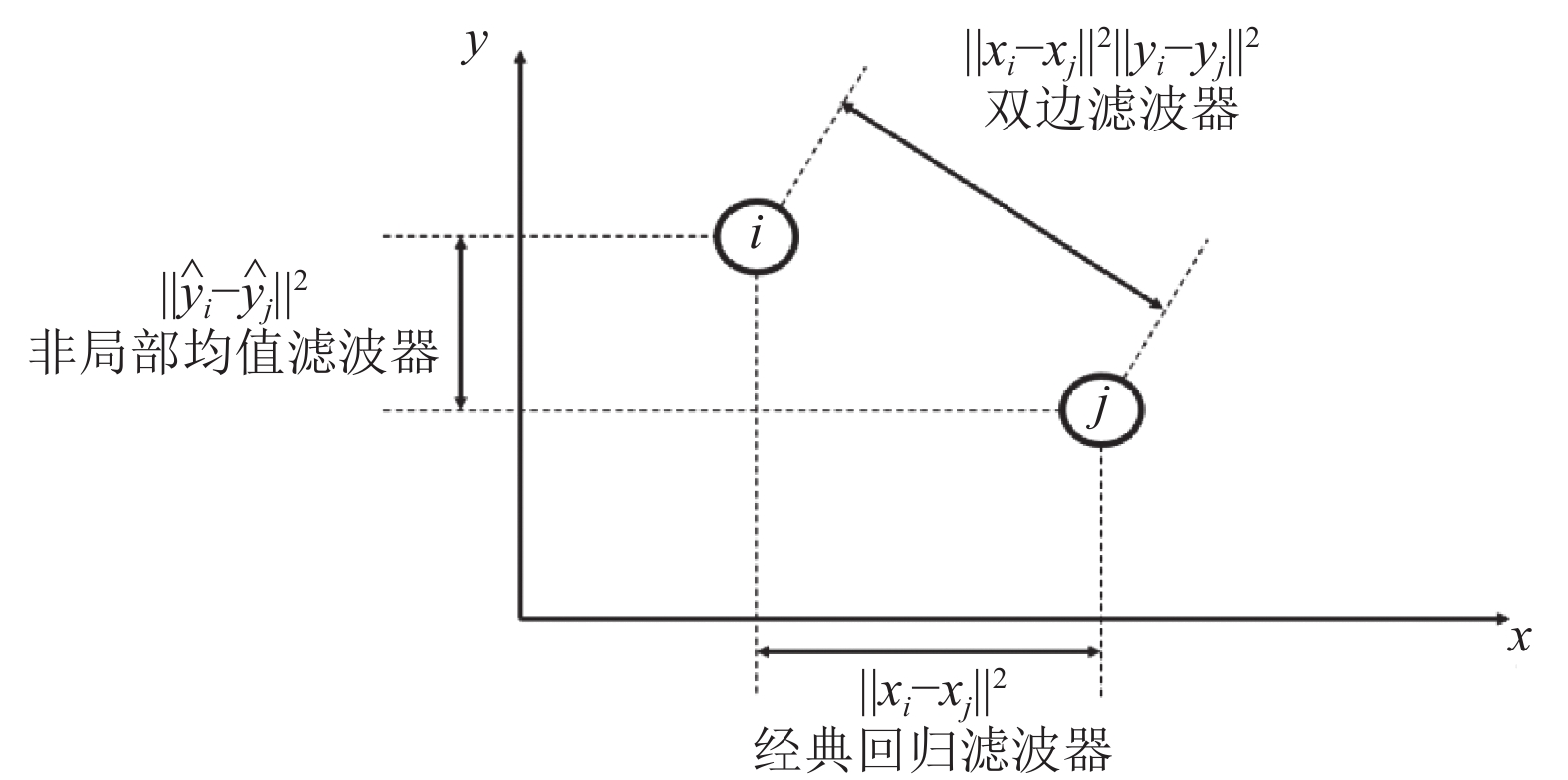
|
图 2 常用距离度量的图形解释 |
3 基于图滤波的图像去噪算法 3.1 图信号的谱分析
图信号处理中的一个重要算子是图拉普拉斯算子
对拉普拉斯矩阵进行特征分解, 有
接下来说明, 对于图信号
由
| $ {u_k}^{\rm{T}}{\lambda _k}{u_k} = {\lambda _k}, k = 1, 2, \cdots, N $ | (4) |
由于拉普拉斯矩阵
换一个角度, 如果将
同理, 由于
本文提出下面的优化问题:
| $ \hat {\textit{z}} = \arg \mathop {\min }\limits_{\textit{z}} {\left( {y - {\textit{z}}} \right)^{\rm{T}}}W\left( {y - {\textit{z}}} \right) + \eta {{\textit{z}}^{\rm{T}}}L{\textit{z}} $ | (5) |
其中, 第一项为数据保真度项, 用来衡量观测输入
对于目标函数
首先计算
| $ \nabla E\left( {\textit{z}} \right) = - W\left( {y - {\textit{z}}} \right) + \eta L{\textit{z}} $ | (6) |
令
| $ \hat {\textit{z}} = {\left( {W + \eta L} \right)^{ - 1}}Wy $ | (7) |
考虑到权重矩阵
由式(6), 迭代更新表达式为:
| $ \begin{split} {{\textit{z}}_k} &= {{\textit{z}}_{k - 1}} - {\mu _k}\nabla E\left( {{{\textit{z}}_{k - 1}}} \right) \\ & = {{\textit{z}}_{k - 1}} + {\mu _k}\left[ {W\left( {y - {{\textit{z}}_{k - 1}}} \right) - \eta L{{\textit{z}}_{k - 1}}} \right] \\ \end{split} $ | (8) |
其中,
如果每一轮都要求出最优的
总结归纳后得到算法1.
算法1. 基于图结构滤波的图像去噪算法
1) 非局部均值核计算输入图像
2) 根据权重矩阵
3) 循环执行下列迭代直到收敛:
4) 得到输出图像近似等于
算法1中, 步长
为了验证本文所提出的方法的性能, 使用图3中的6张灰度图像作为测试图像, 如果要推广至彩色图像去噪, 将算法分别应用于各个通道即可. 在这些图像上添加加性高斯白噪声, 均值为0, 噪声方差从0.2到400, 从而得到噪声图像. 对照算法分别选用NLM[3], BM3D[9], WNNM[10], 这3种算法都是去噪效果较好且比较常用的算法. NLM的基本思想是基于图像块构建图像的逐点估计. WNNM基于加权核范数进行去噪. BM3D基于图像块进行三维滤波. 所有实验都是基于Matlab, 运行在LENOVO 82DN环境下, 所使用的处理器是Intel Core i5-10210U.

|
图 3 用于评估算法性能的一组图像 |
其中,
对于图像恢复效果的衡量, 使用峰值信噪比(
| $ {\textit{PSNR}} = 10{\lg}\frac{{{{\left( {{2^n} - 1} \right)}^2}}}{\textit{MSE}} $ | (9) |
表2中给出了不同方法的
视觉上的主观比较如图4, 以Goldhill叠加方差为400的噪声为例. 使用本文的方法所生成的图像纹理更加清晰. 相比WNNM, 本文的方法没有造成过度模糊, 相比NLM, 本文的方法显然能更好地去除噪声, 相比BM3D, 本文的方法消除了其中的振铃效应. 因此, 使用本文的方法可以获得更好的细节, 极大抑制了噪声且避免了振铃, 同时纹理信息清晰可见.
| 表 2 基于图滤波去噪算法, NLM, BM3D, WNNM的PSNR性能 (dB) |

|
图 4 Goldhill图像的去噪示例 |
5 结论与展望
本文提出了一种基于图信号的图像去噪通用方法. 这个方法基于以下两点分析: (1)将基于NLM滤波计算得到的图结构用于描述图像的内在框架. (2) 基于图像计算的权重矩阵和拉普拉斯矩阵分别可以看作自适应低通和高通滤波器, 可用于表征图信号的特征. 我们创新性地提出了一种基于图信号的目标函数用于去噪, 对于所提出的目标函数, 给出了理论的最优解和迭代逼近算法. 实验表明, 本文所提出的方法在数值指标和视觉效果上都优于BM3D和WNNM等前沿去噪算法.
| [1] |
Lebrun M, Colom M, Buades A, et al. Secrets of image denoising cuisine. Acta Numerica, 2012, 21: 475-576, 2012. DOI:10.1017/S0962492912000062 |
| [2] |
Yağan AC, Özgen MT. A spectral graph wiener filter in graph fourier domain for improved image denoising. 2016 IEEE Global Conference on Signal and Information Processing. Washington: IEEE, 2016. 450–454.
|
| [3] |
Dong WS, Zhang L, Shi GM, et al. Nonlocally centralized sparse representation for image restoration. IEEE Transactions on Image Processing, 2013, 22(4): 1620-1630. DOI:10.1109/TIP.2012.2235847 |
| [4] |
Hu W, Li X, Cheung G, et al. Depth map denoising using graph-based transform and group sparsity. 2013 IEEE 15th International Workshop on Multimedia Signal Processing (MMSP). Pula: IEEE, 2013. 1–6.
|
| [5] |
Meyer FG, Shen XL. Perturbation of the eigenvectors of the graph Laplacian: Application to image denoising. Applied and Computational Harmonic Analysis, 2014, 36(2): 326-334. DOI:10.1016/j.acha.2013.06.004 |
| [6] |
Yan CG, Li ZS, Zhang YB, et al. Depth image denoising using nuclear norm and learning graph model. ACM Transactions on Multimedia Computing, Communications, and Applications, 2021, 16(4): 122. DOI:10.1145/3404374 |
| [7] |
Stanković L, Sejdić E. Vertex-frequency analysis of graph signals. Switzerland: Springer, 2019.
|
| [8] |
Cheung G, Magli E, Tanaka Y, et al. Graph spectral image processing. Proceedings of the IEEE, 2018, 106(5): 907-930. DOI:10.1109/JPROC.2018.2799702 |
| [9] |
Mäkinen Y, Azzari L, Foi A. Collaborative filtering of correlated noise: Exact transform-domain variance for improved shrinkage and patch matching. IEEE Transactions on Image Processing, 2020, 29: 8339-8354. DOI:10.1109/TIP.2020.3014721 |
| [10] |
Gu SH, Zhang L, Zuo WW, et al. Weighted nuclear norm minimization with application to image denoising. 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014. 2862–2869.
|
| [11] |
Bhola VK, Sharma T, Bhatnagar J. Image quality assessment techniques. International Journal of Advanced Research in Computer Science and Software Engineering, May, Special, 2014, 156-161. |
 2022, Vol. 31
2022, Vol. 31


