2. 闽南师范大学 物理与信息工程学院, 漳州 363000
2. School of Physics and Information Engineering, Minnan Normal University, Zhangzhou 363000, China
过去的30年, 房地产行业高速发展, 房屋室内设计需求也随之递增. 传统的室内设计是在房屋交付之后, 由设计师根据户型结构确定设计图开始的. 设计师事先了解用户需求, 在固定结构设计基础上进行平面图绘制, 最终将设计平面图方案提供给用户挑选. 在平面图设计过程中, 用户无法参与其中, 因此, 设计师无法根据用户的需求进行平面设计及时调整. 在精装修房屋交付中, 这种问题表现更加突出, 由于房屋室内设计甚至户型设计无法满足用户的个性化需求, 房屋交付后业主重新规划设计装修的情况比比皆是, 造成了社会资源的极大浪费. 近年来, 国家要求房地产开发商提高精装修房屋交付比例. 住建部印发的《建筑业发展“十三五”规划》中明令要求, 截止到2020年新开工全装修成品住宅面积达到30%, 这类问题愈发严重.
在房屋设计的早期, 特别是室内平面图设计阶段, 引入用户的个性化需求很有必要. 然而, 绝大多数用户缺少专业领域知识, 他们无法准确描述自己的偏好或描绘出喜欢设计样式, 只能用相对口语化、模糊、情绪化的语言来形容, 例如“大气”“温馨”“西式”等过于抽象的词语. 最终, 往往会出现这样的情形: 设计师耗费大量精力设计出好几套方案, 但并不能符合用户的要求, 而用户又说不出哪里不满意. 因此, 在室内平面图的设计过程中让用户及时参与是解决该问题的关键.
室内平面设计可以看成是空间布局问题, 属于典型的优化问题. 早先的文献成果可分为两大研究领域:空间调度和场地布局规划, Thabet等人[1]开发SCaRC(空间约束和资源约束)调度系统, 量化工作空间参数, 定义和合并调度过程中的工作空间可用性. Li等人[2]用遗传算法将施工现场级设施布局问题转化为将预定设施分配到预定地点的问题, Jang等人[3]用遗传算法在前者基础上改进, 整合了空间调度和场地布局规划两个因素. 然而, 传统的空间调度和场地规划不适用于现代房屋空间布局, 原因在于室内设计不光涉及到房间大小或位置排列, 还包含了采光、朝向、房间邻接度等居住舒适度问题和中国传统文化中独有的风水因素, 很难从既定的公式、数据中得到结果, 既耗时又效率低下.
为了解决这类问题, 我们设计了一种房屋平面图生成算法, 将交互式遗传算法(interactive genetic algorithm, IGA)用于生成空间布局图, 让用户参与其中并对其进行评价, 形成一种人机协同工作方式. 算法负责生成布局图, 用户负责评价, 评价的参数反馈到算法中, 再次生成下一代更优的布局图, 最终生成用户满意的图纸. 规避了传统演化算法缺少主观手段的局限性的同时又充分发挥用户的主观能动性, 帮助设计师找到符合用户偏好、直观的模型, 作为讨论的蓝本, 提高工作效率.
1 相关工作 1.1 布局问题布局设计(layout design)问题即对特定对象合理排布与摆放的研究. 现代行业与工程中存在大量布局设计类问题, 如海运码头的集装箱摆放装运问题[4], 仓库的设备材料流动问题[5]与车间调度问题[6], 建筑行业的建筑布局设计问题等. 布局设计具有强烈的需求与庞大的市场空间, 对其布局设计问题的研究具有广泛而深刻的现实意义. 绝大多数布局设计问题都与空间密不可分, 如一维空间的分割问题, 二维空间的室内平面图设计, 三维空间的驾驶舱布局问题[7, 8], 因此空间布局问题占布局设计中的主要部分.
室内空间布局(indoor spatial layout)是室内设计中主要涉及的问题, 也是布局设计中重要的研究方向, 相较于其他类型的布局问题, 室内空间布局更具研究价值和前景. 室内设计[9]、虚拟现实[10]、电脑游戏[11]等领域中已广泛应用室内空间布局中的相关知识. 其中在建筑领域内, 室内空间布局包含布局平面设计(空间分割)及场景优化布局(家居装饰), 传统的室内设计往往都是由设计师事先与用户沟通, 初步了解用户需求之后, 提供类型模板供用户选择, 多以反复试错为主. 因此涉及到以下问题: (1)用户缺少相关的专业知识, 无法术语化表达自己的需求, 与设计师间的沟通存在障碍; (2)设计师需收集、设计大量模板供用户选择, 并在之后的过程中反复试错, 造成时间与资源的浪费; (3)设计工作过于依赖人工, 往往造成大量人力资源的消耗.
在早期的研究中, 对于住宅建筑的室内平面设计, 提出大量约束性研究方法[12-14]. Mirahmadi等人[15]设计了一种演化系统, 根据给定的约束条件生成多组配置, 并根据评价指标对其优先级进行排序之后, 找到室内布局中的最佳配置. Rosser等人[16]提出了一种半自动建模系统, 用于将建筑平面图与实时地图数据集成以生成建筑模型. 除此之外, 专家系统(expert system)[17]实现平面布局图也是研究热点. Río-Cidoncha等人[18]整合人工智能思想和专家系统设计出一类布局设计模型. Kwon等人[19]通过将建筑设计知识与相关设计规范封装入专家系统中, 通过参考和推导基于给定BIM空间信息和现有知识的空间布局, 结合专家系统比较空间布局方案, 确定不同可达性条件下的最佳选择.
然而, 由于组合问题的复杂性, 传统的约束方法与演化算法无法完全匹配布局问题中的约束条件与评价指标, 例如房间邻接舒适度、不同室内风格、风水布局等无法公式化的因素, 并且从整体上用户可以轻易地评价生成的平面图是否满足预期, 但很难着手局部特征的优化. 而IGA中的用户评价模式中, 用户的主观评价取代复杂的数据评价, 使缺少专业知识的普通人也能代入设计师的视角, 相较于他人, 用户更能清楚自身所需, 简化复杂性的同时提高设计效率.
1.2 辅助设计工具虽然室内设计的风格会随着时尚潮流或者社会风气而改变, 但设计师在设计布局时所做的工作并没有太大的变化. 他们根据业主的要求收集材料, 现场勘察, 并设计出相应的草图, 就定好的草图方案与甲方协商进行分析整改, 最后制成最终效果图和施工图. 近些年随着计算机领域的发展和普及, 越来越多的设计软件逐渐应用到人们的日常生活工作当中. 著名的计算机设计软件AutoCAD、3DsMAX和Archicad可以很好地应用于室内设计辅助系统, 大大减少工作量.
然而, 上述辅助设计系统给设计行业提供了很大的便利, 但他们都只是单向操作的工具, 缺少用户与设计师沟通交流的平台, 用户参与程度有限, 并且使用这些工具需要专业的设计基础和软件使用知识, 非专业人士很难掌握, 在使用过程中有一定局限性
1.3 交互式遗传算法20世纪70年代, Holland[20]提出了遗传算法(genetic algorithm, GA), 该算法根据达尔文生物进化论的自然选择和遗传学机理的生物进化过程, 模拟自然界生物优胜劣汰的机制得出更优解. 并已应用于许多优化和分类问题[21, 22].
算法的步骤如下:
步骤1. 初始化种群, 设置个体数量和每个个体中染色体的编码;
步骤2. 设置一个适应度函数, 计算每个个体的适应值(评分);
步骤3. 根据适应值两两配对繁殖出下一代;
步骤4. 交叉和变异;
步骤5. 回到步骤2, 直到得出满意的结果.
两个染色体相互匹配按特定方式交换其部分基因, 从而形成两个全新的子类个体, 子类继承双亲的特征. 除此之外, 设置一个突变概率, 来让种群能够进化出更好的特征. 随着一代又一代的发展, 种群中的每个个体都进化获得更高的适应性.
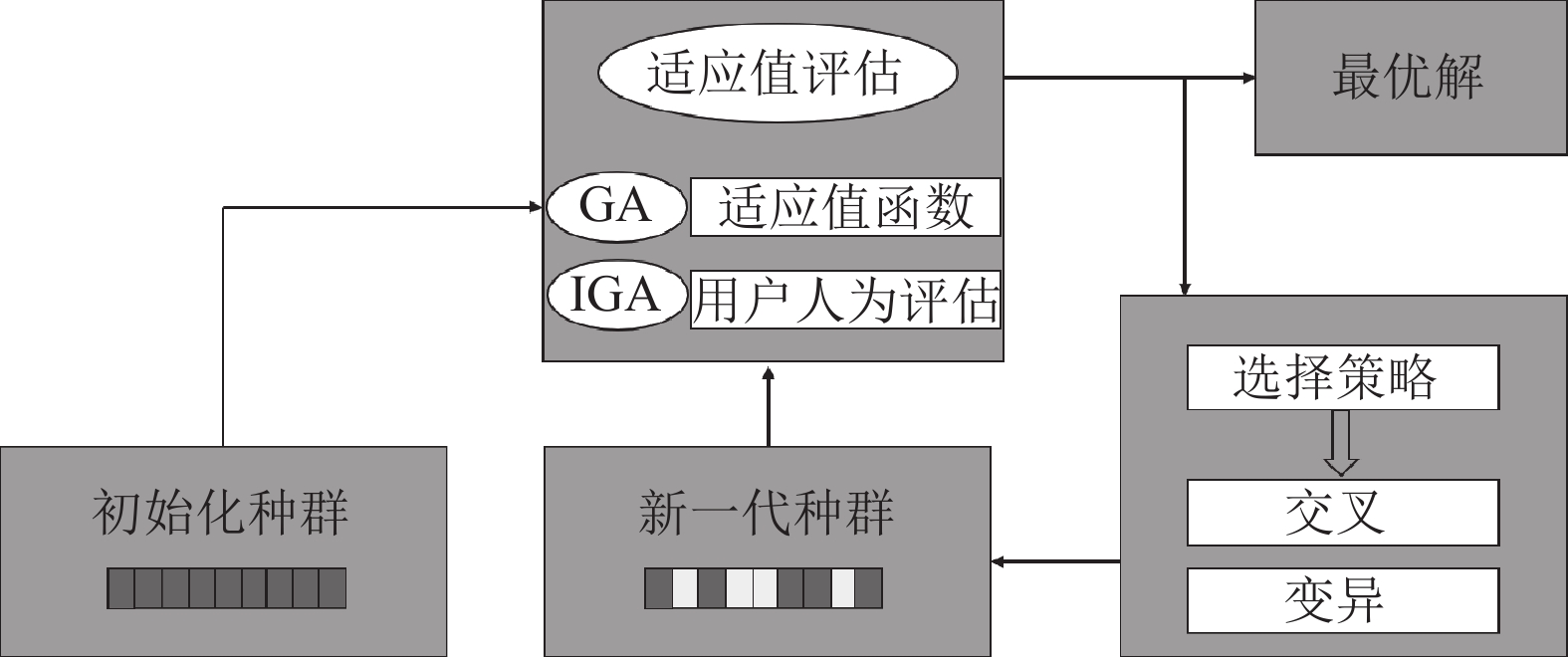
交互式遗传算法(IGA)与遗传算法基本相同, 但是把其中的适应值由适应度函数确定改为由用户主观确定. 因此, 算法可以与用户“互动”, 适应值也不再是由一串机械化的数据决定, 可以在进化过程中感知用户的喜好. 于是, IGA可以解决一般算法不能解决的问题, 如设计和艺术等偏主观类行业[23, 24]. 图1比较了遗传算法和IGA算法的过程.
|
图 1 演化过程 |
2 基于IGA的布局生成算法 2.1 室内设计因素
房屋室内设计一般需要考虑4个因素: (1)面积: 不同的房间具有不同的功能, 里面的家具和装饰也随之变换, 那么相应也就会有不同面积要求, 就算是同一类房间, 按照使用人数来参考也会有两个不同面积的要求, 例如主卧室和副卧室; (2)长宽比: 每个房间都需要合适的长宽比, 通常是为了方便人员的流通和不同形状家具的摆放; (3)位置: 针对每个房间的不同功能, 其在空间上的位置分配也尤为重要, 某些粗略的布局, 例如厨房与卫生间相邻, 卧室靠近大门等, 不光会降低房间功能的使用体验, 还会影响到用户的睡眠质量; (4)风水因素: 风水文化在中国可有上千年的历史流传, 是宇宙观在传统思维范式下的一种表现形式, 从古就有道家“天人合一”“道法自然”等思想, 一个好的风水布局能够帮助改善人们的疲惫情绪、生活氛围, 对生活、事业、学业都有一定的帮助.
可以将房屋室内布局当成多目标优化问题来解决[25]. 因此需要如上述所示考虑不同目标函数间的相对重要性. 在传统的多目标加权法中, 每个目标函数被乘上一个自定义的权重后整合起来作为一个目标, 转化成单目标优化算法求最优解[26]. 在室内设计问题中, 目标权重值作为决策者的一种主观偏好信息, 一般很难预先设定. 运用遗传算法可以得到一组无偏好Pareto最优解, 决策者再根据自己的偏好选择, 但要在这众多可行解中挑选出合适的结果, 无疑会加剧决策者的疲劳感并且效果大打折扣, 且设计、艺术类行业中适应值很难用具体函数确定, 本文采用交互式遗传算法, 其中的“人机交互”模式可以在较复杂的情况下, 让用户的主观选择替换复杂的适应值函数, 演化得到用户满意的个体, 逐步搜索获得满足要求的解. 除此之外, 为解决种群规模小造成的遗传漂变问题, 结合聚类算法将每代种群进行聚类分组, 保持种群多样性的同时不增加用户分配适应值的负担.
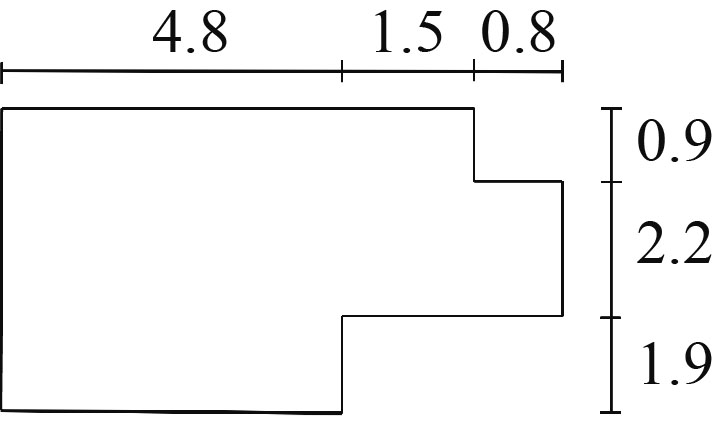
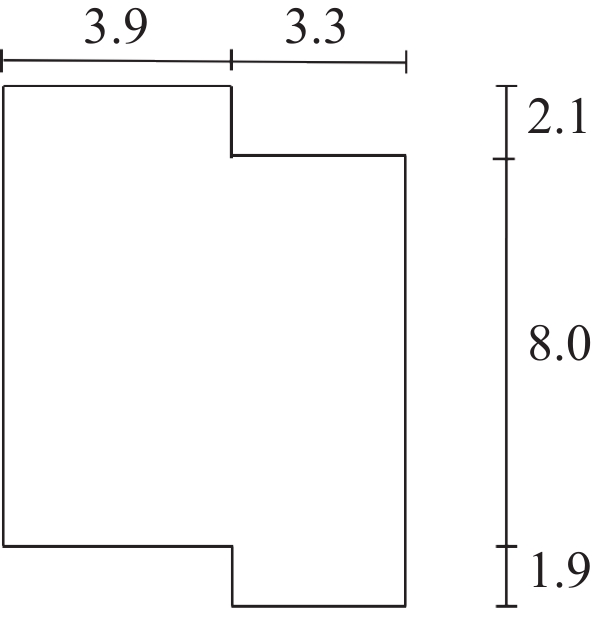
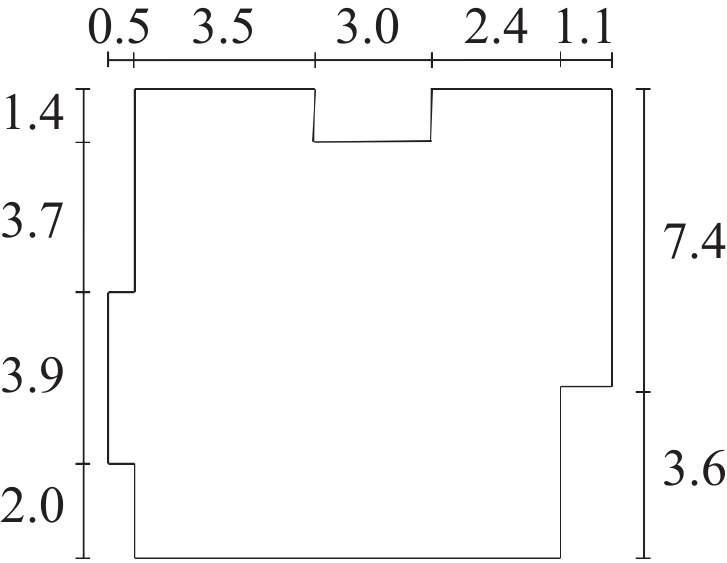
2.2 房屋整体框架房屋平面布局图是指房屋的整体框架以及内部的空间分布情况, 通常在基于外围整体框架固定不变的情况下进行室内设计. 家庭在不同的发展阶段时, 成员构成及居住功能呈阶段性的特点[27]. 据研究所得, 现购房者家庭成员人数及空间需求如表1所示. 户型图根据房屋结构设计呈现出多种形态[28], 可分为一居室、二居室、三居室、多居室等. 表2给出不同类型的代表性框架示意图.
| 表 1 家庭不同阶段空间需求 |
| 表 2 模型框架 |
2.3 遗传编码
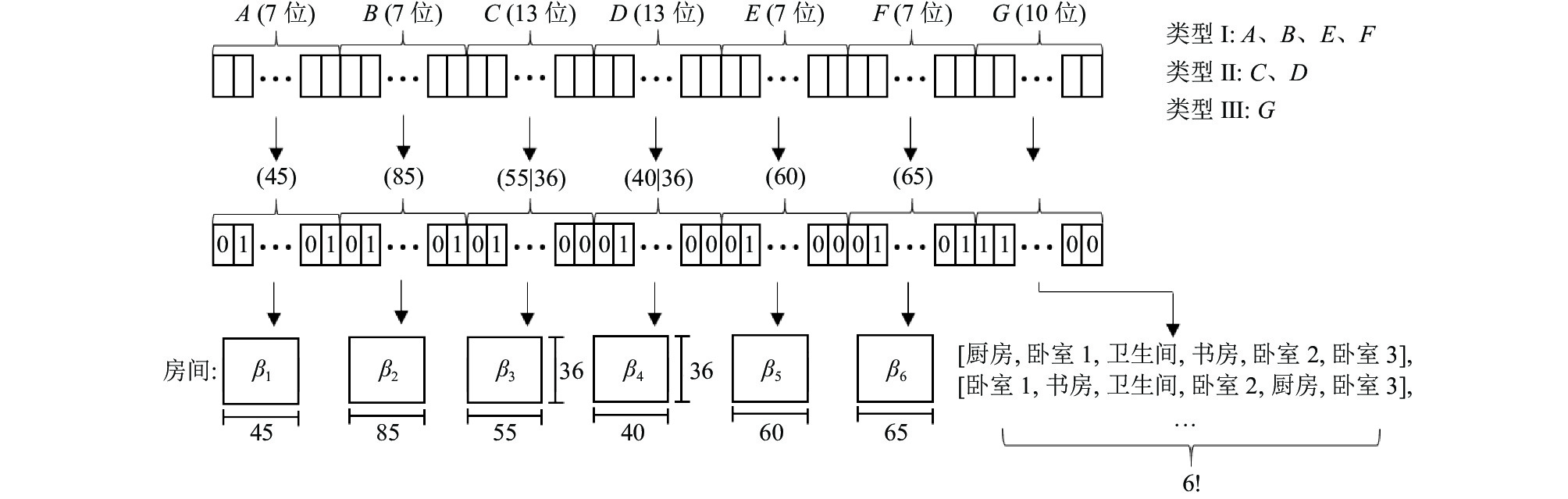
遗传算法中染色体的编码形式有很多[29, 30], 本文采用二进制编码形式, 分布空间的参数以基于字符集{0,1}构成的染色体位串为表现形式. 以表2中④号框图为例, 在外部整体框架不变的情况下, 将平面图分为7个部分: 房间β1–β6和各房间分布位置, 种群的染色体由所有变量的编码排列所构成(如图2), A-F分别对应6个房间, G表示其位置排列, 图3详解了基因对应个体的过程. 房间生成、排列时比例需满足一定的约束关系, 但这种关系绝非特定, 只能按照设计风格、房间类型与用户要求来确定, 本文算法得出的仅为初步设计蓝本图, 为用户和设计师提供一种讨论的可能性, 因此参数与实际可能略有误差. 表3给出了各编码位置对应的显性表示、取值区间与参考依据, HL和HW分别表示房屋总平面图的横、纵向距.
|
图 2 染色体编码 |

|
图 3 编码详解 |
| 表 3 模型参数设置 |
2.4 算法流程
算法1. 改进的交互式遗传算法
(1) 随机产生初始种群, 种群数量pop_size;
(2) 对种群进行循环筛选, 选出不符合要求的重新随机赋值;
(3) 对种群进行评估:
用户在交互界面上给每个个体进行打分, 得到各自的适应值fi; 总适应值为
(4) 产生新的种群:
采用轮盘赌方法, 循环pop_size次, 依次选择个体加入新的种群中, 方法如下:
1) 计算个体被选择的概率为pi=fi/F;
2) 计算个体的累积概率
3) 生成一组位于区间[0, 1]中的随机浮点数r;
4) 若
适应值越高的个体越容易被选择继承下来, 而适应值低的个体也有较小的概率被选择, 增加了新种群的多样性;
(5) 对新种群进行K-means聚类操作:
1) 从种群中随机提取k个个体, 作为k个簇的中心;
2) 分别用欧式距离计算剩下的个体到k个簇中心的相异度, 划分到相异度最低的簇;
3) 根据聚类结果, 重新计算各自中心;
4) 将全部个体按照新的中心重新聚类;
5) 重复第4)步, 直至结果不再变化;
(6) 对新种群应用重组算子——杂交:
用户在系统开始前给定一个杂交概率pc, 循环pop_size次, 每次生成一个区间[0, 1]中的随机浮点数c, 若
(7) 变异:
另存在一个用户给定的变异概率pm, 对种群中个体的每个基因进行遍历, 随即生成一个区间[0, 1]的随机数r, 若
如若用户已发现有满足其偏好的个体存在, 则终止算法操作; 否则跳至步骤(3).
2.5 交互界面设计用户交互界面如图4所示, 设计过程中, 首先用户选择“家具风格”项, 目标参数是用户对室内设计风格的评价, 例如“简约”“欧式”等. 之后用户按照意愿自行修改杂交概率(默认0.65)与变异概率(默认0.05)数值. 系统将按照收到的参数信息不断演化最终得到符合用户主观偏好的平面图.
人机交互模式的核心在于确定个体适应值. 传统的遗传算法缺少交互思想, 适应值由适应值函数确定, 不适用于设计、艺术等主观行业. 而在本系统中, 考虑到不同用户的偏好标准各不相同, 且室内设计中的风水等因素无法简单地用函数体现, 因此由用户评分的形式给出适应值. 系统根据收到的参数信息演化出种群, 用户对种群个体打分确定适应值, 进行下一代的演化. 此外, 系统在每一代演化之后进行自我调节, 比较父代与子代的适应值, 如果适应值提高, 则保留子代个体; 如果降低, 就保留父代抛弃子代. 从而保证演化之后的每代种群适应值的提高, 直到得到满足用户偏好的个体, 提高了算法的有效性.

|
图 4 交互界面 |
3 实验结果与分析 3.1 参数设置
为了使用户在选择时减轻疲劳感的同时增加个体的多样性, 对于实验参数, 设置种群大小为12, 选择概率0.65, 设置0.05的变异概率使基因不局限于某一范围之内, K-means方法中k设置为4, 选择策略采用轮盘赌算法.
3.2 模拟环境下实验为快速验证算法可行性, 假定用户最终满意解为如图5所示的平面图, 即

|
图 5 实验模板 |
演化个体
| $ f\left( x \right) = \sqrt {\mathop \sum \limits_{i = 1}^n {{\left( {{x_i} - {o_i}} \right)}^2}} $ | (1) |
与此同时, 为了解决轮盘赌选择中概率为负的问题, 修改适应值计算公式:
| $ Fit\left( {f\left( x \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {{c_{\rm{max}}} - f\left( x \right), \; f\left( x \right) < {c_{\rm{max}}}} \\ {0, \; {\rm{else}}} \end{array}} \right. $ | (2) |
其中,
同时, 为了验证聚类方法对于算法改进的有效性, 对比了原始遗传算法与改进算法在“简约”风格下对搜索空间寻找目标值的曲线收敛变化情况(图6). 为获取更为准确的对比结果, 模拟实验中设置迭代次数t = 120次. 在
交互式算法中, 除了参数对收敛性的影响之外, 用户的主观选择也起到关键的作用, 收敛性测试的目的是研究在演化过程中用户的主观选择是如何影响收敛性的, 同时为了提高算法的有效性, 对K-means聚类法中的k值分别取3、4、5进行对比实验. 设计、艺术行业偏向主观的特性, 很难对收敛性进行定量的描述, 因此我们采用打分机制, 将分数转换为种群个体的适应值.
测试分别选择“简约”和“欧式”两种目标风格, 10名用户使用本系统对每代种群个体打分, 并求出平均分, 分数越高则表明算法收敛性越强. 图7显示了随着用户的主观选择与k的不同取值, 分数(收敛性)变化的情况. 由图可知, 当迭代次数

|
图 6 模拟评价结果 |

|
图 7 收敛性测试 |
3.4 主观测试
人们的主观审美会随着时间的推移而改变, 那么这些过于主观的测试结果偏差可能会比较大. 本文采用Sheffe的二点检验(pair-test)[31]. 该测试确定一个标准, 通过将演化得到的模型与该标准相对比, 得出用户对实验结果满意程度的调查.
首先, 我们从整个搜索空间中随机选择了500个样本模型分成5等份, 并选出了5名用户, 每人得到100个样本模型, 要求他们根据“简约”“欧式”两种家居风格, 对这100个模型进行打分(0–5), 最后根据平均得分, 各求得10个“简约”和“欧式”个体模型, 作为下一步测试的参考标准. 接下来我们要求10名用户使用本系统寻找风格为“简约”“欧式”的目标个体, 演化代数限定为20, 用户从最后一代种群中选出他们认为最好的个体, 与之前制定的标准进行对比, 并对这些个体进行打分(0–5). 最后, 经过统计分析, 图8显示了92%和97%的可靠性下用户的满意程度. 平均而言, 用户对得到的“简约”目标评分为4.69, 对“欧式”目标评分为3.78, 可以看到用户对测评的满意程度很高. 同时相比于“欧式”风格目标, “简约”风格目标拥有更高的满意度和更窄的置信区间. 因此可以认为, 将IGA应用到非专业人士的室内设计辅助系统中是很有前景的.

|
图 8 满意度均值 |
4 结论与展望
本文使用交互式遗传实现了室内布局平面图的生成, 引入K-means聚类算法对新生成的种群进行聚类划分, 防止了因种群过小而产生的遗传漂变问题, 在合理的迭代次数内获得满意解. 然而, 算法执行过程中由于用户参与交互, 算法迭代次数、种群范围不宜过大, 这限制了搜索空间的广度, 否则会造成用户疲劳感加剧和审美疲劳, 从而影响最终结果. 因此, 如在后续研究中加入筛选机制, 从每代种群中选取代表性解呈现给用户, 将减轻用户评价疲劳. 如何在减缓用户疲劳度和扩大搜索空间中维持平衡将是后续研究中需要进一步探讨的难点.
| [1] |
Thabet WY, Beliveau YJ. SCaRC: Space-constrained resource-constrained scheduling system. Journal of Computing in Civil Engineering, 1997, 11(1): 48-59. DOI:10.1061/(ASCE)0887-3801(1997)11:1(48) |
| [2] |
Li H, Love PED. Genetic search for solving construction site-level unequal-area facility layout problems. Automation in Construction, 2000, 9(2): 217-226. DOI:10.1016/S0926-5805(99)00006-0 |
| [3] |
Jang H, Lee S, Choi S. Optimization of floor-level construction material layout using genetic algorithms. Automation in Construction, 2007, 16(4): 531-545. DOI:10.1016/j.autcon.2006.09.006 |
| [4] |
何静静, 王晓峰. 基于遗传算法的海运集装箱空箱调运成本优化. 计算机系统应用, 2015, 24(1): 123-127. DOI:10.3969/j.issn.1003-3254.2015.01.022 |
| [5] |
杨玮, 刘江, 岳婷, 等. 多载具自动化立体仓库货位分配与作业调度集成优化. 计算机集成制造系统, 2019, 25(1): 247-255. |
| [6] |
陈金广, 马玲叶, 马丽丽. 求解作业车间调度问题的改进遗传算法. 计算机系统应用, 2021, 30(5): 190-195. DOI:10.15888/j.cnki.csa.007921 |
| [7] |
Liu X, Liu Z, Yu SH, et al. Adapted particle swarm optimization algorithm-based layout design optimization of passenger car cockpit for enhancing ergonomic reliability. Advances in Mechanical Engineering, 2019, 11(3).
|
| [8] |
徐刚, 庞丽萍. 特种车辆舱室送风系统布局仿真优化. 化工学报, 2020, 71(S1): 335-340. |
| [9] |
Tang XF. Research on interior design strategy based on optimization of computer renderings production process. Journal of Physics: Conference Series, 2021, 1992: 032104. DOI:10.1088/1742-6596/1992/3/032104 |
| [10] |
Liu HM, Wang ZQ, Mazumdar A, et al. Virtual reality game level layout design for real environment constraints. Graphics and Visual Computing, 2021, 4: 200020. DOI:10.1016/j.gvc.2021.200020 |
| [11] |
Ma CY, Vining N, Lefebvre S, et al. Game level layout from design specification. Computer Graphics Forum, 2014, 33(2): 95-104. DOI:10.1111/cgf.12314 |
| [12] |
Donath D, Böhme LFG. Constraint-based design in participatory housing planning. International Journal of Architectural Computing, 2008, 6(1): 97-117. DOI:10.1260/147807708784640081 |
| [13] |
Zawidzki M, Tateyama K, Nishikawa I. The constraints satisfaction problem approach in the design of an architectural functional layout. Engineering Optimization, 2011, 43(9): 943-966. DOI:10.1080/0305215X.2010.527005 |
| [14] |
刘正龙, 杨艳梅. 基于遗传算法的数值优化约束问题的研究. 计算机系统应用, 2013, 22(5): 139-142, 197. DOI:10.3969/j.issn.1003-3254.2013.05.032 |
| [15] |
Mirahmadi M, Shami A. A novel algorithm for real-time procedural generation of building floor plans. arXiv: 1211.5842v1, 2012.
|
| [16] |
Rosser J, Morley J, Smith G. Modelling of building interiors with mobile phone sensor data. ISPRS International Journal of Geo-Information, 2015, 4(2): 989-1012. DOI:10.3390/ijgi4020989 |
| [17] |
Kamol K, Krung S. Optimizing architectural layout design via mixed integer programming. Proceedings of the 11th International CAAD Futures Conference held at the Vienna University of Technology. Vienna: Springer, 2005. 175–184.
|
| [18] |
del Río-Cidoncha G, Martínez-Palacios J, Iglesias JE. A multidisciplinary model for floorplan design. International Journal of Production Research, 2007, 45(15): 3457-3476. DOI:10.1080/00207540600889550 |
| [19] |
Kwon O, Cho J. BIM space layout optimization by space syntax and expert system. Korean Journal of Computational Design and Engineering, 2017, 22(1): 18-27. DOI:10.7315/CDE.2017.018 |
| [20] |
Holland JH. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. Ann Arbor: University of Michigan Press, 1975.
|
| [21] |
Sun YN, Xue B, Zhang MJ, et al. Automatically designing CNN architectures using the genetic algorithm for image classification. IEEE Transactions on Cybernetics, 2020, 50(9): 3840-3854. DOI:10.1109/TCYB.2020.2983860 |
| [22] |
Su Y, Jin SM, Zhang XP, et al. Stakeholder-oriented multi-objective process optimization based on an improved genetic algorithm. Computers & Chemical Engineering, 2020, 132: 106618. |
| [23] |
Lee JY, Cho SB. Interactive genetic algorithm for content-based image retrieval. Proceedings of Asia Fuzzy Systems Symposium. 1998. 479–484.
|
| [24] |
刘征宏, 鄢吉多, 林芸, 等. 基于感性工学和交互式遗传的产品配色设计方法. 包装工装, 2019, 40(20): 88-94. |
| [25] |
Coello CAC. Evolutionary multiobjective optimization. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2011, 1(5): 444-447. DOI:10.1002/widm.43 |
| [26] |
Cai CS, Chen SR. Framework of vehicle-bridge-wind dynamic analysis. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(7–8): 579-607. DOI:10.1016/j.jweia.2004.03.007 |
| [27] |
文铮, 漆平, 洪惠群. 保障性住房的公共服务体系建构. 建筑学报, 2013(4): 106-109. DOI:10.3969/j.issn.0529-1399.2013.04.019 |
| [28] |
宋纪青. 中小户型住宅设计研究[硕士学位论文]. 合肥: 合肥工业大学, 2013.
|
| [29] |
帅训波, 马书南, 邵艳伟, 等. 基于两种新型遗传算子的优化组合遗传算法. 计算机系统应用, 2010, 19(7): 98-102. DOI:10.3969/j.issn.1003-3254.2010.07.023 |
| [30] |
E ZB, Shi RH, Gan L, et al. Multi-satellites imaging scheduling using individual reconfiguration based integer coding genetic algorithm. Acta Astronautica, 2021, 178: 645-657. DOI:10.1016/j.actaastro.2020.08.041 |
| [31] |
David HA. The Method of Paired Comparison. New York: Hafner Press, 1969.
|
 2022, Vol. 31
2022, Vol. 31