2. 中交一公局集团有限公司, 北京100020;
3. 长安大学 公路学院, 西安 710064;
4. 长安大学 信息工程学院, 西安 710064
2. CCCC First Highway Engineering Group Co. Ltd., Beijing 100020, China;
3. School of Highway, Chang’an University, Xi’an 710064, China;
4. School of Information Engineering, Chang’an University, Xi’an 710064, China
隧道在建设中往往伴随着地质复杂, 工程量大, 建设条件恶劣等因素的影响, 并且在山体结构中时常分布有裂隙发育较严重风化岩体, 这导致隧道施工过程中不可避免地会造成地表沉降, 甚至可能会导致地面沉陷、建筑物开裂及管线破坏等情况的发生[1, 2]. 因此对隧道沉降的变化规律进行科学分析与处理, 对最终沉降量做出准确的预测, 具有十分重要理论意义与实际应用价值[3, 4].
近年来, 国内外学者对隧道沉降量的分析及预测进行了大量的研究并取得了一定的成果[5, 6]. 曾学宏等[7]使用BP (backpropagation)神经网络和长短时记忆网络(long short term memory network, LSTM)两种网络模型独立对实际工程中获取到的两组地铁隧道数据进行了分析研究, 并对两种模型的预测精准度进行了对比. 针对地表沉降的预测, 赵振华等[8]采用回归分析法, 使用Peck公式得到了较好的地表沉降预测. 他们建立的BP神经网络地表沉降预测模型, 同样获得了较为理想的预测结果. 潘恺等[9]提出了动态灰色时序神经网络组合模型. 对于南京二号线的地铁沉降数据, 利用3种算法的组合对其进行分析预测, 并对比了其与动态灰色模型和动态灰色时序模型的预测精准度. 李伟等[10]提出一种Adaboost.RT算法集成多种不同基学习模型的隧道预测方法. 针对非线性回归问题且研究对象是交通隧道沉降的随机性强的小样本数据, 可以使用Adaboost算法得到强学习模型, 以此得到较优的预测精度. 姚凯等[11]利用广义回归神经网络参数少、使用简单的特点, 结合FOA算法预测隧道围岩变形. 明祖涛等[12]分别用规范双曲线、修正双曲线、三点法、Asaoka法和GM(1, 1) 模型, 结合某高速铁路桥隧的沉降观测数据, 对各模型在铁路桥隧的准确性、适用性进行了分析. 毕旋旋等[13]使用了小波分析理论对所得到的隧道沉降数据序列进行分解重构得到高频分量和低频分量, 进而分别构建ARIMA模型进行预测, 最后叠加预测结果得到最终的沉降值. 莫云等[14]发现武汉市轨道交通二号线第24标段的监测数据满足Logistic曲线, 故运用Logistic时间函数模型对隧道“发生”“剧变”“平稳”的过程进行描述.
基于以上研究, 可以发现已有一些基于机器学习的方法对沉降进行预测, 然而以上模型在时间序列规律性的考虑上还有所欠缺, 同时在数据预处理方面未能结合多源数据表中的时空域信息进行修复, 大多是对异常数据直接进行删除. 因此本文首先对采集到原始沉降监测数据通过融合多源异构数据表中的时空信息对缺失及异常数据修复, 然后采用贝叶斯算法优化在众多项目表现较优的XGBoost集成模型[15, 16]对隧道拱顶沉降、地表沉降和周边收敛数据进行演变分析及预测, 最后与原始XGBoost集成模型和常用于时序序列预测的LSTM时间序列模型进行对比, 以证明本文提出的最优沉降量预测模型的有效性, 从而对隧道沉降变化进行科学的监测与预测. 整体实验流程如图1.

|
图 1 整体研究路线 |
1 隧道沉降监测数据集建立 1.1 原始工程数据采集
(1) 工程概况
以沙岭壕隧道、十里坡隧道、中坪隧道以及白家庄隧道的实际工程量测沉降统计数据为依托, 分别对隧道拱顶沉降、地表沉降、周边收敛进行分析, 具体隧道信息如下:
1)沙岭壕隧道: 沙岭壕隧道为郑西高速栾双段在建分离式隧道, 该隧道位于河南省南阳市西峡县, 隧道施工区域穿越浅埋段5条, 地质构造复杂, 隧道内突水涌砂情况频发, 存在6处溢出泉和流塑粉砂层, 围岩通常情况下基本上是Ⅳ、V级围岩, 在实际的施工中会遇到反坡涌水、围岩破碎、地形条件复杂等困难, 施工难度大, 安全风险高. 隧道左线桩号ZK102+290–ZK103+609, 全长1 319 m; 右线桩号K102+228–K103+438, 全长1 210 m.
2)十里坡隧道: 十里坡隧道为郑西高速栾双段在建分离式隧道, 该隧道位于河南省南阳市西峡县, 隧道左线桩号ZK109+840–ZK110+094, 全长254 m; 右线桩号K109+733–K109+994, 全长261 m.
3)中坪隧道: 中坪隧道是郑西高速栾双段在建分离式隧道, 该隧道位于河南省南阳市西峡县, 位于两河口附近, 隧道紧邻311国道, 爆破作业安全等级要求高. 隧道左线桩号ZK108+702–ZK109+159, 全长457 m;右线桩号K108+612–K109+115, 全长503 m.
4)白家庄隧道: 白家庄隧道为郑西高速栾双段在建分离式隧道, 该隧道位于河南省南阳市西峡县, 隧道左线桩号ZK104+214–ZK105+526, 全长1 312 m; 右线桩号K104+116–K105+416, 全长1 300 m.
(2) 原始数据分析
本文选择上述4段隧道为试验对象. 每段隧道选取左右两个部分, 每个部分又具体的分为地表、拱顶及周边监测位置, 这里以白家庄隧道部分采集数据为样例, 见表1.
从原始数据可知: 前15次测量是每天不间断测量, 从第16次之后, 测量周期改为每两天测一次. 对于不同空间信息的监测点, 时间采样信息也不一致, 存在时空尺度不对齐的问题. 同时研究表中沉降监测量演变规律可以发现, 监测初期, 隧道每天的累计沉降量都在增加, 但增加速率逐渐放缓; 在进行20次左右的测量即25天左右后, 隧道沉降趋于收敛, 仅有微小变化量; 在50天之后的沉降测量值基本不再发生变化, 保持稳定. 整体符合“发生”“剧变”“平稳”的变化过程.
1.2 融合时空信息的隧道沉降监测数据修复(1) 时空尺度对齐
由于不同空间位置的沉降监测的采样间隔不同, 首先需要对时间序列数据进行尺度统一. 在这里, 采用平均插值算法对原始数据中第17–21期间隔为2天的采样数据进行插值, 得到采样间隔为1天的共26期沉降监测数据. 同时将采样间隔时间较长的长期稳定不变化的数据去掉.
(2) 数据修复
同时数据中存在一些异常和缺失的情况, 需要首先对原始数据进行修复, 以减少异常和缺失数据对沉降预测精度的影响, 同时避免因数据异常导致程序卡顿等问题. 对于孤立点异常和数据中部缺失(即头尾有合理数据)的监测数据, 采用长短时记忆网络对孤立点异常数据及中间的缺失数据进行修复; 对于其他异常情况和大量数据缺失(后期数据连续缺失)的情况直接对其进行删除.
| 表 1 白家庄隧道部分原始数据 |
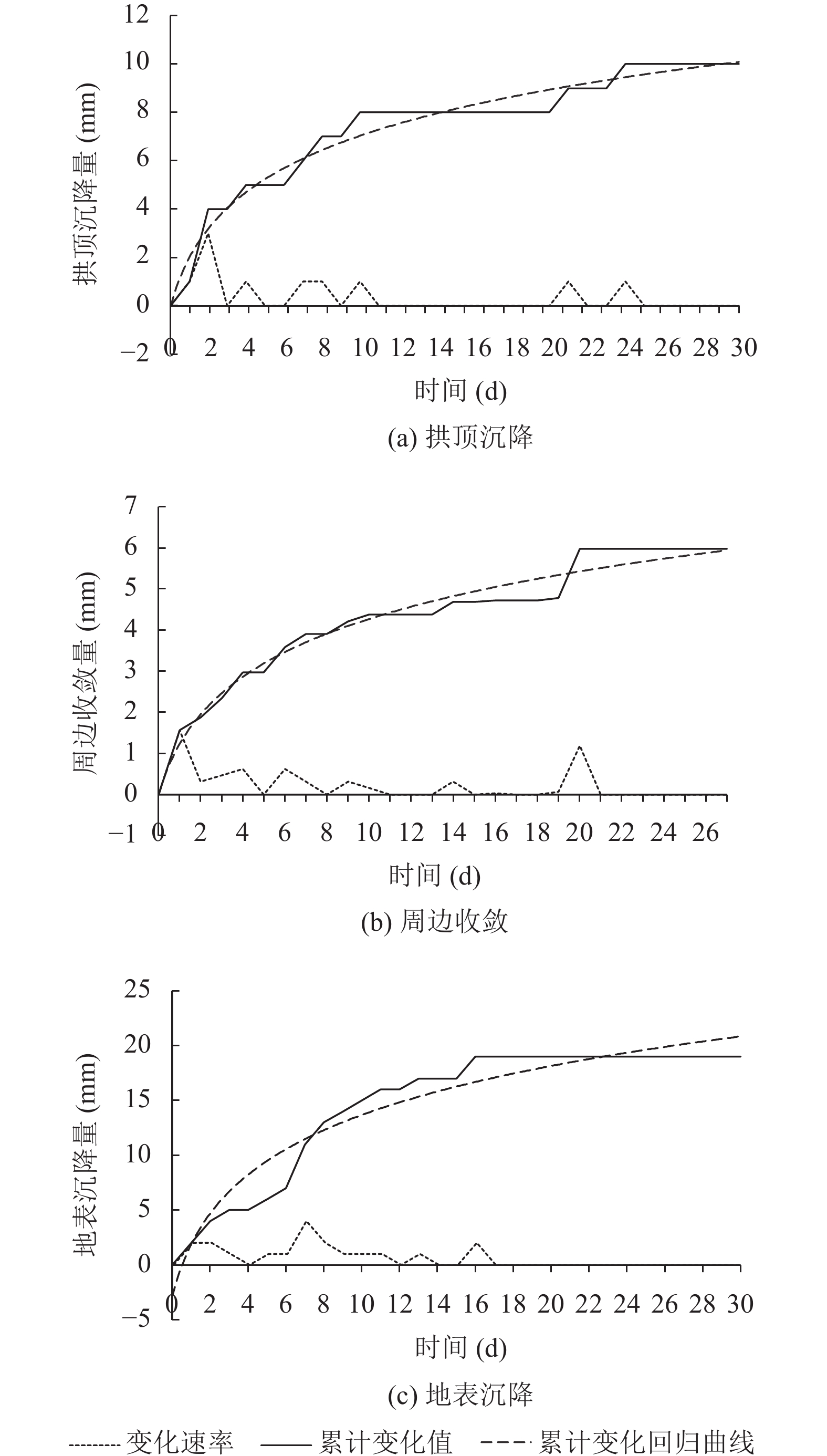
根据修复后的K106-405桩号的监测数据, 分别绘制了该桩号对应的拱顶、地表和周边收敛的沉降量变化速率、沉降量累计变化值、沉降量累计变化回归曲线, 如图2所示. 总体来说, 隧道3个不同位置的变化趋势基本一致, 在25天后就趋于平稳.
2 基于贝叶斯优化的XGBoost隧道沉降预测模型 2.1 XGBoost模型XGBoost模型基于回归决策树, 通过固定第一颗回归树经过第一轮迭代已学习的数据特征, 增加新的回归树以弥补误差提升精度, 前t个集成的模型产生的误差数据, 会被第t+1棵树作为建立时的参考. 即将多个回归树前一个输出与后一棵树的输入连接起来(串联), 以此, 随着回归树的不断加入, 损失函数Obj小于期望阈值, 如式(1).
| $ {Obj}(\theta)=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}\right)+\sum_{k=1}^{K} \Omega\left(f_{k}\right) $ | (1) |
其中,
| $ \hat{y}_{i}=\sum_{k=1}^{K} f_{k}\left(x_{i}\right) $ | (2) |
其中, k是回归树的总量,
整个算法的过程如下: 首先进行初始化, 然后把第1棵树加入预测模型中, 接着把第2棵树加入预测模型中, 以此类推, 直至把第t棵树加入预测模型中:
| $ \left\{\begin{array}{l} \hat{y}_{i}^{(0)}=0 \\ \hat{y}_{i}^{(1)}=f_{1}\left(x_{i}\right)=\hat{y}_{i}^{(0)}+f_{1}\left(x_{i}\right) \\ \hat{y}_{i}^{(2)}=f_{1}\left(x_{i}\right)+f_{2}\left(x_{i}\right)=\hat{y}_{i}^{(1)}+f_{2}\left(x_{i}\right) \\ \qquad\qquad\qquad\vdots \\ \hat{y}_{i}^{(t)}=\displaystyle\mathop \sum \limits_{k = 1}^t f_{k} \left (x_{i} \right) = \hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\end{array}\right. $ | (3) |
其中,
| $ \begin{split} {Obj}(\theta)&=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t)}\right)+\sum_{k=1}^{K} \Omega\left(f_{k}\right) \\ &=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\right)+\Omega\left(f_{t}\right)+C \end{split} $ | (4) |
训练模型的复杂度见式(5):
| $f_{t}(x)=w_{q(x)}, w \in R^{T}, q: R^{d} \rightarrow\{1, 2, \cdots, T\} $ | (5) |
其中, q(x)是样本x在树中的位置, w是树叶的得分值, T是该树叶子结点的数目, 复杂度也可以表示为式(6).
| $ \Omega\left(f_{t}\right)=\gamma T+\frac{1}{2} \lambda \sum_{j=1}^{T} w_{j}^{2} $ | (6) |
其中,
|
图 2 沉降量3项参数变化 |
2.2 贝叶斯优化算法
机器学习算法中每种模型都具有多个超参数, 超参数的设置和组合对模型最终的预测效果有很大影响. 例如层数太多导致梯度消失无法训练, 或者学习率过大可能导致收敛效果差, 过小又可能收敛速度过慢. 调参过程是模型优化的重要思路, 由于本文初始样本点有限, 不适用于遗传算法和PSO这些群体优化算法, 同时网格搜索算法因为要遍历参数的所有组合因此优化效率也不高. 采用贝叶斯算法对XGBoost的超参数进行优化可以在样本点有限的情况下大大提升调参效率, 可以根据当前已经试验的超参数组合来预测下一个可能带来最大收益的组合.
贝叶斯优化框架有两个关键部分: ① 使用概率模型代理原始评估代价高昂的复杂目标函数; ② 利用代理模型的后验信息构造主动选择策略, 即收益函数. 假设超参数优化的函数f(x)服从高斯过程, 根据已有的N组试验的输入输出{x, f(x)}, 计算f(x)的后验分布p(f(x)|x)来估计f(x).
| $ p(f(x)|x) = p(f(x)) p (x |f(x))/ p(x) $ | (7) |
其中, p(f(x))是先验概率; p(x|f(x))是样本x相对于函数 f(x)的条件概率;p(x)是用于归一化的证据因子. 即利用高斯随机过程, 使用贝叶斯定义, 将假设的先验概率分布转换为后验分布. 后验概率分布描述通过已观测数据集对先验进行修正后未知目标函数的置信度.
为了使得后验分布接近其真实分布, 就需要样本空间进行足够多的采样. 但是超参数优化中每一个样本的生成成本很高, 需要用尽可能少的样本使得p(f(x)|x)接近于真实分布. 因此需要定义一个收益函数来判断一个样本能否给建模提供更多的收益, 收益越大, 其修正的高斯过程会越接近目标函数的真实分布. 常用的收益函数有改善概率(PI)、期望改善函数(EI)、高斯过程置信上界(GP-UCB)等. 收益函数将在新的区域和局部最优解附近寻求全局最优解, 优化目标则是在全集A中寻找使f(x)值达到最大或最小的x集合, 如式(8)所示:
| $ x^{*}={\rm arg\;max}_{x\in A}f(x) $ | (8) |
本文使用R2和MAE分别作为评价模型的精确度指标和误差度指标, 计算公式如式(9)和式(10).
| $ R^{2}=\frac{\displaystyle\sum\left(\hat{{y}}_{i}-\overline{{y}}\right)^{2}}{\displaystyle\sum\left({y}_{i}^{2}-\overline{{y}}\right)^{2}} $ | (9) |
| $ M A E=\frac{100 {\text{%}}}{n} \sum_{i=1}^{n}\left|\frac{\hat{y}_{i}-y_{i}}{y_{i}}\right| $ | (10) |
其中,
R2(R-square)决定系数用于衡量原始回归值和预测回归值的相关性, 该值越接近1代表模型拟合效果越好, 模型越优秀.
MAE(mean absolute error)平均绝对误差反映原始回归值和预测回归值的真实误差, 该值越接近0, 表明预测结果与真实情况平均绝对误差越小, 模型预测结果越好.
不同类(精度类、误差类等)评价指标之间没有明确的精度越高误差越小的说法, 例如R2一般会随着样本数量的增加而增加, 不能绝对意义上说明准确程度. 同理, 误差类评价指标受某些异常值影响变化明显, 只能从不同角度大概定量反映预测值与真实值之间的误差. 因此需要结合不同类指标来综合评估模型优劣.
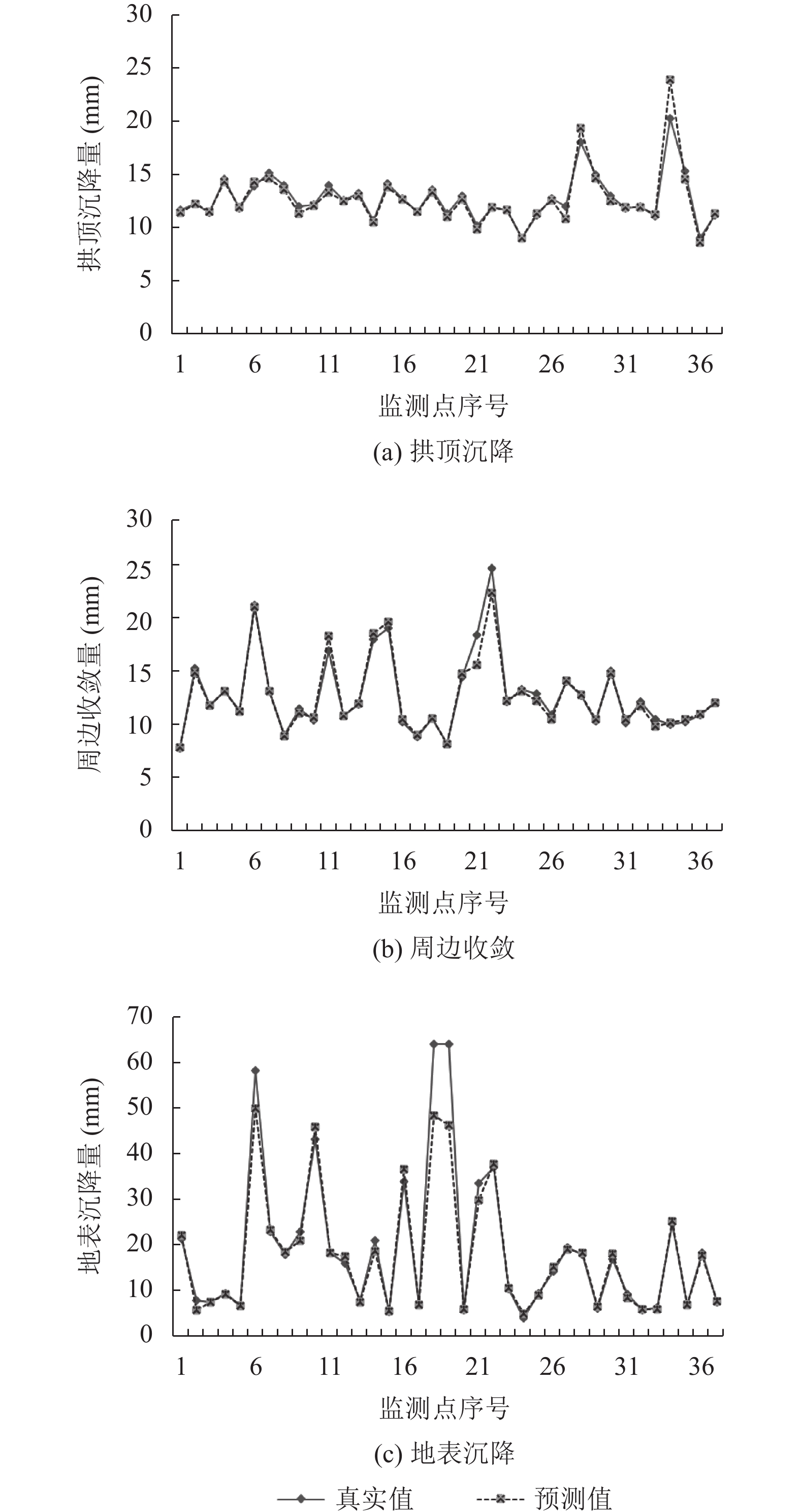
3.2 沉降预测结果本文利用十里坡+沙岭壕+中坪隧道共732条数据来训练模型, 取200条白家庄隧道数据用于测试模型精度, 通过指标计算进行对比分析, 得到基于贝叶斯优化XGBoost最优模型的参数设置, 如表2所示. 同时最优模型的训练集和测试集在不同监测点的真实值和预测值的对比效果如图3所示.
| 表 2 最优参数组 |
图3中黑色曲线为隧道沉降监测真实值, 灰色曲线为贝叶斯优化XGBoost模型的预测结果, 从图中可以发现, 两条曲线重合度较高, 这表明在不同的沉降监测点, 贝叶斯优化的XGBoost沉降预测模型的曲线趋势能够与隧道监测数据的周边收敛、地表沉降和拱顶沉降真实数据高精度吻合, 预测误差较小.
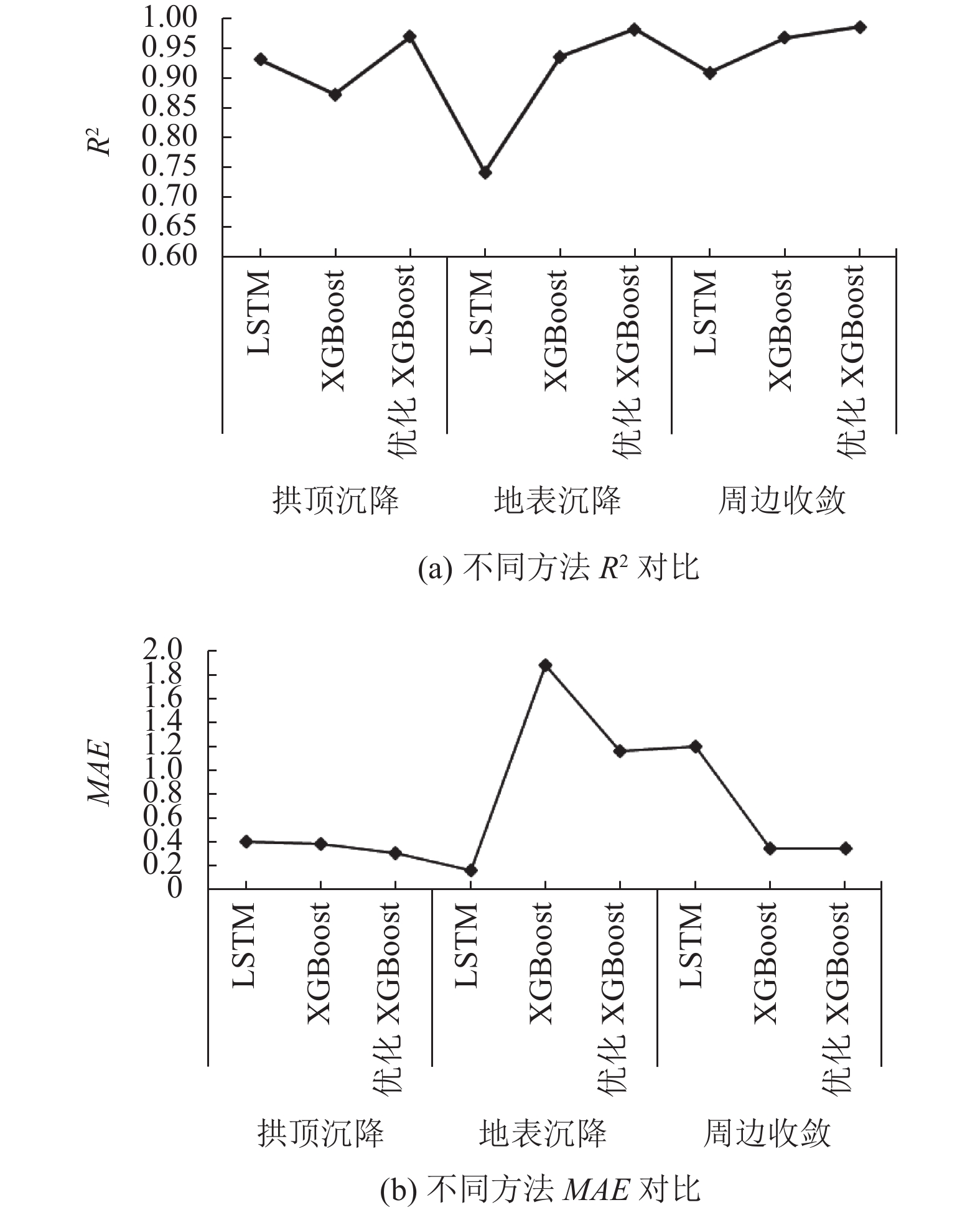
训练时序预测较优的LSTM模型[17, 18]和原始XGBoost模型与贝叶斯优化的XGBoost模型进行对比验证, 预测结果由表3可得: 总体来说基于贝叶斯优化的XGBoost模型对隧道3种不同位置的沉降预测效果最好, 平均精度最高, 达到0.979 4. 同时由图4可得优化的XGBoost模型对拱顶沉降, 地表沉降和周边收敛的预测效果均要优于LSTM. LSTM在对拱顶沉降和周边收敛的预测中精度达到0.9以上, 对地表沉降的预测效果偏低. 综上, 在实际的隧道施工监测工程中, 建立基于贝叶斯优化的XGBoost隧道沉降模型能更好地掌握隧道沉降变化规律, 服务隧道施工工程要求.
4 结论通过对实体工程隧道沉降监测数据进行整理, 对其中的拱顶沉降、周边收敛及地表沉降分别进行预测, 主要有以下结论.
|
图 3 最优模型训练及测试结果 |
(1)采用平均插值方法对时空尺度不对齐的监测数据进行尺度对齐, 对于孤立点异常和部分缺失监测数据, 融合时间空间信息采用长短时记忆网络对其进行修复, 大大提高后期沉降预测的准确性和程序可执行性.
(2)以沙岭壕隧道、十里坡隧道、中坪隧道以及白家庄隧道的监测点实测数据为样本建立贝叶斯优化的XGBoost模型, 分析结果表明在不同位置的沉降预测中贝叶斯优化的XGBoost模型表现均优于LSTM和原始XGBoost模型, 精度可以达到0.979 4, 能够达到工程监测要求.
在未来的研究中, 可以将重点转向隧道使用过程中的沉降变化量监测, 检测和采集更多指标数据构建隧道使用过程中各项指标的演变模型.
| 表 3 不同方法预测结果对比 |
|
图 4 不同方法预测结果对比 |
| [1] |
林晓东, 林浩. 考虑序列关联性的公路隧道沉降预测模型. 中外公路, 2019, 39(5): 183-188. |
| [2] |
周立俊, 黄腾, 王思捷, 等. 基于GA-SVR的地铁隧道沉降预测. 地理空间信息, 2021, 19(3): 115-117. DOI:10.3969/j.issn.1672-4623.2021.03.032 |
| [3] |
岳岭, 刘方, 刘辉, 等. 基于人工神经网络的大直径盾构隧道施工地层变形预测分析. 铁道标准设计, 2020, 64(1): 122-126. |
| [4] |
赵紫龙. 基于小波分解的差分灰色神经网络-AR模型及其在地铁隧道沉降预测中应用研究. 测绘通报, 2020(S1): 99-103. |
| [5] |
宋方方. 盾构双线隧道不同步施工对地表沉降的影响效应研究. 铁道建筑技术, 2020(9): 40-44, 74. DOI:10.3969/j.issn.1009-4539.2020.09.009 |
| [6] |
吴大勇. 小寨山隧道洞口段塌方成因分析及变形预测. 长江科学院院报, 2020, 37(9): 79-86, 95. DOI:10.11988/ckyyb.20190561 |
| [7] |
曾学宏, 赵义花. LSTM网络在地铁隧道沉降预测中的应用研究. 甘肃科学学报, 2019, 31(6): 117-122. |
| [8] |
赵振华, 胡锡鹏, 孙鹤明, 等. 城市盾构隧道施工地表沉降BP神经网络预测应用研究. 路基工程, 2020(4): 170-175. |
| [9] |
潘恺, 田林亚, 李成成. 动态灰色时序神经网络组合模型在地铁运营期沉降预测效果分析. 勘察科学技术, 2019(2): 49-52. DOI:10.3969/j.issn.1001-3946.2019.02.011 |
| [10] |
李伟, 严珂, 陆慧娟, 等. 基于Adaboost. RT算法的隧道沉降时间序列预测研究. 中国计量大学学报, 2019, 30(3): 331-336. |
| [11] |
姚凯, 朱向阳, 张克宏, 等. 基于FOA-GRNN的软岩隧道围岩变形预测模型. 地下空间与工程学报, 2019, 15(S2): 908-913. |
| [12] |
明祖涛, 游振兴, 张届, 等. 高速铁路桥隧沉降预测模型的研究. 测绘通报, 2011(8): 17-19, 41. |
| [13] |
毕旋旋, 任超, 邓开元, 等. 小波-ARIMA模型在贵广高铁隧道沉降预测中的应用. 桂林理工大学学报, 2020, 40(1): 156-160. |
| [14] |
莫云, 岳昊, 胡斌, 等. 基于Logistic预测模型的地铁隧道地表沉降预测研究. 工程地球物理学报, 2010, 7(1): 115-119. DOI:10.3969/j.issn.1672-7940.2010.01.024 |
| [15] |
Pei LL, Sun ZY, Yu T, et al. Pavement aggregate shape classification based on extreme gradient boosting. Construction and Building Materials, 2020, 256: 119356. DOI:10.1016/j.conbuildmat.2020.119356 |
| [16] |
徐韧, 苏怀智, 杨立夫. 基于GP-XGBoost的大坝变形预测模型. 水利水电科技进展, 2021, 41(5): 41-46, 70. DOI:10.3880/j.issn.1006.7647.2021.05.007 |
| [17] |
杨青, 王晨蔚. 基于深度学习LSTM神经网络的全球股票指数预测研究. 统计研究, 2019, 36(3): 65-77. |
| [18] |
卢诗扬, 张雷蕾, 潘家荣, 等. 拉曼光谱结合LSTM长短期记忆网络的樱桃产地鉴别研究. 光谱学与光谱分析, 2021, 41(4): 1177-1181. |
 2022, Vol. 31
2022, Vol. 31



