随着社会的发展和科技的进步, 化工过程和设备变得更加复杂与多样化, 故障诊断也成为了当代过程监控中的一项重要任务^{[1, 2]}. 近年来, 由于信息技术的快速发展, 使得工业过程中的数据可以大量采集并保存, 因此基于数据驱动的故障诊断相关方法得到了学者们的广泛关注^{[3, 4]}. 除了基于数据驱动的方法外, 基于数学模型的方法及基于知识的方法也都是常用方法. 然而基于数学模型的方法存在着模型建立难、诊断的结果直接受模型准确性影响等问题, 因此在复杂系统中该类方法的使用受到限制; 基于知识的方法则需要大量的经验和专家知识来建立知识库, 通用性差. 而基于数据驱动的方法直接对数据进行分析, 能够规避上述两类方法存在的问题, 因此目前在复杂系统中使用更多^[5-7].

故障分类技术在数据挖掘和机器学习领域得到快速发展, 但是大多数的分类方法均假设其训练集中的各类样本数相似或相等, 当训练集呈现数据不平衡特征时, 分类性能通常并不令人满意. 张剑飞等^[8]指出不平衡数据的分类问题广泛出现在疾病诊断、垃圾邮件处理、信用卡检测等领域, 但传统的机器学习算法在数据不平衡比过大时, 分类效果会急剧下降. Japkowicz等^[9]指出利用决策树处理不平衡数据时, 训练过程会被多数类的样本主导, 导致对少数类的样本识别率低. 为了提高对不平衡数据的分类性能, 目前常采用的方法主要包括两个方面: 数据层面和算法层面^{[10, 11]}. 在数据层面, 为降低数据的不平衡比, 通常会采取欠采样或过采样的方法改变训练样本的数量. Liu等^[12]提出了一种EasyEnsemble的欠采样方法, 该方法通过从多数类样本中有放回的随机采样出n个每个子集, 使子集的样本数与少数类近似相等, 并将各子集分别与少数类样本合并进行训练, 从而达到保留多数类样本信息的目的. Chawla等^[13]提出了一种SMOTE (synthetic minority oversampling technique)的过采样方法, 通过对少数类中的某个样本及其邻近样本进行叠加, 产生人造样本来降低样本间的不平衡度. 虽然上述方法对部分场景下的不平衡数据问题具有一定的效果, 但是它们仍有一些不足之处需要改进. 由此, 更复杂的重采样技术被提出. 张天翼等^[14]提出了一种改进SMOTE的重采样方法, 通过将合成样本从一维空间扩展至更高维空间, 使新样本更加多样化. 李忠智等^[15]结合卷积神经网络和生成对抗网络, 利用卷积神经网络从故障样本中提取训练特征后输入至对抗网络, 并由解码器网络来生成新的故障样本. Chen等^[16]提出了一种K-means Bayes方法, 利用T阈值K-means在既不减少多数类样本也不增加少数类样本的前提下, 提高对少数类故障的识别能力. 在算法层面, 通常是对现有的分类算法进行修改, 以增强对少数类的学习能力. 如代价敏感学习、集成算法等.

Bayes和SVM是故障诊断领域常用的两种方法. Lemnaru等^[17]指出Bayes和SVM使用的前提是不同类型样本的数据量近似相等, 当数据不平衡严重时, 这两种方法通常会表现出较差的分类性能. Zhang等^[18]将D-S证据理论应用于多分类器实现故障监控, 有效提高了分类性能. 本文主要研究数据不平衡的算法层面, 同时考虑到单一方法在这种数据不平衡条件下的局限性, 提出了一种基于多分类器融合的故障分类方法. 选择K-means Bayes作为分类模型1, AdaBoost-SVM作为分类模型2, 并利用D-S证据理论将二者的分类结果进行融合, 进一步提升分类性能. 将该方法运用在Tennessee Eastman (TE)数据集上, 经仿真和实验证明了所提方法的有效性及可行性.

1 K-means Bayes算法 1.1 Naive Bayes

Naive Bayes是一种基于贝叶斯定理和条件独立性假设的分类方法^[19]. 给定一组训练数据 $T = \{ ({x_1}, {y_1}), ({x_2}, {y_2}), \cdots, ({x_N}, {y_N}){\text{\} }}$ , 其中, $N$ 为训练样本总数, ${x_i} = {\{ x_i^{(1)}, x_i^{(2)}, \cdots, x_i^{(n)}\} ^{\rm T}}$ 为每一个样本数据, ${y_i} = \{ {C_1}, {C_2}, \cdots, {C_k}\}$ 为各样本数据对应的标签, 对于一个测试样本 $x$ , Bayes分类器将后验概率 $P(Y = {C_k}|X = x)$ 最大的类作为 $x$ 的类输出:

$ P(Y = {C_k}|X = x) = \frac{{P(X = x|Y = {C_k})P(Y = {C_k})}}{{P(X = x)}} $

(1)

依据条件独立性假设, 且每个连续变量 ${x^{(j)}}$ 均服从高斯分布:

$ P({X^{(j)}} = {x^{(j)}}|Y = {C_k})\sim N({\mu _{{C_k}, j}}, \sigma _{{C_k}, j}^2) $

(2)

对于样本 $ x $ 的分类结果为:

$ y = \mathop {\arg \max }\limits_{{C_k}} {\kern 1pt} {\kern 1pt} P(Y = {C_k})\prod\limits_{j = 1}^n {P({X^{(j)}} = {x^{(j)}}|Y = {C_k})} $

(3)

1.2 K-means Bayes

K-means Bayes算法^[16]的思想为: 在不改变原始数据集信息的情况下降低数据不平衡性对故障分类带来的影响. 算法步骤如算法1.

算法1. K-means对多数类均分

1) 给定多数类样本 $\scriptstyle X = \left[ {{x_1}, {x_2}, \cdots, {x_m}} \right]$ , 标准化得到 $\scriptstyle {X^{\text{*}}}$ ;

2) 指定 $\scriptstyle k$ 个聚类子集: 从 $\scriptstyle {X^{\text{*}}}$ 中随机选择 $\scriptstyle k$ 个样本点作为初始聚类中心 $\scriptstyle \;\mu $ , 并计算各子集的样本数 $\scriptstyle T = m/k$ ;

3) 设置2个集合 $\scriptstyle U = \left\{ {{U_1}, \cdots, {U_k}} \right\}$ 和 $\scriptstyle {U^{\text{*}}} = \left\{ {U_1^*, \cdots, U_k^*} \right\}$ , 其中 $\scriptstyle {U_i}$ 存放原始样本数据, $\scriptstyle U_i^*$ 存放标准化后的数据;

4) 对 $\scriptstyle {X^*}$ 的各样本 $\scriptstyle {x^{\text{*}}}$ , 计算与各聚类中心的距离, 找出距离最近的 $\scriptstyle \;{\mu _i}$ 及对应的 $\scriptstyle U_i^*$ ;

5) 判断 $\scriptstyle U_i^*$ 的样本数 $\scriptstyle {n_i}$ 是否 $\scriptstyle \leqslant T$ . 若 $\scriptstyle {n_i} \leqslant T$ , 则将 $\scriptstyle {x^{\text{*}}}$ 和对应的 $\scriptstyle x$ 分别分配至 $\scriptstyle U_i^*$ 和 $\scriptstyle {U_i}$ , 并转至4)对下一个样本进行计算; 若 $\scriptstyle {n_i} \geqslant T$ , 则该样本将不再分至 $\scriptstyle {U_i}$ , 并转至4)重新计算;

6) 当所有样本完成分类后, 计算各子集 $\scriptstyle U_i^*$ 的样本均值, 并作为新的聚类中心 $\scriptstyle \;\mu _i^{'}$ , 并判断各 $\scriptstyle \;{\mu _i}$ 与 $\scriptstyle \;\mu _i^{'}$ 是否相等; 若 $\scriptstyle \;{\mu _i} = \mu _i^{'}$ 则算法终止输出结果 $\scriptstyle {U_i}$ , 否则返回3)进行下一轮计算.

对于测试样本 $x$ , 可利用式(3)预测其类别, 再利用式(4)转换成实际类别:

$ {y_{\rm real}} = \left\{ \begin{gathered} 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y \in [1, k] \hfill \\ y - k + 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y \in [k + 1, k + c] \hfill \\ \end{gathered} \right. $

(4)

2 AdaBoost-SVM算法 2.1 SVM

SVM (support vector machine)^[20]是一种有监督的二分类模型, 其思想是寻找到一个分离超平面, 此超平面不仅能正确划分开正负实例点, 还能使离超平面最近的点(支持向量)离超平面尽可能的远. 给定一组线性可分的训练数据集 $T = \{ ({x_1}, {y_1}), \cdots, ({x_N}, {y_N})\} $ , 其中 ${x_i} \in X \in {{R}^n}$ , ${y_i} \in Y \in \{ + 1, - 1\} $ , 则分离超平面为:

$ wx + b = 0 $

(5)

分类决策函数为:

$ f(x) = {\rm sign}(wx + b) $

(6)

为解决多分类问题, 通常将多分类问题进行拆分并利用投票机制进行分类. 常用的拆分策略包括“一对多”和“一对一”, 本文使用“一对一”策略, 这样由少数类构成的子分类器的正类和负类可看成是平衡的, 有利于提高分类性能. 由于可能存在子分类器对某些类的分类能力较差, 影响最终的投票结果, 因此引入AdaBoost分类器替换^{[21, 22]}.

2.2 AdaBoost

AdaBoost (adapative boost)^[23]是提升学习Boosting里的一种, 其思想是通过反复学习得到一系列的弱分类器, 并将这些弱分类器进行加权组合得到一个强分类器.

算法2. AdaBoost-SVM

1) 设置每个子分类器的最低分类正确率 $\scriptstyle A{{c}}{{{c}}_{\min }}$ ;

2) 根据类别总数n构建SVM子分类器, 其中子分类器总数为 $\scriptstyle N = C_n^2$ ;

3) 对各SVM子分类器进行训练, 其中核函数选择径向基核函数(RBF), 并利用网格法和三折交叉验证法进行参数寻优, 选择合适的惩罚参数C及核参数g;

4) 对训练好的分类器在相应的测试集上进行分类, 计算各子分类器的实际正确率 $\scriptstyle A{{c}}{{{c}}_{\rm real}}$ ;

5) 若某个分类器的 $\scriptstyle A{{c}}{{{c}}_{\rm real}} < A{{c}}{{{c}}_{\min }}$ , 则使用AdaBoost分类器对其进行替换. 初始化AdaBoost的弱分类器个数为10个, 各样本的初始化权重 $\scriptstyle w=1/Coun{t}_{样本} $ ;

6) 使用相同的测试集计算AdaBoost分类器的分类正确率 $\scriptstyle A{{cc}}_{{\text{real}}}^*$ , 若 $\scriptstyle A{{cc}}_{{\text{real}}}^* \geqslant A{{c}}{{{c}}_{{\text{real}}}}$ , 则选择替换, 否则不替换.

3 决策融合算法 3.1 故障分类框架

如果能设计出一种在任何情况下都具有良好泛化性能的分类器, 那么单一分类器就已经能够满足需要. 然而实际采集到的数据存在着噪声点、异常等问题, 使得上述的单一分类器难以实现. 因此考虑创建一个故障分类系统, 该系统中存在两个及以上的分类器, 并希望其分类性能优于其中任意单一分类器. 当某个分类器在识别时发生错误, 其他分类器可以纠正该分类器的错误.

图1展示了一种基于D-S证据理论的故障分类框架. 该框架主要分为两个部分: 利用训练数据进行离线建模、利用建立好的模型对数据进行在线分类. 具体来说, 本系统的实施主要包括3个步骤: 1)分类器构建; 2)计算各分类器的融合矩阵; 3)利用D-S证据理论进行决策融合.

3.2 计算各分类器的融合矩阵

为了进行D-S证据理论融合, 应计算出各分类器的融合矩阵^[18]. 假设样本类别集合 $T = \left\{ {{F_1}, {F_2}, \cdots, {F_n}\} } \right.$ , 其中第 $i$ 个类别称为 ${F_i}$ , $i = 1, 2, \cdots, n$ , $n$ 为所有类别的总数. 分类器总个数为 $N$ , 其中第 $k$ 个分类器的融合矩阵表示为 $F{M^k}$ , $k = 1, 2, \cdots, N$ . 则 $F{M^k}$ 可表示如式(7). 其中 $F{M^k}$ 的行代表真实类别 ${F}_{1},{F}_{2},\cdots,{F}_{n}$ , 列代表由该分类器预测出的类别 ${F}_{1},{F}_{2},\cdots,{F}_{n}$ , 元素 $N_{ij}^k$ 表示由该分类器预测类别为 ${F_j}$ 而真实类别为 ${F_i}$ 的样本数之和. 因此对于每个分类器的融合矩阵 $ F{M^k} $ 而言, 矩阵的每列之和为定值1.

$ F{M^k} = \left[ {\begin{array}{*{20}{c}} {\frac{{N_{11}^k}}{{\displaystyle\sum\limits_{i = 1}^n {N_{i1}^k} }}}&{\frac{{N_{12}^k}}{{\displaystyle\sum\limits_{i = 1}^n {N_{i2}^k} }}}& \cdots &{\frac{{N_{1n}^k}}{{\displaystyle\sum\limits_{i = 1}^n {N_{in}^k} }}} \\ {\frac{{N_{21}^k}}{{\displaystyle\sum\limits_{i = 1}^n {N_{i1}^k} }}}&{\frac{{N_{22}^k}}{{\displaystyle\sum\limits_{i = 1}^n {N_{i2}^k} }}}& \cdots &{\frac{{N_{2n}^k}}{{\displaystyle\sum\limits_{i = 1}^n {N_{in}^k} }}} \\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{N_{c1}^k}}{{\displaystyle\sum\limits_{i = 1}^n {N_{i1}^k} }}}&{\frac{{N_{c2}^k}}{{\displaystyle\sum\limits_{i = 1}^n {N_{i2}^k} }}}& \ldots &{\frac{{N_{nn}^k}}{{\displaystyle\sum\limits_{i = 1}^n {N_{in}^k} }}} \end{array}} \right] $

(7)

3.3 基于D-S证据理论的决策融合

1) 计算分类器对某个样本 $x$ 的预测类别为 ${F_j}$ 时对应 ${F_i}$ 的基本概率分配(BPA):

$ {m_k}({F_i}) = \frac{{N_{ij}^k}}{{\displaystyle\sum\limits_{i = 1}^n {N_{ij}^k} }} $

(8)

2) 依据D-S融合规则计算联合BPA值:

$ \left\{ \begin{gathered} BPA(A) = \frac{1}{K}\sum\limits_{{A_1} \cap \cdots \cap {A_n} = A} {{m_1}({A_1}) \cdots {m_n}({A_n})} \hfill \\ K = \sum\limits_{{A_1} \cap \cdots \cap {A_N} \ne \Phi } {{m_1}({A_1}){m_2}({A_2}) \cdots {m_n}({A_n})} \hfill \\ \end{gathered} \right. $

(9)

3) 选择最大的联合BPA值所对应的类别 ${F_i}$ 作为最终决策:

$ Fina{l_{DS}} = \mathop {\arg \max }\limits_{i \in [1, {\kern 1pt} n]} [{m_{1, 2, \cdots, N}}({F_i})] $

(10)

4 仿真实验 4.1 TE过程

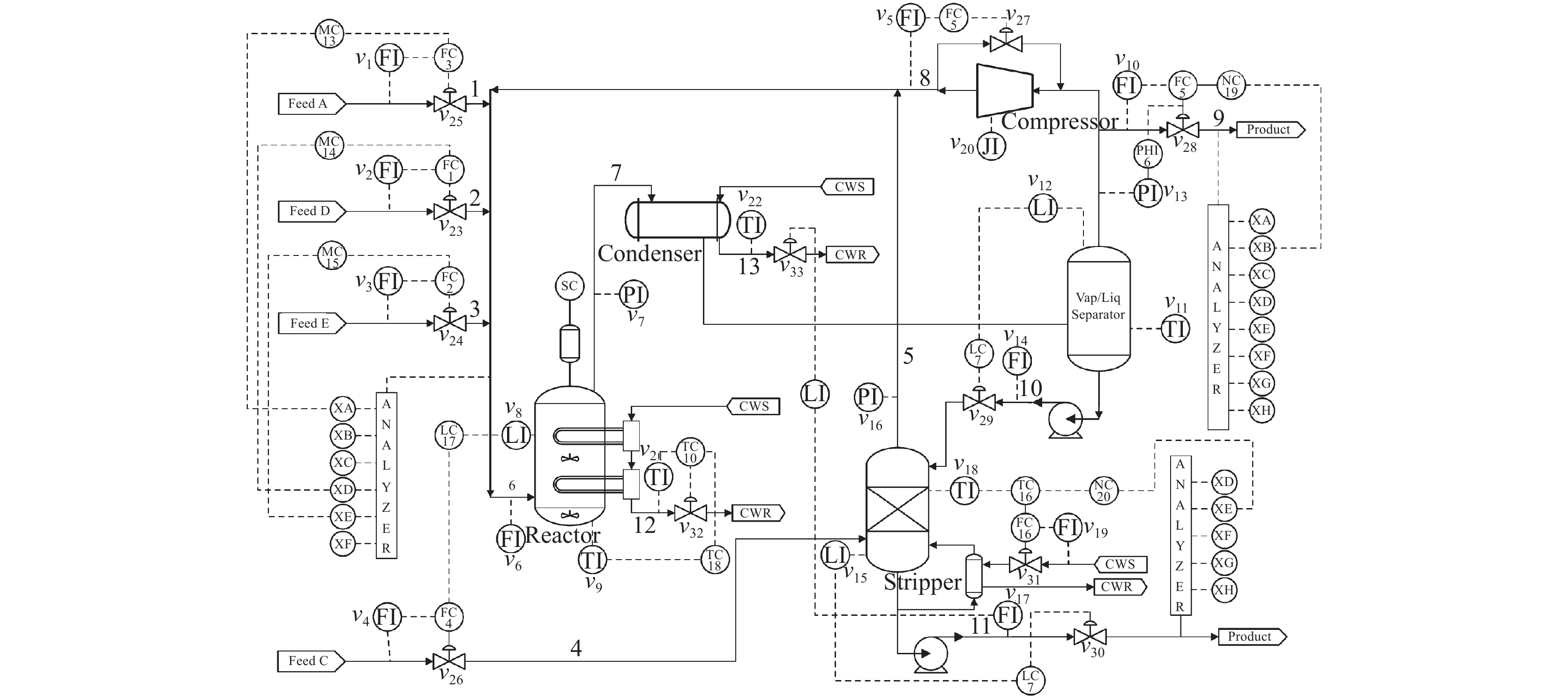
本文所提到算法均以TE过程数据为基础. TE过程由伊斯曼化学公司所创建, 该仿真模型在真实化工过程基础上构建^[24]. 其工艺流图如图2. 该过程通过4种气态反应物(A、C、D、E)和惰性成分B生成产品G、H及副产品F. TE数据可由开源的Simulink代码生成, 数据集共包括41个测量变量和11个控制变量, 数据除正常类型外还包括21种不同类型的故障, 本文所使用的故障类型如表1. 部分仿真结果如图3.

4.2 仿真结果及分析

图3(a)为利用Naive Bayes进行故障分类的结果, 测试集的分类正确率为62.1%, 可以看出该方法在这种不平衡数据下的分类能力较差; 图3(b)为利用EasyEnsemble Bayes的分类结果, 通过EasyEnsemble将正常类样本有放回的抽取15组, 每组10个样本并分别与故障样本组合, 最终的分类正确率为65.4%, 与Naive Bayes相比略有提升, 但故障1和故障14的识别率依然较低, 说明EasyEnsemble方法并不能完全解决数据稀缺性带来的问题; 图3(c)为利用SMOTE Bayes的分类结果, 通过SMOTE为每个少数类增加10个合成样本, 在一定程度上弥补了少数类样本的稀缺性. 但利用这种方式对测试集的分类结果不理想, 甚至低于Naive Bayes, 且经实验仿真发现利用SMOTE分别为每个少数类依次增加20个、30个、40个样本时, 预测的准确率也几乎没有提升, 其原因可能在于所使用的部分训练样本本身处于所在样本集的分布边缘, 则由此及其相邻样本产生的人造样本也会处于这个边缘, 且会越来越边缘化, 从而使分类更加的困难; 图4(d)、图4(e)为利用K-means Bayes的分类结果, 当分类子集数k=450时, 与前几种方法相比正确率得到显著提升, 预测的准确率达到了76.0%, 但对故障1、6的分类能力仍存在一定的缺陷.

SVM是一种经典的二分类学习算法, 在使用SVM之前, 为解决多分类问题, 本文选择“一对一”策略对多分类问题进行拆分, 如表2所示. 通过构建10个子分类器, 对测试集样本进行分类预测, 正确率为70%, 如图4所示, 且对故障1和故障14的分类能力差. 通过分析各SVM子分类器的分类性能, 发现C1、C4、C6、C7及C10这5个子分类器对对应测试样本的分类能力差.

为克服上述5个子分类器分类能力差的问题, 本文利用AdaBoost算法构建5个强分类器, 分别替代原SVM的C1、C4、C6、C7及C10再重新进行预测, 如图5所示. AdaBoost-SVM的最终预测正确率为80.7%, 除故障14外其余类型样本预测均比较准确, 其原因为利用AdaBoost构建的C4分类器依然无法正确识别故障14类型的样本.

为进一步提高分类性能, 使用本文提出的决策融合算法, 选择K-means Bayes和AdaBoost-SVM的预测结果作为证据体计算融合矩阵, 并进行D-S融合, 分类正确率达到93.1%, 结果如图6、图7所示.

在上述2个融合矩阵中, 矩阵的行表示数据的真实标签分类, 列表示利用模型的预测分类, 矩阵的每一列元素和为1. 由于AdaBoost-SVM对所有测试样本均未分类到故障14, 故融合矩阵中缺少预测为故障14的列. 表3展示了故障分类的部分信息融合过程, 根据各分类器对某个测试样本的预测结果, 选择对应的融合矩阵中的数据实现数据融合.

5 结论与展望

本文针对不平衡数据的故障分类问题, 分别提出了K-means Bayes和AdaBoost-SVM的分类策略. 利用K-means对多数类的样本划分为K个子集, 在不丢失多数类样本信息的前提下降低了不平衡度, 提高了Bayes的分类准确率; 利用AdaBoost对分类能力较差的SVM子分类器进行替换, 提高了SVM的分类准确率; 再利用D-S证据理论对二者的预测结果进行融合, 得到更好的分类结果. 由基于TE过程的仿真结果可知, 本文提出的决策融合算法与单一的传统算法相比具有更好的故障分类性能.