2. 黄山旅游集团水电开发有限公司, 黄山 245899;
3. 南京航空航天大学 经济与管理学院, 南京 211106
2. Huangshan Tourism Group Hydropower Development Co. Ltd., Huangshan 245899, China;
3. School of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China
时间序列预测在许多工业和商业应用中发挥着重要作用, 例如金融市场、网络流量、天气预报和供水行业等. 在这些场景中, 人们可以利用大量关于过去行为的时间序列数据来预测将来的值[1-3]. 时间序列预测的主要挑战是提高预测能力以满足日益增长的多步预测需求. 目前, 时间序列预测在实际应用中关系到经济社会生活的各个方面. 因此, 在这项工作中, 本文将研究时间序列的多步预测性能.
传统的线性回归方法主要包括自回归, 移动平均, 自回归综合移动平均模型(ARIMA)等. 而非线性机器学习模型主要包括人工神经网络、支持向量回归和梯度提升决策树等[4-6], 它们在时间序列预测方面也取得了良好的效果. 目前, 深度学习技术可以更加高效的提取数据的特征. 经典深度学习框架有深度神经网络, 卷积神经网络, 循环神经网络(RNN)[7]等. RNN是一种在时间上进行递归的神经网络, 但它存在梯度消失和梯度爆炸的问题. 长短期记忆网络(LSTM)[8]使用3个门控机制来解决梯度爆炸和梯度消失问题, 它在长序列预测中表现得更好. 门控循环单元(GRU)[9]作为LSTM的变体, GRU与LSTM具有相似的性能, 它简化了LSTM的门控结构, 降低了网络的训练时间. 然而这些方法在对序列数据中的长期和复杂关系进行建模时仍然具有局限性. 为了提高预测精度很多信号处理方法被用于时间序列预测, 在这些模型中, 信号处理方法将时间序列进行分解和去噪处理[10, 11]. 在时间序列数据中, 不同的数据分量可能具有不同的特征, 现有的常见混合模型无法充分利用不同分量的特征.
为了解决上述问题, 本文提出了一种新型的混合多步预测模型. 通过采用奇异谱分析对数据进行预处理, 再结合本文设计的自动编码器网络结构对预处理后的数据进行预测, 可以实现对复杂数据建模的能力. 主要贡献如下:
1) 提出了一种端到端的时间序列预测混合模型, 该模型可以用于时间序列数据的多步预测. 该混合模型的预测精度优于单一模型.
2) 采用SSA将原始时间序列数据分解为不同的趋势分量, SSA可以从原始数据中提取数据的不同趋势信息. 同时设计了新的基于ConvLSTM和BiGRU自动编码器结构, 该模型能够进行短期和长期特征学习.
3) 使用真实世界的2个供水数据集和3个公开的时间序列数据集评价所提出的模型. 实验结果表明, 与所有基线方法相比, 该模型在多步预测评价指标下几乎都获得了最好的预测性能, 证明了模型在时间序列预测方面的优越性.
本文的其余部分安排如下: 第1节介绍了相关的工作. 第2节阐述了所提出模型的设计与实现. 第3节评价了模型的预测性能, 并对实验结果进行了详细讨论. 第4节对本文进行总结.
1 相关工作目前, 为了更好地提高时间序列预测的准确性, 很多信号处理的方法被用于时间序列预测. 例如, Zhang等人[12]采用小波变换(WT)获取交通流的时变和周期性特征, 建立了季节性ARIMA进行预测. Ahani等人[13]提出了一种多步预测系统, 集成了经验模式分解(EEMD), 最小二乘支持向量回归(LSSVR)和长短期记忆神经网络(LSTM). Chang等人[14]提出了一种基于小波变换和Adam优化的LSTM神经网络混合模型, 用于时间序列数据预测. 此外, 很多方法采用了数据分解技术来提取数据不同的趋势信息进行预测. 例如, Tang等人[15]通过WT和SSA对金融时间序列进行分解重构去噪, 将平滑序列引入LSTM得到预测值. Li等人[16]利用变分模式分解(VMD)将非平稳月降水时间序列分解为几个相对稳定的固有模式函数(IMFs), 然后为每个IMF建立一个极限学习机预测模型, 最后将预测值累加得到预测结果. Liu等人[17]采用SSA将原始数据进行分解, 同时使用CNNGRU和SVR分别预测不同的分量数据. Zhu等人[18]通过VMD来捕捉时间序列的趋势和可变性信息, 通过引入双向门控循环单元实现对天然橡胶期货的短期预测. 在这些信号处理方法中, WT可以提取时频信息, EEMD和VMD可以提取趋势信息. 然而, SSA具有严格的数学理论和少量的参数, 并且可以有效地提取信号的趋势信息, 因此被选为信号处理的方法.
由于深度学习算法在数据特征提取方面的强大功能, 目前也有大量的工作在时间序列预测领域取得了令人瞩目的成绩. 例如, Sagheer等人[19]提出了一种深度长短期记忆(DLSTM)模型用来捕捉时间序列数据中的非线性动态和长期依赖关系. Zhang等人[20]提出了一种基于双向长短期记忆(Bi-LSTM)网络模型用于时间序列数据的预测. Hu等人[21]采用了一种将卷积神经网络与双向长短期记忆网络相结合的模型, 用于预测城市的用水需求. Essien等人[22]提出了一种用于多步预测的端到端模型, 该模型包含一个深度ConvLSTM编码器-解码器架构, 应用于智能工厂时间序列数据的预测. Salinas等人[23]提出了DeepAR, 这是一种产生精确概率预测的方法, 基于对大量相关时间序列训练自动回归的递归网络模型. 因此, 深度学习方法在时间序列预测方面具有广泛的应用. 同时, 它们使用由多个非线性变换组成的架构来映射数据中的高级抽象.
根据以上文献, 信号处理方法和深度学习方法在时间序列预测方面有着广泛的使用. 然而, 由于不同数据具有不同的特征, 单一的深度学习方法在对数据中的长期和复杂关系进行建模时具有一定的局限性. 基于此背景, 在本研究中, 提出了一种新的混合模型. 使用奇异谱分析对数据进行预处理, 再结合本文设计的自动编码器网络用于对预处理后的数据进行预测, 该模型可用于供水数据的预测, 同时模型也可以应用于其他时间序列数据的预测任务.
2 方法 2.1 问题描述在本研究中, 多步(即序列到序列)预测是一个重要的时间序列预测问题, 本文将时间序列预测制定为有监督的机器学习任务. 多步时间序列预测的目标是使用大量关于过去行为的时间序列数据来预测将来的值, 给定一个一维的单变量时间序列,
| $ \hat Y = ({y_{t + 1}}, {y_{t + 2}} \cdots , {y_{t{\text{ + }}k}}) = f({x_{t - w + 1}}, \cdots , {x_{t - 1}}, {x_t}) $ | (1) |
其中,
在本节中, 将描述如何使用SSA-ConvBiAE模型实现时间序列数据的预测任务. SSA-ConvBiAE模型的总体流程如图1所示. 首先, 对原始数据进行处理, 主要是对数据的缺失值进行填充和归一化操作, 处理后的数据被划分为训练集和测试集; 通过数据分解步骤, 将训练集和测试集进行分解和重构, 来获取不同趋势的分量数据; 然后, 将获取到的训练集不同的分量数据分别输入到自动编码器网络用于模型的训练, 经过迭代保存训练好的模型. 最后, 将测试集分量输入到对应训练好的模型中用于预测, 将不同分量的预测结果相加得到最终的预测结果.
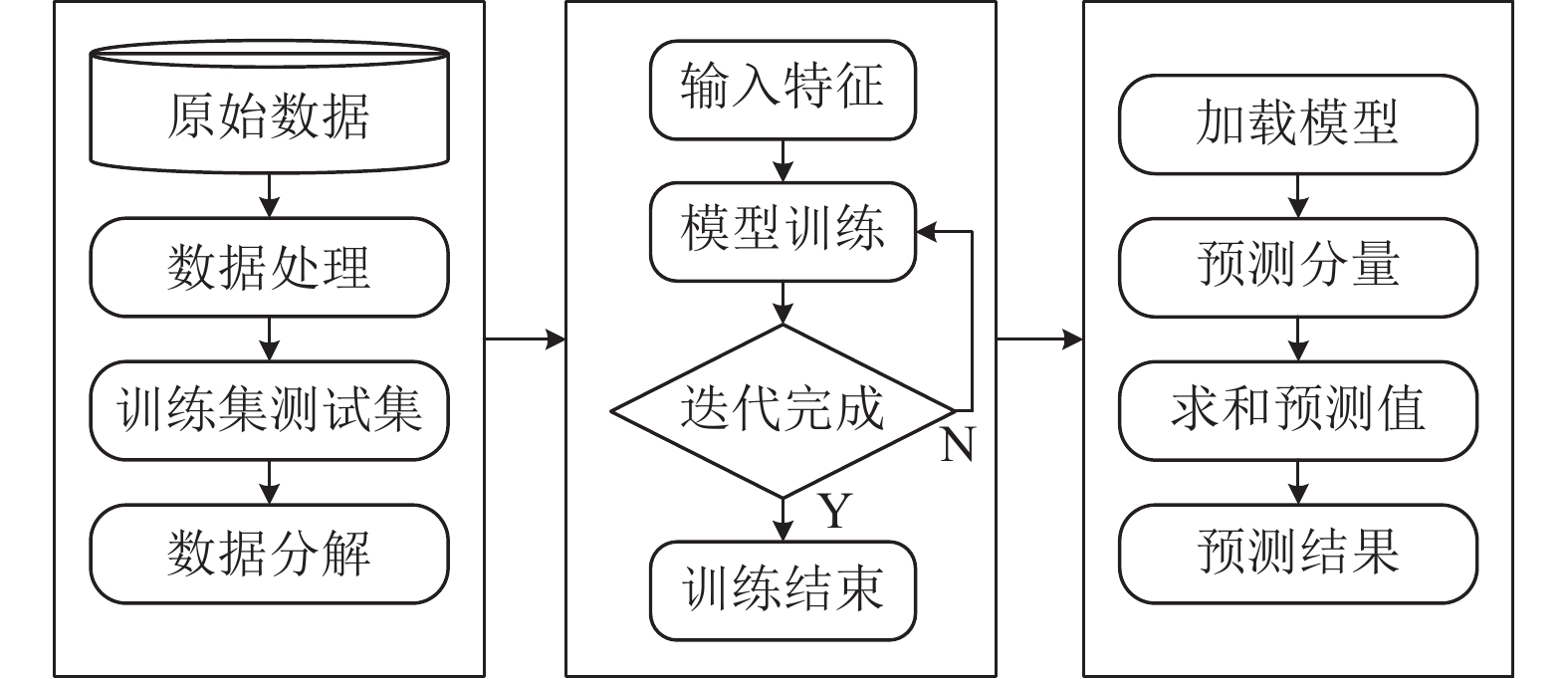
|
图 1 总体预测模型的管线图 |
2.3 提出的模型
本文提出的SSA-ConvBiAE模型的整个过程如图2所示, 详细说明如下.
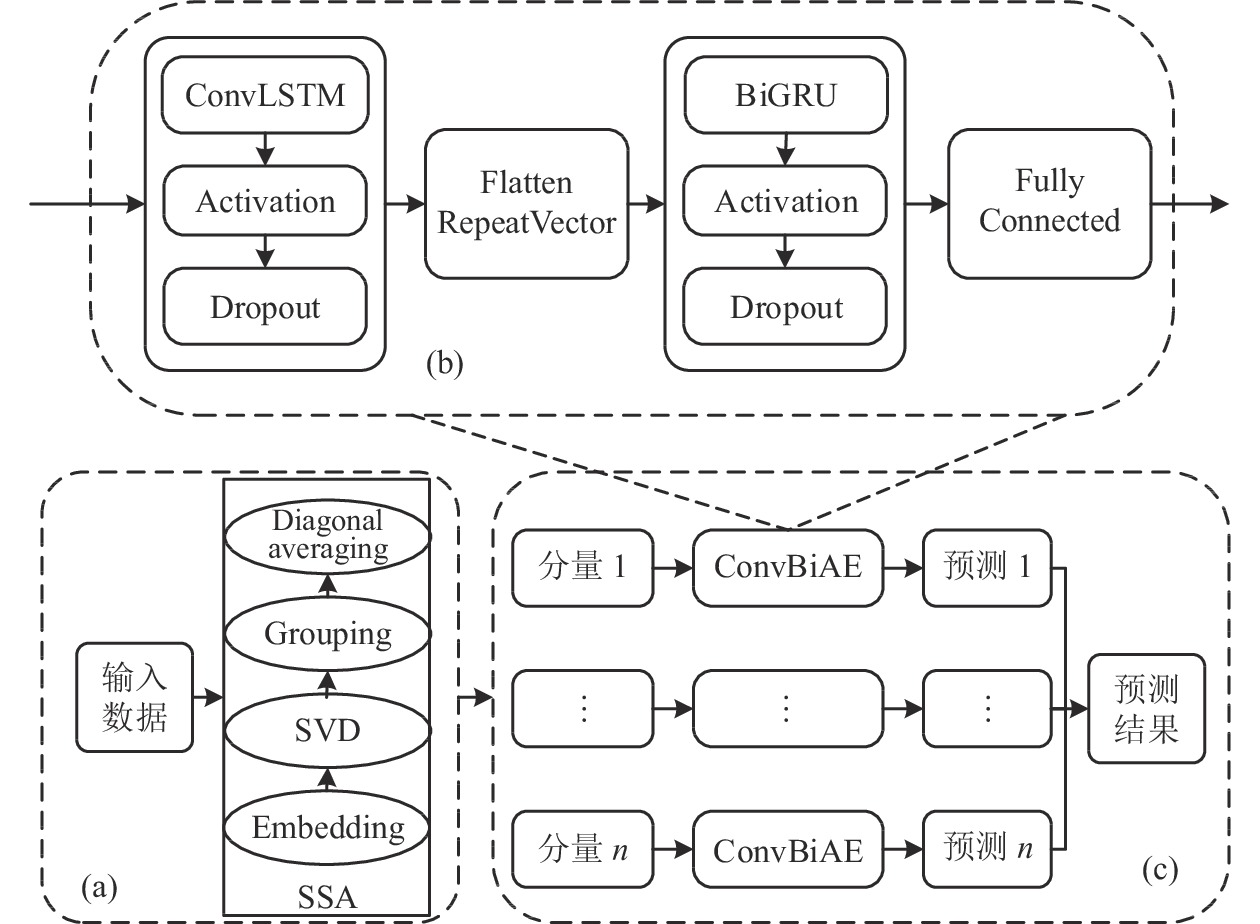
|
图 2 SSA-ConvBiAE模型结构图 |
2.3.1 数据分解
为了提高模型预测的准确性, 采用SSA信号处理方法将原始的时间序列数据进行预处理, SSA是用于时间序列分析有效的非参数算法, SSA可以有效地实现信号的分解和重构. 此外, SSA具有严格的数学理论和较少的参数, 并且可以很好地识别时间序列的周期、准周期和趋势信息. 本文选择这种非参数方法将原始的时间序列分解并从原始数据中提取不同的趋势分量. 具体如图2(a)所示, SSA经过4个步骤分别是: 嵌入(embedding)、奇异值分解(SVD)、分组(grouping)和对角平均化(diagonal averaging), 可以将原始的时间序列数据进行分解和重构, 并获取数据不同的趋势信息, 用于模型的训练和预测. SSA的详细步骤描述如下:
1) 嵌入. 首先选择适当的窗口长度
| $ Z = \left( {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_K}} \\ {{x_2}}&{{x_3}}& \cdots &{{x_{K + 1}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{x_L}}&{{x_{L + 1}}}& \cdots &{{x_N}} \end{array}} \right) $ | (2) |
可以看出矩阵
2) 奇异值分解. 通过SVD, 轨迹矩阵
| $ Z = {Z_1} + {Z_2} + \cdots + {Z_d} $ | (3) |
其中,
3) 分组. 该过程将区间
| $ Z = {Z_{{I_1}}} + {Z_{{I_2}}} + \cdots + {Z_{{I_m}}} $ | (4) |
4) 对角平均化. 该过程旨在将分组序列的每个矩阵转换为长度为
| $ r{s_n}=\left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{n}\displaystyle\sum\limits_{m = 1}^n {{\textit{z}}_{m, n - m + 1}^ * , 1 \leqslant n \leqslant {L^ * }} } \\ {\dfrac{1}{{{L^ * }}}\displaystyle\sum\limits_{m = 1}^{{L^ * }} {{\textit{z}}_{m, n - m + 1}^ * , {L^ * } \leqslant n \leqslant {K^ * }} } \\ {\dfrac{1}{{N - n{\text{ + }}1}}\displaystyle\sum\limits_{m = n - {K^ * } + 1}^{N - {K^ * } + 1} {{\textit{z}}_{m, n - m + 1}^ * , {K^ * } \leqslant n \leqslant N} } \end{array}} \right. $ | (5) |
自动编码器可以解决序列到序列建模的问题, 其中输入和输出均为序列. 本文设计了基于ConvLSTM和BiGRU的自动编码器结构, 具体如图2(b)所示, 提出的网络模型结构主要分为编码器和解码器.
1) 编码器有一层ConvLSTM, 一层激活函数tanh和一层Dropout函数堆叠在一起作为编码层. ConvLSTM[24]作为LSTM的一种变体, 虽然LSTM可以有利地捕获长输入序列的长期依赖, 但它的各个门控结构之间采用的是由全连接的方式构建的, 因此模型在训练时需要更多的参数. 而ConvLSTM用卷积算子替换了全连接层算子, 使得它在输入到隐藏状态以及与各个门控结构之间的转换都具有卷积操作. ConvLSTM继承了卷积算子中稀疏连接和参数共享的优点, 可以减少全连接结构的冗余. 此外, ConvLSTM不仅能够提取时间特征, 通过卷积操作还可以有效对空间信息进行特征提取. 同时, ConvLSTM通过门控机制克服了梯度消失的问题, 也保留了LSTM可以捕获长时间记忆的优点. 因此, 本文选择ConvLSTM作为编码器. 它的计算公式如下:
| $ {i_t} = \sigma ({W_{xi}} * x{}_t + {W_{hi}} * {h_{t - 1}} + {W_{ci}} \circ {C_{t - 1}} + {b_i}) $ | (6) |
| $ {f_t} = \sigma ({W_{xf}} * x{}_t + {W_{hf}} * {h_{t - 1}} + {W_{cf}} \circ {C_{t - 1}} + {b_f}) $ | (7) |
| $ {C_t} = {f_t} \circ {C_{t - 1}} + {i_t} \circ \tanh ({W_{xc}} * {x_t} + {W_{hc}} * {h_{t - 1}} + {b_c}) $ | (8) |
| $ {o_t} = \sigma ({W_{xo}} * x{}_t + {W_{ho}} * {h_{t - 1}} + {W_{co}} \circ {C_t} + {b_o}) $ | (9) |
| $ {h_t} = {o_t} \circ \tanh ({C_t}) $ | (10) |
其中,
2) 解码器由一层BiGRU、一层激活函数tanh和一层Dropout函数堆叠在一起作为解码层. BiGRU模型一种双向循环神经网络, 它可以利用正向和反向信息. 双向门控循环单元将两个传输方向相反的隐藏层连接到同一个输出层. 因此, 输出层具有输入序列中每个点的过去和未来状态的完整信息, 从而做出更准确的预测. BiGRU是在GRU基础上进行正向和反向训练并将结果进行线性融合, 这样不但可以提取过去的特征, 也可以提取未来的特征, 同时数据复用, 而且每个时刻输出值是由两个方向的GRU共同决定. BiGRU的思想是将常规GRU神经元分为前向状态和后向状态. GRU的计算公式如下所示:
| $ {{\textit{z}}_t} = \sigma ({W_{\textit{z}}} [{h_{t - 1}}, {x_t}] + {b_{\textit{z}}}) $ | (11) |
| $ {r_t} = \sigma ({W_r} [{h_{t - 1}}, {x_t}] + {b_r}) $ | (12) |
| $ \widetilde {{h_t}} = \tanh ({W_h} [{r_t} * {h_{t - 1}}, {x_t}] + {b_h}) $ | (13) |
| $ {h_t} = (1 - {{\textit{z}}_t}) * {h_{t - 1}} + {{\textit{z}}_t} * \widetilde {{h_t}} $ | (14) |
其中,
为了使编码层的输出可以作为解码层的输入, 在编码层之后通过使用一个重复向量层(repeat vector). 该层的主要功能是重复来自编码层的最终输出向量, 以便解码层能够重建原始输入序列. 最后, 在解码层之后通过一个全连接层, 用来输出数据的预测值.
2.3.3 预测分量多个分量的预测过程, 具体如图2(c)所示, 将SSA获取到的n个分量数据分别作为每个自动编码器模型的输入数据进行模型的训练, 保存训练好的模型. 将不同的测试集分量分别输入到对应的训练好的自动编码器模型中进行预测, 最后将不同分量的预测值进行求和, 得到最终的预测结果.
SSA-ConvBiAE模型是一个健壮的, 可扩展的端到端时间序列多步预测模型. 奇异谱分析可以从原始数据中提取数据不同的趋势信息, 同时本文设计的自动编码器网络结构能够进行短期和长期特征学习, 该混合模型可以用于时间序列的多步预测.
2.4 损失函数为了更好地反映出模型的预测值跟真实值的差距, 在SSA-ConvBiAE模型中采用的损失函数是均方误差. 同时, 使用了基于随机梯度的优化算法Adam, 每次迭代时更新模型参数. 损失函数的计算方法如下:
| $ Loss = \frac{1}{n}\sum\limits_{i = 1}^n {{{({{\hat y}_i} - {y_i})}^2}} $ | (15) |
其中,
本文的实验环境是基于Windows操作系统, 使用Python语言对代码进行实现. 深度学习框架主要采用了TensorFlow, 模型算法的实现是使用Keras, 它是基于TensorFlow的深度学习库. 硬件环境的配置是Intel(R) Core(TM)i7-7700K CPU @4.20 GHz、32.0 GB内存和NVIDIA GeForce RTX 2080 8 GB GPU.
3.2 数据描述本文提出的模型在5个数据集进行了实验, 其中包括2个真实的供水数据集和3个公开的时间序列数据集. TH-reservoir 和 XH-waterworks 是由黄山旅游集团水电开发有限公司提供的黄山风景区供水数据集. Milan-air[25], Delhi-meantemp[26]和Global-power[27]是从Kaggle网站获得的公开的时间序列数据集. 5个数据集的详细描述如下所示:
1) TH-reservoir: 该数据集是黄山风景区某水库的水位值, 数据集包含了黄山风景区某水库2017年1月1日到2019年12月31日每天的水位值.
2) XH-waterworks: 该数据集是黄山风景区某水厂的供水量, 数据集包含了黄山风景区某水厂2017年1月1日到2019年12月31日每天的供水量.
3) Milan-air: 该数据集是米兰空气中PM2.5浓度数据, 数据集包含2020年7月24日到2020年9月20日每小时PM2.5浓度的平均值.
4) Delhi-meantemp: 该数据集是印度德里市的天气温度数据, 数据集包含2013年1月1日至2017年1月1日每天温度的平均值.
5) Global-power: 该数据集是一个家庭在4年内的有功功率电力消耗数据, 数据是每分钟收集一次, 经过累加计算得出每天的消耗量, 数据集包含2006年12月16日至2010年11月26日每天消耗量的值.
上述黄山风景区供水数据集包含少量的缺失数据, 因此使用线性插值的方法进行填充. 在实验中, 将80%的数据用作训练集, 其余20%用作测试集. 为了评价模型的多步预测性能. 在本文中, 使用了输入步长大小为18的滑动窗口机制, 进行多步预测. 另外, 将输入数据进行归一化处理, 其公式如下所示:
| $ {x_{\rm{nor}}} = \frac{{x - {x_{\min}}}}{{{x_{\max}} - {x_{\min}}}} $ | (16) |
其中,
为了验证所提出模型的预测性能, 本文进行了5个实验. 在每个实验中, 将SSA-ConvBiAE模型的预测性能与以下基线方法进行比较:
1) SVR[5]: 支持向量回归, 它使用历史数据来训练模型并对数据进行预测.
2) XGBoost[6]: 它是一个端到端的梯度提升决策树模型, 是一种高效且广泛使用的机器学习方法.
3) GRU[9]: 门控循环单元, GRU通过简化门控结构使得网络更易计算, 降低了模型的训练时间.
4) DLSTM[19]: 通过堆叠多个LSTM块, 构建一个深度LSTM神经网络.
5) Bi-LSTM[20]: 主要使用前向和后向LSTM来捕捉过去和未来隐含的信息, 然后将两部分结合起来形成最终的预测输出.
6) SSA-ConvLSTM: 消融实验. 奇异谱分析和ConvLSTM的混合模型, 详细描述请参见第2.3节.
7) SSA-BiGRU: 消融实验. 奇异谱分析和BiGRU的混合模型, 详细描述请参见第2.3节.
本实验采用3种评价指标对模型的预测结果进行评价, 具体如下:
平均绝对误差(MAE):
| $ MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{{\hat y}_i} - {y_i}} \right|} $ | (17) |
均方根误差(RMSE):
| $ {\textit{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} } $ | (18) |
平均绝对百分比误差(MAPE):
| $ {\textit{MAPE}} = \frac{{100{\text{%}} }}{n}\sum\limits_{i = 1}^n {\left| {\frac{{\left( {{{\hat y}_i} - {y_i}} \right)}}{{{y_i}}}} \right|} $ | (19) |
其中,
在本节中, 为了研究所提出模型的多步预测性能, 对涉及到的所有模型进行1-step到4-step的预测. 表1, 表2和表3给出了2个真实的供水数据和3个公开时间序列数据在几种不同模型上的预测误差评价结果.
| 表 1 SSA-ConvBiAE模型和基线方法对TH-reservoir和XH-waterworks数据集的预测结果 |
通过表1的实验结果, 可以发现: 在供水数据案例研究中, SSA-ConvBiAE模型可以实现准确的多步预测结果, 混合模型的预测精度优于单一模型. 这表明SSA对数据的分解, 可以获取数据不同趋势的分量信息, 从而降低了时间序列的复杂度, 提高了模型的预测精度. 与其他几种基线方法相比, SSA-ConvBiAE模型的多步预测几乎具有最好的预测精度, 这表明设计的基于ConvLSTM和BiGRU结构的自动编码器模型可以有效地提取数据特征, 适用于时间序列预测. 同时, 为了验证模型不仅可以用于供水数据预测, 本文也在3个公开的时间序列数据进行了实验, 通过表2和表3的实验结果可以发现, 所提出的模型在公开的数据集上都有优异的表现, 表明模型具有一定的泛化能力.
表1, 表2和表3显示了SSA-ConvBiAE模型和其他基线方法在5个时间序列数据集上的多步预测任务的性能. 可以看出, SSA-ConvBiAE模型在多步预测范围的评价指标下几乎都获得了最好的预测性能. 模型与其他基线方法预测结果相比, 详细描述如下.
| 表 2 SSA-ConvBiAE模型和基线方法对Milan-air和Delhi-meantemp数据集的预测结果 |
1) 预测精度. 以TH-reservoir数据集为例, 从表1中可以看出: 所提出的模型SSA-ConvBiAE极大地提高了多步预测的性能, 这表明该模型在长期预测能力方面取得了优异的效果. 例如, 对于1-step的供水数据预测任务, SSA-ConvBiAE模型和SVR和XGBoost模型相比, RMSE误差降低了约71.45%和71.27%. 这主要是由于SVR和XGBoost等方法难以处理复杂的非平稳时间序列数据. SSA-ConvBiAE模型和GRU模型、DLSTM模型和BiLSTM模型相比, RMSE误差降低了约72.28%、71.39%和72.21%, 这主要是由于针对具有不同特征的时间序列数据, 这几种模型的预测结果会有所降低. 从表1可以看出, 经过SSA进行数据分解, 预测精度得到了明显提高, 这表明提出的混合模型是有效的.
2) 消融分析. 为了验证SSA-ConvBiAE模型采用自动编码器网络结构的有效性, 将SSA-ConvBiAE与SSA-ConvLSTM和SSA-BiGRU模型进行了比较. 以TH-reservoir数据集为例, 从图3中可以看出, 在RMSE和MAPE两种不同的实验评价指标下, 可以清楚地看到提出的SSA-ConvBiAE比SSA-ConvLSTM和SSA-BiGRU具有更好的预测结果. SSA-ConvBiAE与SSA-ConvLSTM和SSA-BiGRU模型相比, 从1-step预测可以看出, RMSE分别降低了约7.22%和17.80%. 实验表明, ConvLSTM充分捕捉了序列数据的时间和空间分布, 同时模型中结合BiGRU, 使输出层具有输入序列中每个点的过去和未来状态的完整信息, 可以融合更多的序列特征, 提高了模型的预测性能. 因此, 表明了本文提出的自动编码器网络结构可以有效地提取数据特征.
| 表 3 SSA-ConvBiAE模型和基线方法对Global-power数据集的预测结果 |

|
图 3 消融实验预测结果对比 |
3) 多步预测. 从以上的实验结果可以看出, 在5个不同的数据集上SSA-ConvBiAE模型预测精度在多步预测范围内明显要高于其他基线方法. 以TH-reservoir和XH-waterworks数据集为例, 从表1中可以看出, 本文提出的SSA-ConvBiAE模型在1-step到4-step的预测结果几乎都获得了最好的预测性能, 这表明提出的混合模型是可行的. 因此, 该模型可以用于供水数据和其他时间序列任务的预测, 同时本文提出的SSA-ConvBiAE模型不仅可以用于短期预测, 还可以用于中长期预测.
3.5 模型参数选择在本节中, 将选择SSA-ConvBiAE模型的相关参数. SSA-ConvBiAE模型的超参数主要包括: 批次大小、训练次数、隐藏层单元数、卷积核的尺寸、Dropout和数据分量个数. 在实验中, 将批次大小设置为32, 训练次数设置为100, 隐藏层单元设置为128, 卷积核的尺寸设置为1×3, Dropout参数设置为0.1.
数据分量的个数是SSA-ConvBiAE模型的一个非常重要的参数, 本文通过尝试不同的数据进行对比预测实验来选择最佳值. 在实验中, 从[2, 3, 4, 5, 6, 7]中选择不同的分量个数并分析预测精度的变化. 如图4和图5所示, 横轴代表不同的分量个数, 纵轴代表RMSE和MAE两种不同的评价指标的变化. 图4(a)和图4(b)分别显示了数据集TH-reservoir和XH-waterworks不同分量个数的RMSE和MAE的预测结果. 可以看出, 当分量个数为5时, 误差最小. 同样图5(a)和图5(b)分别显示了数据集Milan-air和Delhi-meantemp的预测结果, 当个数为6时, 结果达到最小值, 图5(c)显示了数据集Global-power的预测结果, 当个数为4时, 结果达到最小值. 这表明不同的分量个数会极大地影响预测精度, 因此需要通过不同参数的对比实验来选择最佳值.
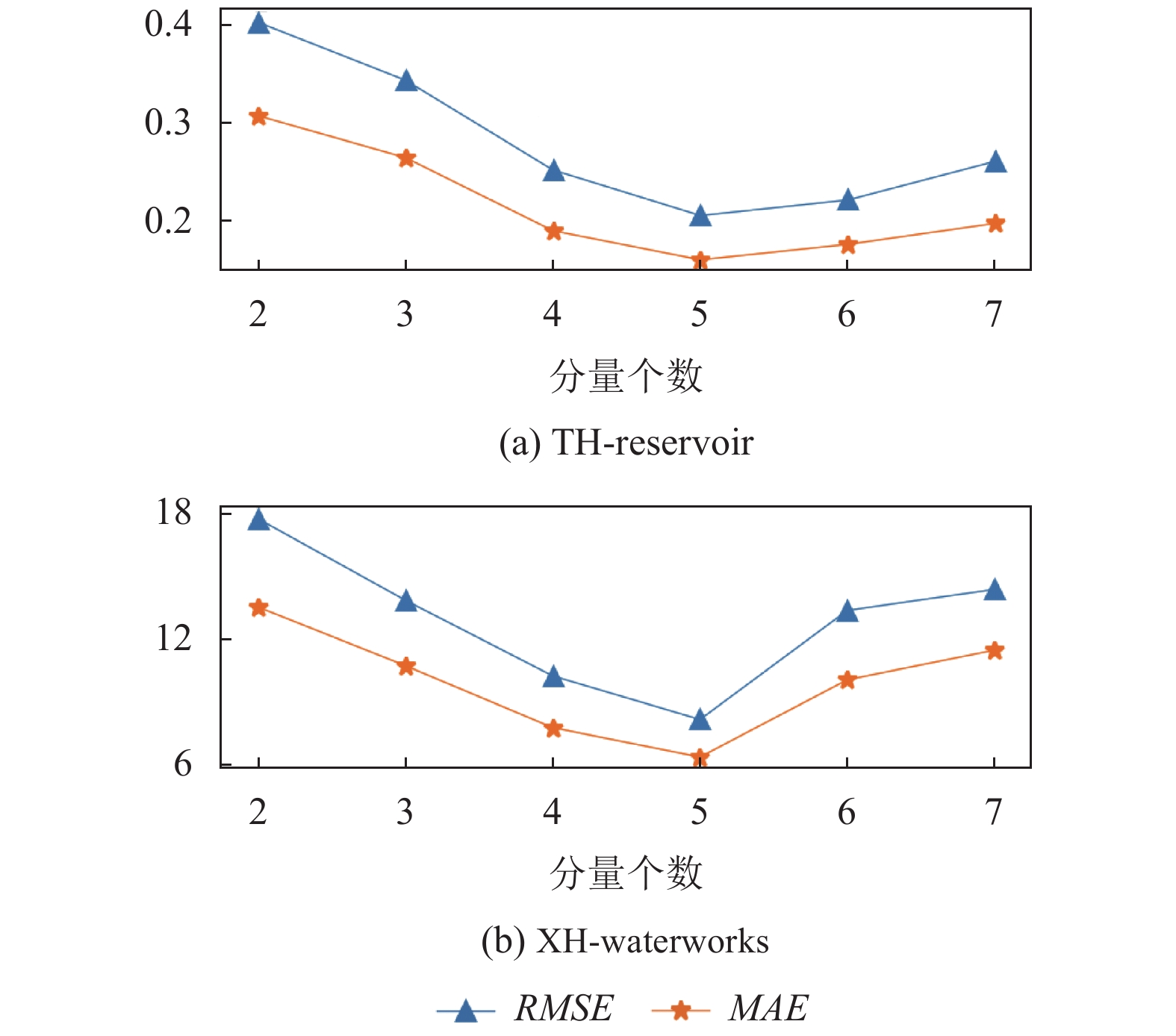
|
图 4 不同的SSA分量在TH-reservoir和XH-waterworks数据集上的预测性能比较 |
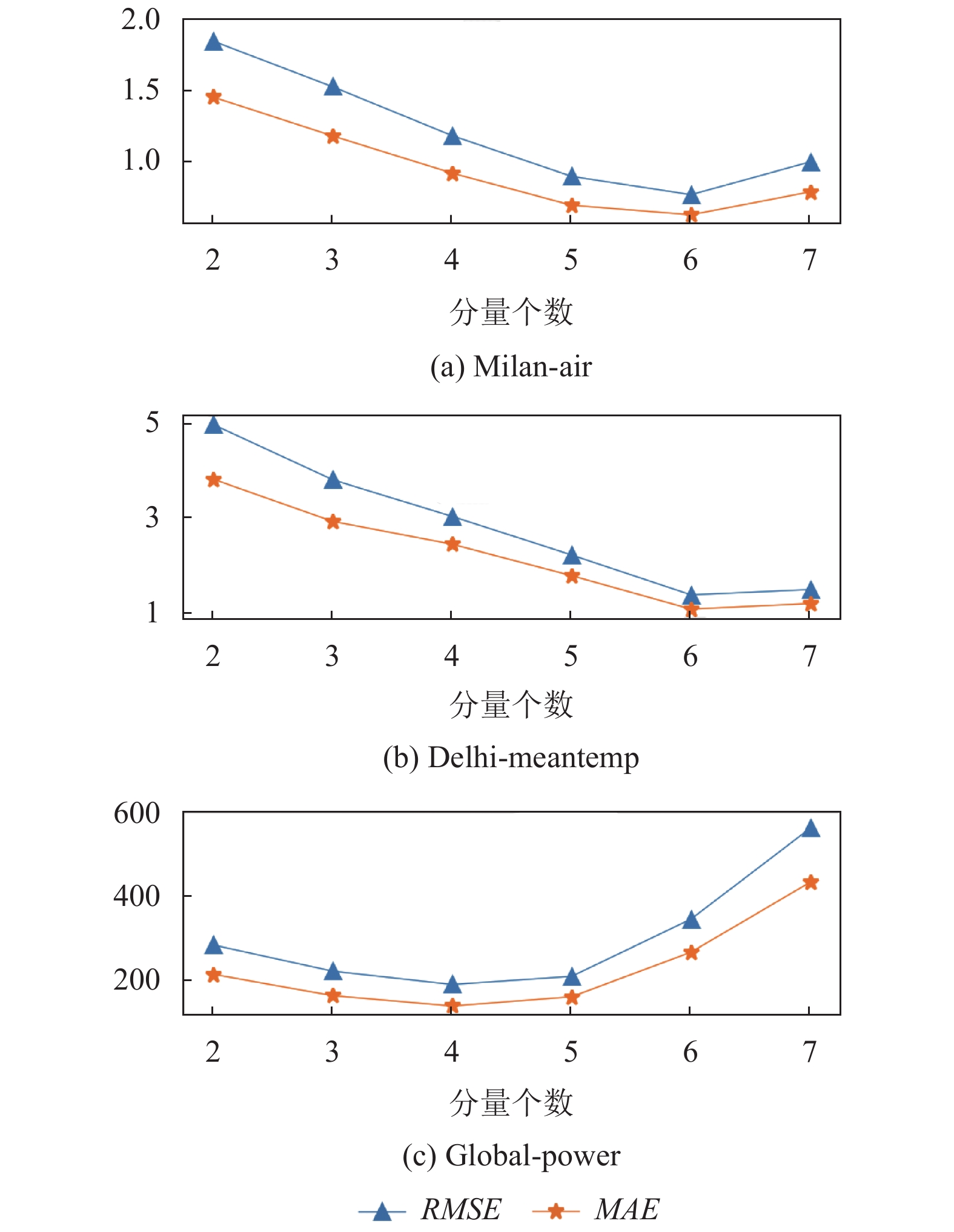
|
图 5 不同的SSA分量在Milan-air, Delhi-meantemp和Global-power数据集上的预测性能比较 |
3.6 模型解释
为了更好的理解SSA-ConvBiAE模型的预测结果, 选择对TH-reservoir的部分测试集样本数据进行预测结果可视化, 图6(a)–图6(d)分别显示了模型1-step到4-step的预测范围的可视化结果.
从图6中1-step和2-step预测的可视化结果来看, SSA-ConvBiAE模型在数据的局部最小值和局部最大值处的预测结果都非常的接近真实值, 这表明SSA将数据分解成不同的趋势分量后, 自动编码器结构中ConvLSTM充分捕捉了序列数据的空间和时间分布, 具有自动特征提取方面的优势, 而BiGRU可以融合更多的序列特征, 提高了模型的预测性能. 从图6中3-step和4-step的预测可视化结果来看, 模型预测的总体趋势接近真实值, 但在局部最小值和局部最大值处的预测结果要低于前两步预测. 尽管ConvLSTM, BiGRU可以捕捉数据集中的长期依赖性, 但针对复杂数据的预测, 长期预测的结果也会有所降低. 从图6中的1-step到4-step的预测结果, 可以看出奇异谱分析与自动编码器网络的结合是有效的, 该模型可以提取序列数据的时间特征, 可以很好地拟合数据, 以及准确预测数据的变化趋势. 同时, 在5个数据集上的预测结果可以看出, 在针对具有不同特征的时间序列数据, 本文提出的模型在预测结果方面都具有优异的表现.

|
图 6 SSA-ConvBiAE模型的可视化预测结果(其中, 纵坐标表示水位 (m)) |
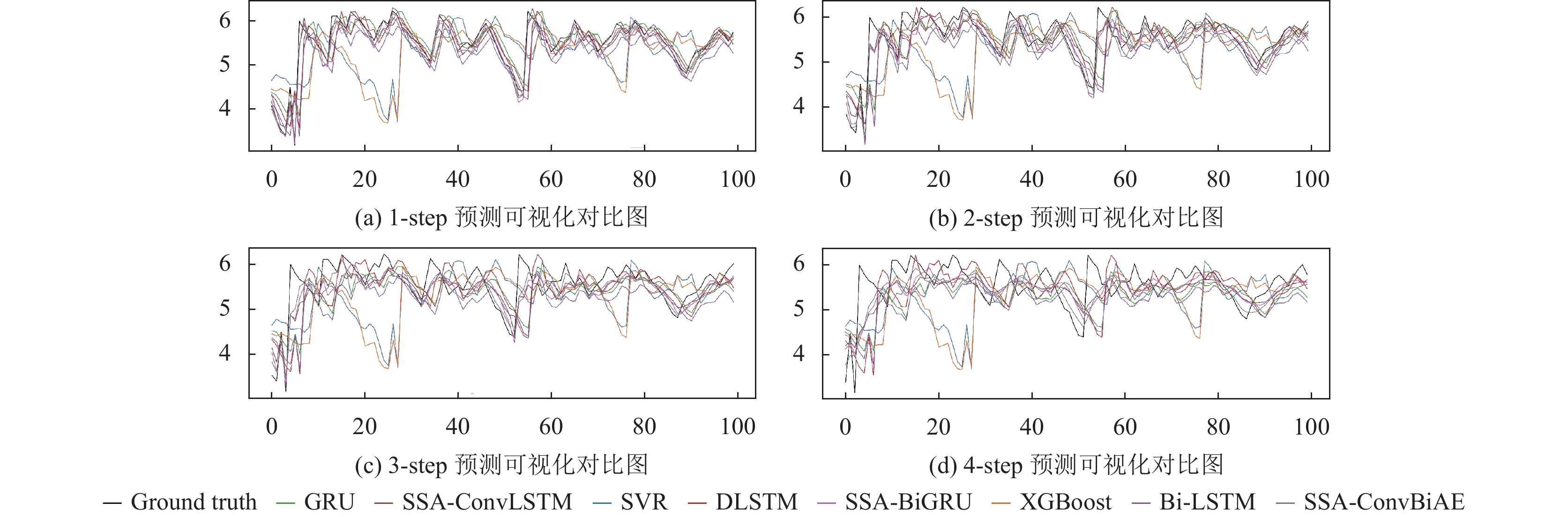
为进一步表明模型的预测结果, 选择SSA-ConvBiAE模型与其他基线方法的预测结果进行可视化对比, 如图7(a)–图7(d)所示, 不同的模型对TH-reservoir数据集进行1-step到4-step预测结果可视化, 可以看出, 采用SSA对数据进行处理后, 混合模型的预测结果明显优于单一模型, 预测结果更接近真实值, 与SSA-ConvLSTM和SSA-BiGRU模型相比, SSA-ConvBiAE模型在多步预测范围内获得了更好的预测性能. 同时本文也选择了对Milan-air数据集进行预测结果可视化, 如图8(a)–图8(d)所示, 展示了不同模型的预测结果.
4 结论本文提出的一种端到端的时间序列预测混合模型, SSA-ConvBiAE模型是一个健壮的, 可扩展的端到端模型可以用于时间序列数据的多步预测. 在提出的SSA-ConvBiAE模型中, 采用SSA将原始时间序列数据分解为不同的趋势分量, SSA可以从原始数据中提取数据不同的趋势信息, 同时本文设计了新的基于ConvLSTM和BiGRU自动编码器结构, 模型能够进行短期和长期特征学习, 该混合模型的预测精度优于单一模型. 在真实世界的2个供水数据集和3个公开的时间序列数据集上进行实验来评价所提出的模型. 实验结果表明, 与所有基线方法相比, 该模型在多步预测评价指标下几乎都获得了最好的预测性能, 证明了SSA-ConvBiAE模型在时间序列预测方面的优越性. 这表明提出的模型不仅可以应用于供水预测领域, 同时对于其他时间序列数据预测也具有一定的适用性. 在未来的研究计划中将继续深化研究SSA-ConvBiAE模型在时间序列数据方面的预测性能, 特别是针对多变量的时间序列预测问题.
|
图 7 SSA-ConvBiAE模型与基线方法对TH-reservoir数据集的预测结果可视化对比图 (其中, 纵坐标表示水位 (m), 横坐标表示样本数目) |

|
图 8 SSA-ConvBiAE模型与基线方法对Milan-air数据集的预测结果可视化对比图 (纵坐标表示: PM2.5浓度 (μg/m³), 横坐标表示样本数目) |
| [1] |
Tealab A. Time series forecasting using artificial neural networks methodologies: A systematic review. Future Computing and Informatics Journal, 2018, 3(2): 334-340. DOI:10.1016/j.fcij.2018.10.003 |
| [2] |
Lim B, Zohren S. Time-series forecasting with deep learning: A survey. arXiv: 2004.13408, 2020.
|
| [3] |
Han Z, Zhao J, Leung H, et al. A review of deep learning models for time series prediction. IEEE Sensors Journal, 2019, 21(6): 7833-7848. DOI:10.1109/JSEN.2019.2923982 |
| [4] |
Zhang G, Patuwo BE, Hu MY. Forecasting with artificial neural networks: The state of the art. International journal of forecasting, 1998, 14(1): 35-62. DOI:10.1016/S0169-2070(97)00044-7 |
| [5] |
Smola AJ, Schölkopf B. A tutorial on support vector regression. Statistics and computing, 2004, 14(3): 199-222. DOI:10.1023/B:STCO.0000035301.49549.88 |
| [6] |
Chen T, Guestrin C. XGBoost: A scalable tree boosting system. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM. 2016. 785–794.
|
| [7] |
Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature, 1986, 323(6088): 533-536. DOI:10.1038/323533a0 |
| [8] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [9] |
Cho K, Van Merriënboer B, Bahdanau D, et al. On the properties of neural machine translation: Encoder-decoder approaches. arXiv: 1409.1259, 2014.
|
| [10] |
Xu M, Han M, Lin H. Wavelet-denoising multiple echo state networks for multivariate time series prediction. Information Sciences, 2018, 465: 439-458. DOI:10.1016/j.ins.2018.07.015 |
| [11] |
Zhang Y, Chen B, Pan G, et al. A novel hybrid model based on VMD-WT and PCA-BP-RBF neural network for short-term wind speed forecasting. Energy Conversion and Management, 2019, 195: 180-197. DOI:10.1016/j.enconman.2019.05.005 |
| [12] |
Zhang H, Wang X, Cao J, et al. A multivariate short-term traffic flow forecasting method based on wavelet analysis and seasonal time series. Applied Intelligence, 2018, 48(10): 3827-3838. DOI:10.1007/s10489-018-1181-7 |
| [13] |
Ahani I K, Salari M, Shadman A. An ensemble multi-step-ahead forecasting system for fine particulate matter in urban areas. Journal of Cleaner Production, 2020, 263: 120983. DOI:10.1016/j.jclepro.2020.120983 |
| [14] |
Chang Z, Zhang Y, Chen W. Electricity price prediction based on hybrid model of adam optimized LSTM neural network and wavelet transform. Energy, 2019, 187: 115804. DOI:10.1016/j.energy.2019.07.134 |
| [15] |
Tang Q, Shi R, Fan T, et al. Prediction of financial time series based on LSTM using wavelet transform and singular spectrum analysis. Mathematical Problems in Engineering, 2021, 2021: 1-13. DOI:10.1155/2021/9942410 |
| [16] |
Li G, Ma X, Yang H. A hybrid model for monthly precipitation time series forecasting based on variational mode decomposition with extreme learning machine. Information, 2018, 9(7): 177. DOI:10.3390/info9070177 |
| [17] |
Liu H, Mi X, Li Y, et al. Smart wind speed deep learning based multi-step forecasting model using singular spectrum analysis, convolutional gated recurrent unit network and support vector regression. Renewable Energy, 2019, 143: 842-854. DOI:10.1016/j.renene.2019.05.039 |
| [18] |
Zhu Q, Zhang F, Liu S, et al. A hybrid VMD–BiGRU model for rubber futures time series forecasting. Applied Soft Computing, 2019, 84: 105739. DOI:10.1016/j.asoc.2019.105739 |
| [19] |
Sagheer A, Kotb M. Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing, 2019, 323: 203-213. DOI:10.1016/j.neucom.2018.09.082 |
| [20] |
Zhang M, Wu D, Xue R. Hourly prediction of PM 2.5 concentration in Beijing based on Bi-LSTM neural network, Multimedia Tools and Applications, 2021.
|
| [21] |
Hu P, Tong J, Wang J, et al. A hybrid model based on CNN and Bi-LSTM for urban water demand prediction. IEEE Congress on Evolutionary Computation (CEC). Wellington: IEEE. 2019. 1088–1094.
|
| [22] |
Essien A, Giannetti C. A deep learning model for smart manufacturing using convolutional LSTM neural network autoencoders. IEEE Transactions on Industrial Informatics, 2020, 16(9): 6069-6078. DOI:10.1109/TII.2020.2967556 |
| [23] |
Salinas D, Flunkert V, Gasthaus J. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. arXiv: 1704.04110, 2019.
|
| [24] |
Shi X, Chen Z, Wang H, et al. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Proceedings of the 28th International Conference on Neural Information Processing Systems. Cambridge: MIT Press. 2015. 802–810.
|
| [25] |
Milan-air数据集下载官方网址. https://www.kaggle.com/wiseair/air-quality-in-milan-summer-2020.
|
| [26] |
Delhi-meantemp数据集下载官方网址. https://www.kaggle.com/sumanthvrao/daily-climate-time-series-data.
|
| [27] |
Global-power数据集下载官方网址. https://www.kaggle.com/uciml/electric-power-consumption-data-set.
|
 2022, Vol. 31
2022, Vol. 31


