多元时间序列是指以相同间隔按指定采样率对某过程进行采集的一组变量, 且按时间先后顺序排列. 在实际处理多元时间序列时, 需要分析各变量之间潜在的复杂关系和变化规律, 才能对其做出有效预测. 但现有方法常因为多元时间序列复杂的变化规律难以捕捉, 所以导致预测精度较低. 如何对其做出有效预测, 成为国内外诸多学者关注的问题.

早期传统多元时间序列预测方法主要采用灰色模型^[1]、自回归综合移动平均模型(ARMA)^[2]、自回归移动平均模型(ARIMA)^[3]等. 这些方法虽然结构简单, 但都属于线性方法, 不能较好反映时间序列中非线性因素的影响. 为了克服这一缺陷, 人们将神经网络引入对多元时间的序列的预测. 例如, Meng等人^[4]使用BP神经网络实现了对股价走势的预测. 这种模型可以较好反映出多元时间序列中非线性因素对结果的影响, 但无法联系多元时序数据间的潜在的内部关联. 邓玉婧等人^[5]采用了循环神经网络(RNN)实现了对航班客座率的预测, 证明了RNN神经网络在时序预测方面的有效性, 这种模型可以解决无法联系多元时序数据关系的缺点, 但在预测较长序列时经常会出现梯度爆炸的缺陷, 使模型无法从训练数据中得到较高的学习效率. 廖志伟等人^[6]使用LSTM神经网络实现了对短期电煤价格预测, 这种模型在RNN神经网络的基础上增加了不同的门控单元来实现长期信息记忆功能, 成功减缓了RNN神经网络梯度爆炸问题. 周莽等人^[7]使用GRU神经网络实现了对短期电力负荷的预测, 这种模型是LSTM模型的一种流行变体, 不仅同样可以克服RNN模型梯度爆炸问题, 其结构较LSTM模型还更为简易, 更易训练. BiLSTM神经网络作为近年来神经网络中的新型模型^{[8, 9]}, 它创新性地将一个正向LSTM模型和一个反向LSTM模型相结合, 实现了特征之间潜在关系的双向挖掘. 与LSTM相比, BiLSTM模型在预测多元时序序列时, 其预测精度明显提高. 江知航等人^[10]使用BiLSTM神经网络对棉花价格进行了预测, 但没有考虑多维特征与预测目标的相关性以及无关特征对预测结果的影响, 导致预测精度并未大幅提升. 陈宇韶等人^[11]在预测股票价格前使用了PCC相关系数, 在庞杂多维特征中分析出与预测目标高度相关的特征, 消除了无关特征对预测结果的影响, 降低了模型复杂度的同时有效地改善了最终的预测效果.

基于以上, 为了更有效地对多元时序序列进行预测, 本文将PCC-BiLSTM-GRU-Attention组合模型的预测方法进行了探讨和验证. 具体来说, 该方法首先利用PCC相关系数对输入特征进行筛选, 删除无关变量, 避免无关变量对结果精度的影响. 其次使用BiLSTM神经网络双向获取输入特征之间潜在的关联关系. 最后使用GRU神经网络融合Attention机制, 进一步深入学习双向时序特征的变化规律, 更精准的捕获关键时刻的信息以及非线性动力系统的复杂变化规律. 为了验证此方法在多元时间序列中的预测效果, 本文以股票价格预测^[12-15]为实验场景, 以各模型的平均绝对百分比误差值和决定系数值作为衡量标准进行对比实验, 验证结果表明, 相比于其他5种模型, PCC-BiLSTM-GRU-Attention组合模型的预测方法拟合程度更高, 预测效果更好.

1 PCC-BiLSTM-GRU-Attention组合预测模型 1.1 PCC相关系数

根据文献[16]可知, 在预测多元时间序列前, 建立初始化指标体系后进行相关性筛选可以有效减少的数据复杂度和无关变量对预测结果的影响. Cai等人^[17]根据PCC相关系数计算出变量间的相关程度来删除冗余变量. 因此本文选择PCC相关系数对实验进行特征选择, PCC相关系数的公式为:

$ {r_{X, T}} = \frac{{\displaystyle\sum\limits_{i = 1}^k {{X_i}{Y_i} - \frac{{\displaystyle\sum\limits_{i = 1}^k {{X_i}} \displaystyle\sum\limits_{i = 1}^k {{Y_i}} }}{k}} }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^k {X_i^2} - \frac{{{{\left( {\displaystyle\sum\limits_{i = 1}^k {{X_i}} } \right)}^2}}}{k}} \sqrt {\displaystyle\sum\limits_{i = 1}^k {Y_i^2} - \frac{{{{\left( {\displaystyle\sum\limits_{i = 1}^k {{Y_i}} } \right)}^2}}}{k}} }} $

(1)

其中, $ {r_{X, Y}} $ 为变量X, Y的相关系数, $ {X_i} $ 为自变量, $ {Y_i} $ 为因变量. 变量的相关程度可由相关系数的绝对值表示, 具体如表1所示.

1.2 BiLSTM神经网络

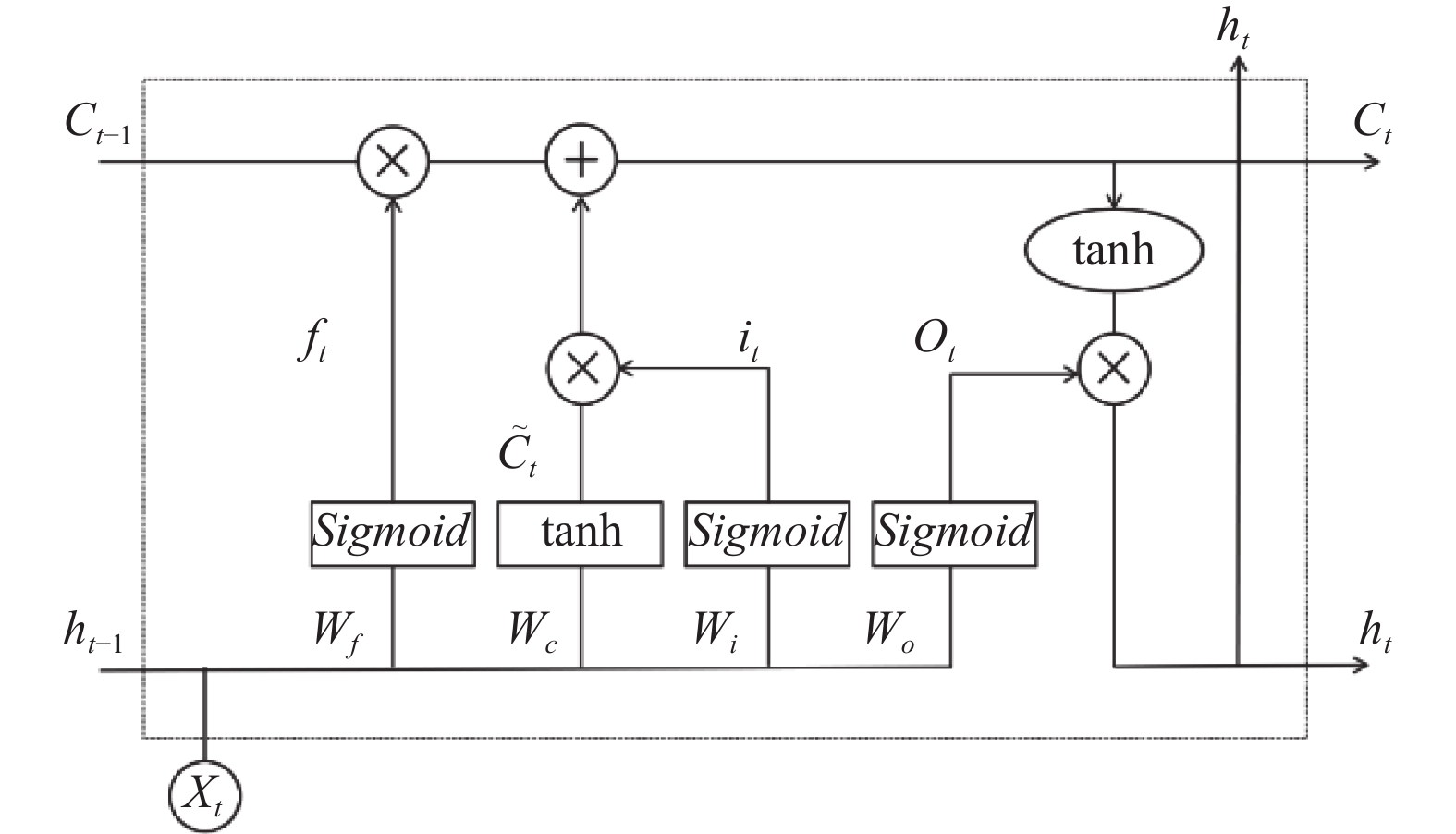
BiLSTM神经网络由两个LSTM神经网络叠加组成^[18]. LSTM神经网络是另一种RNN神经网络, 在处理时间序列方面具备显著优势^[19], 它具有遗忘门、输入门、输出门和细胞状态等部分, 其结构如图1所示. 细胞状态用来存储和传递时序特征信息, 3种门结构在训练过程中会学习如何去保存、遗忘和输出时序特征信息^[20]. 这种结构使得在LSTM神经网络中早期单元的特征信息一样可以传递至后期单元的细胞状态中, 实现了LSTM神经网络可长时间记忆特征信息的优势.

$ {f_t} = {\textit{Sigmoid}}\left( {{W_f} \cdot \left[ {{h_{t - 1}}, {X_t}} \right] + {b_f}} \right) $

(2)

$ {i_t} = {\textit{Sigmoid}}\left( {{W_i} \cdot \left[ {{h_{t - 1}}, {X_t}} \right] + {b_i}} \right) $

(3)

$ {\widetilde C_t} = \tanh \left( {{W_c} \cdot \left[ {{h_{t - 1}}, {X_t}} \right] + {b_c}} \right) $

(4)

$ {C_t} = {f_t} \cdot {C_{t - 1}} + {i_t} \cdot \widetilde {{C_t}} $

(5)

$ {o_t} = {\textit{Sigmoid}}\left( {{W_o} \cdot \left[ {{h_{t - 1}}, {X_t}} \right] + {b_o}} \right) $

(6)

$ {h_t} = {o_t} \cdot \tanh \left( {{C_t}} \right) $

(7)

其中, $ {W_f} $ 、 $ {W_i} $ 、 $ {W_c} $ 、 $ {W_o} $ 和 $ {b_f} $ 、 $ {b_i} $ 、 $ {b_c} $ 、 $ {b_o} $ 分别对应各门结构的权重矩阵与偏置, 其运行原理首先是遗忘门通过式(2)计算当前细胞状态需要遗忘的信息 $ {f_t} $ , 然后输入门通过式(3)计算当前细胞状态需要存放的信息 $ {i_t} $ , 并通过式(4)、式(5)在tanh层中创建候选值加入到细胞状态中并且将单元状态从 $ {C_{t - 1}} $ 更新为 $ {C_t} $ , 最后输出门通过式(6)、式(7)计算出当前LSTM单元的输出 $ {h_t} $ .

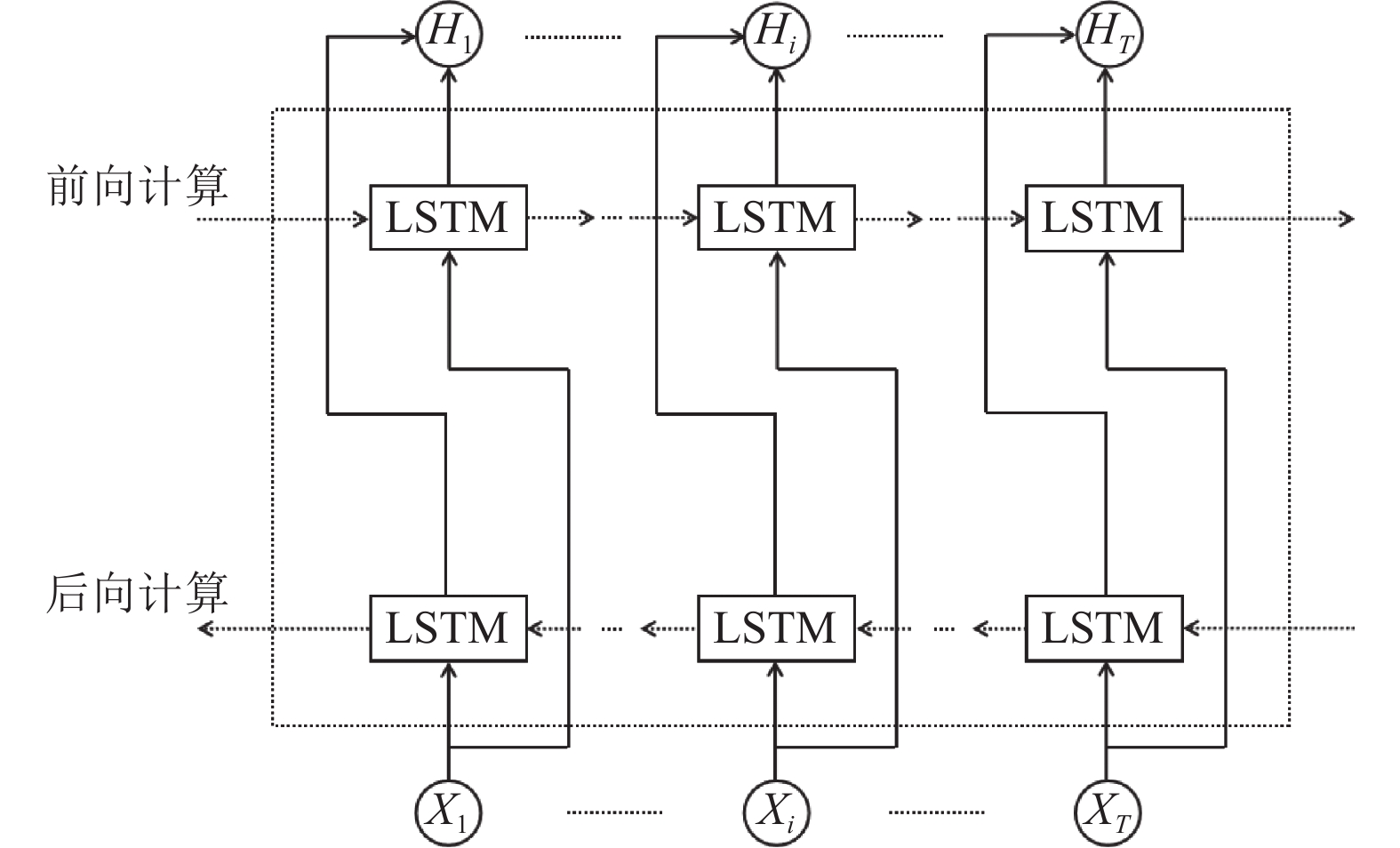
图2是BiLSTM神经网络结构图, 它由一个前向LSTM计算层一个为后向LSTM计算层. 这种结构可对时序序列关系进行较长时间的双向挖掘, 提取双向时序特征.

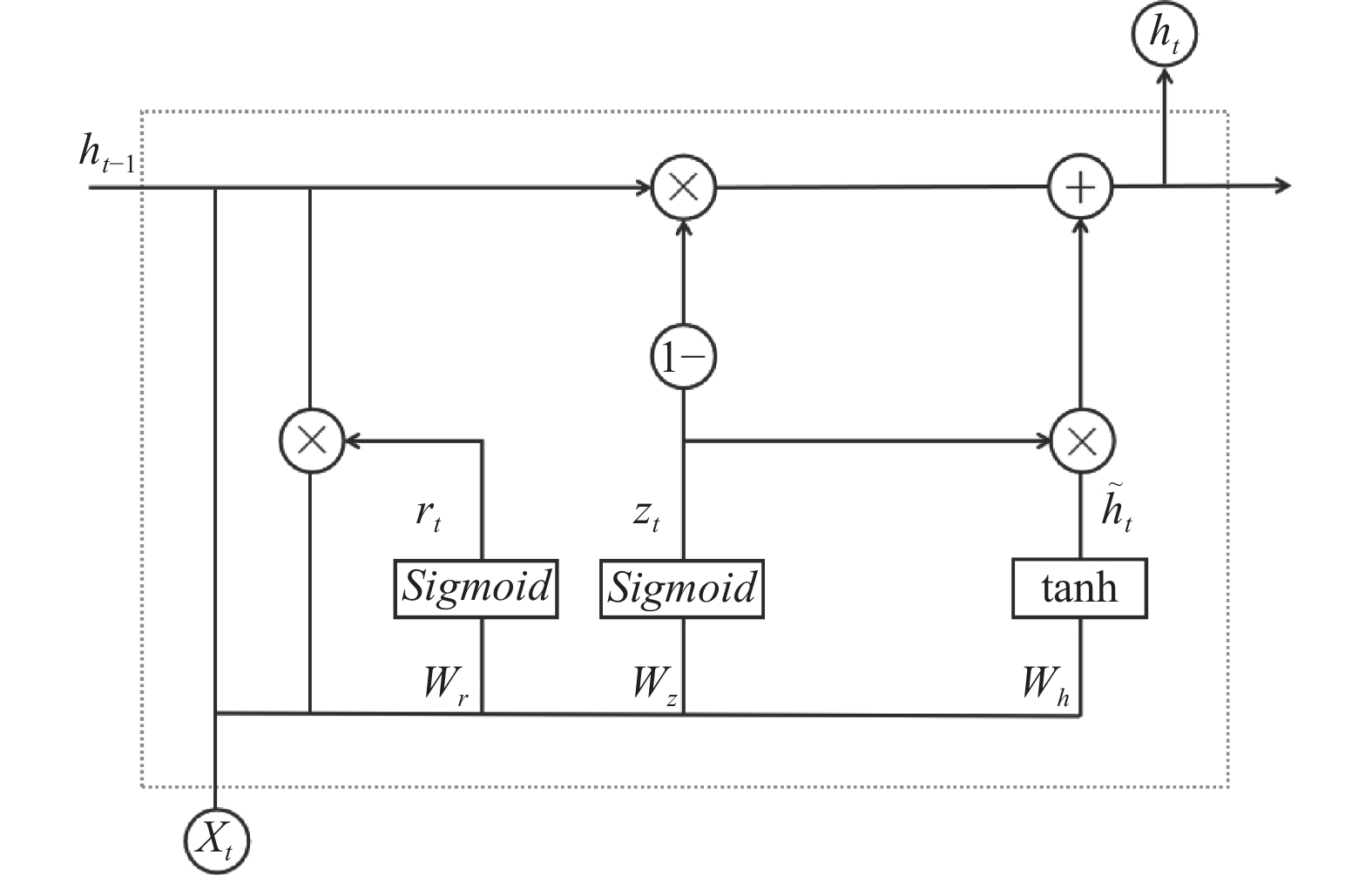
1.3 GRU神经网络

GRU神经网络对LSTM内部进行了有效简化, 引入了重置门、更新门的概念, 这使其在保留原LSTM神经网络预测效果的同时变得更易训练^[21], 其结构如图3所示.

$ {r_t} = {\textit{Sigmoid}}\left( {{W_r} \cdot \left[ {{h_{t - 1}}, {X_t}} \right] + {b_r}} \right) $

(8)

$ {\widetilde h_t} = \tanh \left( {{W_h} \cdot \left[ {r * {h_{t - 1}}, {X_t}} \right] + {b_h}} \right) $

(9)

$ {{\textit{z}}_t} = {\textit{Sigmoid}}\left( {{W_{\textit{z}}} \cdot \left[ {{h_{t - 1}}, {X_t}} \right] + {b_{\textit{z}}}} \right) $

(10)

$ {h_t} = \left( {1 - {{\textit{z}}_t}} \right) * {h_{t - 1}} + {{\textit{z}}_t} * {\widetilde h_t} $

(11)

其中, $ {X_{{t}}} $ 代表当前时刻的输入, $ {h_{t - 1}} $ 代表上一时刻GRU单元的隐藏状态, $ {h_t} $ 代表当前GRU单元计算出的隐藏状态, $ {W_r} $ 、 $ {W_h} $ 、 ${W_{\textit{z}}}$ 和 $ {b_r} $ 、 $ {b_h} $ 、 ${b_{\textit{z}}}$ 为各门结构对应的权重矩阵和偏置, GRU神经网络单元的运行原理首先是通过式(8)计算出重置门的取值, 再通过式(9)计算候选状态. 若重置门取值接近0, 则候选值会选择忽略前一个隐藏状态的信息, 这有效地使隐藏状态具有丢弃不相关的特征信息的能力. 计算出候选值后, 通过式(10)使更新门控制特征信息需要传递多少信息至当前隐藏状态, 实现了单元的长期记忆功能, 最后通过式(11)计算出当前隐藏状态的最终值.

1.4 Attention注意力机制

Attention机制通过不同特征对于预测结果影响的大小来为神经网络中的隐藏单元赋予不同权重, 使对预测结果有突出影响的因素获得更高关注, 为后续再次处理数据提供更好的参考^[22-24], 大大减少了对资源的消耗, 提高了预测精度, 其结构具体如图4所示.

$ {e_i} = \tanh \left( {W{h_{\text{i}}} + b} \right) $

(12)

$ {a_i} = \frac{{\exp \left( {{e_i}} \right)}}{{\displaystyle\sum\limits_{j = 1}^T {\exp \left( {{e_{{j}}}} \right)} }} $

(13)

$ {c_t} = \sum\limits_{i = 1}^T {{a_i}{h_i}} $

(14)

其中, $ W $ 、 $ b $ 为权重系数和偏置系数, $ {h_i} $ 为GRU神经网络中t时刻中输出的第i个隐藏单元状态值. Attention机制首先根据GRU神经网络输出每个隐层单元的值 $ {h_i} $ 计算式(12)后得到每个隐层单元的得分 $ {e_i} $ , 再通过式(13)对注意力得分值进行归一化, 最终计算式(14)将归一化后的得分值 $ {a_i} $ 和隐层单元 $ h_i $ 进行加权求和得到t时刻这一时间步长内的隐藏层状态值 $ {c_t} $ .

1.5 PCC-BiLSTM-GRU-Attention组合预测模型

PCC-BiLSTM-GRU-Attention组合模型的预测方法主要由6个阶段构成, 具体层级结构如图5所示.

(1) PCC相关系数: 将原始数据中的自变量逐一与预测的因变量进行PCC相关性分析, 删除与因变量无关的特征, 具体表示为:

$ {X_i} = \left[ {{x_1}, \cdots , {x_i}, \cdots , {x_N}, p} \right] $

(15)

$ {X_i} = \left[ {{x_1}, \cdots , {x_i}, \cdots , {x_n}, p} \right] $

(16)

其中, $ {X_i} $ 表示某时刻中的第i天的输入序列, $ {x_i} $ 为第i个特征值, N为未降维选优时的总特征数, n为降维后的总特征数. $ p $ 为某时刻第i天的预测值, 未经过筛选时 $ {X_i} $ 可表示为式(15), 经过PCC相关性分析筛选出不相关的特征后, $ {X_i} $ 可表示为式(16).

(2)输入层: 将经过特征值筛选后的特征以及因变量作为本文模型的输入, 在t时刻中的输入序列具体为:

$ {X_t} = {\left[ {{X_1}, \cdots , {X_i}, \cdots , {X_T}} \right]^{\rm{T}}} $

(17)

其中, $ {X_t} $ 为t时刻的输入序列, T为时间步数.

(3)BiLSTM层: 在前向层中输入正向 $ {X_t} $ 序列 ${\left[ {{X_1}, \cdots , {X_i}, \cdots , {X_T}} \right]^{\rm{T}}}$ 计算出该层第i个输出的隐藏状态 $ \overrightarrow {{H_i}} $ , 在后向层中输入反向 $ {X_t} $ 序列 ${\left[ {{X_T}, \cdots , {X_i}, \cdots , {X_1}} \right]^{\rm{T}}}$ 计算出该层第i个输出的隐藏状态 $ \overleftarrow {{H_i}} $ :

$ \overrightarrow {{H_i}} = \overrightarrow {LSTM} \left( {\overrightarrow {{H_{i - 1}}} , {X_t}, \overrightarrow {{C_{i - 1}}} } \right) $

(18)

$ \overleftarrow {{H_i}} = \overleftarrow {LSTM} \left( {\overleftarrow {{H_{i + 1}}} , {X_t}, \overleftarrow {{C_{i + 1}}} } \right) $

(19)

$ {H_i} = \left[ {\overrightarrow {{H_i}} \oplus \overleftarrow {{H_i}} } \right] $

(20)

$ {H_t} = {\left[ {{H_1}, \cdots , {H_i}, \cdots , {H_T}} \right]^{\rm{T}}} $

(21)

其中, 通过式(18)使用对应t时刻的输入序列 $ {X_t} $ 、第i–1个输入时间步的前向LSTM层中的隐藏单元状态 $ \overrightarrow {{H_{i - 1}}} $ 以及第i–1个输入时间步的前向LSTM层中的细胞状态 $ \overrightarrow {{C_{i - 1}}} $ , 计算出在t时刻的前向LSTM层中第i个输出的隐藏状态 $ \overrightarrow {{H_i}} $ . 通过式(19)使用对应t时刻的输入序列 $ {X_t} $ 、第i+1个输入时间步的后向LSTM层中的隐藏单元状态 $ \overleftarrow {{H_{i + 1}}} $ 以及第i+1个输入时间步的后向LSTM层中的细胞状态 $ \overleftarrow {{C_{i + 1}}} $ , 计算出在t时刻的后向LSTM层中第i个输出状态 $ \overleftarrow {{H_i}} $ , 通过式(20)计算出BiLSTM层在t时刻的第i个隐藏单元状态值, 将式(21)中 $ {H_t} $ 最终作为t时刻上提取的双向时序序列.

(4) GRU: 将BiLSTM层中输出的双向时序序列 $ {H_t} $ 作为GRU层的输入序列进行进一步学习:

$ {h_i} = GRU\left( {{H_{i - 1}}, {H_i}} \right) $

(22)

$ {h_t} = \left[ {{h_1}, \cdots , {h_i}, \cdots , {h_T}} \right] $

(23)

其中, 记 $ {h_i} $ 为t时刻中第i个GRU层的隐层状态, 式(23)中 $ {h_t} $ 为最终在t时刻上GRU层的隐层状态.

(5) Attention机制: 将GRU层输出的隐层状态 $ {h_t} $ 作为Attention机制的输入, 每个隐层单元的得分 $ {e_i} $ 、归一化后得分 $ {a_i} $ 和最终Attention层输出 $ {c_t} $ 由式(12)–式(14)计算而来.

(6)输出层: 选择Sigmoid函数作为激活全连接层的函数, 输出最终t时刻最终预测值, 记作 $ {y_t} $ :

$ {y_t} = {\textit{Sigmoid}}\left( {\omega {c_t} + b} \right) $

(24)

2 实验分析 2.1 数据来源

本文选取某银行从2006年1月5日至2019年6月5日这一时段内所有交易日的股指数据作为实验数据集. 采集数据主要包括: 开盘价、最高价、最低价、涨幅率、振幅率、总手数、交易金额、换手率、成交次数和收盘价, 最终将股票收盘价作为目标变量. 此数据集大且全面, 具有多元特性, 在连续的时间序列上呈现一定的变化规律. 本文将数据集选取前80%的数据为训练集, 后20%的数据为测试集.

2.2 数据预处理

本文对数据的预处理分为两个步骤, 归一化和特征数据的降维选优:

(1)为了消除特征参数之间数值与单位的差异性, 以对每个特征进行同等对待, 本文对原始特征数据进行归一化处理来提升预测精度, 归一化公式如下:

$ {x_i} = \frac{{{x_i} - min }}{{max - min }} $

(25)

其中, min代表特征 $ x $ 在时序序列中的最小值, max代表在时序序列中的最大值.

(2)将归一化后的特征数据进行PCC相关性分析. 如表2可以看出各特征与股票收盘价的PCC相关程度, 为了消除无关变量对模型预测带来的噪声影响, 决定选取开盘价、最高价、最低价、总手数、交易金额和成交次数这些具有相关性的因素作为神经网络输入参数, 删除无关因素来实现对特征数据的降维选优.

2.3 参数设置

基于本文提出方法训练中的优化目标为平均绝对百分比误差MAPE最小化, 即决定采用Adam优化算法对模型中的权重进行迭代更新. 模型各参数选用经验数据且通过多次实验进行调整, 最终确定BiLSTM神经网络层的隐层节点个数为64个, GRU神经网络层的隐层节点个数为16个, 迭代次数为100次, batch-size大小为64, 滑动窗口长度为5, 学习率为0.01.

2.4 评价指标

本文选用的评价指标为平均绝对百分比误差(MAPE)和决定系数( ${R^2}_{{\text{score}}}$ )两种指标来评价模型的优劣性, 两种指标公式如下:

$ MAPE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{y_{\rm{true}}}\left( i \right) - {y_{\rm{pre}}}\left( i \right)}}{{{y_{\rm{true}}}\left( i \right)}}} \right|} \times 100{\text{%}}$

(26)

$ {R^2}_{{\text{score}}} = 1 - \frac{{{{\displaystyle\sum\limits_{i = 1}^n {\left( {{y_{\rm{true}}}\left( i \right) - {y_{\rm{pre}}}\left( i \right)} \right)} }^2}}}{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{y_{\rm{true}}}\left( i \right) - \frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{y_{\rm{true}}}\left( i \right)} } \right)}^2}} }} $

(27)

其中, n为样本个数, ${y_{\rm{true}}}\left( i \right)$ 为i时刻的实际值, ${y_{\rm{pre}}}\left( i \right)$ 为i时刻的预测值. MAPE的值代表预测值与真实值产生的误差值与真实值之间的比例, 当比例越接近0%时, 表明预测误差越小. ${R^2}_{{\text{score}}}$ 的值表示预测值曲线与真实值曲线的拟合优度, 当 ${R^2}_{{\text{score}}}$ 的值越接近1时拟合优度越好.

2.5 多模型对比

为了验证PCC-BiLSTM-GRU-Attention组合模型的预测方法的预测性能, 将该方法与BP、LSTM、GRU、BiLSTM-GRU、BiLSTM-GRU- Attention等神经网络模型放在股票价格预测场景中进行对比实验, 观察不同模型对某银行测试集的预测效果. 为了减少结果中的偶然因素对各神经网络精度的影响, 本文对每种神经网络进行了多次实验, 记录下每种模型在测试集预测的最优结果, 实验结果如表3所示.

从表3可观察到, PCC-BiLSTM-GRU-Attention组合模型的预测方法在MAPE与决定系数两种评估指标上计算的结果均优于其他神经网络. 该方法的MAPE指标为2.484%, 与BP、LSTM、GRU、BiLSTM-GRU、BiLSTM-GRU-Attention等神经网络相比, 其MAPE指标分别下降了7.285%、5.462%、5.369%、2.216%、0.372%. 该方法的决定系数指标为0.966, 与BP、LSTM、GRU、BiLSTM-GRU、BiLSTM-GRU-Attention等神经网络进行对比后, 决定系数分别提高了0.343、0.268、0.208、0.028、0.02, 由此可见, 实验的结果验证了PCC-BiLSTM-GRU-Attention组合模型的预测方法可以有效提高对多元时间序列的预测. 此外, 将PCC-BiLSTM-GRU-Attention组合模型的预测方法与BiLSTM-GRU-Attention神经网络模型相比较, MAPE指标降低了0.372%, 决定系数提高了0.02, 证明了使用PCC相关性系数剔除无关变量可有效减少其对预测精度的影响. 将BiLSTM-GRU-Attention神经网络模型与BiLSTM-GRU神经网络模型相比较, MAPE指标降低了1.844%, 决定系数提高了0.008, 证明了Attention机制神经网络的加入能够有效捕捉关键时刻的信息. 图6为PCC-BiLSTM-GRU-Attention组合模型的预测方法与其他模型的预测结果图, 可以看出该方法相较于其他模型预测的结果同真实值的波动更为拟合.

3 结论

本文将PCC-BiLSTM-GRU-Attention组合模型的预测方法进行了探讨和验证. 该方法首先利用PCC相关系数将特征数据进行筛选, 删除冗余无关特征对实验结果精度的影响, 实现多元数据的降维选优. 其次选取BiLSTM神经网络双向学习时序序列的变化规律, 再使用GRU融合Attention机制进一步深度学习双向时序特征的变化规律, 同时更精准的捕获关键时刻的信息, 最后通过全连接层输出最后预测值. 本文结合PCC相关系数、BiLSTM神经网络、GRU神经网络、Attention机制进一步提高了对多元时序序列的预测精度. 将该方法通过实验与BP、LSTM、GRU、BiLSTM-GRU、BiLSTM-GRU-Attention五种模型进行对比, 验证结果表明, PCC-BiLSTM-GRU-Attention组合模型的预测方法在MAPE和决定系数两种指标上有显著优势, 与真实值具有更高的拟合性, 实际预测精度最佳.