2. 江苏万安电力科技有限公司, 南通 210018
2. Jiangsu Wanan Electric Technology Co. Ltd., Nantong 210018, China
对真实世界的三维数字化是虚拟现实的核心研究任务之一. 高质量三维重建将可显著提升虚拟现实场景的真实感并简化建模过程, 并广泛应用于其他领域, 如现场勘测、遥感航拍和消费电子等. 对真实场景的三维重建有多种方法, 如结构光法、立体法、明暗法、光场法等. 在这些方法当中, 立体方法(shape from stereo)通过场景不同角度的图像信息进行场景的三维重建, 具有低成本、易于部署和扩展性好等优势. 特别地, 随着数码相机和手机相机的发展, 图片质量和分辨率均得到显著提高, 捕获场景图像\视频数据变得非常便捷. 在这一背景下, 立体方法, 特别是多视角方法, 日益成为对真实世界的重要三维感知手段. 多视角立体方法需要用户在多个角度拍摄图片或围绕场景进行视频的录制, 需保证图片间具有足够的基线以实现精确的三维重建. 宽基线假设增加了用户拍摄和三维获取的成本, 并且在某些空间受限情况下, 大范围的移动相机并不可行.
与经典的多视角立体方法不同, 本文考虑如下场景: 手持相机或智能手机进行拍照时, 由于手部抖动或拍摄者对摄影画面的局部调整, 不可避免的导致相机发生微小运动(small motion), 如图1所示. 对于此类包含极小视差的数据, 主流三维重建方法, 如COLMAP, 将会由于较窄的基线导致重建过程失败. 特别地, 一些相机和数码相机在拍照的同时可以直接记录这样的微小运动视频(small motion clips), 如iPhone的实况照片(LivePhoto), 松下相机的4K预连拍和GoPro相机的实况连拍(LiveBurst)等. 这类包含微小运动的极短视频数据已经成为介于宽基线(wide-baseline)视频和单目图像之间的一类数据形式. 一方面, 微运动视频蕴含的视差信息可以有助于恢复三维场景; 另一方面, 由于小基高比特性(相机的位移远小于相机距离场景的距离), 对应点的三角化过程易受噪声影响, 导致三维点重建过程具有较高的不确定性.
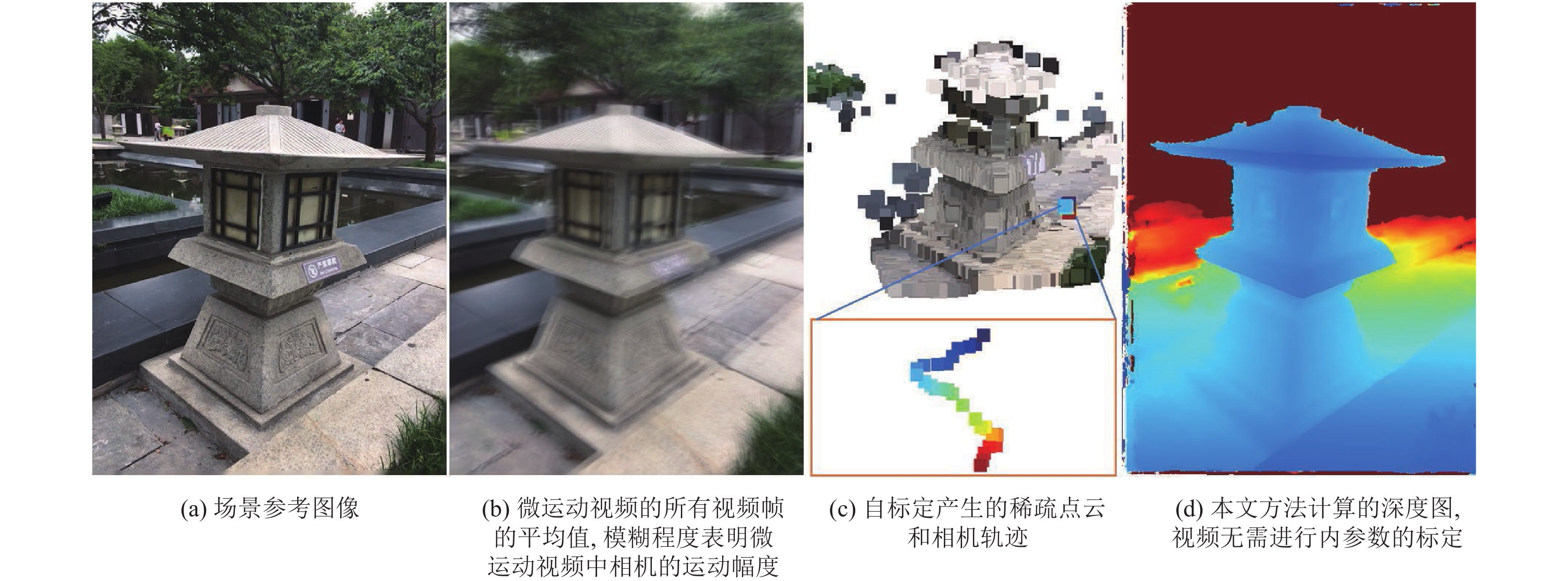
|
图 1 微运动视频三维重建示意图 |
为了解决微运动视频三维重建问题, 学术界已提出了一系列专门的方法. Yu等[1]首次提出针对小运动视频的三维重建方法, 他们的方法首先基于小运动假设简化旋转矩阵的参数, 在此基础上提出基于特征跟踪—光束平差重建—条件随机场稠密深度估计的重建流程. Im等[2]提出一种高效的小运动视频稠密重建方法, 其中包括一种法线约束和颜色信息引导的从稀疏到稠密插值方法, 可以获得场景的光滑深度. 文献[3]进一步在文献[2]的基础上, 引入基于平面扫描(plane-sweep)的精化操作, 提升在特征分布稀少区域的稠密重建效果. 以上方法需要假设相机内参数已知(焦距和畸变系数等), 限制了方法在任意相机模型和拍摄场景中的应用. Ha等[4]提出面向无标定微运动视频的方法, 采用D-U畸变模型来简化畸变系数估计所带来的复杂优化, 并提出基于方差最小化成本函数的平面扫描法获得深度图. 文献[5]进一步将深度学习方法引入微运动视频的稠密重建中, 实现对弱纹理的鲁棒性. 针对城市场景, Li等[6]提出一种鲁棒的微运动视频三维重建方法, 包括基于线段特征约束的相机自标定和对噪声鲁棒的PatchMatch稠密重建方法, 并通过加权平均多个关键帧的深度图进一步减小噪声的影响.
虽然以上工作针对微运动视频提出了一系列改进方法, 逐渐提升了重建质量, 然而这些方法[1-6]没有考虑微运动视频重建过程中的不确定性, 赋予微运动视频中不同邻域视频帧相同的权重, 导致重建结果容易受到噪声的影响, 同时在稠密重建阶段, 缺乏一种有效的正则化方法来平滑噪声的同时保持几何结构. 针对这些问题, 本文提出一种高精度的微运动三维重建方法, 将不确定性显示地考虑进重建过程中, 在自标定阶段, 提出一种视点加权方法, 减少窄基线的负面影响, 在稠密重建阶段, 提出基于广义全变分的深度图平滑方法, 提升稠密重建质量. 本文方法技术流程图如图2所示, 主要贡献总结如下.
(1) 将窄基线的重建不确定性引入相机自标定, 提出一种视点加权的光束平差方法, 通过赋予较窄基线的邻域视点较小的不确定性, 提升相机自标定精度.
(2) 提出基于广义全变分的深度估计方法, 在抑制深度图噪声的同时保持倾斜结构和精细几何特征.
本文在真实数据和合成上与主流方法进行了定量和定性评估实验, 验证了提出方法的有效性.
本文余下内容组织如下: 第2节论述相关工作, 第3节介绍提出的算法, 第4节给出实验评估结果, 第5节对全文进行总结.

|
图 2 提出的微运动视频三维重建方法的技术流程图. |
2 相关工作
基于图像的立体三维重建是图像生成的逆过程, 旨在通过匹配多视角图像间的对应点, 估计场景的三维表面. 基于立体线索信息的三维重建可以分为两个主要步骤: 从运动恢复结构(structure from motion, SFM)和多视角立体稠密重建(multi-view stereo, MVS). 针对这两个子问题, 已经提出了大量的研究工作[7-14], 尝试解决基于图像的三维重建中存在的若干关键问题, 包括: 弱纹理、大尺度重建、高反光重建等, 逐渐提升了重建精度. 这些方法需要假设图像间包含足够的视差, 以准确复原有效像素对应点. 然而, 对于微小运动视频, 其运动幅度所诱导的视差非常小, 对当前主流重建方法提出了挑战.
针对微运动视频的三维重建问题, 学术界已经提出了若干重建方法. Yu等[1]首次研究这一问题, 提出简化的旋转矩阵参数化来减少问题的复杂性, 并提出使用逆深度来约束深度的不确定性对优化过程的影响, 提出基于能量最小化的深度估计方法改善噪声的影响. 该方法可复原由于手部抖动造成的微小运动, 但其需要假设相机的内参数已知, 并依赖耗时的能量优化过程. Im等[2]提出了从稀疏到稠密的插值方法避免了耗时的稠密重建过程, 其方法首先提出一种基于微小运动复原结构(strucure from small motion, SFSM)重建一组三维稀疏点, 在此基础上将三维稀疏点的二维投影当作是控制点, 通过求解基于法线约束的权重最小平方的能量函数来补全缺失的深度. 这一方法依赖SFSM阶段重建的稀疏三维特征点的分布和密度, 如果稀疏三维特征点数量过少, 则插值结果将偏离真实表面. Im等[3]在其改进工作中, 提出采用插值结果作为初始值, 在此基础上执行局部的平面扫描立体算法, 提升了表明细节的重建效果. 文献[15]将相机模型从透视模型宽展到球面模型, 尝试解决全景相机的微运动三维重建问题. 文献[2, 3,15]的方法也需要假设相机的内参数已经标定并且输入图像为已经过畸变矫正的图像, 然而在真实场景下相机的焦距和畸变系数可能和标定时不一样(如对近景的焦距不适合远景), 因此固定相机内参数限制了方法在真实场景下的适用性.
为了增强方法处理真实拍摄场景下的灵活性, Ha等[4]提出了面向无标定微小运动视频的三维重建方法. 为了将相机内参, 如焦距和畸变系数引入SFSM的优化过程中, 他们提出采用D-U畸变模型来简化畸变系数带来的复杂的非线性优化问题. 在稠密重建阶段, 文献[4]提出一种基于方差成本最小化的平面扫描方法, 并通过基于最小生成树的深度精化算法[16]来平滑噪声和补全空洞. Im等[5]将文献[4]中的稠密重建步骤替换为深度学习方法, 提升了弱纹理表面的重建完整度, 但是由于深度学习的泛化能力问题, 方法在一些与训练数据差异较大的场景下表现较差, 并且无法复原物体表面的细致结构. 针对城市场景, Li等[6]提出基于点特征和线特征共同约束的SFSM方法, 提升了相机自标定的准确性, 并提出一种对噪声鲁棒的PatchMatch深度图估计方法快速复原一组关键帧的深度图, 通过多帧深度图的加权平均进一步减小重建噪声.
窄基线立体视差计算问题在遥感领域获得了关注[17-19], 用于遥感影像中的小基高比建筑物的视差, 然而此类方法需要预先极线校正的立体图像对作为输入. 微运动视频也可以看作是光场问题的特例, 在光场问题中, 经过内参数和位姿标定的相机阵列稠密且均匀分布在空间中, 光场方法[20, 21]通过这一均匀且稠密的相机分布特性来计算图像间的遮挡. 然而, 微运动视频相比窄基线立体视觉和光场问题更具挑战性, 这是因为其运动轨迹是任意的, 并且相机参数未知. 因此从微运动复原三维结构不仅需要进行深度的估计还需要考虑相机的标定问题.
虽然方法[4-6]可以处理无标定的微运动视频, 但是这些方法在光束平差过程中, 将所有邻域视频帧相同对待, 忽略了不同视频帧由于相对参考图像的基线不同而具有不同可信度的事实, 导致较差的重建精度. 并且在稠密重建阶段, 文献[1–5]提出方法的重建结果忽略了场景的表面几何细节和倾斜结构, 而文献[6]的方法缺乏有效的噪声平滑手段, 其重建结果仍包含明显噪声. 本文提出一种高精度的微运动视频三维重建方法, 包含视点加权的光束平差方法和基于广义全变分的稠密深度估计方法, 可提升对窄基线所造成的噪声的鲁棒性.
3 提出的方法 3.1 问题定义假设输入微运动视频序列为
针对微运动视频, 本文提出的三维重建方法包括: (a)相机自标定和(b)稠密重建. 其中相机自标定将根据输入视频序列估计对应的相机位置姿态(旋转和平移)和相机内参数(焦距和畸变系数); 而稠密重建计算参考图像的稠密深度图. 在第3.2节和第3.3节, 将对这两个步骤分别详细介绍.
3.2 基于视点加权的微运动视频的自标定根据文献[4], 给定参考图像
步骤1. 特征点检测和匹配. 首先, 使用Harris角点检测方法在参考图像上检测特征点, 设特征集合为
步骤2. 光束平差. 假设在拍摄瞬间的相机焦距和镜头畸变固定不变, 即所有输入视频帧
| $ \mathop {\arg \min }\limits_{f, {k_1}, {k_2}, {{r}}, {{t}}, \omega } \sum\limits_{i = 1}^{|\mathcal{J}|} {\sum\limits_{m = 0}^{{M_p}} \rho } \left( {{{p}}_m^i\mathcal{F}\left( {\frac{{{{p}}_m^i}}{f}} \right) - f \cdot {\pi _i}\left( {{{{x}}_m}, {{{r}}_i}, {{{t}}_i}} \right)} \right) $ | (1) |
其中,
| $ R({r_i}) = \left[ {\begin{array}{*{20}{c}} 1&{ - {r_{i, 3}}}&{{r_{i, 2}}} \\ {{r_{i, 3}}}&1&{ - {r_{i, 1}}} \\ { - {r_{i, 2}}}&{{r_{i, 1}}}&1 \end{array}} \right] $ | (2) |
其中,
| $ \mathop {\arg \min }\limits_{f, {k_1}, {k_2}, {{r}}, {{t}}, \omega } \sum\limits_{i = 1}^{|\mathcal{J}| - 1} {{w_i}} \cdot \sum\limits_{m = 0}^{{M_p}} \rho \left( {{{p}}_m^i\mathcal{F}\left( {\frac{{{{p}}_m^i}}{f}} \right) - f \cdot {\pi _i}\left( {{{{x}}_m}, {{{r}}_i}, {{{t}}_i}} \right)} \right) $ | (3) |
在实验部分本文将对所提出的视点加权的光束平差方法与主流方法进行详细的实验比较, 由于本文方法将视点不确定性考虑进优化过程, 可显著提升相机自标定的精度. 需要指出的是, 相比基准方法, 所提出的视点加权方法仅需要额外计算视角权重, 因此并不显著增加计算量.
3.3 基于广义全变分的稠密重建稠密重建的目标是基于SFSM估计的相机参数和
首先, 对于像素
| $ \begin{split} {\psi _j}\left( {s, t} \right) =& \left( {{{1 - }}\alpha } \right) \cdot \min \left( {\left\| {{I_i}\left( s \right) - {I_j}\left( t \right)} \right\|, \;{\tau _c}} \right) \hfill \\ &+\alpha \cdot \min \left( {\left\| {\nabla {I_i}\left( s \right) - \nabla {I_j}\left( t \right)} \right\|, \;{\tau _g}} \right) \end{split} $ | (4) |
| $ {\rho _j} = \sum\limits_{s \in {R_p}, t \in {R_{{q_j}}}} {\xi _p^s\psi \left( {s, t} \right)} $ | (5) |
其中,
对于小运动视频, 由于各帧之间视差很小, 可以忽略遮挡的影响, 则关于像素
| $ {g^*}\left( {{d_p}, {n_p}} \right) = \frac{1}{{\left| \mathcal{J} \right|}}\sum\limits_{j \in \mathcal{J}} {{\rho _j}} $ | (6) |
PatchMatch首先随机初始化深度和法线值, 方法通过交替执行邻域传播(propagation)和精化(refinement)步骤来不断地优化深度和法线假设. 在文献[22]所提出的方法中, 采用一种基于GPU的红黑棋盘格传播算法, 可以在整幅图像上并行的传播邻域的深度与法线假设. 其中精化操作采用二分法, 不断地在更小的区间内随机寻找更优的深度和法线. Li等[6]在文献[8]的基础上提出一种噪声鲁棒的PatchMatch算法(noise-aware PatchMatch, N-PM), 通过成本松弛和局部假设更新来改善噪声的影响, 并通过加权融合一组关键帧的深度图实现对噪声的进一步抑制. 然而由于窄基线的影响, 重建的深度图
| $ \mathop {\arg \min }\limits_{{\textit{z}}, v} \left\{ {{\alpha _1}\sum\limits_{{\boldsymbol{p}} \in \Omega } {\left| {\nabla {{\textit{z}}_p} - v} \right|} + {\alpha _0}\sum\limits_{{\boldsymbol{p}} \in \Omega } {\left| {\eta (v)} \right|} + \sum\limits_{{\boldsymbol{p}} \in \Omega } {{{\left| {{{\textit{z}}_p} - {\textit{z}}_p^0} \right|}_\delta }} } \right\} $ | (7) |
其中,
本文在多种数据集上对微运动视频的自标定和稠密重建进行了定性和定量对比实验. 数据集包括来自主流方法[3, 4]的公开数据集和合成数据集, 以及本文作者捕获的数据集.
4.1 自标定算法评估首先, 本文对所提出的视点加权的自标定方法进行评估. 本文方法和基准方法[4, 6]均采用30帧微运动视频帧作为输入.
由于真实数据的外部参数未知, 根据文献[4,6]所提出的策略评估相机内参数估计的准确度, 包含焦距和畸变系数. 其中焦距的评价包含了在数据集上的平均值、最大值和最小值. 畸变系数的估计采用文献[4]所提出的策略: 首先在图像阈建立一张均匀网格, 使用真值畸变系数对网格进行形变, 然后采用算法估计的畸变系数对其进行去畸变, 计算去除畸变后的网格和原始网格的误差, 从而得到畸变系数的误差. 本文给出各个算法在数据集上的平均畸变误差、最大畸变误差和最小畸变误差.
本文分别在文献[3]所给出的Canon 60D数据集(4个视频片段), 文献[6]所给出的Nikon D5500数据集(10个视频片段)和本文作者捕获的Nikon D600数据集(18个视频片段)上进行了定量评价. 其中Canon 60D数据集如图3所示, Nikon D5500数据集如图4所示, 本文捕获数据集如图5所示. 这3个数据集的视频规格均为30帧, 1920×1080, 数据拍摄时候保持镜头焦距固定, 数据集的内参数的真值采用棋盘格法[23]获得. 对于Canon 60D和Nikon D600数据集, 本文使用Ha等提出的方法[4]作为基准方法. 对于Nikon D5500数据集, 由于其弱纹理等挑战性, 文献[4]方法容易导致较大重建误差, 为此选用文献[6]的线特征约束的SFSM方法作为基准方法, 在此方法基础上引入本文提出的视点加权策略. 对于每个数据集, 执行SFSM之前的焦距的初始值等于图像维度的最大值, 畸变系数设置为0.

|
图 3 Canon 60D数据集[3] |

|
图 4 Nikon D5500数据集[6] |

|
图 5 本文捕获的Nikon D600数据集部分样例 |
表1–表3分别展示了本文方法和基准方法[4, 6]在3个数据集上的量化对比. 从实验结果可以看出本文提出的视点加权方法在不同相机拍摄的室内和室外视频片段中均可以实现高质量的自标定, 在绝大多数量化指标项上实现了比基准方法更好的结果, 本文分析这是由于所提出的视点加权的光束平差方法考虑了不同邻域视点的基线大小导致的重建不确定性, 可以减小窄基线视点的影响同时增大较宽基线视点的权重, 从而有效地减弱了微运动视频的窄基线对自标定的影响, 提升了自标定的精度.
| 表 1 Canon 60D数据集上的自标定结果(像素) |
| 表 2 在Nikon D600 数据集上的自标定结果(像素) |
| 表 3 在Nikon D5500 数据集上的自标定结果(像素) |
4.2 稠密重建算法评估
进一步地, 本文对稠密重建算法进行评估. 首先在合成数据集上进行定量评价. 合成数据集来自文献[6], 其使用Blender 软件对真实感场景沿一条直线上均匀分布的视点进行渲染, 获得微运动相机轨迹. 合成数据总共包含5组相机轨迹和对应图像数据, 每组包含31张图像, 并提供了深度真实值. 相机的基高比使用基线与最小深度比值的log10来刻画, 分别为: −3.0, −2.5, −2.0, −1.5 和−1.0, 值越小则基高比越小, 重建的不确定性越大. 为了专注于稠密重建算法本身的误差, 稠密重建算法相机参数采用数据集提供的真值参数. 误差度量指标包括R1和MAD. 其中MAD 表示估计深度与真值深度的平均绝对差异值, 该指越小越好, 而R1表示像素的深度估计值与真值深度的误差值小于最大真值深度的1%的像素比例, 该值越大越好. 量化评估结果如表4所示. 在表4中, 本文分别给出了主流方法[4–6]的重建结果, 其中, R1指标越大越好, MAD 指标越小越好. 可以看出, 本文方法显著提升了重建精度, 在不同基线下均实现最好的重建结果, 证明了方法的有效性.
| 表 4 合成数据集上不同基高比的量化评价结果 |
除了定量比较, 本文还定性地比较了在不同基高比下, 提出的方法和对比方法[4-6]的重建结果, 如图6所示. 其中数据集的基高比为–2.0. 为了帮助可视化, 深度图使用法线图形式进行渲染. 可以看出本文方法显著减少了重建误差, 重建结果更加平滑且保留倾斜结构和丰富的几何细节. 本文还在真实数据集上进行了稠密重建的定性比较实验, 如图7所示, 平滑的重建结果进一步验证了方法的有效性.

|
图 6 合成数据上的深度估计 (第2行为对应的R1误差图) |

|
图 7 真实数据集上的定性评估, 数据集来自文献[4] |
4.3 iPhone实况照片的重建结果
特别地, 本文采用iPhone 6S的实况照片模式捕获了一组真实场景的微运动视频数据. 在实况照片模式下, 用户手持手机按下快门, 可同时拍摄一张照片和一个记录了拍摄瞬间前1.5 s和后1.5 s的视频. 首先将视频等间隔采样, 获得30帧数据. 在此数据基础上, 执行本文提出的视点选择和稠密重建, 获得的重建结果如图8和图9所示. 可以看出针对不同的场景下拍摄的实况照片, 本文方法可以实现高质量的三维重建, 验证了方法的有效性.

|
图 8 针对iPhone实况照片拍摄的猫雕塑数据的重建结果 |
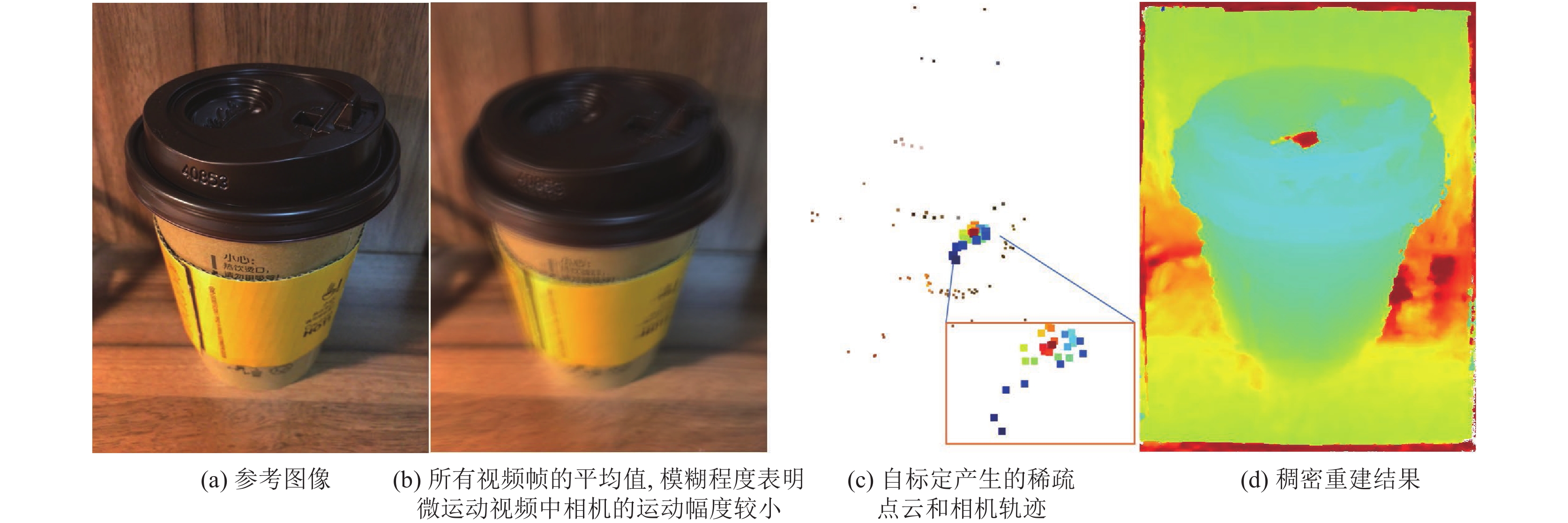
|
图 9 针对iPhone实况照片拍摄的咖啡杯数据的重建结果 |
5 结论与展望
微运动视频来自拍摄瞬间的手部抖动, 提供了一种获取场景深度信息的便捷方式, 同时极小的基线也为三维重建算法提出了挑战. 本文提出一种高精度的微运动重建方法, 包括一种基于不确定性的视点加权相机自标定精度, 以及一种基于广义全变分的稠密重建算法, 提升了重建算法对于窄基线所诱导的噪声的鲁棒性. 此外提出的整个系统框架还可以应用于手机自带的动态照片, 可方便的重建场景的深度图. 基于重建的深度图, 提出的方法可潜在地应用于场景建模、照片重定焦、局部着色等任务.
| [1] |
Yu F, Gallup D. 3D reconstruction from accidental motion. 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014. 1–8.
|
| [2] |
Im S, Ha H, Choe G, et al. High quality structure from small motion for rolling shutter cameras. 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015. 837–845.
|
| [3] |
Im S, Ha H, Choe G, Jeon H, et al. Accurate 3D reconstruction from small motion clip for rolling shutter cameras. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(4): 775-787. DOI:10.1109/TPAMI.2018.2819679 |
| [4] |
Ha H, Im S, Park J, et al. High-quality depth from uncalibrated small motion clip. 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 5413–5421.
|
| [5] |
Im S, Ha H, Jeon HG, et al. Deep depth from uncalibrated small motion clip. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 1(1): 1-14. |
| [6] |
Li ZX, Zuo WM, Wang ZQ, et al. Robust 3D reconstruction from uncalibrated small motion clips. The Visual Computer, 2022, 38(5): 1589–1605.
|
| [7] |
Schönberger JL, Frahm JM. Structure-from-motion revisited. 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 4104–4113.
|
| [8] |
Seitz SM, Curless B, Diebel J, et al. A comparison and evaluation of multi-view stereo reconstruction algorithms. 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06). New York: IEEE, 2006. 519–528.
|
| [9] |
Strecha C, von Hansen LW, van Gool L, et al. Thoennessen U. On benchmarking camera calibration and multi-view stereo for high resolution imagery. 2008 IEEE Conference on Computer Vision and Pattern Recognition. Anchorage: IEEE, 2008. 1–8.
|
| [10] |
Schöps T, Schönberger JL, Galliani S, et al. A multi-view stereo benchmark with high-resolution images and multi-camera videos. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017. 2538–2547.
|
| [11] |
Furukawa Y, Ponce J. Accurate, dense, and robust multiview stereopsis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 32(8): 1362-1376. |
| [12] |
Li ZX, Zuo WM, Wang ZQ, et al. Confidence-based large-scale dense multi-view stereo. IEEE Transactions on Image Processing, 2020, 29: 7176-7191. DOI:10.1109/TIP.2020.2999853 |
| [13] |
Snavely N, Seitz SM, Szeliski R. Photo Tourism: Exploring photo collections in 3D. ACM Transactions on Graphics, 2006, 25(3): 835-846. DOI:10.1145/1141911.1141964 |
| [14] |
Wu CC. Towards linear-time incremental structure from motion. 2013 International Conference on 3D Vision—3DV 2013. Seattle: IEEE, 2013. 127–134.
|
| [15] |
Im S, Ha H, Rameau F, et al. All-around depth from small motion with a spherical panoramic camera. 2016 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 156–172.
|
| [16] |
Yang QX. A non-local cost aggregation method for stereo matching. 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence: IEEE, 2012. 1402–1409.
|
| [17] |
刘雨晨, 贺金平, 胡斌, 等. 小基高比立体测绘仿真与分析. 航天返回与遥感, 2016, 37(5): 95-101. DOI:10.3969/j.issn.1009-8518.2016.05.011 |
| [18] |
申二华, 范大昭, 孙晓昱. 基于SGM和相位相关的小基高比影像匹配. 中国矿业大学学报, 2015, 44(1): 183-188. |
| [19] |
马宁, 门宇博, 门朝光, 等. 基于扩展相位相关的小基高比立体匹配方法. 电子学报, 2017, 45(8): 1827-1835. DOI:10.3969/j.issn.0372-2112.2017.08.004 |
| [20] |
Zhang S, Sheng H, Li C, et al. Robust depth estimation for light field via spinning parallelogram operator. Computer Vision and Image Understanding, 2016, 145(1): 148-159. |
| [21] |
Schilling H, Diebold M, Rother C, et al. Trust your model: Light field depth estimation with inline occlusion handling. IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 4530–4538.
|
| [22] |
Galliani S, Lasinger K, Schindler K. Massively parallel multiview stereopsis by surface normal diffusion. 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015. 873–881.
|
| [23] |
Zhang Z. A flexible new technique for camera calibration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. DOI:10.1109/34.888718 |
 2022, Vol. 31
2022, Vol. 31


