随着多媒体技术和3D打印技术的快速发展, 三维模型[1]已广泛应用于医学影像、工业制造和游戏等领域. 此外, 在文物保护、化学和生物等领域, 三维模型的应用也越来越普遍. 它成为继图像、视频、音频3大主流数据类型之后的数据类型. 但在使用和传播这些数字产品的同时盗版和侵权等问题也随之而来, 使得如何安全有效的保护数字产品的版权成为学者研究的一个重点问题.
数字水印作为信息隐藏的一个重要分支, 在数字产品的版权保护方面发挥了重要作用. 1997年, 在ACM国际会议上Ohbuchi等[2]首次提出将数字水印技术应用到三维模型, 为三维数字产品的版权保护提供了新思路. 此后, 越来越多的学者开始研究三维网格模型数字水印技术.
根据水印算法是否修改原始模型的数据, 可将其分为嵌入式水印算法[3-7]和零水印算法[8-10]. 大部分水印算法为嵌入式水印算法, 它通过对模型进行细微的修改来嵌入水印信息. Cho等[3]提出了一种改变所有顶点与质心之间欧氏距离分布的统计水印方法. 该方法能够很好地抵抗相似变换和顶点重排序这种无失真的攻击. 之后, Bors等[11]对基于统计的水印进行了扩展, 通过Levenberg-Marquardt优化方案进行最优保存, 使目标表面畸变最小化. 该方案对常见的网格攻击具有很强的鲁棒性, 同时保证了曲面的最小失真. 为了增强鲁棒性, Liu等[12]提出了一种对三角网格模型进行多分辨率曲面自适应参数化的鲁棒水印算法. Liu等将模型的所有顶点分为两组. 一个是粗糙层, 它可以建立一个不变量空间. 二是作为水印嵌入特征的精细层次. 该算法具有很强的隐蔽性, 对常见攻击具有很强的鲁棒性. 但这些算法对裁剪攻击的鲁棒性相对较弱, 而且嵌入式水印算法不可避免地要修改原始模型信息, 无法应用到对数据精度要求较高的模型; 并且嵌入式水印算法嵌入水印的强度难以控制, 若嵌入强度过低, 算法的鲁棒性较差, 嵌入强度过高, 又会影响模型的视觉效果. 所以, 如何平衡水印的透明性与鲁棒性之间的矛盾是嵌入式水印算法研究的一个难点问题.
为解决上述问题, 温泉等[13]提出了零水印算法, 零水印算法不需要对原始模型进行修改, 而是利用模型本身特征构造水印信息, 并将水印信息在知识产权(intellectual property rights, IPR)信息数据库中注册; 当需要对版权进行验证时, 再利用零水印算法构造水印信息, 并与IPR数据库中的水印信息进行对比, 以此验证模型所有者. 零水印算法并没有将信息嵌入到模型中, 从而避免了透明性和鲁棒性之间的矛盾.
目前, 在图像方面关于零水印算法的研究[14, 15]比较多, 由于三维模型数据的不规则性, 并且表示方法有多种, 使得构造稳定的水印存在一定困难, 三维模型零水印算法较少. 徐涛等[16]利用网格空域特征的提取和变换域二次能量集中构造水印信息. 王新宇[17]提出一种三维网格模型空域零水印算法, 该算法利用模型顶点范数以及该顶点的邻域顶点范数构造水印信息. 这两种算法对剪切攻击的抵抗能力都比较弱. 为了使算法能够在抵抗旋转、平移、缩放等常见攻击的同时也能够抵抗网格简化和剪切攻击, 本文提出一种基于矢量长度比的零水印算法.
1 算法思想由于零水印算法不改变原始模型信息, 而是利用模型自身属性造水印信息, 构造信息的鲁棒性直接影响算法的鲁棒性, 因此, 构造鲁棒的特征对零水印算法至关重要[18]. 顶点范数是三维模型的一种全局特征, 它能够反映模型的整体形状. 一般对模型进行攻击的时候不会改变模型的全局特征, 否则模型的视觉效果就破坏, 从而失去使用价值. 但仅利用这一特征构造水印, 在水印检测阶段, 需要对模型进行重定位和重采样操作, 否则就无法提取水印, 重定位是为了使受到几何攻击的模型恢复到原始位置, 重采样是为了使拓扑结构发生改变的模型恢复原样. 将顶点范数和顶点领域以及比例相结合, 就可以避免对模型进行重定位和重采样. 若直接选择模型质心作为构造水印的基元, 算法容易受到剪切攻击的影响, 为了抵抗剪切攻击, 可以对模型分块[19], 然后用块质心代替模型质心, 接着计算均值, 弱化受攻击后模型顶点改变带来的影响.
三维网格模型由顶点集合和这些顶点之间的连接组成. 为了避免顶点均匀缩放、平移、旋转等相似变换的影响, 可以对三维模型进行预处理, 即将顶点的笛卡尔坐标转换为球坐标, 然后依据需要构造的水印长度以及经度分量对顶点进行分块, 对分块中的每个顶点计算出该顶点到块质心的距离和邻域顶点到块质心的平均距离, 接着计算这两个长度之比, 利用长度之比和密钥构造水印信息. 水印构造的流程如图1所示.
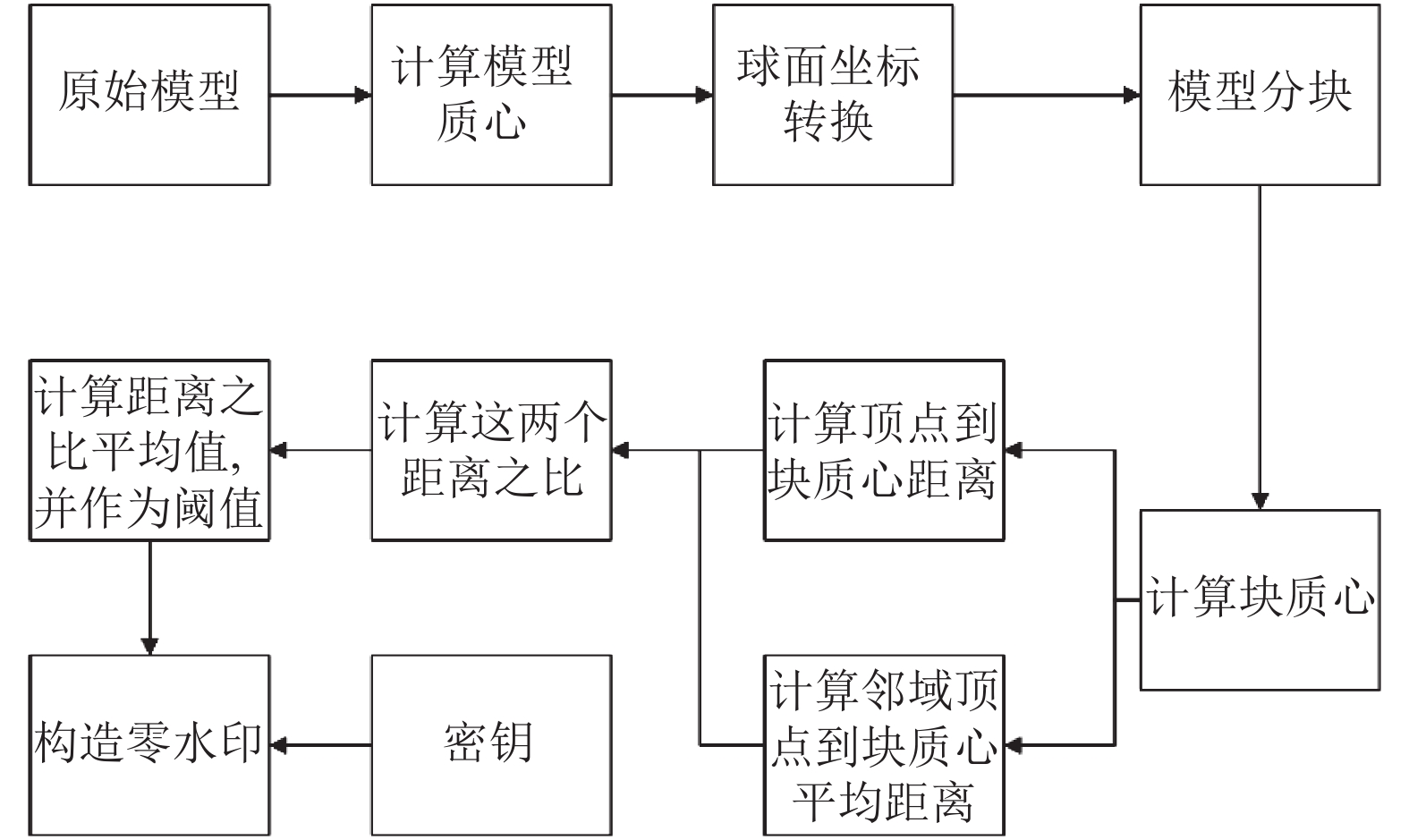
|
图 1 水印构造流程图 |
2 基于长度比的零水印算法
三维网格模型可以表示为
为了更方便地对三维模型进行零水印的构造, 需要对三维模型进行预处理, 将三维模型的直角坐标系转换为球面坐标系, 并根据经度分量对模型分块. 预处理步骤如下.
(1)为了实现三维模型坐标转换, 需要计算三维模型质心坐标, 由于三维模型受到攻击后可能造成模型的顶点分布不均匀, 使模型质心改变, 以三角形面积为权重的方法可以弱化这种影响, 获得较稳健的质心. 因此, 本文算法采用基于面积矩的方法计算三维模型的质心, 计算公式如式(1).
| $ {V_c} = \frac{{\displaystyle\sum\limits_{{{i}} = 1}^{{N_v}} {A({V_i}){V_i}} }}{{\displaystyle\sum\limits_{{{i}} = 1}^{{N_v}} {A({V_i})} }} $ | (1) |
其中,
(2)平移模型即将三维模型质心与直角坐标系原点重合, 计算公式如式(2).
| $ \left\{ \begin{gathered} {{{{x}'}}_i} = {x_i} - {x_c} \hfill \\ {{{{y}'}}_i} = {y_i} - {y_c} \hfill \\ {{{{\textit{z}}\text{}'}}_i} = {{\textit{z}}_i} - {{\textit{z}}_c} \hfill \\ \end{gathered} \right., 0 \leqslant i \leqslant {N_v} - 1 $ | (2) |
(3)接着转换为球面坐标系, 计算公式如式(3).
| $ \left\{ \begin{gathered} {\rho _{{i}}} = \sqrt {{{x{'}}_i} + {{y{'}}_i} + {{{\textit{z}}{'}}_i}} \hfill \\ {\theta _i} = \arctan \left( {\dfrac{{{{y{'}}_i}}}{{{{x{'}}_i}}}} \right) \hfill \\ {\phi _i} = \arccos \left( {\dfrac{{{{{\textit{z}}{'}}_i}}}{{{\rho _{{i}}}}}} \right) \hfill \\ \end{gathered} \right., 0 \leqslant {{i}} \leqslant {N_v} - 1 $ | (3) |
其中,
(4)利用模型现有的条件经度分量对模型进行分块. 根据经度坐标分量将模型等分为块, 然后根据θ的取值将模型的顶点进行分块, 建立顶点与θ之间的映射关系. 第i个顶点分块的表示如式(4)所示.
| $ \begin{split} & {B_{\theta , {{j}}}} = \left\{ {{V_{i, j}}|{V_{i, j}} \in \frac{{2\pi }}{{{N_\theta }}} \cdot i \lt {\theta _{i, j}} \lt \frac{{2\pi }}{{{N_\theta }}} \cdot \left( {i + 1} \right)} \right\}, \\ &\quad\quad 0 \leqslant i \leqslant {N_\theta } - 1, 0 \leqslant j \leqslant {N_{\theta , {{j}}}} - 1 \\ \end{split} $ | (4) |
其中,
(5)计算每个分块中的质心
零水印的构造过程如下.
(1)对分块中的每个顶点进行以下操作.
1)计算每个顶点
2)计算
3)计算这两个长度的比值
| $ {Q_{{i}}} = {{{D_{cl}}} \mathord{\left/ {\vphantom {{{D_{cl}}} {{{\overline D}_{cl}}}}} \right. } {{{\overline D}_{cl}}}} $ | (5) |
(2)计算每个顶点处长度之比的平均值
| $ \overline Q = \dfrac{1}{N}\sum\limits_{i = 0}^{N - 1} {{Q_i}} $ | (6) |
(3)构建顶点的状态序列
| $ {S}_{{i}}=\left\{ { \begin{array}{l}0,\; 若{Q}_{{i}} < {\overline{Q}}_{{i}}\\ 1, \;若{Q}_{{i}} \geqslant {\overline{Q}}_{{i}}\end{array}, 0 \leqslant i \leqslant N-1 } \right. $ | (7) |
(4)统计每个分块中0和1的数目, 若1的个数大于0的个数, 则本块构造的水印为1, 否则为0, 最后得出水印序列
(5)将版权信息转换成与构造的水印长度相同的密钥
(6)将密钥与生成的水印序列进行异或, 按式(8)生成最终的水印序列
| $ {\textit{z}}ero\_watermark = {L_i} \oplus {S_i} $ | (8) |
(7)将生成的零水印信息和密钥交给知识产权信息数据库IPR进行保存, 当发生版权纠纷时根据数据库中的水印信息和密钥就可以确定模型的所有者.
2.3 零水印检测当无法确定三维模型的版权所有者时, 就需要用零水印检测算法对模型进行版权验证. 零水印是一种特殊的盲水印, 检测时不需要原始模型的参与. 它的检测过程与构造过程相同, 结合密钥, 重复水印的构造过程, 最终得到水印序列Wd, 然后将Wd与数据库中的水印序列W进行比较, 判定模型的版权归属.
在使用模型的时候可能对模型进行有意或无意的操作, 从而使模型发生改变, 使构造出的水印信息与原始水印信息不一致, 难以判断水印是否存在, 因此为了评价算法的鲁棒性, 需要一个衡量指标, 即相关性系数Corr, 来判断待检测水印与原始水印之间的相关性. 计算方法如式(9)所示.
| $ Corr = \frac{{\displaystyle\sum\limits_{i = 0}^{N - 1} {(w_i^d - {{\overline w}^d})(w_i^o - {{\overline w}^o})} }}{{\sqrt {\displaystyle\sum\limits_{i = 0}^{N - 1} {{{(w_i^d - {{\overline w}^d})}^2}\displaystyle\sum\limits_{i = 0}^{N - 1} {{{(w_i^o - {{\overline w}^o})}^2}} } } }} $ | (9) |
其中,
本文算法是使用Visual Studio 2013开发平台以及OpenGL库来实现的. 选取了bunny、dragon、rabbit、venus这4个具有代表性的模型进行相关实验. 模型的数据信息如表1所示, 在实验中, 水印长度W=64.
3.1 鲁棒性实验为了验证零水印算法的鲁棒性, 本文使用LIRIS实验室提供的攻击软件和MeshLab软件对三维模型分别进行相似变换、随机噪声、平滑攻击、网格简化等多种类型的攻击, 对攻击后的模型重新构造水印序列, 然后与原始模型水印序列进行比较, 通过计算相关性系数来衡量算法的鲁棒性, 相关性系数的计算如式(9)所示. 图2为原始三维模型.
| 表 1 三维模型数据信息 |

|
图 2 原始模型 |
(1)相似变换
因为本文使用的是三维模型顶点的矢量长度之比这一几何变量, 它不受平移, 旋转和均匀缩放的影响, 而且在构造水印之前已经对模型进行了预处理, 所以能够很好地抵抗相似变换的攻击, 即在受到这类攻击后的模型构造出来的水印与原始水印完全相同, 实验结果如表2所示.
| 表 2 相似变换的相关系数结果 |
(2)平滑攻击
平滑攻击是对模型的顶点进行轻微扰动, 使模型表面变光滑, 它会轻微改变模型质心以及模型到块质心的距离, 导致水印错误, 但该攻击不会改变模型的整体形状, 本文选择的矢量长度比能够反应模型整体形状, 因此对该类攻击具有较高的容忍性, 并且当该类攻击造成模型顶点发生剧烈变化, 构造的水印严重错误时, 模型必然已失去使用价值, 无须再对模型进行保护. 分别对模型平滑迭代10次、20次和30次, 部分攻击后的venus模型如图3所示, 实验结果如表3所示, 实验表明, 攻击后的模型构造出的水印信息仍与原始水印信息具有较高的相关性, 即水印算法对平滑攻击具有鲁棒性.
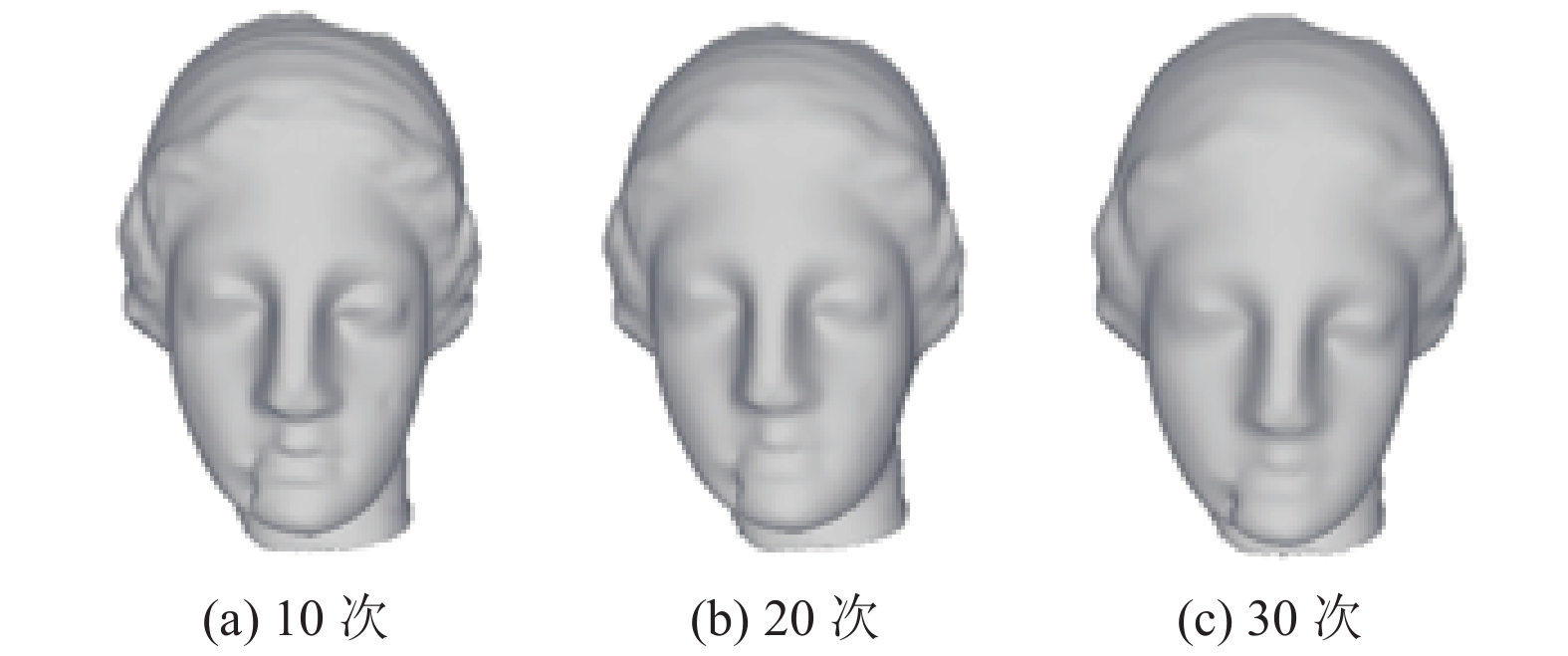
|
图 3 平滑攻击后的venus模型 |
| 表 3 平滑攻击的相关系数结果 |
(3)随机噪声
针对噪声攻击, 分别对三维模型的每个顶点添加一个0.05%、0.1%、0.2%的随机噪声, 图4显示的是不同强度噪声攻击后的bunny模型, 噪声攻击测试的实验结果如表4所示. 噪声攻击对三维模型影响比较大, 容易造成模型表面失真, 从而使模型的视觉效果变差. 它与平滑攻击类似都属于信号处理攻击, 所以选取矢量长度比这一特征也能够抵抗该类攻击. 实验结果显示, 当噪声攻击达到0.2%时, 本文的算法对噪声攻击具有鲁棒性.

|
图 4 噪声攻击后的模型 |
| 表 4 噪声攻击的相关系数结果 |
(4)简化攻击
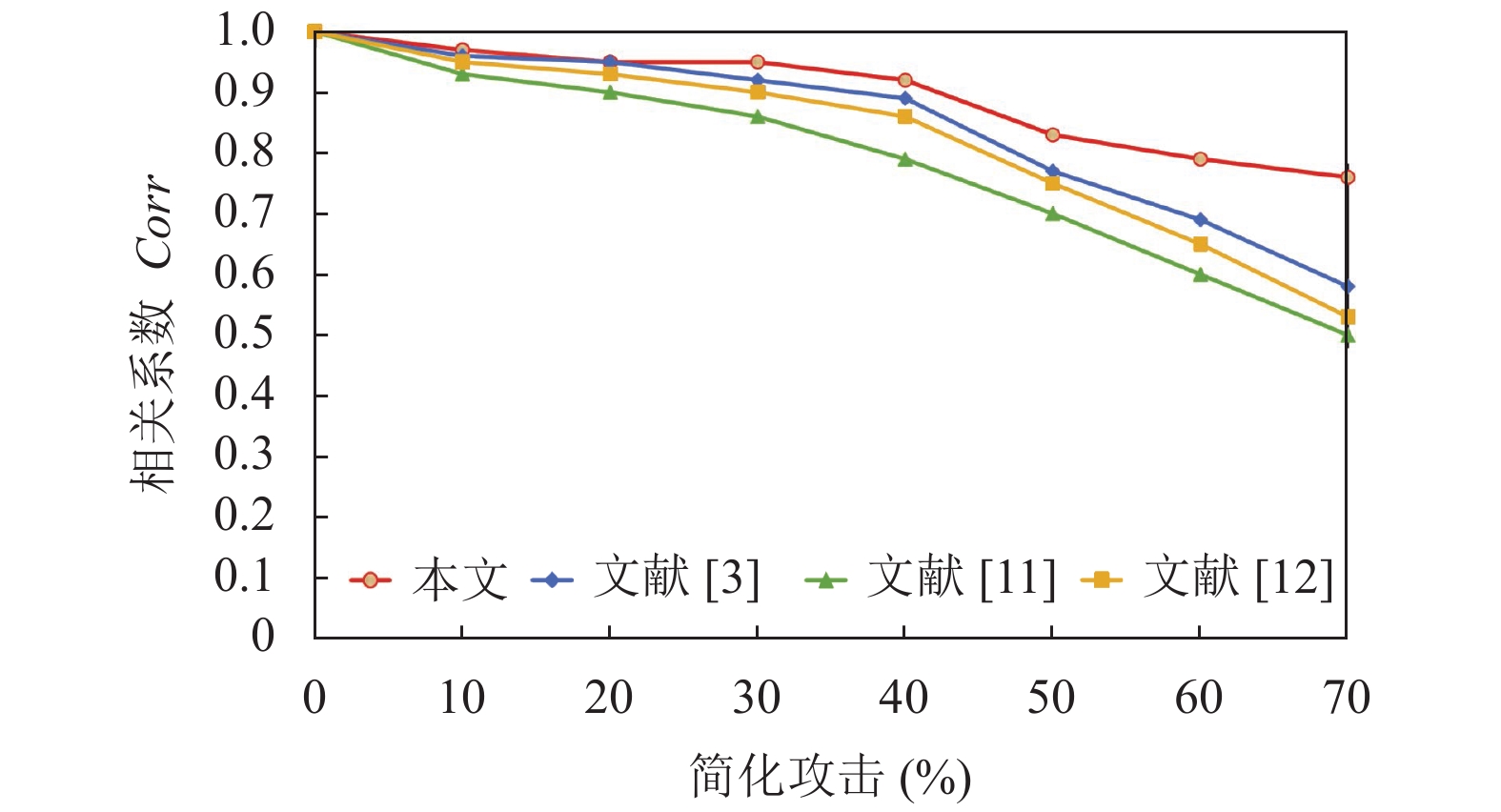
简化攻击是在保持模型整体形状的前提下, 减少模型点、线、面的个数, 这种减少是近乎等比例的减少, 本文选择的矢量长度的向量比, 是模型的全局几何特征, 能够很好地抵抗简化攻击, 并且在对模型进行预处理时使用面积矩计算模型的质心, 能够弱化简化攻击后模型顶点分布不均带来的影响, 进而加强对抗简化攻击的能力. 分别将模型的顶点数目简化30%、50%、70%, 简化后的部分dragon模型如图5所示, 实验结果如表5所示, 实验表明, 随着模型简化率的增高, 受攻击后的模型构造出的水印信息与原始水印信息仍然具有较高的相关性, 即使简化率高达80%, 本算法仍具有较好的鲁棒性.

|
图 5 简化攻击后的dragon模型 |
| 表 5 简化攻击的相关系数结果 |
(5)剪切攻击
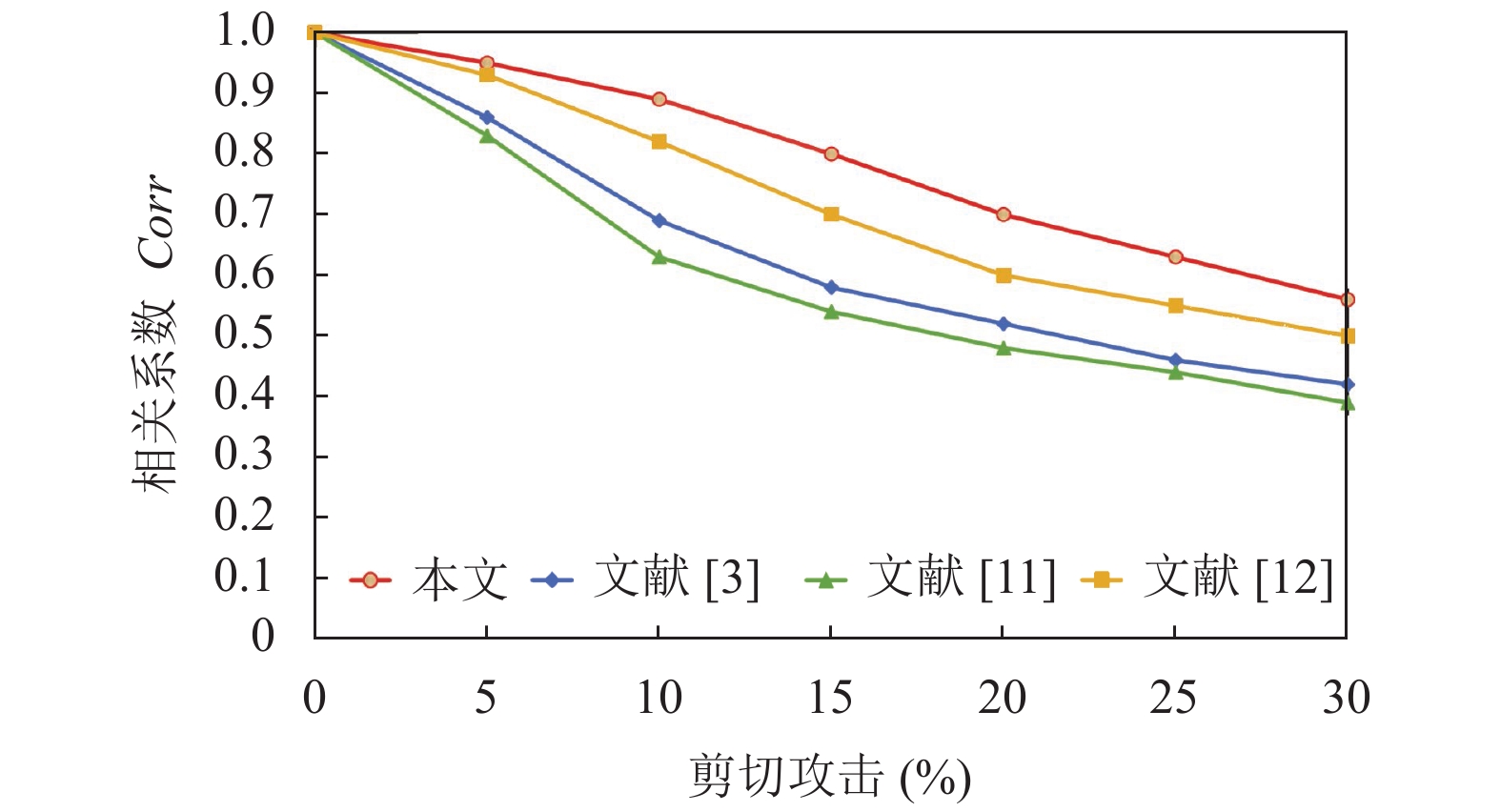
剪切攻击是将模型的部分点和面的信息切除, 从而使模型的整体形状改变, 丢失的是局部信息, 并且随着剪切比例的升高, 模型的质心会发生偏移, 使得对模型质心依赖较大的算法难以提取出正确的水印信息. 分别选取三维模型的3个不同位置对三维模型进行10%、20%、30%的剪切, 剪切后的部分bunny模型如图6所示, 实验结果如表6所示. 本文算法选取分块后的块质心并取均值, 能够减小对模型质心的依赖, 从而较好的抵抗剪切攻击, 但随着剪切比例的升高, 会对模型的分块产生较大的影响, 所以本算法只能够抵抗较低比例的剪切攻击. 实验结果显示, 当模型被剪切30%时, 本文算法仍具有较高的相关性系数, 能很好地提取出水印信息. 因此, 本文算法在非对称模型失去保护价值之前对剪切攻击仍具有鲁棒性.
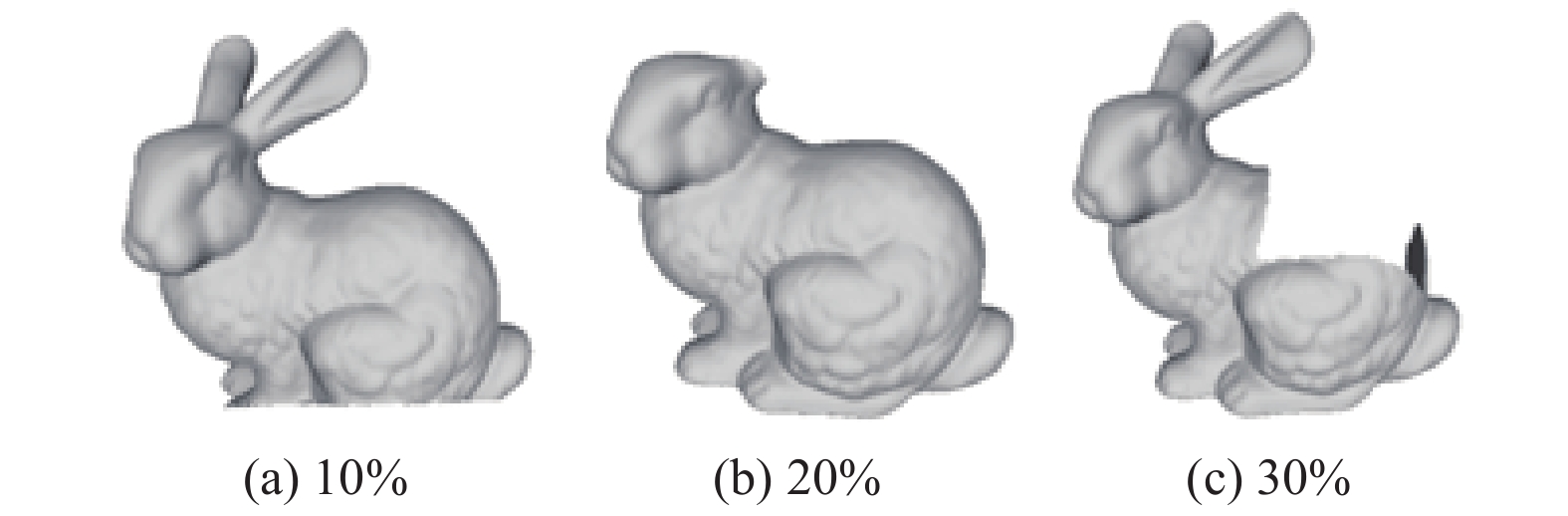
|
图 6 剪切攻击后的bunny模型 |
| 表 6 剪切攻击的相关系数结果 |
3.2 相关工作比较
为了更好地验证本文算法的鲁棒性, 本小节将本文的实验结果与比较经典的水印算法的实验结果进行了对比. bunny模型的对比实验结果如图7–图10所示. 表7为5种水印算法鲁棒性比较.
对于相似变换, 本文使用矢量长度之比这一变量, 它不受旋转、平移和缩放攻击的影响, 所以能很好的抵抗这类攻击, 而对于文献[12]的算法是利用网格的低层分辨率建立不变空间, 当模型受到攻击后, 这些点顶点可能发生轻微扰动, 所以该算法受旋转缩放攻击的影响.
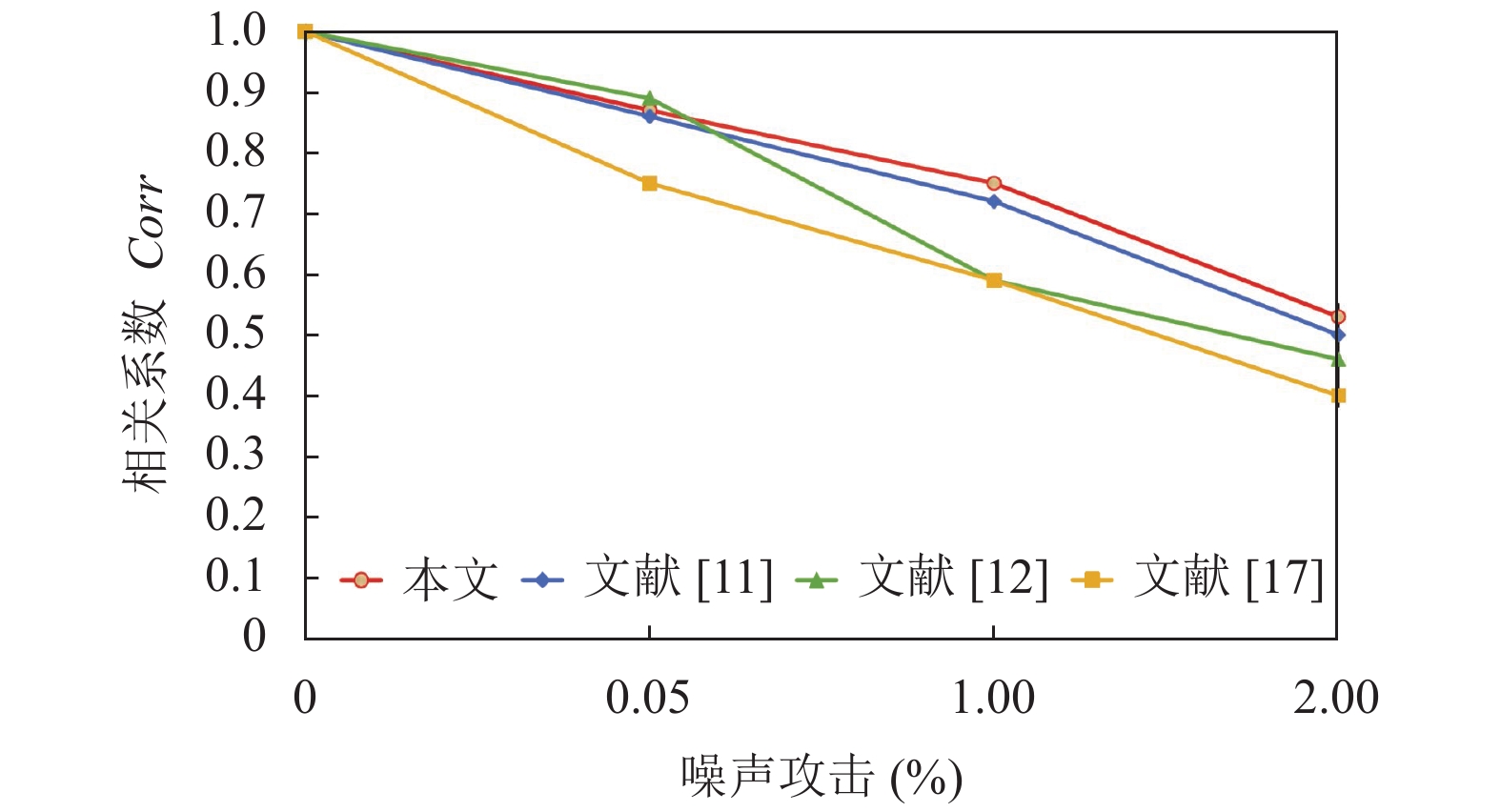
|
图 7 噪声攻击 |

|
图 8 平滑攻击 |
如图7–图9所示, 本文算法在抵抗网格简化和剪切攻击方面的优势比较明显. 由于本文算法在对模型进行预处理时使用面积矩计算模型的中心, 并且在实现过程中加入了顶点与顶点邻域之间的比值, 使算法对抗不同程度的采样能力加强, 所以本文算法对简化攻击具有很强的鲁棒性. 相对于其他算法, 本文算法对模型中心的依赖更小, 所以能较好地抵抗剪切攻击. 对于噪声和平滑攻击, 本文算法在模型失去使用价值之前, 检测出的阈值大于无法辨别模型归属的阈值0.5, 所以本文算法也能够抵抗噪声和平滑攻击. 总体来说, 本文提出的算法不需要考虑透明性问题, 能够抵抗常见类型的攻击, 并且对简化攻击有很强的鲁棒性, 也能够抵抗一定比例的剪切攻击.
|
图 9 简化攻击 |
|
图 10 剪切攻击 |
| 表 7 5种水印算法的鲁棒性比较 (%) |
4 结论
本文提出了一种基于矢量长度比的三维网格模型零水印算法, 该算法首先对三维网格模型进行分块并计算每块质心, 用块质心代替模型质心, 利用顶点到块质心距离与邻域顶点到块质心的平均距离构造出鲁棒的水印序列. 实验结果表明本算法能够抵抗相似变换、噪声、平滑、剪切等常见的攻击, 并且在简化攻击和剪切攻击方面的优势比较突出. 本文算法可应用于对精度要求较高的三维模型中. 下一步计划是加强算法抵抗攻击的种类以及它们的联合攻击, 进一步加强算法的鲁棒性.
| [1] |
Kariya K. The next generation EDA system for 3D printing technologies. 2017 International Conference on Electronics Packaging (ICEP). Yamagata: IEEE, 2017. 3–4.
|
| [2] |
Ohbuchi R, Masuda H, Aono M. Watermaking three-dimensional polygonal models. Proceedings of the 5th ACM International Conference on Multimedia. Seattle: ACM, 1997. 261–272.
|
| [3] |
Cho JW, Prost R, Jung HY. An oblivious watermarking for 3-D polygonal meshes using distribution of vertex norms. IEEE Transactions on Signal Processing, 2007, 55(1): 142-155. DOI:10.1109/TSP.2006.882111 |
| [4] |
胡敏, 谢颖, 许良凤, 等. 基于几何特征的自适应三维模型数字水印算法. 计算机辅助设计与图形学学报, 2008, 20(3): 390-394, 402. |
| [5] |
Zhan YZ, Li YT, Wang XY, et al. A blind watermarking algorithm for 3D mesh models based on vertex curvature. Journal of Zhejiang University Science C, 2014, 15(5): 351-362. DOI:10.1631/jzus.C1300306 |
| [6] |
王启垒. 针对三维模型的数字水印技术研究[硕士学位论文]. 深圳: 深圳大学, 2018.
|
| [7] |
Liu J, Yang YJ, Ma DL, et al. A novel watermarking algorithm for three-dimensional point-cloud models based on vertex curvature. International Journal of Distributed Sensor Networks, 2019, 15(1).
|
| [8] |
张君瑾. 三维网格模型的零水印算法研究[硕士学位论文]. 天津: 天津大学, 2008.
|
| [9] |
高龙, 王孝通, 徐晓刚, 等. 一种基于仿射不变量的模型零水印算法. 2011年亚太青年通信学术会议论文集, 2011. 325–328.
|
| [10] |
Cui CC, Ni RR, Zhao Y. Robust zero watermarking for 3D triangular mesh models based on spherical Integral invariants. 16th International Workshop on Digital Forensics and Watermarking. Magdeburg: Springer, 2017. 318–330.
|
| [11] |
Bors AG, Luo M. Optimized 3D watermarking for minimal surface distortion. IEEE Transactions on Image Processing, 2013, 22(5): 1822-1835. DOI:10.1109/TIP.2012.2236345 |
| [12] |
Liu J, Wang YH, Li Y, et al. A robust and blind 3D watermarking algorithm using multiresolution adaptive parameterization of surface. Neurocomputing, 2017, 237: 304-315. DOI:10.1016/j.neucom.2016.12.065 |
| [13] |
温泉, 孙锬锋, 王树勋. 零水印的概念与应用. 电子学报, 2003, 31(2): 214–216.
|
| [14] |
曲长波, 杨晓陶, 袁铎. 小波域视觉密码零水印算法. 中国图象图形学报, 2014(03): 37-44. |
| [15] |
Kang XB, Zhao F, Chen YJ, et al. Combining polar harmonic transforms and 2D compound chaotic map for distinguishable and robust color image zero-watermarking algorithm. Journal of Visual Communication and Image Representation, 2020, 70: 102804. DOI:10.1016/j.jvcir.2020.102804 |
| [16] |
徐涛, 张艳宁. 三维网格模型零水印技术. 吉林大学学报(工学版), 2007, 37(4): 901-904. |
| [17] |
王新宇. 三维网格模型数字水印算法研究[硕士学位论文]. 镇江: 江苏大学, 2006.18
|
| [18] |
王新宇, 詹永照. 面向三维点云模型的鲁棒零水印技术. 计算机工程与应用, 2011, 47(28): 7-11. |
| [19] |
林克正,卜雪娜, 唐远新. 块矢量的三维模型数字水印. 计算机工程与应用, 2021, 46(031): 188-191. |
 2022, Vol. 31
2022, Vol. 31



