大规模的车辆轨迹数据可通过GPS、手机信令、视频监控、感应线圈等技术获取[1]. 利用地理信息系统(geographic information system, GIS)将这些轨迹数据投影在电子地图上, 能直观地显示交通环境, 进行实时的交通智能信息分析. 同时, 深入分析车辆轨迹数据还可获取道路起讫点(origin-destination, OD)、出行偏好等信息. 为公路规划、建设养护等工作提供重要决策支撑[2].
在上述的交通信息采集技术中, 使用部署在道路上的摄像采集设备, 通过自动车牌识别技术能获取车辆的行驶状态, 如时间、车牌号、速度、车道和方向. 这些行驶状态, 结合道路网络拓扑结构, 即可得到车辆时序轨迹数据. 与基于GPS[3, 4]、手机信令[5]、感应线圈[6]等方法相比, 使用摄像采集技术具有覆盖面积广、安装维护便捷、连续性强、样本量大的优势. 同时还可提供可视化图像, 以保证数据的精准性[7]. 由此产生了大量基于车牌识别数据的交通特性分析研究, 但现有的研究[7-10]主要集中在交通小区交通量、出入站情况、通行效率等宏观特性提取, 很少有研究关注到微观的车辆出行轨迹提取与分析. 然而, 完整可靠的车辆出行轨迹蕴含丰富的交通运行状态信息, 能系统、全面地再现复杂的道路交通运行场景, 对交通管控至关重要.
基于车牌识别数据的出行轨迹的研究具有很大挑战, 主要原因在于以下2点: 1)受设备采样频率、信号质量、天气环境等多种因素影响, 导致部分轨迹数据错误或者漏检, 使得车辆轨迹数据呈现稀疏不完整性. 2)以往的出行路径还原方法没有充分利用视频图像检测器获取的驾驶状态, 忽略了出行者路径决策的主观行为.
直观地说, 针对稀疏不完整的车牌轨迹数据, 充分考虑每2个监测点之间不同的路线选择方案, 以挖掘驾驶员潜在的行驶规律, 可有效提升算法的鲁棒性. 为实现此目标, 本文提出一种新的OD轨迹还原算法. 该算法的主要贡献有: 1) 设计一种基于K则最短路径算法(K shortest paths, KSP)的候选路径生成方法, 以模拟出行者复杂的路径决策行为. 2) 应用变分自编码器(variational auto-encoder, VAE)对多个候选轨迹就行最优化估计, 以此重建还原车辆的完整通行轨迹. 该算法在杭州市萧山区实际交通小区进行验证评估. 实验结果表明, 该方法在轨迹还原精准度上准达到了95%, 远高于用于对比的基准模型. 此外, 该方法还被证明能有效适应数据缺失率高的场景, 在基于稀疏数据的轨迹重建上显示出巨大的应用前景.
1 OD轨迹还原算法本文提出了一种基于稀疏车牌数据的轨迹还原算法. 如图1, 该算法框架主要由4个模块组成: 1) 出行链验证分离; 2) 候选路径生成; 3) 路径校验; 4) 路径决策. 本节将对以上模块展开详细描述.

|
图 1 OD轨迹还原算法框架 |
为了便于描述, 设定
对识别到的所有行驶状态按车牌号进行分组, 再以检测时间排序, 可得到采样时间段内每辆车的出行链. 如图2所示, 该出行链来自于多个时间段统计聚合, 可能包含多个不同目的的OD出行. 本节首先对整个出行链进行验证, 结合相邻样本间空间距离与通行间隔将原始时序数据划分为多个OD片段, 从而保证轨迹推导模型数据的真实可靠.

|
图 2 多OD出行链示例 |
具体来说, 给予一辆车在统计时间内的出行链, 即车牌时序序列
| $ {v}_{i, i+1}=d/\Delta t $ | (1) |
然后, 判定
出行链经过验证分离转化为仅包含一个O点和D点的独立轨迹片段. 在实际道路环境中, 设备的未覆盖、漏检或者错检, 导致这些独立的OD片段往往呈现出稀疏不完整的性质. 为获取完整的OD轨迹供后续分析使用, 需要对缺失的轨迹数据进行补全还原.
如图3所示, 车辆在两个间断点有多条距离相当的可选通行路径, 直接假设车辆以最短路径行驶显然不再适用. 本文设计了一种新的路径还原思路. 对两个间断样本点潜在路径求解, 以模拟真实道路交通场景下, 出行者复杂的道路选择; 再对候选路径进行校验, 择优, 以获取最终的通行路径.
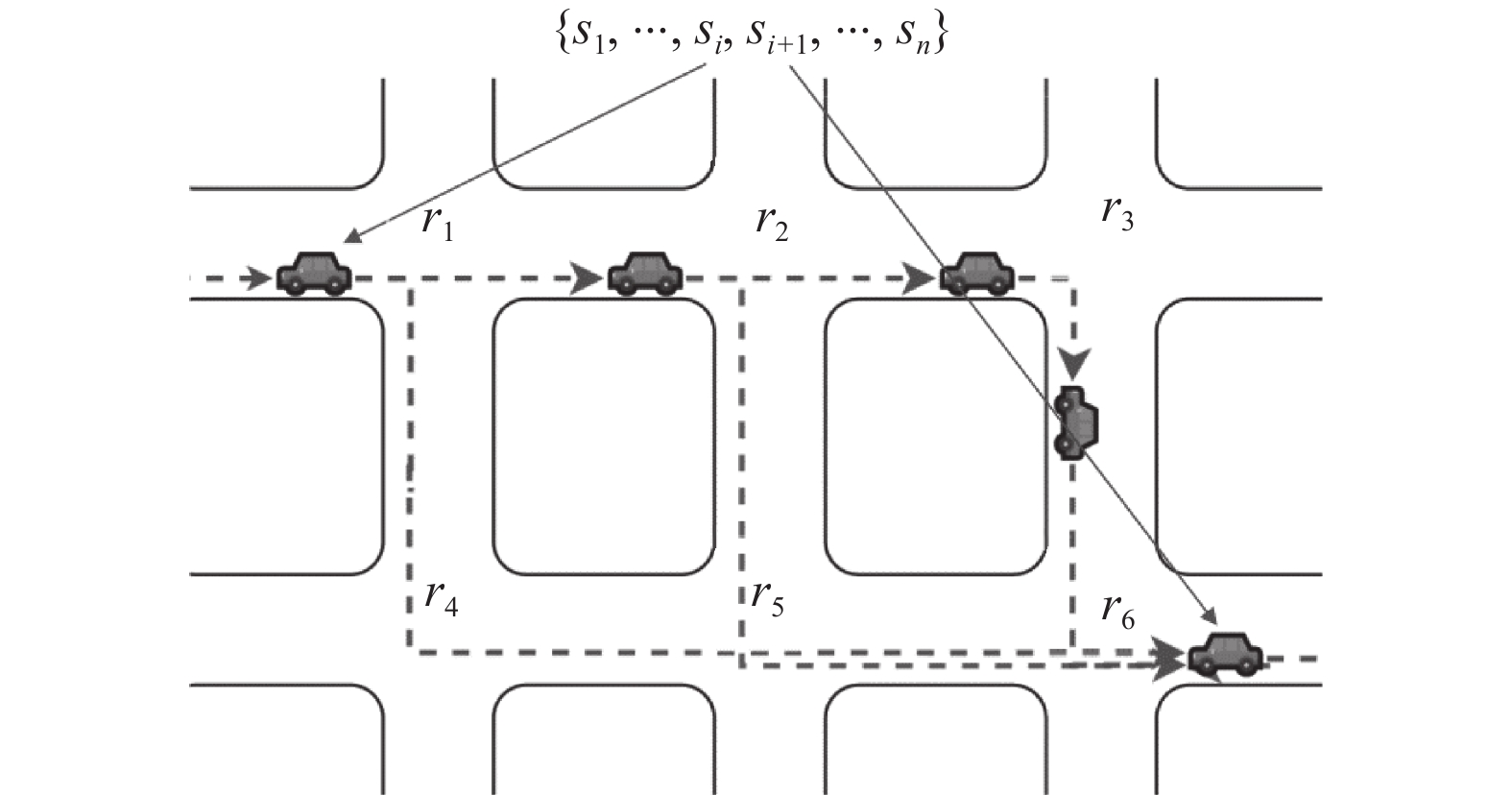
|
图 3 OD缺失拓扑图 |
具体来说, 给予分割后的OD轨迹序列
步骤1: 判断
步骤2: 如果存在有
步骤3: 汇总并排列组合, 得到
生成候选路径的方式将求解完整出行轨迹的问题转化为从多个可行路径中选取一条最符合出行者驾驶风格路径的问题. 为此, 本文构建了一系列的决策指标以模拟出行者路径选择决策过程. 从实际出行决策角度, 需要考虑的主要因素包括: 路径距离、通行时间、含信号交叉口、转弯次数等[11-13]. 然而, 以上因素同属于静态因素, 缺乏与出行者固有行驶习惯的关联.
为解决这个问题, 本文特别设计了通行时间一致性和轨迹偏好2个动态指标. 其中, 通行时间一致性表示当前候选OD轨迹先验的平均通行时间
| $ {T}{C}\left({{q}}_{i}\right)=1-\left|\frac{{\stackrel-{t}}_{qi}-{\Delta t}_{qi}}{{\stackrel-{t}}_{qi}}\right| $ | (2) |
值越大表示该候选路径与实际通行路径越接近. 而轨迹偏好程度用于描述该候选轨迹的实际通行情况占所有轨迹通行情况的比例, 求解过程可以描述为:
| $ {T}{P}\left({{q}}_{i}\right)=\frac{number\left({{q}}_{i}\right)}{\displaystyle\sum _{k=0}^{n}number\left({{q}}_{k}\right)} $ | (3) |
其中, 函数
此外, 为区分每个指标内部的显著性, 本文使用z-score方法对所有指标进行归一化:
| $ {\textit{z}}=\frac{{e}_{i}-\mu }{\sqrt{\dfrac{1}{M}\displaystyle\sum _{j=1}^{M}({{e}_{j}-\mu )}^{2}}} $ | (4) |
其中,
通过候选OD轨迹的各项校验指标可计算得到最合适的行驶轨迹, 这本质上可视为多属性决策问题. 以往通常使用主成分分析、灰色关联分析等方法进行多属性决策的研究, 但这样的方法存在计算复杂度高, 特征提取效率低等缺陷. 受Wu等人[14]的启发, 他们在风格迁移任务中首次提出图像的风格可以由实例的均值和方差来表示. 基于此, 本文设计了一种基于VAE模型的多属性路径决策方法. 该方法可以通过VAE算法的编码器得到输入候选轨迹校验指标的均值和方差, 并以此作为出行者固定的风格习惯, 从而将最符出行者出行风格的路径中候选路径中挑选出来.
图4展示了VAE模型的计算流程. 基于VAE的路径决策方法以候选轨迹的指标组成的多维向量作为输入, 通过模型学习轨迹指标之间的分布关系. 最终, 每条候选轨迹计算得到的均值和方差会与代表出行者出行固有习惯的先验值比较, 越接近代表越符合最优路径, 如图5所示.
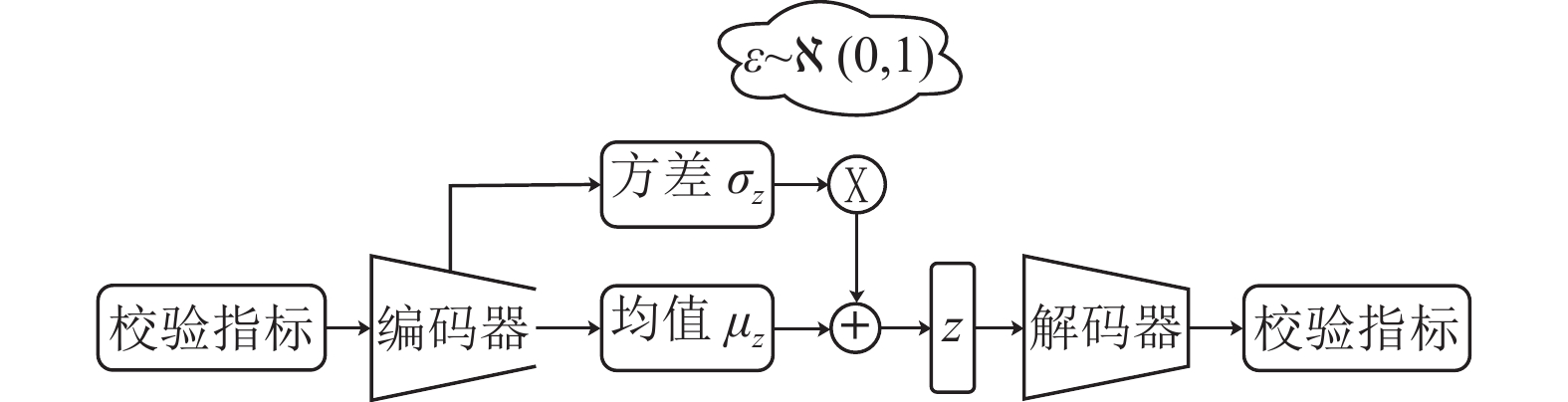
|
图 4 VAE模型流程图 |
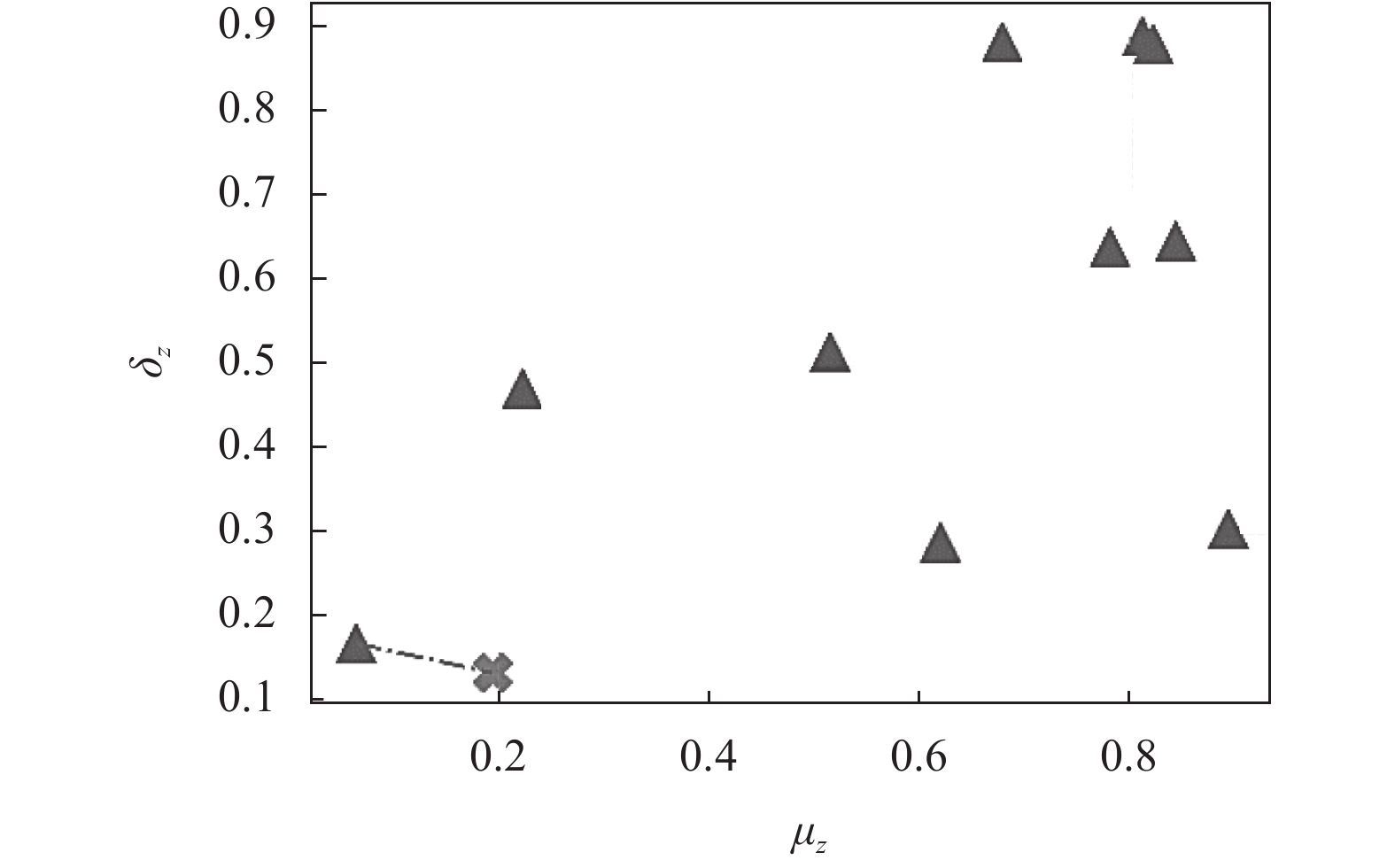
|
图 5 候选轨迹均值方差(▲)与先验值(X)的空间分布 |
通过VAE优化校验指标的目标函数可以表示为:
| $ \vartheta = {E_{x \sim \tilde p\left( x \right)}}\left[ {{E_{{\textit{z}} \sim p\left( {{\textit{z}}|x} \right)}}} \right[ - {\rm{log}}q(x|{\textit{z}})] + KL(p({\textit{z}}|x)\left| {} \right|q\left( {\textit{z}} \right))] $ | (5) |
本文所述算法在杭州萧山S103交通小区进行测试验证. 实施范围如图6所示, 该路网包括34个路口、50个路段. 每个路段皆配备1–2个摄像采集设备, 总计117个. 在2021年5月6日至2021年8月6日时间范围内, 通过自动车牌识别技术对该交通小区路网内车辆的交通状态进行提取. 所提取识别数据中包含乱码信息、逻辑关系混乱 、以及车牌不符合规范等异常轨迹信息, 剔除后最终得到259219条可用的稀疏车辆行驶轨迹序列. 每条序列包含了检测设备编码、时间、地点、车牌号等信息, 详细数据如表1所示.

|
图 6 杭州萧山S103交通小区 |
| 表 1 预处理后的车牌识别 |
2.2 实验结果
本小节将展示一系列的数值化和可视化结果, 对本文提出的OD还原算法进行评估.
2.2.1 轨迹还原对比实验本文选取了几个比较有竞争力的模型作为基准来验证算法性能. 包括: (1) 最短路径法(SP)[15], 以间断点最短路径作为补全还原的路径; (2) 主成分分析法(PCA)[16], 将每个候选轨迹的校验指标映射到2个维度, 并以此作为均值方差的替代; (3) 自编码器(AE)[17], 同PCA, 可自动学习数据映射规律, 并映射到2个维度.
验证使用的数据集是原始车牌识别数据的子集, 包括了1208辆车的总计15812条不存在间断点的轨迹数据, 且每辆车的每个OD内的轨迹满足检测样本数不小于10. 对于每个完整OD轨迹
| $ {Accuracy}_{k}=\dfrac{\displaystyle\sum _{i=1}^{m}bool({S}_{i}', {S}_{i}'')}{m} $ | (6) |
其中, 函数
表2展示了对比实验的结果, 从表中可以发现, SP算法在轨迹还原的精准度上表现最差, 随着节点缺失率的增加, SP具有最大的降幅(如图7所示). 主要原因在于, SP算法假设驾驶车辆以最短的路径行驶, 忽略了出行者主观决策等对驾驶路径的影响. 而PCA、AE和文本提出的算法通过候选轨迹生成模拟出行者的路线选择过程, 在指标上明显优于SP算法. 相较于PCA和AE, 本文使用VAE对每条候选轨迹计算抽象意义的均值和方差, 以此作为出行者的出行风格、固有习惯, 这促使本文所提出的算法取得更优越的性能. 此外, 从表2最后一行指标和图7的可视化视图, 还可以发现, 与表现最好的对比模型AE相比, 在缺失样本点低(不超过5个)时, 两个算法取得了相当的性能. 但在节点缺失率更高时, 本文的算法表现出更强大的适应能力(在缺失节点为7时, 优于表现最好的AE算法11%).
| 表 2 本文提出算法与对比算法的准确率表现 |
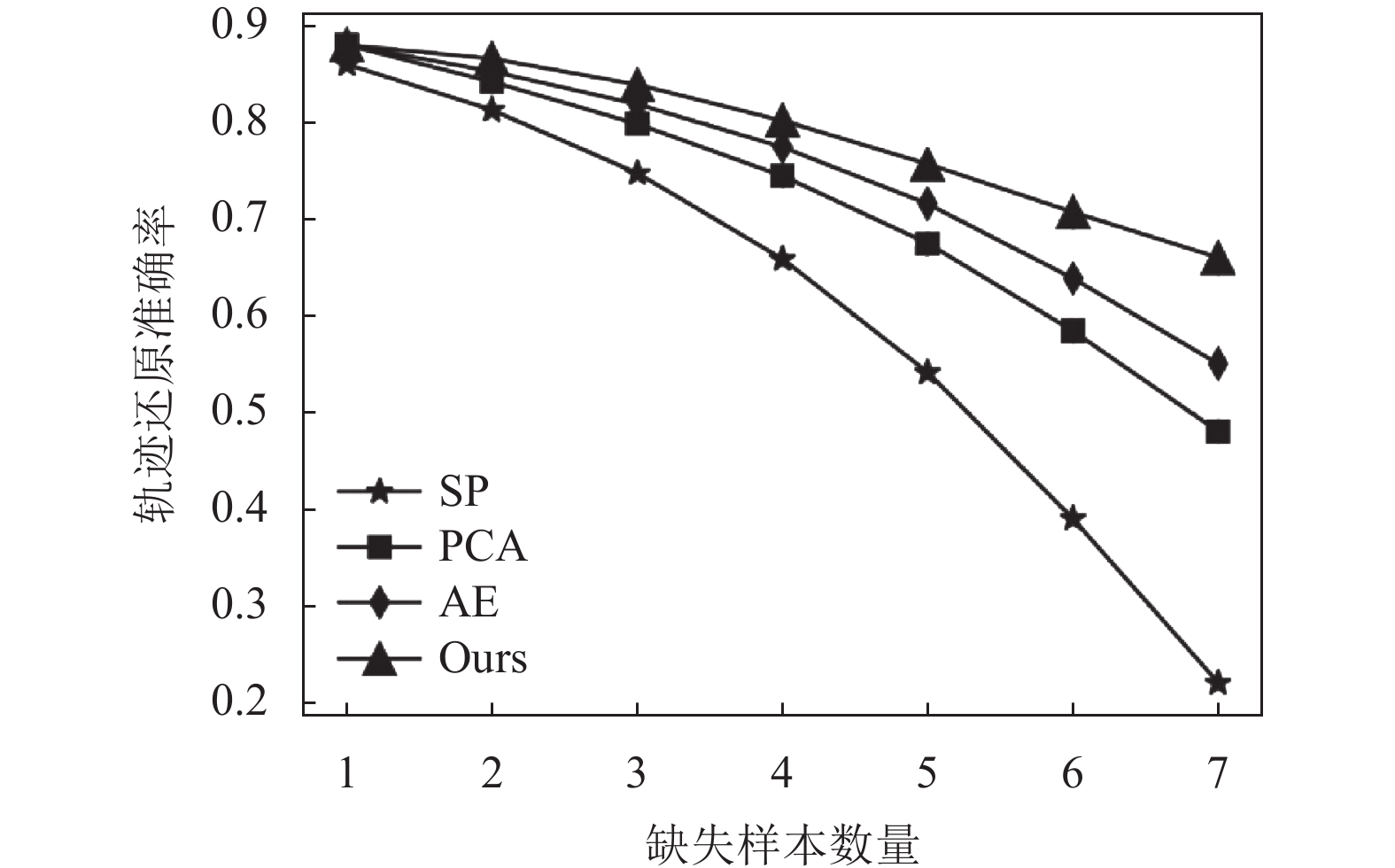
|
图 7 不同算法的准确率表现 |
表3展示了各个算法的时空消耗表现. 尽管SP算法拥有极高的运算效率, 但在精度上面很难满足实际需求. 在精度相对比较高的PCA、AE和本文的算法中, 本文算法与AE算法在运行效率上都明显优于PCA算法. 尽管本文所提出的算法拥有最高的参数量, 但减少一定运算的时空效率给算法带来的是大幅度的精度上的提升.
| 表 3 本文提出算法与对比算法的时空消耗 |
2.2.2 摄像采集设备覆盖率分析
利用大数据技术、车牌自动识别技术, 借助当前高密度、高精度的监测设备, 深挖车牌照的自动识别信息, 实现OD数据与交通运行数据的智能化提取, 是适应当前复杂的交通发展状况与精确的交通数据需求的思路. 但在实际道路交通中, 并非每个路口、路段都已部署摄像采集设备. 研究不同覆盖率与轨迹还原准确率的关系, 可以在保证达到识别性能和还原效果的情况下, 降低设备覆盖率, 让轨迹分析系统以更经济、高效的方式运行.
由此, 本文进一步测试了不同摄像采集设备覆盖率下车辆OD轨迹还原的准确率. 从交通小区所有采集设备中随机删除10%、20%、30%、40%、60%、60%和70%的设备以及这些设备对应的识别数据, 模拟90%至40%之间以10%为间隔的不同设备覆盖率情况, 并通过本文提出算法和对比模型中表现最好的自动编码器(AE)进行轨迹的还原重建. 图8展示了不同设备覆盖率下本文提出算法与AE算法轨迹还原的精准度变化情况. 从图中可以发现, 随着设备覆盖率的减少, 两者轨迹还原的精度都有所下降. 且覆盖率越低, 对应的下降幅度越大. 不同的是: (1) 本文提出的算法在所有覆盖率下的精度都优与AE算法; (2) 在90%–50%的覆盖率间, 本文提出的算法随覆盖率下降带来的准确率的衰退不超过6.6%, 而AE在覆盖率由70%减少60%时, 精度就大幅度的衰退了10.3%. (3) 在覆盖率50%-30%之间, 虽然两者精度都大幅衰退, 本文算法始终保值更高的精度以及更小的下降幅度. 以上这些观察证明, 在覆盖率高的情况下, 本文算法更加准确、有效. 且在覆盖率低的情况下, 本文算法依然具有非常良好的适应能力.

|
图 8 不同摄像点位覆盖率下本文提出算法准确率表现 |
2.2.3 敏感性分析
第1.3节介绍了影响最终最优路径决策的6个关键性指标: 路径距离、通行时间、含信号交叉口、转弯次数、通行时间一致性和轨迹偏好. 计算选择路径与以上指标的相关系数可以得到每个指标对最终决策的影响程度. 图9展示了各校验指标与决策路径的相关系数矩阵, 其中, 颜色越深代表相关性越强.

|
图 9 各校验指标与决策路径之间的相关系数矩阵 |
由图9可知, 本文所提出的时间一致性和轨迹偏好2个动态性指标最终的决策路径保持着较高的相关稀疏, 分别为0.65和0.77. 在通用的静态决策指标中, 含信号灯交叉路口数对最终决策的影响最高, 为0.65. 总的来说, 本文所提出的2个动态性指标, 在最终的轨迹还原中起到了非常积极的促进作用.
3 总结本文提出一种基于车牌识别数据的城市交通网络车辆轨迹重建算法. 基于车牌识别时序序列, 该方法充分考虑到出行者出行过程中复杂道路选择决策过程, 从而拟合产生最适合出行者主观行驶风格的通行路径. 通过杭州市萧山区实际交通小区对该方法进行校验, 综合实验结果表明了算法时鲁棒可靠的, 为稀疏车牌数据的轨迹还原提供了一个强有力的基准.
| [1] |
王龙飞. 基于车牌照的车辆出行轨迹分析方法与实践研究[博士学位论文]. 西安: 长安大学, 2011.
|
| [2] |
Zhang Z, Liu HQ, Rai L, et al. Vehicle trajectory prediction method based on license plate information obtained from video-imaging detectors in urban road environment. Sensors, 2020, 20(5): 1258. DOI:10.3390/s20051258 |
| [3] |
李广耀, 黄正锋, 楼乐依. 基于贝叶斯网络的稀疏出租车GPS轨迹路径还原方法. 宁波大学学报(理工版), 2021, 34(2): 17-24. |
| [4] |
詹起林, 高峻, 王磊. 基于货运车辆GPS数据的交通调查技术研究. 地理与地理信息科学, 2011, 27(3): 30-33, 37. |
| [5] |
胡永恺. 基于手机信令的轨道交通乘客出行行为分析方法研究[博士学位论文]. 南京: 东南大学, 2017.
|
| [6] |
李力伟. 基于超声波传感器的行车轨迹检测器的设计. 科技经济导刊, 2016(24): 69. |
| [7] |
鞠鹏, 周晶, 张俊婷, 等. 基于车牌识别数据的城市交通流时空特性分析. 统计与信息论坛, 2014, 29(10): 66-72. DOI:10.3969/j.issn.1007-3116.2014.10.012 |
| [8] |
杨文军, 孟凡冬, 李游, 等. 基于车辆轨迹OD数据分析乘客出行特征的研究. 测绘与空间地理信息, 2020, 43(S1): 144-147, 150. |
| [9] |
王振, 张志敏, 禚保玲, 等. 基于车辆牌照识别数据的城市居民出行特征研究——以青岛市为例. 青岛理工大学学报, 2020, 41(2): 130-137. DOI:10.3969/j.issn.1673-4602.2020.02.019 |
| [10] |
Rao WM, Wu YJ, Xia JG, et al. Origin-destination pattern estimation based on trajectory reconstruction using automatic license plate recognition data. Transportation Research Part C: Emerging Technologies, 2018, 95: 29-46. DOI:10.1016/j.trc.2018.07.002 |
| [11] |
Ahmed MM, Abdel-Aty MA. The viability of using automatic vehicle identification data for real-time crash prediction. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 459-468. DOI:10.1109/TITS.2011.2171052 |
| [12] |
Feng Y, Jian S, Chen P. Vehicle trajectory reconstruction using automatic vehicle identification and traffic count data. Journal of Advanced Transportation, 2015, 49(2): 174-194. DOI:10.1002/atr.1260 |
| [13] |
Wafy M, Madbouly AMM. Efficient method for vehicle license plate identification based on learning a morphological feature. IET Intelligent Transport Systems, 2016, 10(6): 389-395. DOI:10.1049/iet-its.2015.0064 |
| [14] |
Wu ZX, Wang X, Gonzalez J, et al. ACE: Adapting to changing environments for semantic segmentation. 2019 IEEE/CVF International Conference on Computer Vision (ICCV). Seoul: IEEE, 2019. 2121–2130.
|
| [15] |
徐鹏, 程钢, 黎旻懿. Dijkstra算法在GIS中的优化与应用. 北京测绘, 2021, 35(6): 737-740. |
| [16] |
Shlens J. A tutorial on principal component analysis. arXiv: 1404.1100, 2014.
|
| [17] |
杨云开, 范文兵, 彭东旭. 基于一维卷积神经网络和降噪自编码器的驾驶行为识别. 计算机应用与软件, 2020, 37(8): 171-176. DOI:10.3969/j.issn.1000-386x.2020.08.030 |
 2022, Vol. 31
2022, Vol. 31


