1 前言

混合式教学是一种线上与线下相结合的新兴教学模式, 既通过在智慧教学平台上发布任务, 上传资源等发挥教师的主导作用, 又通过学生线上自主学习、完成任务等, 引导学生积极主动学习. 目前正被各大高校积极推广^[1]. 学生可以不受时空限制, 通过多种方式登录学习平台学习, 所产生的学习行为数据被平台记录保存^[2]. 学习行为数据反映学生的学习状态和习惯. 而日常的学习状态和习惯对最终的学习成绩有着重要影响^[3]. 混合式学习对学生的自觉性要求较高, 在实际实施过程中, 学生的参与度受各种因素干扰而参差不齐^{[4, 5]}. 因此, 如何利用平台记录的学习行为数据分析出学生学习状态, 掌握学生的学习情况, 引导学生积极主动学习, 成为教学管理中急需解决的问题.

通过对学生学习行为数据进行挖掘和分析, 可以找出隐藏的规律, 进而对学生成绩进行分类预测, 及时发现学困生并干预指导, 提高教学质量^{[6, 7]}. 近年来, 众多学者基于在线学习行为数据对学习成绩预测的方法进行了多方面探索. 喻铁朔等采用支持向量机回归对成绩进行预测, 并在其基础上实现学业预警^[8]. 吕品等对比感知机, 支持向量机和神经网络等分类算法的预测效果, 发现基于支持向量机的成绩预测模型具有更高的准确率^[9]. 王凤芹等利用登录次数, 视频观看时间等10个行为特征验证K近邻优化算法在预测MOOC学习成绩的有效性^[10].

虽然通过优化算法和调节算法参数可以比原有的单一算法模型具有更高的精度, 泛化能力也有所增强^{[11, 12]}. 但由于线上线下相结合的学习行为数据相对复杂多变, 异常值较多, 单一的预测算法有自身的局限性. 为了提高单一算法模型的泛化能力, 有学者尝试通过融合算法来建立成绩预测模型. 贾靖怡等利用MOOC课程数据和RapidMiner大数据挖掘平台构建基于AdaBoost算法的学习成绩预测模型^[13]. 宋洁通过实验对比了SVR、RF、GBDT和 XGBoost四种不同算法模型在学习成绩预测中的效果, 最终得出具有集成特点的XGBoost算法预测效果最佳^[14]. 但XGBOOST和AdaBoost属于同质算法的集成模型, 主要通过线性化融合算法, 无法将各个算法的差异与优势相融合, 其泛化能力仍需加强^{[15, 16]}.

为提高模型的泛化能力, 充分发挥个体学习器的优势, 本文采用Stacking集成方法, 对多项式朴素贝叶斯、AdaBoost、Gradient boosting与逻辑斯蒂回归4个异质学习器进行非线性组合, 构建两层Stacking集成学习模型, 基于超星平台的混合式教学中产生的数据集. 通过对比Stacking集成学习模型与多项式朴素贝叶斯、AdaBoost、Gradient boosting和逻辑斯蒂回归在数据集上的预测准确率、召回率、精确率和F1得分等评价指标, 验证Stacking集成学习模型的有效性.

2 Stacking集成学习预测模型

集成学习是通过一定的方式组合多个弱学习器, 构造出比单一学习器性能更好的强学习器. 常见的集成学习方法有Bagging, Boosting和Stacking等. Bagging和Boosting采用线性集成策略, 根据确定性算法组合同质弱学习器形成强学习器. 与Bagging和Boosting不同的是, Stacking采用非线性集成策略, 通过组合异质学习器构成多层次强学习器, 高层学习器能够通过低层学习器的输出结果对模型进一步泛化增强^[17].

2.1 Stacking集成学习算法原理

Stacking集成学习算法是一种叠加式分层集成算法, 以两层为例, 在第1层中使用不同的初级学习器对数据进行训练, 在训练数据集时, 为了避免因测试集比例划分过小造成泛化能力不强问题, 通常采用交叉验证方式进行训练. 然后将第1层产生的多次训练的数据结果作为新的训练集和测试集, 第2层次级学习器采用新的训练集与测试集进行训练和预测. 具体算法如算法1所示.

算法1. Stacking集成学习算法

输入: 数据集 $\scriptstyle D = \left\{ {\left( {{x_1}, {y_1}} \right), \left( {{x_2}, {y_2}} \right), \cdots , \left( {{x_m}, {y_m}} \right)} \right\} $ , 初级学习器 $\scriptstyle {\varsigma }_{1}, \cdots , {\varsigma }_{T} $ , 次级学习器 $\scriptstyle {\varsigma _{}}$

1. 　for $\scriptstyle t = 1, 2, \cdots , T$ do

2. 　　 $\scriptstyle {h_t} = {\varsigma _t}\left( D \right)$

3.　 end for

4. 　 $\scriptstyle D' = \emptyset $

5. 　for $\scriptstyle i = 1, \cdots , m $ do

6. 　　for $\scriptstyle t = 1, \cdots , T $ do

7. 　　　　 $\scriptstyle {{\textit{z}}_{it}} = {h_t}\left( {{x_i}} \right) $

8.　　 end for

9. 　　 $\scriptstyle D' = D' \cup \left( {\left( {{{\textit{z}}_{i1}}, \cdots , {{\textit{z}}_{iT}}} \right), {y_i}} \right) $

10. 　end for

11.　 $\scriptstyle h' = {\varsigma _{}}\left( {D'} \right)$

输出: 最终分类器 $\scriptstyle H\left( x \right){\text{ = }}h'\left( {{h_1}\left( x \right), \cdots , {h_T}\left( x \right)} \right)$

2.2 两层Stacking集成学习成绩预测模型设计

Stacking集成学习模型采用的是多层次结构, 每一层的输出作为下一层的输入, 但构造的层数越多, 模型越复杂, 训练的速度也会越慢. 因此, 本文选择采用两层结构. 在第1层, 为了保证模型的多元化, 初级学习器选用多项式朴素贝叶斯, AdaBoost和Gradient boosting三种学习器, 其中多项式朴素贝叶斯为一种适用于离散特征概率计算的学习器, AdaBoost和Gradient boosting为基于Boosting集成学习方式的学习器^{[18, 19]}; 在第2层, 为了防止发生过拟合现象, 采用简单的逻辑蒂斯回归分类器作为次级学习器, 次级学习器对初级学习器融合得到Stacking集成学习模型. Stacking集成学习模型中的个体学习器在训练过程中, 通过sklearn库中的GridSearchCV (网格搜索法)选取个体学习器的最优参数. 集成学习模型框架如图1所示.

两层Stacking集成学习模型的具体步骤如下:

步骤1. 对学生的原始特征数据集进行预处理与特征变换, 将目标特征即学生期末成绩转换为0和1, 结合皮尔逊相关性分析选择有效特征构建新的数据集^[20].

步骤2. 选择AdaBoost, 多项式朴素贝叶斯和Gradient boosting作为初级学习器.

步骤3. 将经过特征工程处理过的混合式教学下产生的学生特征数据集以一定比例切分为训练集 $D$ 和测试集B. 并将处理好的训练集平均分为5份数据集 ${D_i},\; i \in \left\{ {1, 2, 3, 4, 5} \right\}$ .

步骤 4. 在第一层预测模型中, 将3个初级学习器分别采用5折交叉验证进行训练. 以AdaBoost为例, 每次交叉验证包含两个过程. 首先用其中的4份数据集作为AdaBoost训练集进行训练, 剩下的1份作为AdaBoost模型预测的测试集, 得到预测数据集 ${a_i}\;(i \in \left\{ {1, 2, 3, 4, 5} \right\})$ , 将其整合为1列记为 ${A_1}$ . 然后再由上一步基于4份数据集训练的AdaBoost模型对测试集 $B$ 进行预测, 得到预测数据集 ${p_i}\;(i \in \left\{ {1, 2, 3, 4, 5} \right\})$ , 再对5次预测的结果 ${p_i}\; (i \in \left\{ {1, 2, 3, 4, 5} \right\})$ 按行相加取均值, 得到数据集 ${P_1}$ .

步骤 5. 在3个初级学习器完成训练及预测后会得到 $ ({A}_{1}, {A}_{2}, {A}_{3}) $ 和 $ ({P}_{1}, {P}_{2}, {P}_{3}) $ 两个新的矩阵数据集. 在第二层, 次级学习器逻辑斯蒂回归以 $ ({A}_{1}, {A}_{2}, {A}_{3}) $ 矩阵作为训练集, $ ({P}_{1}, {P}_{2}, {P}_{3}) $ 矩阵作为测试集, 以其为基础进行训练, 得到最终预测结果, 即学生能否通过期末检测(0不通过, 1通过).

3 特征工程

特征工程指的是从原始数据集中提取实验特征的过程, 提取的特征能够较好的描述数集的内容, 其一般包括数据预处理和特征分析与选择等.

3.1 数据集介绍

本文数据采集自学校超星平台与教务系统, 共229名学生, 近6万多条线上学习记录和229条学生线下成绩记录. 数据集中学生特征共有16个维度, 分为学生的基本信息特征和学习行为特征两类, 分别如表1和表2所示.

3.2 数据预处理

由于混合式学习特征数据多样化, 需要根据数据与算法模型的特点, 对数据进行预处理. 数据预处理主要包括不同考核标准特征数据的归一化和连续型数据的离散化等. 本文在预处理过程中使用了Python中的sklearn、pandas和numpy等库.

3.2.1 归一化

每个开课班级在超星学习通上课程设置的任务点、学习资源以及课堂活动等有所差别, 从而造成特征的数值区间范围也不同, 需采用区间缩放法将数据映射到同一区间. 区间缩放法是归一化的一种方式, 本文利用特征数据的两个最值(最大值和最小值)进行缩放. 缩放公式如下.

$ {x_i}' = \frac{{{x_i} - \min (x)}}{{\max (x) - \min (x)}}, i = 1, 2, \cdots , m $

(1)

其中, $x$ 为同一特征集合, 共有 $ m $ 个特征变量, $ {x_i} $ 为该特征集合中的第 $ i $ 个特征变量, $ {x_i}' $ 为 $ {x_i} $ 缩放后的值, $\max (x)$ 为该集合特征变量的最大值, $\min (x)$ 为该集合特征变量的最小值.

3.2.2 特征转换

本文使用的数据集中的数据主要为varchar (可变字符型)、int (整数型)和double (浮点型) 3种类型, 而sklearn库要求模型输入的数据类型必须是数值型数据, 且本文采用的预测模型为集成分类预测模型, 其中个体算法模型AdaBoost和Gradient boosting为树模型结构, 为了保证模型输入数据类型的一致性, 需使用分箱操作对连续型特征数据离散化. 为此, 本文通过pandas库中的cut()函数对表2的11个int型和double型数据特征等宽划分离散化处理, 并对其进行数值型映射. 由于表1的5个特征数据为varchar型定性离散变量, 故直接将其映射为数值型变量.

3.3 特征相关性分析

在使用模型对目标预测前, 通常需要先进行特征选择, 通过特征选择可以移除不相关的特征, 降低计算复杂度以及提高模型的可解释性. 为此, 本文通过皮尔逊系数计算特征之间的相关性. 皮尔逊系数主要衡量变量之间的线性相关性, 结果的取值区间为[−1, 1], −1表示完全的负相关, +1表示完全的正相关^[21]. 实验获取的数据共有16个特征, 包括学生的基本信息特征和学习行为特征, 在经过数据预处理后, 通过皮尔逊系数计算特征之间的相关性系数, 并将相关性系数的结果以热力图的形式输出, 其结果如图2所示.

由图2可以看出semester, gender, faculty, class与目标特征final_mark之间的相关性系数小于0.2, 相关性较弱, 其中semester和faculty与目标特征的相关性系数皆为0, 无相关性. 与final_mark之间的相关性系数大于0.4的特征有midterm, study_count, group_task, 其中特征midterm代表期中考试的成绩, 与目标特征final_mark的相关性最高, 达到了0.46. discussion, course_point, answer_mark, chapter_quiz等7个特征与final_mark的相关性相对较一般. 故本文将相关性为0的无用特征semester和faculty删除, 保留midterm, group_task, class_test等13个相对重要的特征.

4 实验及结果分析

本实验在处理器为Intel i7-8750U, 运行内存为16 GB的电脑上进行, 操作环境是64位的Windows 10系统. 算法实现工具为Pycharm, 编程语言为Python 3.7.0. 算法实现过程中使用到Python的工具库有: numpy、pandas、matplotlib、seaborn和sklearn等. 将数据集中的229条学生行为数据随机切分出70%, 共160条作为模型的训练集, 剩余的30%作为模型的测试集, 用于模型的验证.

4.1 模型的泛化能力评估指标

本文的目的在于通过相关的学生特征来预测学生能否通过期末检测, 将预测结果分为通过(pass)和挂科(failed)两类, 这是一个二分类预测问题. 二分类预测问题的混淆矩阵分析表如表3所示.

本文采用准确率(A), 召回率(R), 精确率(P), F1得分(F1) 4个指标评价算法的预测结果. 准确率虽然能够判断整体模型预测的正确率, 但相比于通过学生, 本文更加关注真正挂科学生的预测情况, 因此应当引入召回率作为评估指标, 但若只注重召回率的提升, 会减少成功预测真正通过学生的情况, 即会导致精确率下降, 模型变得虚高^[22]. 召回率与精准率是一对相对矛盾的变量, 为此引入F1得分来平衡召回率与精确率, 更为客观的对模型进行评价. 各项指标的计算方法的公式如式(2)–式(5).

$ A = \frac{{TP + TN}}{{TP + TN + FP + FN}} $

(2)

$ P = \frac{{TP}}{{TP + FP}} $

(3)

$ R = \frac{{TP}}{{TP + FN}} $

(4)

$ F1 = \frac{{2P \times R}}{{P + R}} $

(5)

4.2 模型参数设置

超参数是模型在开始学习之前设置的函数参数, 选择合适的参数可以在一定程度上提高模型的分类能力. 本文Stacking集成学习模型中的个体学习器在训练集中训练时, 采用机器学习库sklearn中的GridSearchCV(网格搜索法), 以准确率(A)作为各学习器预测效果的评价标准, 在各学习器的所有候选的参数选项中循环遍历, 并结合5折交叉验证方式, 通过对比在测试集中的预测效果, 寻找模型的最优参数. 各学习器的最优超参数集及其预测准确率如表4所示.

4.3 模型的泛化能力分析

集成学习的目的是通过一定的策略集合各个初级分类器的优势, 取长去短, 提高分类器的分类效果, 因此集成后的分类效果应好于单个基分类器的分类效果. 为验证所构建的Stacking集成学习预测模型的预测性能, 通过对比多项式朴素贝叶斯、AdaBoost、Gradient boosting、逻辑斯蒂回归和Stacking集成学习预测模型在数据集上的预测效果来验证本文所设计的模型的优越性. 最后根据第4.1节中的式(2)–式(5), 对各分类器的分类效果通过准确率、召回率、精确率和F1得分等评价指标对各模型的预测性能进行对比分析验证, 各指标结果如图3、图4和图5所示. 在对比分析验证过程中, 多项式朴素贝叶斯、AdaBoost、Gradient boosting和逻辑斯蒂回归以及Stacking集成分类器中的初级学习器与次级学习器在训练与预测中所采用的参数如表4, 各参数为通过机器学习库sklearn中的GridSearchCV (网格搜索法)中搜寻的最优参数.

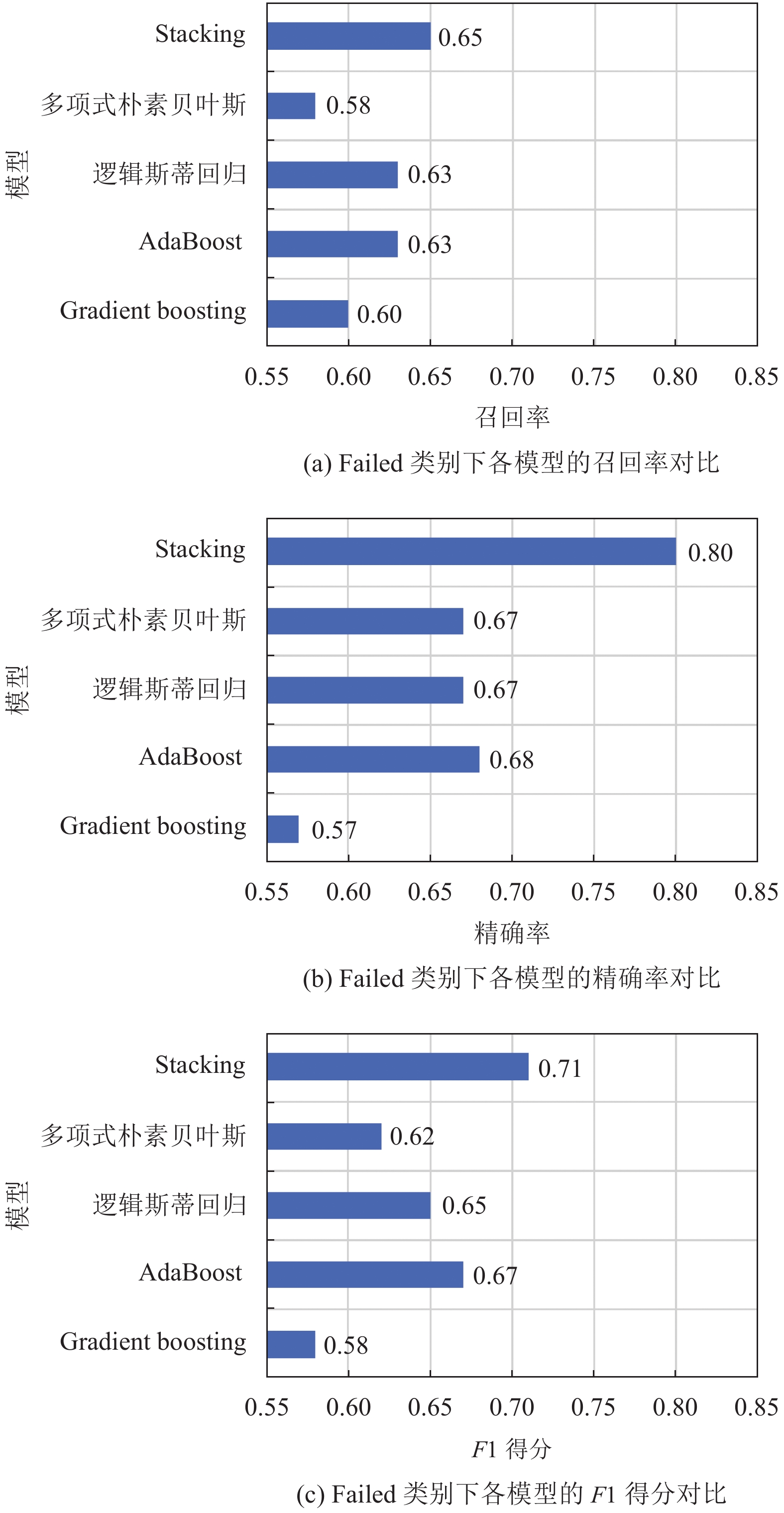
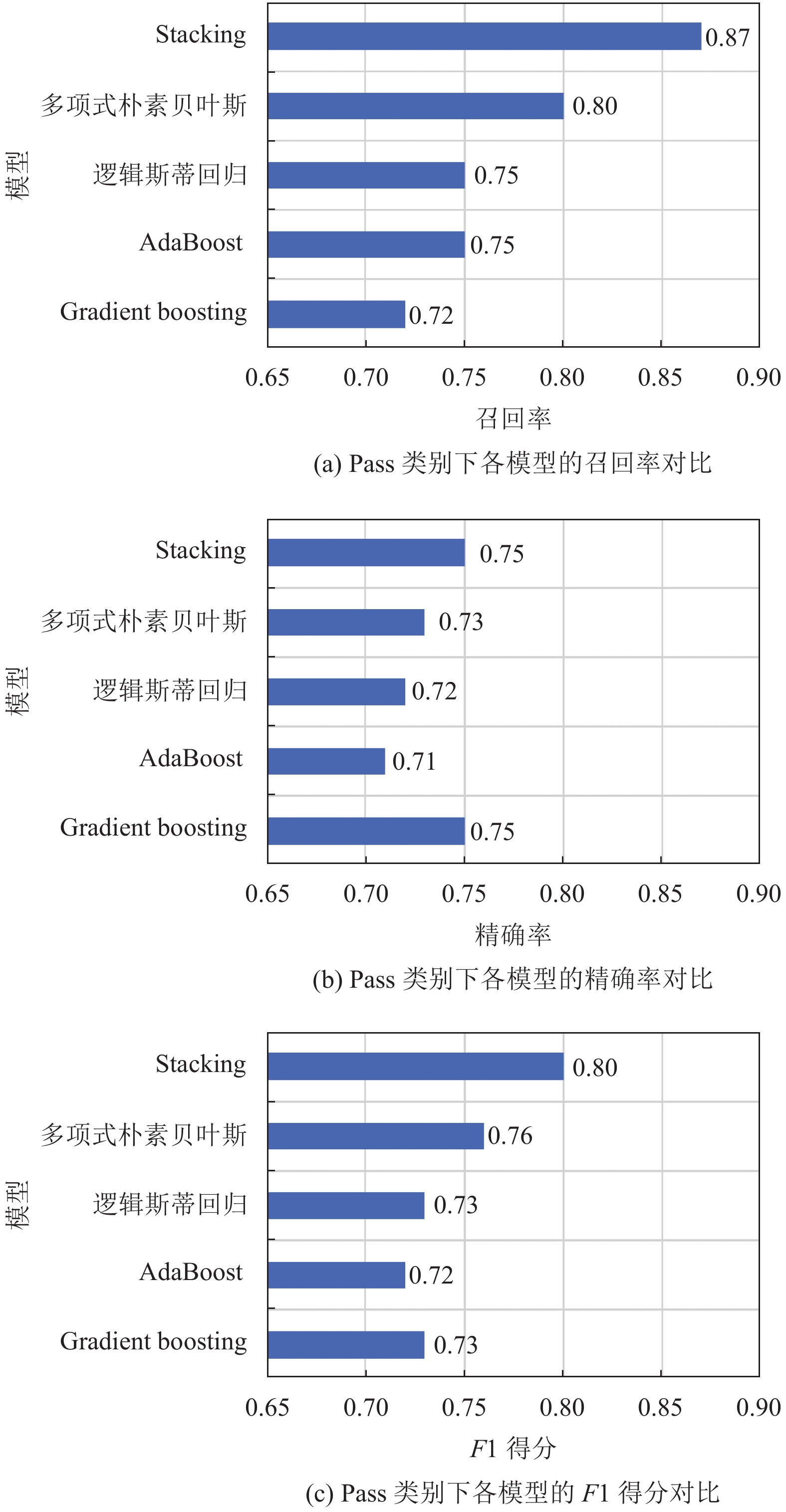
从图3、图4和图5中可以看出Stacking集成学习模型的各分类结果评价指标均明显高于多项式朴素贝叶斯、AdaBoost、Gradient boosting和逻辑斯蒂回归4个单一分类模型. 其中, 在召回率上, Stacking集成学习模型在Pass类别中的召回率为87%, 高于单一分类模型中表现最好的多项式朴素贝叶斯7%; 在Failed类别中的召回率为65%, 比单一分类模型中表现最好的模型AdaBoost高出2%. 在F1得分上, Stacking集成学习模型在Pass类别中的F1得分为80%, 分别高于多项式朴素贝叶斯, AdaBoost, Gradient boosting和逻辑斯蒂回归4个单一分类模型4%、8%、7%和7%; 在Failed类别中的F1得分为71%, 分别高于多项式朴素贝叶斯、AdaBoost、Gradient boosting和逻辑斯蒂回归4个单一分类模型9%、4%、13%和6%. Stacking集成学习模型的整体分类准确率为76%, 分别高于多项式朴素贝叶斯、AdaBoost、Gradient boosting和逻辑斯蒂回归4个单一分类模型5%、6%、9%和6%.

从以上实验结果来看, 通过Stacking融合多项式朴素贝叶斯、AdaBoost、Gradient boosting和逻辑回归分类模型能够有效弥补单一算法模型的泛化能力不强问题, 这是由于Stacking集成学习模型通过学习几个不同的初级学习器, 然后通过学习一个次级学习器来组合初级学习器, 基于初级学习器的预测结果输出最终预测结果. 从理论层面看, Stacking集成学习模型优于个体模型的主要原因是Stacking集成学习模型可以充分发挥各个学习器的自身优势, 对于个体学习器在测试集中预测较差的部分采用舍弃策略, Stacking集成学习模型采用多而不同的个体学习器, 取长补短, 可以在一定程度上有效减少单一模型泛化性能不佳的风险. 另一方面, 从模型优化角度看, 单一模型训练的优化过程中, 模型往往会有陷入局部最小点的风险, 有的局部极小点所对应的模型泛化性能可能较差, 而通过多个基学习器运行之后进行结合, 可有效减少陷入局部极小点的风险. 此外, 从图3和图4的Failed类别与Pass类别预测的同一指标两种类别之间差异性可看出Failed类别与Pass类别数据分布较不平衡, 混合式教学过程中产生的数据一般分布较不平衡, Failed类别样本数据较少, 而Stacking 集成学习模型相比于个体学习模型多了一层学习模型, 可以在同样训练数据下进一步进行学习, 因此, 采用Stacking集成学习方式后预测精度有所提升. 本质上Stacking集成学习模型是通过不同的方式分析数据, 然后根据学习器自生的算法规则建立模型, 次级学习器能够根据初级学习器的输出结果对模型进一步泛化增强, 当初级学习器得到了错误的预测结果时, 次级学习器可以将错误纠正回来. 因此, 融合差异性大的个体学习器可以充分发挥不同个体学习器的优势, 使得集成后的模型比单一算法模型具有更强的泛化能力.

5 总结

本文针对单一算法预测模型在学生成绩分类预测中存在泛化性能不强的问题, 提出一种Stacking集成学习模型, 其采用两层结构, 第一层通过融合多项式朴素贝叶斯, AdaBoost和Gradient boosting三个初级学习器, 第二层次级学习器采用逻辑斯蒂回归分类模型. 基于超星平台与教务系统获取的学生相关特征数据, 通过特征的皮尔逊相关性分析选择有效特征, 通过实验对Stacking集成学习模型与多项式朴素贝叶斯, AdaBoost和Gradient boosting和逻辑斯蒂回归进行比较. 结果表明, Stacking集成学习模型的召回率, 准确率等各项预测性能指标皆高于单个初级学习器, 在混合式教学的成绩分类预测中具有较好的应用价值. 但本文训练的数据量不是足够大, 且所选取特征的相关性相对较一般, 后期可以尝试加入提交作业时间先后等更多相关性较强的特征, 以及积累更多的训练数据来提高模型的总体分类预测效果.