CPU厂商纷纷推出了与自身硬件平台相对应的数学库软件, 国产申威芯片同样需要一个功能完备、性能优越的数学库软件. 基础数学函数库用以支撑在国产处理器平台上科学计算方面的应用课题的可靠高效运行, 并作为系统核心支持软件集成到单机编译器之中. 同时, 基础数学函数库软件为基础语言编译和优化编程提供支撑. 目前, 已经研发了多个面向申威26010众核处理器[1]深度优化、符合IEEE 754标准[2]和ISO C99规范的高效基础数学函数库版本, 并将其投入到申威1621多核处理器中使用. 数学函数在浮点运算[3]过程中, 会出现浮点异常的情况, 如何高效处理则至关重要. 文献[4, 5]充分证明了一个数值计算软件要达到没有浮点异常产生的效果, 其实现困难程度巨大. 在验证软件的可靠性方面, 文献[6–8]提出了测试工具DART, CUTE等, 其中DART可以对任何编译的程序进行自动化测试. 文献[9, 10]提出了浮点标准形式化的工具Coq, Gappa等, 文献[10]提出的Gappa使用区间算法自动评估和传播舍入误差, 并且演示了该工具在浮点程序类中的实际使用, 即为数学库中基本函数的实现, 遗憾的是缺乏直接针对浮点计算实现的形式化分析方法. Xia等人[11]依照浮点运算规则计算出了特殊数参与运算后的返回值, 从而为浮点数值软件的异常分析奠定了基石.
文献[12]提出了一种新的异常处理表示法, 该方法能够以合理的效率同样很好地满足故障、结果分类和监控异常的需求. 文献[13]成功实现应用后, 其原理的变化是微乎其微的. 文献[14, 15]对这类与异常领域相关的学术性研究和工程性探索也进行了详细的对比分析. 文献[16]对基于IEEE 754规范下的浮点异常问题进行了深入研究, 分析并总结出面向C语言环境中的不同运算操作的异常产生的条件. 以上的很多研究有一个明显的局限性, 大都基于C++, Java等面向对象语言实现, 缺乏基于面向汇编语言的实现.
此后许瑾晨等人[17]提出了一种分段式异常处理方法, 这种方法不仅是面向汇编函数而且是针对浮点运算, 恰好弥补了上述研究的局限性. 为了保证方法的高效性, 其先进行浮点异常编码, 然后将异常处理过程分为3 个阶段, 巧妙地将异常处理过程和核心运算分离开来, 并应用于申威1621基础数学库. 吴凡[18]在基础数学库适配申威1621的过程中为了解决fcvtdl_z 指令产生的INE 异常问题, 提出一种浮点小数取整法, 提前将浮点小数转换为浮点整数, 但这种方法有一定的局限性, 它只可应用于绝对值大于1的浮点小数, 因此对于像floor 、ceil 、round 等数值函数来说, 要保证定义域内所有数据的正确性, 就需要用到本文提出的数据集分段处理方法.
申威1621作为一款高性能的多核处理器, 并且具有自主知识产权, 近年来已相继推出了与之对应的国产数学软件, 但是在异常处理方面还并不完善. 而glibc 数学库作为目前最大的开源数学库, 已经形成了一套成熟的功能体系, 并且获得了大多数CPU厂商的认可. 为了使基础数学库更好的适配申威1621芯片, 应用于市场用户的研发以及生态体系的构建, 在让申威数学库保证功能上的完备性的同时兼顾其高效率, 并完全通过glibc测试集、gcc工具链以及SPEC[19]等市场上主流的测试软件的测试, 需要先将glibc开源库移植到申威平台, 再把基础数学库集成到glibc中, 并用开源测试数据集对其进行功能测试, 最后对其异常处理. 本文将针对申威1621现有数学库功能测试出的不精确异常问题从检测、分析和处理3个角度详细展开叙述.
本文主要贡献:
(1)对主流开源的glibc 测试标准和机制进行理论研究, 总结出了一套详细测试流程, 为国产数学库在不同的架构中进行扩展提供了可能.
(2)提出一种数据集分段式处理的方法, 应用于需要消除INE异常的函数, 使基础数学库同时符合了IEEE 754标准和glibc测试标准, 经过算法改进后的函数平均性能加速比达到148%.
为了更加清晰的表述本文问题, 第1节详细介绍了glibc的异常检测机制, 总结出一套融合异常检测的浮点函数算法; 第2节利用浮点控制寄存器(floating-point control register, FPCR)跟踪定位非精确结果异常(inexact exception, INE)产生的位置并且分析其原因; 第3节提出一种数据集分段处理的思想, 对数值函数进行算法改进, 高效解决了INE异常; 第4节进行正确性测试和性能测试, 对比INE异常在应用此方法前后的区别以及性能的变化情况, 以此来说明以上方法的可行性; 第5节是总结与展望.
1 glibc 异常检测机制刘剑[20]提出了一种浮点异常检测方法, 通过词法与语法来分析源代码的语义, 并利用修改规则模板, 对源代码进行转化, 同时利用状态标志位记录其检测的行号, 从而生成含有浮点异常检测的新程序. 以上的过程有一定局限性, 它只能通过半自动的代码转换程序完成, 且只能检测出异常类型以及出现源码的位置.
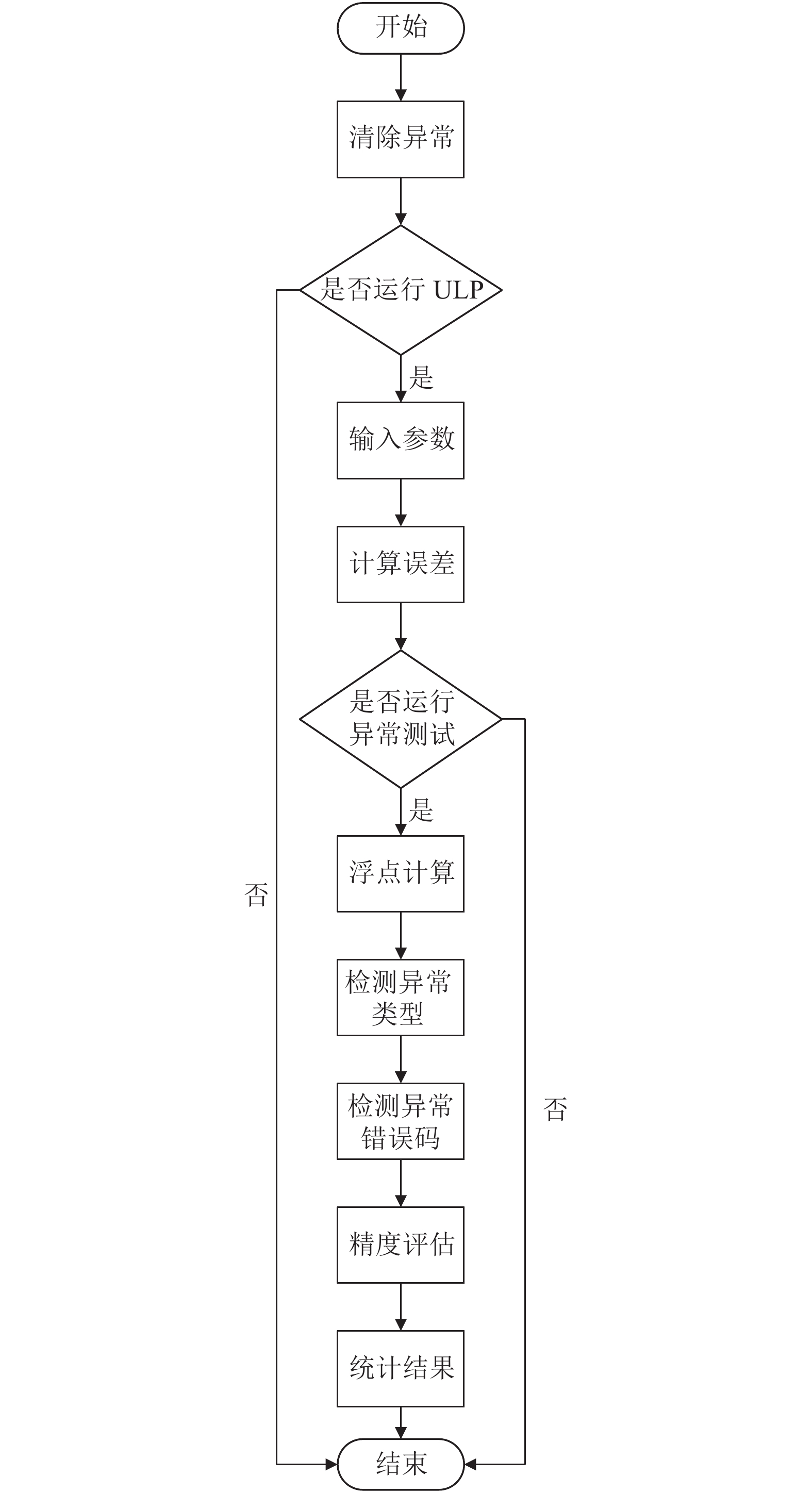
为了更清晰的说明如何检测出的异常以及后续的处理方法, 下面介绍glibc数学库的异常检测机制, 该检测流程在进入具体函数实现之前先将所有异常清除和检测ULP是否按照预期的方式进行或者中止; 在经过初始化后正式进入具体函数的测试集进行逐一检测, 针对于某个函数的某个参数先计算其最大能允许的精度误差; 在正常运算的过程中, 通过将调用基础数学库计算的值和glibc 给出的期望值进行一系列对比, 从而完成异常类型、异常错误码以及计算精度问题的检测. 最后对检测结果总数进行统计, 输出异常和errno的测试数量. 其基本流程如图1所示.
|
图 1 glibc 数学库异常测试机制 |
本文研究的异常检测机制相比于现有的异常检测机制, 它的创新性在于可以在全自动的程序中快速完成, 并且检测到的异常信息更加全面, 主要异常信息包括异常类型、异常错误码以及异常返回值, 其基本算法如算法1所示. 该算法在初始化后对不同异常的类型, 不同异常的错误码以及计算精度结果进行检测. check_ULP函数验证ulp() 实现是否按预期运行或中止; enable_test函数根据异常标记参数判断是否需要进行接下来的一系列的异常测试; check_exception、check_errno、ulpdiff 三个函数都是将实际值和glibc期望的值进行比较, 如果不同则返回相应的异常类型、异常错误码以及误差范围; COUNT_ARRAY为测试集的个数, EXCEPTIONS为异常标记参数, Computed 为实际的值, expected为glibc 期望的值.
算法1. Exception detection
1. TEST_INIT;//清除异常位的设置
2. if check_ULP()≠ 0 then
3. for 1…COUNT_ARRAY do
4. if enabe_test(EXCEPTIONS)≠0 then
5. if check_exception(computed, expected)=true then
6. return E; //返回异常类型
7. end if
8. if check_errno(computed, expected)=true then
9. return E; //返回异常错误码
10. end if
11. if ulpdiff (computed, expected)=true then
12. return ULP;//返回误差范围
13. end if
14. end if
15. end for
16. end if
17. TEST_FINISH;//统计检测结果
2 FPCR 寄存器分析法glibc异常检测机制可以较全面的检测出程序中的INE异常, 为了更好的处理这些异常, 本文提出了基于FPCR寄存器的分析方法, 对触发异常的指令和算法进行了详细分析. gdb作为调试工具, 它可以在程序中追踪查看变量、寄存器、内存及堆栈, 更进一步甚至可以修改变量及内存值. 因此, 我们在进行浮点运算时, 可以依托这样功能强大的调试器, 在不同的舍入模式下, 对比FPCR寄存器第56位值的变化, 从而定位到程序中INE异常的触发位置. 经过以上分析, 我们可以将触发的INE异常分为以下两类:
(1)指令触发
fcvtdl_n $f16, $f11 //触发INE异常
以floor 函数为例, fcvtdl_n 指令将D-浮点数转化成长字, 结果负无穷舍入, 在完成向下取整功能的同时也触发了INE异常.
(2)算法触发
faddd $f16, $f1, $f10 //触发INE异常
以ceil 函数为例, faddd 指令计算的结果舍去了小数位, 造成了结果的不精确表示. 表1例举了特殊数4 503 599 627 370 496 前后部分浮点格式的16进制和10进制的数据对应关系, 发现一个规律, 以浮点数0x4330000000000000 为分界点, 对于此浮点数的浮点格式有效位每加1, 其10进制也就加1, 比如0.5加上4 503 599 627 370 496 本该等于4 503 599 627 370 496.5, 但浮点格式的有效位已经无法表示如此精确的计算结果, 自动将其近似4 503 599 627 370 497, 这样就实现了函数ceil 向上取整的功能, 同理原算法中任何一个小数加上这样一个特殊数, 浮点格式的有效位就不足以容纳精确的计算结果, 从而触发INE异常. 后面第4节将以round函数为例, 进一步分析这种由本身算法设计带来的INE异常, 并提出一种数据集分段处理方法将对现有算法进行改进, 以达到消除这种INE异常的目的.
| 表 1 IEEE 754 数据转换 |
3 数据集分段处理
数据集分段处理的核心就是首先进行输入参数检测, 如果遇到无穷、非数等异常数直接处理并结束程序; 如果检测到的是浮点有限数, 则根据数据集不同的定义域区间分别处理并返回.
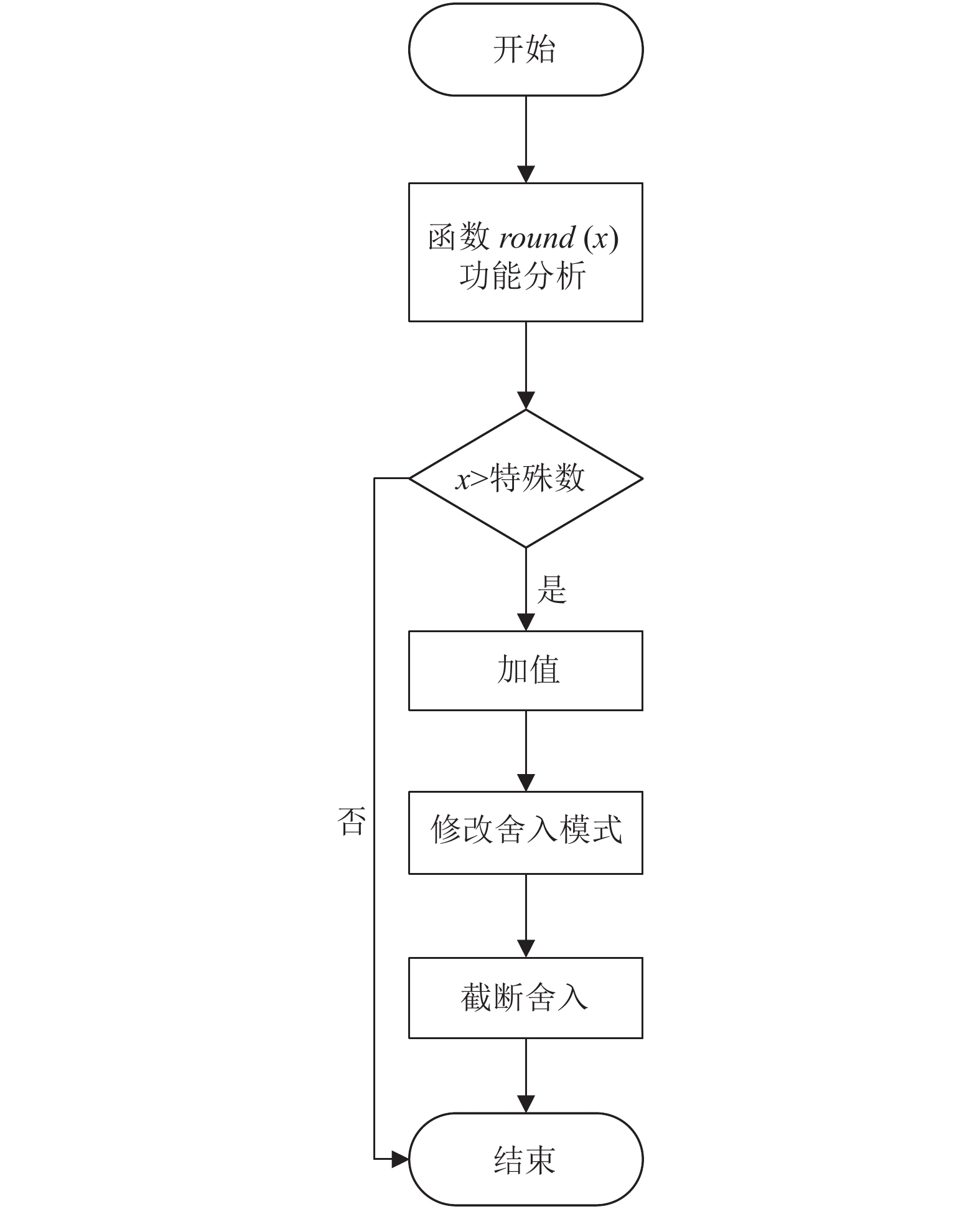
依据 IEEE-754 的规范标准, 在十进制数运算的四舍五入中, round函数的使用功能介绍为根据四舍五入取整数原则选择最贴近x的整数. 在申威1621处理器现有的基础数学库中,round函数现有算法流程图如图2所示.
现有round函数的算法都是先判断输入值是否大于特殊数4 503 599 627 370 496, 大于这个特殊数的值寄存器会根据默认的舍入模式进行舍入, 因此直接返回即可. 小于这个特殊数的输入值, 会经过加值、修改舍入模式、截断舍入3步完成函数的功能.
Step 1. 加值
在输入值的基础上加上一个值的大小为0.5的数, 其符号位与输入值的符号位保持一致.
Step 2. 修改舍入模式
先用rfpcr 指令读取浮点舍入模式的状态标志位, 然后通过移位、与非等逻辑操作修改浮点舍入模式的状态标志位, 最后用wfpcr指令将其写回, 从而将四舍五入改为向0舍入.
Step 3. 截断舍入
通过加上特殊数4 503 599 627 370 496, 舍去小数位.
|
图 2 round函数现有算法流程图 |
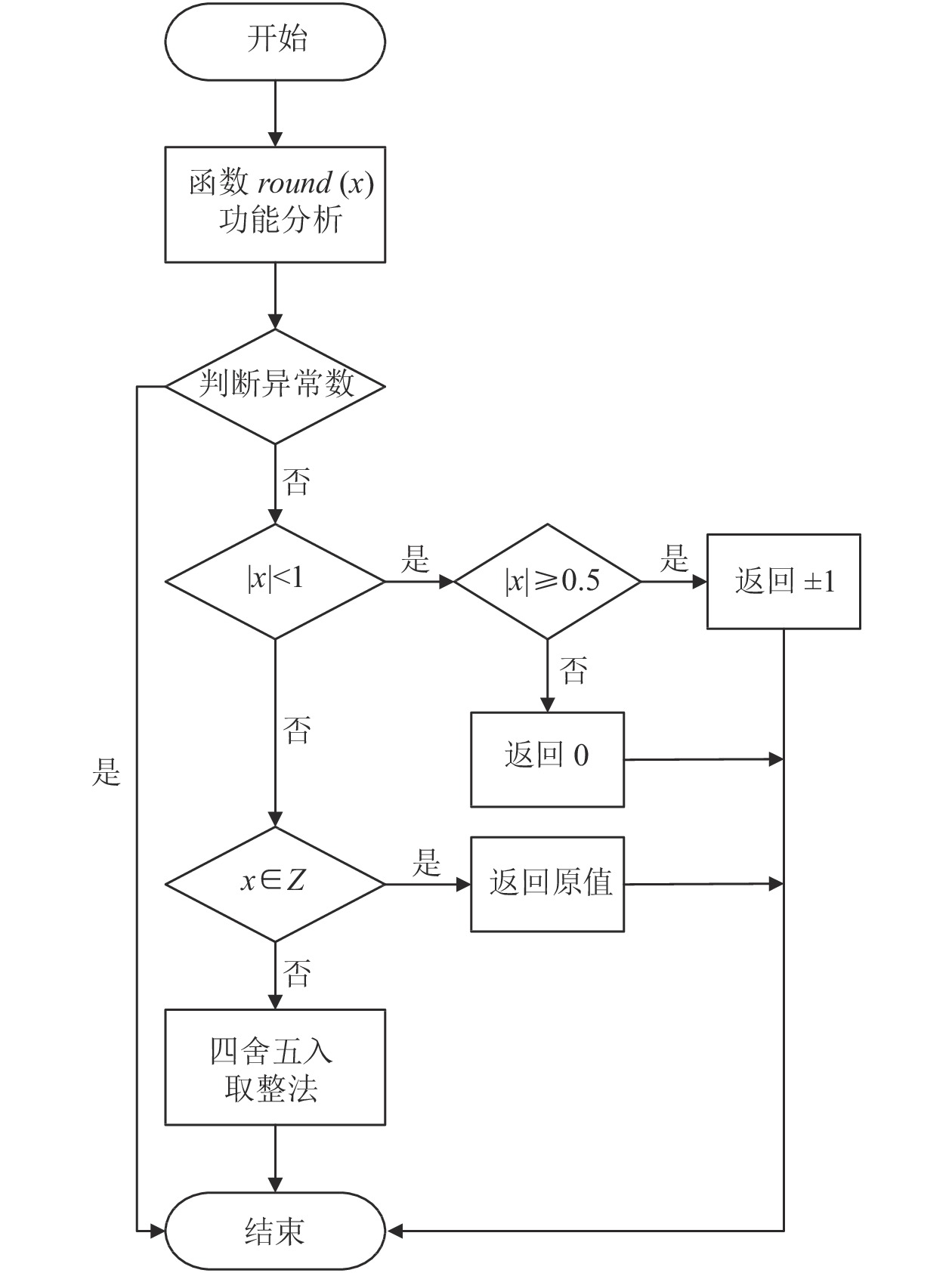
经过以上3步, 原本是1.0–1.4 的小数加上0.5再截断舍入就为1, 1.5–1.9的小数加上0.5 再截断舍入则为2, 从而实现了小数域四舍五入的功能. 然而, 在第3步截断舍入时, 用faddd指令舍去小数位的同时, 也造成了计算结果的不精确表示, 引发了INE异常, 下面运用数据集分段处理的思想, 详细阐述如何消除此处的INE异常. 改进后round函数算法流程如图3所示.
图3相比于现有的算法, 利用申威1621 处理器的硬件特性, 首先通过以下代码段对异常数检测并处理, 然后根据数据集不同的定义域区间分别处理并返回.
fcmpeq $f16, $f16, $f14
fbeq $f14, L$9
….
L$9:
faddd $f16, $f16, $f0
ret
对于绝对值小于的1的浮点小数来说, 四舍五入的实现主要和指数有关, 若浮点数的指数减去1 023的十进制值是–1, 那么浮点小数的绝对值应为[0.5, 1), 若浮点数的指数减去1 023的十进制值小于–1, 那么浮点小数的绝对值应为[0, 0.5).
|
图 3 改进后round函数算法流程 |
数值大于 1 的浮点数, 整数和小数位共同构建了浮点数的尾数位,其中构成浮点数整数部分的位数和浮点数的指数位密切相关. 从双精度浮点数的数据类型不难得出, 如果浮点数的指数位减去值为1 023 后的数表示为x, 那么小数部分占用尾数的 0~(51–x)位, 尾数(51–x)+1~51 则用来表示整数. 如果将小数点后的所有数字都更改为零, 则会得到小数点后的整数. 同样相对于绝对值大于1的二进制数字而言, 将小数点后面的位全部置为 0, 也就是将双精度浮点数的[0, 51–x]位置0, 则该二进制浮点数就变成了一个浮点整数[18].
下面重点介绍round函数数据集分段处理中所使用的整数判断法和四舍五入取整法的具体步骤.
3.1 整数判断法假设是对双精度浮点数f1 进行整数位的判断:
Step 1. 将f1 传进二进制数t1; 再将t1右移52位得到t0;生成一个十进制值为2 047的t2, 将t2与t0相与得到f1指数位的十进制值x1.
Step 2. 将x1和十进制为 1 023 的值相减, 计算出浮点数的尾数部分整数占据的位数n.
Step 3. 构造符号位、指数位全0, 尾数位全1的二进制数t3; 再将其右移n位, 得到尾数位表示整数位
Step 4. 将t3和t1进行逻辑与操作; 如果浮点数f1是整数, 那么二进制t1表示小数的位上应为全0, 与操作后得到数也应为全0; 反之, 则判断浮点数f1 不为整数.
3.2 四舍五入取整法以上算法中浮点小数根据四舍五入原则取最接近x整数的具体步骤如下.
如果遵循四舍五入的原则进行取整的是双精度浮点小数 f1:
Step 1. 取得f1的指数e1, 取得浮点数1的指数e2; 然后将e1–e2 得到的十进制数值用n表示, 从而计算出浮点数的整数部分所占的位数.
Step 2. 构造符号位、指数位全0, 尾数位全1的二进制数t2; 再将t2右移n 位, 计算出表示浮点数的整数位上全0 的二进制t3.
Step 3. 构造浮点最小值f2, 将其对应的二进制数右移n位得到t4; 接着将t4加上t1得到二进制数t1, 完成了四舍五入前的加值操作.
Step 4. 将表示浮点数整数位上全0 的二进制t3按位取反, 得到表示小数位上全0的二进制数t3.
Step 5. 将二进制数t3与t1相与, 得到的二进制数传给f1, 从而完成了浮点小数f1的四舍五入.
其他数值函数floor, ceil, nearbyint, nextafter, 算法改进的方法和round函数类似. 用开源测试数据集测试的INE异常不需要设置的所有函数, 通过这样的算法改进, 完全可以消除INE异常.
4 测试结果及分析为了更直观地验证本文采用的数据集分段处理方法的可行性, 将测试平台选为申威 1621 处理器, 表2详尽的例举出了处理器相关配置信息.
| 表 2 申威1621 实验平台 |
浮点计算程序的正确性和性能都得到了验证. 正确性测试根据 glibc 异常检测机制, 将异常处理前后的计算结果进行比较; 性能测试分别对异常处理前和异常处理后的测试结果进行对比, 并求得经过算法改进后的函数平均加速比.
注意这里性能加速比的计算公式和其他文献计算的方式不同, 具体如下:
性能加速比=(算法改进前节拍/算法改进后节拍)×100%
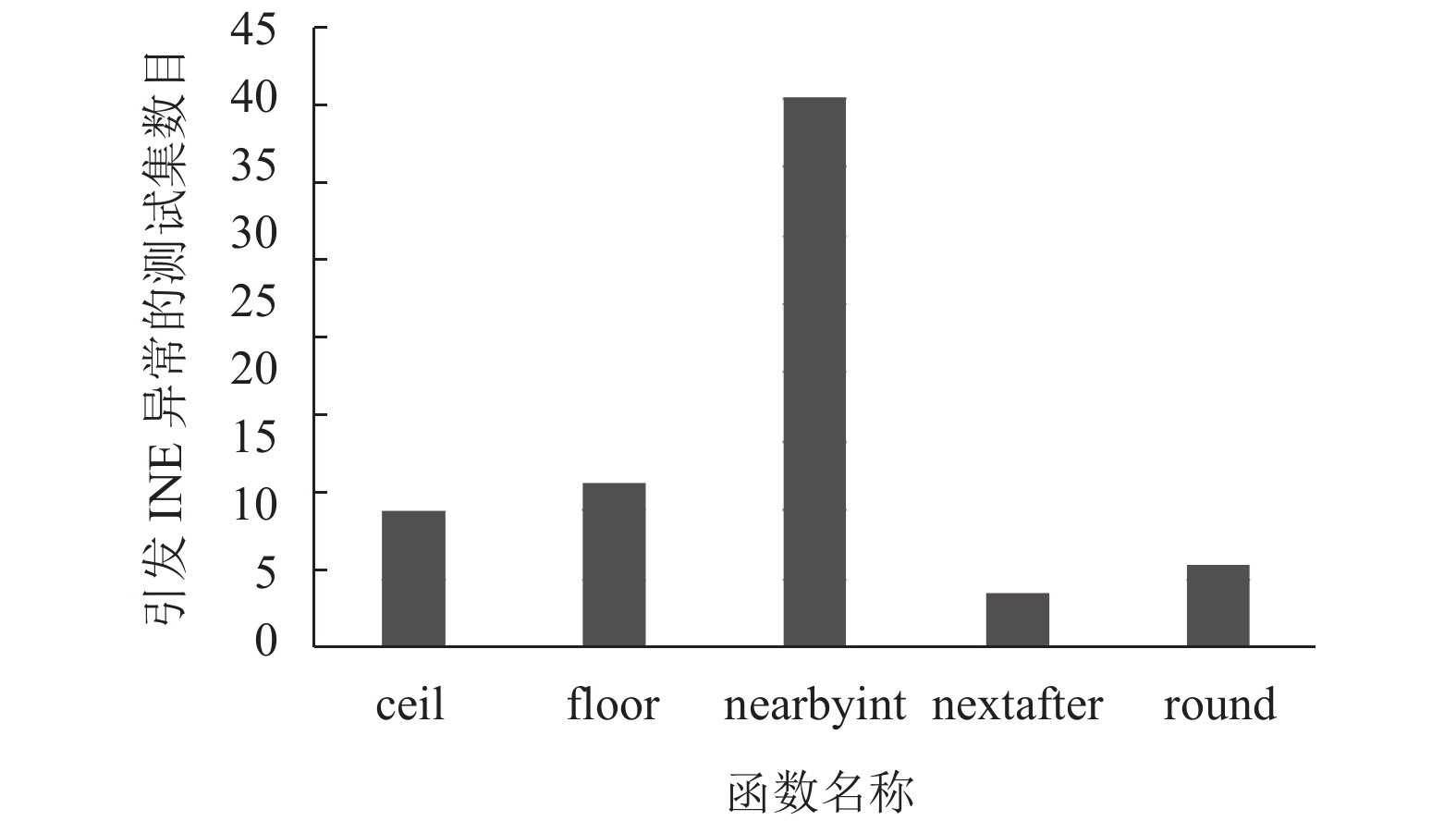
4.1 正确性测试在验证glibc-2.28 libm和基础数学库函数功能是否一致的过程中, 用开源测试数据集测试出基础函数库中INE异常需要消除的函数, 图4以double类型为例, 例举了5个不同函数INE异常需要消除的测试集个数, 横坐标表示了函数名称, 纵坐标表示引发INE异常的测试集的数目.
|
图 4 INE异常测试集统计 |
从图4中不难发现, INE异常需要消除的函数全部集中在数值函数中, 通过应用以上数据集分段处理的方法, 再进行测试则发现将图4检测到的5个函数不同测试集的所有INE异常消除.
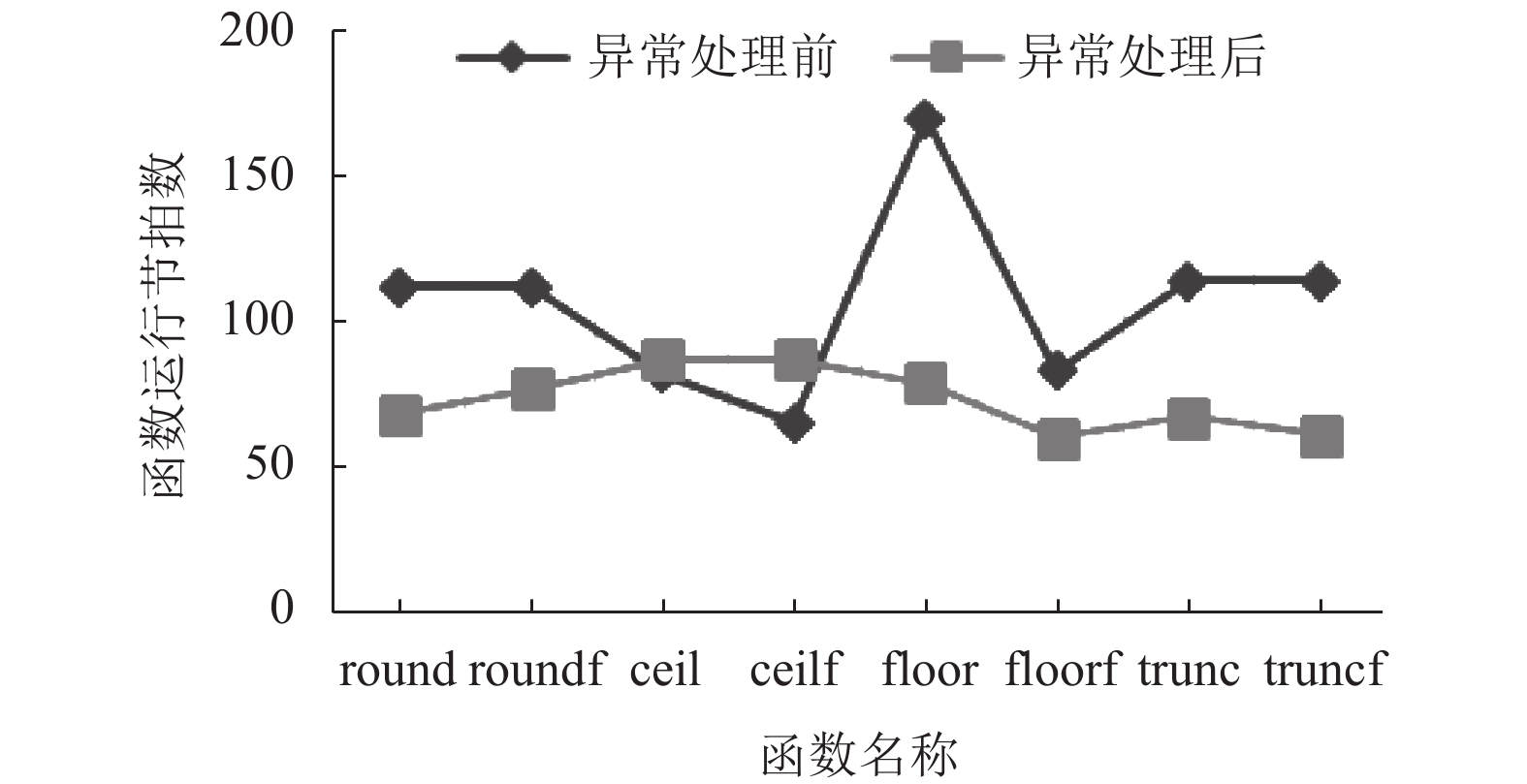
4.2 性能测试申威1621处理器整数部件中有一个控制状态寄存器TC, 作为周期计数器. rpcc 指令作为如今超级计算机衡量性能的通用计时指令, 通过插桩采样来计算被测函数的运算节拍数来判断性能的高低. 为了保证性能测量结果能够涵盖所有被测函数的热点路径, 首先进行热点分析, 并检查数据集主要使用的是随机浮点数, 其特点为都在0–1区间范围内均匀分布, 以测试基础数学库中运行上百次以上的总节拍数[18]. 为了排除误差较大的测试数据对性能测试结果的干扰, 采用 4D 检测法[21]对测试结果数据进行相关处理, 从而求得算术平均值. 测试结果如图5所示, 横坐标表示函数名称, 纵坐标表示函数运行节拍数.
|
图 5 算法改进前后性能对比 |
从图5的性能测试结果来看, 除了ceil, ceilf以外函数的性能还是有所提升的, 并且可以算出平均加速比为148%, 以此证明了这种方法的高效性. floor 函数性能提升的效果最为明显, 加速比达到了213.75%, floor 函数原来算法中相比于别的同类数值函数多了一条 SETFPEC0指令, 这个指令会导致流水线中断, 严重降低函数性能, 因此算法改进前运行节拍数就达到了171 cycles, 节拍数远远大于其他同类数值函数, 从而使得性能提升最为明显; ceilf 函数算法改进前由于不存在任何断流水的指令, 运行节拍数就为66 cycles, 属于同类函数中节拍数最小, 经过数据集分段处理后, 判断分支明显增多, 导致性能加速比为75%, 相比于异常处理前性能有一定的下降.
综合正确性测试和性能测试的测试结果分析, 可以得出数据集分段处理的方法, 在保证了功能的前提下还兼顾了性能, 足以说明这种方法的有效性.
5 总结与展望本文提出一种数据集分段处理的方法, 并应用于floor、ceil、trunc、round等8个数值函数, 同时以round函数为例进行算法改进, 归纳出其中用到的整数判断法和四舍五入取整法. 测试结果表明, 此方法消除了所有INE异常, 且相对于算法改进前平均性能加速比达到了148%. 下一步, 我们将试图从理论检验的视角全面证实本文方法的可行性, 并且把以上异常处理方式推广至更多的浮点运算型数值软件系统之中.
| [1] |
曹代, 郭绍忠, 张辛. 基于申威26010处理器的扩展函数库实现与优化. 计算机工程, 2017, 43(1): 61-66, 71. DOI:10.3969/j.issn.1000-3428.2017.01.011 |
| [2] |
Rajaraman V. IEEE standard for floating point numbers. Resonance, 2016, 21(1): 11-30. DOI:10.1007/s12045-016-0292-x |
| [3] |
刘纯根. 浮点计算编程原理、实现与应用. 北京: 机械工业出版社, 2008, 68. |
| [4] |
Goldberg D. What every computer scientist should know about floating-point arithmetic. ACM Computing Surveys, 1991, 23(1): 5-48. DOI:10.1145/103162.103163 |
| [5] |
Hauser JR. Handling floating-point exceptions in numeric programs. ACM Transactions on Programming Languages and Systems, 1996, 18(2): 139-174. DOI:10.1145/227699.227701 |
| [6] |
Cadar C, Dunbar D, Engler D. KLEE: Unassisted and automatic generation of high-coverage tests for complex systems programs. Proceedings of the 8th USENIX Conference on Operating Systems Design and Implementation. San Diego: USENIX Association, 2008. 209–224.
|
| [7] |
Godefroid P, Klarlund N, Sen K. DART: Directed automated random testing. ACM SIGPLAN Notices, 2005, 40(6): 213-223. DOI:10.1145/1065010.1065036 |
| [8] |
Sen K, Marinov D, Agha G. CUTE: A concolic unit testing engine for C. ACM SIGSOFT Software Engineering Notes, 2005, 30(5): 263-272. DOI:10.1145/1081706.1081750 |
| [9] |
Boldo S, Melquiond G. Flocq: A unified library for proving floating-point algorithms in Coq. Proceedings of the 2011 IEEE 20th Symposium on Computer Arithmetic. Tuebingen: IEEE, 2011. 243–252.
|
| [10] |
de Dinechin F, Lauter C, Melquiond G. Certifying the floating-point implementation of an elementary function using Gappa. IEEE Transactions on Computers, 2011, 60(2): 242-253. DOI:10.1109/TC.2010.128 |
| [11] |
Xia H, Wang CY, Yan JY. Analysis and research of floating-point exceptions. Proceedings of the 2nd International Conference on Information Science and Engineering. Hangzhou: IEEE, 2010. 1851–1854.
|
| [12] |
Goodenough JB. Exception handling: Issues and a proposed notation. Communications of the ACM, 1975, 18(12): 683-696. DOI:10.1145/361227.361230 |
| [13] |
Cristian F. Exception handling and software fault tolerance. IEEE Transactions on Computers, 1982, 31(6): 531-540. DOI:10.1109/TC.1982.1676035 |
| [14] |
Garcia AF, Rubira CMF, Romanovsky A, et al. A comparative study of exception handling mechanisms for building dependable object-oriented software. Journal of Systems and Software, 2001, 59(2): 197-222. DOI:10.1016/S0164-1212(01)00062-0 |
| [15] |
Cabral B, Marques P. Exception handling: A field study in Java and .Net. Proceedings of the 21st European Conference on Object-oriented Programming. Berlin, Heidelberg: Springer, 2007. 151–175.
|
| [16] |
袁浩. 基于符号执行与区间运算的浮点异常检测[硕士学位论文]. 上海: 华东师范大学, 2016.
|
| [17] |
许瑾晨, 郭绍忠, 黄永忠, 等. 浮点数学函数异常处理方法. 软件学报, 2015, 26(12): 3088-3103. DOI:10.13328/j.cnki.jos.004814 |
| [18] |
吴凡. 基于申威1621的基础数学库流水线中断优化研究[硕士学位论文]. 郑州: 中原工学院, 2021.
|
| [19] |
Álvares AR, Amarral JN, Pereira FMQ. Instruction visibility in SPEC CPU2017. Journal of Computer Languages, 2021, 66: 101062. DOI:10.1016/j.cola.2021.101062 |
| [20] |
刘剑. 基于区间分析的浮点计算误差估计与异常检测[硕士学位论文]. 上海: 华东师范大学, 2015.
|
| [21] |
许瑾晨, 黄永忠, 郭绍忠, 等. 一个浮点数学函数库测试平台. 软件学报, 2015, 26(6): 1306-1321. DOI:10.13328/j.cnki.jos.004589 |
 2022, Vol. 31
2022, Vol. 31


