绩效评价是基于特定的标准和指标, 采取科学的方法, 对员工过去的工作行为及取得的工作业绩进行评估, 是企业高效管理、激励员工的必要手段. 如何基于一线员工工作内容、工作质量等建立一套合理、公正的绩效评价体系, 是电力企业发展中非常重要和紧迫的课题.
近年来, 滕学军[1]以符合电力系统实际需求的KPI应用软件为基础, 研制制定绩效管理系统奖惩办法的策略; 彭佳惠等[2]引入EVA绩效考核制度, 提出了优化电力企业绩效考核的措施; 查杰等[3]介绍了平衡计分卡及其在供电公司绩效管理中的应用; 蒋丽等[4]提出了基于战略导向的项目制绩效考核的设计思路与过程, 结合关键绩效指标考核法完善绩效考核体系; 杨子等[5]将OKR管理模式引入绩效考核以构建更为完善、科学的绩效考核模式; 张峰[6]以某大型电力企业实施一线员工“工作积分制”绩效考核入手, 探讨其在优化系统设置及系统积分应用方面积累的经验.
目前, 传统的绩效评价体系往往容易陷入“过于量化”, 有时为了寻求客观科学的评价结果, 需要考核人员基于各类复杂的测算指标进行评价计算, 耗时耗力, 且考核人员的主观经验等绩效评价过程中价值信息却很难挖掘并予以应用. 本文提出了一套基于工单的绩效评价模型, 通过对同类工作项基于多维评价属性简单定性进行纵向计数量化, 对不同工作项基于班组长的主观评估权重进行横向聚类, 充分挖掘考核人员主观评估中隐含的价值信息, 解决考核人员评测难、过于量化的问题. 同时, 本文提出基于平均度数的动态随机种群拓扑PSO算法对模型进行求解, 对算法中粒子编码方式、约束条件处理、策略具体实现等展开了深入的探究.
1 聚类与班组绩效考核聚类分析是数据挖掘和知识发现的一种基本方法, 可在无先验知识无指导下进行数据无监督分类. 通过聚类分析, 可基于样本各维度属性数据将样本区分为自然的群体, 并给出每个群体特征描述, 有利于发掘数据中潜藏的价值信息.
聚类分析的算法很多, 比较著名的有模糊K-均值算法、K-中心点算法、C均值算法、FCM算法等. 作为典型的组合优化问题, 近年来国内外学者将蚁群算法[7-9]、遗传算法[10, 11]等群智能算法应用到聚类分析中, 为求解聚类分析提供了一种新思路.
在班组周期考核中, 班组长一般基于班组成员工作项及非工作项业绩给出考核分, 再对考核分排序, 结合总人数比例, 评定班员的绩效考核等级(A/B/C). 由于各工作分项重要程度、工作项与非工作项重要程度很难确定一个对所有班组都适用的科学、客观的评价权重系数, 班组长在实际操作中要给班员打出一个绝对量化的具体数值难度较大.
实际上, 班组绩效考核结果相当于依据班员在各类工作项、非工作项中的表现情况对班员划分出A、B、C等级3个聚类. 我们可以将绩效考核从“绝对”量化转化为“相对”量化, 从考核周期班组长对班员的绩效等级划分倒推挖掘出班组长对各类工作分项和非工作项的主观评价系数, 再基于评价系数对k+1考核周期班员绩效等级进行聚类划分.
本文选取PSO算法作为聚类分析主要工具, 并结合班组绩效考核实际情况建立了基于PSO算法的电力一线员工绩效评价模型.
2 电力一线员工绩效评价模型构建电力一线员工根据业务工作内容划分为生产、调度、营销等类型, 本文以生产域一线员工为例, 探讨绩效评价模型的构建.
2.1 基于评价系数的同类工单计件法电力生产一线员工的工作项可基于PMS2.5系统获取详细台账数据, 如操作票、带电作业票、变电一种票、巡线记录、缺陷管理、测温测负等. 不同班组根据班组类型(变电运维、变电检修、输电运检、配电运检、配电抢修等)关联其中某几种类型的工单数据. 可基于数据中台服务获取各班组所有班员的工单数据, 进而综合考虑各项工作技术难度、风险因素、人员参与角色等进行定性或定量评价.
本文采用的基于评价系数的同类工单计件法如图1所示. 班组长可自行定义各类工单的评价因子, 以及各项评价因子的衡量级别及衡量系数. 由于是针对同类工单的评价, 且只需针对各评价因子给出班员纵向所属级别, 相对明确易判断, 评价过程对班组长而言友好易操作. 由此可得到某考核周期内各班员在各类工单上的基于评价系数的计件数.
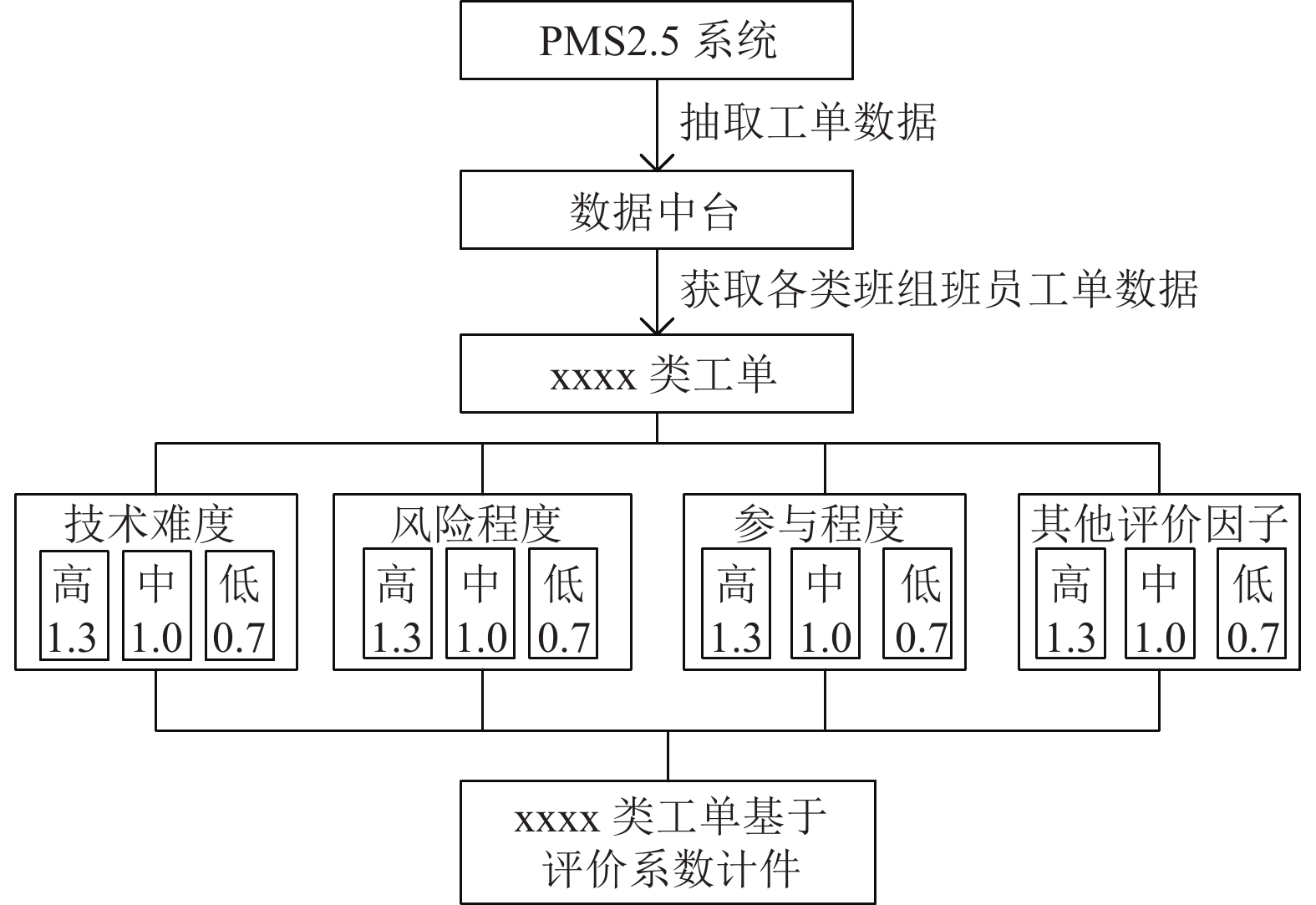
|
图 1 基于评价系数的同类工单计件法 |
2.2 基于PSO聚类算法的绩效等级评价
在实际考核中, 生产域班组考核内容主要分为两大类: 工作项与非工作项. 工作项基于从PMS2.5获取的工单进行统计分析, 非工作项由班组长定义各指标分项并进行评价.
对同类工单, 技术难度、风险程度、参与角色重要性可以给出清晰的评价准则. 但工作项不同类型工单之间, 工作项与非工作项之间, 如何以科学、合理的方式综合评价给出班员周期考核成绩是班组绩效考核中的难点. 本文从班组长抽象化的主观评价方式入手, 探索挖掘量化出班组长对各类工作/非工作项的主观评价系数.
本文提出的基于PSO聚类算法的绩效等级评价模型如图2所示. 对班组内m个班员采用基于评价系数的计件法求得t类工单计件数, 班组长基于非工作项指标体系综合给出每个班员的非工作项评分, 从而为每个班员生成了一个t+1维的评价数据. 根据k考核周期, 班组长对班员绩效等级划分的结果数据, 通过PSO聚类算法求解出t+1维的评价系数. 基于评价系数, 采用PSO聚类算法对k+1考核周期班员绩效考核等级进行评价, 班组长可基于全省同类班组主观偏好对评价系数进行调整, 可手动调整班员绩效考核等级, 调整结果自动更新到班组考核评价系数中, 作为下一次聚类评测依据.

|
图 2 基于PSO聚类算法的绩效等级评估模型 |
此外, 通过这种与自身历史主观评价系数比较、与同类班组主观评价系数比较的方式, 一方面促进了模型本身参数的更新优化, 另一方面也约束、促进班组长不断思考, 寻求更为客观、科学的评价标准.
3 基于随机拓扑策略的PSO算法 3.1 PSO算法基本原理PSO算法最初由Kennedy等[12]于1995年提出. 算法通过个体间协作来寻找解空间最优位置. 首先在解空间随机初始化一群粒子的位置向量, 根据目标函数评价粒子位置的优劣, 粒子结合种群中最优位置和自身历史最优位置进行迁移, 经过一定的进化次数后收敛到最优位置.
PSO算法具有计算简单、易于工程实现等诸多优点, 但在实际应用中, 存在易陷入局部最优值、解空间探索能力不稳定等问题. 针对这些缺点, 国内外学者提出了各类PSO算法变体, 例如, 由Shi等[13]提出的带惯性权重的WPSO算法, 由Clerc[14]提出的带压缩因子的CPSO算法, 由Liang等[15]提出的基于综合学习策略的CLPSO算法, 由朱国晖等[16]、Li等[17]提出的引入异构多种群策略的PSO算法, 由Tsujimoto等[18]、倪庆剑等[19]、Lu等[20] 提出的引入随机种群拓扑策略的PSO算法. 通过各种策略, 综合挖掘粒子的“个体认知”和“社会认知”能力, 从而提高粒子对解空间的探索能力.
3.2 基于动态随机拓策略的PSO算法在PSO算法的诸多应用中, 大多采用的种群拓扑结构是静态的全连接型拓扑和环型拓扑, 如图3所示.

|
图 3 经典静态种群拓扑结构 |
采用全连接型拓扑结构, 在进化过程中最优解粒子的位置信息会被迅速传播到整个种群中, 算法的收敛速度非常快, 容易陷入局部最优解. 采用环型拓扑结构, 每个粒子的邻居只有相邻的两个粒子, 种群中信息的传递速度较慢, 有助于对解空间充分挖掘, 但是算法收敛速度较慢.
本文PSO算法中引入动态随机种群拓扑策略(RPT-PSO), 在种群进化过程中, 动态改变拓扑结构, 一方面帮助粒子跳出局部最优解, 另一方面推动信息在粒子及其新的邻域粒子间充分传递.
设计基于平均度数的动态随机种群拓扑策略如下: 每隔一定代数M, 随机生成一个种群拓扑结构. 为了避免早熟收敛, 增强粒子在解空间的搜索能力, 在算法进化初期, 平均度数AD可以设为2, 随着粒子不断进化, 算法开始收敛, 此时平均度数AD应该不断增大, 来产生新的种群拓扑结构. 最终, AD增加到最大值, 产生了一个全接连型的种群拓扑结构. 具体算法如算法1.
算法1. 基于平均度数的动态随机种群拓扑算法
1) 对于一个包含S个粒子的种群, 创建一个S×S维的矩阵L, 设置L(i,i)=1;
2) 设置平均度数AD的值;
3) 随机排列所有粒子的编号, 若i和j是序列中两个相邻的编号, 则设置L(i,j)=1, 从而产生了一个连通图. 设置当前平均度数CurrentAD=2;
4) 设置进化代数计数器的值为0;
5) while 算法不满足终止条件 do
6) 种群中粒子继续进行进化操作;
7) 记增进化代数计数器的值;
8) if 进化代数计数器的值能被M整除 then
9) 线性增加AD的值;
10) 生成一个新的平均度数为AD的随机种群拓扑.
4 PSO算法求解绩效等级评价模型本节采用基于平均度数的动态随机种群拓扑PSO算法, 根据绩效等级评估模型特点, 提出求解该模型的完整算法.
4.1 基于聚类结果求解多维评价系数对于k考核周期, 由班组长基于t种类型工单的统计结果和非工作项评价将n个班员评定为A、B、C三个绩效等级, 相当于一个有n个样本的样本集{X1, X2, …, Xn}, 每个样本有t+1个特征值, 被划分为3个模式分类{S1, S2, S3}, 每个模式分类Si中的样本到各自聚类中心Ci距离之和最小. 目标函数为:
| $ f = {\rm min}\sum\nolimits_{i = 1}^3 {\sum\nolimits_{{X_i} \in {S_i}} {D({X_i}, {C_i})} } $ | (1) |
其中,
定义特征值评价系数向量(w1, w2, …, wt+1). 由于各维度特征值具有不同的评价系数, 本文中聚类中心计算方式为:
| $ {C_{id}} = \sum\nolimits_{j = 1}^n {{w_d}{y_{ji}}{X_j}\Bigg/\sum\nolimits_{j = 1}^n {{y_{ji}}} } $ | (2) |
样本与其聚类中心的距离计算方式为:
| $ D({X_i}, {C_i}) = \sqrt {\sum\nolimits_{d = 1}^{t + 1} {{{({w_d}{X_{id}} - {w_d}{C_{id}})}^2}} } $ | (3) |
其中,
| $ {y}_{ji}=\left\{ {\begin{array}{l}1, 模式样本j分配给模式分类{S}_{i}\\ 0, 模式样本j未分配给模式分类{S}_{i}\end{array} } \right. $ | (4) |
用每个粒子p的位置代表评价系数向量, 即: (xp1, xp2, xp3, …
综上, 给出PSO算法求解多维评价系数的完整算法如算法2所示.
算法2. PSO求解多维评价系数算法
1) 记S为种群中粒子总数, M为某一拓扑结构下种群进化代数;
2) 初始化拓扑结构为环形拓扑, 平均度数AD=2;
3) 对每个粒子p的位置向量每一维度xpi生成[1, 10]间的随机数;
4) for
5)
6) 随机初始化粒子速度, 校验粒子速度绝对值不超过最大值vpmax;
7) 计算粒子适应值
8) 更新粒子自身最优值fpbest及粒子群全局最优值f
9) 设置进化的总次数GNum;
10) for
11) for
12) for
13) 更新粒子速度vpi, 更新粒子位置xpi;
14) 将粒子位置归一化处理为权重向量;
15) 计算粒子适应值;
16) 更新粒子自身最优值fpbest及最优值位置
17) 更新粒子群全局最优值fgbest及最优值位置;
18) if GNum能被M整除 then
19) 线性增加AD的值, 生成一个新的平均度数为AD的随机种群拓扑.
4.2 基于多维度评价系数求解班组绩效基于k考核周期求出的班组多维评价系数, k+1周期t种类型工单的统计结果和非工作项评价, 将n个班员k+1周期的考核结果评定为A、B、C三个绩效等级. 相当于一个有n个样本的样本集{X1, X2, …, Xn}, 每个样本有t+1个特征值, 各特征值评价系数向量为(w1, w2, …, wt+1), 需要将其划分为3个模式分类{S1, S2, S3}, 使得每个模式分类Si中的样本到各自聚类中心Ci距离之和最小. 目标函数、聚类中心、样本与其聚类中心距离的计算方式同第4.1节.
用每个粒子p的位置代表n个样本分别属于哪种模式分类, 即: (xp1, xp2, xp3…, xpn). 对应的, 粒子p的速度表示为向量: (vp1, vp2, vp3…, vpn). 使用PSO算法求解的流程与第4.1节相似, 只是粒子位置向量初始化或更新后, 要通过对其整数部分对3取余数映射为模式分类1、2、3.
定义3个类别的模式样本值如下:
(1) 第 1 类: A级(优秀). 对每类工作类别取排名前20%的得分取平均值作为样本各维度数值.
(2) 第 2 类: B级(良好). 对每类工作类别取排名介于后15%和前20%的得分取平均值作为样本各维度数值.
(3) 第 3 类: C级(合格). 对每类工作类别取排名后15%的得分取平均值作为样本各维度数值.
使用PSO算法进行聚类分析时, 将这3类标准模式样本值也加入到总的员工样本中进行聚类, 聚类结果出来后, 如果某个员工和某个标准模式样本处于同一个类别群体, 那么该员工就属于该类员工. 例如: 员工张三和第1类标准模式样本处于同一个类别群体, 那么张三就属于“第 1 类: A级(优秀)”. 通过这种方法, 就可以将员工具体属于哪一个档次分类出来.
5 实验分析选取省内5个同类型班组, 获取班员k考核周期内的工单数据, 根据第2.1节中提出的基于评价系数的同类工单计件法, 由班组长参与对工作情况进行定性评价, 求得所有班员各类工作项统计值. 同时, 班组长对班员进行非工作项考核打分. 基于工作项和工作项统计结果, 由班组长对班员进行绩效等级评价. 以配电运检1班为例, 具体数据如表1所示. 其中F1–F7对应不同类型的工作项, F8为非工作项评价.
通过PSO算求解评价系数向量. 对PSO算法, 设置粒子总数为100, 实验进化次数设置为500次. 实验编码采用C++语言, 实验环境为Intel(R) i7-4790处理器, CPU为3.6 GHz, 内存为8 GB. 得到评价系数向量w=(0.0923, 0.0612, 0.2555, 0.0545, 0.1738, 0.1086, 0.1486, 0.1055).
获取班员k+1考核周期内的工单数据, 完成所有班员各类工作项统计值及班员非工作项的评价. 根据评价系数向量, 通过PSO聚类算法求解班员绩效等级, 并由班组长结合各项数据根据个人主观判断对班员绩效等级进行评价. 以配电运检1班为例, 得到考核结果数据如表2所示.
| 表 1 配电运检1班工单计件值及非工作项评价 |
| 表 2 配电运检1班k+1周期PSO聚类结果及班组长考核结果 |
从表2可以看到, PSO聚类算法求解得到的班员绩效等级, A等级人员完全一致, C等级3人中有两个与班组长评价结果一致.
定义某绩效等级X评价命中率为: 评定为X等级的班员中与实际班组长评定为X等级一致的人数/X等级总人数. 对5个班组k+1考核周期绩效测算情况统计得到表3.
通过在5个同类型班组绩效考核中对本文提出的模型有效性进行验证, 可以发现模型总体测算性能良好, 尤其对A等级测算命中率相对较为稳定.
实验证明, 对班组长主观判断偏好进行挖掘并通过聚类方式规避了对绩效评判的绝对量化后, 测算出的绩效等级与班组长实际评价较为接近. 同时, 将同一类型班组班组长评价偏好进行综合统计分析, 可为班组长提供一种相对客观的评价衡量标准, 有助于促进班组长对绩效评判更为公平的认知.
| 表 3 5个班组k+1考核周期绩效测算命中率(%) |
6 结论与展望
本文针对电力一线员工绩效考核问题, 构建了一套基于工单的绩效评价模型, 提出了基于平均度数的动态随机种群拓扑PSO算法求解该模型, 得出以下结论:
(1)通过对同类工作项基于多维评价属性简单定性进行纵向计数量化, 对不同工作项基于班组长的经验等主观评估权重进行横向抽象聚类, 可为班组成员绩效等级评定提供一种有效的测算工具.
(2)对PSO算法基于聚类结果反向求解多维评价系数、基于多维度评价系数评测班组绩效等级提出了完整的编码规则、聚类中心及距离计算规则、算法流程, 可有效对模型进行求解.
未来的研究中, 将更为深入地结合电力一线员工工作内容、工作性质、安全风险等, 探索构建更为客观、科学的一线员工绩效评价模型, 推动落实班组精细管理.
| [1] |
滕学军. 基于KPI的电力企业员工绩效管理体系研究. 电力设备管理, 2019(10): 115-117. |
| [2] |
彭佳惠, 李佩瑜. 基于EVA的电力企业绩效评价研究. 财经界, 2020(27): 46-47. |
| [3] |
查杰, 娜比拉·海萨尔. 基于平衡计分卡的供电公司绩效考核体系研究. 营销界, 2020(48): 121-122. |
| [4] |
蒋丽, 王伟玉. 基于战略导向的电力企业项目制绩效考核体系设计——以HL公司为例. 现代营销, 2021(3): 190-191. |
| [5] |
杨子, 李歆. 基于OKR方法的绩效考核模式优化研究——以宁夏电科院为例. 企业改革与管理, 2021(12): 62-63. |
| [6] |
张峰. 一线员工绩效管理在电力企业的探索. 人力资源管理, 2015(12): 128-129. DOI:10.3969/j.issn.1673-8209.2015.12.107 |
| [7] |
冯志雨, 游晓明, 刘升. 分层递进的改进聚类蚁群算法解决TSP问题. 计算机科学与探索, 2019, 13(8): 1280-1294. DOI:10.3778/j.issn.1673-9418.1901022 |
| [8] |
李伟. 基于划分的蚁群聚类算法研究. 信息与电脑, 2019(2): 45-47. |
| [9] |
武书舟, 闫丽娜, 张秋艳, 等. 基于改进蚁群算法的聚类分析方法研究. 计算机与数字工程, 2018, 46(9): 1721-1725, 1849. DOI:10.3969/j.issn.1672-9722.2018.09.005 |
| [10] |
冯劲, 姚远. 融合相似度计算与改进遗传算法的聚类分析. 计算机仿真, 2020, 37(9): 226-230. DOI:10.3969/j.issn.1006-9348.2020.09.047 |
| [11] |
孙雨萌, 柏丽娜, 张旭秀. 核模糊聚类划分子种群的双种群遗传算法. 大连工业大学学报, 2021, 40(1): 67-73. |
| [12] |
Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of 1995 International Conference on Neural Networks. Perth: IEEE, 1995. 1942–1948.
|
| [13] |
Shi Y, Eberhart RC. Empirical study of particle swarm optimization. Proceedings of 1999 IEEE Congress on Evolutionary Computation (CEC). Washington: IEEE, 1999. 1945–1950.
|
| [14] |
Clerc M. The swarm and the queen: Towards a deterministic and adaptive particle swarm optimization. Proceedings of 1999 IEEE Congress on Evolutionary Computation (CEC). Washington: IEEE, 1999. 1951–1957.
|
| [15] |
Liang JJ, Qin AK, Suganthan PN, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Transactions on Evolutionary Computation, 2006, 10(3): 281-295. DOI:10.1109/TEVC.2005.857610 |
| [16] |
朱国晖, 刘茹文, 杨瑛. 多种群粒子群的SDN控制器故障恢复算法. 计算机工程与应用. http://kns.cnki.net/kcms/detail/11.2127.TP.20210326.1634.004.html. [2021-09-15].
|
| [17] |
Li GQ, Wang WL, Zhang WW, et al. Grid search based multi-population particle swarm optimization algorithm for multimodal multi-objective optimization. Swarm and Evolutionary Computation, 2021, 62: 100843. DOI:10.1016/j.swevo.2021.100843 |
| [18] |
Tsujimoto T, Shindo T, Kimura T, et al. A relationship between network topology and search performance of PSO. Proceedings of 2012 IEEE Congress on Evolutionary Computation (CEC). Brisbane: IEEE, 2012. 1–6.
|
| [19] |
倪庆剑, 邓建明, 邢汉承. 基于异构多种群策略的动态概率粒子群优化算法. 模式识别与人工智能, 2014, 27(2): 146-152. DOI:10.3969/j.issn.1003-6059.2014.02.008 |
| [20] |
Lu JN, Chen YH. Particle swarm optimization (PSO) based topology optimization of part design with fuzzy parameter tuning. Computer-Aided Design and Applications, 2014, 11(1): 62-68. DOI:10.1080/16864360.2013.834139 |
 2022, Vol. 31
2022, Vol. 31


