金融时间序列预测是金融领域中一个重要研究方向, 可以为二级股票市场投资提供市场走势、风险和入场出场时机的预测. 传统金融时间序列预测方法包括技术分析和计量经济学模型. 技术分析是利用技术指标或者结合多种技术指标对未来一段时间股票走势进行方向性预测, 计量经济学方法是利用多元线性回归、ARIMA模型等模型对历史股票数据进行最优化拟合, 然后对未来进行预测.

人工智能可以学习到时间序列中的非线性关系, 能够有效处理金融数据中低信噪比问题, 在金融时间序列预测上具有显著的优势, 尤其是以大数据为背景的神经网络类模型. 国外相关文献主要以宏观经济数据和股票价格预测为主, Ahmed等利用传统机器学习模型对宏观经济中M3时间序列进行预测^[1]; Cao等利用EMD分解和LSTM模型对美国股票价格时间序列进行预测, 获得了较高的预测精度^[2]; Siami-Namini等比较了LSTM模型和ARIMA模型在美国重要股票指数上的预测水平差异^[3]; Dingli等研究了CNN模型在美国股票价格序列上的预测能力^[4]; Kumar等测试了LSTM对纳斯达克股票价格的预测能力^[5]; Shen等比较了GRU和SVM在美国和欧洲不同股票指数上的预测能力^[6]. 国内相关文献主要以单只股票指数预测为主, 谷丽琼等利用结合注意机制的GRU模型对科大讯飞股票价格进行预测, 预测效果优于其他模型^[7]; 乔若羽比较研究神经网络在上证指数上的预测能力, 研究了模型优化方向^[8]; 李坤等利用支持向量机对A股大盘指数和个股进行预测^[9]; 王文波等结合EMD分解和神经网络对上证指数和深证成指进行预测^[10].

本文在传统神经网络(NN)、RNN、LSTM和GRU等模型基础上, 构建集成学习模型, 研究神经网络类模型和集成学习模型在金融时间序列预测上的表现.本文选择ARIMA模型和线性回归模型为基准模型, 选择16只A股市场和全球重要发达国家和地区股票市场指数为样本, 研究模型在长期、中期和短期3种不同预测期间上的预测能力, 比较模型在不同国家和地区的适用情况.

1 模型构建 1.1 传统神经网络模型

神经网络模型由全连接层组成, 按照全连接层作用分类, 可以分为输入层, 隐藏层和输出层, 如图1(a). 神经网络中的节点是非线性转换单元, 负责对输入进行线性组合并且利用激活函数进行非线性输出, 如图1(b).

激活函数是神经网络可以进行非线性拟合的核心, 常见激活函数有S型函数(Sigmoid)、双曲正切函数(tanh)和修正线性单元(ReLU), 如式(1).

$ \left\{ {\begin{split} & {\textit{Sigmoid}}(x) = \frac{1}{{1 + {{\rm{e}}^{ - x}}}} \hfill \\ & \tanh (x) = \frac{2}{{1 + {{\rm{e}}^{ - 2x}}}} - 1 \hfill \\ & ReLU(x) = \max (0, x) \end{split}} \right. $

(1)

1.2 循环神经网络

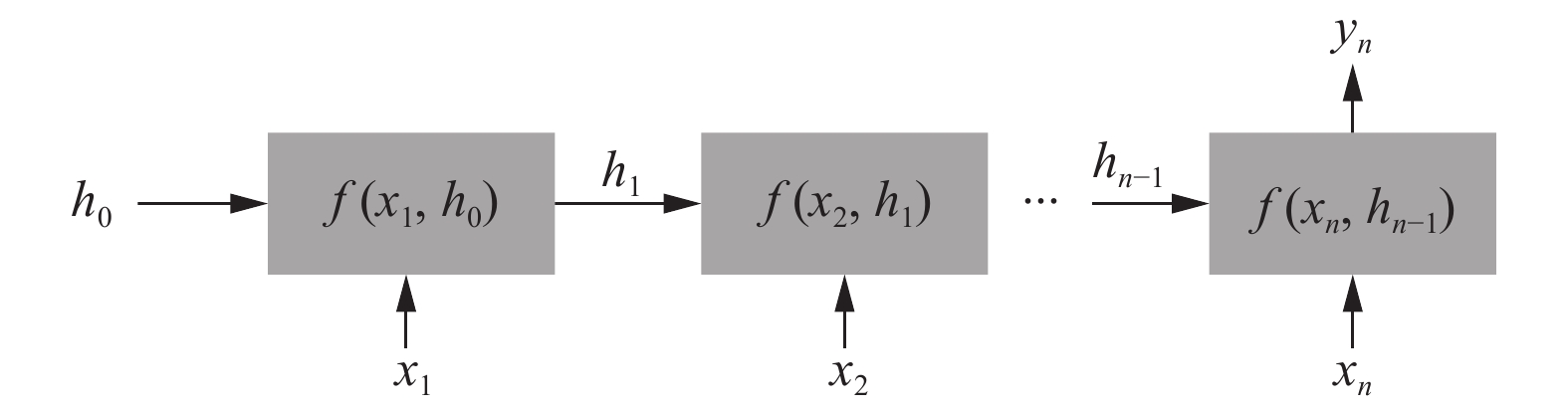
传统神经网络的输入是同质的, 无法区分输入序列的先后关系, RNN将输入看成一个新的维度, 允许模型按照时间顺序输入特征, 如图2所示.

RNN模型输入向量为 $({x_1}, {x_2}, \cdots , {x_n})$ , 输出为 ${y_n}$ , 记忆向量为 ${h_t}$ , RNN前向运算过程如式(2)和式(3), 其中 ${W_{hh}}, {W_{xh}}, {W_{hy}}$ 是权重共享的参数矩阵, 是RNN最后的输出^[11].

$ {h_t} = \tanh({W_{hh}}{h_{t - 1}} + {W_{xh}}{x_t}) $

(2)

$ {y_t} = {W_{hy}}{h_t} + b $

(3)

RNN虽然可以利用状态向量拥有记忆能力, 但是记忆能力有限, 只能记忆当前时刻最近的状态, 无法处理长期依赖问题. LSTM模型解决了长期依赖问题, 拥有长期记忆能力, 同时也解决了RNN梯度爆炸和梯度离散的问题.

LSTM由遗忘门 ${f_t}$ , 输入门 ${i_t}$ , 输出门 ${o_t}$ 组成, 输入当前时刻输入 ${x_t}$ , 上一时刻单元状态 ${c_{t - 1}}$ 和隐藏状态 ${h_{t - 1}}$ , 输出 ${c_t}$ , ${h_t}$ 和 ${y_t}$ . LSTM前向运算如图3所示, 其中, $*$ 表示矩阵对应元素乘法, $ + $ 表示矩阵加法^[12-14]. LSTM数学运算过程如式(4).

$ \left\{ {\begin{split} & {f_t} = \sigma ({W_f}[{h_{t - 1}}, {x_t}] + {b_f}) \\ & {i_t} = \sigma ({W_i}[{h_{t - 1}}, {x_t}] + {b_i}) \\ & {o_t} = \sigma ({W_o}[{h_{t - 1}}, {x_t}] + {b_o}) \\ & {{\textit{z}}_t} = \tanh({W_{\textit{z}}}[{h_{t - 1}}, {x_t}] + {b_{\textit{z}}}) \\ & {c_t} = {f_t}*{c_{t - 1}} + {i_t}*{{\textit{z}}_t} \\ & {h_t} = {o_t}*\tanh({c_t}) \end{split}} \right. $

(4)

其中, $\sigma $ 是Sigmoid激活函数, 输出在0到1之间, tanh是激活函数, 输出在−1到1之间, $*$ 表示矩阵中对应元素相乘. LSTM依然采用权值共享机制, 不同时刻的参数矩阵相同.

GRU是LSTM的简化版本, 性能与LSTM类似, 但是大大减少了计算复杂度, 提高了计算效率^[15]. GRU减少了门控的数量并且去掉了状态向量 ${c_t}$ , 只保留重置门 ${r_t}$ 和更新门 ${{\textit{z}}_t}$ , 如图4所示.

GRU输入为 ${h_{t - 1}}$ 和 ${x_t}$ , 输出为 ${h_t}$ 和 ${y_t}$ , ${h_t}$ 作为下一个时刻的输入, ${y_t}$ 作为最终输出结果, GRU的数据运算过程如式(5).

$ \left\{ {\begin{split} & {{\textit{z}}_t} = \sigma ({W_{\textit{z}}}[{h_{t - 1}}, {x_t}] + {b_{\textit{z}}}) \\ & {r_t} = \sigma ({W_r}[{h_{t - 1}}, {x_t}] + {b_r}) \\ & {s_t} = \tanh({W_s}[{h_{t - 1}}*{r_t}, {x_t}] + {b_s}) \\ & {h_t} = (1 - {{\textit{z}}_t})*{h_{t - 1}} + {{\textit{z}}_t}*{s_t} \end{split} } \right.$

(5)

其中, ${W_{\textit{z}}}$ , ${W_r}$ , ${W_s}$ 是参数矩阵, ${b_{\textit{z}}}$ , ${b_r}$ , ${b_s}$ 是偏置向量, ${{\textit{z}}_t}$ , ${r_t}$ 分别代表更新门和重置门, ${s_t}$ 是中间变量, ${h_t}$ 是GRU的输出, 最后时刻的 ${h_t}$ 是GRU最终输出 ${y_t}$ , $*$ 表示矩阵中对应元素相乘.

1.3 集成学习

股票指数在不同的资本市场和不同的时期会呈现出不同的趋势和特点. 机器学习模型有其各自的优缺点和最优的适用场景, 单一机器学习模型很难适用于股票市场中的所有情况. 集成学习(ensemble learning)可以结合多个基学习器, 获得一个表现稳定且优异的强学习器, 能够同时减少预测偏差和方差^[16].

本文选择传统神经网络(NN)、RNN、LSTM和GRU 4个模型作为基学习器, 利用bagging集成学习构建强学习器, 如图5所示.

假设金融时间序列为 $\{ {x_t}\} (t = 1, 2, 3, \cdots)$ , 第 $i\;(i = 1, 2, 3, 4)$ 个基学习器如式(6)所示:

$ x_t^i = {f_i}({x_{t - 1}}, {x_{t - 2}}, \cdots , {x_{t - n}}) $

(6)

其中, 输入为 ${x_{t - 1}}, {x_{t - 2}},\cdots, {x_{t - n}}$ , 输出 $x_t^i$ 为第 $i$ 个基学习器在 $t$ 时刻的预测值. 由于股票指数时间序列具有渐进独立性, 所以本文选择n等于30, 即前30个交易日为自变量, 第31个交易日为因变量, 构建神经网络集成学习模型.

集成学习在 $t$ 时刻的最终预测值 ${\hat x_t}$ 等于4个基学习器的预测值的简单算数平均数, 如式(7):

$ {\hat x_t} = \frac{1}{4}\sum\limits_{i = 1}^4 {x_t^i} $

(7)

1.4 传统金融时间序列模型

传统金融时间序列模型主要包括n阶自回归模型(AR(n)模型)和差分自回归移动平均模型(ARIMA(p, d, q)模型).

假设金融时间序列为 $\{ {x_t}\}\; (t = 1, 2, 3,\cdots)$ , ${\varepsilon _t}$ 为白噪声, AR(n)模型表达式如式(8)所示, 其本质是多元线性回归模型. 为了与神经网络模型保持一致, 本文选择AR(30)模型作为基准模型.

$ {x_t} = {a_t}{x_{t - 1}} + {a_2}{x_{t - 2}} + \cdots + {a _n}{x_{t - n}} + {\varepsilon _t} $

(8)

ARMA(p, q)模型表达式如式(9)所示:

$ {x_t} = \sum\limits_{i = 1}^p {{a_i}{x_{t - i}}} + \sum\limits_{j = 1}^q {{b_j}{\varepsilon _{t - j}} + {\varepsilon _t}} $

(9)

对于非平稳金融时间序列, 传统金融计量经济学引用d阶差分来平稳化金融时间序列, 并且使用经过差分后的金融时间序列进行ARMA(p, q)建模, 即ARIMA(p, d, q)模型^{[17, 18]}.

2 实证研究 2.1 数据选取

本文数据来源是wind数据库, 样本时间范围为2005年1月1日到2020年12月31日. 本文选择7只我国A股市场指数和9只国际市场指数共计16只重要股票指数作为样本, 比较机器学习模型和传统时间序列预测模型在不同市场和拥有不同成分股的股票指数上的预测能力, 增加了结论的可靠性和稳健性.

我国A股市场指数分别为上证综指(000001), 上证50 (000016), 上证180 (000010), 沪深300 (000300), 深证成指 (399001), 创业板指(399006)和中小板指(399005)^[19]; 全球市场指数分别为道琼斯工业指数(DJI), 标普500 (SPX), 纳斯达克指数(IXIC), 恒生指数(HSI), 法国CAC40 (FCHI), 英国富士100 (FTSE), 德国DAX(GDAXI), 日经225 (N225)和韩国综合指数(KS11).

2.2 评价指标与DM检验

本文使用平均绝对误差(MAE)度量模型预测能力, 并且比较神经网络集成学习(EL)与传统金融时间序列预测模型直接预测误差MAE衡量EL性能提升水平. 本文进一步使用Diebold-Mariano检验来对模型预测能力进行统计显著性检验, 比较神经网络类模型和集成学习是否显著优于传统ARIMA和AR模型^{[20, 21]}.

MAE用于衡量预测值与真实值误差绝对值的均值, 可以比较模型预测能力的优劣, 本文为了便于展示, 将MAE结果扩大了100倍, 如式(10).

$ MAE = \frac{1}{n}\sum\limits_{i = 1}^{\text{n}} {|{y_{\text{i}}} - {{\hat y}_i}|} \times 100 $

(10)

EL性能提升水平是基于模型预测误差MAE计算的模型预测误差提升百分比, 如式(11), 其中 $MA{E_{\rm{other}}}$ 代表其他模型的预测误差MAE, $MA{E_{\rm{EL}}}$ 代表神经网络集成学习模型预测误差MAE.

$ E{L_{\rm{Growth}}} = \frac{{MA{E_{\rm{other}}} - MA{E_{\rm{EL}}}}}{{MA{E_{\rm{EL}}}}} \times 100{\text{%}} $

(11)

Diebold和Mariano (2002)^[22]提出DM检验, 检验两个模型预测精度是否存在显著的差异. DM检验假设模型与模型在时间跨度的预测误差序列向量分别为: ${{\boldsymbol{e}}_{\boldsymbol{A}}} = ({a _1}, {a_2},\cdots, {a_T})$ , ${{\boldsymbol{e}}_{\boldsymbol{B}}} = ({b _1}, {b_2}, \cdots, {b_T})$ , 二者的差值序列向量为: ${\boldsymbol{d}} = ({d _1}, {d_2}, \cdots, {d_T})$ , 其中 ${d_i} = {a_i} - {b_i}\;(i = 1, 2,\cdots, T)$ . DM统计量表达式如式(12).

$ DM = \frac{{\sqrt T {\boldsymbol{\bar d}}}}{{\sigma ({\boldsymbol{d}})}} $

(12)

其中, $\sigma ({\boldsymbol{d}})$ 为差值序列向量 ${\boldsymbol{d}}$ 的标准差, ${\boldsymbol{\bar d}}$ 为差值序列向量 ${\boldsymbol{d}}$ 均值, DM统计量的分布服从标准正态分布.

2.3 模型参数

神经网络模型超参数包括隐藏层层数、神经元个数、激活函数和模型优化器等. 为了提高模型的收敛速度, 本文对数据进行最大最小值标准化, 对神经网络类模型采用随机梯度下降(SGD)优化器, 并且配合学习率递减策略^[23]. 4种基学习器的具体超参数取值如表1所示. 本文基准模型选择ARIMA(p, d, q)模型和AR(n)模型, 两个基准模型的参数优化及选择如表2和表3所示.

2.4 实证结果

本文选择全球16只重要的股票价格指数时间序列为样本, 时间跨度为2005年1月1日到2020年12月31日, 共计3889个交易日, 由于我国A股市场某些指数编制起始时间不同, 交易日个数略少, 具体如表4.

本文将样本划分为不同长度的训练集和测试集, 用以检验神经网络集成学习模型在不同预测期间长度上的表现, 具体可分为长期预测(100个交易日预测), 中期预测(50个交易日预测)和短期预测(30个交易日预测), 即选择样本中最后100、50和30个交易日数据作为测试集, 其他交易日数据作为训练集.

实证结果如表5–表7所示. 表5–表7以MAE为评价指标, 分别展示了神经网络类模型和神经网络集成学习模型在全球不同市场不同股票指数下, 在不同预测期间的预测能力, 比较了神经网络集成学习(EL)相比于传统金融时间序列预测模型ARIMA和AR模型的性能提升水平.

由表5–表7可知, NN、RNN、LSTM、GRU和集成学习模型的样本外预测能力显著优于传统ARIMA和线性回归模型, 在不同股票指数和不同预测时间长度上的表现都优于传统模型, 其平均预测性能提升大约35%.

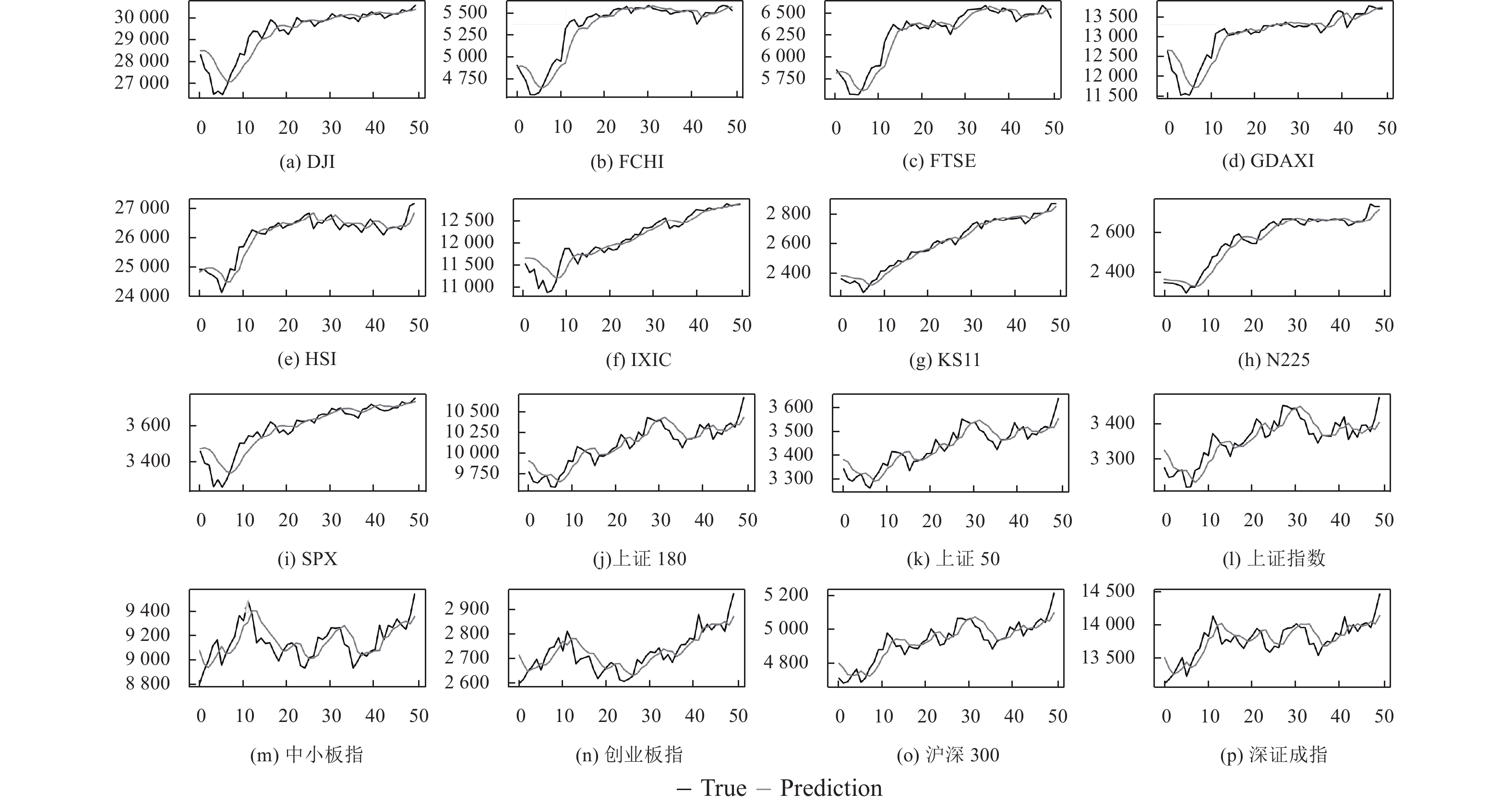
LSTM和GRU模型在英国富士100和日经225等极少数股票指数上表现不如线性回归模型, 其他情况下都优于ARIMA和AR模型. 其中原因是股票指数与近期股市表现相关性最强, 与长期表现相关性变弱, 导致具有长期记忆能力的LSTM和GRU模型预测能力下降. 集成学习作为强学习器, 在预测稳定性和预测精度上优于其他神经网络类模型, 集成学习在不同期限上的样本外预测值和真实值的时间序列, 如图6–图8所示.

神经网络类模型和集成学习在不同国家和地区的股票市场中的表现具有一定的差异. 在中国股票市场和美国股票市场上, 神经网络类模型和集成学习比ARIMA模型性能提升大约45%, 比AR模型性能提升大约35%; 在其他发达国家股票市场上, 神经网络类模型和集成学习比ARIMA模型依然有显著的优势, 性能提升大约70%, 但是比AR模型性能提升只有15%左右.

本文利用DM检验, 进一步检验神经网络类模型和集成学习在不同预测期间和不同国家股票市场上的表现的是否显著优于传统时间序列预测模型, 结果如表8所示. 表8检验了在不同预测期限上, 神经网络类模型和集成学习分别在中国股票市场、美国股票市场和其他发达国家股票市场上相比于传统时间序列模型是否存在显著的优势. NN、RNN、LSTM、GRU和集成学习模型在中国市场和美国市场上的预测能力显著优于传统时间序列模型, 但是在其他发达国家市场的表现不具有统计显著性.

2.5 结果分析

ARIMA和AR等传统金融时间序列预测模型只能捕获时间序列中的线性关系, 无法捕获时间序列中的非线性关系. 股票指数是包含了众多噪音在内的非线性时间序列, 线性模型只能预测股票指数的线性趋势部分, 无法预测股票指数非线性趋势部分.

神经网络类模型可以捕获时间序列中的非线性关系, 集成学习可以有效地降低单一神经网络模型的过拟合风险. 基于神经网络类模型的集成学习不仅仅可以有效地识别出股票指数中的非线性关系, 还可以避免模型拟合过多的噪音, 增强模型的泛化能力. 所以神经网络集成学习在金融时间序列预测上的表现远远优于传统金融时间序列预测模型.

3 结论

本文以7只A股市场指数和9只国际市场指数为样本, 研究了神经网络类模型和基于神经网络的集成学习在金融时间序列上的预测能力与传统时间序列模型的预测能力的差异, 提出基于神经网络类模型的集成学习时间序列预测模型, 提高了金融时间序列的样本外预测能力.

本文主要结论如下: (1) 神经网络类模型显著优于ARIMA模型和线性回归模型. LSTM和GRU模型在英国富士100和日经225等极少数股票指数上表现不如线性回归模型, 在其他股票指数上的表现显著优于ARIMA和AR等传统时间序列模型. NN、RNN和集成学习模型显著优于传统时间序列模型. (2) 基于神经网络类的集成学习模型在所有机器学习模型中表现最稳定, 在短期预测、中期预测和长期预测和全部股票市场指数上的表现显著优于传统时间序列模型. (3) 神经网络类模型和基于神经网络的集成学习模型在中国股票市场和美国股票市场中的表现显著优于其他发达国家股票市场.

本文的研究拓展了金融时间序列预测的理论研究, 为股票投资提供风险参考和入场出场时机参考. 在宏观上, 本文研究可以为投资者提供股票走势的预测和风险预测; 在微观上, 本文研究可以减少股票市场不必要的波动, 促进中国股票市场合理定价, 促进中国股票市场繁荣稳定发展.