三维网格模型在计算机图形学、计算机动画、虚拟现实等领域有着广泛应用, 然而复杂场景的三维模型极大地消耗了带宽资源、增加了处理时间, 不利于模型的存储、计算、渲染等. 因此, 通过使用相对简单的模型代替原始的高细节模型, 即对网格模型进行简化成为当前的主流方案[1]. 网格简化指通过删除或修改对视觉影响不大的点、边、面来减少网格面片数量[2], 对几何模型在各领域的应用有着重要意义.
自Clark[3]于1976年提出网格简化思想以来, 国内外学者对简化算法进行了广泛而深入的研究. 其中, 1997年由Garland和Heckbert提出的二次误差测度(QEM)算法是目前使用最广泛的网格简化算法之一. QEM算法运算速度快, 简化后的模型质量较高, 是一种兼顾速度、质量和通用性的较理想的算法[4]. 然而, 该算法仅以点到相关平面距离的二次方作为误差测度, 容易使简化后的模型失去局部特征和几何结构, 并且易产生狭长三角面, 导致渲染效果差. 针对上述问题, 很多学者提出改进方案. Kim等人[5]将离散曲率范数与距离度量结合共同作为边折叠代价, 保留了原始网格的高曲率区域. Tang等人[6]选择引入反向成本概念增加高、低曲率差异, 并选择中点作为新顶点使算法更简单、直观. 王继东等人[7]把三角形法向量约束因子嵌入误差矩阵中, 让体积变化平方作为误差度量, 并自动分配网格疏密, 保留模型局部特征. Li等人[8]提出考虑纹理的边缘折叠改进方法, 并提前计算模型边界以保留模型基本拓扑结构. Mao等人[9]利用平均二次误差代替累积误差作为折叠代价. Tang等人[10]引入高斯曲率作为简化因子, 以此保留网格细节特征.
综上所述, QEM算法的改进方向多是通过优化误差度量来保持三维网格模型特征, 没有重点解决简化后模型的三角面异常问题. 基于此, 本文提出一种结合边分割的网格简化算法. 实验表明, 该算法简化后的模型视觉效果更好, 高简化率下的模型精度更高.
1 QEM网格简化算法QEM算法实际上是一种基于边折叠的网格简化算法. 算法通过顶点对的迭代收缩来简化三维模型, 即选择合适的边进行折叠, 而边折叠顺序依赖于误差.
1.1 边折叠操作边折叠是一种基于网格边代价的迭代收缩算法. 该算法具有可逆性且折叠代价的计算和更新仅依靠局部信息, 使得算法效率较高.
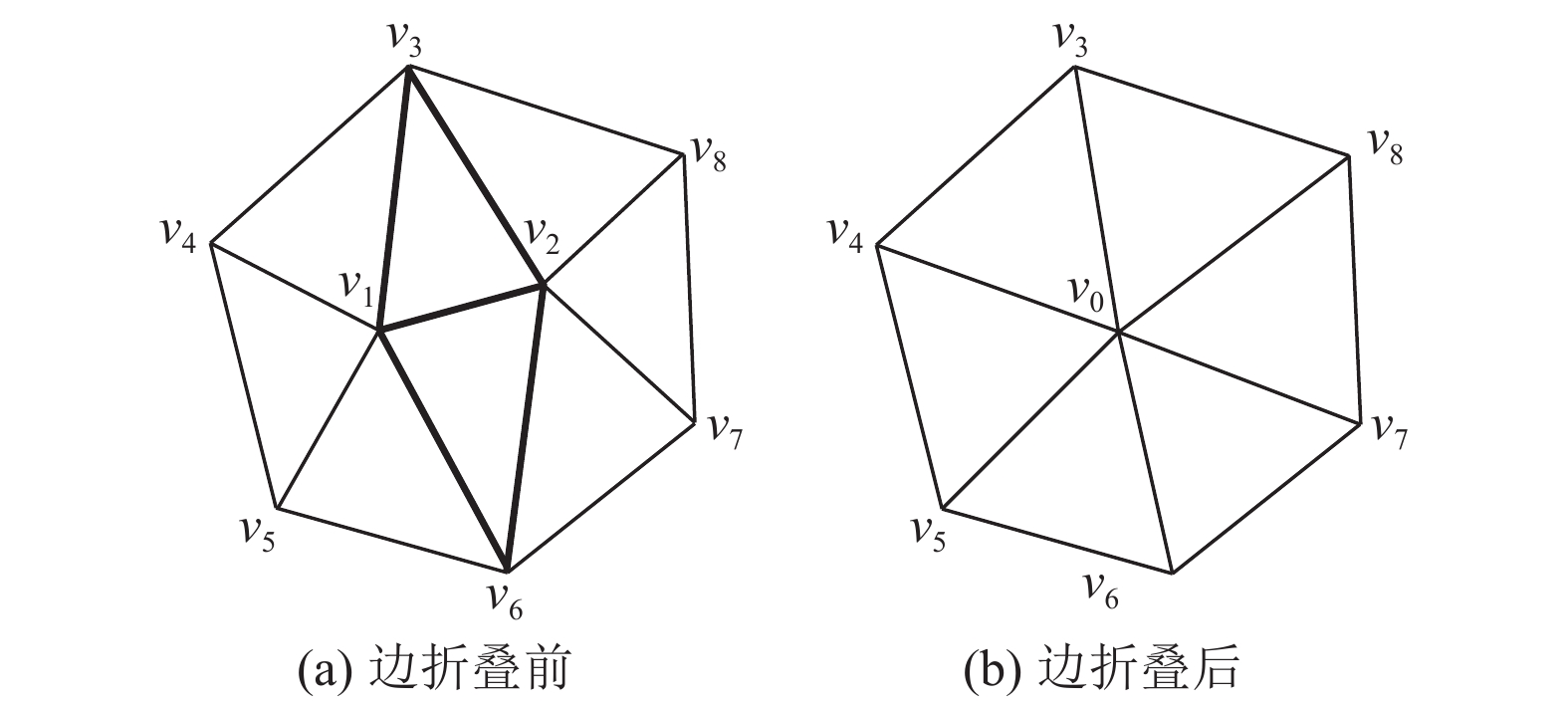
边折叠操作前提是计算三角网格边的折叠代价, 每次操作取出队列最顶端的边(即折叠代价最小的边), 进行边折叠操作[11]. 如图1所示, 边v1v2为选中的折叠代价最小的边.
|
图 1 边折叠示意图 |
根据边v1v2的两个端点v1、v2和局部信息计算出误差最小的新顶点v0的位置. 删除顶点v1、v2及两点所在三角网格v1v2v3和v1v2v6, 删除相应的边v1v3 、v2v3、v1v6、v2v6. 添加新顶点v0和新生成的边v0v3、v0v6, 更新顶点v0的局部顶点信息、边信息的拓扑结构. 重复上述步骤, 直至三角网格数量达到要求.
1.2 QEM算法QEM算法中的顶点对迭代收缩是边折叠的扩展, 顶点对的折叠代价即为边折叠代价. Garland等人[4]将顶点误差定义为点到点所在平面集距离的二次方和, 并用二次矩阵保留当前模型的每个顶点近似误差.
故预先对网格中的每一个顶点定义一个4×4的误差矩阵Q, 则顶点v=[vxvyvz 1]T的误差形式确定为其二次项(v)=vTQv. 将空间中的每个顶点与其所在平面相关联, 定义误差为点与平面集距离的二次方和, 如式(1)所示:
| $ \vartriangle \left( v \right) = \vartriangle \left( {\mathop {\left[ v_x \; v_y \; v_{\textit{z}} \; 1 \right]}\nolimits^{\rm{T}} } \right) = \displaystyle\sum\limits_{p \in {\textit{planes}}\left( v \right)} {\mathop {\left( {\mathop p\nolimits^{\rm{T}} v} \right)}\nolimits^2 } $ | (1) |
其中, planes(v)是包含顶点v的所有三角平面集; p=[a b c d]T表示由方程ax+by+cz+d=0所定义的平面, 且a2+b2+c2=1. 由式(1)中的误差度量可重写为二次形式:
| $ \begin{split}\Delta \left(v\right)&={\displaystyle \sum _{p\in {\textit{planes}}\left(v\right)}\left({{\displaystyle v}}^{\rm{T}}p\right)\left({{\displaystyle p}}^{T}v\right)}\\ &={\displaystyle \sum _{p\in {\textit{planes}}\left(v\right)}{{\displaystyle v}}^{\rm{T}}\left(p{{\displaystyle p}}^{\rm{T}}\right)v}\\ &={{\displaystyle v}}^{\rm{T}}\left({\displaystyle \sum _{p\in {\textit{planes}}\left(v\right)}{{\displaystyle K}}_{p}}\right)v\end{split} $ | (2) |
其中, Kp表示平面p的基本二次误差矩阵, 如式(3)所示:
| $ \mathop K\nolimits_p =p p^{\rm{T}} = \left[ {\begin{array}{*{20}{c}} {\mathop a\nolimits^2 }&{ab}&{ac}&{ad} \\ {ab}&{\mathop b\nolimits^2 }&{bc}&{bd} \\ {ac}&{bc}&{\mathop c\nolimits^2 }&{cd} \\ {ad}&{bd}&{cd}&{\mathop d\nolimits^2 } \end{array}} \right] $ | (3) |
通过Kp计算空间中任意顶点到该三角面的距离平方, 则顶点的二次误差矩阵Q可表示为:
| $ \mathop Q\nolimits_{\left( v \right)} = \sum\limits_{p \in {\textit{planes}}\left( v \right)} {\mathop K\nolimits_p } $ | (4) |
对于给定的顶点收缩对
| $ \mathop Q\nolimits_{\overline v } = \mathop Q\nolimits_{\mathop v\nolimits_1 } + \mathop Q\nolimits_{\mathop v\nolimits_2 } = \left[ {\begin{array}{*{20}{c}} {\mathop q\nolimits_{11} }&{\mathop q\nolimits_{12} }&{\mathop q\nolimits_{13} }&{\mathop q\nolimits_{14} } \\ {\mathop q\nolimits_{21} }&{\mathop q\nolimits_{22} }&{\mathop q\nolimits_{23} }&{\mathop q\nolimits_{24} } \\ {\mathop q\nolimits_{31} }&{\mathop q\nolimits_{32} }&{\mathop q\nolimits_{33} }&{\mathop q\nolimits_{34} } \\ {\mathop q\nolimits_{41} }&{\mathop q\nolimits_{42} }&{\mathop q\nolimits_{43} }&{\mathop q\nolimits_{44} } \end{array}} \right] $ | (5) |
| $ \Delta \left( {\overline v } \right) = \mathop {\overline v }\nolimits^{\rm{T}} \left( {\mathop Q\nolimits_{\mathop v\nolimits_1 } + \mathop Q\nolimits_{\mathop v\nolimits_2 } } \right)\overline v $ | (6) |
通过计算
| $ \overline v = \mathop {\left[ {\begin{array}{*{20}{c}} {\mathop q\nolimits_{11} }&{\mathop q\nolimits_{12} }&{\mathop q\nolimits_{13} }&{\mathop q\nolimits_{14} } \\ {\mathop q\nolimits_{21} }&{\mathop q\nolimits_{22} }&{\mathop q\nolimits_{23} }&{\mathop q\nolimits_{24} } \\ {\mathop q\nolimits_{31} }&{\mathop q\nolimits_{32} }&{\mathop q\nolimits_{33} }&{\mathop q\nolimits_{34} } \\ 0&0&0&1 \end{array}} \right]}\nolimits^{ - 1} \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ 1 \end{array}} \right] $ | (7) |
当
综上, QEM算法边折叠代价实则为顶点对(v1v2)收缩后产生的新顶点
针对原始QEM网格简化算法所存在的问题引入高斯曲率算子和边缘分割操作, 提出结合边分割的二次误差测度(ESQEM)算法.
首先, 只考虑距离度量的QEM算法会使简化后的网格和顶点均匀分布, 不利于边缘特征保留. 因此将能反应顶点尖锐度的顶点高斯曲率加入二次误差度量中, 并提取和保留网格模型边界点, 以此维护高曲率区域特征和几何结构. 其次, 在简化过程中添加边长查询机制, 根据网格模型平均边长设置目标长度、边中点作为分割点, 对异常三角形进行边分割操作, 以此消除不规则的边.
2.1 添加高斯曲率算子高斯曲率反应了曲面局部弯曲程度, 三角网格上某点的高斯曲率反应该点的尖锐程度, 因而不均匀区域和特征边缘的高斯曲率较大. 本文采用Kim等人[12]提出的方法来计算网格中内顶点和边界顶点的高斯曲率, 顶点高斯曲率与其相连的角度和面积有关, 如图2.

|
图 2 顶点高斯曲率 |
图2中θi是三角形fi的内角, 三角形面积用Si表示, n表示与顶点v相连的三角形个数. 则三角网格中内顶点和边界顶点的高斯曲率计算公式如式(8)、式(9)所示:
| $ K({{v}}){\rm{ = }}\frac{{2\pi - \displaystyle\sum\limits_{i = 1}^{{n}} {\theta _i} }}{{\dfrac{1}{3}\displaystyle\sum\limits_{i = 1}^n {S_i} }} $ | (8) |
| $ K({{v}}){\rm{ = }}\frac{{\pi - \displaystyle\sum\limits_{i = 1}^{{n}} {\theta _i} }}{{\dfrac{1}{3}\displaystyle\sum\limits_{i = 1}^n {S_i} }} $ | (9) |
若边e由顶点v1和顶点v2组成, 而边的高斯曲率与边上的顶点相关[13], 则e的高斯曲率可通过式(10)计算:
| $ K\left( e \right) = \left| {K\left( {\mathop v\nolimits_1 } \right)} \right| \times \mathop \omega \nolimits_1 + \left| {K\left( {\mathop v\nolimits_2 } \right)} \right| \times \mathop \omega \nolimits_2 $ | (10) |
其中, K(v1)和K(v2)分别代表边e两个端点v1和v2的高斯曲率, 且权重ωi可通过式(11)计算:
| $ \mathop \omega \nolimits_i = \frac{{\displaystyle\sum\limits_{i = 1}^n {\mathop s\nolimits_i \left( {\mathop v\nolimits_i } \right)} }}{{\displaystyle\sum\limits_{i = 1}^n {\mathop s\nolimits_i \left( {\mathop v\nolimits_1 } \right) + \displaystyle\sum\limits_{i = 1}^n {\mathop s\nolimits_i \left( {\mathop v\nolimits_2 } \right)} } }} $ | (11) |
在QEM算法中, 选择最小的边代价进行边缘折叠操作, 以获得最佳近似结果. 当在边折叠代价中加入高斯曲率算子后, 便能有效规避具有显著特征的边被折叠. 将二次误差和高斯曲率结合, 获得新的边塌陷成本, 如式(12)所示:
| $ {Cos} t\left( e \right) = K\left( e \right) \times \omega + Q\left( e \right) $ | (12) |
其中, 权重ω用来平衡高斯曲率K(e)和二次误差Q(e), 且ω可通过式(13)计算:
| $ w = \frac{{a \times \mathop Q\nolimits_{\rm{avg}} }}{{\mathop K\nolimits_{\rm{avg}} }} $ | (13) |
其中, Qavg和Kavg分别是所有边的平均二次误差和平均高斯曲率, 而参数a用于调整K(e)和Q(e)的数量级关系, 通常将高斯曲率设为比二次误差小两个数量级.
2.2 边分割策略边分割是三角剖分的一种经典操作. 实质是将离散的点集连接成一定大小的三角形, 而Delaunay三角剖分的应用最为广泛. Dyer等人[14]定义非Delaunay边为两个对角之和大于π的边, 并通过递归分割非Delaunay边将任意一个流形三角网格转化为Delaunay网格; Liu等人[15]考虑到非Delaunay边的蝴蝶形区域提出了一种计算最优分割点的方法. 张顺岚等人[16]利用Delaunay三角形剖分技术实现了战场仿真模型的局部三角化. 若对已知三维网格中进行边分割操作需要确定要分割的边及分割点的位置.
因此, 为了消除由QEM算法产生的狭长三角面, 提出一种基于网格边长的边分割方法. 该方法对简化后网格的边进行遍历以获取边长信息, 根据网格平均边长求出目标长度, 并将目标边的中点作为分割点进行边缘分割操作, 边分割流程如图3所示.

|
图 3 基于网格边长的边分割流程图 |
Step 1. 读取三维网格模型;
Step 2. 计算网格平均边长AvgLength, 令目标长度TargetLength为b倍AvgLength. 其中, 倍数b可根据实际模型做适当调整;
Step 3. 遍历网格中的每条边, 获取每条边的长度EdgeLength;
Step 4. 判断边长是否大于目标长度, 若EdgeLength大于TargetLength, 进入Step 5, 否则跳至Step 8;
Step 5. 计算当前边的中点位置, 设中点为分割点vertex_split;
Step 6. 获取当前边所在三角面的顶点坐标v[0]、v[1]、v[2]、v[3];
Step 7. 删除以点v[0]、v[1]、v[2]和v[0]、v[2]、v[3]组成的2个旧三角面, 添加由点v[0]、v[1]、vertex_split, 点v[1]、v[2]、vertex_split, 点v[2]、v[3]、vertex_split和点v[3]、v[0]、vertex_split组成的4个新三角面;
Step 8. 判断当前边是否为最后一条边, 如果是则进入Step 9, 否则跳至Step 3;
Step 9. 保存边分割后的网格信息;
Step 10. 输出模型.
2.3 算法描述综上所述, 改进的二次误差测度算法描述如算法1.
算法1. ESQEM算法
1) 读取网格文件, 获取原始三维网格信息.
2) 遍历网格中的每个顶点, 计算每个顶点的二次误差矩阵Q.
3) 区分网格内顶点和边界顶点, 根据式(8)和式(9)计算内定点和边界顶点的高斯曲率, 并根据式(10)计算每条边的高斯曲率.
4) 计算
5) 边折叠操作. 从堆顶删除代价最小的边, 添加新顶点
6) 边分割操作. 遍历网格的每条边, 当EdgeLength大于TargetLength时, 删除两个旧的三角面, 同时根据顶点和中点位置添加4个新的三角面; 当EdgeLength小于TargetLength时, 继续判断下一条边, 直至循环结束.
7) 保存简化后的网格模型.
算法1不但可以通过参数ω调整网格特征保留情况, 还能通过边长判断异常三角面. TargetLength通常为AvgLength的4/3倍, 也可以根据原始网格模型调整最佳TargetLength值, 使简化后的三角面更均匀.
3 实验分析实验分别采用QEM算法和ESQEM算法对Cow模型和Dinosaur模型进行简化, 通过对比两种算法的简化效果及简化前后的Hausdorff距离来验证ESQEM算法在维持模型边缘、避免异常三角面和保留局部特征方面比原始算法更有效.
3.1 简化效果对比ESQEM算法是基于VS 2019开发平台在QEM算法源码基础上进行改进的. 为增加可信度, 实验所测试机相同(Intel(R) Core(TM) i5-8265U CPU 1.60 GHz, RAM 8 GB), 输入数据相同, 控制参数相同, 且未对改进算法做任何加速处理. 为保证在相同简化率的情况下进行比较, 参数ω允许的最大误差不超过0.01个精度, 参数b为固定值. 简化后模型以白模和网格两种形式进行整体和局部对比展示, 随着简化率增高, 网格模型信息不断变动, 表1为实验过程中的网格数据.
| 表 1 实验模型数据基本信息 |
Cow的原始模型如图4所示. 采用两种算法对Cow模型进行简化, 结果见图5和图6. 由图4可知, 简化后的模型边缘始终保持完整, 从图5(a)到图5(c)简化率由58.03%升到82.77%, 此过程中模型逐渐变得棱角分明, 却并无异常面和异常拓扑产生. 当简化率超过90%时, 图5(d)中牛的脚部和面部特征出现模糊, 但曲率更高的牛角处仍然清晰可见, 且未产生细长三角面. 对比图6(d), 当使用QEM算法简化率超过90%时, 牛的脚部及面部特征退化, 而牛角的上半部分直接消失, 此外还产生了多个细长三角面. 而图6(c)中, 虽然边缘特征仍在, 但出现孔洞及异常三角面.

|
图 4 Cow原始模型 |
为了更清晰的观察两种算法的简化效果, 将Cow模型的局部位置进行放大比较. 如图7、图8所示, 图7(a)和图7(b)为Cow模型在简化率为58.03%时的背部对比图, 图8(a)和图8(b)为Cow模型在简化率为92.69%时的头部对比图. 可以看出, ESQEM算法能消除异常三角面和保留高曲率特征.
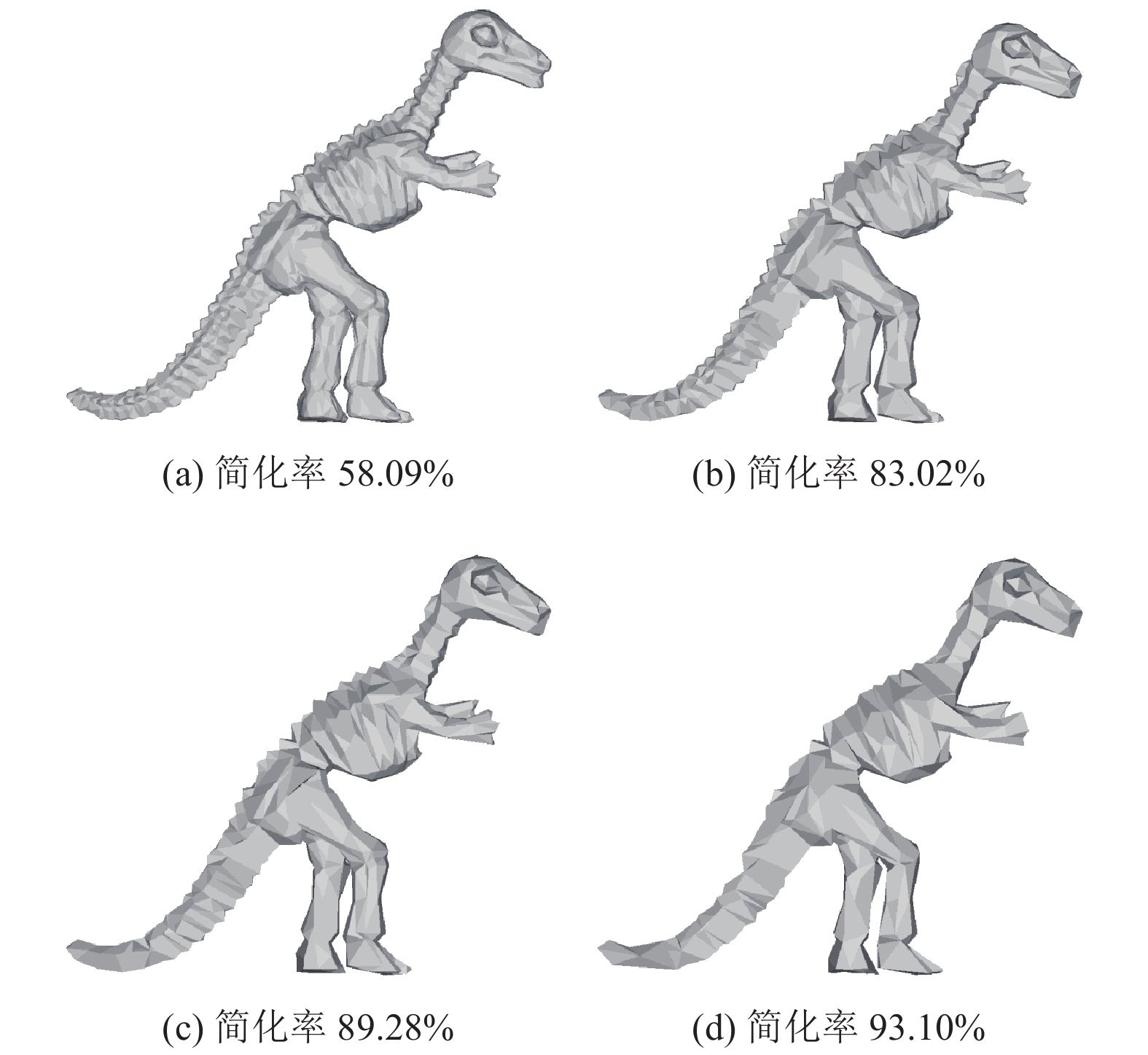
Dinosaur的原始模型如图9所示. 图10为ESQEM算法对Dinosaur模型的简化效果图, 图10(a)到图10(c)的简化率从58.09%到89.28%, 在此过程中模型外表逐渐锋利, 但几何结构与局部特征依旧清晰可辨. 而当简化率超过90%时, 从图10(d)可以看出模型面部、手部等轮廓依旧清晰, 且三角面和拓扑也并无异常. 图11为QEM算法对Dinosaur模型的简化效果图, 从图11(a)到图11(d)的模型轮廓无显著变化, 但在简化过程中产生了细长三角面. 并且当简化率超过90%时, 由图11(d)明显看到, 模型部分手部特征消失, 恐龙的爪子由3个退化成2个.
为了更清晰的对比两种算法的不同效果, 将Dinosaur模型的局部位置进行放大比较. 图12和图13是简化率为93.10%时, Dinosaur模型的背部和手部对比图, 从红圈标注的位置可以看出, ESQEM算法不仅能更多地保留模型局部特征, 还能将较大的三角面进行分割.

|
图 5 Cow模型ESQEM算法简化结果 |

|
图 6 Cow模型QEM算法简化结果 |
3.2 Hausdorff距离对比
Hausdorff距离是用来测量欧氏空间中两个点集之间距离的一种量度. 在三维网格模型简化过程中, 通常使用Hausdorff距离来比较简化前和简化后模型的相似程度, Hausdorff距离越小, 则简化前后的模型就越相似, 精度就越高, 反之, 简化模型的精度就越低. 因此, 在使用两种不同算法的情况下, 计算简化前后模型的Hausdorff距离, 能有效对比ESQEM算法和QEM算法简化后的模型精度. 图14和图15为两种算法简化Cow模型和Dinosaur模型的Hausdorff距离值. 其中, 横坐标代表模型简化率, 纵坐标代表Hausdorff距离.

|
图 7 Cow模型背部对比图 |

|
图 8 Cow模型头部对比图 |

|
图 9 Dinosaur原始模型 |
由图14可知, 当简化率低于75%时, 使用ESQEM算法得到的模型精度整体略低于QEM算法.尤其当简化率在35%–75%时, Hausdorff距离相差较大. 然而, 当到简化率超过75%时, ESQEM算法的精度开始高于QEM算法, 且简化率越大, 精度越高.
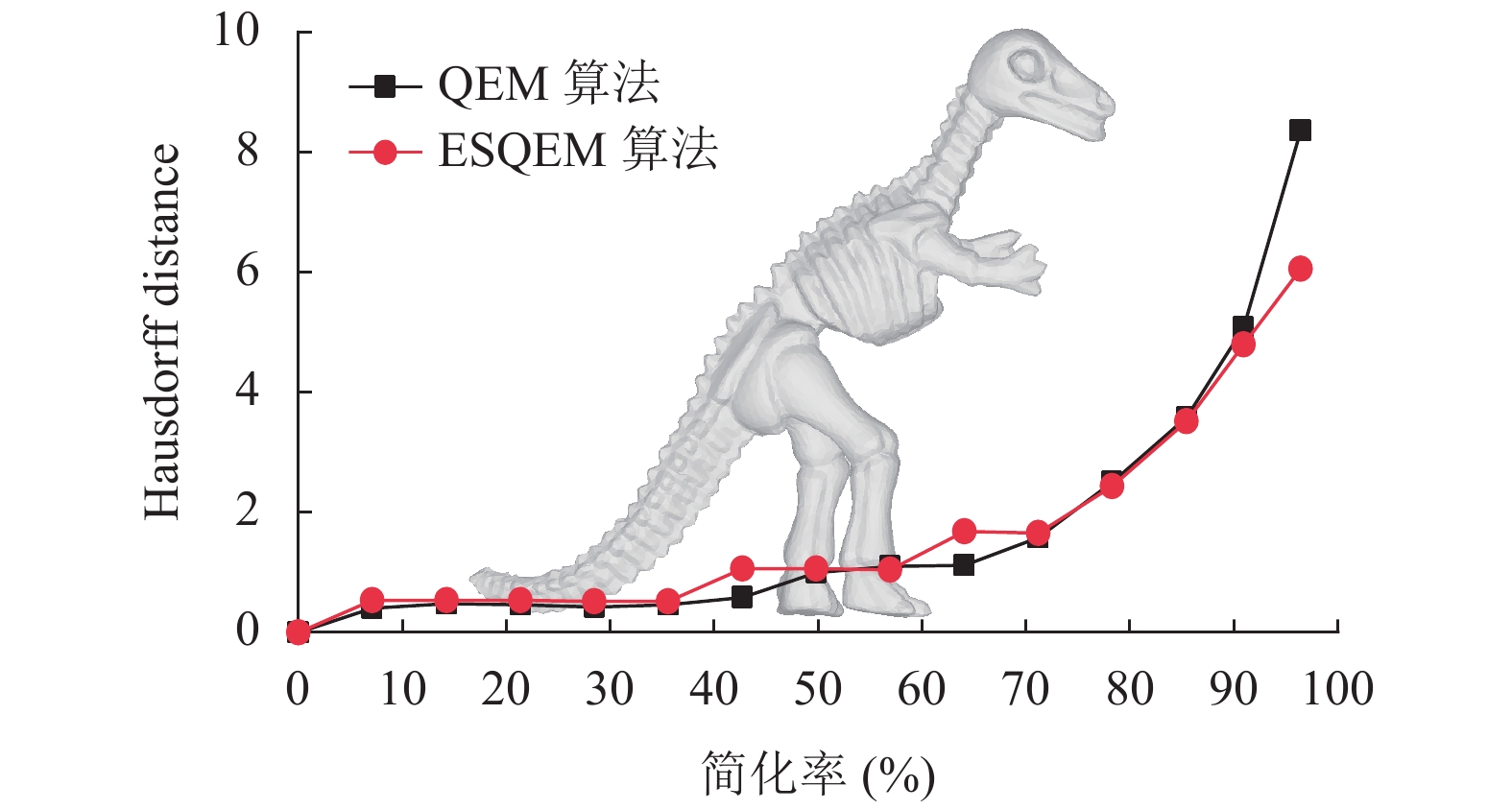
图15反映了相似的情况, 前期简化率较低时, 两种算法的Hausdorff距离值相差不大. 简化率在50%左右时, 使用ESQEM算法所得的Hausdorff距离值出现波动, 模型精度不够稳定. 当简化率超过70%时, 使用ESQEM算法所得模型精度开始高于QEM算法. 综上所述, ESQEM算法更适合高简化率的简化需求, 模型所需面数越少, ESQEM算法较QEM算法的优势就越大.

|
图 10 Dinosaur模型ESQEM算法简化结果 |
|
图 11 Dinosaur模型QEM算法简化结果 |

|
图 12 Dinosaur模型背部对比图 |

|
图 13 Dinosaur模型手部对比图 |

|
图 14 Cow的Hausdorff距离 |
|
图 15 Dinosaur的Hausdorff距离 |
4 结论与展望
针对QEM算法难以保留简化后模型的细节特征、几何结构和容易产生异常三角面等缺点, 提出一种结合边分割操作的改进算法(ESQEM). 该算法加入了高斯曲率算子和长边分割操作, 在维持几何结构的基础上, 通过调整参数保留模型局部特征、优化异常三角面. 实验证明ESQEM算法具有更好的简化效果, 能更多的保留模型细节、均匀三角面, 并在高简化率的条件下, 简化后的模型精度比QEM算法更高. 在接下来的研究中, 将会考虑重新计算边的分割点. 如第3.2小节所示, 仅以边中点作为分割点无法在低简化率条件下保证模型精度. 为了在简化过程中始终能得到较高精度的模型, 后续会考虑引入边分割代价, 以保证新的分割点与原始模型相同位置的点最接近.
| [1] |
黄飞鸿. 基于法向量和体积的半边折叠简化算法. 计算机应用研究, 2020, 37(S1): 334-336. |
| [2] |
董方敏, 张蕊, 刘勇, 等. 网格模型简化算法综述. 中国学术期刊文摘, 2007, 13(14): 8. |
| [3] |
Clark J. Hierarchical geometric models for visible surface algorithms. Communications of the ACM, 1976, 19(10): 547-554. DOI:10.1145/360349.360354 |
| [4] |
Garland M, Heckbert P S. Surface simplification using quadric error metrics. Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 1997. 209–216.
|
| [5] |
Kim SJ, Kim CH, Levin D. Surface simplification using a discrete curvature norm. Computers & Graphics, 2002, 26(5): 657-663. DOI:10.1016/S0097-8493(02)00121-8 |
| [6] |
Tang Z, Yan S, Lan C. A new method of mesh simplification algorithm based on QEM. Information Technology Journal, 2010, 9(2): 391-394. DOI:10.3923/itj.2010.391.394 |
| [7] |
王继东, 张芸, 杨斌. 一种新的边折叠网格模型简化算法. 计算机工程与应用, 2013, 49(1): 195-198. DOI:10.3778/j.issn.1002-8331.1105-0364 |
| [8] |
Li XX, Wan WG, Wang L. Using canny algorithm in QEM simplification for textured 3D models. IET International Communication Conference on Wireless Mobile and Computing (CCWMC 2011). Shanghai: IET, 2011. 315–319.
|
| [9] |
Mao YL, Yang J, Zhu BP, et al. A new mesh simplification algorithm based on quadric error metric. 2015 IEEE 5th International Conference on Consumer Electronics-Berlin (ICCE-Berlin). Berlin: IEEE, 2015. 463–466.
|
| [10] |
Tang Y, Zhang QC. Edge-collapse mesh simplification method based on Gauss curvature. 2011 International Conference on Internet of Things and 4th International Conference on Cyber, Physical and Social Computing. Dalian: IEEE, 2011. 660–662.
|
| [11] |
李世俊, 姜晓彤, 唐慧. 保持细节特征的带纹理模型的高质量简化算法. 计算机应用研究, 2020, 37(1): 300-303, 312. DOI:10.19734/j.issn.1001-3695.2018.04.0481 |
| [12] |
Kim SJ, Jeong WK, Kim CH. LOD generation with discrete curvature error metric. Proceedings of 2nd Korea Israel Bi-National Conference on Geometrical Modeling and Computer Graphics in the WWW Era. 1999. 97–104.
|
| [13] |
Liang YQ, He FZ, Zeng XT. 3D mesh simplification with feature preservation based on whale optimization algorithm and differential evolution. Integrated Computer-Aided Engineering, 2020, 27(4): 417-435. DOI:10.3233/ICA-200641 |
| [14] |
Dyer R, Zhang H, Möller T. Delaunay mesh construction. Proceedings of the 5th Eurographics Symposium on Geometry Processing. Goslar: Eurographics Association, 2007. 273–282.
|
| [15] |
Liu YJ, Xu CX, Fan D, et al. Efficient construction and simplification of Delaunay meshes. ACM Transactions on Graphics (TOG), 2015, 34(6): 1-13. DOI:10.1145/2816795.2818076 |
| [16] |
张顺岚, 刘钊, 韩传久. 基于点删除网格简化算法在战场仿真中的应用. 计算机系统应用, 2005, 14(4): 28-31. DOI:10.3969/j.issn.1003-3254.2005.04.008 |
 2022, Vol. 31
2022, Vol. 31


