网约车是一种新兴的共享出行服务, 可显著提高城市交通容量, 例如, 中国的一个主要网约车平台在 2020 年的日出行量已超过 5000 万^[1]. 网约车服务由司机、乘客和平台组成, 平台将乘客提交给司机与出租车请求进行匹配, 出租车请求和司机之间匹配, 也就是任务分配, 是网约车研究的核心问题^[2].

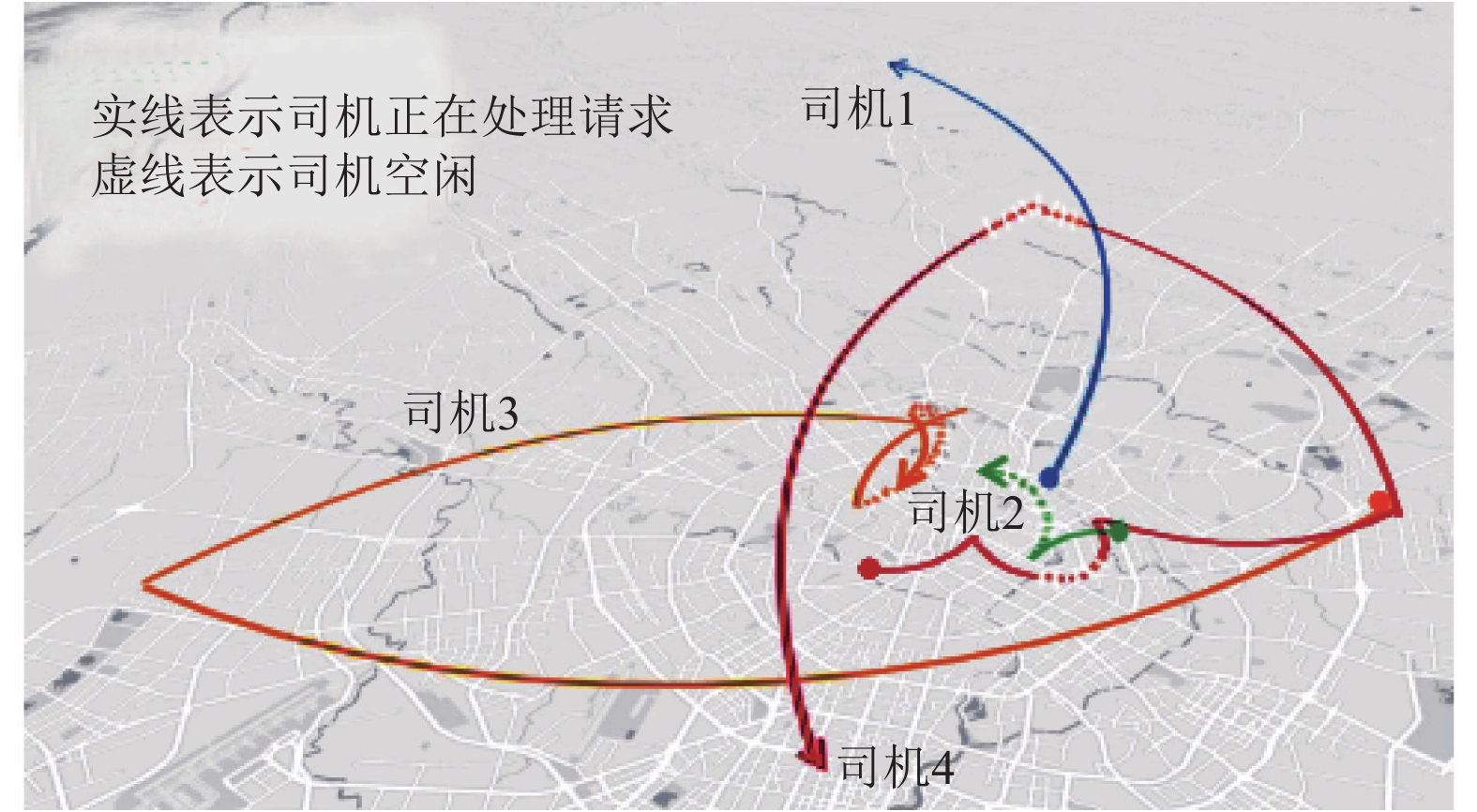
现有研究主要从平台或乘客的角度优化任务分配, 而很少从驾驶员的角度研究问题, 例如, 已经设计了许多分配算法来最大化效用^{[2, 3]}或最小化旅行成本^[4]或乘客的等待时间^[5], 直到最近, 先行工作^[6]才探索司机的收益公平性, 例如在任务分配期间平衡司机之间的收入. 本文认为, 盲目地将司机分配到最大化效用的任务可能会损害司机之间显著的收入差距^[7]. 图1通过仅最大化效用的分配算法模拟了4个驾驶员的轨迹, 司机1首先被分配一个请求, 该请求在偏远区域结束, 完成这个订单后, 他很难回到繁忙的地区, 导致他每小时收入很低; 相比之下, 司机3很幸运, 在繁忙区域结束一个订单后, 又立即被分配到另一个繁忙区域请求, 他可以获得更高的每小时收入; 司机2留在繁忙区域, 但很少被分配到请求, 长时间的空闲时间导致他低小时收入; 相比之下, 司机4碰巧被分配了许多请求, 而且空闲时间短有助于提高每小时收入. 司机之间的这种每小时收入差距(在本例中为司机 1、司机2 与司机 3、司机4)可能会使司机气馁并导致不公平的任务分配.

尽管在云计算中的负载平衡^[8]等应用领域中, 任务分配的公平性得到了广泛的研究, 但网约车中的公平任务分配面临着独特的挑战: (1) 在线设置: 网约车是一种双向在线分配场景, 具有高时空依赖性和变化^[9]; (2) 双目标优化: 一个理想的网约车分配算法应该在各种实际约束下优化司机之间的效用和公平性; (3) 高效率要求: 现实世界的网约车平台需要对城市规模的数据进行快速分配. 最先进的网约车公平分配算法^{[6, 10]}未能解决所有这些挑战. 首先, 这些解决方案是短视的, 也就是说, 他们忽略了当前分配对未来分配的影响, 这在很大程度上缩小了优化空间, 从而显著降低了可实现的效用和公平性; 其次, 它们要么依赖于线性规划^[6], 要么需要多轮重新分配^[10], 这使得它们对于大规模数据的实时响应效率低下.

本文提出了公平分配学习(learning to assign with fairness, LAF)方法, 一个有效和高效的任务分配方案, 优化了效用(以所有司机的期望总收入衡量)和公平(以司机之间的时间收入公平衡量). LAF通过强化学习, 学习未来感知分配策略, 明确地说明了作业之间的依赖性, 这种学习分配策略可以整体优化效用和公平性. 为了实现高效分配, LAF将公平性和效用优化嵌入到相同的赋值操作中, 并利用二部图的稀疏性进一步加速. 值得一提的是, 本文提出了一个加权平摊公平度量而不是传统的未加权^[6]来表征司机在更细的时间粒度上的收入公平性, 如小时收入公平性.

评价结果显示, 在公平和效用方面, 比普通水平分别提高了45.7%–86.7%和7.7%–29.1%^{[6, 10]}. 本文的LAF也比文献[6, 10]快到700. 本文主要贡献如下:

(1)据本文所知, 这是第一个明确考虑当前和未来任务之间的依赖性的工作, 以提高公平的任务分配在网约车服务的表现;

(2)提出了一种新的基于强化学习的公平任务分配方案LAF, 该方案适应高度动态的交通, 符合实际设置, 适合大规模的网约车应用;

(3)广泛的评估表明, 本文的LAF在公平性、效用和效率方面远远优于最先进的文献[6, 10].

本文其余部分组织如下: 第1节回顾相关工作, 第2节介绍本文的问题, 第3节解释本文的方法, 第4节给出评估, 第5节进行总结.

1 相关工作

本文的工作主要涉及两个研究方向: 网约车中的任务分配和分配问题的公平性.

1.1 任务分配

由于打车服务在大城市的快速扩张, 引起了广泛的研究兴趣, 其中一个核心课题是为特定的优化对象向司机分配打车请求. 网约车的共同目标包括最大化利润^{[3, 11]}、最小化旅行成本^{[9, 12]}、最小化乘客等待时间^{[1, 5]}等. 许多任务分配算法关注于提供理论上的性能保证^[5], 然而, 他们经常会做出假设——比如司机和任务之间的独立性, 这往往会阻止他们在现实世界的应用程序中实现预期的性能. 一个很有前途的替代方案是, 在很少的假设下, 自动学习从历史数据中优化分配, 例如, 文献[13]最近的一些工作通过使用强化学习优化效用实现了最先进的性能. 在这项工作中, 本文也针对适合大规模应用的实际任务分配算法, 但本文是第一个设计基于强化学习的解决方案, 以优化效用和公平性.

1.2 分配任务的公平性

在各种应用中, 公平一直是分配问题的一个重要因素^{[14, 15]}. 关于公平分配的研究可以根据任务和员工是静态的还是动态的而分为两类. 在静态公平任务分配中, 工作者和任务都是静态的; 动态公平分配比较困难, 因为其中一方或双方都是动态的, 这个设置适用于云计算^[16]和Web请求分配^[8]等应用程序, 它们的目标是平衡服务器的负载. 一些工作(如文献[17])研究了空间众包中的公平分配, 公平意味着员工承担相同数量或价值的任务, 这个公平的目标不适合网约车, 因为不同的出租车司机有不同的工作时间.

网约车公平属于动态公平分配问题, 特别令人感兴趣的是司机收入的公平性^{[6, 10]}. 由于任务和司机的强烈时空动态, 网约车中的公平分配具有挑战性. 在这项工作中, 本文提出了一种新的驾驶员收入公平指标, 该指标解释了这种时空动态, 并设计了高效且有效的分配算法, 其性能明显优于最先进的公平分配算法^{[6, 10]}.

2 问题陈述

与之前的研究(文献 [6, 10]) 一样, 本文考虑将司机批量分配给请求, 令W和R是感兴趣的时间范围T中的司机和请求的集合, 在每个批次t中, 该批次中可用的请求R(t)和司机W(t)之间的分配被表述为二部图匹配问题, 以优化效用和公平性, 批量设置在现实世界的大规模乘车应用中被广泛采用^{[2, 13]}.

定义1 (请求). 一辆出租车请求r∈R, 表示为一个元组< $ {o_{r, }}{d_r}, {p_r}, {\tau _r} $ >, $ {o_{r, }}\;{d_r},\; {p_r},\; {\tau _r} $ 分别代表出发地、目的地、价格和持续时间.

在现实世界的网约车应用中, 请求的来源和目的地由乘客输入并上传到平台上, 本文对请求的来源和目的地不作任何假设, 平台收到请求后, 根据行程距离和交通拥堵等因素, 确定价格并估计请求持续时间, 为简单起见, 本文假设持续时间是t的倍数, 如果请求被分配给一个司机, 则比值p_r/τ_r决定他的每批收益, 本文将在下面解释.

定义2 (司机). 一个出租车司机w∈W表示为一个元组< $ \ell _w^{(t)}, u_w^t, a_w^{(t)} $ >, $ \ell _w^{(t)}, \;u_w^t,\; a_w^{(t)} $ 分别代表当前位置、收入和第t批次的状态.

状态 $ a_w^{(t)} $ 为0或1的二进制指示灯, $ a_w^{(t)} $ = 0, 代表司机处于非活动状态, 即不在平台上; $ a_w^{(t)} $ = 1代表司机是活动的, 它可以是空闲的或服务一个请求. 本文假设 $ a_w^{(t)} $ 在一个批处理中保持不变, 因为实际批处理的大小很小(例如2 s). 如果司机处于空闲状态, 则收益为 $ u_w^{(t)} $ = 0, 如果批量发送请求r, 则收益为 $ a_w^{(t)} $ =p_r/τ_r. 不像先前的研究^{[9, 5]}, 假设独立的司机跨批分布, 本文考虑一个更现实的依赖司机设置, 即未来批次的司机分布受当前批次司机分布和当前分配的影响.

定义3 (二部图). 本文使用二部图G^(t)= < R^(t), W^(t), E^(t)>, 表示候选人之间的作业司机和第t批次的请求, 节点集R^(t) 请求被分配到第t批次的可用司机W^(t). 如果请求r可以分配给司机w, 则有一个边(r, w)∈E^(t), 带有一个权重θ_{r, w}.

根据之前关于网约车^[11]中任务分配的研究, 为了避免乘客等待时间过长, 只有当请求-司机距离在某一阈值内时才存在优势. 本文还为每条边(r, w)指定了一个拒绝率λ_r,w, 以考虑其他与用户体验相关的因素, 距离阈值和拒绝率由平台设置, 权重θ_r,w初始设定为请求r的价格p_r.

本文的目标是为每个批次t∈{1, 2, ···, T}找到一个匹配M^(t)的候选分配G^(t), 优化总效用和时间收入公平性, 定义如下.

定义4 (总效用). 给定可重用的司机集W和动态出现的请求集R, 总实用程序是所有司机在T批之前的预期累积收益, 即:

$ U = \sum\limits_{w \in W} E \left[ {\sum\limits_{t \in T} {u_w^{(t)}} } \right] $

(1)

其中, E[·]代表期望, 司机w的期望累计收益 $ E\left[ {\displaystyle\sum\limits_{t \in T} {u_w^{(t)}} } \right] $ 由匹配结果决定:

$ E\left[ {\sum\limits_{t \in T} {u_w^{(t)}} } \right] = \sum\limits_{t \in T} {} \sum\limits_{(r, w) \in {M^{(t)}}} {(1 - {\lambda _{w, r}}} ) \cdot {p_r} $

(2)

本文最大化U以优化司机的整体收益.

采用摊销公平性^[6]的概念来描述驾驶员之间的时间收益公平性, 摊销公平性是指驾驶者在活动时间 $\displaystyle \sum t \in {T^{u_w^t}}\Bigg/\displaystyle\sum t \in {T^{a_w^t}} $ 期间的累计收益, 然而, 本文认为, 这种朴素的平摊公平可能对有不同工作时间偏好 (例如白天、晚上或高峰时间)的司机不公平, 由于一天中不同时间的出租车需求不同, 潜在收益也不同, 因此, 实行与活动时间成比例的平等收入会导致司机之间的收入不平等, 例如主要在白天工作的司机和主要在晚上工作的司机. 作为补救措施, 本文建议使用如下定义的加权平公平平摊.

定义5 (加权公平平摊). 驾驶员w的加权摊销公平性为其累计收益除以其加权活跃时间:

$ {F_w} = \tfrac{{\displaystyle\sum {t \in {T^{u_w^{(t)}}}/{\xi ^{(t)}}} }}{{\displaystyle\sum {t \in {T^{a_w^{(t)}}}} }} $

(3)

其中, ξ^(t)是与收益相关的权重, 用于将一天中不同时段的潜在收益变化正常化, 通常, 关注的时间范围T是一天, 批次t以秒为刻度(例如2 s), 时间权重ξ^(t)以每小时为基础变化, 这是因为报告显示, 出租车司机在决策时关注小时和日工资, 研究表明出租车需求按小时大幅波动. 为简单起见, 本文使用包含批次t的当前小时内司机收入的中位数为ξ^(t).

为了量化各司机间的公平性分布, 本文定义了基于权重摊销的时间收益公平性, 如定义6所示.

定义6 (时间收益公平). 给定可重用的司机集W和动态出现的请求集R, W之间的时间收益公平性由加权平摊公平性的熵变量来度量:

$ F = - \sum\limits_{w \in W} \log \left(\frac{{{F_w}}}{{{{\max }_w} \in {W^{{F_w}}}}} \right) $

(4)

较大的F表示驾驶员之间的分散加权平摊公平, 即高收入不平等. 因此, 本文的目标是最小化F.

对大型网约车应用的总效用U和时间收益公平性F进行分析是具有挑战性的, 以往的解决方案^{[6, 10]}有以下局限性:

(1)忽视当前和未来作业之间的时间依赖性: 许多现有的建议通过假设新司机在时间范围内独立到达来简化问题设置. 然而, 司机在下一批中的可用性和位置会受到当前批中的分配的影响, 这种依赖关系会影响效用和公平性的优化, 特别是在短期内, 出租车的供需可能会在空间和时间上发生剧烈波动.

(2)对于大规模应用程序来说效率低下: 以往的研究采用线性规划的方法来解决双目标匹配问题, 这可能会导致大规模叫车的实时响应速度较慢.

3 建议的方法

在本节中, 介绍了LAF方法, 这是一种新的解决方案, 用于优化大规模网约车应用的总效用和时间收入公平. LAF采用一种基于强化学习的重新加权方案, 明确地考虑了匹配过程中当前和未来任务之间的时间依赖性. 该方案采用在线方式实现, 以适应出租车供需的动态变化. LAF还包含了一组剪枝和加速策略, 用于大规模数据上的高效双目标(效用和公平性)分配. 本文在第3.1节对LAF进行了概述, 并在第3.2节和第3.3节详细阐述了细节.

3.1 公平分配学习(LAF)概述

LAF由一个基于学习的重新加权模块和一个有效的双目标分配模块组成, 见图2.

在每个批次中, 基于学习的重新加权模块首先考虑分配之间的时间依赖性, 重新调整给定二部图的边权重, 然后高效的双目标分配模块通过公平增强和其他加速技术找到分配, 最后, 基于学习的重新加权模块根据分配结果更新权重, 并在必要时引导空闲驾驶员.

基于学习的重新加权模块(第 3.2 节)细化二部图中的边权重, 这些边权重被初始化为旅行价格(见定义 3), 以反映当前分配对未来效用和公平性的影响, 权重细化策略是通过在线强化学习获得的, 本文还设计了一个驾驶员指导方案来缓解在线学习的冷启动问题.

高效的双目标分配模块(第 3.3 节)将出租车请求分配给司机, 同时考虑实用性和公平性, 它的核心是公平增强算法, 它应用 Kuhn-Munkres 算法^[18]来最大化效用并检查司机的收入率以确保公平.

在每个批次中, LAF 分4个阶段运行: 评估、分配、指导和学习(如图2), 每个批次都从评估开始, 给定一个边权重由旅行价格初始化的二部图, 基于学习的重新加权模块将更新权重, 以便权重反映当前和未来的收益, 然后在分配阶段, 高效的双目标分配模块在细化的二部图上计算新的匹配, 同时考虑效用和公平性. 由于: (1) 更新的权重考虑了当前分配对未来分配的影响; (2) 分配算法是双目标的, 因此产生的分配以整体方式优化了效用和公平性; 最后是学习和指导阶段. 重新加权模块将从匹配结果中学习以改进其下一批的重新加权策略, 并引导空闲驾驶员到繁忙区域以避免在线学习的冷启动.

3.2 基于学习的重新加权

本小节解释了如何应用在线强化学习来模拟当前分配对未来效用和公平性的影响, 第3.2.1节介绍基本公式, 第3.2.2节至第3.2.4节讨论实际问题, 第3.2.5节介绍完整的设计.

3.2.1 基于在线强化学习的公式

强化学习^[8] 是一种智能体, 随时间与环境交互的学习方法, 代理每一步都采取行动并从环境中获得奖励, 基于奖励, 代理更新其价值函数 $ V_w^\pi $ , 如果代理按照策略 π 采取行动, 该函数将从代理 w 的状态映射到预期的累积奖励, 可以通过评估与环境交互获得的奖励来学习最优策略.

在本文的上下文中, 每个主动司机都被视为一个代理, 在每一批, 一个代理(即司机)可以采取两种行动, 接受出租车请求r或保持空闲, 奖励分别为p_r或0. 司机w的状态由他的位置代表 $ \ell _w^{(t)} $ 和t批次处理为( $ \ell _w^{(t)} $ , t). 本文对司机 w 的价值函数 $ V_w^\pi $ ( $ \ell _w^{(t)} $ , t) 感兴趣, 其状态 ( $ \ell _w^{(t)} $ , t) 遵循优化总效用和时间收益公平性的策略π, 由于公平目标和司机之间的潜在行为冲突, 明确推导出策略π具有挑战性, 因此, 本文在不考虑策略的情况下从奖励中迭代更新价值函数, 如下所示:

$ V_w^\pi (\ell _w^{(t)}, t) \leftarrow V_w^\pi (\ell _w^{(t)}, t) + \beta .{\Delta w}({\forall w} \in W) $

(5)

其中, β是学习率, Δw由以下因素决定:

$ {\nabla }{w}=\left\{\begin{array}{l}{p}_{r}+{V}_{w}^{\pi }({d}_{r}, t+{\tau }_{r})-{V}_{w}^{\pi }({\ell }_{w}, t),\;\;如果w获取r\\ 0,\;\;如果w是空闲的\end{array}\right. $

(6)

由于本文的目标不是明确的策略π, 为了简洁起见, 在其余的论文中省略了上标π. 另请注意, 本文采用在线强化学习模型来适应城市交通的短期动态, 将交通模式预测与强化学习相结合超出了本文的范围.

3.2.2 减少状态数

上面的公式有太多的状态供智能体探索, 这阻碍了有效的强化学习. 简单的状态离散化是不够的, 状态总数是空间状态数N_s乘以时间状态数N_T, 考虑将一个城市划分为 1 km² 的方块, 将一天的时间范围划分为跨度为 20 min (平均旅行持续时间)的片段, 那么N_s和N_T将分别约为 8 000 和 72, 导致超过总共 500 000 个方块, 这超出了代理在一天 25 200 次操作中的探索, 假设活动时间为 14 h (允许的最大工作时间)并每 2 s探索一个状态(一批), 如果排除服务请求的时间, 实际探索次数要低得多.

本文通过两种方法减少状态数:

(1)空间值近似函数: 本文将时空状态空间中的原始价值函数近似为空间状态空间, 即V_w(d_r, t+τ_r)=V_w(d_r, t), 这是合理的, 因为大多数请求持续时间不到半小时, 价值函数的变化可以忽略不计. 因此, 更新方程可以改写为:

${\nabla }{w}=\left\{\begin{array}{l}{p}_{r}+{\gamma }^{{\tau }_{r}}{V}_{w}({d}_{r})-{V}_{w}({\ell }_{w}),\;\;如果w获取r\\ 0,\;\;如果w是空闲的\end{array} \right.　 　 $

(7)

折扣因子γ纠正了长时间请求的近似误差.

(2)代理之间的信息共享: 使用一个结合所有代理的价值函数的共享价值函数, 这是合理的, 因为处于相似时空状态的驾驶员应该对位置具有相似的评估, 因此, 更新方程进一步简化为:

$ V(\ell ) \leftarrow V(\ell ) + {\beta '} \cdot \sum\limits_{w:\ell _w^{(t)} \in \ell } {{\nabla w}} $

(8)

其中, β′是归一化的学习比率, 而 $ \ell $ 代表价值函数的所有可能位置.

第1种方法将状态总数从N_T·N_s 减少到N_s; 第2种方法使所有司机探索相同的价值函数以扩展探索, 由于城市中司机的数量可能在 10 000 的数量级, 每个方块平均会被探索一百次, 这足以收敛.

3.2.3 适应不同的城市布局

在实际的网约车应用中, 空间通常是离散的^{[2, 13]}, 这限制了价值函数在城市布局上的变化, 为了消除这些限制, 本文从不同方向对价值函数进行平滑, 这包括两个步骤: (1) 将位置离散为一个两层结构; (2)对不同层值进行平滑.

在LAF中, 这两层分别是六边形层和正方形层, 城市在这两层中分别被分割成六边形和正方形. 这两种形状提供了不同的平滑特性: 六边形有更多的方向, 通过这些方向的平滑有利于不规则的城市布局; 正方形的边界与经纬度平行, 适用于规则区域. 如图3所示, 六边形层为与主干道形状一致的径向模式(图3(a)), 而正方形层为区域模式(图3(b)), 表示部分繁忙区域.

最后, 本文将价值函数平滑如下:

$ \begin{gathered} V(\ell ) = \frac{1}{{|DI{R_H}| + |DI{R_S}|}}\left(\sum\limits_{x \in DI{R_H}} {H(\ell + x)} + \sum\limits_{x \in DI{R_S}} {S(\ell + X)} \right) \end{gathered} $

(9)

其中, H和s为六边形和正方形的价值函数, 由式(8)更新, DIR_H和DIR_s为两层的平滑方向偏移量.

3.2.4 在线学习中避免冷启动

由于在线学习的方式, 价值函数被初始化为零, 导致值评估退化为初始权值(出行价格), 这样的冷启动禁止初始批的分配是未来感知的, 为此, 本文建议提前指引司机前往适当地点, 适当的区域由价值函数的距离和增量决定(即算法3中的第4行). 为简单起见, 本文使用价值函数H中的六边形区域(A_h)作为候选的引导目的地.

3.2.5 再加权模块

基于学习的再加权模块由评估、学习和指导3个阶段组成. 算法1、算法2和算法3分别说明了过程, 在算法3的第4行中, 函数dist计算距离. 重新加权模块利用强化学习明确考虑当前作业对未来作业的影响, 它不会直接促进公平. 在LAF中, 公平目标的优化嵌入到总效用的优化中, 将在下面解释.

算法1. 重新加权模块的评估阶段

输入: 二部图G(t)= < W^(t), R^(t), E^(t)>, 拒绝概率λ, 六边形H价值函数, S方值函数

输出: 重权后的二部图G^(t) =<W^(t), R^(t), E′^(t) >

E′(t) ← Ø

for w, r, θ_w, r ∈ E^(t) do

　　calculate V(l_w) and V(d_r) by Eq(9)

　　 θ_{w, r} ← (1−λ_{w, r})·(p_r+γ^τ_rV(d_r)−V(l_w))

　　 E′(t) ← E′(t) $ \cup $ (w, r, θ_{w, r})

end

Return E′^(t)

算法2. 重权模块的学习阶段

输入: 赋值结果M^(t), 司机W^(t), 六边形值函数H, 正方形值函数S

输出: 更新后的值函数H和S

for w in W^(t) do

　　if there exists an order r, s.t. (w, r) ∈ M^(t) then

　　　　ΔH ← p_r + γ^τ_r H(d_r ) − H(l_w)

　　　　ΔS ← p_r + γ^τ_r S(d_r ) − S(l_w)

　　end

　　else

　　　　ΔH ← 0, ΔS ← 0

　　end

　　 H ← H + β · ΔH, S ← S + β · ΔS

end

return H, S

算法3. 重称重模块引导阶段

输入: 空闲司机 $\scriptstyle w_i^t $ , 候选目的地A_h, 从第1批到当前批t的权重ξ

输出: 指导方案δ

δ← Ø

基于 $\scriptstyle \frac{{\sum\nolimits_{i = 1}^t {u_w^{(i)}/{\xi ^{(i)}}} }}{{\sum\nolimits_{i = 1}^t {a_w^{(i)}} }}x $ 递增排序司机

for w ∈ W ^(t) do

　　 $\scriptstyle g \leftarrow \arg {\max _{g'}} \in {A_h}\frac{{V(g') - V({\ell _w})}}{{dist(g', {\ell _w})}} $

　　 $\scriptstyle \delta \leftarrow \delta \cup (w, g) $

end

Return $\scriptstyle \delta $

3.3 有效的双目标分配

本节介绍了优化效用和公平性的分配算法.

3.3.1 公平增长

不像以前的双目标解决方案, 要么依赖于缓慢的线性规划^[16], 要么在公平和效用^[5]的单独优化之间进行重复的重新分配, 本文建议直接将公平检查嵌入到过程中, 以最大化更快的分配的效用.

在二部图上寻找效用最大化的匹配的标准方法是Kuhn-Munkras算法^[8], 其中的基本操作是增长, 即首先尝试找到一条由匹配边和不匹配边交替组成的路径, 而未匹配边的权值之和大于已匹配边的权值之和, 如果发现, 则将未匹配边和已匹配边进行切换, 以增加总效用. 本文的公平增长算法的思想是, 在寻找增长路径时, 检查驾驶员的未来收益率, 拒绝收益率方差较大的增长, 然而, 拒绝增长可能会损害已实现的效用, 考虑一个新上线的司机在增长路径上, 由于他的空闲时间几乎为零, 所以他在服务请求后的收益比会非常大, 导致增长频繁被拒绝. 还要注意, 在找到一个扩展路径后, 检查所有司机的方差是非常耗时的, 因此, 本文不检查所有的司机, 只检查增长路径中相邻的两个司机, 一旦发现方差比, 立即中断并停止增长. 算法4说明了公平的增长算法, 时间复杂度为O(N2M), 其中, $ M = \max (\left| {\left. {W(t), } \right|} \right. $ $ \left| {\left. {R(t)} \right|2, N = \min (\left| {\left. {W(t)} \right|, \left| {\left. {R(t)} \right|} \right.} \right.} \right. $ .

3.3.2 加速度

算法5利用二部图的稀疏性, 进一步加速了均匀增长算法, 具体地说, 执行广度优先搜索(BFS), 将as分配图分成几个部分, 其中很多部分只包含一个司机(请求), 所以本文使用特殊的判断来快速地为单个节点找到最佳的请求(司机).

算法4. 公平增长

输入: 二部图G^(t)= < W^(t), R^(t), E^(t)>, 当前批t, 权重ξ, t从第一批

输出: 作业M^(t)

M^(t) ← Ø

for w ∈ W ^(t) do

　　while there exists an augment Path P do

　　　　 accept ← True

　　　　for every pair of adjacent drivers w_pre, w_cur do

　　　　　　 r_pre ← current assigned request of w_pre

　　　　　　 r_cur ← current assigned request of w_cur

　　　　　　 $\scriptstyle {\rm{if}} \; \left | \frac{{\sum\nolimits_{i = 1}^t {\frac{{u_{{w_{\rm{pre}}}}^{(i)}}}{{{\xi ^{(i)}}}} + \frac{{p{r_{\rm{pre}}}}}{{{\xi ^{(t)}}}}} }}{{\sum\nolimits_{i = 1}^t {a_{wpre}^{(i)} + {\tau _{rpre}}} }} - \frac{{\sum\nolimits_{i = 1}^t {\frac{{u_{{w_{\rm{cur}}}}^{(i)}}}{{{\xi ^{(i)}}}} + \frac{{p{r_{\rm{cur}}}}}{{{\xi ^{(t)}}}}} }}{{\sum\nolimits_{i = 1}^t {a_{{w_{\rm{cur}}}}^{(i)} + {\tau _{{r_{\rm{pre}}}}}} }} \right | > {\text{ }}$ ε

　　　　　　then

　　　　　　　　 accept ← False

　　　　　　　break

　　　　　end

　　　　end

　　　　If accept then

　　　　　　Update M^(t) based on P

　　　　end

　　end

end

Return M^(t)

算法5. 分配算法

输入: 二部图 G^(t) =<W ^(t), R^(t), E^(t) >

输出: 作业M^(t)

P^(t) ← split G^(t) by BFS.

M^(t) ← Ø

for p ∈ P^(t) do

　　if there is only one driver w (request r) then

　　　　 M_p ← < w(best driver), best request(r)>

　　end

　　else

　　　　 M_p ← Fair Augmentation(p)

　　end

　　 M^(t) ← M^(t) $ \cup $ M_p

end

return M^(t)

4 评价 4.1 实验设置

验证环境: 在一个大型网约车平台的模拟器上进行了实验, 在3个城市进行了21天的实验, 该模拟器生成请求, 模拟驾驶员和乘客的行为(即空闲驾驶员转换和乘客拒绝), 构建二部图, 并执行本文的分配算法.

基线: 将本文的方法与以下基线进行比较:

(1)距离贪婪(DG): 它将每个请求分配给它最近的可用司机, 这是一个广泛使用的基线叫车.

(2)收益比率贪婪(ERG): 它首先按加权摊销公平性 F_w 按降序对所有可用司机进行排序, 然后按每批次的奖励(p_r /τ_r)降序对请求进行排序, 然后它根据顺序将请求分别分配给司机.

(3)整数线性规划(ILP)^[6]: 这是第一个应用摊销公平性来评估网约车收益公平性的工作, 它将问题转换为整数线性规划问题. 为了公平比较, 本文从其优化目标中省略了乘客侧的公平性.

(4)重新分配(REA)^[10]: 它首先分别计算优化效用和公平性的两个分配(调整为 min_w F_w 以进行相等比较), 然后它将匹配从一个分配重新分配到另一个分配, 以找到效用和公平之间的权衡. 这是最先进的解决方案, 可优化网约车服务的实用性和公平性.

评价指标: 本文通过公平、效用和效率来评估不同方法的性能, 其中, 公平是通过时间收益公平(定义6)来衡量; 效用是通过总效用(定义4)来衡量; 效率是通过每小时累积的分配消耗时间来衡量的.

实现: 所有算法都是在Python 3中实现的, 本文将折扣因子γ (式(7))设为0.9, 学习率β' (式(8))设为0.025. 实验在Intel Xeon CPU E5-2630 v4 @ 2.20 GHz, 12 GB内存上进行.

4.2 总体性能

表1总结了3个城市数据集上不同分配方法的公平性和效用指标, 总体而言, LAF在工作日比基线提高了45.7%–81.4%, 在周末提高了52.0%–86.7%. LAF总效用最高, 工作日比基线高7.7%–29.1%, 周末比基线高11.3%–28.5%. 特别是, 本文的LAF在公平性和效用方面分别比ILP平均高出68.4%和22.1%. 对于REA, LAF在公平性和效用上的平均提高分别为69.3%和20.1%. 此外, LAF在这3个城市的表现都优于基线.

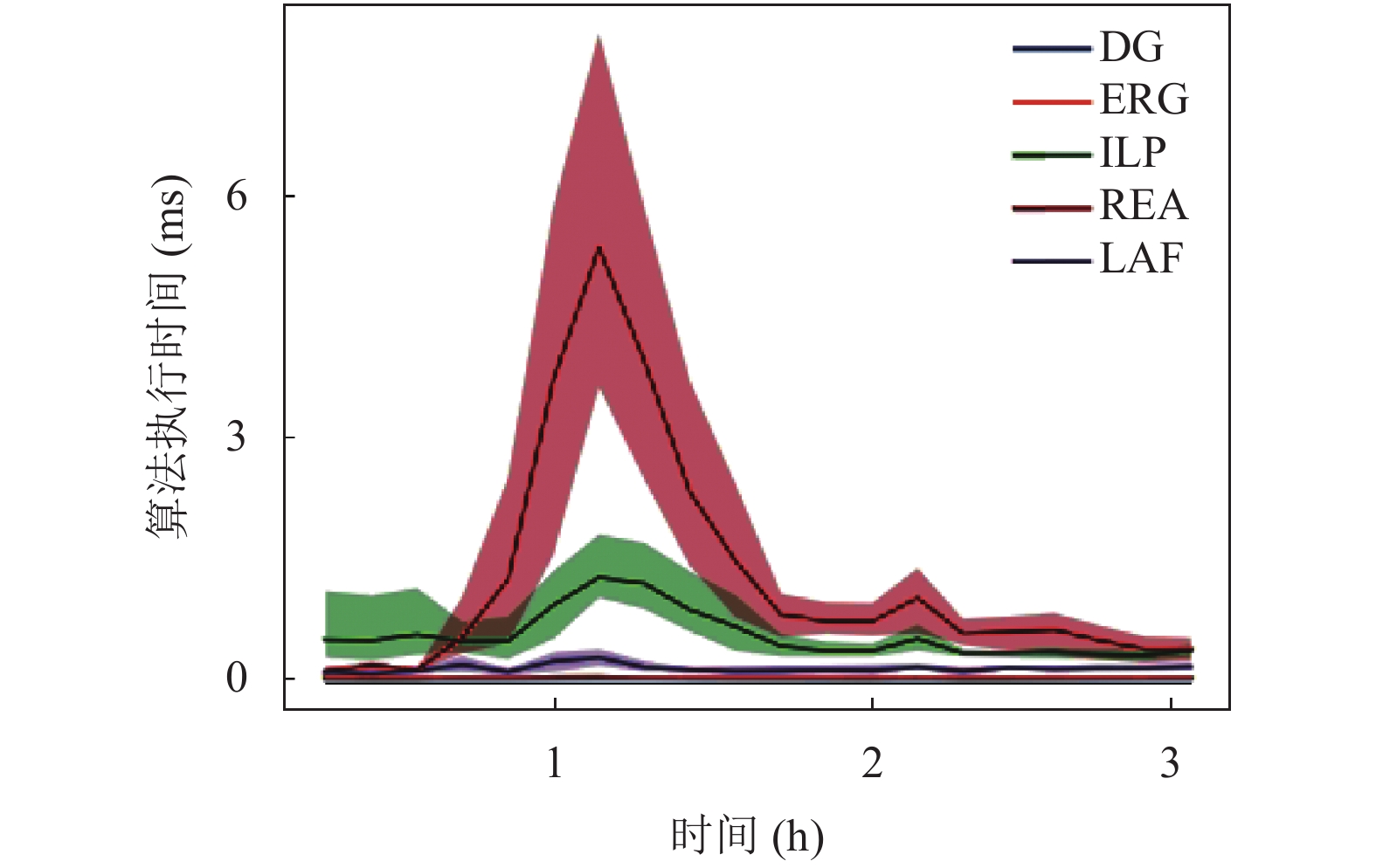
图4比较了不同算法的效率, 简单基线DG和ERG的时间复杂度分别为O(|E| log |E|)和O(|W| log |W|), 但在公平方面表现不佳, 在周末, 公平和效用方面, 本文这两个简单的解决方案几乎一样快, LAF的运行时间相对稳定, ILP和REA比LAF慢797%. 此外, 他们的运行时间是敏感的变化, 交通在高峰期, 当请求数量急剧增加时, 这两种方法的时间成本也会显著增加.

4.3 实验结果分析

现在深入研究不同方法在3个城市中规模最大的城市Ａ的数据集上的性能, 以进一步了解本文方法的有效性.

4.3.1 LAF与其他算法的差异

为了说明不同分配算法之间的差异, 本文在图5中绘制了驾驶员的轨迹.

(1) DG不顾公平, 将最近的请求分配给司机, 第2次分配后, 驾驶员被困在偏远地区, 无法返回进行其他请求(图5(a)); ERG将收益比率最低的驾驶员分配给最高的p_r/τ_r, 在第2个请求后, 司机的收益比较低, 并被分配到一个长途请求(图5(b)).

(2) ILP对这个司机做了与DG相同的分配(图5(c)), 这是因为司机在完成长途请求后, 其收益比较高, 导致下一批请求的距离较近, 而在偏远地区, 由于两次服务后的收入比较高, 司机很难再接到另一次服务.

(3) REA兼顾了公平性和实用性, 实用程序的优化增加了分配给司机的请求数量(图5(d)), 但是, REA仍然不知道目的地, 司机只能选择一个短距离的请求, 可能被困在偏远地区.

(4)本文的LAF通过考虑它们对未来任务的影响来进行任务, 该指导还避免了司机被困在偏远地区. 如图5(e)所示, 在繁忙区域服务了一些请求后, 司机的收益比相对较高, 然后, 为了公平起见, 将请求分配给其他驾驶员, 然后, 为了避免长时间的闲置, 司机会被引导到他/她可以得到请求的区域, 然后返回到繁忙的区域.

4.3.2 流量动态与公平性的相关性

本文的贡献之一是使用加权平摊公平F_w作为公平度量(定义5), 通过显示F_w中的权重ξ⁻¹(t)与流量动态之间的相关性来证明本文的加权平摊公平度量的优势.

图6(a)绘制了一天中不同时间内司机和请求的数量以及权重ξ⁻¹(t), 司机和请求的数量反映了交通的变化, 如图６所示, 交通流量从早上6点到8点上升, 白天波动, 晚上下降, 权重ξ⁻¹(t)也呈现出同样的趋势. 这表明本文在高峰时段更注重公平, 因为那里有更多的司机, 因此需要更多的公平. 还需要注意的是, 司机在当前小时内的收入中值, 如ξ是一个不错的选择, 因为它的变化略早于交通, 这是因为有经验的司机往往在高峰时间之前更早开始活跃, 导致收入中值提前下降, 因此权重ξ可以预见地增加.

图6(b)显示了随机抽样的3500名司机的时薪, 如图所示, 以公平性度量作为优化目标时, 驾驶员的时薪分布相对均匀, 而LAF算法在减少时薪极高/极低的驾驶员数量方面表现最好.

4.3.3 优化未加权平摊公平的有效性

表2比较了优化未加权平摊公平性(即在所有时间t内将ξ^(t)设置为1)和效用的不同算法, DG被排除在外是因为它不公平, 算法的效用结果与表2相同. 结果表明, 尽管ILP和REA的设计是为了优化未加权平摊公平性, 但LAF的公平性提高了57.9%–62.2%, 效用提高了17.3%–17.6%. 因此, 本文的LAF在未加权和加权摊销公平性方面都优于目前的水平.

5 结论

在本文中, 提出了公平分配学习(LAF)方法, 它有效地优化了总效用(驾驶员的预期总收入)和驾驶员的公平性(驾驶员收入的加权摊销公平性). 关键的创新之处在于应用强化学习来进行分配, 这些分配明确说明了分配之间的依赖性, 从而可以从整体角度优化效用和公平性. LAF 还结合了一组技术来适应交通动态和不同的城市布局, 并在大规模数据上进行快速分配. 实验结果表明, LAF 在公平性、实用性和效率方面比最先进的网约车公平分配算法提高了 86.7%、29.1% 和 797%. 此工作将成为在现实世界网约车应用中实际采用公平任务分配的指南.