化石燃料正处在耗尽的边缘, 世界各国都意识到开发和使用可再生的清洁能源才是持久之道[1]. 目前, 可再生能源发电形式有很多, 风电是所有方法中最成熟的一种, 将风电大规模加入到电网中, 可以大大减轻社会的能源负担[2]. 对短期风电功率的准确预测, 不但能够节约电网运行的本钱, 同时使电网系统可靠性更上一层楼[3]. 风速的短期预测, 能够在一定程度上为电网调度提供参考, 是现代社会风电场以及电网运行和维护中不可缺少的一大助力.
早期的风速预测, 物理方法占据了半壁江山, 另一半为统计学方法. 物理方法需要采集大量的风机及天气信息, 利用数学表达式计算出风速预测值, 由于数据量庞大, 需要使用高性能计算机进行运算, 预测难度和经费预算都比较大; 统计学方法需根据历史信息建立模型, 预测精度受样本量限制, 样本量越大, 预测精度越高. 统计学方法擅长处理线性数据, 而风速数据是非线性的, 使用统计学方法预测风速准确度不够高.
近年来, 使用机器学习(如SVM[4]、随机森林[5]、极限学习机[6]等)、深度学习(如BP[7]、RNN[8]、LSTM[9]等)预测方法受到国内外学者的偏爱. 文献[10]在对短期风速进行预测时, 使用到了支持回归向量机(SVR)方法, 具有较好的仿真效果. 文献[11]使用了SVM预测模型, 其中核函数选择了RBF, 并通过算法对惩罚因子(C)和RBF自带参数(gamma)进行寻优, 预测结果较为理想. 文献[12]提出一种基于正则化极限学习机的风电场短期风速预测新方法, 相较于标准的ELM和BP神经网络, 该方法具有更好的预测精度. 文献[13]使用了BP预测模型, 不同于一般做法, 在使用了风速历史数据的同时, 还收集了风速周围的时空信息, 将这两种数据同时使用到风速预测中, 取得了较好的结果. 上述机器学习、深度学习方法在对风速数据进行预测时, 均取得了不错的结果, 但在实际场景的风速预测中, 仅运用单一模型, 预测的精度很难满足需求.
针对上述方法存在的问题, 组合预测模型目前被大量使用, 通过对不同单一预测模型的组合, 实现各模型之间优势互补, 以此提高预测精度. 文献[14]为了使非平稳风电功率信号相对平稳化, 使用EMD方法对其进行分解, 得到n个平稳序列, 分别送入ARIMA预测模型, 累加所有模型预测结果, 得到风速预测值. 文献[15]采用LSTM结构的循环神经网络对超短期风力发电进行预测. 文献[16]使用EMD方法和堆叠的长短期记忆网络的组合模型, 对短时风速进行预测. 上述组合模型均在一定程度上提升了预测精度, 但也存在一些问题, 文献[14]和文献[16]采用的EMD分解方法分解风速信号, 容易被异常信号干扰, 导致模态混叠现象, 文献[15]仅采用LSTM网络预测, 在一些风速数据预测上可能存在滞后问题.
本文提出基于EEMD-GRU的短期风速预测模型. 首先, 对原始风速时间数据进行异常数据剔除操作, 使用EEMD分解方法, 将原始数据分解成若干分量, 然后将分解得到的分量分别送入GRU模型进行预测, 接着将所有分量的预测结果进行累加, 风速预测最终结果由此得到. 对于EMD分解方法产生的模态混叠现象, 本文使用EEMD分解方法来解决此问题; 对于单一LSTM预测方法可能产生的预测结果滞后现象, 使用EEMD与GRU相结合的组合预测方法来解决. 最后与EEMD-LSTM、EMD-LSTM、EMD-GRU等模型对比, 进行指标分析与评价, 实验证明本文的方法, 在对时间序列预测时, 准确度更高, 预测能力更强.
1 相关理论 1.1 经验模态分解经验模态分解是一种比较智能的自适应算法(empirical mode decomposition, EMD), 在对原信号进行拆分时, 分解得到的分量能够自动匹配自己应在的尺度, 若分解得到分量还可继续拆分, 则继续分解, 直到不可分解为止, 这时就得到了原始信号经EMD方法分解后的所有分量[17]. 这种分解方法能够挖掘出信号内部更详细的细节, 非常适用于处理不稳定的数据. EMD分解的具体步骤如下:
(1) 将原始风速时间数据Y(t)里面包含的全部局部极大值以及极小值找出来;
(2) 对原始数据进行插值操作, 求得上下包络线 U(t)和D(t);
(3) 求出上下包络线的平均值M(t);
| $ M(t) = \dfrac{{\left[ {U(t) - D(t)} \right]}}{2} $ | (1) |
(4) 用Y(t)减去M(t), 求得类距平值H(t);
| $ H(t) = Y(t) - M(t) $ | (2) |
(5) 对步骤(4)得到的序列H(t)进行检查, 看其能否达到IMF标准, 若不达标, 则将H(t)作为新的初始序列, 从头进行步骤(1)–(4), 直到所得结果都达到标准, 若条件达标, 则得到初始风速时间序列分解的t时刻第n个分量Cn(t);
| $ {C_n}(t) = H(t) $ | (3) |
(6) 从原始序列中将Cn(t)去除, 得到剩余序列R(t);
| $ R(t) = Y(t) - {C_n}(t) $ | (4) |
(7) 将R(t)作为新的初始序列, 循环执行上述步骤, 直到得到所有不可拆分的分量;
(8) 原始风速序列经过EMD分解后可表示为:
| $ Y(t) = \displaystyle \sum\limits_{i = 1}^n {{C_i}} (x) + {R_n}(t) $ | (5) |
EMD分解方法处理非平稳数据时表现良好, 但也存在问题, 分解得到的有些分量会重叠在一起, 即模态混叠. Huang等人为了解决这个缺陷, 在EMD方法的基础上不断改进, 经过大量试验, 发现在原信号中加入噪声, 利用噪声自身的特点, 可以解决模态混叠问题, 由此集合经验模态分解(ensemble empirical mode decomposition, EEMD)方法被提出[18]. EEMD方法的改进之处, 就是将高斯白噪声放到了原始信号中(之所以选择高斯白噪声, 是因为其具有随机性、且频谱均匀分布的特点), 之后就是多次使用EMD方法分解新信号[19]. EEMD的具体步骤如下:
(1) 向风速时间序列中添加噪声, 噪声为服从正态分布的白噪声[20];
(2) 使用EMD方法, 对新序列进行拆分, 结果就是新序列由n个IMF分量和1个残差组成;
(3) 重复步骤(1)和步骤(2), 每次执行时, 将新的正态分布的白噪声序列添加到信号中;
(4) 对所有IMF分量, 做集成平均操作, 得到风速时间序列的IMF分量.
1.3 门控循环单元GRU (gated recurrent unit)是LSTM (long short-term memory)的一种变体[21], 从结构上看, 两者还是有着很大的差别. 与LSTM的三门结构不同, GRU只有两个门, 分别是重置门和更新门[22]. 因为少了一个门结构, 计算时参数数量相比于LSTM会少一些, 训练速度更快. GRU整体结构如图1所示.

|
图 1 GRU网络基本单元 |
GRU的迭代公式如下:
| $ {{\textit{z}}_{{t}}}{\text{ = }}\sigma ({W_{\textit{z}}} \cdot \left[ {{{{h}}_{t - 1}}, {x_t}} \right]) $ | (6) |
| $ {r_t} = \sigma ({W_r} \cdot \left[ {{h_{t - 1}}, {x_t}} \right]) $ | (7) |
| $ \tilde h = \tanh (W \cdot \left[ {{r_t}*{h_{t - 1}}, {x_t}} \right]) $ | (8) |
| $ {h_t} = (1 - {{\textit{z}}_t})*{h_{t - 1}} + {{\textit{z}}_t}*{\tilde h_t} $ | (9) |
其中, 下标t代表t时刻、更新门由z指代, 重置门由r指代. 权重矩阵由W指代, Sigmoid函数由符号σ指代, 输出值由h指代. *代表哈达玛积(Hadamard product).
2 基于EEMD-GRU的短期风速预测模型实现 2.1 EEMD-GRU模型风速序列通常随着时间的变化一直震荡, 呈不平稳状态, 且极容易受现实中周围环境影响, 传统预测方法效果较差. 本文为克服仅使用单一模型预测精度不够高的问题, 使用两种方法相结合的组合模型对风速进行预测. 组合模型由EEMD和GRU方法构成. 首先用孤立森林算法剔除原始风速中的异常点, 然后使用EEMD方法, 将其拆分成不同尺度的信号, 从而大大降低风速信号的震动性、非平稳性, 其次, 将分解得到的各分量信号分别送入GRU模型进行训练得到各自的预测结果, 预测风速最后由所有分量结果累加得到. 具体预测流程如图2所示.
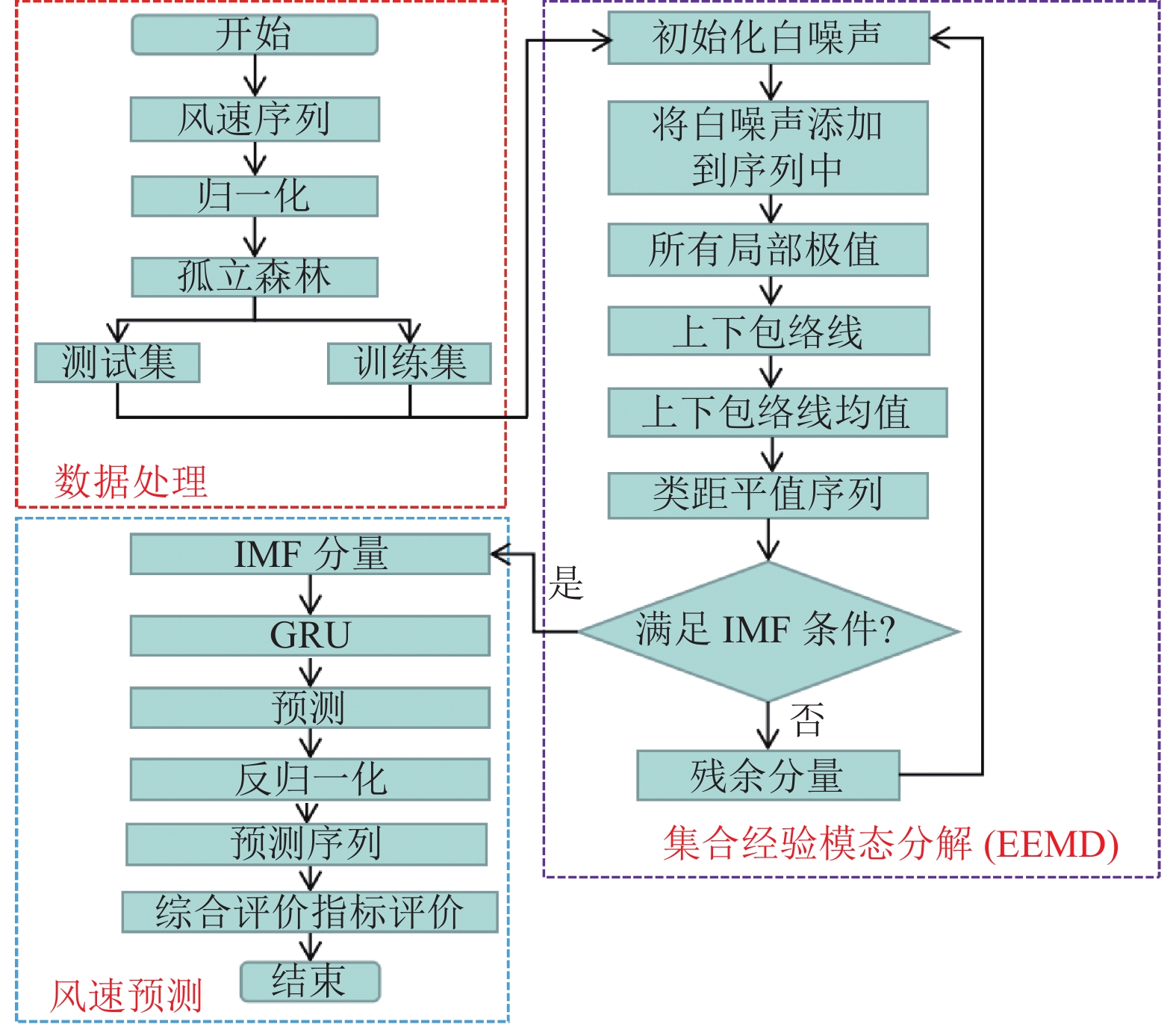
|
图 2 EEMD-GRU组合模型基本结构 |
具体步骤如下:
(1) 获取原始风速时间数据, 归一化处理, 归一化公式如下:
| $ X_i^* = \dfrac{{{X_i} - min }}{{max -min }} $ | (10) |
其中, i为风速序列的第i个元素; 风速的初始值、最大值、最小值由X、max、min分别指代; X*为归一化操作后得到的序列;
(2) 对归一化的数据, 使用孤立森林算法, 标注出全部异常点、剔除全部异常点;
(3) 使用EEMD方法对上述操作得到的结果进行拆分, 得到不同尺度的IMF;
(4) 按照19:1的占比, 将步骤(3)得到的序列划分为训练集和测试集;
(5) GRU网络初始化, 将步骤(4)所得数据分别送入GRU网络进行训练;
(6) 将步骤(5)得到的全部预测结果累加求和, 得到最终风速预测结果.
2.2 模型评价指标为更加直观的评估EEMD-GRU模型在实际问题预测中的表现, 选用了4种评价指标进行评测. 分别是RMSE (均方根误差)、R2 (决定系数)、MAE (平均绝对误差)、MAPE (平均绝对百分误差)[23]. 其中, RMSE、MAPE、MAE数值越小代表模型预测误差越小, R2数值越接近于1, 代表模型表现越好. 4项指标计算公式如下:
| $ {\textit{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{y_{\rm{true}}}(i) - {y_{\rm{pred}}}(i)} \right)}^2}} } $ | (11) |
| $ {R^2} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{y_{\rm{true}}}(i) - {y_{\rm{pred}}}(i)} \right)}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{y_{\rm{true}}}(i) - \mathop y\limits^ - } \right)}^2}} }} $ | (12) |
| $ {\textit{MAE}}{\text{ = }}\frac{1}{n}\sum\limits_{i = 1}^n {\left| {{y_{\rm{true}}}(i) - {y_{\rm{pred}}}(i)} \right|} $ | (13) |
| $ MAPE{\text{ = }}\frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{y_{\rm{true}}}(i) - {y_{\rm{pred}}}(i)}}{{{y_{\rm{true}}}(i)}}} \right|} $ | (14) |
本文算例为我国新疆某地风场2017年的风速实地采样数据, 以15 min对风速数据采样, 每小时提取4条数据. 本次实验使用的2017年5月1日至6月2日的数据, 一共3072条, 原始样本数据如图3. 首先对数据进行归一化操作, 缩小数据之间的量纲差距, 避免训练中产生误差过大. 归一化结果如图4所示.

|
图 3 原始风速序列 |
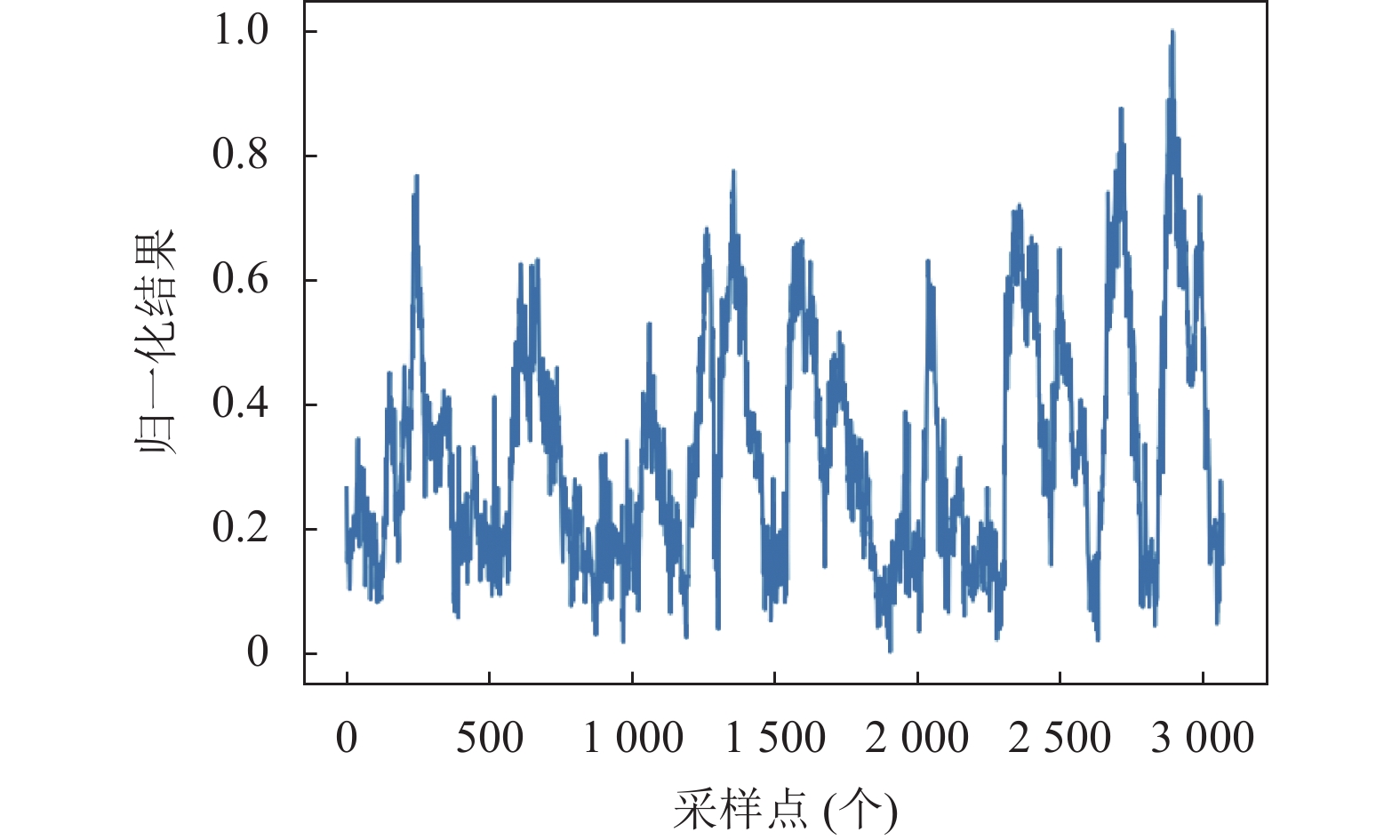
|
图 4 归一化结果 |
原始数据在采集时, 可能因为各种各样的原因(风机故障、操作失误等), 导致样本中存在脏数据, 直接将数据送入网络学习, 网络会将错误信息一起学习, 预测时会产生一定的误差, 因此对异常数据处理显得尤为重要. 对归一化数据, 采用孤立森林算法, 找出异常点153个, 如图5所示, 将异常点去除, 结果如图6所示.
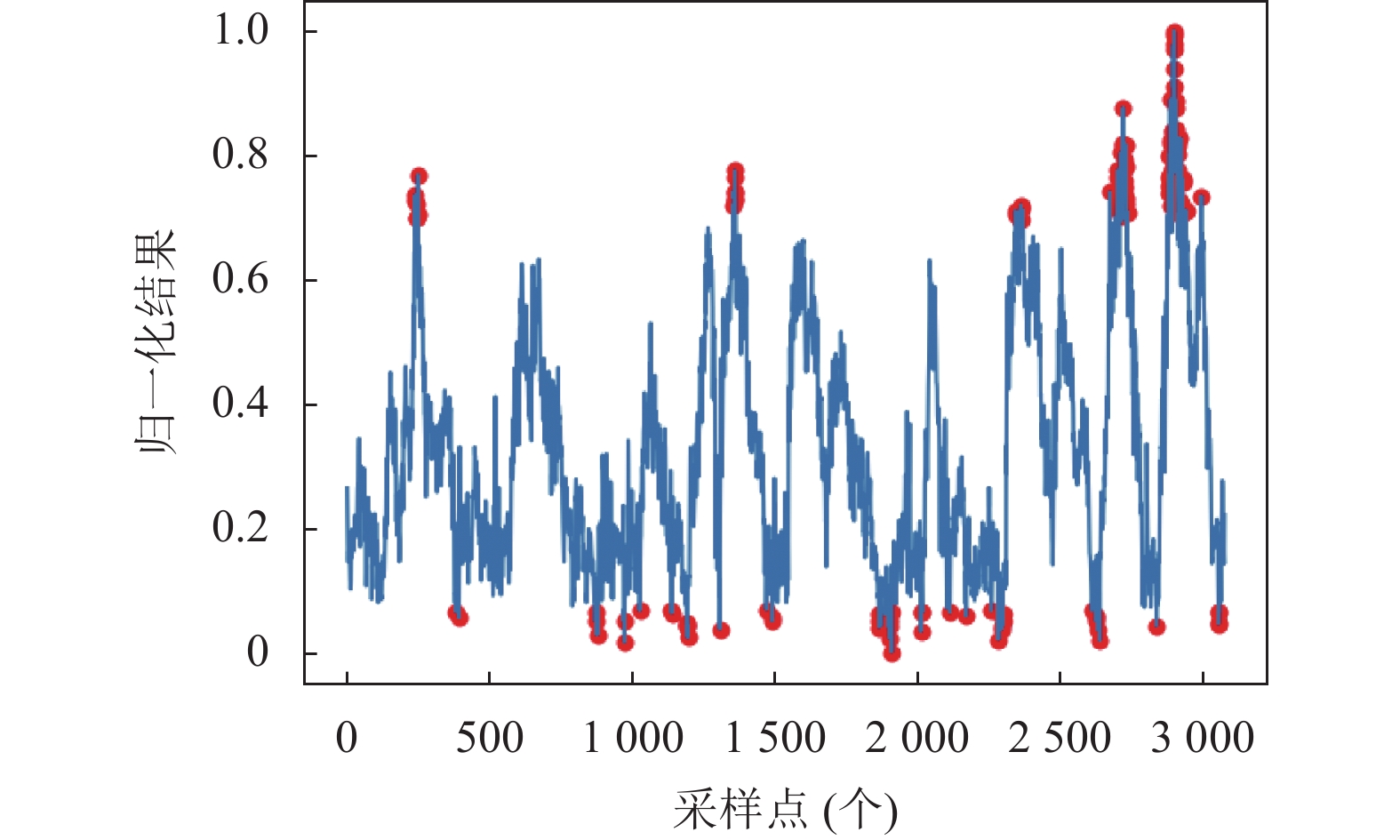
|
图 5 异常点分布 |

|
图 6 去除异常点结果 |
3.2 EEMD分解
异常点去除后, 样本剩余2919, 根据19:1的占比, 将数据划为训练集和测试集. 如图7所示, 原始的震动性极强的序列, 现在由9个IMF和1个残差分量所代替, 并且按照信号频率的大小, 由高到低依次排列, 原始风速序列波动性大、非平稳的缺点被大大克服, 同时经过分解操作得到的分量, 具备较强的稳定性.

|
图 7 EEMD分解结果 (横坐标表示采样点个数, 纵坐标表示信号幅值大小) |
3.3 GRU模型参数选择
深度学习发展至今, 网络结构以及网络参数选择问题, 至今没有定性的理论可参考, 学者们大多根据经验或在实验过程中确定参数. 过于复杂或简单的网络结构、过大或过小的神经元个数, 会导致过拟合或欠拟合现象, 因本文数据量只有3000条左右, 样本量不大, 故GRU网络考虑单层或双层结构, 隐藏层神经元考虑30或50. 为排除随机性误差, 采用10次实验的平均值作为模型结构选择的参考. 如表1所示.
| 表 1 GRU网络参数 |
网络结构确定后, 接下来探索时间步长(TIME_STEP)的合适值. TIME_STEP用来重构风速序列, 形成新的输入集合. TIME_STEP为6, 意思是用前6个风速数据作为模型的输入, 预测第7个风速数据的输出. 不同大小的TIME_STEP, 对模型的预测结果会产生不同的影响, 因此在不同TIME_STEP下, 进行实验.
| 表 2 时间步长 |
从表2可以看出, TIME_STEP=32时, 模型的预测误差比TIME_STEP=20时还要高, 这说明时间步长并不是越大越好. 随着时间步长的增加, 误差呈波浪式变化, 当TIME_STEP为20时RMSE和MAE值均为最小, 故本文时间步长设定为20.
3.4 不同模型对比本文选用EEMD-LSTM、EMD-GRU、EMD-LSTM、LSTM、GRU、BP网络作为EEMD-GRU模型的对比模型. 其中所有模型的网络结构与GRU模型相同, 均为单层结构, 神经元均设为50, Dropout率设为0.2, epoch为50, batch_size为16, 预测结果如图8、图9所示.

|
图 8 不同模型预测结果 |
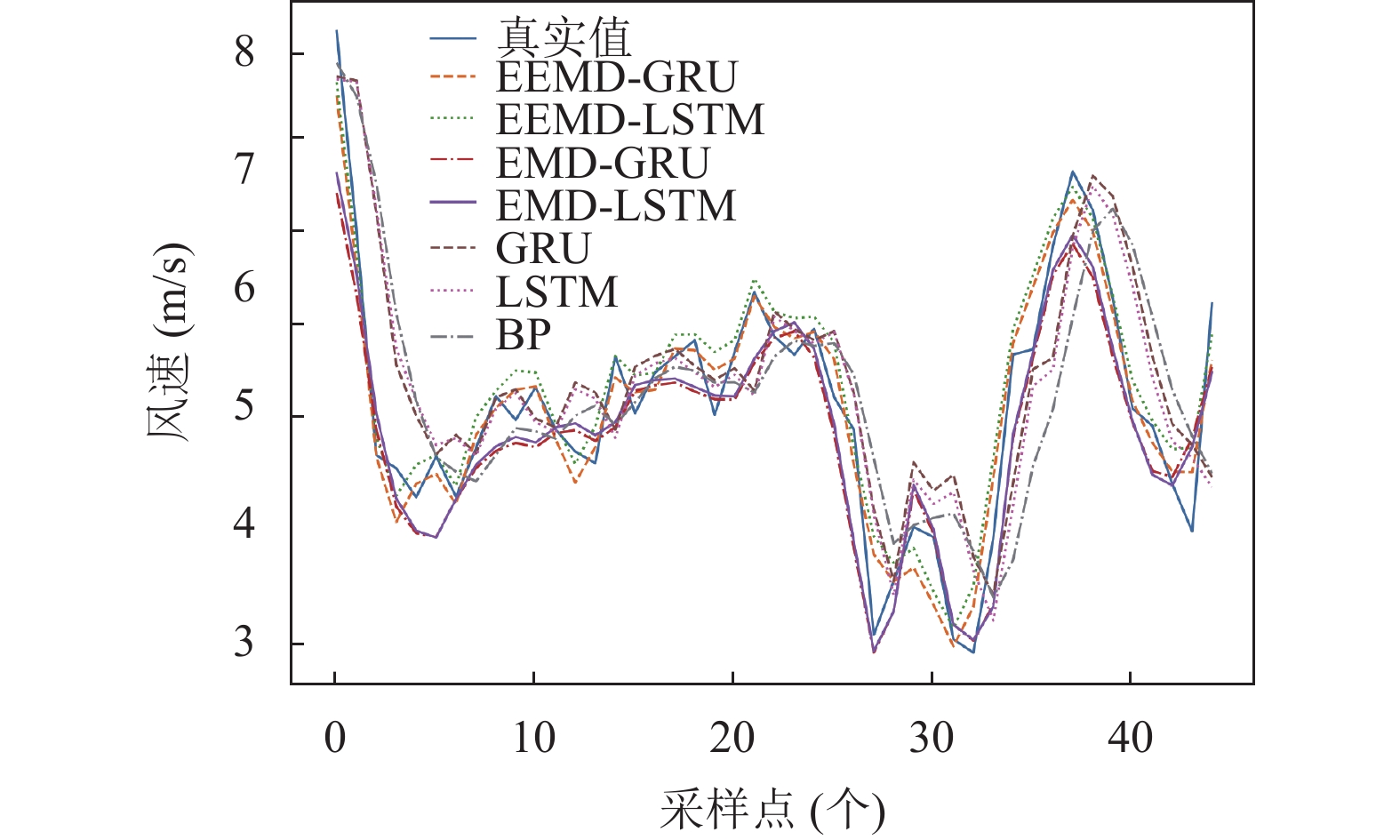
|
图 9 不同模型预测结果放大图 |
从图9可以明显看出EEMD-GRU模型预测的曲线能够更好地跟随真实数据变化, 拟合效果最好. 为了更加直观的比较模型预测精度, 计算了所有模型在相同输入条件下的4种评价指标, 见表3.
| 表 3 不同模型效果对比 |
从RMSE、MAPE、MAE三项指标来看, EEMD-GRU模型相较于EEMD-LSTM模型, 误差分别降低了7.47%、11.99%、7.48%; 相较于EMD-GRU模型, 误差分别降低了16.33%、16.97%、19.74%; 相较于EMD-LSTM模型, 误差分别降低了12.33%、11.51%、15.22%; 相较于GRU模型, 误差分别降低了56.66%、59.17%、56.50%; 相较于LSTM模型, 误差分别降低了57.76%、59.32%、57.22%; 相较于BP模型, 误差分别降低了59.53%、62.09%、59.38%. 从R2来看, EEMD-GRU模型相对于其他模型R2的值更接近1, 综合4种指标, 足以证明EEMD-GRU方法在预测精度上表现的最好.
4 结论本文针对风速的随机性、震动性以及仅使用LSTM预测可能出现的滞后性等问题, 提出了一种基于EEMD-GRU的短期风速预测方法, 采用实地采集的数据进行预测, 得出以下结论:
(1) 对原始风速时间序列分解, 能够很大程度上降低风速数据自身的不稳定性.
(2) EEMD-GRU模型克服了EMD方法在分解非平稳数据(风速序列)时产生的模态混叠问题, 提高了预测精度.
(3) EEMD-GRU模型有效地改善了单一LSTM模型预测出现的滞后性问题.
(4) 通过与EEMD-LSTM、EMD-LSTM、EMD-GRU、LSTM、GRU、BP模型进行比较, 证明了本文提出的EEMD-GRU组合模型在对风速数据预测时, 预测曲线更贴合实际曲线, 预测精度更高, 预测能力更强.
| [1] |
薛阳, 张宁, 俞志程, 等. 基于BiLSTM和Bootstrap方法的风电功率区间预测. 可再生能源, 2020, 38(8): 1059–1064.
|
| [2] |
纪洁, 胡汉, 高远, 等. 基于遗传算法优化参数的支持向量机风电功率预测. 电子测试, 2020(21): 32-35. DOI:10.3969/j.issn.1000-8519.2020.21.011 |
| [3] |
温钊, 张方红, 刘冰冰, 等. 基于小波分析和高斯过程的短期风速预测. 船舶工程, 2020, 42(S2): 192-195, 221. |
| [4] |
陈岩, 周晨, 侯群. SVM算法在风力发电机功率预测中的应用研究. 电子世界, 2021(4): 100-102. |
| [5] |
Vassallo D, Krishnamurthy R, Sherman T, et al. Analysis of random forest modeling strategies for multi-step wind speed forecasting. Energies, 2020, 13(20): 5488. DOI:10.3390/en13205488 |
| [6] |
Zhang YJ, Chen L. A hybrid forecasting model based on modified bat algorithm and ELM: A case study for wind speed forecasting. 2018 2nd International Workshop on Renewable Energy and Development (IWRED 2018). Guilin: IOP Publishing, 2018. 32–37.
|
| [7] |
梅雨, 王红蕾, 王瑾. 基于PSO-BP组合改进模型的短期风电功率预测仿真. 软件, 2020, 41(12): 7-10. DOI:10.3969/j.issn.1003-6970.2020.12.003 |
| [8] |
夏文泽, 冯骁, 王喆, 等. 基于新型联合循环神经网络(RNN)模型的出水总氮预测. 净水技术, 2021, 40(8): 107-113. |
| [9] |
李艳, 彭春华, 傅裕, 等. 基于CNN-LSTM网络模型的风电功率短期预测研究. 华东交通大学学报, 2020, 37(4): 109–115.
|
| [10] |
李霞. 支持向量回归机在风电场短期风速预测中的应用研究[硕士学位论文]. 北京: 华北电力大学, 2013.
|
| [11] |
赵斌, 宋建丽. 基于SVM回归方法的风速预测研究. 电子世界, 2013(6): 83-84. |
| [12] |
袁翀, 戚佳金, 王文霞, 等. 采用正则化极限学习机的短期风速预测. 电网与清洁能源, 2016, 32(11): 62-68. DOI:10.3969/j.issn.1674-3814.2016.11.011 |
| [13] |
周建强, 李玉娜, 屈卫东, 等. 基于风速时空信息的BP神经网络超短期风速预测研究. 电网与清洁能源, 2015, 31(1): 109-112. DOI:10.3969/j.issn.1674-3814.2015.01.019 |
| [14] |
仇琦, 杨兰, 丁旭, 等. 基于改进EMD-ARIMA的光伏发电系统短期功率预测. 电力科学与工程, 2020, 36(8): 42-50. DOI:10.3969/j.ISSN.1672-0792.2020.08.007 |
| [15] |
王炜, 刘宏伟, 陈永杰, 等. 基于LSTM循环神经网络的风力发电预测. 可再生能源, 2020, 38(9): 1187-1191. DOI:10.3969/j.issn.1671-5292.2020.09.009 |
| [16] |
黄元生, 杨磊, 高冲, 等. 基于经验模态分解和误差校正的短期风速预测. 智慧电力, 2020, 48(1): 35-41. |
| [17] |
甘迪, 柯德平, 孙元章, 等. 基于集合经验模式分解和遗传-高斯过程回归的短期风速概率预测. 电工技术学报, 2015, 30(11): 138-147. DOI:10.3969/j.issn.1000-6753.2015.11.017 |
| [18] |
Huang NE, Shen Z, Long SR, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [19] |
于婷, 孙景云. 基于EEMD和PSO方法的我国港口集装箱吞吐量预测. 物流技术, 2021, 40(5): 56-64. DOI:10.3969/j.issn.1005-152X.2021.05.010 |
| [20] |
Sun HY, Wu J, Wu J, et al. Hybrid SVM and ARIMA model for failure time series prediction based on EEMD. International Journal of Performability Engineering, 2019, 15(4): 1161-1170. DOI:10.23940/ijpe.19.04.p11.11611170 |
| [21] |
黄伟建, 李丹阳, 黄远. 基于深度学习的PM2.5浓度长期预测. 计算机应用研究, 2021, 38(6): 1809–1814.
|
| [22] |
余本功, 张培行. 基于双通道特征融合的WPOS-GRU专利分类方法. 计算机应用研究, 2020, 37(3): 655-658. |
| [23] |
胡汉. 风电场风电功率概率预测研究[硕士学位论文]. 南京: 东南大学, 2016.
|
 2022, Vol. 31
2022, Vol. 31


