随着传感器微型化和智能化技术的发展, 智能可穿戴设备在中青年用户群中越来越受到追捧. 根据权威市调机构Canalys最新数据显示, 2020年全球可穿戴式腕带设备增长10%, 达1.85亿台. 许多运动爱好者也非常热衷利用可穿戴设备来了解自己的实时运动状态. 目前市面上流行的智能手环大都是通用型手环, 这样的手环功能单一, 无法为球类爱好者提供运动数据的分析和指导. 因此, 研发一款精确度较高, 且具有专项运动识别功能的智能手环会有较好的市场应用前景.
目前, 已有国内外学者开展各类人体运动识别算法的研究. Ayachi等[1]使用17个传感器捕获全身多处的动作信号, 用以收集成年人9种动作的加速度信号. 祁胜锋[2]提出了基于Boosting算法的人体动作数据识别研究, 采用时域特征和关联特征方法, 快速构建识别模型. 此方法在采集加速度信号时需要使用多个传感器, 用户体验不佳且精确度不高. 吴保锋等[3]提出基于小波阈值去噪算法的原理, 利用软、硬阈值两种函数, 对陀螺的测量数据进行去噪处理, 寻找数据降噪效率最高的方法. 张儒鹏等[4]采用基于OI-LSTM神经网络结构的人体动作识别模型研究, 在Inception的基础上提出O-Inception结构实现对特征的自动提取, 同时利用LSTM捕获动作时序, 提高动作识别准确率. 但基于深度学习的动作识别技术计算量大, 对硬件要求高, 不利于推广. 李元良等[5]通过对动作区间进行分割, 并对数据进行特征提取, 再利用BP神经网络算法对数据样本进行训练, 通过BP神经网络输出动作识别结果. 但BP神经网络存在样本依赖性, 如果样本代表性差, 矛盾样本多等, 就很难达到预期的效果. 吴军等[6]使用了手机内嵌的加速度传感器识别了5种人体运动状态, 并将卷积神经网络用于结果的判别, 增加了识别的准确性.
在基于可穿戴设备人体运动识别研究领域中, 对于专项运动的运动模式识别分析仍有较大可供完善的空间. 本文聚焦的乒乓球运动模式实时识别研究方法基于ESP32传感器, 能够实时响应并反馈运动员在进行乒乓球运动时正手攻球、反手攻球、正手搓球、反手搓球等四种运动模式, 为后期帮助乒乓球运动员及爱好者方便快捷的了解和掌握个人运动数据, 根据数据信息制定符合自身特点的训练方案, 提高运动效率奠定良好的基础.
1 乒乓球运动模式实时识别系统介绍本系统对乒乓球运动的原始加速度信号采集只需佩戴单个基于ESP32的智能手环即可实现, 简单便携, 对硬件设备要求不高. 手环如图1所示. 首先通过手环内嵌的MPU6886获取4种乒乓球击球动作产生的原始加速度信号并通过传感器的蓝牙模块实时发送到计算机端, 接着将采集到的原始加速度信号作为样本, 通过加窗和滑动均值滤波完成对样本数据的预处理, 再分别对每个动作进行特征提取. 通过主成分分析法(PCA)对提取的特征进行分析归纳, 以实现特征的降维处理, 提高系统的计算效率. 最后用决策树算法训练出最佳分类模型, 实现对4种运动模式的分类与实时显示. 整个流程分为6个模块, 各模块间的关系如图2所示.
2 加速度信号预处理及特征工程 2.1 原始加速度信号实时采集和传输方法要实现加速度信号的实时采集和传输, 首先需要ESP32微处理器利用内部集成电路(I2C)总线采集加速度传感器MPU6886的数据信号并利用蓝牙模块将原始加速度信号发送给智能手机; 再通过智能手机转发到计算机端, 在计算机端对信号进行数据预处理、特征工程和动作的识别与显示. 程序每隔200个样本点(约2 s)调用一次运动识别算法, 并将分类结果显示在计算机端. 本实验中, 原始加速度信号的采集与发送和数据处理、特征提取与降维以及动作的分类识别算法均由Python语言实现.

|
图 1 基于ESP32的智能手环佩戴示意图 |
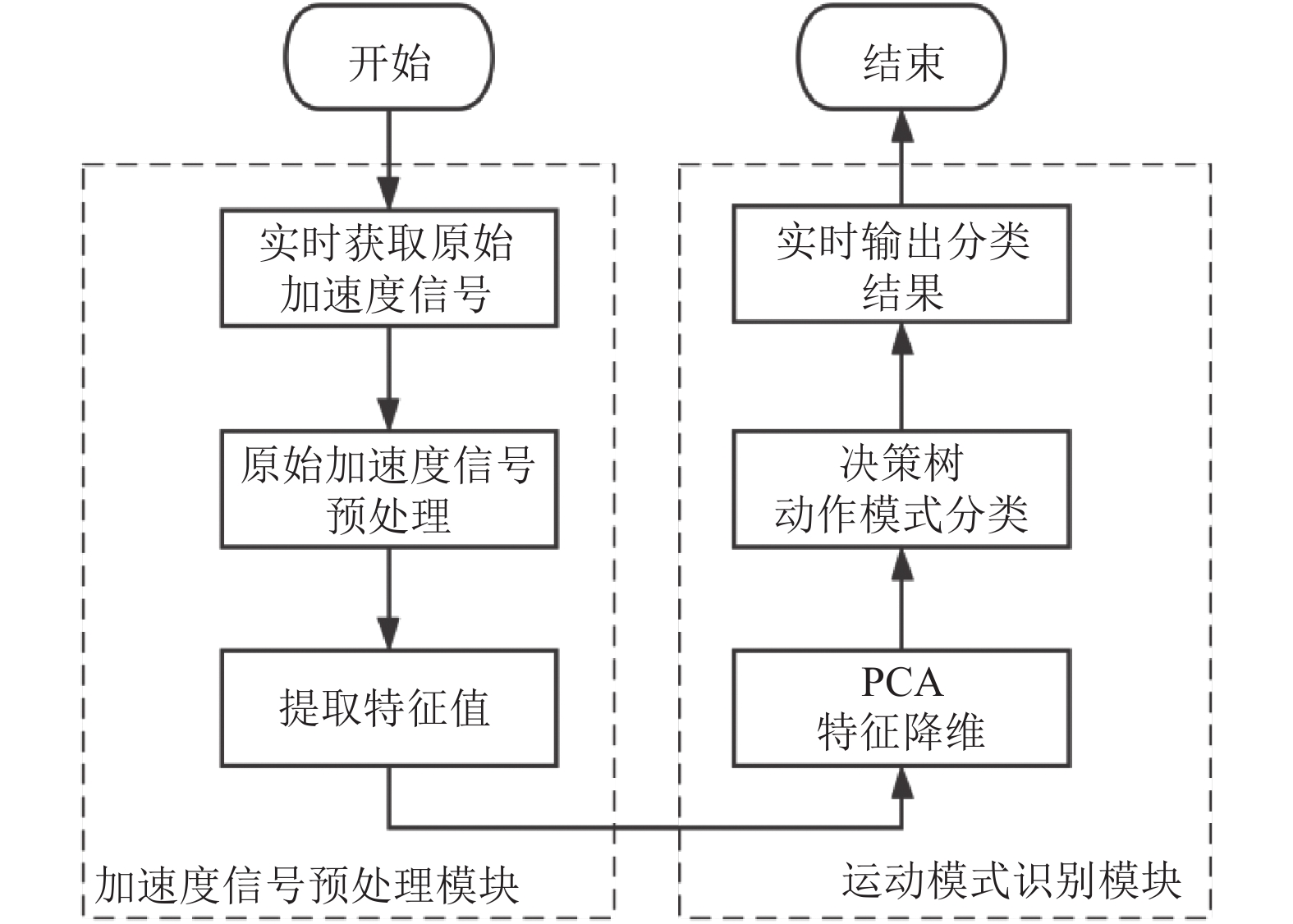
|
图 2 乒乓球运动模式实时识别算法流程图 |
2.1.1 加速度信号实时采集方法
搭载ESP32芯片体系和集成IMU姿态传感器MPU6886的M5stack开发板为本次实验使用的加速度信号采集工具. ESP32核心电路图如图3所示.
开发板内置3轴陀螺仪和3轴加速计, 可连接各类外设配合使用. 通过手环按键控制开发板内的MPU6886传感器实时收集用户击球过程中在X、Y、Z, 3个方向上产生的加速度信号. 对于乒乓球运动而言, 加速度的传输频率要足够高才能保证采集到足够的动作信息. 实验中, 将ESP32开发板传感器频率设为90 Hz左右, 这样的频率能够包含更多有效信息.
当用户按下手环上的开始按键时, MPU6886传感器随即开始收集用户运动时产生的3轴加速度信号, 并通过I2C总线完成与ESP32的通信, 再利用ESP32的蓝牙模块将采集到的加速度信号发送到计算机端, 加速度信号采集模块如图4所示.

|
图 3 ESP32核心电路图 |
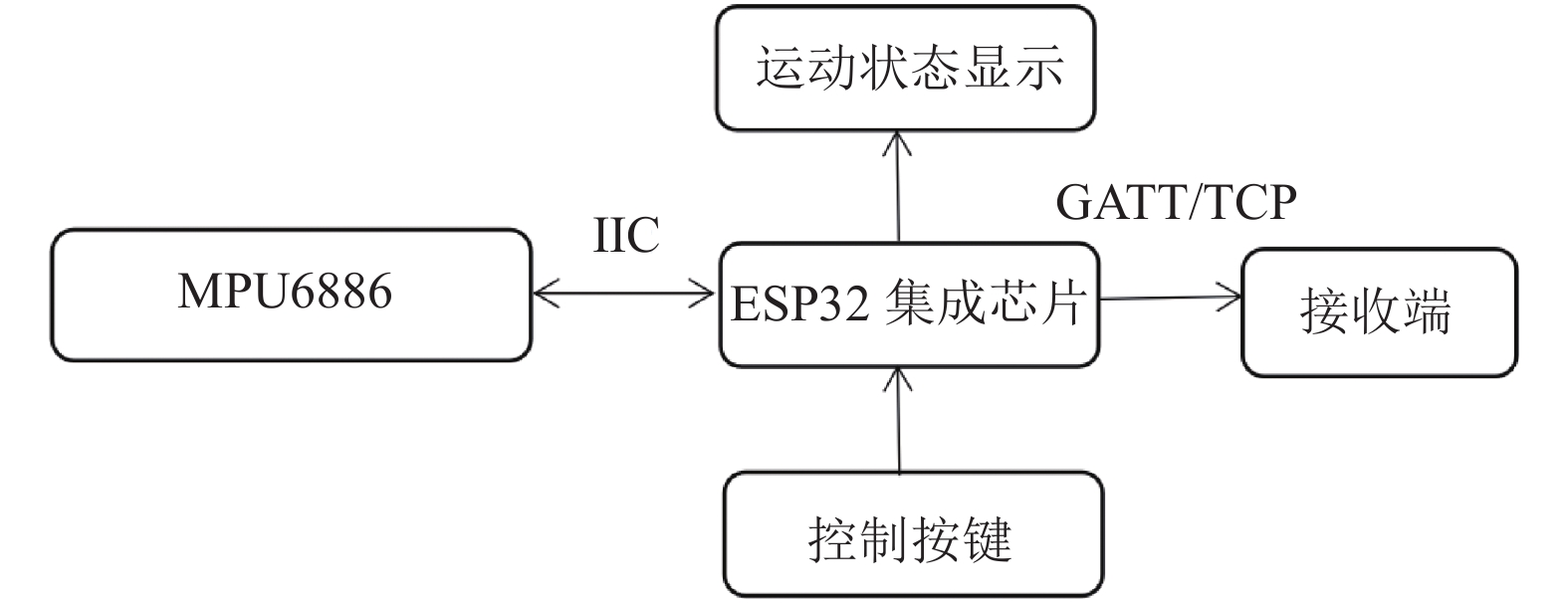
|
图 4 加速度信号采集模块 |
I2C总线(inter-integrated circuit, I2C)是一个双向的两线连接总线, 提供集成电路之间的通信线路. I2C总线物理拓扑结构和时序图分别如图5和图6所示.
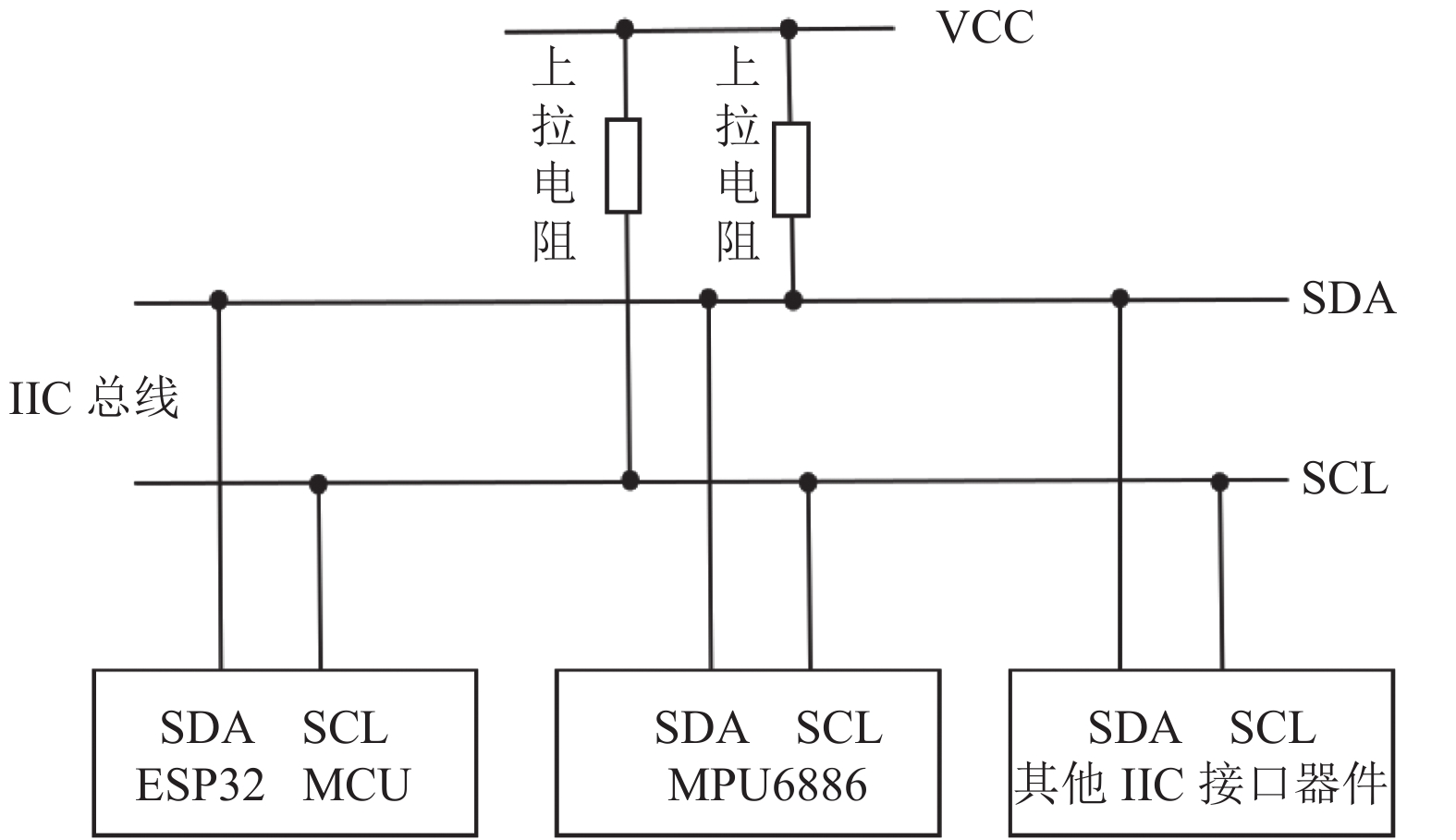
|
图 5 I2C总线物理拓扑结构 |
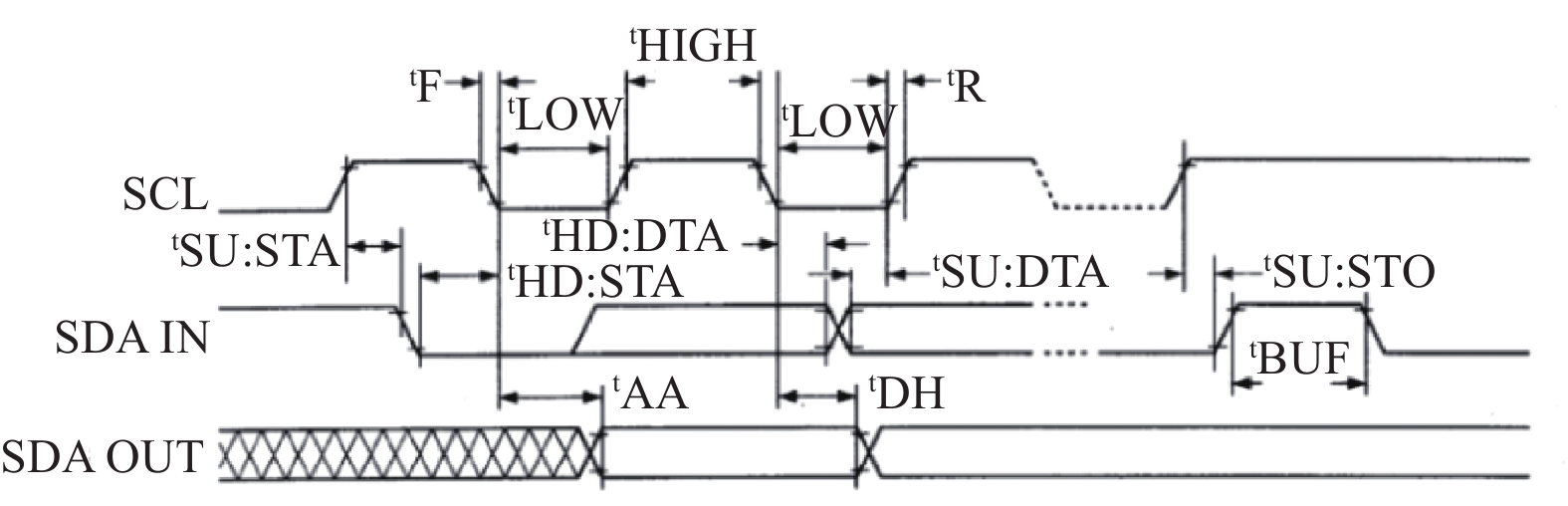
|
图 6 I2C总线时序图 |
2.1.2 加速度信号实时传输方法
实时采集到加速度信号后, 利用GATT协议通过蓝牙模块将数据发送到手机端, 并在手机端显示实时运动数据和传输频率, 如图7. 再利用TCP/IP协议, 通过WiFi与计算机建立通信.

|
图 7 手机端实时显示运动数据和传输频率 |
(1)低功耗蓝牙GATT协议
GATT协议(generic attribute profile)建立在 ATT (attribute protocol)协议的基础上. 在本实验中, 利用MAC地址匹配设备, 在传感器与手机端之间建立连接. 图8为GATT协议的网络拓扑结构图.
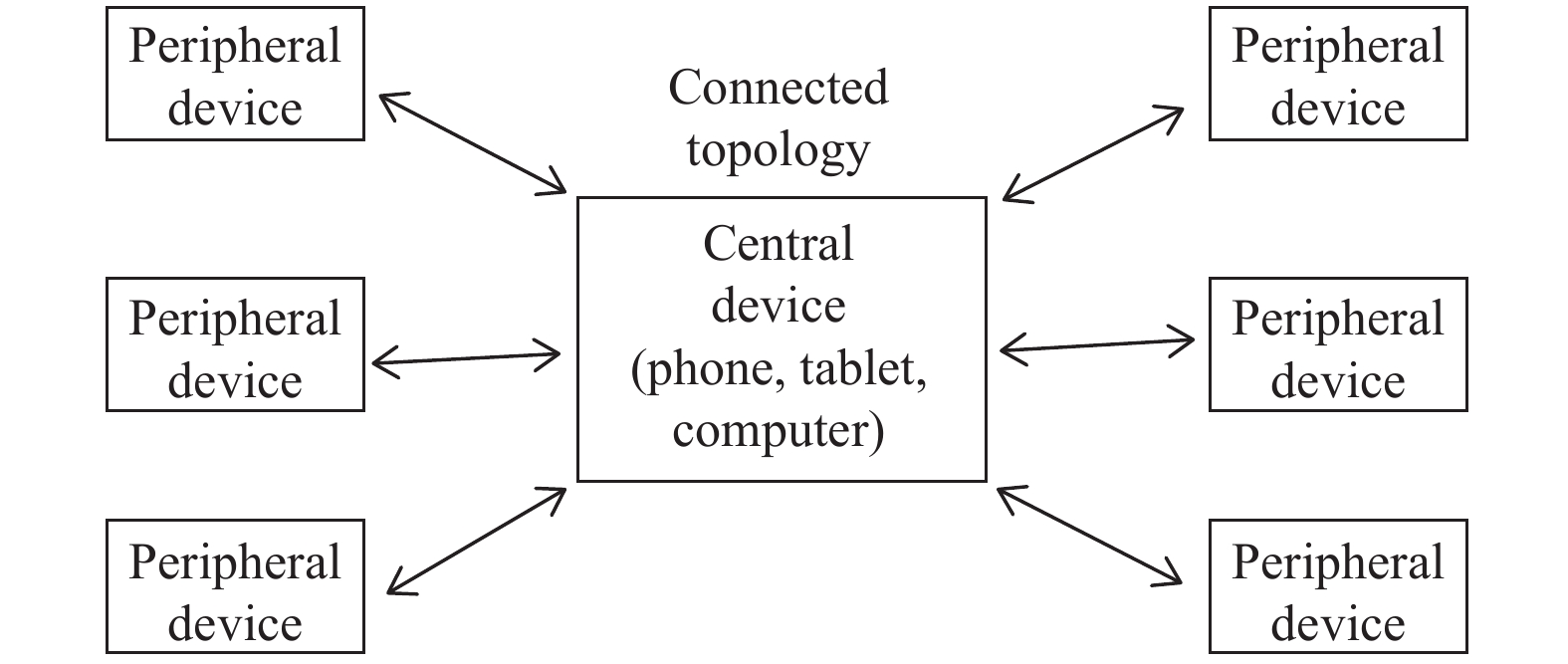
|
图 8 GATT协议网络拓扑结构 |
(2)基于TCP协议的Socket通信
应用程序可通过Socket通信向网络发送请求或应答网络请求. 本次实验主要是利用Socket通信, 将数据信息从手机端转发到计算机, 并在计算机端完成对数据的实时接收和处理.
在完成对原始加速度信号的发送和存储后, 需要对不同的动作数据打上标签, 实验中使用数字“0, 1, 2, 3”分别对“正手攻球, 反手攻球, 正手搓球和反手搓球”4个动作进行标记.
2.2 加速度信号预处理 2.2.1 加速度信号加窗处理为实现对原始加速度信号的数据分割和特征提取, 使用加窗法分割加速度信号. 这种方法经常被用于人体运动识别中, 用一个窗口长度为200个样本点的矩形窗分割原始加速度数据, 相邻窗之间重叠半个窗长. 经过加窗后, 单个窗口数据段包含200个采样点. 实验中, 加速度信号传输到计算机端的频率为90–100 Hz, 加窗后, 每个窗口数据段的时间跨度为2–2.2 s, 足以包含单个完整动作.
2.2.2 加速度信号滤波处理在实际的应用中, 由于加速度传感器产生的随机漂移、无效动作和抖动产生的噪声信号以及传输过程中因为丢包等原因导致的数据失真等[7]都将会对动作的分类产生干扰. 直接对未经处理的加速度信号提取特征, 得到的特征数值误差大、干扰多, 对动作的分割和分类会产生负面影响. 因此, 在进行动作分割和分类之前要对加速度信号进行降噪处理[8, 9]. 在选择对数据进行预处理的方法时, 有选择切比雪夫 I 型数字低通滤波器对原始加速度信号进行了滤波处理, 滤除高频噪声[10]; 有通过快速傅里叶变换法和归一法提取数据频率, 减少外界因素引起的数据大小差异[11]; 还有利用小波变换和小波阈值完成对原始数据的降噪[12].
滑动均值滤波算法具有结构简单, 适合去除信号中的毛刺等高频噪声干扰等[13]优点, 对滤除混杂在原始加速度信号上的随机干扰噪声非常有效. 为有效降低信号噪声, 使特征提取的加速度信号更接近于真实值, 实验采用滑动均值滤波算法实现加速度信号的滤波处理. 滑动均值滤波算法是把连续取得的N个样本进行算术平均运算, 获得新的滤波结果, 同时每采样得到一个新的数据放入队尾, 并扔掉原来队首的一个数据, 计算公式如式(1):
| $ {{y}}(n) = \frac{1}{{2m + 1}}\sum\limits_{k = - m}^m {x(n - k)} $ | (1) |
其中,
选取运动员做乒乓球反手搓球运动时y轴方向上的1000个加速度信号样本点用式(1)进行滤波处理. 滤波前后加速度信号波形图如图9和图10所示.
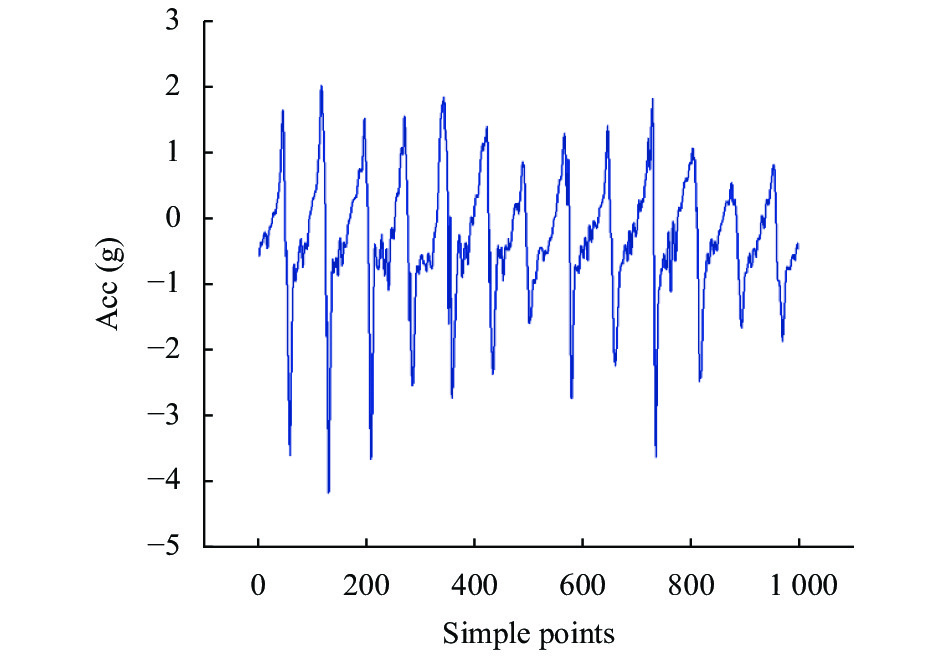
|
图 9 滤波前的加速度信号 |
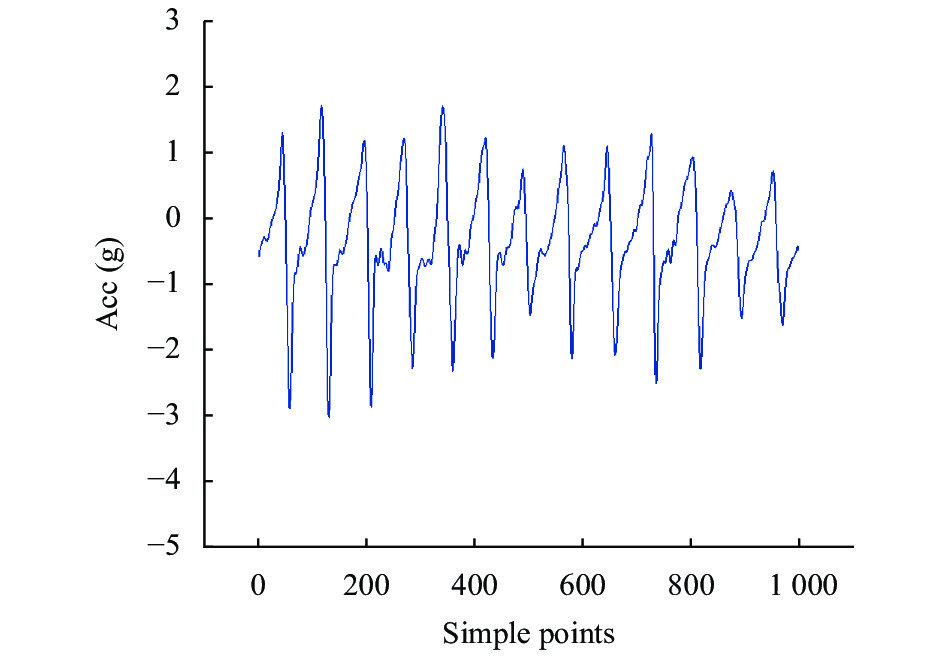
|
图 10 滤波后的加速度信号 |
从上述两幅图可以看出, 图9的原始加速度波形图毛刺和干扰信号较多, 这会影响后续特征提取和动作分类的准确性, 在利用滑均值滤波算法对加速度信号进行处理后, 可以明显看到滤波后的图10较图9平滑很多. 两图前后对比可以看出, 滑动均值滤波对原始加速度信号中的毛刺和干扰信号的滤除有较好的效果.
2.3 特征工程要实现动作的分类, 主要依赖加速度计发送到计算机端的实时加速度信号, 而加速度信号在时域内以数据流的形式呈现, 常规的分类器无法直接处理时间序列的数据[14], 此时就需要从时域中提取相关的特征量. 在完成对原始加速度信号的加窗和平滑等预处理工作后, 接下来就要提取相关特征值. 本实验从X、Y、Z三个方向上收集加速度信号, 提取包括3个方向上的加速度均值、方差、标准差、最大最小值、峰谷值、合成加速度模的均值、相关系数等共22个特征值.
2.3.1 特征提取方法X、Y、Z方向上加速度的平均值
| $ \overline {\mathop a\nolimits_x } = \frac{{\displaystyle\sum\limits_{k = 1}^m {\mathop a\nolimits_{x, k} } }}{m} $ | (2) |
| $ \overline {\mathop a\nolimits_{{y}} } = \frac{{\displaystyle\sum\limits_{k = 1}^m {\mathop a\nolimits_{y, k} } }}{m} $ | (3) |
| $ \overline {\mathop a\nolimits_{\textit{z}} } = \frac{{\displaystyle\sum\limits_{k = 1}^m {\mathop a\nolimits_{{\textit{z}}, k} } }}{m} $ | (4) |
其中,
3个方向上的加速度信号方差计算公式为:
| $ \mathop s\nolimits_x^2 = \frac{{\displaystyle\sum\limits_{k = 1}^m {\mathop {(a_{x, k} - \overline {a_{x}} )}\nolimits^2 } }}{m} $ | (5) |
| $ \mathop s\nolimits_{{y}}^2 = \frac{{\displaystyle\sum\limits_{k = 1}^m {\mathop {(a_{y, k} - \overline {a_{y}} )}\nolimits^2 } }}{m} $ | (6) |
| $ \mathop s\nolimits_{\textit{z}}^2 = \frac{{\displaystyle\sum\limits_{k = 1}^m {\mathop {(a_{{\textit{z}}, k} - \overline {a_{\textit{z}}} )}\nolimits^2 } }}{m} $ | (7) |
同样, 可获得3个方向上加速度的标准差计算公式为:
| $ \sigma _{{x}} = \sqrt {s_x} $ | (8) |
| $ \sigma {_{y}} = \sqrt {s_y} $ | (9) |
| $ \sigma _{\textit{z}} = \sqrt {s_{\textit{z}}} $ | (10) |
加速度波峰和波谷的差值可用于排除一些无效的峰谷数值. 用
| $ a_{pv} = \max(a) - \min(a) $ | (11) |
通过式(11)可以计算出3个方向上加速度信号的峰谷值.
为了综合体现运动的剧烈程度, 创建合成加速度模的均值特征, 公式如下:
| $ \mathop a\nolimits_k = \sqrt {\mathop a\nolimits_{x, k}^2 + \mathop a\nolimits_{y, k}^2 + \mathop a\nolimits_{{\textit{z}}, k}^2 } $ | (12) |
| $ \overline a = \frac{{\displaystyle\sum\limits_{k = 1}^m {\mathop a\nolimits_k } }}{m} $ | (13) |
其中,
根据相关系数公式, 可计算出3个方向上加速度信号两两之间的相关系数分别为:
| $ \rho (x, y) = \frac{{{cov} (x, y)}}{{\sqrt {\sigma _x\sigma _{{y}}} }} $ | (14) |
| $ \rho (x, {\textit{z}}) = \frac{{{cov} (x, {\textit{z}})}}{{\sqrt {\sigma_x \sigma_ {\textit{z}}} }} $ | (15) |
| $ \rho (y, {\textit{z}}) = \frac{{{cov} (y, {\textit{z}})}}{{\sqrt {\sigma_y \sigma_ {\textit{z}}} }} $ | (16) |
其中,
特征值过多会造成过拟合现象, 完成特征提取后便要用特征降维来减少维度, 避免训练过程中的过拟合现象. 特征降维主要分为特征选择和特征抽取.
为了尽量减少降维过程中样本信息丢失, 使得抽取后的特征能够精确的表示样本信息, 本实验采用PCA算法实现特征降维.
PCA算法的主要目标是确定一个最有意义的主成分来重新表达一个数据集, 使原本复杂的数据简单化, 又不丢失重要信息[15].
PCA算法的降维过程主要包括: 对所有特征进行中心化(去均值), 求协方差矩阵, 计算特征值和特征向量, 将原始特征值投影到特征向量上, 得到降维后的新特征.
PCA算法首先对所有的特征进行中心化, 又叫去均值法. 即求每一个特征的平均值, 对所有的样本, 每个特征都减去自身的均值, 公式如下:
| $ \overline {\mathop x\nolimits_k } = \frac{{\displaystyle\sum\limits_{i = 1}^m {\mathop x\nolimits_k^i } }}{m} $ | (17) |
其中,
计算出平均值后, 每个特征都要减去自身的均值, 生成新的值
| $ \mathop {x'_k} = \mathop x\nolimits_k - \overline {\mathop x\nolimits_k } $ | (18) |
接着, 利用式(19)求协方差C:
| $ C = \left[ {\begin{array}{*{20}{c}} {cov({x_1},{x_1}),}&{cov({x_1},{x_2}),}&{ \cdots ,}&{cov({x_1},{x_k})}\\ {cov({x_2},{x_1}),}&{cov({x_2},{x_2}),}&{ \cdots ,}&{cov({x_2},{x_k})}\\ \vdots & \vdots & \ddots & \vdots \\ {cov({x_k},{x_1}),}&{cov({x_k},{x_2}),}&{ \cdots ,}&{cov({x_k},{x_k})} \end{array}} \right] $ | (19) |
其中, k =1, 2, …, 22.
| $ {cov} (x_i, x_j) = \frac{{\displaystyle\sum\limits_{l = 1}^M {(\mathop x\nolimits_i^l - \overline {\mathop x\nolimits_j } )(\mathop x\nolimits_j^l - \overline {\mathop x\nolimits_j } )} }}{{M - 1}} $ | (20) |
通过式(19)和式(20)可得M个样本在22维特征下的协方差矩阵C.
接着, 求协方差矩阵C的特征值
| $ Cu = \lambda u $ | (21) |
每一个特征值都对应一个特征向量. 本实验中, 特征值
最后将原始特征投影到选取的特征向量上, 得到降维后的新k维特征, 新的特征计算公式如式(22)所示:
| $ \left[ \begin{array}{c} \mathop y\nolimits_1^i \\ \mathop y\nolimits_2^i \\ \vdots\\ \mathop y\nolimits_k^i \end{array} \right] = \left[ \begin{array}{c} \mathop u\nolimits_1^{\rm{T}} {\rm{\cdot}}\mathop {{\rm{(}}\mathop x\nolimits_1^i {\rm{, }}\mathop x\nolimits_2^i {\rm{, }} \cdots {\rm{, }}\mathop x\nolimits_n^i {\rm{)}}}\nolimits^{\rm{T}} \\ \mathop u\nolimits_2^{\rm{T}} {\rm{\cdot}}\mathop {{\rm{(}}\mathop x\nolimits_1^i {\rm{, }}\mathop x\nolimits_2^i {\rm{, }} \cdots {\rm{, }}\mathop x\nolimits_n^i {\rm{)}}}\nolimits^{\rm{T}} \\ \vdots\\ \mathop u\nolimits_k^{\rm{T}} {\rm{\cdot}}\mathop {{\rm{(}}\mathop x\nolimits_1^i {\rm{, }}\mathop x\nolimits_2^i {\rm{, }} \cdots {\rm{, }}\mathop x\nolimits_n^i {\rm{)}}}\nolimits^{\rm{T}} \end{array} \right] $ | (22) |
对于每个样本xi而言, 投影之后的新特征是
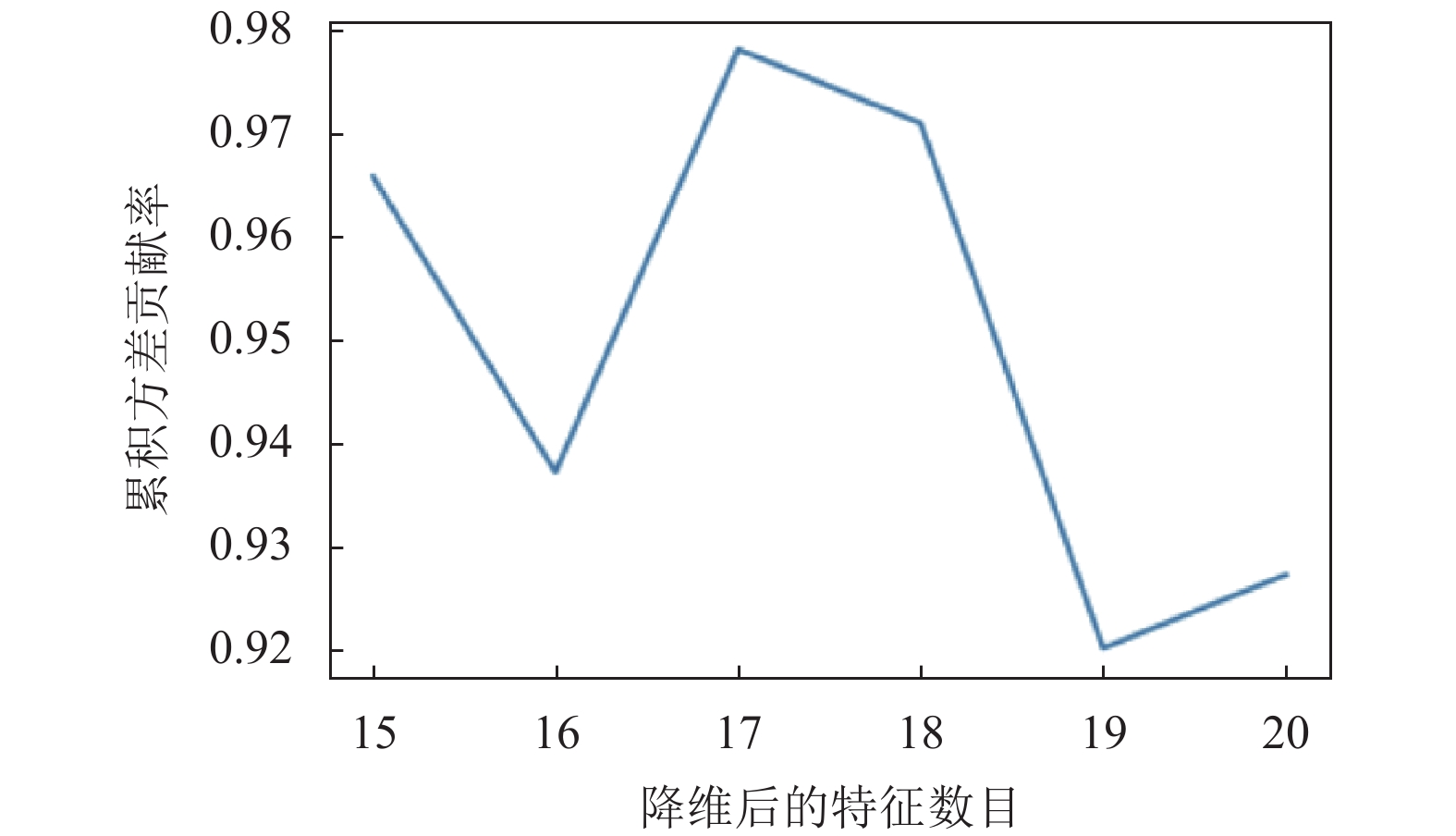
对特征数据降维后, 可通过绘制累积方差贡献率曲线找到最优维度. 图11和图12均为累积方差贡献率曲线. 其中, 横轴为降维后保留的特征个数, 纵轴为降维后新特征矩阵捕捉到的方差贡献率, 累积方差贡献率最高的点所对应的特征个数即为希望保留的降维后的特征个数.
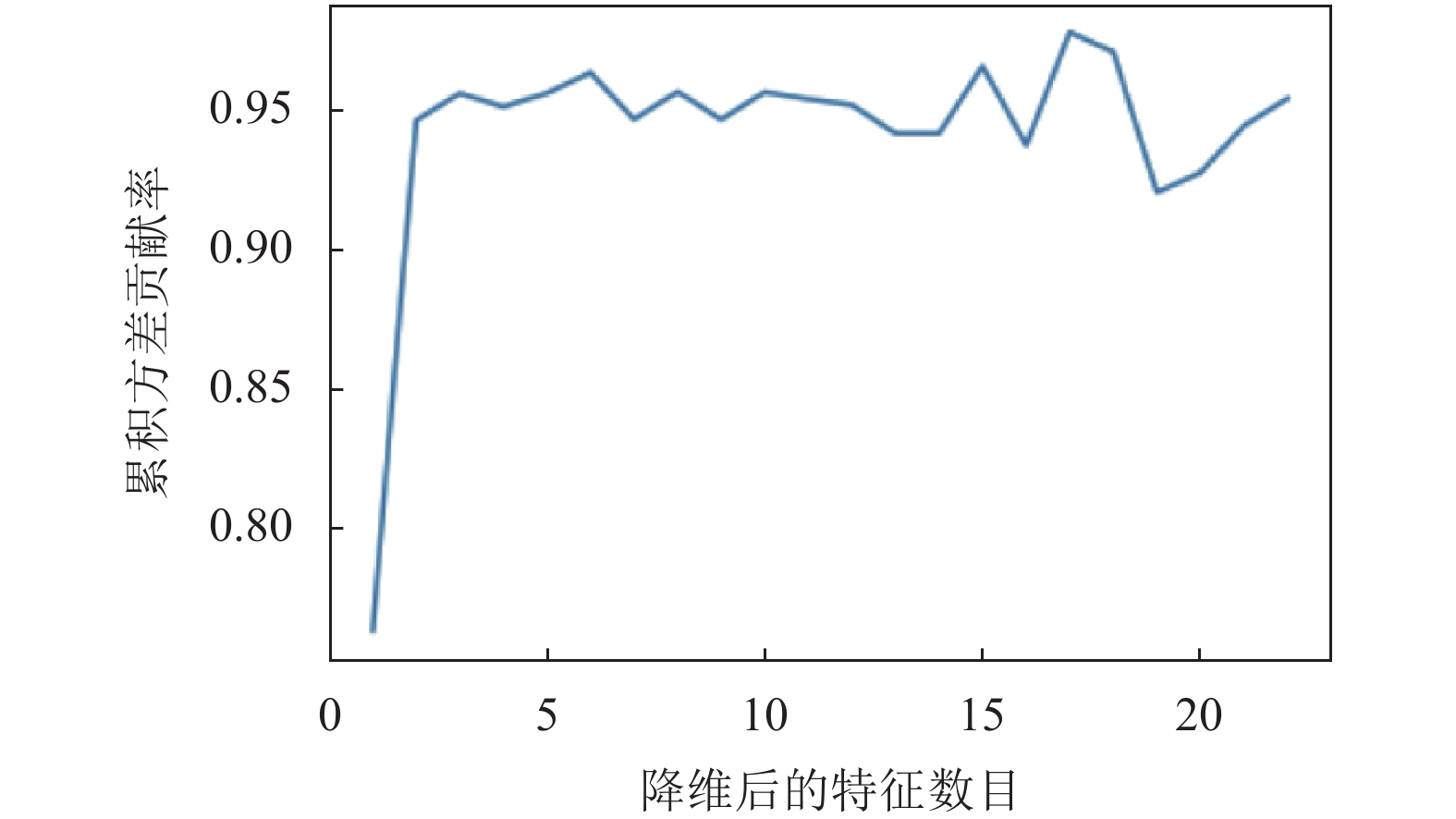
|
图 11 k=0, 1, 2, …, 22时累积方差贡献率曲线 |
|
图 12 k=15, 16, …, 20时累积方差贡献率曲线 |
当降维后保留的特征个数k=0, 1, 2, …, 22时, 累积方差贡献率曲线如图11所示.
通过图11可以看出, 当特征数15<k<20时, 模型的准确率达到最高点, 所以最佳维度保留的特征个数k应该在(15, 20)中.
当降维后保留的特征个数k=15, 16, …, 20时, 累积方差贡献率曲线如图12所示.
通过图12可以清晰地看出, 当k=17时, 模型的可解释方差贡献率最高(大于97%), 故在本实验中, PCA降维后的特征维度应为17.
当PCA降维算法中的k=17时, 用随机森林分类器对降维后的特征数据进行交叉验证, 准确率可达97.80%.
通过PCA降维算法对特征进行降维, 一定程度上能去除噪声, 减少由于特征较多导致的冗余问题, 进一步降低算法的开销. 而选择最佳k值使得数据在压缩的同时让信息损失最小化, 使得训练出的模型拥有更高更稳定的识别效率.
3 运动模式识别实验及结果分析本实验选用决策树算法对运动模式进行分类识别. 决策树算法是一种非参数的有监督机器学习算法, 主要包括: 特征选择、决策树的生成和决策树的修剪等, 可用以解决分类和回归问题. 本实验使用的是分类决策树模型, 通过借助树形结构中的叶子结点进行属性判定, 并通过不断判定进而得出最终的决策分类结果. 本实验中, 决策树得出的最终决策结果即为当前的乒乓球击球动作.
本实验选用决策树模型进行分类, 是因为它具有效率高、计算量相对较小, 且通常不需要受训数据外的信息, 鲁棒性强等特点, 适合处理实际运动过程中产生的数量较大的数据样本.
在第2节中已经完成对原始运动加速度信号的预处理和特征提取. 接下来就要把降维后的特征值作为训练样本集和测试样本集. 利用训练样本集训练决策树学习模型, 并通过测试集检验决策树学习模型是否符合预期, 当正确率达到一定标准时, 即可将此决策树学习模型投放到实时运动模式识别中. 构造决策树学习模型的步骤如下:
(1)随机选取特征样本集中70%的数据作为训练集, 30%的数据为测试集.
(2)构造决策树分类器学习模型对步骤(1)中的训练集进行训练, 主要通过不断选择最优属性, 提高节点分类纯度, 由上至下形成一个树型结构学习分类模型, 并利用步骤(1)中的测试集对模型准确度进行测试, 返回预测准确度.
(3)利用剪枝策略对决策树进行剪枝优化, 确定最优参数, 使生成的决策树具有更好的泛化性和更高的准确性. 包括对树的最大深度、对叶子节点的最小样本数和分割内部节点所需的最小样本数以及分枝时的特征个数和信息增益的大小限制等. 当决策树正确率达到较高水平时, 便可将它作为最终的分类器学习模型投入到乒乓球运动模式的实时分类和显示.
运动者将ESP32智能手环佩戴在持拍手腕, 做乒乓球正手攻球、反手攻球、正手搓球、反手搓球4种动作, 决策树分类模型可以实现对乒乓球4种运动模式的实时识别与显示. 决策树分类模型对411组乒乓球运动模式的实时识别结果统计如表1所示.
| 表 1 乒乓球4种运动模式实时识别结果统计 |
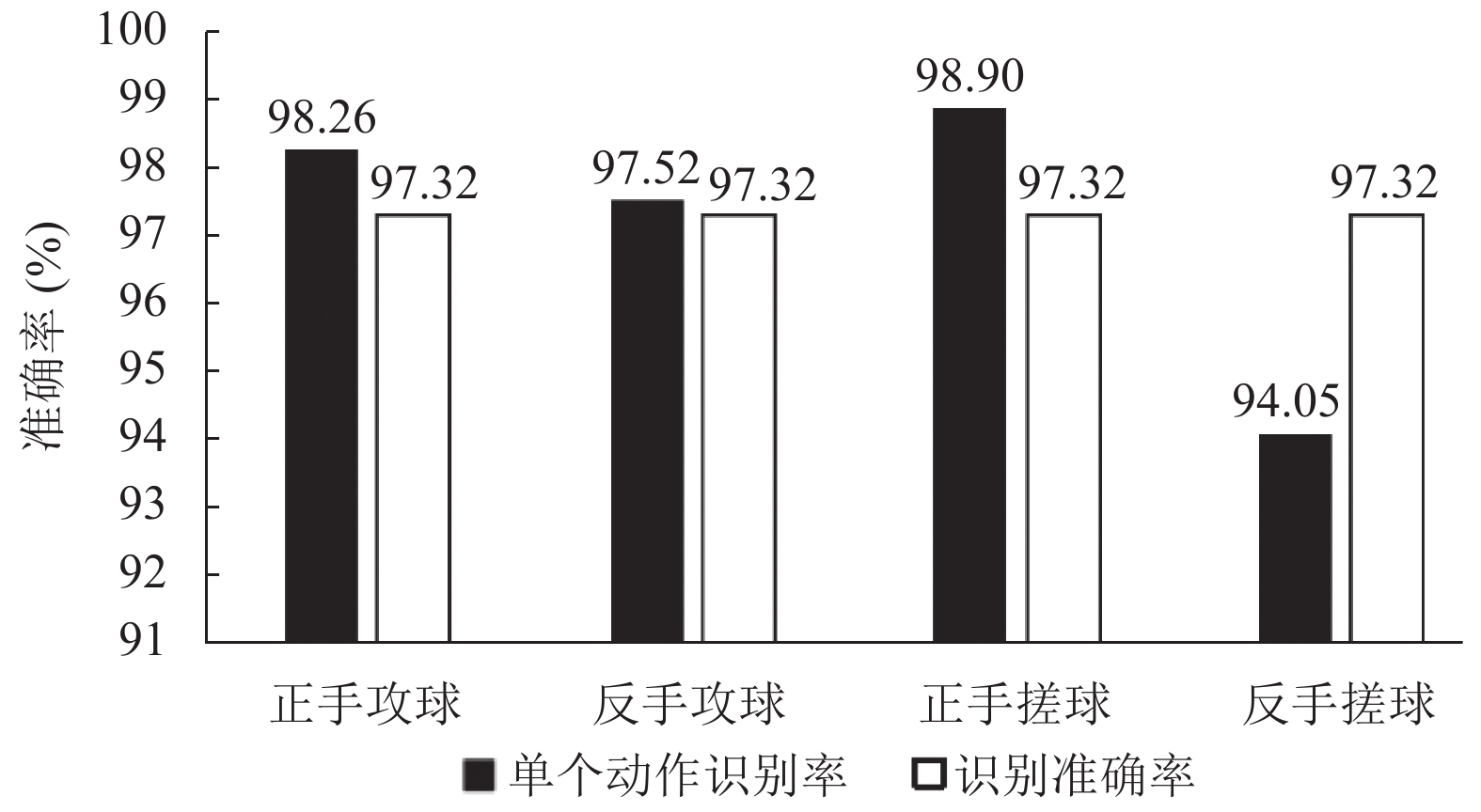
从表1中可以看出, 少量的正手攻球和正手搓球会被误分类为反手攻球, 少量的反手攻球会被误判为正手攻球和正手搓球, 个别反手搓球可能被误识别为正手搓球. 但总的来说, 识别效果较好. 图13的柱状图表示的是决策树算法分别对4种运动模式进行实时分类时的单个动作识别率和识别准确率的比较.
|
图 13 决策树学习模型对乒乓球4种动作的识别准确率 |
由图13可得, 决策树模型对正手攻球和正手搓球动作识别率较高, 分别达到98.26%和98.9%; 对反手搓球识别率最低, 但也有94.05%的准确率. 总体上看, 该模型对乒乓球正手攻球、反手攻球、正手搓球、反手搓球4种运动模式的实时识别准确率较高, 可达97.32%, 故本文中提出的实时运动模式识别方法对以上乒乓球4种运动模式的实时识别具有较好的效果.
4 结论与展望本文围绕乒乓球运动的4种模式: 正手攻球、反手攻球、正手搓球、反手搓球的实时识别展开研究. 首先, 参与数据采集的实验人员大量重复的做4种乒乓球击球动作并实时采集运动的加速度信号, 然后将采集到的加速度信号作为样本数据集实时传输到计算机端进行数据预处理和特征提取, 再实现特征降维, 最后使用决策树算法实现对运动模式的实时识别和分析.
获取运动原始加速度信号后, 通过低功耗蓝牙GATT协议和TCP/IP协议将采集的加速度信号实时发送到计算机端. 计算机端接收原始加速度信号, 并对加速度信号进行加窗和滤波处理. 接着, 提取预处理后加速度信号的时域特征, 并对特征进行综合分析, 将原本22个特征利用PCA算法降为17个, 既避免出现过拟合现象又保证了较高的准确率. 最后通过对决策树进行剪枝优化, 训练生成最优的决策树模型投入到对运动模式的实时识别中. 结果显示, 本方法对乒乓球正手攻球、反手攻球、正手搓球、反手搓球4种动作的识别准确率可达97.32%.
本文研究的乒乓球运动模式实时识别方法, 可运用于基于ESP32的智能手环中, 通过实时采集转发运动加速度信号, 自动分析数据实现对用户运动的模式识别, 及时反馈用户的运动信息, 让用户能更好地了解自己的运动习惯, 有针对性地开展各项训练. 接下来的研究中将会考虑引入更多分类模型, 减少识别误差, 优化模型性能, 同时丰富动作识别的种类, 以期能够识别更多种类的球类运动.
| [1] |
Ayachi FS, Nguyen HP, de Brugiere EG, et al. The use of empirical mode decomposition-based algorithm and inertial measurement units to auto-detect daily living activities of healthy adults. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2016, 24(10): 1060-1070. DOI:10.1109/TNSRE.2016.2519413 |
| [2] |
祁胜锋. 基于Boosting算法的人体动作数据识别研究[硕士学位论文]. 武汉: 武汉纺织大学, 2019.
|
| [3] |
吴保锋, 夏林元, 吴东金, 等. MEMS陀螺仪随机误差分析与小波阈值去噪研究. 电子设计工程, 2020, 28(15): 1-5. |
| [4] |
张儒鹏, 于亚新, 张康, 等. 基于OI-LSTM神经网络结构的人类动作识别模型研究. 计算机科学与探索, 2018, 12(12): 1926-1939. DOI:10.3778/j.issn.1673-9418.1807045 |
| [5] |
李元良, 史中权, 李少辉, 等. 基于MEMS传感器的人体运动识别系统. 计算机应用与软件, 2018, 35(8): 243-248, 285. DOI:10.3969/j.issn.1000-386x.2018.08.044 |
| [6] |
吴军, 肖克聪. 基于深度卷积神经网络的人体动作识别. 华中科技大学学报(自然科学版), 2016, 44(S1): 190-194. |
| [7] |
韩盈党, 李哲. MEMS加速度传感器的数据采集和预处理. 仪表技术与传感器, 2015(2): 16-19. DOI:10.3969/j.issn.1002-1841.2015.02.007 |
| [8] |
孙宇航, 周建钦, 张学锋. 基于加速度传感器的人体运动模式识别. 计算机系统应用, 2020, 29(6): 196-203. DOI:10.15888/j.cnki.csa.007443 |
| [9] |
黄刘松, 储岳中, 张学锋. 基于加速度传感器的乒乓球击球动作识别. 传感器与微系统, 2016, 35(1): 56-58, 61. |
| [10] |
徐川龙, 顾勤龙, 姚明海. 一种基于三维加速度传感器的人体行为识别方法. 计算机系统应用, 2013, 22(6): 132-135. |
| [11] |
李锋, 潘敬奎. 基于三轴加速度传感器的人体运动识别. 计算机研究与发展, 2016, 53(3): 621-631. |
| [12] |
王泰雷. 基于MEMS传感器的人体上肢运动捕捉与识别方法研究[硕士学位论文]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [13] |
邵兴臣, 段发阶, 蒋佳佳, 等. 基于自适应滑动均值和小波阈值的叶尖间隙信号降噪方法. 传感技术学报, 2021, 34(1): 34-40. |
| [14] |
杨世文. 基于可穿戴设备的动作识别方法研究[硕士学位论文]. 福州: 福州大学, 2018.
|
| [15] |
黄秀霞. C4.5决策树算法优化及其应用[硕士学位论文]. 无锡: 江南大学, 2017.
|
 2022, Vol. 31
2022, Vol. 31


